Hall and ion slip effects and chemical reaction on MHD rotating convective flow past an infinite vertical porous plate with ramped wall and uniform wall temperatures

Abstract

In this paper, we discussed the chemical reaction influences on the radiating MHD convective flow of an incompressible viscous electrically conducting fluid past an exponentially accelerated perpendicular surface under the influences of slip velocity in the revolving structure taking Hall and ion slip impacts into account. A steady homogeneous magnetic field is applied under the presumption of less magnetic Reynolds number. The ramped wall temperature and time altering concentration at the plate is constructing into consideration. First order consistent chemical reaction and heat absorption are also regarded. Laplace transformation technique is engaged on the non-dimensional governing equations for the closed form solutions. Supporting on these results, the phrases for non-dimensional shear stresses and rate of heat and mass transport are also found. The graphical profiles are represented to examine the impacts of physical parameters on the important physical flow features. The computational quantities of the shear stress and rate of heat and mass transportations near the surface are tabulated by a variety of implanted parameters. The resulting velocity is growing by an increase in heat and solutal buoyancy force, while rotation and slip parameters have reverse outcomes on this. The resulting velocity is falling by an increasing in the Hartmann number while the penetrability parameters and Hall and ion slip effects have overturn impacts on this. The temperatures and the thickness of thermal boundary layer decrease on an enhancing heat source parameter for together ramped wall temperature and uniformed wall temperature. The heat absorptions increase the Nusselt number near the surface.

1 Introduction

The recent developments in technology require the pioneering revolutions in the domain of heat transport. In spite of the difficulty of Newtonian fluids, realistic mathematicians and engineering scholars are affiliated in Newtonian fluid dynamics, since the stream and heat transport characteristics of these fluids are important to plentiful and various systems in bio-technology, pharmacy, and chemical engineering, etc. In wide-ranging, Newtonian modelling has linear relation-ship flanked by stress and rates of strain. The mechanically characteristics of Newtonians liquids, both with thin and/or shear thickness, usually stress differences, and chemical reactions, may not be depicted with the conservation theory; therefore, an innovatively and effectually prediction is requisite. Different constitutive type equations have been advised to portray the progress and heat transport mechanism; by these, Newtonian models have developed an immense deal acceptances. This model became Newtonians fluid to the explorers since those of wide-range applications in the range of bio-medical and industrial engineering, energy construction, and geo-physical fluid mechanics and dynamics.

Magnetohydrodynamic (MHD) flows are of interest and use because they are used to treat injury and cancer tumours, reduce bleeding during surgeries, deliver certain drugs using magnetic particles, and determine disease using MRI (magnetic resonance imaging). MHD is the study of how magnetic fields interact with fluid flow, and it is a branch of physics. MHD viscous flows with temperature and mass transport have risen due to their use in a wide range of engineering and technology sectors and astronomy, geophysics, and nuclear studies. A large number of experimental and computational researches have been published in MHD flow in chemical engineering. The concept of chemical reaction and Hall and ion slip effects on unsteady hydromagnetic convection flow past permeable medium is in the momentous regions of bio-engineering, renewable energy, and environmental protections. The development of investigations and applications in thermo-chemical renovation and physical and chemical adaptations with bio-chemical conversions, jointly with each and every one essential action for the provisions and preparations of the biomass and all feasible downstream dispensation movements for the ecological sound and economical viable provision of energy and chemical manufacture possessions.

The gyratory fluids are essential because they occur in a variety of predicted phenomena and technological needs due to the Coriolis forces action. Many of the most critical qualities in rotating fluids may be found across the broadest areas of various disciplines. The influences of the Coriolis forces are the most important than the effects of gelatinous and non-reactive forces. Furthermore, the magnetic and Coriolis strengths are equivalent in their terrible character. According to the definition of the Hall effects, it is the generation of the voltage differential (the Hall voltages) transversely an electrically conductor when the electrical current flows through the conductor and the magnetic domain vertical to the wind is applied to the conductor. Edwin Hall found it in 1879 and published his findings in 1880. The effects of ion slips on a flow of Newtonians fluids had received microscopic study in the literature. A macroscopic wall slide is particularly noticeable in polymer melts. In technical application they are, the polish of simulated heart valve, rarefied fluid difficulties, and flow across numerous surfaces, boundary ion slip fluids are critical to understand and manipulate. The ion slips of the fluid near the unyielding walls are a term that is used to explain the macroscopic consequences of certain molecular events in the investigation of liquid-solids surface interaction. Thermal radiating on usual central heating has become tremendously appropriate. Ram et al. [1] discussed closed form solutions for porosity significance of an Oldroyd-B fluid flow transport between parallel plates. The effects of radiation and Hall current on an unsteady MHD free convective flow in a vertical channel filled with a porous medium have been studied by Krishna et al. [2]. The Hall current, heat generation/absorption, and thermo-diffusion on an unsteady free convective MHD flow of radiating and chemically reactive second grade fluid near an infinite vertical plate have been studied by Krishna and Chamkha [3]. Chamka et al. [4] discussed a modelling and is used for the nanoliquids with the effect of Brownian movement and thermophoretics. Samad and Rahman [5] explored the interactions of thermal radiating on the unstable MHD flows past a porous plate with the time dependent suction. Hamad [6] explored the analytical solutions of MHD normal convective flow of the nanoliquids past the linear lengthening sheets. Krishna et al. [7] explored the radiating and magnetic field impacts on unstable normal convective flows of the nanoliquid over an unbounded vertical plate. Krishna and Chamkha [8] investigated the diffusion-thermo, radiation-absorption and Hall and ion slip effects on MHD free convective rotating flow of nano-fluids past a semi-infinite permeable moving plate with constant heat source. Chamkha and Aly [9] explored the MHD free convective flow of the nanoliquid over a perpendicular plate with the warmth generating and/or absorption impacts. Sheikholeslami et al. [10] inspected the heat transport of MHD flow of nanofluids with the effects of Brownians movement. Krishna [11] investigated the radiation absorption, chemical reaction; Hall and ion slip impacts on MHD free convection flow past a semi-infinite moving porous surface. The effects of Hall and ion slip on the radiative MHD rotating flow of viscous incompressible electrically conducting Jeffrey fluid over an infinite vertical flat porous surface by the ramped wall velocity and temperature, and isothermal plate have been explored by Krishna [12]. Mustafa et al. [13] explored the influences of unstable MHD normal convection frontier stratum fluids past a lengthening piece with glutinous dissipations. The influences on MHD nanoliquid flows of the wedge by a porous slips and the media have been examined by Pandey and Kumar [14]. Upreti et al. [15] discussed the MHD flow of Ag-water nanofluid over a flat porous plate with viscous-Ohmic dissipation, suction/injection and heat generation/absorption. Krishna [16] explored the radiative MHD flow of an incompressible viscous electrically conducting non-Newtonian Casson hybrid nanofluid over an exponentially accelerated vertical porous surface. Mishra et al. [17] examined the impacts of Ohmic glutinous dissipation and slip impacts on nanoliquid flows past the lengthening cylinder by a suction and/or injection. Motsumi and Makinde [18] deliberated the impacts of thermal radiating and gelatinous dissipation on boundary layered flows of nanoliquids past a porous moving smooth plate. Haroun et al. [19] scrutinized the unsteady MHD assorted convective in the nanofluids owing to a stretching and/or shrinking surfaces by suction and/or injections. Farooq et al. [20] conferred the influences of transpiration and glutinous dissipation on entropy flows past the nonlinear and radial stretching disks. Kuznetsov and Nield [21] have deliberated the normal convection frontier stratum flows of a nanoliquid over a perpendicular plate. Hamad and Pop [22] explored the unstable MHD complimentary convective flows of the nanofluids over the perpendicular porous smooth plate in the revolving frame. The MHD free convective flow of the nanofluids over the perpendicular half-unbounded smooth plate have been examined by Hamad et al. [23]. Turkyilmazoglu [24] has found the investigative solution for warmth and mass transport of MHD slip flow in nanoliquids. Nandkeolyar et al. [25] have represented the unsteady MHD radiating flows of the nanoliquid over a smooth plate by the ramped wall temperature.

Recently, Shankar et al. [26] discussed the two dimensional mixed convection non-Darcy model with radiation effect in a nanofluid over an inclined wavy surface. Radiation effect on MHD Casson fluid flow over an inclined non-linear surface with chemical reaction in a Forchheimer porous medium has been studied by Shankar et al. [27]. The thermal radiation impact of MHD boundary layer flow of Williamson nanofluid along a stretching surface with porous medium taken into account of velocity and thermal slips has been discussed numerically by Reddy et al. [28]. Reddy et al. [29] explored the multiple slip effects on steady MHD flow past a non-isothermal stretching surface in presence of Soret, Dufour with suction/injection. Reddy et al. [30] discussed the transport properties of a hydromagnetic radiative stagnation point flow of a nanofluid past a stretching surface. Kumar et al. [31] thermal radiation impact on MHD heat transfer natural convective nanofluid flow over an impulsively started vertical plate. Kumar et al. [32] discussed an impact on non-Newtonian free convective MHD Casson fluid flow past a vertical porous plate in the existence of Soret, Dufour, and chemical reaction. Reddy et al. [33] explored the influence of radiation and viscous dissipation on MHD heat transfer Casson nanofluid flow along a nonlinear stretching surface with chemical reaction.

Singh et al. [34] discussed the numerical results of stagnation point flow of micropolar fluid over a porous stretchable surface due to the physical effects of internal heat generation/absorption, melting heat transfer and chemical reaction via Keller-Box method. Singh et al. [35] investigated a numerical solution to the melting heat transfer on micropolar fluid flow over a stretchable porous medium. Singh et al. [36] explored the numerical approach for chemical reaction and suction/injection impacts on magnetic micropolar fluid flow through porous wedge with Hall and ion-slip using Keller Box method. Singh et al. [37] explored the slip flow of micro-polar fluid through a permeable wedge due to the effects of chemical reaction and heat source/sink with Hall and ion-slip currents. Joshi et al. [38] discussed the combined impact of thermal radiation and suction/blowing on the MHD flow of Cu-Ag/H₂O-C₂H₆O₂ hybrid nanofluid through a stretchable surface in Darcy-Forchheimer porous medium. Joshi et al. [39] discussed the mixed convection flow of magnetic hybrid nanofluid over a bidirectional porous surface with internal heat generation and a higher-order chemical reaction. Natural convection and thermal radiation influence on nanofluid flow over a stretching cylinder in a porous medium with viscous dissipation have been explored by Pandey and Kumar [40]. Pandey and Kumar [41] discussed the boundary layer flow and heat transfer on Cu-water nanofluid flow over a stretching cylinder with slip effects. Joshi et al. [42] discussed the heat and mass transfer assessment of magnetic hybrid nanofluid flow via bidirectional porous surface with volumetric heat generation. Upreti et al. [43] explored the unsteady squeezing flow of magnetic hybrid nanofluids within parallel plates and entropy generation. Thermophoresis and suction/injection roles on free convective MHD flow of Ag–kerosene oil nanofluid have been explored by Upreti et al. [44].

Analytic expression for unsteady hydromagnetic boundary layer flow past an oscillating vertical plate in optically thick nanofluid in presence of thermal radiation and uniform transverse magnetic field has been obtained by Kataria and Mittal [45]. Kataria and Mittal [46] discussed the mathematical modeling of flow, heat and mass transfer in the unsteady natural convection MHD flow of electrically conducting nano fluid, past over an oscillating vertical plate. Sheikholeslami et al. [47] scrutinized three dimensional Al₂O₃-Water nanofluid flow and heat transfer features between two horizontal parallel plates in the presence of magnetic field through porous medium. Sheikholeslami et al. [48] studied the thermal diffusion and heat generation effects on the unsteady MHD flow of radiating and electrically conducting nanofluid past over an oscillating vertical plate through porous medium. Three dimensional CuO–water nanofluid flow considering Brownian motion in presence of radiation has been discussed by Mittal and Kataria [49]. Two dimensional mixed convective MHD stagnation point flow of Casson fluid past an infinite plate in porous medium has been discussed by Mittal and Patel [50]. Mittal et al. [51] discussed the mixed convection micropolar ferrofluid flow with viscous dissipation, joule heating and convective boundary conditions. Patel et al. [52] explored the MHD flow of micropolar nanofluid model with microstructure and inertial features of the substructure particles. MHD flow of a nanofluid through a permeable duct is analyzed through the mesoscopic approach by Li et al. [53]. Mittal [54] discussed heat and mass transfer of three-dimensional water-based composite MHD nanofluid flow through two horizontal parallel plates in a rotating system.

Shamshuddin et al. [55] discussed the computation of reactive thermo-solutal micro-polar nanofluid Sakiadis convection flow with gold/silver metallic nanoparticles. Shamshuddin et al. [56] explored the thermal and solutal performance of nanoparticles on a non-linear radiating stretching surface with heat source/sink and varying chemical reaction effects. Shamshuddin et al. [57] investigated the thermo-magnetic reactive ethylene glycol-metallic nanofluid transport from a convectively heated porous surface with Ohmic dissipation, heat source, thermophoresis, and Brownian motion effects. Shamshuddin and Eid [58] explored the nth order reactive nanofluids through convective elongated sheet under mixed convection flow by the joule heating effects. Radiative heat energy exploration on Casson-type nanoliquid induced by a convectively heated porous plate in conjunction with thermophoresis and Brownian movements has been discussed by Shamshuddin et al. [59]. Shamshuddin et al. [60] discussed the computation of reactive mixed convection radiative viscoelastic nanofluid thermo-solutal transport from a stretching sheet with Joule heating. Patil et al. [61] explored double diffusive time-dependent MHD Prandtl nanofluid flow due to linear stretching sheet with convective boundary conditions. Humane et al. [62] dynamics of multiple slip boundaries effect on MHD Casson-Williamson double-diffusive nanofluid flow past an inclined magnetic stretching sheet. Nakamura and Sawada [63] discussed numerical study on the flows of non-Newtonian liquids during the axisymmetric stenosis. Krishna and Vajravelu [64] explored the MHD free convection and oscillating flows of second graded fluids during two corresponding porous walls.

Keeping on the top of stated details, the chemical reaction influences on the radiating MHD convective flow of an incompressible viscous electrically conducting fluid past an exponentially accelerated perpendicular surface under the influences of slip velocity in the revolving structure taking Hall and ion slip impacts into account have not been explored yet. Therefore, in the present investigation, it is discussed the chemical reaction influences on the radiating MHD convective flow of an incompressible viscous electrically conducting fluid past an exponentially accelerated perpendicular surface under the influences of slip velocity in the revolving structure taking Hall and ion slip impacts into account. The governing equations are solved making use of Laplace transforms technique and computationally discussed with reference to the pertinent parameters.

2 Formulation and solution of the problem

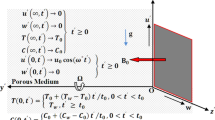
We considered the chemical reaction influences on the radiating MHD convective flow of an incompressible viscous electrically conducting fluid past an exponentially accelerated perpendicular surface under the influences of slip velocity in the revolving structure taking Hall and ion slip impacts into account. The physical modelling of a current study is represented by Fig. 1. Considered the x-direction is acquired through the surface in the perpendicular growing direction, the z-direction vertical to the surfaces and the y-direction are at right angle to the xz-plane. The plate and the fluid have been regarded in the situations of nonflexible body revolving by the uniformed angular speed Ω along z-directions. The consequences of revolving concerning the z-directions put in the transversal body strengths for the stream, that in terms produced transversal speed gradient, and the stream became 2-dimensionalised. The flow of fluids underneath contemplations is subject to the sturdy uniformed transversal magnetic strength B₀ parallel to the z-direction. The strengths of the provoked magnetic domain owing to liquid flow is presumed to be not significant in contrasted to apply the magnetic domain. Underneath the beyond referenced presumptions, and presuming Boussinesqs approximation for the body strength expression, the momentum equation leading the unstable MHD strength of liquids by porous medium in the revolving structure are as pursues (Singh and Srinivasa [65]).

Fig. 1

Physical model

$$\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}=0,$$

(1)

$$\frac{\partial u}{\partial t}-2\Omega v=\nu \frac{{\partial }^{2}u}{\partial {z}^{2}}+\frac{{B}_{0}{J}_{y}}{\rho }u-\frac{\nu }{k}u+g{\beta }_{T}\left(T-{T}_{\infty }\right)+g{\beta }_{C}\left(C-{C}_{\infty }\right),$$

(2)

$$\frac{\partial v}{\partial t}+2\Omega u=\nu \frac{{\partial }^{2}v}{\partial {z}^{2}}-\frac{{B}_{0}{J}_{x}}{\rho }v-\frac{\nu }{k}v$$

(3)

$$\rho {C}_{p}\frac{\partial T}{\partial t}={k}_{1}\frac{{\partial }^{2}T}{\partial {z}^{2}}-{Q}_{0}\left(T-{T}_{\infty }\right),$$

(4)

$$\frac{\partial C}{\partial t}=D\frac{{\partial }^{2}C}{\partial {z}^{2}}-K{r}^{*}\left(C-{C}_{\infty }\right),$$

(5)

The primary and boundary stipulations for the flows past the electrical non-conducting plates with slip impacts are,

$$u=v=0,T=T_\infty,C=C_\infty,\;\;\;\;t\leq0,\;z>0,$$

(6)

$$u=u_0e^{t/t_0}+\lambda_0\frac{\partial u}{\partial z},\;\;\;v=\lambda_0\frac{\partial v}{\partial z}\;\;\;\;at\;\;z=0,$$

(7)

$$T=\left\{\begin{array}{l}T_\infty+\left(T_w-T_\infty\right)\left(t/t_0\right),\;\;\;\;if\;0<t\leq t_0\\T_w\;\;\;\;\;if\;\;\;t>t_0\end{array}\right.\;\;\;at\;\;z=0,\;$$

(8)

$$C=C_\infty+\left(C_w-C_\infty\right)(t/t_0)\;\;\;\;at\;\;\;z=0,$$

(9)

$$u\rightarrow0,v\rightarrow0,T\rightarrow T_\infty,C\rightarrow C_\infty,\;\;\;t>0,\;\;\;\;as\;\;\;\;\;z\rightarrow\infty.$$

(10)

Here, ${\lambda }_{0}(\ge 0)$ is the slip coefficient and negative quantities of ${\lambda }_{0}$ did not keep in touch to physical case (Khaled and Vafai [66]) and the characteristic time t₀ may be defined in accordance for the non-dimensional process as ${t}_{0}=\nu /{u}_{0}^{2}$. The slip coefficient is depending on the variety of substantial issues, they are defer the phases in the rheological behaviour of the fluid (Lauge et al. [67]).

The electrons and atoms collision occurrence is assumed to be enormously prominent; subsequently, the Hall and ion slip impacts might not be abandoned. For that cause, the Hall and ion slip consequence increases to the velocity in the y-direction. If the strength for the magnetic field are extensively larger, the comprehensively Ohms law is tailored to included Hall and ion slip effects be (Sutton and Sherman [68]),

$$J=\sigma (E+V\times B)-\frac{{\omega }_{e}{\tau }_{e}}{{B}_{0}}(J\times B)+\frac{{\omega }_{e}{\tau }_{e}{\beta }_{i}}{{B}_{0}^{2}}\left((J\times B)\times B)\right),$$

(11)

Furthermore, it is presumed that, ${\omega }_{e}{\tau }_{e}\sim O(1)$ and ${\omega }_{i}{\tau }_{i}<<1,$ in the Eq. (11), the electrons pressure gradients and thermo-electrical impacts are discarded, i.e., the electrical field E = 0 underneath those presumptions, the Eq. (11) compacted to be,

$$(1+{\beta }_{i}{\beta }_{e}){J}_{x}+{\beta }_{e}{J}_{y}=\sigma {B}_{0}v,$$

(12)

$$(1+{\beta }_{i}{\beta }_{e}){J}_{y}-{\beta }_{e}{J}_{x}=-\sigma {B}_{0}u,$$

(13)

On solving Eqs. (12) and (13), it is acquired as,

$${J}_{x}=\sigma {B}_{0}({\alpha }_{2}u+{\alpha }_{1}v),$$

(14)

$${J}_{y}=-\sigma {B}_{0}({\alpha }_{2}v-{\alpha }_{1}u),$$

(15)

where, $\alpha_1=\frac{1+\beta_e\beta_i}{{(1+\beta_e\beta_i)}^2+\beta_e^2}\;and\;\alpha_2=\frac{\beta_e}{{(1+\beta_e\beta_i)}^2+\beta_e^2}.$  

Substituting the Eqs. (14) and (15) in (3) and (2) accordingly, it is acquired the momentum equation equations are,

$$\frac{\partial u}{\partial t}-2\Omega v=\nu \frac{{\partial }^{2}u}{\partial {z}^{2}}+\frac{\sigma {B}_{0}^{2}({\alpha }_{2}v-{\alpha }_{1}u)}{\rho }-\frac{\nu }{k}u+g{\beta }_{T}\left(T-{T}_{\infty }\right)+g{\beta }_{C}\left(C-{C}_{\infty }\right),$$

(16)

$$\frac{\partial v}{\partial t}+2\Omega u=\nu \frac{{\partial }^{2}v}{\partial {z}^{2}}-\frac{\sigma {B}_{0}^{2}({\alpha }_{2}u+{\alpha }_{1}v)}{\rho }-\frac{\nu }{k}v,$$

(17)

Combining the Eqs. (16) and (17), let q = u + iv, it is acquired be,

$$\frac{\partial q}{\partial t}+2i\Omega q=\nu \frac{{\partial }^{2}q}{\partial {z}^{2}}-\frac{\sigma {B}_{0}^{2}({\alpha }_{1}+i{\alpha }_{2})}{\rho }q-\frac{\nu }{k}q+g{\beta }_{T}\left(T-{T}_{\infty }\right)+g{\beta }_{C}\left(C-{C}_{\infty }\right),$$

(18)

The non-dimensional variables are introduced as

$$u*=\frac{u}{{u}_{0}},v*=\frac{v}{{u}_{0}},z*=\frac{z}{\sqrt{v{t}_{0}}},t*=\frac{t}{{t}_{0}},\theta =\frac{T-{T}_{\infty }}{{T}_{w}-{T}_{\infty }},\phi =\frac{C-{C}_{\infty }}{{C}_{w}-{C}_{\infty }},{M}^{2}=\frac{\sigma {B}_{0}^{2}v}{\rho {u}_{0}^{2}},Sc=\frac{v}{D},Kc=\frac{K{r}^{*}v}{{u}_{0}^{2}}{R}^{2}=\frac{\Omega v}{{u}_{0}^{2}},K=\frac{k{u}_{0}^{2}}{{v}^{2}},Gr=\frac{g{\beta }_{T}v\left({T}_{w}-{T}_{\infty }\right)}{{u}_{0}^{3}},Gc=\frac{g{\beta }_{C}v\left({C}_{w}-{C}_{\infty }\right)}{{u}_{0}^{3}},\mathrm{Pr}=\frac{\mu {C}_{p}}{{k}_{1}},Q=\frac{{Q}_{0}v}{\rho {C}_{p}{u}_{0}^{2}}.$$

Using the non-dimensional quantities, we obtained the revised non-dimensional leading equations and are given by,

$$\frac{\partial q}{\partial t}=\frac{{\partial }^{2}q}{\partial {z}^{2}}-\left({M}^{2}({\alpha }_{1}+i{\alpha }_{2})+2i{R}^{2}+\frac{1}{K}\right)q+Gr\theta +Gc\phi ,$$

(19)

$$\frac{\partial \theta }{\partial t}=\frac{1}{\mathrm{Pr}}\frac{{\partial }^{2}\theta }{\partial {z}^{2}}-Q\theta ,$$

(20)

$$\frac{\partial \phi }{\partial t}=\frac{1}{Sc}\frac{{\partial }^{2}\phi }{\partial {z}^{2}}-Kc\phi ,$$

(21)

The relevant non-dimensional primary and boundary conditions are:

$$q=0,\theta=0,\phi=0\;for\;all\;z>0\;and\;t\leq0,$$

(22)

$$q=e^t+\lambda\frac{\partial q}{\partial z},\theta=\left\{\begin{array}{l}t\;\;\;if\;\;\;0<\tau\leq1\\1\;\;if\;\;\;\;\;\;\;\;\;\tau>1\end{array}\right.,\phi=t\;\;\;at\;\;\;\;z=0,$$

(23)

$$q\rightarrow0,\theta\rightarrow0,\phi\rightarrow0\;\;\;\;as\;\;\;\;z\rightarrow\infty\;\;\;for\;\;\;\;t>0.$$

(24)

where, $\lambda =\frac{{\lambda }_{0}{u}_{0}}{v}$ is the slip parameter.

To solve the governing Eqs. (19) - (21) by making use the Laplace transform method with the initial and boundary conditions (22) – (24). The transformed differential equations become,

$${a}_{1}\frac{{d}^{2}\overline{q}}{d{z }^{2}}-(s+{\lambda }_{1})\overline{q }=-{a}_{2}\overline{\theta }-{a}_{3}\overline{\phi },$$

(25)

$$\frac{{d}^{2}\overline{\theta }}{d{z}^{2}}-(s+{a}_{5}){a}_{4}\overline{\theta }=0,$$

(26)

$$\frac{{d}^{2}\overline{\phi }}{d{z}^{2}}-(s+{a}_{1}){a}_{10}\overline{\phi }=0,$$

(27)

The boundary stipulations in terms of changed variable are,

$$\overline q=\frac1{s-1}+\lambda\frac{d\overline q}{dz},\overline\theta=\frac1{s^2}\left(1-e^{-s}\right),\overline\phi=\frac1{s^2}\;\;\;\;at\;\;\;\;z=0,$$

(28)

$$\overline q\rightarrow0,\overline\theta\rightarrow0,\overline\phi\rightarrow0\;\;\;\;as\;\;\;\;z\rightarrow\infty,$$

(29)

Solving the differential Eqs. (25) – (27) with the frontier conditions (28) – (29), we acquire the transformed solutions for the velocity, temperature, and concentration $\overline q\left(z,s\right),\overline\theta\left(z,s\right)\;and\;\overline\phi\left(z,s\right)$ are,

$$\overline{q }\left(z,s\right)=\left\{{\left(1+\lambda {b}_{5}\right)}^{-1}\left[\frac{1}{s-1}+{b}_{3}+{b}_{4}+\lambda ({b}_{1}+{b}_{2})\right]\right\}{e}^{-{b}_{5}z}-{b}_{3}{e}^{-{b}_{1}z}-{b}_{4}{e}^{-{b}_{2}z},$$

(30)

$$\overline{\theta }(z,s)=\frac{1}{{s}^{2}}\left(1-{e}^{-s}\right){e}^{-\sqrt{(s+{a}_{5}){a}_{4}}z},$$

(31)

$$\overline{\phi }(z,s)=\frac{1}{{s}^{2}}{e}^{-\sqrt{(s+{a}_{1}){a}_{10}}z}.$$

(32)

Captivating the inverse Laplace transforms for the Eqs. (30) – (32), it is acquired the solutions for the velocity distribution, temperature, and concentration distribution afterwards moving on the t-path for the flow near a perpendicular surface by the ramped wall temperature précised by,

$$q(z,t)={q}_{1}(z,t)-H(t-1){q}_{1}(z,t-1),$$

(33)

$$\theta (z,t)={f}_{1}({\alpha }_{2},{a}_{5},t)-H(t-1){f}_{1}({\alpha }_{3},{a}_{5},t-1),$$

(34)

$$\phi (z,t)={f}_{1}({\alpha }_{3},{a}_{1},t).$$

(35)

Initiate to emphasize the consequence of the ramped wall temperature on a flow domain, it may be consequentially to contrasts a fluid flow due to uniformed wall temperature. In the current case, the initial and boundary conditions (22)–(24) are the identically exclude the condition $\theta(0,t)=1,for\;t=0$. The temperature and velocity for the flow over the plate surface with the uniform wall temperature may be obtained as,

$$q(z,t)={q}_{2}(z,t),$$

(36)

$$\theta (z,t)={f}_{7}({\alpha }_{1},{a}_{5},0,t).$$

(37)

Equations (36) and (37) designated the velocity and temperature distribution for a uniform wall temperature and the time altering concentration distribution.

In support of engineering inquisitiveness, the non-dimensional shear stresses due to the initial and secondary flow at a plate (z = 0) are calculated by the Eqs. (33) and (36).

For the ramped wall temperature,

$$\tau ={\tau }_{x}+i{\tau }_{y}={\left(\frac{\partial q}{\partial z}\right)}_{z=0}={q}_{3}(t)-H(t-1){q}_{3}(t-1),$$

(38)

For the uniform wall temperature

$$\tau ={\tau }_{x}+i{\tau }_{y}={\left(\frac{\partial q}{\partial z}\right)}_{z=0}={q}_{4}(t).$$

(39)

The Nusselt number in terms of rate of heat transport at the plate surface (z = 0) for ramped wall temperature and for uniform wall temperature is calculated by the Eqs. (34) and (37), and are specified by

$${\theta }^{^{\prime}}\left(0,t\right)=-{\left(\frac{\partial \theta }{\partial z}\right)}_{z=0}=-\sqrt{{a}_{4}\left({g}_{1}\left({a}_{5},t\right)-H\left(t-1\right){g}_{1}\left({a}_{5},t-1\right)\right),}$$

(40)

$${\theta }^{^{\prime}}(0,t)=-{\left(\frac{\partial \theta }{\partial z}\right)}_{z=0}=-\sqrt{{a}_{4}}\;{g}_{7}({a}_{5},0,t).$$

(41)

The Sherwood number in terms of rate of mass transport at the plate surface (z = 0) is calculated through the Eq. (35) also specified as,

$${\Phi }^{^{\prime}}(0,t)=-{\left(\frac{\partial \phi }{\partial z}\right)}_{z=0}=-\sqrt{{a}_{10}}\;{g}_{1}({a}_{1},t).$$

(42)

All the constant expressions are mentioned in the appendix.

3 Results and discussion

It is regarded as the chemical reaction influences on the radiating MHD convective flow of an incompressible viscous electrically conducting fluid past an exponentially accelerated perpendicular surface under the influences of slip velocity in the revolving structure taking Hall and ion slip impacts into account. The precise solutions of the leading equations are accomplished with the Laplace transform procedure. The fluid flow is presided by the non-dimensional parameters named as, viz. Hartmann quantity M, permeability parameter K, revolution parameter R, slip parameter λ, thermal Grashofs quantity Gr, mass Grashofs quantity Gm, temperature source parameter Q, chemical reaction parameter Kc, Schmidt quantity Sc, and time t. Figures (2, 3, 4, 5, 6, 7, 8 and 9), (10 and 11), and (12 and 13) present the sketches of velocity, temperature for ramped wall temperature and uniform wall temperature, and concentration profiles correspondingly. The resultant velocity is executed a distinguished higher quantity near the surface of the plate and then diminishes suitably on increasing frontier layers co-ordinates z to reaches free stream conditions. This is also observed that, the resultant velocity is slowly downs in a case of ramped wall temperature plate than that of uniform wall temperature. The skin friction, Nusselt number on together ramped wall temperature and uniform wall temperature, and Sherwood number are also evaluated and exhibited in Tables 1, 2 and 3. Table 4 represents the comparison of the results.

Table 1 Shear stresses (τ) (Pr = 0.71, Kc = 2, t = 0.5)

Table 2 Nusselt number (Nu)

Table 3 Sherwood number (Sh)

Table 4 Comparison of results for principal velocity for the ramped wall temperature (Kc = 0,${\upbeta }_{\mathrm{e}}=0,{\upbeta }_{\mathrm{i}}=0$, Sc = 0, Q = 0, Gm = 0, R = 0)

It is look upon that of the values of Hartmann parameter $0<M\le 8$; the values of the permeability parameter are $0<K\le 3$; revolution parameter $0<R\le 3$; slip parameter $0<\lambda <1$; thermal Grashofs quantity $0<Gr\le 20$, mass Grashofs quantity $0<Gm\le 12$; heat source parameter $0<Q\le 8$; the quantities of the Hall parameter ${\beta }_{e}$ are 1 to 4 $({\omega }_{e}{\tau }_{e}\approx O(1))$; the quantities of ion slip parameter ${\beta }_{i}$ are 0 to less than 1 $({\omega }_{i}{\tau }_{i}<<1)$; the Schmidt number as Sc = 0.220, 0.30, 0.60, 0.780 this analogous to H₂, He, H₂O- vapour, and NH₃ respectively; chemical reaction parameter $0<Kc\le 4$ (Krishna [69] and Seth et al. [70]). For computational purposes, fixing values, M = 2, K = 0.5, R = 1, λ = 0.2, Gr = 5,Gm = 3, Q = 2, Kc = 1, Sc = 0.22, β_e = 1, β_i = 0.2, t = 0.6, while it is illustrated the profiles on each of the parameters varied over the range.

Figure 2 exhibits the consequences of the Hartmann quantity on resultant velocity with together kinds of ramped wall temperature and uniform wall temperature. It is evidently that, in both cases, the resultant velocity is reducing over the plate with the analogous performance throughout the liquid medium. Subsequently, unpredicted reduction in the velocity is noticed in a neighbourhood of a surface in the manifestation of the magnetic field. In addition, this has been cleared that, that occurrence diminishes the velocity distributions throughout the liquid medium. These reflected to known that, the appearances of a magnetic field vertically toward the movement paths, an inclination on or attractions to produce the resistances distinguished as Lorentz forces, it is shown the propensity to refuse to gone together with the flow field throughout the fluid media. As the consequences, it is attained as the applications of the magnetic field strength in the manifestation of porous materials, support the lessening outcomes on the thicknesses of the momentums frontier layer.

Fig. 2

The velocity profiles against M

Figure 3 demonstrates that, the consequences of permeability parameters K on a resultant speed for together ramped wall temperature and uniform wall temperature. This is perceived that, the resultant velocity is enhancing by an increment in permeability parameters K throughout the liquid environment. This is obviously that, in generally, proportional values of K developed the resultant velocity rapidity and thus an enlargement in the momentum boundary layer thickness. Lower the penetrability reasons lesser the liquid velocity is scrutinized within the flow medium engaged by the fluid.

Fig. 3

The velocity profiles against K

Figure 4 displays that the consequences of rotation parameter R on a resultant velocity for together ramped wall temperature and uniform wall temperature. It is observed that, on both cases, the resultant velocity lessens on increasing in the rotation parameters in the liquid environment from a plate. This is due to a reason that, the Coriolis strength is predominant in the fluid medium at the direction of rotation.

Fig. 4

The velocity profiles against R

The outcome of slip velocity for the resultant velocity for mutually ramped wall temperature and uniformed wall temperature is depicted in Fig. 5. The resulting velocity reduces and thickness of momentum frontier layers increase by a rising in slip parameter throughout a fluid region.

Fig. 5

The velocity profiles against λ

Figures 6 and 7 depict the specially consequence of thermal and concentration buoyancy strengths, the resulting velocity for both cases of temperature are increasing with an enlargement in the thermal Grashofs quantity Gr or the mass Grashofs quantity Gm. Thermal Grashofs quantity described as the relative forces of the thermal buoyancy to the viscous, similarly, mass Grashofs quantity signify a comparative strength of concentration buoyancy forces to gelatinous forces. Therefore, thermal Grashofs quantity Gr or the mass Grashofs quantity Gm are enhancing on a boost up in the potency of thermal and mass buoyancy forces accordingly. Therefore, the thickness of the momentum boundary layer is enhanced for both kinds.

Fig. 6

The velocity profiles against Gr

Fig. 7

The velocity profiles against Gm

This is professed from Figs. 8 and 9 that, for together ramped walls temperatures and uniformed walls temperatures, the resultant velocity boosts on a growing in Hall and ion slip parameters β_e and β_i throughout the fluid medium. This is noticeable that, as reinforcement in the Hall parameter and the ion slip parameters, this results, increased the resultant velocity and the momentum frontier layered thickness during the fluid medium. The inclusions of Hall parameter retard the effective conductivity and as a result downgrade the magnetic renitent ferocity. Also, the proficient conductivity increased as increases in the ion slip parameter, for that motivation, the attenuation strengths are reducing; consequently, velocity intensifies in the fluid region.

Fig. 8

The velocity profiles against β_e

Fig. 9

The velocity profiles against β_i

The computational quantities of temperature θ are evaluated from the systematic resolutions (33) and (36) and are displayed diagrammatically through Figs. 10 and 11 for a variety of values of heat source parameters Q and Prandtl number Pr. This is apparent through Fig. 10 that liquid temperature and the thickness of thermal boundary layer decrease on an enhancing heat source parameter Q for together ramped wall temperature and uniform wall temperature. It might be established from Fig. 11 that, this is divulged that fluid temperature lessens with mounting in Prandtl number. Therefore, in both case, thermal diffusion has a tendency to augment fluid temperature during the boundary layer region. At the highest values of Prandtl numbers have less velocities, this is in revolve also imply that, at lesser fluid velocity, the species diffusion are relatively lower, and therefore, the highest species concentrations is examined at higher Prandtl numbers.

Fig. 10

The temperature profiles against Q

Fig. 11

The temperature profiles against Pr

Figures 12 and 13 exhibit to the influences of Schmidt quantity Sc, chemical reaction parameter Kc on concentration profiles. The concentration distribution and these boundary stratum thickness are diminished by an enhancement in Schmidt quantity. Actually, Schmidt quantity is linear relation to the ratio of the momentum diffusivity to the mass diffusivity. Schmidt number hence measured the relative efficiency of momentum and mass transportation during diffusion to the hydrodynamic boundary layers. The reduction into the concentration graphs is supplementary with immediate diminution in the concentration frontier stratum thickness. The concentration sketches are reducing for an enhancing in chemical reaction parameter Kc. The largest values of Kc lead to reduce the diffusion coefficients of mixture chemical species; it reduced concentration and boundary stratum thickness. Actually, for a harmful case (Kc > 0), reliable chemical reaction acquires position through lot of disturbances.

Fig. 12

The concentration profiles against Sc

Fig. 13

The concentration profiles against Kc

The computation results for shear stresses at the surface of a plate are shown by Table 1 for some quantities of important parameters. This is examined by Table 1 that for together ramped and uniformed wall temperatures, the shear stresses at the surface of a plate enhanced with a boosting in Hartmann number, penetrability parameter, slip parameter, and thermal and concentration buoyancy forces, β_e and β_i, and lessen by an growing in rotation parameter. Also, the shear stress of ramped wall temperatures is lower than towards the uniformed wall temperature. The computational results of Nusselt quantity at the surface of a plate for together ramped and uniform wall temperature are publicized into Table 2. This is noticed that, the Nusselt quantity is increasing with an enhancing in temperature source parameters Q, Prandtl number Pr for together temperature cases where as it is reduced with an increase in time. Additionally, the Nusselt number near the plate is moderately lowered for ramped wall temperature than that of uniform wall temperature. The computational assessments of the Sherwood number for different values of Schmidt number, chemical reaction parameter Kc, and time t are representing in Table 3. The Sherwood number at a plate is boosting by an increment in Schmidt number Sc, chemical reaction parameter Kc, and reduced with time t.

Figures 14, 15, 16, 17 and 18 expose the stream lines associated with the digressions in the magnetic field parameter, rotation parameter, permeability parameter, and Hall and ion slip parameters. This is recognized from Figs. 14 and 15 that, the streamlines are comprehensively more, vertically, with inferior strength if growing higher choices of magnetic field and rotations. Truly, enormous strengths of magnetic field and rotation tried to counter-balances the significances of free convection; Hall and ion slip impacts. It is perceived that, with an enhancement of Hartmann number and/or rotation parameter, the quantities of stream functions trim down. As a rising in Hartmann number induced the strongest magnetic fields, this in turns fabricated the Lorentz forces in flow domain; this retarded the reinforcement of flow, explicitly, slighter the convective currents in the perpendicular absorbent plate. Additionally, from Figs. 16, 17 and 18, it is notified that, the streamlines were spreading in the porous plate through the prominent stream function quantities due to the higher penetrability of absorbent medium; Hall and ion slip impacts. It designated that, stronger convection on greater penetrability and Hall and ion slip parameters.

Fig. 14

The stream lines against M

Fig. 15

The stream lines against R

Fig. 16

The stream lines against K

Fig. 17

The stream lines against β_e

Fig. 18

The stream lines against β_i

4 Code validation

In applied mathematics and all branches of engineering, analytical methods for finding exact solution to the boundary value problem using Laplace transform methodology. Analytical methods are used in a wide range of field, and reach its most sophisticated and advanced structures in all engineering regions. The field in general remains actively and heavily researched across multiple disciplines. The exactitude of numerical code is simulated for propriety, by the MATHEMATICA 10.4 software through the computational mechanism. Using this code, it is obtained that the primary velocity distributions are shown in Table 4 for quite a few values of pertinent parameters namely Hartmann number, permeability parameter, thermal Grashof number, and time. Again, by using same code for the previous work (Seth [70]), the same results are obtained nearly described above and are shown in Table 4 respectively for numerous values of pertinent parameters. The rigorously identical results are distinguished for both the research problems. Thus, the sensitivity of coding achieved accuracy (Fig. 19).

Fig. 19

Comparison of primary velocity u with $\mathrm{Sc}=\mathrm{Kc}=\mathrm{Gm}=\mathrm{R}=\mathrm{Q}=0,\mathrm{M}=2,\mathrm{K}=0.5,\mathrm{Gr}=5,\mathrm{Pr}=0.71,\uplambda =2,{\upbeta }_{\mathrm{e}}=0,{\upbeta }_{\mathrm{i}}=0,\mathrm{t}=0.5$  

5 Conclusions

It is regarded as chemical reaction influence on the radiative MHD flow of an incompressible viscous electrically conducting fluid past an exponentially accelerated perpendicular plate under the influences of slip velocity in the revolving structure taking Hall and ion slip effects into account. The terminations are finished as the subsequent.

• The resulting velocity is growing by an increase in heat and solutal buoyancy force, while revolution as well as slip parameters have reverse outcomes on it.

• The resulting velocity is falling by an increasing in the Hartmann number while the penetrability parameters and Hall and ion slip effects have overturn impacts on it.

• The temperatures and the thickness of thermal boundary layer decrease on an enhancing heat source parameter for together ramped wall temperature and uniformed wall temperature.

• The fluid temperature lessens with mounting in Prandtl number. Species concentration of fluid is reduced by an increased through Schmidt number as well as chemical reaction parameter.

• The shear stresses are enlarged by a growing in Hartmann number, slip parameter, and thermal and concentration buoyancy strengths and it is diminished by an increasing in Coriolis force.

• The heat absorptions increase the Nusselt number near the surface.

• The Sherwood number at the surface is superior with chemical reaction parameter.

• The current research has more applications with magnetic materials dispensation, electrical performing polymers mechanics, and purifications of molten metal through non-metallic.

• The research in the biomass conversion is mostly concentrated on steam gasification, entrained flow gasification’s, applications of thermo-chemical cycle, and/or conversions of ethanol as well as bio-oils.

• The present work is also extended for nanofluids and hybrid nanofluids.

Appendix

$${\lambda }_{1}={M}^{2}\left({\alpha }_{1}+i{\alpha }_{2}\right)+2i{R}^{2}+\frac{1}{K};$$

$${\alpha }_{1}=z\sqrt{{\lambda }_{1}},{\alpha }_{2}=z\sqrt{{a}_{4}},{\alpha }_{3}=z\sqrt{{a}_{10}},$$

$${b}_{1}=\sqrt{(s+{a}_{5}){a}_{4}},{b}_{2}=\sqrt{(s+{a}_{1}){a}_{10}}, {b}_{3}=\frac{1}{{b}_{1}^{2}-(s+{\lambda }_{1})}\left(\frac{1-{e}^{-s}}{{s}^{2}}\right),{b}_{4}=\frac{1}{{b}_{2}^{2}-(s+{\lambda }_{1})}\left(\frac{1}{{s}^{2}}\right), {b}_{5}=\sqrt{(s+{\lambda }_{1})},{b}_{6}=\frac{1}{\lambda },$$

$${a}_{1}=Kc {,a}_{2}=Gr, {a}_{3}=Gm{, a}_{4}=\frac{1}{\mathrm{Pr}},{a}_{5}=Q; {a}_{6}=\frac{{\lambda }_{1}-{a}_{4}{a}_{5}}{{a}_{4}-1}; {a}_{7}=\frac{{\lambda }_{1}-{a}_{10}{a}_{1}}{{a}_{10}-1}; {a}_{8}={a}_{2}\sqrt{{a}_{4}}; {a}_{9}={a}_{3}\sqrt{{a}_{10}};{a}_{10}=Sc, {a}_{11}=\frac{{b}_{6}{a}_{2}}{{a}_{6}^{2}},{a}_{12}=\frac{{b}_{6}{a}_{3}}{{a}_{7}^{2}}, {a}_{13}=\frac{{a}_{8}({a}_{5}+{a}_{6})}{{a}_{6}^{2}},{a}_{14}=\frac{{a}_{9}(Kc+{a}_{7})}{{a}_{7}^{2}},$$

$$\begin{array}{c}{q}_{1}(z,t)={b}_{6}{f}_{3}({\alpha }_{1},{\lambda }_{1},1,{b}_{6},t)-{a}_{2}{f}_{2}({\alpha }_{2},{a}_{5},{a}_{6},t)-{a}_{3}{f}_{2}({\alpha }_{3},{a}_{1},{a}_{7},t)\\ +{a}_{11}\left({f}_{3}({\alpha }_{1},{\lambda }_{1},{a}_{6},{b}_{6},t)-{f}_{3}({\alpha }_{1},{\lambda }_{1},0,{b}_{6},t)-{a}_{6}{f}_{4}({\alpha }_{1},{\lambda }_{1},{b}_{6},t)\right)\\ \begin{array}{c}+{a}_{12}\left({f}_{3}({\alpha }_{1},{\lambda }_{1},{a}_{7},{b}_{6},t)-{f}_{3}({\alpha }_{1},{\lambda }_{1},0,{b}_{6},t)-{a}_{7}{f}_{4}({\alpha }_{1},{\lambda }_{1},{b}_{6},t)\right)\\ +{a}_{13}\left({f}_{5}({\alpha }_{1},{\lambda }_{1},{a}_{6},{b}_{6},t)-{f}_{5}({\alpha }_{1},{\lambda }_{1},0,{b}_{6},t)-{a}_{6}{f}_{6}({\alpha }_{1},{\lambda }_{1},{a}_{5},{b}_{6},t)\right)\\ +{a}_{8}{f}_{6}({\alpha }_{1},{\lambda }_{1},{a}_{5},{b}_{6},t)+{a}_{9}{f}_{6}({\alpha }_{1},{\lambda }_{1},{a}_{1},{b}_{6},t)\end{array}\end{array}$$

$$\begin{array}{c}{q}_{2}(z,t)={b}_{6}{f}_{3}({\alpha }_{1},{\lambda }_{1},1,{b}_{6},t)-{a}_{3}{f}_{2}({\alpha }_{3},{a}_{1},{a}_{7},t)+{a}_{8}{f}_{5}({\alpha }_{1},{\lambda }_{1},0,{a}_{5},{b}_{6},t)\\ +{a}_{11}\left({f}_{3}({\alpha }_{1},{\lambda }_{1},{a}_{6},{b}_{6},t)-{f}_{3}{\alpha }_{1},{\lambda }_{1},0,{b}_{6},t)\right)\\ \begin{array}{c}+{a}_{12}\left({f}_{3}({\alpha }_{1},{\lambda }_{1},{a}_{7},{b}_{6},t)-{f}_{3}({\alpha }_{1},{\lambda }_{1},0,{b}_{6},t)-{a}_{7}{f}_{4}({\alpha }_{1},{\lambda }_{1},{b}_{6},t)\right)\\ +{a}_{13}\left({f}_{5}({\alpha }_{1},{\lambda }_{1},{a}_{6},{b}_{6},t)-{f}_{5}({\alpha }_{1},{\lambda }_{1},0,{b}_{6},t)\right)\\ +{a}_{14}\left({f}_{5}({\alpha }_{1},{\lambda }_{1},{a}_{7},{a}_{1},{b}_{6},t)-{f}_{5}({\alpha }_{1},{\lambda }_{1},0,{a}_{1},{b}_{6},t)-{a}_{7}{f}_{6}({\alpha }_{1},{\lambda }_{1},{a}_{1},{b}_{6},t)\right)\end{array}\end{array}$$

$$\begin{array}{c}{q}_{3}(t)={b}_{6}{g}_{3}({\lambda }_{1},1,{b}_{6},t)-{a}_{2}\sqrt{{a}_{4}}{g}_{2}({a}_{5},{a}_{6},t)-{a}_{3}\sqrt{{a}_{10}}{g}_{2}({a}_{1},{a}_{7},t)\\ +{a}_{11}\left({g}_{3}({\lambda }_{1},{a}_{6},{b}_{6},t)-{g}_{3}({\lambda }_{1},0,{b}_{6},t)-{a}_{6}{g}_{4}({\lambda }_{1},{b}_{6},t)\right)\\ \begin{array}{c}+{a}_{12}\left({g}_{3}({\lambda }_{1},{a}_{7},{b}_{6},t)-{g}_{3}({\lambda }_{1},0,{b}_{6},t)-{a}_{7}{g}_{4}({\lambda }_{1},{b}_{6},t)\right)\\ +{a}_{13}\left({g}_{5}({\lambda }_{1},{a}_{6},{a}_{5},{b}_{6},t)-{g}_{5}({\lambda }_{1},0,{a}_{5},{b}_{6},t)-{a}_{6}{g}_{6}({\lambda }_{1},{a}_{5},{b}_{6},t)\right)\\ \begin{array}{c}+{a}_{14}\left({g}_{5}({\lambda }_{1},{a}_{7},{a}_{1},{b}_{6},t)-{g}_{5}({\lambda }_{1},0,{a}_{1},{b}_{6},t)-{a}_{7}{g}_{6}({\lambda }_{1},{a}_{1},{b}_{6},t)\right)\\ +{a}_{2}\sqrt{{a}_{4}}{g}_{6}({\lambda }_{1},{a}_{5},{b}_{6},t)+{a}_{3}\sqrt{{a}_{10}}{g}_{6}({\lambda }_{1},{a}_{1},{b}_{6},t)\end{array}\end{array}\end{array}$$

$$\begin{array}{c}{q}_{4}(t)={b}_{6}{g}_{3}({\lambda }_{1},1,{b}_{6},t)-{a}_{3}\sqrt{{a}_{10}}{g}_{2}({a}_{1},{a}_{7},t)\\ +{a}_{11}\left({g}_{3}({\lambda }_{1},{a}_{6},{b}_{6},t)-{g}_{3}({\lambda }_{1},0,{b}_{6},t)\right)\\ \begin{array}{c}+{a}_{12}{g}_{3}({\lambda }_{1},{a}_{7},{b}_{6},t)-{g}_{3}({\lambda }_{1},0,{b}_{6},t)-{a}_{7}{g}_{4}({\lambda }_{1},{b}_{6},t)\\ +{a}_{13}\left({g}_{5}({\lambda }_{1},{a}_{6},{a}_{5},{b}_{6},t)-{g}_{5}({\lambda }_{1},0,{a}_{5},{b}_{6},t)\right)\\ \begin{array}{c}+{a}_{14}\left({g}_{5}({\lambda }_{1},{a}_{7},{a}_{1},{b}_{6},t)-{g}_{5}({\lambda }_{1},0,{a}_{1},{b}_{6},t)-{a}_{7}{g}_{6}({\lambda }_{1},{a}_{1},{b}_{6},t)\right)\\ +{a}_{2}\sqrt{{a}_{4}}{g}_{5}({\lambda }_{1},0,{a}_{5},{b}_{6},t)+{a}_{3}\sqrt{{a}_{10}}{g}_{6}({\lambda }_{1},{a}_{1},{b}_{6},t)\end{array}\end{array}\end{array}$$

$${f}_{1}\left(x,y,z\right)=\frac{1}{2}\left[\left(z+\frac{x}{2\sqrt{y}}\right){e}^{x\sqrt{y}}erfc\left(\frac{x}{2\sqrt{z}}+\sqrt{yz}\right)+\left(z-\frac{x}{2\sqrt{y}}\right){e}^{x\sqrt{y}}erfc\left(\frac{x}{2\sqrt{z}}-\sqrt{yz}\right)\right];$$

$$\begin{array}{c}{f}_{2}\left(x,y,z,u\right)=\frac{{e}^{zu}}{2{z}^{2}}\left[{e}^{x\sqrt{y+z}}erfc\left(\frac{x}{2\sqrt{u}}+\sqrt{u\left(y+z\right)}\right)+{e}^{-x\sqrt{y+z}}erfc\left(\frac{x}{2\sqrt{u}}-\sqrt{u\left(y+z\right)}\right)\right]\\ -\frac{1}{2z}\left[\left(u+\frac{1}{z}+\frac{x}{2\sqrt{y}}\right){e}^{x\sqrt{y}}erfc\left(\frac{x}{2\sqrt{u}}+\sqrt{yu}\right)+\left(u+\frac{1}{z}-\frac{x}{2\sqrt{y}}\right){e}^{-x\sqrt{y}}erfc\left(\frac{x}{2\sqrt{u}}-\sqrt{yu}\right)\right]\end{array};$$

$$\begin{array}{c}{f}_{3}\left(x,y,z,u,v\right)={L}^{-1}\left[\frac{{e}^{-x\sqrt{s+y}}}{\left(s-z\right)\left(u+\sqrt{s+y}\right)}\right]\\ =-\frac{u{e}^{\left({u}^{2}-y\right)\tau +ux}}{{u}^{2}-y-z}erfc\left(\frac{x}{2\sqrt{v}}+u\sqrt{v}\right)+\frac{{e}^{zv}}{2\left({u}^{2}-y-z\right)}\times \\ \left[\left(u+\sqrt{y+z}\right){e}^{x\sqrt{y+z}}erfc\left(\frac{x}{2\sqrt{v}}+\sqrt{v\left(y+z\right)}\right)+\left(u-\sqrt{y+z}\right){e}^{-x\sqrt{y+z}}erfc\left(\frac{x}{2\sqrt{v}}-\sqrt{v\left(y+z\right)}\right)\right]\end{array};$$

$$\begin{array}{c}{f}_{4}\left(x,y,z,u\right)={L}^{-1}\left[\frac{{e}^{-x\sqrt{s+y}}}{{s}^{2}\left(z+\sqrt{s+y}\right)}\right]\\ =-\frac{z{e}^{u\left({z}^{2}-y\right)+zx}}{{\left({z}^{2}-y\right)}^{2}}erfc\left(\frac{x}{2\sqrt{u}}+z\sqrt{u}\right)-\frac{1}{\left({z}^{2}-y\right)}\sqrt{\frac{u}{\pi }}{e}^{-\left(\frac{{x}^{2}}{4u}+yu\right)}\\ \begin{array}{c}+\frac{1}{4\sqrt{y}\left(z-\sqrt{y}\right)}\left(2u\sqrt{y}+x+\frac{1}{z-\sqrt{y}}\right){e}^{x\sqrt{y}}erfc\left(\frac{x}{2\sqrt{u}}+\sqrt{yu}\right)\\ +\frac{1}{4\sqrt{y}\left(z+\sqrt{y}\right)}\left(2u\sqrt{y}-x-\frac{1}{z+\sqrt{y}}\right){e}^{-x\sqrt{y}}erfc\left(\frac{x}{2\sqrt{u}}-\sqrt{yu}\right)\end{array}\end{array};$$

$$\begin{array}{c}{f}_{5}\left(x,y,z,u,v,w\right)={L}^{-1}\left[\frac{{e}^{-x\sqrt{s+y}}}{\left(s-z\right)\sqrt{s+u}\left(v+\sqrt{s+y}\right)}\right]\\ =\frac{{v}^{2}{e}^{w\left({v}^{2}-y\right)+vx}}{\left({v}^{2}-y+u\right)\left({v}^{2}-y-z\right)}erfc\left(\frac{x}{2\sqrt{w}}+v\sqrt{w}\right)+\frac{\left(y-u\right){e}^{-u\tau }}{2\left({v}^{2}-y+u\right)\left(z+u\right)}\times \\ \begin{array}{c}\left[\left(1+\frac{v}{\sqrt{y-u}}\right){e}^{x\sqrt{y-u}}erfc\left(\frac{x}{2\sqrt{w}}+\sqrt{w\left(y-u\right)}\right)+\left(1-\frac{v}{\sqrt{y-u}}\right){e}^{-x\sqrt{y-u}}erfc\left(\frac{x}{2\sqrt{w}}-\sqrt{w\left(y-u\right)}\right)\right]\\ -\frac{\left(y+z\right){e}^{zw}}{2\left({v}^{2}-y-z\right)\left(z+u\right)}\times \\ \left[\left(1+\frac{v}{\sqrt{y+z}}\right){e}^{x\sqrt{y+z}}erfc\left(\frac{x}{2\sqrt{w}}+\sqrt{w\left(y+z\right)}\right)+\left(1-\frac{v}{\sqrt{y+z}}\right){e}^{-x\sqrt{y+z}}erfc\left(\frac{x}{2\sqrt{w}}-\sqrt{w\left(y+z\right)}\right)\right]\end{array}\end{array};$$

$$\begin{array}{c}{f}_{6}\left(x,y,z,u,v,w\right)={L}^{-1}\left[\frac{{e}^{-x\sqrt{s+y}}}{{s}^{2}\sqrt{s+y}\left(v+\sqrt{s+y}\right)}\right]\\ =\frac{{v}^{2}{e}^{w\left({v}^{2}-y\right)+vx}}{{\left({v}^{2}-y\right)}^{2}\left({v}^{2}-y+u\right)}efrc\left(\frac{x}{2\sqrt{w}}+v\sqrt{w}\right)+\frac{v}{u\left({v}^{2}-y\right)}\sqrt{\frac{w}{\pi }}{e}^{-\left(\frac{{x}^{2}}{4w}+yw\right)}-\\ \begin{array}{c}\frac{\left(y-u\right){e}^{-uw}}{2\left({v}^{2}-y+u\right){u}^{2}}\times \\ \left\{\left(1+\frac{v}{\sqrt{y-u}}\right){e}^{x\sqrt{y-u}}erfc\left(\frac{x}{2\sqrt{w}}+\sqrt{w\left(y-u\right)}\right)+\right.\\ \begin{array}{c}\left.\left(1-\frac{v}{\sqrt{y-u}}\right){e}^{-x\sqrt{y-u}}erfc\left(\frac{x}{2\sqrt{w}}-\sqrt{w\left(y-u\right)}\right)\right\}\\ -\frac{1}{4u\left(v-\sqrt{y}\right)}\left[2\frac{{v}^{2}{u}^{2}-\left(y-u\right){\left({v}^{2}-y\right)}^{2}}{\sqrt{y}u\left({v}^{2}-y\right)\left({v}^{2}-y+u\right)}+\left(2w\sqrt{y}+x-\frac{v}{\sqrt{y}\left(v+\sqrt{y}\right)}\right)\right]\\ \begin{array}{c}{e}^{x\sqrt{y}}erfc\left(\frac{x}{2\sqrt{w}}+\sqrt{yw}\right)\\ \begin{array}{c}+\frac{1}{4u\left(v+\sqrt{y}\right)}\left[2\frac{{v}^{2}{u}^{2}-\left(y-u\right){\left({v}^{2}-y\right)}^{2}}{\sqrt{y}u\left({v}^{2}-y\right)\left({v}^{2}-y+u\right)}+\left(2w\sqrt{y}-x-\frac{v}{\sqrt{y}\left(v-\sqrt{y}\right)}\right)\right]\\ {e}^{-x\sqrt{y}}erfc\left(\frac{x}{2\sqrt{w}}-\sqrt{yw}\right)\end{array}\end{array}\end{array}\end{array}\end{array};$$

$${f}_{7}\left(x,y,z,u\right)=\frac{{e}^{zu}}{2}\left[{e}^{x\sqrt{y+z}}erfc\left(\frac{x}{2\sqrt{u}}+\sqrt{u\left(y+z\right)}\right)+{e}^{-x\sqrt{y+z}}erfc\left(\frac{x}{2\sqrt{u}}-\sqrt{u\left(y+z\right)}\right)\right];$$

$${g}_{1}\left(x,y\right)=-\left[\left(\tau \sqrt{x}+\frac{1}{2\sqrt{x}}\right)erfc\left(\sqrt{xy}\right)+\sqrt{\frac{y}{\pi }}{e}^{-xy}\right];$$

$$\begin{array}{c}{g}_{2}\left(x,y,z\right)=-\frac{{e}^{yz}}{{y}^{2}}\left[\sqrt{x+y}erf\left(\sqrt{z\left(x+y\right)}\right)+\frac{1}{\sqrt{\pi z}}{e}^{-z\left(x+y\right)}\right]+\\ \frac{1}{y}\left[\left\{\sqrt{x}\left(\tau +\frac{1}{y}\right)+\frac{1}{2\sqrt{y}}\right\}erf\left(\sqrt{zx}\right)+\frac{1}{\sqrt{\pi z}}\left(z+\frac{1}{y}\right){e}^{-zx}\right]\end{array};$$

$$\begin{array}{c}{g}_{3}\left(x,y,z,u\right)=-\frac{z{e}^{u\left({z}^{2}-x\right)}}{{z}^{2}-x-y}\left[zerfc\left(z\sqrt{u}\right)-\frac{{e}^{-{z}^{2}u}}{\sqrt{\pi u}}\right]-\\ \frac{{e}^{yu}}{{z}^{2}-x-y}\left[z\sqrt{x+y}erf\left(u\sqrt{x+y}\right)-\left(x+y\right)+\frac{{e}^{-u\left(x+y\right)}}{\sqrt{\pi u}}\right]\end{array};$$

$$\begin{array}{c}{g}_{4}\left(x,y,z\right)=-\frac{y{e}^{z\left({y}^{2}-x\right)}}{{\left({y}^{2}-x\right)}^{2}}\left[yerfc\left(y\sqrt{z}\right)-\frac{{e}^{-{y}^{2}z}}{\sqrt{\pi z}}\right]+\\ \frac{1}{2\sqrt{y}\left({y}^{2}-x\right)}\left[2\sqrt{x}\left(xz+\frac{{y}^{2}}{\left({y}^{2}-x\right)}\right)-y\left(2xz+\frac{{y}^{2}+{x}^{2}}{{y}^{2}-{x}^{2}}\right)erf\sqrt{xz}-2y\sqrt{x}\left(z+\frac{1}{{y}^{2}-x}\right)\frac{{e}^{-xz}}{\sqrt{\pi z}}\right]\end{array};$$

$$\begin{array}{c}{g}_{5}\left(x,y,z,u,v\right)=\frac{{u}^{2}{e}^{\left({u}^{2}-x\right)\tau }}{\left({u}^{2}-x+z\right)\left({u}^{2}-x-y\right)}\left[uerfc\left(u\sqrt{v}\right)-\frac{{e}^{-{u}^{2}v}}{\sqrt{\pi v}}\right]-\\ \frac{\left(x-z\right){e}^{-zv}}{\left(y+z\right)\left({u}^{2}-x+z\right)}\left[\sqrt{x-z}erf\left(\sqrt{v\left(x-z\right)}\right)-u+\frac{{e}^{-v\left(x-z\right)}}{\sqrt{\pi v}}\right]+\\ \frac{\left(x+yu\right){e}^{yv}}{\left(y+z\right)\left({u}^{2}-x-y\right)}\left[\sqrt{x+z}erf\left(\sqrt{v\left(x+y\right)}\right)-u+\frac{{e}^{-v\left(x+y\right)}}{\sqrt{\pi v}}\right]\end{array};$$

$$\begin{array}{c}{g}_{6}\left(x,y,z,u\right)=\frac{{z}^{2}{e}^{u\left({z}^{2}-x\right)}}{\left({z}^{2}-x+y\right){\left({z}^{2}-x\right)}^{2}}\left[zerfc\left(z\sqrt{u}\right)-\frac{{e}^{-{z}^{2}u}}{\sqrt{\pi u}}\right]-\\ \frac{\left(x-y\right){e}^{-yu}}{{y}^{2}\left({z}^{2}-x+y\right)}\left[\sqrt{\left(x-y\right)}erf\left(\sqrt{u\left(x-y\right)}\right)-z+\frac{{e}^{-u\left(x-y\right)}}{\sqrt{\pi u}}\right]+\\ \begin{array}{c}\frac{1}{y\left({z}^{2}-x\right)}\left\{\sqrt{x}\left\{xu+\frac{1}{2}+\frac{{z}^{2}{y}^{2}-\left(x-y\right){\left({z}^{2}-x\right)}^{2}}{y\left({z}^{2}-x\right)\left({z}^{2}-x+y\right)}\right\}erf\left(\sqrt{xu}\right)-\right.\\ \left.\left\{xu+\frac{{z}^{2}{y}^{2}-\left(x-y\right){\left({z}^{2}-x\right)}^{2}}{y\left({z}^{2}-x\right)\left({z}^{2}-x+y\right)}\right\}\left(z-\frac{{e}^{-xu}}{\sqrt{\pi u}}\right)\right\}\end{array}\end{array}$$

$${g}_{7}\left(x,y,z\right)=-{e}^{yz}\left[\sqrt{x+y}erf\left(\sqrt{x+y}\tau \right)+\frac{{e}^{-z\left(x+y\right)}}{\sqrt{\pi z}}\right].$$