Introduction

Nowadays researchers paid too much attention in the analysis of heat and mass transfer due to their plenteous applications in the field of engineering and industrial appliances such as cooling of nuclear reactor, heat exchanger, refrigerator, polymer process, plastics extrusion. Fourier’s and Fick’s laws are the basic fundamental mathematical relations which are used to describe the mechanism of the transport of heat and mass in given medium due to temperature and concentration difference, respectively. Fourier’s law lead to parabolic-type equation for the temperature field which means heat transport has infinite speed and propagate throughout the medium with initial disturbance. To resolve this heat transport paradox, the Fourier’s law needs the some modifications. Many attempts have taken to clear up this paradox but not at all have been successful. Cattaneo [1] modified the Fourier’s law by introducing the thermal relaxation time parameter multiply with time derivative of heat flux which yields to the hyperbolic-type equation for heat transport phenomenon and as results, transport of heat has finite speed in the entire medium. This new model termed as Maxwell–Cattaneo (MC) model. In order to make this model frame invariant, Christov [2] amend the MC model by replacing time derivative to upper-convective time derivative which includes the higher spatial gradients. Yousif et al. [3] numerically studied the momentum and heat transport by using Fourier’s law in the flow Carreau nanofluid under the influence of magnetic field and internal sink/source. Sarafraz et al. [4] examined the characteristics of heat transport by employing Fourier’s law of heat conduction in the process of pool boiling in the presence of constant magnetic field.

Recently, scientists explored the heat and mass transport phenomena by using the Cattaneo–Christov double diffusion theory for the flow of both Newtonian and non-Newtonian fluids in different geometries. Han et al. [5] studied the flow of viscoelastic fluid with the impact of Cattaneo–Christov theory. They found the graphical outcomes for temperature and concentration fields. MHD flow of viscous fluid with Cattaneo–Christov model over the stretching sheet was explored by Upadhya et al. [6] Reduction in the heat transfer is observed for higher values of thermal relaxation parameter. Cattaneo–Christov double diffusion theory employed to the rotating flow of Oldroyd-B fluid over the stretching sheet with variable thermal conductivity by Khan et al. [7] Numerical investigation was performed by Ibrahim [8] on the 3D rotating flow of Powell-Eyring fluid and heat transfer with the help of non-Fourier’s law. Farooq et al. [9] analyzed the Cattaneo–Christov theory for the flow of viscous fluid with variable thermal conductivity and mass diffusivity. Their results revealed that both temperature and concentration fields decline for thermal and mass relaxation time parameters. Alamri et al. [10] investigated the flow of second-grade fluid over stretching cylinder with the perspective of Cattaneo–Christov heat flux model. Furthermore, numerous investigation has been performed for the analysis of Fourier’s law and Cattaneo–Christov double diffusion theory for the heat transport in the flow of various fluid models (see Refs. [11,12,13,14,15,16,17,18,19,20]). In the recent study of heat transfer enhancement, Khan et al. [21] scrutinized the effect of nanoparticles with different shapes in the peristaltic MHD flow of nanofluid.

Due to wide range applications of non-Newtonian fluids in engineering process attracted the researchers to investigate their perplexing rheology and also transport of thermal and solutal energy behaviors. Many engineering equipments used the non-Newtonian fluids, e.g., for reduction in friction in oil-pipe line, soldiers suits fill with some non-Newtonian fluids that turns into solid when built hit them, use as surfactant for large-scale heating and cooling systems, use in manufacturing lubricants for vehicles. As non-Newtonian fluids change their flow behavior under the applied stress, thus the researchers give various empirical models to describe the behavior of the non-Newtonian fluids. The constitutive equations for flow are highly complicated and nonlinear. The numerous analytical and numerical techniques are employed to tackle the flow equations for these nonlinear fluids. Raju et al. [22] studied the flow of non-Newtonian nanofluid over the cone under the influence of magnetic field. Flow of Maxwell fluid with heat transport with the influence of viscous dissipation and radiation was analyzed by Hsiao [23]. Application of Carreau nanofluid flow to enhance the heat transport in thermal extrusion manufacturing system was explored by Hsiao [24]. Ahmed et al. [25] numerically investigated the stagnation point flow of Maxwell fluid over the permeable rotating and stretching disk, and their results revealed that radial velocity increases with higher values of velocity ratio parameter. Moshkin et al. [26] analyzed the transient stagnation point 2D flow of Maxwell fluid.

In the subject of fluid dynamics, the flow of various fluid models with different dynamical properties induced by stretching surfaces attract the researcher to investigate its characteristics due to its diverse applications in engineering mechanism such as wire drawing, glass fiber, hot rolling, paper production, etc. In a wide range of applications such as plastic extrusion process flow over stretching cylinders is also critically important. Hsiao [27] investigated the mixed convection stagnation point flow over stretching sheet with slip boundary condition under the impact of uniform magnetic field. Numerical results were obtained by using finite difference scheme (FDM). The higher rate of heat transport was observed in case of more value of stagnation parameter. Flow of MHD micropolar fluid induced above the stretching sheet in addition to viscous dissipation was studied by Hsiao [28]. Application of Darcy–Forchheimer law to the flow nanofluid over curved stretching surface was investigated by Saif et al. [29]. The outcomes revealed that skin friction coefficient boosts up for higher porosity parameter and inertia coefficient. Ahmed et al. [30] numerically studied the unsteady flow of CNT nanofluid over shrinking surface by considering the variable viscosity of fluid and heat transport in it.

In view of the above detailed studies, we proposed this note to investigate the heat and mass transport in Maxwell fluid flow over the stretched cylinder in unsteady state. For the formation of energy and concentration equations, we utilize the Cattaneo–Christov double diffusion theory. Numerical solutions with the help of bvp4c function are obtained for governing physical problem. The outcomes for velocity, temperature and concentration fields are presented graphically and discussed in detail with the help of physical justification.

Mathematical formulation

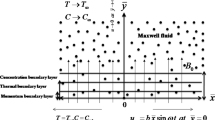
Consider the unsteady laminar 2D flow of an incompressible Maxwell fluid with variable thermal conductivity influenced by stretching cylinder of radius \(R_{1}\). Suppose that u and w are velocity components along z-axis (axis of cylinder) and r-axis (normal to z-axis), respectively as presented in Fig. 1. The time-dependent stretching velocity of the cylinder is assumed to be \(u_{\text{w}}(t,z)=\frac{az}{1-\gamma t}\) where \(a,\gamma >0\). Thermal and solutal energy transport in the flow is conducted by using Cattaneo–Christov double diffusion theory. The Maxwell fluid model is defined as [31]

$$\begin{aligned} \left( 1+\lambda _{1}\frac{\mathrm{D}}{\mathrm{D}t}\right) {\mathbf {S}}=\mu {\mathbf {A}}_{1}, \end{aligned}$$
(1)

where \(\lambda _{1}\) is the relaxation time, \(\frac{\mathrm{D}}{\mathrm{D}t}\) signifies the Oldroyd derivative, S the extra stress tensor, \({\mathbf {A}}_{1}=\mathbf\nabla {\mathbf {V}}+(\mathbf\nabla {\mathbf {V}})^{\mathrm{T}}\) the first Rivlin–Erickson tensor and \(\mu\) the viscosity of the fluid. If \(\lambda _{1}=0\) in Eq. (1) we recover the Newtonian fluid model.

The Cattaneo–Christov model for conduction of heat and mass are used rather than classical Fourier’s and Fick’s laws. If \({\mathbf {q}}\) and \({\mathbf {J}}\) are heat and mass fluxes, respectively, then both satisfy the following mathematical expressions [9, 10]

$$\begin{aligned}&{\mathbf {q}}+\lambda _{\mathrm{t}}\left( \frac{\partial {\mathbf {q}}}{\partial t}+{\mathbf {V}}\cdot\mathbf \nabla \mathbf {q}+({\mathbf {\nabla }} \mathbf {V})\mathbf {q} -{\mathbf {q}}\cdot \mathbf \nabla {\mathbf {V}} \right) \nonumber \\&\quad =-\,K(T)\mathbf \nabla T,\end{aligned}$$
(2)
$$\begin{aligned}&{\mathbf {J}}+\lambda _{\mathrm{c}}\left( \frac{\partial {\mathbf {J}}}{\partial t}+\mathbf { V}\cdot \mathbf \nabla \mathbf {J}+({\mathbf {\nabla }} \cdot \mathbf {V})\mathbf {J} -{\mathbf {J}}\cdot\mathbf \nabla {\mathbf {V}} \right) \nonumber \\&\quad =-\,D_{\mathrm{B}}\mathbf \nabla C. \end{aligned}$$
(3)

In the above equations \(\lambda _{\mathrm{t}}\) is the thermal time relaxation and \(\lambda _{\mathrm{c}}\) the mass time relaxation, \(K(T)=k_{\infty }(1+\epsilon \theta )\) the variable thermal conductivity (\(k_{\infty }\) free stream conductivity, \(\epsilon\) small conductivity parameter and \(\theta\) the dimensionless temperature) and \(D_{\mathrm{B}}\) the Brownian diffusion coefficient. If \(\lambda _{\mathrm{t}}=\lambda _{\mathrm{c}}=0\) then both Eqs. (2) and (3) reduce to classical Fourier’s and Ficks’s laws, respectively. For an incompressible fluid, Eqs. (2) and (3) become

$$\begin{aligned}&{\mathbf {q}}+\lambda _{\mathrm{t}}\left( \frac{\partial {\mathbf {q}}}{\partial t}+\mathbf { V}\cdot \mathbf \nabla {\mathbf {q}}-{\mathbf {q}}\cdot \mathbf \nabla {\mathbf {V}}\right) =-K(T)\mathbf \nabla T,\end{aligned}$$
(4)
$$\begin{aligned}&{\mathbf {J}}+\lambda _{\mathrm{c}}\left( \frac{\partial {\mathbf {J}}}{\partial t}+\mathbf { V}\cdot \mathbf \nabla \mathbf {J}-{\mathbf {J}}\cdot \mathbf \nabla {\mathbf {V}}\right) =-D_{\mathrm{B}}\mathbf \nabla C. \end{aligned}$$
(5)

The basic transport equations for flow, heat and mass transport found by conservation laws are

$$\begin{aligned}&\rho \frac{\mathrm{d}{\mathbf {V}}}{\mathrm{d}t}=-\mathbf \nabla \mathbf {p}+\mathbf \nabla \cdot \mathbf {S}, \end{aligned}$$
(6)
$$\begin{aligned}&(\rho c_{\text{p}})\frac{\mathrm{d}T}{\mathrm{d}t}=-\mathbf \nabla \cdot \mathbf {q}, \end{aligned}$$
(7)
$$\begin{aligned}&\frac{\mathrm{d}C}{\mathrm{d}t}=-\mathbf \nabla \cdot \mathbf {J}. \end{aligned}$$
(8)

By applying the law of conservation of mass, momentum and energy to the whole system of flow problem and eliminating \({\mathbf {S}}\) in Eqs. (1) and (6), \({\mathbf {q}}\) in Eqs. (2) and (7) and \({\mathbf {J}}\) in Eqs. (3) and (8), respectively, we arrived at following set of governing partial differential equations (Fig. 1):

$$\begin{aligned}&\frac{\partial (ru)}{\partial z}+\frac{\partial \left( rw\right) }{\partial r }=0, \end{aligned}$$
(9)
$$\begin{aligned}&\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial z}+w\frac{ \partial u}{\partial r}=\nu \left[ \frac{\partial ^{2}u}{\partial r^{2}}+ \frac{1}{r}\frac{\partial u}{\partial r}\right] \nonumber \\&\qquad -\,\lambda _{1}\left[ \frac{\partial ^{2}u}{\partial t^{2}}+2u\frac{\partial ^{2}u}{\partial t\partial z}+2w\frac{\partial ^{2}u}{\partial r\partial t} +2uw\frac{\partial ^{2}u}{\partial r\partial z}\right. \nonumber \\&\qquad \left. +\,w^{2}\frac{\partial ^{2}u}{ \partial r^{2}}+u^{2}\frac{\partial ^{2}u}{\partial z^{2}}\right] , \end{aligned}$$
(10)
$$\begin{aligned}&\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial z}+w\frac{ \partial T}{\partial r}+\lambda _{\mathrm{t}}\nonumber \\&\qquad \left[ \begin{array}{ll} &{}\frac{\partial ^{2}T}{\partial t^{2}}+\frac{\partial u}{\partial t}\frac{ \partial T}{\partial z}+2u\frac{\partial ^{2}T}{\partial t\partial z}\\ &{}\quad +\,\frac{\partial w}{\partial t}\frac{\partial T}{\partial r}+2w\frac{\partial ^{2}T}{ \partial t\partial r}+2uw\frac{\partial ^{2}T}{\partial r\partial z} \\ &{}\quad +\,w^{2}\frac{\partial ^{2}T}{\partial r^{2}}+u^{2}\frac{\partial ^{2}T}{ \partial z^{2}}+u\frac{\partial u}{\partial z}\frac{\partial T}{\partial z}\\ &{}\quad +\,w \frac{\partial u}{\partial r}\frac{\partial T}{\partial z}+u\frac{\partial w }{\partial z}\frac{\partial T}{\partial r}+w\frac{\partial w}{\partial r} \frac{\partial T}{\partial r} \end{array} \right] \nonumber \\&\quad =\frac{1}{(\rho c_{p})_{f}}\frac{1}{r}\frac{\partial }{\partial r}\left[ K(T)(r\frac{\partial T}{\partial r})\right] , \end{aligned}$$
(11)
$$\begin{aligned}&\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial z}+w\frac{ \partial C}{\partial r}+\lambda _{\mathrm{c}}\nonumber \\&\qquad \left[ \begin{array}{ll} &{}\frac{\partial ^{2}C}{\partial t^{2}}+\frac{\partial u}{\partial t}\frac{ \partial C}{\partial z}+2u\frac{\partial ^{2}C}{\partial t\partial z}+\frac{ \partial w}{\partial t}\frac{\partial C}{\partial r}\\ &{}\quad +\,2w\frac{\partial ^{2}C}{ \partial t\partial r}+2uw\frac{\partial ^{2}C}{\partial r\partial z} \\ &{}\quad +\,w^{2}\frac{\partial ^{2}C}{\partial r^{2}}+u^{2}\frac{\partial ^{2}C}{ \partial z^{2}}+u\frac{\partial u}{\partial z}\frac{\partial C}{\partial z}\\ &{}\quad +\,w \frac{\partial u}{\partial r}\frac{\partial C}{\partial z}+u\frac{\partial w }{\partial z}\frac{\partial C}{\partial r}+w\frac{\partial w}{\partial r} \frac{\partial C}{\partial r} \end{array} \right] \nonumber \\&\quad =D_{\mathrm{B}}\frac{1}{r}\frac{\partial }{\partial r}\left[ \left( r\frac{\partial C }{\partial r}\right) \right] . \end{aligned}$$
(12)

The corresponding boundary conditions for given problems are

$$\begin{aligned}&u(t,z,r)=u_{\text{w}}(t,z)=\frac{az}{1-\gamma t},\quad w(t,z,r)=0,\nonumber \\&\quad T=T_{\text{w}},\quad C=C_{\text{w}}\quad \text {at }r=R_{1}, \end{aligned}$$
(13)
$$\begin{aligned}&u\rightarrow 0,\quad T\rightarrow T_{\infty },\text { } C\rightarrow C_{\infty }\quad \text {as }r\rightarrow \infty . \end{aligned}$$
(14)

Here \(\nu\) is the kinematic viscosity, \(T_{\text{w}}\) and \(C_{\text{w}}\) are temperature and concentration at the wall, respectively, \(T_{\infty }\) and \(C_{\infty }\) the free stream temperature and concentration, respectively, \(\rho\) the fluid density and \(c_{\text{p}}\) the specific heat capacity at constant pressure.

Fig. 1
figure 1

Flow configuration and coordinate system

Full size image

With the help of following conversion parameters

$$\begin{aligned}&u=-\frac{R_{1}}{r}\sqrt{\frac{a\nu }{1-\gamma t}}f(\eta ),\quad w= \frac{az}{1-\gamma t}f^{\prime }(\eta ),\nonumber \\&\quad \theta (\eta )=\frac{ T-T_{\infty }}{T_{w}-T_{\infty }} \nonumber \\&\quad \phi (\eta )=\frac{C-C_{\infty }}{C_{w}-C_{\infty }},\quad \eta = \sqrt{\frac{a}{\nu (1-\gamma t)}}\left( \frac{r^{2}-R_{1}^{2}}{2R_{1}} \right) , \end{aligned}$$
(15)

Equation (9) is satisfied automatically and Eqs. (10)–(14) yield

$$\begin{aligned}&(1+2\alpha \eta )f^{\prime \prime \prime }+2\alpha ff^{\prime \prime }- \frac{S}{2}\eta f^{\prime \prime }-Sf^{\prime }-f^{\prime 2}\nonumber \\&\quad +\,ff^{\prime \prime }-\frac{7}{4}\beta _{1}S^{2}\eta f^{\prime \prime } \nonumber \\&\quad -\,\frac{\beta _{1}}{4}\eta ^{2}S^{2}f^{\prime \prime \prime }-2\beta _{1}S^{2}f^{\prime }-2S\beta _{1}f^{\prime 2}-\beta _{1}\eta Sf^{\prime }f^{\prime \prime }\nonumber \\&\quad +\,S\beta _{1}\eta ff^{\prime \prime \prime } \nonumber \\&\quad +\,3S\beta _{1}ff^{\prime \prime }+2\beta _{1}ff^{\prime }f^{\prime \prime }- \frac{\alpha \beta _{1}}{1+2\alpha \eta }f^{2}f^{\prime \prime }\nonumber \\&\quad -\,\beta _{1}f^{2}f^{\prime \prime \prime }=0, \end{aligned}$$
(16)
$$\begin{aligned}&(1+2\alpha \eta )\theta ^{\prime \prime }+\Pr \left( f\theta ^{\prime }-\frac{S}{2 }\eta \theta ^{\prime }\right) +(1+2\alpha \eta )(\theta \theta ^{\prime \prime }+\theta ^{\prime 2})\epsilon \nonumber \\&\quad +\,2\alpha \theta ^{\prime }+2\alpha \epsilon \theta \theta ^{\prime }-\Pr \beta _{\mathrm{t}}\left( \frac{3}{4}S^{2}\eta \theta ^{\prime }-\frac{3S}{2}\theta ^{\prime }f-\frac{S}{2}\eta \theta ^{\prime }f^{\prime } \right. \nonumber \\&\quad \left. +\,\frac{1}{4}S^{2}\eta ^{2}\theta ^{\prime \prime }-S\eta f\theta ^{\prime \prime }+\theta ^{\prime \prime }f^{2}+\theta ^{\prime }ff^{\prime }\right) =0, \end{aligned}$$
(17)
$$\begin{aligned}&(1+2\alpha \eta )\phi ^{\prime \prime }+\mathrm{Le}\Pr \left( f\phi ^{\prime }-\frac{S}{2} \eta \phi ^{\prime }\right) +2\alpha \phi ^{\prime } \nonumber \\&\quad -\,\mathrm{Le}\Pr \beta _{\mathrm{c}}\left( \frac{3}{4}S^{2}\eta \phi ^{\prime }-\frac{3S}{2}\phi ^{\prime }f-\frac{S}{2}\eta \phi ^{\prime }f^{\prime } \right. \nonumber \\&\quad \left. +\,\frac{1}{4}S^{2}\eta ^{2}\phi ^{\prime \prime }-S\eta f\phi ^{\prime \prime }+\phi ^{\prime \prime }f^{2}+\phi ^{\prime }ff^{\prime }\right) =0, \end{aligned}$$
(18)
$$\begin{aligned}&f(0)=0,\quad f'(0)=1,\quad \theta \left( 0\right) =1,\ \ \ \phi (0)=1, \end{aligned}$$
(19)
$$\begin{aligned}&f^{\prime }(\infty )=0,\quad \theta (\infty )=0,\quad \phi (\infty )=0. \end{aligned}$$
(20)

In the above equations \(S\, (=\frac{\gamma }{a})\) is the unsteadiness parameter, \(\alpha \,\left( =\frac{1}{R_{1}}\sqrt{\frac{\nu (1-\gamma t)}{a} }\right)\) the curvature parameter, \(\beta _{1}\) \(\left( =\frac{\lambda _{1}a}{1-\gamma t}\right)\) the Maxwell parameter, \(\Pr \, \left( =\frac{ \nu }{\alpha _{1}}\right)\) the Prandtl number, \(\beta _{\mathrm{t}}\) \(\left( =\frac{ \lambda _{\mathrm{t}}a}{1-\gamma t}\right)\) the thermal relaxation time parameter, \(\beta _{\mathrm{c}}\) \(\left( =\frac{\lambda _{\mathrm{c}}a}{1-\gamma t}\right)\) the mass relaxation time parameter and \(\mathrm{Le}\) \(\left( =\frac{\alpha _{1}}{D_{\mathrm{B}}}\right)\) the Lewis number.

Solution procedure

This section is proposed for the solution of established ODEs for flow, energy and concentration Eqs. (16), (17) and (18) along with corresponding boundary conditions given in Eqs. (19) and (20) the numerically. Bvp4c built in MATLAB technique is used to acquire the numerical results. For this we transformed the governing ODEs to the system of first-order ordinary differential equations. For this, we used the transformed variables as

$$\begin{aligned} f= & {} y_{1},\quad f^{\prime }=y_{2},\quad f^{\prime \prime }=y_{3},\quad f^{\prime \prime \prime }=yy_{1}, \end{aligned}$$
(21)
$$\begin{aligned} \theta= & {} y_{4},\theta ^{\prime }=y_{5},\theta ^{\prime \prime }=yy_{2}, \end{aligned}$$
(22)
$$\begin{aligned} \phi= & {} y_{6},\quad \phi ^{\prime }=y_{7,}\quad \phi ^{\prime \prime }=yy_{3}. \end{aligned}$$
(23)

The resulting first-order ODEs are as follows

$$\begin{aligned} yy_{1}= & {} \frac{ \begin{array}{l} y_{2}^{2}-y_{1}y_{3}+Sy_{2}+\frac{S}{2}\eta y_{3}-2\alpha y_{1}y_{3}+\frac{7 }{4}\beta _{1}S^{2}\eta y_{3}+2\beta _{1}S^{2}y_{2} \\ +\,2\beta _{1}Sy_{1}^{2}+\beta _{1}\eta Sy_{1}y_{3}-3\beta _{1}Sy_{1}y_{3}-2\beta _{1}y_{1}y_{2}y_{3}+\frac{\alpha \beta _{1}}{1+2\alpha \eta }y_{1}^{2}y_{3} \end{array} }{a_{1}}, \end{aligned}$$
(24)
$$\begin{aligned} yy_{2}= & {} \frac{ \begin{array}{l} \Pr \beta _{\mathrm{t}}\left( y_{1}y_{2}y_{5}-\frac{3}{2}Sy_{5}y_{1}-\frac{S}{2}\eta y_{2}y_{5}+\frac{3}{4}S^{2}\eta y_{5}\right) \\ +\,\Pr \left( \frac{S}{2}\eta y_{5}-y_{1}y_{5}\right) -2\alpha y_{5} \end{array} }{a_{2}}, \end{aligned}$$
(25)
$$\begin{aligned} yy_{3}= & {} \frac{ \begin{array}{l} \mathrm{Le}\Pr \beta _{\mathrm{c}}\left( y_{1}y_{2}y_{7}-\frac{3}{2}Sy_{1}y_{7}-\frac{S}{2}\eta y_{2}y_{7}+\frac{3}{4}S^{2}\eta y_{7}\right) \\ +\,\mathrm{Le}\Pr \left( \frac{S}{2}\eta y_{7}-y_{1}y_{7}\right) -2\alpha y_{7}\end{array} }{a_{3}}, \end{aligned}$$
(26)

where

$$\begin{aligned} a_{1}= & {} 1+2\alpha \eta -\frac{\beta _{1}}{4}\eta ^{2}S^{2}+S\beta _{1}\eta y_{1}-\beta _{1}y_{1}^{2},\\ a_{2}= & {} 1+2\alpha \eta -\frac{\Pr }{4}\beta _{\mathrm{t}}S^{2}\eta ^{2}\\&+\,\beta _{\mathrm{t}}S\Pr \eta y_{1}+(1+2\alpha \eta )\epsilon y_{4}-\Pr \beta _{\mathrm{t}}y_{1}^{2}, \\ a_{3}= & {} 1+2\alpha \eta -\frac{\mathrm{Le}\Pr }{4}\beta _{\mathrm{c}}S^{2}\eta ^{2}+\mathrm{Le}\beta _{\mathrm{c}}S\Pr \eta y_{1}-\mathrm{Le}\Pr \beta _{\mathrm{c}}y_{1}^{2}. \end{aligned}$$

Boundary conditions for the above first-order differential system are

$$\begin{aligned}&y_{1}(0)=0,\quad y_{2}(0)=1,\quad y_{4}(0)=1,\quad y_{6}(0)=1, \end{aligned}$$
(27)
$$\begin{aligned}&y_{2}(\infty )=0,\quad y_{4}(\infty )=0,\quad y_{6}(\infty )=0. \end{aligned}$$
(28)

Discussion of results

The flow velocity, temperature distribution and mass transport in Maxwell liquid are the key points of our analysis. Impact of pertinent parameters with following fixed values \(S=\epsilon =0.01,\) \(\beta _{1}=\beta _{\mathrm{t}}=\beta _{\mathrm{c}}=0.5,\) \(\Pr =6.5,\) \(\mathrm{Le}=6.5\) on the velocity, temperature and concentration fields are presented graphically with the comparison of cylinder and sheet. It is observed that there is higher energy transport in case of cylinder than sheet. Figure 2a–c explores the impact of curvature parameter on velocity, temperature and concentration, respectively. For higher values of curvature parameter \(\alpha,\) we noted the increasing trend in velocity, temperature and concentration fields. Physically, higher value of \(\alpha\) reduces the radius of cylinder; thus, the influence of boundary in fluid motion decreases. Hence as result velocity of fluid increases and corresponding heat and mass transport in the fluid enhance. The increasing trend is observed for temperature and concentration fields for growing values of Maxwell parameter \(\beta _{1}\). The adverse behavior is found in case of flow field as shown in Fig. 3a–c. Physically, the Maxwell parameter \(\beta _{1}\) describes the rheology of viscoelastic-type material. The Maxwell parameter \(\beta _{1}\) is the dimensionless relaxation time. The relaxation time is used to depict the phenomena of stress relaxation and stress relaxation (retain in deformation of material after sudden applied stress) observed due to elasticity of material. Therefore, material for higher value of \(\beta _{1}\) behaves like a solid. It means the more time is required for material to retain its deformation, thus, in result the decline in fluid velocity is observed due to higher value of \(\beta _{1}\). On the other hand, energy transport phenomenon boost up for same trend of \(\beta _{1}\) due to increase in heat conduction rate. Plots in Fig. 4a, b described the effect of unsteadiness parameter S on heat and mass transportation mechanisms. Both the temperature and concentration fields boost up for increasing values of S. Figure 5a, b is sketched to depict the impact on heat and mass transfer rate of thermal and mass relaxation time parameters \(\beta _{\mathrm{t}}\) and \(\beta _{\mathrm{c}}\). Increasing values of both thermal relaxation time and solutal relaxation time parameter declines the temperature and concentration fields, respectively. Physically, higher values of relaxation time parameter in Cattaneo–Christov heat flux model control the instant propagation of heat waves in given medium. Therefore, the fluid with enlarging value of relaxation time parameters required more time for the transport of heat and mass. Consequently, the temperature and concentration fields decrease. The relative importance of momentum, thermal and mass diffusivity is described by Prandtl number \(\Pr\) and Lewis number \(\mathrm{Le}\). Figure 6a, b is indicated to show the variation in temperature and concentration profiles via Prandtl and Lewis numbers, respectively. We conclude that both temperature and concentration fields decrease for the enhance values of \(\Pr\) and \(\mathrm{Le}\), respectively. Physically, the higher values of Prandtl number reduce the thermal diffusivity of the fluid and increasing values of \(\mathrm{Le}\) decrease the mass diffusion coefficient. Thus, in result heat and mass transfer decrease in the fluid. The thermal conductivity parameter \(\varepsilon\) boost up the heat transfer rate of the fluid and thus in consequence the temperature filed enhances as shown in Fig. 7. A comparison is given in Table 1 for reduced \(-\,f^{\prime \prime }(0)\) with varying values of \(\beta _{1}\) which assure the validation of our results. Table 2 is provided for the numerical values of thermal and solutal gradients at the surface of cylinder with varying values of pertinent parameters. It is noted that both gradients decrease with higher values of unsteadiness parameter and increase for Prandtl and Lewis numbers, respectively.

Fig. 2
figure 2

a–c The velocity, temperature and concentration profiles via curvature parameter \(\alpha\)

Full size image
Fig. 3
figure 3

a–c The velocity, temperature and concentration profiles via Maxwell parameter \(\beta _{1}\)

Full size image
Fig. 4
figure 4

a, b The temperature and concentration profiles via unsteadiness parameter S

Full size image
Fig. 5
figure 5

a, b The temperature and concentration profiles via \(\beta _{\mathrm{t}}\) and \(\beta _{\mathrm{c}}\), respectively

Full size image
Fig. 6
figure 6

a, b The temperature and concentration profiles via Prandtl number \(\Pr\) and Lewis number \(\mathrm{Le}\), respectively

Full size image
Fig. 7
figure 7

The temperature profile via small thermal conductivity parameter \(\epsilon\)

Full size image
Table 1 Numerical values of \(-\,f^{\prime \prime }(0)\) for different values of \(\beta _{1}\) when \(\alpha =S=0\)
Full size table
Table 2 Numerical values of \(-\,\theta ^{\prime }(0)\) and \(-\,\phi ^{\prime }(0)\) in the limiting case for \(\beta _{\mathrm{t}}=\beta _{\mathrm{c}}=0\) and \(\alpha =1\)
Full size table

Final remarks

The final conclusions have been drawn for the problem of 2D unsteady flow of Maxwell fluid over the stretched cylinder. The Cattaneo–Christov theory is employed for heat and mass transport mechanisms. The thermal conductivity of fluid is assumed to be variable (temperature dependent). The following conclusions are drawn

  • A similar manner is reported for flow, thermal and concentration fields for varying curvature parameter \(\alpha\).

  • Maxwell parameter \(\beta _{1}\) declines the flow field but it boosts up the thermal and concentration distributions.

  • The heat and mass transport decreases with higher values of thermal and mass relaxation parameters \(\beta _{\mathrm{t}}\) and \(\beta _{\mathrm{c}},\) respectively.

  • The thermal diffusivity decreases for higher Prandtl number \(\Pr\) and thus the transport of thermal energy in fluid is lower.