1 Introduction

In nature, heat transfer in a fluid has a significant effect which happens due to difference in temperature within the same body or between two bodies. Many researchers have worth seeing contributions in this regard such as [1,2,3,4,5,6,7,8]. In various practical situations, Fourier’s model provides the basis to analyze the heat transfer phenomenon. But its major drawback was parabolic energy equation which yields that the initial disturbance can affect the whole system. To counter this shortcoming, Cattaneo [9] amalgamates the thermal relaxation time into the classical Fourier’s law in order to get the hyperbolic energy equation. By introducing thermal relaxation time instead of diffusion in Fourier’s law, heat transfer in the form of waves with finite speed is observed. In order to obtain invariant formulation of the material, Christov [10] modified the Cattaneo law by thermal relaxation time along with Oldroyd’s upper-convected derivatives. The study of thermal convection in the Cattaneo–Christov model was carried by Straughan [11]. For the incompressible fluid, Tibullo and Zampoli [12] explained the uniqueness of Cattaneo–Christov heat flux model. Han et al. [13] studied the coupled flow and heat transfer in upper-convected Maxwell fluid over a stretching sheet by employing Cattaneo–Christov heat flux model. Khan et al. [14] investigated the upper-convected Maxwell fluid combined with heat transfer effects over an exponentially stretching surface by taking Cattaneo–Christov heat flux model.

The flow surrounded by a stagnation point has gained a considerable attention among several researchers during the past few decades. It has extensive applications at industrial level, e.g., nuclear reactors cooling all along emergency restrain, solar central receivers unprotected to wind currents, electronic devices cooling by fans and several hydrodynamic processes. Initially Hiemenz [15] proposed the concept of stagnation point flow. According to his theory, stagnation point flow describes the motion of fluid particles which are adjacent to the stagnation region of a solid surface for both fixed and moving bodies. Idea of Hiemenz was further extended by Homann [16] by considering the effect of stagnation point flow in three-dimensional geometry. Recently Turkyilmazoglu [5] investigated the stagnation point flow along with the slip effects on the MHD Jeffrey fluid and heat transfer over deformable surfaces.

Maxwell fluid has received a prominent consideration of researchers in recent era. The main advantage of Maxwell fluid is that it incorporates the relaxation time for the viscoelastic fluid in boundary layer flow. Choi et al. [17] investigated the flow of Maxwell fluid in a channel, in which, by increasing Deborah number, the viscoelasticity affects the velocity profiles in the same pattern as inertia in a Newtonian fluid with a fixed Reynolds number. Boundary layer flow of MHD upper-convected Maxwell fluid over a porous channel was analyzed by Abbas et al. [18], in which they considered the combined effects of viscoelasticity, inertia and applied magnetic field to yield an analytical solution. The impact of MHD and thermal radiation on Maxwell fluid over a stretching sheet was discussed by Aliakbar et al. [19]. According to their observation, an increase in the magnetic parameter and elasticity number causes an enhancement in the heat transfer rate from the stretching sheet to the fluid. Mustafa [20] considered an upper-convected Maxwell fluid for rotating flow and heat transfer in the presence of Cattaneo–Christov heat flux model. Kumaria et al. [21] investigated the MHD mixed convection stagnation point flow of an upper-convected Maxwell fluid. They concluded that with the increase in the elasticity number, reduction in the surface heat transfer, surface velocity gradient and displacement thickness was experienced. Sadeghy et al. [22] examined the stagnation point flow of upper-convected Maxwell fluid, in which they negate the previously well-established prediction about the stagnation point flow of viscoelastic fluids, which states that the velocity inside the boundary layer may exceed from the outside layer. Hayat et al. [23] studied the stagnation point flow of an upper-convected Maxwell fluid for mass transfer. Effect on stagnation point flow of an upper-convected Maxwell fluid for heat transfer over a stretching sheet was analyzed by Hayat et al. [24]. Hayat et al. [25] discussed the stagnation point flow and heat flux in the Cattaneo–Christov model over a nonlinear stretching surface with variable thickness along with homogeneous–heterogeneous reactions in Maxwell fluid having variable thermal conductivity.

The main aspiration of the present study is to sort out the numerical solution of boundary layer stagnation point flow and heat transfer of viscoelastic fluid. Two models namely upper-convected Maxwell fluid model and Cattaneo–Christov heat flux model are considered for the formulation of momentum and energy equation. To obtain the numerical solution of the problem, similarity transformation and shooting method play a key role. However, these types of problems in a limiting case can be solved analytically. Turkyilmazoglu [6] proposed multipleness of the analytical solution by considering the exponential and algebraic type solutions. Turkyilmazoglu [8] presented the some equivalences between the stretching plate problems over different configuration in two–three dimensions. According to his study, he proposed three different geometrical configurations which are mathematically equivalent to two-dimensional system. The influence of physical parameters on temperature and velocity profiles is investigated.

2 Mathematical model

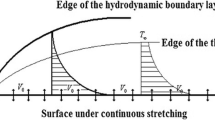
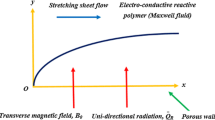
Consider two-dimensional steady, laminar and incompressible stagnation point flow of a viscoelastic fluid over a semi-infinite plate coinciding with the plane y = 0. The plate is supposed to have a constant temperature T w and the ambient fluid temperature T ∞ as shown in Fig. 1. Magnetic field of strength B 0 is applied normally to the direction of flow. Due to the consideration of small magnetic Reynolds number, the electric field is absent and induced magnetic field is neglected. Further first-order velocity slip condition is assumed at the wall. The heat flux model introduced by Cattaneo–Christov is taken into consideration. By using standard boundary layer approximations, the governing equations for the continuity, momentum and temperature flow are [5, 13] and [23]:

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 $$
(1)
$$ u\frac{\partial u}{\partial x} + \frac{\partial u}{\partial y} + \lambda_{1} \left( {u^{2} \frac{{\partial u^{2} }}{{\partial x^{2} }} + v^{2} \frac{{\partial u^{2} }}{{\partial y^{2} }} + 2uv\frac{{\partial u^{2} }}{\partial x\partial y}} \right) = v\frac{{\partial^{2} u}}{{\partial y^{2} }} + u_{\text{e}} \frac{{{\text{d}}u_{\text{e}} }}{{{\text{d}}x}} + \frac{{\sigma B_{0}^{2} }}{\rho }\left( {u_{\text{e}} - u - \lambda_{1} v\frac{\partial u}{\partial y}} \right) $$
(2)
$$ \begin{aligned} & \\ \rho c_{\text{p}} {\mathbf{V}}.\nabla T = - \nabla .{\mathbf{q}}. \\ \end{aligned} $$
(3)

The corresponding velocity slip boundary conditions [26] are:

$$ \left. \begin{aligned} & u = ax + \lambda_{0} \frac{{2 - \sigma_{\text{v}} }}{{\sigma_{\text{v}} }}\frac{\partial u}{\partial y},\,\;v = 0,\,\;T = T_{\text{w}} \;{\text{at}}\;\;y = 0, \\ & u_{e} (x) = cx,\,\;\;\;T \to T_{\infty } \;\;{\text{as }}\;\;y \to \infty . \\ \end{aligned} \right\} $$
(4)

The heat flux \( {\mathbf{q}} \) satisfies the following relation:

$$ {\mathbf{q}} + \lambda_{2} \left[ {\frac{{\partial {\mathbf{q}}}}{\partial t} + {\mathbf{V}}.\nabla {\mathbf{q}} - {\mathbf{q}}.\nabla {\mathbf{V}} + \left( {\nabla .{\mathbf{V}}} \right){\mathbf{q}}} \right] = - k\nabla T, $$
(5)

where \( {\mathbf{V}} = (u,\,v) \) is the velocity vector of the Maxwell fluid. If we choose λ 2 = 0, Eq. (5) corresponds to Fourier’s law. Continuity equation for the incompressible fluid implies \( \nabla .{\mathbf{V}} = 0 \), which when used in Eq. (5) yields the following:

$$ {\mathbf{q}} + \lambda_{2} \left[ {\frac{{\partial {\mathbf{q}}}}{\partial t} + {\mathbf{V}}.\nabla {\mathbf{q}} - {\mathbf{q}}.\nabla {\mathbf{V}}} \right] = - k\nabla T, $$
(6)

Eliminating \( {\mathbf{q}} \) from Eqs. (3) and (6), we get:

$$ u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} + \lambda_{2} \left( {\left( {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right)\frac{\partial T}{\partial x} + \left( {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}} \right)\frac{\partial T}{\partial y} + u^{2} \frac{{\partial^{2} T}}{{\partial x^{2} }} + v^{2} \frac{{\partial^{2} T}}{{\partial y^{2} }} + 2uv\frac{{\partial^{2} T}}{\partial x\partial y}} \right) = \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }} $$
(7)

Introducing the following dimensionless variables:

$$ \eta = \sqrt {\frac{a}{v}} y,\;\,\psi = \sqrt {av} \,xf\left( \eta \right),\;\;\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }} $$
(8)

After simplification we come forth with the following ordinary differential equations:

$$ f^{\prime\prime\prime} + ff^{\prime\prime} - f^{\prime 2} + \beta (2ff^{\prime}f^{\prime\prime} - f^{2} f^{\prime\prime\prime}) + M(e - f^{\prime} + \beta ff^{\prime\prime}) + e^{2} = 0 $$
(9)
$$ \frac{1}{\Pr }\theta^{\prime\prime} + f\theta^{\prime} - \gamma \left( {ff^{\prime}\theta^{\prime} + f^{2} \theta^{\prime\prime}} \right) = 0. $$
(10)

The transformed boundary conditions of (4) are:

$$ \left. \begin{aligned} & f^{\prime}(0) = 1 + bf^{\prime\prime}(0),\;f(0) = 0,\theta (0) = 1, \,\,\,\, f^{\prime}(\infty ) = e,\theta (\infty ) = 0. \\ \end{aligned} \right\} $$
(11)

Different dimensionless parameters appearing in Eqs. (9)–(11) are defined as:

$$ \begin{aligned} & \beta = \lambda_{1} a,\,\;\;\gamma = \lambda_{2} a,\,\;\;e = \frac{c}{a},\,\;\;M = \frac{{\sigma B_{0}^{2} }}{a\rho },\,\,Pr = \frac{\nu }{\alpha } = \frac{{\mu c_{\text{p}} }}{k},\,\;\;b = \lambda_{0} \frac{{2 - \sigma_{\text{v}} }}{{\sigma_{\text{v}} }}\sqrt {\frac{a}{\nu }} . \\ \\ \end{aligned} $$
(12)

The skin friction coefficient C f and local Nusselt number Nu are defined as:

$$ C_{\text{f}} = \frac{{\tau_{\text{w}} }}{{\rho (ax)^{2} }},\,\quad {\text{Nu}} = \frac{{xq_{\text{w}} }}{{\alpha (T_{\text{w}} - T_{\infty } )}}. $$
(13)

Here the wall shear stress τ w and the heat flux q w are defined as:

$$ \tau_{\text{w}} = \mu (1 + \beta )\left( {\frac{\partial u}{\partial y}} \right)_{y = 0} ,\,\quad q_{\text{w}} = - \alpha \left( {\frac{\partial T}{\partial y}} \right)_{y = 0} . $$
(14)

The dimensionless form of skin friction and Nusselt number is:

$$ \text{Re}_{x}^{1/2} C_{\text{f}} = (1 + \beta )f^{\prime\prime}(0),\,\quad \text{Re}_{x}^{ - 1/2} {\text{Nu}}_{x} = - \theta^{\prime}(0). $$
(15)
Fig. 1
figure 1

Geometry of the model

Full size image

3 Numerical solution

The resulting nonlinear system of ordinary differential Eqs. (9) and (10) subject to the conditions (11) has been explored numerically through shooting method [27] for various values of the concerned parameters. On the basis of number of computational experiments, as there is no significant difference in the results after η = 7, we are considering [0, 7] as the domain of the problem instead of [0, ∞). We have chosen the following nomenclature for converting the boundary value problem to the initial value problem consisting of five first-order ordinary differential equations.

$$ f = y_{1,\;} \;f^{\prime} = y_{2} ,\;f^{\prime\prime} = y_{3} ,\;\theta = y_{4} ,\;\theta^{\prime} = y_{5} $$
(16)

The coupled nonlinear momentum and heat equations are transformed into the following system of five first-order differential equations along with initial conditions.

$$ \left. \begin{aligned} & y_{1}^{\prime } = y_{2} , \,\,\,\,y_{1} (0) = 0 \\ & y_{2}^{\prime } = y_{3} , \,\,\,\,y_{2} (0) = 1 + by_{3} (0) \\ & y_{3}^{\prime } = \frac{{[ - y_{1} y_{3} (1 + 2\beta y_{2} ) + y_{2}^{2} - M(e - y_{2} + \beta y_{1} y_{3} ) - e^{2} ]}}{{1 - \beta y_{1}^{2} }}, \,\,\,\,y_{3} (0) = s \\ & y_{4}^{\prime } = y_{5} , \,\,\,\,y_{4} (0) = 1 \\ & y_{5}^{\prime } = \frac{{\Pr y_{1} y_{5} (\gamma y_{2} - 1)}}{{1 - \gamma \Pr y_{1}^{2} }}. \,\,\,\,y_{5} (0) = t \\ \\ \end{aligned} \right\} $$
(17)

We apply the Runge–Kutta method of order four to solve the above initial value problem. To refine the values of s and t, we apply the Newton’s method until we meet the following criteria.

$$ \mathop {\hbox{max} }\limits \{ |y_{2} (7) - e|,|y_{4} (7) - 0|\} < \varepsilon , $$
(18)

where ɛ > 0 is a small positive real number. All the numerical results in this paper are achieved with ɛ = 10−5.

4 Results and discussion

In this article, we utilized the upper-convected Maxwell fluid with Cattaneo–Christov heat flux model to explore the boundary layer flow and heat transfer above a stretching plate with velocity slip boundary condition. Although we have achieved almost the same numerical results for different quantities of interest by two different techniques, for more gratification, we feel a need to validate our MATLAB code by implementation on some published work of the similar nature. For this purpose, we reproduced the numerical values of skin friction for the models investigated by Sadeghy et al. [22] and Abel et al. [28]. An impressively convincing agreement of our results with those of Sadeghy et al. and Abel et al. is given in Table 1. Table 2 presents the values of skin friction and Nusselt number for different emerging parameters. Temperature gradient at the sheet shows increasing behavior for the stretching ratio parameter, Prandtl number and thermal relaxation time, while it depicts inverse behavior for elasticity number, slip coefficient and magnetic parameter. Similarly skin friction seems to have an increasing trend for elasticity number and magnetic parameter and decreasing for slip coefficient and stretching ratio parameter.

Table 1 Comparison of numerical values of –f″(0) with [15] and [21] for M = e = γ = b = 0 and Pr = 1
Full size table
Table 2 Numerical values of −(1 + β)f″(0)and –θ ′(0) for different parameters
Full size table

A relation between upper-convected Maxwell and Newtonian fluid models is set up by an elastic term. Heat transfer and fluid flow are influenced by elastic force. Figures 2 and 3 depict the influence of elasticity number β on velocity and temperature profile. Viscoelastic fluid turns into Newtonian fluid by ignoring the effects of elastic force β. With an increase in the value of β, the elastic forces strengthen up. By enhancement in β, velocity profile shows decreasing and temperature distribution possesses an increasing flow patterns in the viscous fluid. It is because of the fact that an increase in the elasticity number leads to the stronger viscous force which opposes the fluid motion and as a result the velocity displays decreasing pattern. Figures 4 and 5 illustrate the influence of magnetic parameter M on velocity and temperature boundary layer flow. Magnetic field is applied along normal to the fluid flow. It is observed that magnetic field opposes the fluid motion and enhances the temperature distribution. Figures 6 and 7 present the slip effects on velocity and temperature profile. Velocity shows the decreasing behavior for increment in the value of b and converse for the temperature profile. Figures 8 and 9 show the effect of stretching ratio e over velocity and temperature distribution. With the increase in the stretching ratio, we experienced an increase in the velocity profile and decrement in the thermal boundary layer. When e < 1, the stretching sheet velocity axis is greater than the velocity of the far stream cx. Figure 10 presents the effects of thermal relaxation time γ on temperature profile. Temperature profile shows decreasing behavior for enhancement in the thermal relaxation time. Fourier’s Law can be deduced from the present model by applying γ = 0. It is noticed that the temperature in Cattaneo–Christov heat flux model is smaller than the Fourier’s model. Figure 11 shows that with the increase in Prandtl number Pr the temperature boundary layer becomes thinner, because Prandtl number has an inverse relationship with the thermal diffusivity. Figure 12 represents the relationship of Nusselt number in accordance with the Prandtl number Pr and thermal relaxation time γ, with the increase in the Prandtl number Pr thermal relaxation time γ depicts an increasing behavior. All the calculations are performed in hp(i5) machine with 4 GB RAM, and it takes 1.561 s to plot a single graph.

Fig. 2
figure 2

Influence of β on f′(η)

Full size image
Fig. 3
figure 3

Influence of β on θ(η)

Full size image
Fig. 4
figure 4

Impact of M on f′(η)

Full size image
Fig. 5
figure 5

Influence of M on θ(η)

Full size image
Fig. 6
figure 6

Impact of b on f′(η)

Full size image
Fig. 7
figure 7

Influence of b on θ(η)

Full size image
Fig. 8
figure 8

Effect of e on f′(η)

Full size image
Fig. 9
figure 9

Effect of e on θ(η)

Full size image
Fig. 10
figure 10

Effect of γ on θ(η)

Full size image
Fig. 11
figure 11

Effect of Pr on θ(η)

Full size image
Fig. 12
figure 12

Influence of Pr and γ on \( Nu_{x} \text{Re}_{x}^{{ - \frac{1}{2}}} \)

Full size image

5 Concluding remarks

The present model addresses the magnetic effects in stagnation point flow on upper-convected Maxwell fluid along with the Cattaneo–Christov heat flux model. To solve the system of coupled ordinary differential equations, we adopted shooting method. To strengthen the results, we also employed MATLAB built-in function bvp4c. The main observations are summarized as follows:

  • By increasing the magnetic field intensity, velocity profile exhibits decreasing pattern and opposite behavior is seen in thermal boundary layer.

  • Increase in the elasticity number and slip coefficients causes the decrease in velocity phenomenon and opposite behavior is observed in temperature profile.

  • Enhancement in the stretching ratio parameter results in decrease in wall shear stress and an increment in Nusselt number.

  • By increasing the thermal relaxation time, temperature raises up.