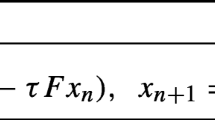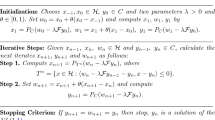1 Introduction

In this paper, we study the Quasi-Variational Inequality (QVI) problem, which generalizes the classical Variational Inequality (VI) problem of Fichera [1, 2] and Stampacchia [3] (see also Kinderlehrer and Stampacchia [4]). In a QVI, the associated feasible set of the problem is not fixed, but varies according to some explicit or implicit rule. For example, in many applications, the feasible set is defined as a “moving set,” i.e., there is a closed and convex set, also known as the core set, that is shifted by another single-valued mapping; see, for example, [5,6,7,8,9] and the references therein. In such a setting, the problem is often called “moving set” QVI.

There exist many techniques for solving QVIs; for example, very recently, Antipin et al. [5] presented gradient projection and extragradient methods for solving QVIs under the assumptions of strong monotonicity and Lipschitz continuity of the associated mappings. The main disadvantage of the extragradient method, with respect to the classical gradient projection algorithm, is that the number of orthogonal projections and mapping evaluations is doubled per each iteration. Moreover, while in the context of VIs, the extra projection and evaluation per iteration of the extragradient method guarantee convergence under weaker assumptions than strong monotonicity of the associated mapping, for QVIs, this is not the case and thus the extragradient does not have any advantage over the gradient projection method.

A more general gradient projection method, with strong convergence, for solving QVIs in real Hilbert spaces, is introduced by Mijajlović et al. in [10]. This method holds great potential since it works well on different practical applications. Other efficient solution methods for solving QVIs can be found in [11,12,13,14].

In the field of continuous optimization, inertial-type algorithms attracted much interest in recent years mainly due to their convergence properties. The idea is derived from the field of second-order dissipative dynamical systems [15, 16]. It is shown that such inertial terms speed up the convergence rate of the existing algorithms; see, e.g., the inertial proximal point algorithm [17,18,19,20,21], the inertial forward–backward splitting method [22,23,24], the inertial Douglas–Rachford splitting method [25, 26], the inertial ADMM [27, 28], and the inertial forward–backward–forward method [29].

Motivated by the above results, we wish to present a new inertial-type algorithm for solving QVIs with the following three major advantages.

  1. 1.

    We consider general QVIs, in contrast to what is done; e.g., in [5] where only the “moving set” case, described above, is analyzed.

  2. 2.

    Our new proposed scheme requires only one operator evaluation and one projection per each iteration, in contrast to other methods such as those provided in [5, 10], just to name a few.

  3. 3.

    The convergence speed of our proposed method is better than other projection methods for solving QVIs; see e.g., [10].

The outline of the paper is as follows. In Sect.  2 we list some basic facts, concepts, and lemmas, which are needed for the rest of the paper. In Sect.  3 the new method with two different inertial and relaxation parameters is presented and analyzed. In Sect. 4, numerical examples illustrate the practical behavior of the proposed schemes and, finally, in Sect.  5 conclusion is given.

2 Preliminaries

Let \(\mathcal {H}\) be a real Hilbert space with inner product \(\langle \cdot ,\cdot \rangle \) and norm \(\Vert \cdot \Vert \). Let \(\mathcal {F}:\mathcal {H}\rightarrow \mathcal {H}\) be a nonlinear operator and \(K:\mathcal {H}\rightrightarrows \mathcal {H}\) be a set-valued mapping which, for any element \(u\in \mathcal {H}\), associates a closed and convex set \(K(u)\subset \mathcal {H}\). With the above data, we are concerned with the following Quasi-Variational Inequality (QVI), which consists of finding a point \(u^{*}\in \mathcal {H}\) such that \(u^{*}\in K(u^{*})\) and

$$\begin{aligned} \left\langle \mathcal {F}(u^{*}),v-u^{*}\right\rangle \ge 0\quad \text { for all }\quad v\in K(u^{*}). \end{aligned}$$
(1)

Clearly, if \(K(u)\equiv K\) for all \(u\in \mathcal {H}\), then the problem reduces to the classical variational inequality; that is, finding a point \(u^{*}\in K\) such that

$$\begin{aligned} \left\langle \mathcal {F}(u^{*}),v-u^{*}\right\rangle \ge 0\quad \text { for all }\quad v\in K. \end{aligned}$$
(2)

Definition 2.1

Let \(T:\mathcal {H}\rightarrow \mathcal {H}\) be a given mapping.

  • The mapping T is called L-Lipschitz continuous (\(L>0\)), if

    $$\begin{aligned} \Vert F(x)-F(y)\Vert \le L \Vert x-y\Vert \quad \text { for all }\quad x,y\in \mathcal {H}. \end{aligned}$$
    (3)

  • The mapping T is called \(\mu \)-strongly monotone (\(\mu >0\)), if

    $$\begin{aligned} \langle T(x)-T(y),x-y\rangle \ge \mu \Vert x-y\Vert ^{2}\quad \text { for all }\quad x,y\in \mathcal {H}. \end{aligned}$$
    (4)

  • The mapping T is called monotone, if

    $$\begin{aligned} \langle F(x)-F(y),x-y\rangle \ge 0 \quad \text { for all }\quad x,y\in \mathcal {H}. \end{aligned}$$
    (5)

Let K be a nonempty, closed, and convex subset of \(\mathcal {H}\). For each point \(x\in \mathcal {H}\), there exists a unique nearest point in K, denoted by \(P_{K}(x)\), such that

$$\begin{aligned} \Vert x-P_{K}(x)\Vert \le \Vert x-y\Vert \quad \text { for all }\quad y\in K. \end{aligned}$$
(6)

The mapping \(P_{K}:\mathcal {H}\rightarrow K\) is called the metric projection of \(\mathcal {H}\) onto K and is characterized; see e.g., [30, Section 3], by the following two properties:

$$\begin{aligned} P_{K}(x)\in K \end{aligned}$$
(7)

and

$$\begin{aligned} \left\langle x-P_{K}\left( x\right) ,P_{K}\left( x\right) -y\right\rangle \ge 0 \quad \text { for all } \quad x\in \mathcal {H}, \quad y\in K, \end{aligned}$$
(8)

and if K is a hyper-plane, then (8) becomes an equality.

The following result, which is proved in [31], gives sufficient conditions for the existence of solutions of QVIs (1).

Lemma 2.1

Let \(\mathcal {F}:\mathcal {H}\rightarrow \mathcal {H}\) be L-Lipschitz continuous and \(\mu \)-strongly monotone on \(\mathcal {H}\), and \(K(\cdot )\) be a set-valued mapping with nonempty, closed, and convex values such that there exists \(\lambda \ge 0\) such that

$$\begin{aligned} \Vert P_{K(x)}(z)-P_{K(y)}(z)\Vert \le \lambda \Vert x-y\Vert ,~~x,y,z \in \mathcal {H}, \quad \lambda +\sqrt{1-\frac{\mu ^2}{L^2}}<1. \end{aligned}$$
(9)

Then the QVI (1) has a unique solution.

The next result is a fixed point formulation characterizing the solutions of the QVI (1).

Lemma 2.2

Let \(K(\cdot )\) be a set-valued mapping with nonempty, closed and convex values in \(\mathcal {H}\). Then \(x^* \in K(x^*)\) is a solution of the QVI (1) if and only if for any \(\gamma >0\) it holds that

$$\begin{aligned} x^* =P_{K(x^*)}(x^*-\gamma \mathcal {F}(x^*)). \end{aligned}$$

A technical result, which is useful for our analysis, is given next; see [32].

Lemma 2.3

Let \(\{a_k\}\) be a sequence of nonnegative real numbers satisfying the following relation:

$$\begin{aligned} a_{k+1}\le (1-\alpha _k)a_k+\alpha _k\sigma _k+\gamma _k,~~k \ge 1, \end{aligned}$$

where

  1. (a)

    \(\{\alpha _k\}\subset [0,1],\)\( \sum _{k=1}^{\infty } \alpha _k=\infty ;\)

  2. (b)

    \(\limsup \sigma _k \le 0\);

  3. (c)

    \(\gamma _k \ge 0 \ (n \ge 1),\)\( \sum _{k=1}^{\infty } \gamma _k <\infty .\)

Then, \(a_k\rightarrow 0\) as \(k\rightarrow \infty \).

3 Inertial Method

In this section, we introduce the inertial-type method and establish its strong convergence theorems.

Algorithm 3.1

Initialization: Select arbitrary starting points \(x^0,x^1 \in \mathcal {H}\).Iterative step: Given the iterates \(x^k\) and \(x^{k-1}\), compute the next iterate \(x^{k+1}\) as follows

$$\begin{aligned} y^{k}= & {} x^{k}+\theta _k(x^{k}-x^{k-1}), \nonumber \\ x^{k+1}= & {} (1-\alpha _k)y^k+\alpha _k P_{K(y^k)}(y^k-\gamma \mathcal {F}(y^k)) \end{aligned}$$
(10)

Set \(k\leftarrow k+1\) and go to the Iterative step.

In Algorithm 3.1, \(\{\theta _k\}\) and \(\{\alpha _k\}\) are sequences that must satisfy different conditions, specified in the results below, to get convergence to solutions of the QVI.

Remark 3.1

  1. 1.

    If \(\theta _k=0\) for all \(k\ge 1\), in Algorithm 3.1, then [10, Algorithm 1] is obtained. Thus, Algorithm 3.1 is actually [10, Algorithm 1] with an inertial extrapolation step \(y^k\).

  2. 2.

    If both \(\theta _k=0\) and \(\alpha _k=1\), for all \(k\ge 1\) in Algorithm 3.1, we obtain the procedure [5, Eq. (5)] (also studied in [7, 33,34,35]).

We start the strong convergence analysis of Algorithm 3.1 with the special choice of parameters:

$$\begin{aligned} 0\le \theta _k \le \bar{\theta _k}, \quad \bar{\theta _k}:=\left\{ \begin{array}{ll} \min \left\{ \frac{k-1}{k+\eta -1}, \frac{\epsilon _k}{\Vert x^{k}-x^{k-1}\Vert }\right\} , &{}\quad \text {if }\, x^{k}\ne x^{k-1}, \\ \frac{k-1}{k+\eta -1}, &{}\quad \text {if }\, x^{k}= x^{k-1}, \end{array}\right. \end{aligned}$$
(11)

for some \(\eta \ge 3\) and \(\epsilon _k \in ]0,\infty [\).

We observe that in this case Algorithm 3.1 generates a sequence such that \(\sum _{k=1}^{\infty }\theta _k\Vert x^{k}-x^{k-1}\Vert <\infty ,\) because for every \(k\ge 1\) we get \(\theta _k\Vert x^{k}-x^{k-1}\Vert \le \epsilon _k\) when \(x^{k}\ne x^{k-1}\) and \(\theta _k\Vert x^{k}-x^{k-1}\Vert =0\) when \(x^{k}= x^{k-1}\).

Theorem 3.1

Consider the QVI (1) with \(\mathcal {F}\) being \(\mu \)-strongly monotone and L-Lipschitz continuous and assume there exists \(\lambda \ge 0\) such that (9) holds. Let \(\{x^k\}\) be any sequence generated by Algorithm 3.1 with the updating rule given by (11). Assume in addition that \(\gamma \ge 0\) satisfies

$$\begin{aligned} \left| \gamma -\frac{\mu }{L^2}\right| <\frac{\sqrt{\mu ^2-L^2\lambda (2-\lambda )}}{L^2}, \end{aligned}$$
(12)

the sequence \(\{\alpha _k\}\subseteq ]0,1]\) is such that \(\sum _{k=1}^{\infty }\alpha _k=\infty \), and the sequence \(\{\epsilon _k\}\) satisfies \(\sum _{k=1}^{\infty }\epsilon _k<\infty \), then \(\{x^k\}\) converges strongly to the unique solution \(x^* \in K(x^*)\) of the QVI (1).

Proof

We know that

$$\begin{aligned} x^*=(1-\alpha _k)x^*+\alpha _k P_{K(x^*)}(x^*-\gamma \mathcal {F}(x^*)). \end{aligned}$$

Now,

$$\begin{aligned} \Vert x^{k+1}-x^* \Vert= & {} \Vert (1-\alpha _k)y^k+\alpha _k P_{K(y^k)}(y^k-\gamma \mathcal {F}(y^k)) \nonumber \\&\quad -\,(1-\alpha _k)x^*+\alpha _k P_{K(x^*)}(x^*-\gamma \mathcal {F}(x^*))\Vert \nonumber \\\le & {} \Vert (1-\alpha _k)(y^k-x^*)\Vert + \alpha _k\Vert P_{K(y^k)}(y^k-\gamma \mathcal {F}(y^k))-P_{K(x^*)}(x^*-\gamma \mathcal {F}(x^*)) \Vert \nonumber \\\le & {} (1-\alpha _k)\Vert y^k-x^*\Vert +\alpha _k \Vert P_{K(y^k)}(y^k-\gamma \mathcal {F}(y^k))-P_{K(x^*)}(y^k-\gamma \mathcal {F}(y^k))\Vert \nonumber \\&\quad +\,\alpha _k \Vert P_{K(x^*)}(y^k-\gamma \mathcal {F}(y^k))-P_{K(x^*)}(x^*-\gamma \mathcal {F}(x^*))\Vert \nonumber \\\le & {} (1-\alpha _k)\Vert y^k-x^*\Vert + \alpha _k \lambda \Vert y^k-x^*\Vert \nonumber \\&\quad +\,\alpha _k \Vert (y^k-\gamma \mathcal {F}(y^k))-(x^*-\gamma \mathcal {F}(x^*))\Vert . \end{aligned}$$
(13)

Using the fact that \(\mathcal {F}\) is \(\mu \)-strongly monotone and L-Lipschitz continuous, we obtain

$$\begin{aligned} \Vert (y^k-\gamma \mathcal {F}(y^k))-(x^*-\gamma \mathcal {F}(x^*))\Vert ^2= & {} \Vert y^k-x^*\Vert ^2-2\gamma \langle \mathcal {F}(y^k)-\mathcal {F}(x^*), y^k-x^* \rangle \nonumber \\&+\,\gamma ^2\Vert \mathcal {F}(y^k)-\mathcal {F}(x^*)\Vert ^2 \nonumber \\\le & {} (1-2\mu \gamma +\gamma ^2L^2)\Vert y^k-x^*\Vert ^2. \end{aligned}$$
(14)

Combining (13) and (14), we get

$$\begin{aligned} \Vert x^{k+1}-x^* \Vert\le & {} (1-\alpha _k)\Vert y^k-x^*\Vert + \alpha _k \lambda \Vert y^k-x^*\Vert \nonumber \\&+\,\alpha _k \sqrt{1-2\mu \gamma +\gamma ^2L^2}\Vert y^k-x^*\Vert \nonumber \\= & {} (1-\alpha _k)\Vert y^k-x^*\Vert + \alpha _k \beta \Vert y^k-x^*\Vert , \end{aligned}$$
(15)

where \(\beta := \sqrt{1-2\mu \gamma +\gamma ^2L^2}+\lambda \). Now,

$$\begin{aligned} \Vert y^{k}-x^* \Vert= & {} \Vert x^k-x^*+\theta _k(x^{k}-x^{k-1})\Vert \nonumber \\\le & {} \Vert x^k-x^*\Vert +\theta _k\Vert x^{k}-x^{k-1}\Vert . \end{aligned}$$
(16)

Plugging (16) into (15), we get

$$\begin{aligned} \Vert x^{k+1}-x^* \Vert\le & {} (1-\alpha _k)\Vert y^k-x^*\Vert + \alpha _k \beta \Vert y^k-x^*\Vert \nonumber \\= & {} (1-\alpha _k(1-\beta ))\Vert y^k-x^*\Vert \nonumber \\\le & {} (1-\alpha _k(1-\beta ))(\Vert x^k-x^*\Vert +\theta _k\Vert x^{k}-x^{k-1}\Vert )\nonumber \\\le & {} (1-\alpha _k(1-\beta ))\Vert x^k-x^*\Vert +\theta _k\Vert x^{k}-x^{k-1}\Vert . \end{aligned}$$
(17)

Observe that by (12), we have \(0<\beta <1\). Since \(\sum _{k=1}^{\infty }\theta _k\Vert x^{k}-x^{k-1} \Vert < \infty \), using Lemma 2.3, we get that \(x^k\rightarrow x^*, k\rightarrow \infty \), and the proof is complete. \(\square \)

Remark 3.2

Inequality (condition) (12) can always be satisfied by setting \(\gamma \) sufficiently close to the ratio \(\frac{\mu }{L^2}\).

Moreover, Theorem 3.1 still holds if in (11) the term \(\frac{k-1}{k+\eta -1}\) is replaced with some constant in [0, 1[. The idea of using it with \(\eta \ge 3\) derives from the recent inertial extrapolated step introduced in [19, 36].

Next we present the complexity bound of Algorithm 3.1 with the updating rule (11).

Theorem 3.2

Consider the QVI (1) with the same assumptions as in Theorem 3.1. Let \(\{x^k\}\) be any sequence generated by Algorithm 3.1 with the updating rule (11) and let \(x^* \in K(x^*)\) be the unique solution of the QVI (1). Let \(\alpha _k = \alpha \) and \(\epsilon _k = \epsilon \) be constant. Then, given \(\rho \in ]0,\alpha (1-\beta )[\), for any

$$\begin{aligned} k \ge \bar{k} := \Big \lfloor \log _{(1-\rho )} \left( \left( \frac{\epsilon }{\Vert x^0 - x^*\Vert } \right) \left( \frac{1-\alpha (1-\beta )}{\alpha (1-\beta ) - \rho } \right) \right) \Big \rfloor , \end{aligned}$$

assuming \(\bar{k} \ge 0\), it holds that

$$\begin{aligned} \Vert x^k - x^*\Vert \le \epsilon \left( \frac{1-\alpha (1-\beta )}{\alpha (1-\beta ) - \rho } + 1 \right) . \end{aligned}$$
(18)

Proof

From the proof of Theorem 3.1, for any \(k\ge 1\), we get

$$\begin{aligned} \Vert x^{k+1}-x^* \Vert\le & {} (1-\alpha (1-\beta ))(\Vert x^k-x^*\Vert +\theta _k\Vert x^{k}-x^{k-1}\Vert )\nonumber \\\le & {} (1-\alpha (1-\beta ))(\Vert x^k-x^*\Vert +\epsilon ), \end{aligned}$$
(19)

because \((1-\alpha (1-\beta )) \ge 0\). Without the loss of generality, assume that for every \(k < \bar{k}\) we get

$$\begin{aligned} \Vert x^k - x^*\Vert \ge \epsilon \frac{1-\alpha (1-\beta )}{\alpha (1-\beta ) - \rho }. \end{aligned}$$
(20)

Concatenating (19) and (20), we obtain, for every \(k < \bar{k}\),

$$\begin{aligned} \Vert x^{k+1}-x^* \Vert\le & {} (1-\alpha (1-\beta )) \left( 1 + \frac{\alpha (1-\beta ) - \rho }{1-\alpha (1-\beta )} \right) \Vert x^k-x^*\Vert \nonumber \\= & {} (1-\rho ) \Vert x^k-x^*\Vert . \end{aligned}$$
(21)

Therefore, by the definition of \(\bar{k}\), it holds that

$$\begin{aligned}&\Vert x^{\bar{k}}-x^* \Vert \le (1-\rho )^{\bar{k}} \Vert x^0-x^*\Vert \le \epsilon \frac{1-\alpha (1-\beta )}{\alpha (1-\beta ) - \rho }. \end{aligned}$$

For any \(k > \bar{k}\), there are two possibilities. If

$$\begin{aligned}&\Vert x^{k-1} - x^*\Vert \le \epsilon \frac{1-\alpha (1-\beta )}{\alpha (1-\beta ) - \rho }, \end{aligned}$$

then, by (19) and recalling that \((1-\alpha (1-\beta )) \le 1\), we obtain that \(x^k\) satisfies (18). Otherwise, if

$$\begin{aligned}&\epsilon \frac{1-\alpha (1-\beta )}{\alpha (1-\beta ) - \rho } \le \Vert x^{k-1} - x^*\Vert \le \epsilon \left( \frac{1-\alpha (1-\beta )}{\alpha (1-\beta ) - \rho } + 1 \right) , \end{aligned}$$

then

$$\begin{aligned}&\Vert x^{k}-x^* \Vert \le (1-\rho ) \Vert x^{k-1}-x^*\Vert \le \Vert x^{k-1}-x^*\Vert , \end{aligned}$$

and the desired result holds. \(\square \)

Remark 3.3

We observe that, in contradiction with the assumptions of Theorem 3.1, in Theorem 3.2 the summability of \(\{\epsilon _k\}\) is not required. However if one wants a good bound in (18) then a small value of \(\epsilon \) must be set; but in this case, small values of \(\theta _k\) are allowed.

Now, we present another convergence theorem for Algorithm 3.1 under different conditions on the inertial terms.

Theorem 3.3

Consider the QVI (1) with \(\mathcal {F}\) being \(\mu \)-strongly monotone and L-Lipschitz continuous and assume there exists \(\lambda \ge 0\) such that (9) holds. Let \(\{x^k\}\) be any sequence generated by Algorithm 3.1 with \(\gamma \ge 0\) satisfying (12), and \(\{\alpha _k\}\) and \(\{\theta _k\}\) satisfying the following conditions for some \(\epsilon \in ]0,1[\):

  1. 1.

    \(0<\frac{1}{2(1-\beta )}\le \alpha _k < \frac{1}{1+\epsilon }\), with \(\beta := \sqrt{1-2\mu \gamma +\gamma ^2L^2}+\lambda \), and \(\sum _{k=1}^{\infty }\alpha _k=\infty \);

  2. 2.

    \(0\le \theta _k\le \theta _{k+1}\le \theta<\frac{\sqrt{1+8\epsilon }-1-2\epsilon }{2(1-\epsilon )}<1\).

Then \(\{x^k\}\) converges strongly to the unique solution \(x^* \in K(x^*)\) of the QVI (1).

Proof

Define \(T(y^k):=P_{K(y^k)}(y^k-\gamma \mathcal {F}(y^k))\). Then for the unique solution \(x^*\) of (1), we obtain

$$\begin{aligned} \Vert T(y^{k})-T(x^*) \Vert= & {} \Vert P_{K(y^k)}(y^k-\gamma \mathcal {F}(y^k))-P_{K(x^*)}(x^*-\gamma \mathcal {F}(x^*))\Vert \nonumber \\\le & {} \Vert P_{K(y^k)}(y^k-\gamma \mathcal {F}(y^k))-P_{K(x^*)}(y^k-\gamma \mathcal {F}(y^k))\Vert \nonumber \\&+\,\Vert P_{K(x^*)}(y^k-\gamma \mathcal {F}(y^k))-P_{K(x^*)}(x^*-\gamma \mathcal {F}(x^*))\Vert \nonumber \\\le & {} \lambda \Vert y^k-x^*\Vert +\Vert y^k-x^*+\gamma (\mathcal {F}(x^*)-\mathcal {F}(y^k))\Vert . \end{aligned}$$
(22)

Since \(\mathcal {F}\) is \(\mu \)-strongly monotone and \(L-\)Lipschitz continuous, we get

$$\begin{aligned} \Vert y^k-x^*-\gamma (\mathcal {F}(x^*)-\mathcal {F}(y^k))\Vert ^2= & {} \Vert y^k-x^*\Vert ^2-2\gamma \langle \mathcal {F}(y^k)-\mathcal {F}(x^*), y^k-x^* \rangle \nonumber \\&+\,\gamma ^2\Vert \mathcal {F}(y^k)-\mathcal {F}(x^*)\Vert ^2 \nonumber \\\le & {} (1-2\mu \gamma +\gamma ^2L^2)\Vert y^k-x^*\Vert ^2. \end{aligned}$$
(23)

Combining (22) and (23), we get

$$\begin{aligned} \Vert T(y^k)-T(x^*) \Vert\le & {} \lambda \Vert y^k-x^*\Vert +\sqrt{1-2\mu \gamma +\gamma ^2L^2}\Vert y^k-x^*\Vert \nonumber \\= & {} \beta \Vert y^k-x^*\Vert \nonumber \\\le & {} \Vert y^k-x^*\Vert . \end{aligned}$$
(24)

From the definition of Algorithm 3.1, we get

$$\begin{aligned} \Vert x^{k+1}-x^* \Vert ^2= & {} (1-\alpha _k)\Vert y^k-x^*\Vert ^2+ \alpha _k \Vert T(y^k)-x^*\Vert ^2\nonumber \\&-\,\alpha _k(1-\alpha _k)\Vert y^k-T(y^k)\Vert ^2\nonumber \\\le & {} \Vert y^k-x^*\Vert ^2- \alpha _k(1-\alpha _k)\Vert y^k-T(y^k)\Vert ^2. \end{aligned}$$
(25)

Now,

$$\begin{aligned} \Vert y^{k}-x^* \Vert ^2= & {} \Vert x^k+\theta _k(x^{k}-x^{k-1})-x^*\Vert ^2\nonumber \\= & {} \Vert (1+\theta _k)(x^k-x^*)-\theta _k(x^{k-1}-x^*)\Vert ^2\nonumber \\= & {} (1+\theta _k)\Vert x^k-x^*\Vert ^2-\theta _k\Vert x^{k-1}-x^*\Vert ^2\nonumber \\&+\,\theta _k(1+\theta _k)\Vert x^{k}-x^{k-1}\Vert ^2. \end{aligned}$$
(26)

Observe that

$$\begin{aligned}&\Vert x^{k+1}-y^{k}\Vert ^2=\alpha _k^2\Vert y^k-T(y^k)\Vert ^2 \end{aligned}$$

and so

$$\begin{aligned}&\Vert y^k-T(y^k)\Vert ^2=\frac{1}{\alpha _k^2}\Vert x^{k+1}-y^{k}\Vert ^2. \end{aligned}$$
(27)

Combining (27) with (25) yields

$$\begin{aligned} \Vert x^{k+1}-x^* \Vert ^2\le & {} \Vert y^k-x^*\Vert ^2-\frac{\alpha _k(1-\alpha _k)}{\alpha _k^2}\Vert x^{k+1}-y^{k}\Vert ^2\nonumber \\= & {} \Vert y^k-x^*\Vert ^2-\frac{(1-\alpha _k)}{\alpha _k}\Vert x^{k+1}-y^{k}\Vert ^2. \end{aligned}$$
(28)

Now,

$$\begin{aligned} \Vert x^{k+1}-y^k \Vert ^2= & {} \Vert x^{k+1}-x^{k}-\theta _k(x^{k}-x^{k-1})\Vert ^2\nonumber \\= & {} \Vert x^{k+1}-x^{k}\Vert ^2+\theta _k^2\Vert x^{k}-x^{k-1}\Vert ^2-2\theta _k \langle x^{k+1}-x^{k},x^{k}-x^{k-1} \rangle \nonumber \\\ge & {} \Vert x^{k+1}-x^{k}\Vert ^2+\theta _k^2\Vert x^{k}-x^{k-1}\Vert ^2-2\theta _k \Vert x^{k+1}-x^{k}\Vert \Vert x^{k}-x^{k-1}\Vert \nonumber \\\ge & {} (1- \theta _k) \Vert x^{k+1}-x^{k}\Vert ^2+(\theta _k^2-\theta _k)\Vert x^{k}-x^{k-1}\Vert ^2. \end{aligned}$$
(29)

Using (26) and (29) with (28), we get

$$\begin{aligned} \Vert x^{k+1}-x^* \Vert ^2\le & {} (1+\theta _k)\Vert x^k-x^*\Vert ^2-\theta _k\Vert x^{k-1}-x^*\Vert ^2\nonumber \\&+\,\theta _k(1+\theta _k)\Vert x^{k}-x^{k-1}\Vert ^2-\frac{(1-\alpha _k)}{\alpha _k}\Big [(1- \theta _k) \Vert x^{k+1}-x^{k}\Vert ^2 \nonumber \\&+\,(\theta _k^2-\theta _k)\Vert x^{k}-x^{k-1}\Vert ^2\Big ]\nonumber \\= & {} (1+\theta _k)\Vert x^k-x^*\Vert ^2-\theta _k\Vert x^{k-1}-x^*\Vert ^2\nonumber \\&-\frac{(1-\alpha _k)}{\alpha _k}(1- \theta _k) \Vert x^{k+1}-x^{k}\Vert ^2\nonumber \\&+\,\Big [\theta _k(1+\theta _k)-\frac{(1-\alpha _k)}{\alpha _k}(\theta _k^2-\theta _k) \Big ]\Vert x^{k}-x^{k-1}\Vert ^2\nonumber \\= & {} (1+\theta _k)\Vert x^k-x^*\Vert ^2-\theta _k\Vert x^{k-1}-x^*\Vert ^2\nonumber \\&-\,\rho _k\Vert x^{k+1}-x^{k}\Vert ^2+\sigma _k\Vert x^{k}-x^{k-1}\Vert ^2, \end{aligned}$$
(30)

where \(\rho _k:=\frac{(1-\alpha _k)}{\alpha _k}(1- \theta _k)\) and \(\sigma _k:=\theta _k(1+\theta _k)-\frac{(1-\alpha _k)}{\alpha _k}(\theta _k^2-\theta _k)\).

Let \(\Gamma _k:=\Vert x^k-x^*\Vert ^2-\theta _k\Vert x^{k-1}-x^*\Vert ^2+\sigma _k\Vert x^{k}-x^{k-1}\Vert ^2\). Then we obtain from (30) that

$$\begin{aligned} \Gamma _{k+1}-\Gamma _k= & {} \Vert x^{k+1}-x^* \Vert ^2-(1+\theta _{k+1})\Vert x^k-x^*\Vert ^2\nonumber \\&+\,\theta _k\Vert x^{k-1}-x^*\Vert ^2+\sigma _{k+1}\Vert x^{k+1}-x^{k}\Vert ^2-\sigma _k\Vert x^{k}-x^{k-1}\Vert ^2\nonumber \\\le & {} \Vert x^{k+1}-x^* \Vert ^2-(1+\theta _k)\Vert x^k-x^*\Vert ^2\nonumber \\&+\,\theta _k\Vert x^{k-1}-x^*\Vert ^2+\sigma _{k+1}\Vert x^{k+1}-x^{k}\Vert ^2-\sigma _k\Vert x^{k}-x^{k-1}\Vert ^2\nonumber \\\le & {} -\,(\rho _k-\sigma _{k+1})\Vert x^{k+1}-x^{k}\Vert ^2. \end{aligned}$$
(31)

Since \(0 \le \theta _k \le \theta _{k+1} <\theta \), we have

$$\begin{aligned} \rho _k-\sigma _{k+1}= & {} \frac{(1-\alpha _k)}{\alpha _k}(1-\theta _k)-\theta _{k+1}(1+\theta _{k+1})\nonumber \\&+\,\frac{(1-\alpha _{k+1})}{\alpha _{k+1}}(\theta _{k+1}^2-\theta _{k+1}) \nonumber \\\ge & {} \frac{(1-\alpha _k)}{\alpha _k}(1-\theta _{k+1})-\theta _{k+1}(1+\theta _{k+1})\nonumber \\&+\,\frac{(1-\alpha _{k+1})}{\alpha _{k+1}}(\theta _{k+1}^2-\theta _{k+1})\nonumber \\\ge & {} \epsilon (1-\theta )-\theta (1+\theta )+\epsilon (\theta ^2-\theta )\nonumber \\= & {} \epsilon -2\epsilon \theta -\theta -\theta ^2+\epsilon \theta ^2\nonumber \\= & {} -\,(1-\epsilon )\theta ^2-(1+2\epsilon )\theta +\epsilon . \end{aligned}$$
(32)

Combining (31) and (32), we get

$$\begin{aligned}&\Gamma _{k+1}-\Gamma _k\le -\delta \Vert x^{k+1}-x^{k}\Vert ^2, \end{aligned}$$
(33)

where \(\delta :=-(1-\epsilon )\theta ^2-(1+2\epsilon )\theta +\epsilon \). Therefore, \(\Gamma _{k+1}\le \Gamma _k\). Hence \(\{\Gamma _k\}\) is nonincreasing. Furthermore,

$$\begin{aligned} \Gamma _k= & {} \Vert x^k-x^*\Vert ^2-\theta _k\Vert x^{k-1}-x^*\Vert ^2+\sigma _n\Vert x^{k}-x^{k-1}\Vert ^2\\\ge & {} \Vert x^k-x^*\Vert ^2-\theta _k\Vert x^{k-1}-x^*\Vert ^2. \end{aligned}$$

Therefore,

$$\begin{aligned} \Vert x^k-x^*\Vert ^2\le & {} \theta _k\Vert x^{k-1}-x^*\Vert ^2+\Gamma _k \nonumber \\\le & {} \theta \Vert x^{k-1}-x^*\Vert ^2+\Gamma _1 \nonumber \\&\vdots&\nonumber \\\le & {} \theta ^k\Vert x^0-x^*\Vert ^2+\Gamma _1(\theta ^{k-1}+\theta ^{k-2}+\ldots +1)\nonumber \\\le & {} \theta ^k\Vert x^0-x^*\Vert ^2+\frac{\Gamma _1}{1-\theta } \end{aligned}$$
(34)

and it can also be seen that

$$\begin{aligned} -\theta \Vert x^{k-1}-x^*\Vert ^2\le & {} \Vert x^k-x^*\Vert ^2-\theta \Vert x^{k-1}-x^*\Vert ^2 \nonumber \\\le & {} \Gamma _k\le \Gamma _1. \end{aligned}$$
(35)

Note that

$$\begin{aligned} \Gamma _{k+1}= & {} \Vert x^{k+1}-x^* \Vert ^2-\theta _{k+1}\Vert x^k-x^*\Vert ^2+\sigma _{k+1}\Vert x^{k+1}-x^{k}\Vert ^2\nonumber \\\ge & {} -\,\theta _{k+1}\Vert x^k-x^*\Vert ^2. \end{aligned}$$
(36)

Using (34) and (36), we get

$$\begin{aligned} -\,\Gamma _{k+1}\le & {} \theta _{k+1}\Vert x^k-x^*\Vert ^2\le \theta \Vert x^k-x^*\Vert ^2 \\\le & {} \theta ^{k+1}\Vert x^0-x^*\Vert ^2+\frac{\theta \Gamma _1}{1-\theta }. \end{aligned}$$

By (33), we have

$$\begin{aligned}&\delta \Vert x^{k+1}-x^{k}\Vert ^2\le \Gamma _k-\Gamma _{k+1}, \end{aligned}$$

and so by (34) and (35), we get

$$\begin{aligned}&\delta \sum _{j=1}^{k} \Vert x^{j+1}-x^{j}\Vert ^2\le \Gamma _1-\Gamma _{k+1}\\\le & {} \Gamma _1+\theta \Vert x^k-x^*\Vert ^2\\\le & {} \Gamma _1+\theta ^{k+1}\Vert x^0-x^*\Vert ^2+\frac{\theta \Gamma _1}{1-\theta }\\= & {} \theta ^{k+1}\Vert x^0-x^*\Vert ^2+\frac{\Gamma _1}{1-\theta }. \end{aligned}$$

This shows that

$$\begin{aligned}&\sum _{k=1}^{\infty } \Vert x^{k+1}-x^{k}\Vert ^2 < \infty \end{aligned}$$

and hence also,

$$\begin{aligned}&\sum _{k=1}^{\infty } \theta _{k}\Vert x^{k+1}-x^{k}\Vert ^2 < \infty . \end{aligned}$$

From the above, we deduce that \(\lim _{k \rightarrow \infty } \Vert x^{k+1}-x^{k}\Vert =0\). Following the same arguments derived (17) from the proof of Theorem 3.1, we obtain

$$\begin{aligned} \Vert x^{k+1}-x^* \Vert ^2\le & {} (1-\alpha _k(1-\beta ))\Vert y^k-x^*\Vert ^2\nonumber \\\le & {} (1-\alpha _k(1-\beta ))(\Vert x^k-x^*\Vert +\theta _k\Vert x^{k}-x^{k-1}\Vert )^2\nonumber \\\le & {} (1-\alpha _k(1-\beta ))(\Vert x^k-x^*\Vert ^2+2\theta _k\Vert x^k-x^*\Vert \Vert x^{k}-x^{k-1}\Vert \nonumber \\&+\,\theta _k\Vert x^{k}-x^{k-1}\Vert ^2). \end{aligned}$$
(37)

Since \(2\alpha _k(1-\beta )\ge 1\), it implies that

$$\begin{aligned} \Vert x^{k+1}-x^* \Vert ^2\le & {} (1-\alpha _k(1-\beta ))\Vert x^k-x^*\Vert ^2 \nonumber \\&+\,2(1-\alpha _k(1-\beta ))\theta _k\Vert x^k-x^*\Vert \Vert x^{k}-x^{k-1}\Vert +\theta _k\Vert x^{k}-\,x^{k-1}\Vert ^2\nonumber \\\le & {} (1-\alpha _k(1-\beta ))\Vert x^k-x^*\Vert ^2 \nonumber \\&+\,2\alpha _k(1-\beta )\theta _k\Vert x^k-x^*\Vert \Vert x^{k}-x^{k-1}\Vert +\theta _k\Vert x^{k}-x^{k-1}\Vert ^2. \end{aligned}$$
(38)

Observe that

$$\begin{aligned}&\limsup _{k\rightarrow \infty }(2\alpha _k(1-\beta )\theta _k\Vert x^k-x^*\Vert \Vert x^{k}-x^{k-1}\Vert )\\&= \lim _{k\rightarrow \infty }(2\alpha _k(1-\beta )\theta _k\Vert x^k-x^*\Vert \Vert x^{k}-x^{k-1}\Vert ) \\&=0, \end{aligned}$$

since \(\{x^k\}\) is bounded and \(\lim _{n \rightarrow \infty } \Vert x^{k+1}-x^{k}\Vert =0\). Applying Lemma 2.3 to (38), we get that \(x^k\rightarrow x^*, k\rightarrow \infty \) and the desired result is obtained. \(\square \)

We discuss some relationships between the sets of assumptions of \(\{\theta _k\}\) given in Theorems 3.1 and 3.3 in the following remark.

Remark 3.4

  1. 1.

    One can see from the choices of \(\{\theta _k\}\) in Theorem 3.1 (see (11)) and Theorem 3.3 that the two choices of \(\{\theta _k\}\) are independent of each other. For example, when \(x^k=x^{k-1}\), one can see from (11) that

    $$\begin{aligned}&\theta _k \le \theta _{k+1} ~~\mathrm{but}~~\theta _{k+1} \nleqslant \frac{\sqrt{1+8\epsilon }-1-2\epsilon }{2(1-\epsilon )} \end{aligned}$$

    for all \(k\ge 1\) and \(\epsilon \in ]0,1[\). This negates the second assumption in Theorem 3.3.

  2. 2.

    Also, from the proof of Theorem 3.3, we can see that \(\sum _{k=1}^{\infty } \theta _{k}\Vert x^{k+1}-x^{k}\Vert ^2 < \infty \), while in Theorem 3.1, we have \(\sum _{k=1}^{\infty } \theta _{k}\Vert x^{k+1}-x^{k}\Vert < \infty \).

4 Numerical Experiments

In this section, we compare the performances of our proposed scheme (Algorithm 3.1) with those of Algorithms 1 and 2 proposed in [10], and the extragradient method studied in [5].

We choose to use the test problem library QVILIB taken from [37]; the feasible map K is assumed to be given by \(K(x):=\{z \in \mathbb {R}^n \, : \, g(z,x) \le 0 \}\). We implemented Algorithm 3.1 in MATLAB/Octave. We implemented the projection over a convex set as the solution of a convex program. We considered the following performance measures for optimality and feasibility:

$$\begin{aligned} \text {opt}(x):= & {} - \min _z \{\mathcal{F}(x)^T (z-x) \, : \, z \in K(x) \}, \;\; \text {feas}(x) := \Vert \max \{0,g(x,x)\}\Vert _\infty . \end{aligned}$$

A point \(x^*\) is considered as a solution of the QVI if opt\((x^*) \le \)1e-3 and feas\((x^*) \le \)1e-3. As a nonlinear programming solver, we used the built-in function sqp with maxiter = 1000. All the experiments were carried out on an Intel Core i7-4702MQ CPU @ 2.20GHz x 8 with Ubuntu 14.04 LTS 64-bit and using GNU Octave version 3.8.1.

In Table 1 the results of Algorithm 3.1 with \(\gamma = 0.5\) and constant sequences \(\{\alpha _k=\alpha \}\) and \(\{\theta _k=\theta \}\) are presented. Different values for \(\alpha \) and \(\theta \) are considered, and we also report in Table 1 the number of iterations the algorithm requires to reach the stopping criterion. A failure is reported whenever the algorithm does not converge within 5000 iterations. We remark that when \(\alpha =1\) and \(\theta =0\) we obtain the classical gradient projection algorithm, and, more in general, when \(\theta = 0\) [10, Algorithm 1] is obtained.

It can be seen in Table 1 that small values of \(\alpha \) increase the robustness of the algorithm. Specifically, we observe only 5 successes when \(\alpha =1\), 20 successes when \(\alpha =0.2\), and 22-24 successes when \(\alpha = 0.05\). On the other hand, these results also show that the inertial step can significantly improve the performances of the projected gradient method. In Table 1, we report the performance measure iter./success that gives the average number of iterations needed to get a run successfully solved. These results clearly show that the algorithm with the inertial parameter \(\theta = 0.75\) outperforms the case with \(\alpha = 0\); i.e., Algorithm 1 in [10].

Table 1 Numerical results of Algorithm 3.1 with \(\gamma = 0.5\): number of iterations needed for satisfying the stopping criterion
Full size table

In Table 2, we compare our algorithm’s performances with \(\theta = 0.75\) and [10, Algorithm 2]. Recall that [10, Algorithm 2] requires an additional projection onto a closed and convex set per each iteration compared to Algorithm 3.1; i.e., one additional convex program needs to be solved at each iteration. Following this reasoning, we report in Table 2 the time in seconds needed for the algorithms to reach the stopping criterion. The number of iterations of [10, Algorithm 2] is however reported in brackets. Hence, clearly, the performance of Algorithm 3.1 is much better than [10, Algorithm 2].

Table 2 Comparison between Algorithm 2 in [10] and Algorithm 3.1 with \(\gamma = 0.5\): time in seconds to satisfy the stopping criterion. (Alg2 [10] in brackets is the number of iterations)
Full size table

We also tested the extragradient method proposed in [5] on the same benchmark problems, but we do not report these results here since this algorithm does not work well with the stepsizes considered for the other methods, and it is really slow with smaller stepsizes.

The experiments made here clearly show how the usage of \(\alpha \) makes Algorithm 3.1 robust, while the inertial parameter \(\theta \) can be used to speed up the method. Relying on these considerations, we tested Algorithm 3.1 with diminishing sequences \(\{\alpha _k\}\) and \(\{\theta _k\}\). Specifically, we set \(\alpha _0 = 0.5\), \(\theta _0 = 1\), and \(\alpha _{k+1} = 0.99 \alpha _k\), \(\theta _{k+1} = 0.99 \theta _k\) for \(k \ge 0\). Performances of this version of the algorithm can be found in Table 3. Comparing these performances with those reported in Tables 1 and 2 indicates that this variant is the fastest one at solving all the test problems.

We also report in Table 3 the performances of Algorithm 3.1 with the updating rule from (11). For this algorithm we set \(\theta _k = \bar{\theta }_k\), \(\eta = 3\), and \(\{\epsilon _k\}\) such that \(\epsilon _0 = 1\) and \(\epsilon _{k+1} = 0.99 \epsilon _k\).

Table 3 Performances of Algorithm 3.1 with diminishing rule and \(\gamma = 0.5\), and with updating rule (11), \(\alpha _k = 0.2\), or 0.05, and \(\gamma = 0.5\): time in seconds to satisfy the stopping criterion and, in brackets, the number of iterations
Full size table

5 Conclusions

In this paper, we propose a generalized gradient-type method with an inertial extrapolation step for solving QVIs in real Hilbert spaces and obtained strong convergence results with different updating rules. Throughout this paper, we do not assume that the set-valued mapping \(K(\cdot )\) is of the form \(K(u)=K+m(u)\) for all \(u\in \mathcal {H}\), as is commonly assumed in most published papers in this subject area. Our numerical experiments show that our suggested method outperforms most of the recently proposed gradient-type methods for solving QVIs in real Hilbert spaces when \(\mathcal {F}\) is strongly monotone and Lipschitz continuous.