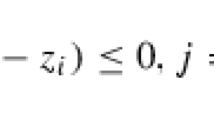Keywords

1 Introduction

It is well known that if the standard primal and dual semidefinite programs satisfy the Slater conditions, then both the primal and dual programs have optimal solutions and there is a zero duality gap between them. However, such Slater-type conditions are not always true for semidefinite primal-dual pairs. There has been interest in a unified duality theory without any Slater-type conditions in conic linear optimization and semidefinite optimization, see [1–8]. The idea behind the construction of a primal-dual pair, which guarantees strong duality (that is zero duality gap and dual attainment), is to use the so-called minimal cone to replace the cone which appears in the original problem so that the generalized Slater condition holds for the consistent primal program. The process of eliminating the possibility of a “duality gap” for consistent programs is called a regularization in the literature. In [2], a regularization for an abstract convex program was studied and a theoretical algorithm for computing the minimal cone was also developed. In [4], an exact duality model called the Extended Lagrange-Slater dual (ELSD) was derived, and the zero duality gap was proved for a consistent program pair (D)–(ELSD) without any Slater-type conditions, where (D) is the standard dual semidefinite program. Unlike the dual in [2], where the minimal cone is used explicitly, (ELSD) can be written explicitly in terms of equality and inequality constraints. In [3, 5], the relation between these two approaches was discussed. The equivalence between the dual formulated using the minimal cone and (ELSD) was obtained under the assumption that (D) is consistent. Though (ELSD) was originally obtained by working directly with semidefinite programming primal-dual pair in [4], it is the expression of the orthogonal complement of a face of the cone of positive semidefinite matrices completely in terms of a system of semidefinite inequalities that gives the possibility to write the strong dual problem in polynomial times, which plays an critical role in formulating an embedding problem that can be used to solve a semidefinite optimization problem without the Slater-type condition [9].

In [10], a recursive algorithm is discussed to obtain the minimal cone for the constraint system of conic linear optimization. As an example of this process, semidefinite optimization problems are studied and (ELSD) are obtained using this recursive algorithm. In the formulation of the strong dual of a semidefinite optimization problem, an expression of the orthogonal complement of a face of a cone, that is the dual cone of a face of the cone of positive semidefinite matrices, in terms of a system of semidefinite inequalities is used in [10]. However, a proof was not given there. In this paper, we give a complete proof of this result together with a conclusion that gives an expression of the orthogonal complement of a face of a cone that is a face of the cone of positive semidefinite matrices.

In the rest of this section, we introduce some basic concepts in convex analysis. For other concepts and notation used in this paper, the reader is referred to [11]. Let \(\mathcal{R}\) denote the set of all real numbers, \(\mathcal{R}_{+}\) the set of all nonnegative numbers, and \(\mathcal{R}^{m\times n}\) the set of all m × n matrices. Let \(\mathcal{V}\) be an inner product vector space with an inner product denoted by \(\langle x,y\rangle\) for \(x,y \in \mathcal{V}\). For any set \(\mathcal{D}\) in \(\mathcal{V}\), we use \(ri\ \mathcal{D}\) to denote the relative interior of \(\mathcal{D}\). Let \(\mathcal{K}\) be a convex cone in \(\mathcal{V}\). \(\mathcal{K}\) can be used to define a partial order in \(\mathcal{V}\): \(x\succeq _{\mathcal{K}}y\) (\(x\succeq y\) if \(\mathcal{K}\) is apparent from the context) if and only if \(x - y \in \mathcal{K}\). A subcone \(\mathcal{K}_{1}\) of \(\mathcal{K}\) is called a face of \(\mathcal{K}\) if \(x \in \mathcal{K}_{1},\ x\succeq y\succeq 0\) implies \(y \in \mathcal{K}_{1}\), where 0 represents the zero vector in \(\mathcal{V}\). For a given face \(\mathcal{K}_{1}\) of \(\mathcal{K}\), the complementary (or conjugate) face of \(\mathcal{K}_{1}\) is defined to be \(\mathcal{K}_{1}^{c} \equiv \{ z \in \mathcal{K}^{{\ast}}\ \vert \ \langle z,x\rangle = 0\mbox{ for all }x \in \mathcal{K}_{1}\} = \mathcal{K}^{{\ast}}\cap \mathcal{K}_{1}^{\perp }\), where \(\mathcal{K}^{{\ast}}\) is the dual cone of \(\mathcal{K}\), that is, \(\mathcal{K}^{{\ast}} =\{ y \in \mathcal{V}\ \vert \ \langle x,y\rangle \geq 0\mbox{ for all }x \in \mathcal{K}\}\), and \(\mathcal{K}^{\perp } = \mathcal{K}^{{\ast}}\cap (-\mathcal{K}^{{\ast}})\). The complementary face of a face in \(\mathcal{K}^{{\ast}}\) is defined similarly. We write \(\mathcal{K}_{1}^{c\perp }\) for \((\mathcal{K}_{1}^{c})^{\perp }\). If \(\mathcal{C}\) is a convex set of \(\mathcal{K}\), then the minimal face of \(\mathcal{C}\), denoted by \(F(\mathcal{C},\mathcal{K})\), is the smallest face of \(\mathcal{K}\) containing \(\mathcal{C}\). Let n be a positive integer. We let \(\mathcal{S}^{n\times n}\) denote the real linear vector space of n × n symmetric matrices. An inner product in this space is defined by \(\langle U,\ W\rangle \equiv U\bullet W = Tr\ (UW)\), where UW denotes ordinary, dimension-compatible matrix multiplication for U and \(W \in \mathcal{S}^{n\times n}\), and Tr (U) represents the trace of U. \(U\succeq W\) means that U − W is positive semidefinite. We use \(\mathcal{S}_{+}^{n\times n}\) to denote the cone of all n × n positive semidefinite matrices.

2 Description of Orthogonal Complement of a Face

In general, a description of the orthogonal complement of a face of a cone in a finite dimensional space cannot be obtained. However, if the cone of positive semidefinite matrices is considered, a description of the orthogonal complement of a face in terms of matrix inequalities is available due to the following theorem proved by Ramana et al. [5, Lemma 2.1]. This theorem makes a strong dual of a semidefinite problem explicit in terms of inequality and equality constraints.

Lemma 1.

[5, Lemma 2.1] Suppose that \(\mathcal{C}\) is a convex cone and \(\mathcal{C}\subseteq \mathcal{S}_{+}^{n\times n}\) . Let \(\mathcal{K}\equiv \{W + W^{T}\ \vert \ W\in \mathcal{R}^{n\times n}\ \mbox{ and}\ U\succeq WW^{T}\mbox{ for some }U \in \mathcal{C}\}\) . Then  \(F(\mathcal{C},\mathcal{S}_{+}^{n\times n})^{c\perp } = \mathcal{K}\) .

We would like to see if this description can be extended to cones, which are either a face of \(\mathcal{S}_{+}^{n\times n}\) or the dual cone of a face of \(\mathcal{S}_{+}^{n\times n}\). We start with the description of a face and the dual cone of a face for the cone of positive semidefinite matrices.

Lemma 2.

Suppose that \(\mathcal{P}\) is a face of \(\mathcal{S}_{+}^{n\times n}\) . Then there is \(r \in \mathcal{N}\) (the set of all natural numbers) and \(Q \in \mathcal{R}^{n\times n}\) with Q T Q = I, such that

$$\displaystyle{\mathcal{P} = \left \{Q\left (\begin{array}{*{10}c} B &0\\ 0 &0 \end{array} \right )Q^{T}\ \left \vert \ B \in \mathcal{S}_{ +}^{r\times r}\right.\right \}.}$$

Proof.

Let \(U \in ri(\mathcal{P})\). Then there is a \(Q \in \mathcal{R}^{n\times n}\) and \(D = \left (\begin{array}{*{10}c} d_{1} & 0 &\cdots & 0 \\ 0 &d_{2} & \cdots & 0\\ \cdots & \cdots &\cdots & \cdots \\ 0 & 0 &\cdots &d_{r} \end{array} \right )\) with d i  > 0 for i = 1, 2, …, r, such that \(U = Q\left (\begin{array}{*{10}c} D & 0^{r\times (n-r)} \\ 0^{(n-r)\times r}&0^{(n-r)\times (n-r)} \end{array} \right )Q^{T},\) where 0m×n represents 0 matrix with m rows and n columns. We sometimes use 0 to represent the 0 matrix if the dimension of the matrix is clear in the context. Of course,

$$\displaystyle{ \mathcal{P}\supseteq \left \{Q\left (\begin{array}{*{10}c} B &0\\ 0 &0 \end{array} \right )Q^{T}\ \left \vert \ B \in \mathcal{S}_{ +}^{r\times r}\right.\right \} }$$
(1)

due to the assumption that \(U \in ri(\mathcal{P})\) and that \(\mathcal{P}\) is a face of \(\mathcal{S}_{+}^{n\times n}\). Next we prove that

$$\displaystyle{ \mathcal{P}\subseteq \left \{Q\left (\begin{array}{*{10}c} B &0\\ 0 &0 \end{array} \right )Q^{T}\ \left \vert \ B \in \mathcal{S}_{ +}^{r\times r}\right.\right \}. }$$
(2)

We choose any \(M \in \mathcal{P}\). Then M = Q(Q T MQ)Q T. We need to prove that Q T MQ has the form \(\left (\begin{array}{*{10}c} B &0\\ 0 &0 \end{array} \right )\) with \(B \in \mathcal{S}_{+}^{r\times r}\). We achieve this by using the assumption that \(U \in ri(\mathcal{P})\). In other words, there exists a \(\lambda < 0\), such that \((1-\lambda )U +\lambda M \in \mathcal{P}\). Therefore,

$$\displaystyle{ (1-\lambda )Q\left (\begin{array}{*{10}c} D&0\\ 0 &0 \end{array} \right )Q^{T}+\lambda Q\left (\begin{array}{*{10}c} M_{11} & M_{12} \\ M_{12}^{T}&M_{22} \end{array} \right )Q^{T} \in \mathcal{P}\subseteq \mathcal{S}_{ +}^{n\times n}, }$$
(3)

where \(Q^{T}MQ = \left (\begin{array}{*{10}c} M_{11} & M_{12} \\ M_{12}^{T}&M_{22} \end{array} \right )\) with \(M_{11} \in \mathcal{S}^{r\times r}\). Because \(M \in \mathcal{P}\), we know that \(M_{22} \in \mathcal{S}_{+}^{(n-r)\times (n-r)}\), and hence, M 22 = 0 by (3), which further implies that M 12 = 0. \(M_{11} \in \mathcal{S}_{+}^{r\times r}\) follows from the assumption that \(M \in \mathcal{P}\). Therefore, (2) holds. By combining (1) and (2), we know the conclusion of the theorem is true.

Lemma 3.

Suppose that \(\mathcal{P}\) is a face of \(\mathcal{S}_{+}^{n\times n}\) . Then there is \(r \in \mathcal{N}\) and \(Q \in \mathcal{S}^{n\times n}\) with QQ T = I, such that

$$\displaystyle\begin{array}{rcl} & & \mathcal{P}^{{\ast}} = \left \{Q\left (\begin{array}{*{10}c} B_{11} & B_{12} \\ B_{12}^{T}&B_{22} \end{array} \right )Q^{T}\ \left \vert \ B_{ 11} \in \mathcal{S}_{+}^{r\times r},B_{ 12} \in \mathcal{R}^{r\times (n-r)},\right.\right. {}\\ & & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \left.\mbox{ and }B_{22} \in \mathcal{S}^{(n-r)\times (n-r)}\right \}. {}\\ \end{array}$$

Proof.

By Lemma 2, we know that there is \(Q \in \mathcal{R}^{n\times n}\) and \(r \in \mathcal{N}\), such that

$$\displaystyle{\mathcal{P} = \left \{Q\left (\begin{array}{*{10}c} B &0\\ 0 &0 \end{array} \right )Q^{T}\ \left \vert \ B \in \mathcal{S}_{ +}^{r\times r}\right.\right \}.}$$

It is easy to see that

$$\displaystyle\begin{array}{rcl} & & \mathcal{P}^{{\ast}}\supseteq \left \{Q\left (\begin{array}{*{10}c} B_{11} & B_{12} \\ B_{12}^{T}&B_{22} \end{array} \right )Q^{T}\ \left \vert \ B_{ 11} \in \mathcal{S}_{+}^{r\times r},B_{ 12} \in \mathcal{R}^{r\times (n-r)},\right.\right. {}\\ & & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \left.\mbox{ and }B_{22} \in \mathcal{S}^{(n-r)\times (n-r)}\right \}. {}\\ \end{array}$$

We now prove the converse inclusion. We choose any \(N \in \mathcal{P}^{{\ast}}\). Let N = Q(Q T NQ)Q T and \(Q^{T}NQ = \left (\begin{array}{*{10}c} N_{11} & N_{12} \\ N_{12}^{T}&N_{22} \end{array} \right )\) with \(N_{11} \in \mathcal{S}^{r\times r},\) \(N_{12} \in \mathcal{R}^{r\times (n-r)},\) and \(N_{22} \in \mathcal{S}^{(n-r)\times (n-r)}\). Then \(N_{11} \in \mathcal{S}_{+}^{r\times r}\). Otherwise, there is \(B \in \mathcal{S}_{+}^{r\times r}\) such that B•N < 0 contradicting the assumption that \(N \in \mathcal{P}^{{\ast}}\). Therefore, N takes the form defined in the lemma.

Of course, \(\mathcal{P}^{{\ast}}\) is a cone which contains \(\mathcal{S}_{+}^{n\times n}\). As a cone, \(\mathcal{P}^{{\ast}}\) has its own faces. The next lemma gives the form of a face of \(\mathcal{P}^{{\ast}}\).

Lemma 4.

Let \(\mathcal{P},Q,r\) be as in Lemma  3. Then a subset \(\mathcal{Q}\) of \(\mathcal{P}^{{\ast}}\) is a face of \(\mathcal{P}^{{\ast}}\) if and only if there is a face \(\mathcal{F}\) of \(\mathcal{S}_{+}^{r\times r}\) such that

$$\displaystyle\begin{array}{rcl} & & \mathcal{Q} = \left \{Q\left (\begin{array}{*{10}c} B_{11} & B_{12} \\ B_{12}^{T}&B_{22} \end{array} \right )Q^{T}\left \vert B_{ 11} \in \mathcal{F},B_{12} \in \mathcal{R}^{r\times (n-r)},\right.\right. \\ & & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \left.\mbox{ and }B_{22} \in \mathcal{S}^{(n-r)\times (n-r)}\right \}. {}\end{array}$$
(4)

Proof.

By Lemma 3 and in a straightforward manner, we can prove that \(\mathcal{Q}\) defined in (4) is a face of \(\mathcal{P}^{{\ast}}\).

Let \(\mathcal{D}\) be a face of \(\mathcal{P}^{{\ast}}\). Assume that \(Q\left (\begin{array}{*{10}c} 2D_{11} & P_{12} \\ P_{12}^{T}&P_{22} \end{array} \right )Q^{T} \in \mathcal{D}\) with \(D_{11} \in \mathcal{S}^{r\times r}\), \(P_{12} \in \mathcal{R}^{r\times (n-r)}\), and \(P_{22} \in \mathcal{S}^{(n-r)\times (n-r)}\). By Lemma 3, we know that \(D_{11} \in \mathcal{S}_{+}^{r\times r}\). Now let \(D_{12} \in \mathcal{R}^{r\times (n-r)}\) and \(D_{22} \in \mathcal{S}^{(n-r)\times (n-r)}\) be any matrices. If we can prove that \(Q\left (\begin{array}{*{10}c} D_{11} & D_{12} \\ D_{12}^{T}&D_{22} \end{array} \right )Q^{T} \in \mathcal{D}\), then we know that

$$\displaystyle{ \left \{Q\left (\begin{array}{*{10}c} D_{11} & B_{12} \\ B_{12}^{T}&B_{22} \end{array} \right )Q^{T}\ \left \vert \ B_{ 12} \in \mathcal{R}^{r\times (n-r)}\mbox{ and }B_{ 22} \in \mathcal{S}^{(n-r)\times (n-r)}\right.\right \} \subseteq \mathcal{D}. }$$
(5)

If we can further prove that

$$\displaystyle\begin{array}{rcl} & & \mathcal{F} = \left \{B_{11}\ \left \vert \ Q\left (\begin{array}{*{10}c} B_{11} & B_{12} \\ B_{12}^{T}&B_{22} \end{array} \right )Q^{T} \in \mathcal{D}\right.\right. \\ & & \qquad \qquad \qquad \qquad \qquad \left.\mbox{ for some }B_{12} \in \mathcal{R}^{r\times (n-r)}\mbox{ and }B_{ 22} \in \mathcal{S}^{(n-r)\times (n-r)}\right \} {}\end{array}$$
(6)

is a face of \(\mathcal{S}_{+}^{r\times r}\), then we know that \(\mathcal{D}\) is of the form of (4).

Now let’s prove (5). By Lemma 3, we know that \(Q\left (\begin{array}{*{10}c} D_{11} & D_{12} \\ D_{12}^{T}&D_{22} \end{array} \right )Q^{T} \in \mathcal{P}^{{\ast}}\) and \(Q\left (\begin{array}{*{10}c} D_{11} & P_{12} - D_{12} \\ P_{12}^{T} - D_{12}^{T}&P_{22} - D_{22} \end{array} \right )Q^{T} \in \mathcal{P}^{{\ast}}\). Since

$$\displaystyle{Q\left (\begin{array}{*{10}c} D_{11} & D_{12} \\ D_{12}^{T}&D_{22} \end{array} \right )Q^{T}+Q\left (\begin{array}{*{10}c} D_{11} & P_{12} - D_{12} \\ P_{12}^{T} - D_{12}^{T}&P_{22} - D_{22} \end{array} \right )Q^{T} = Q\left (\begin{array}{*{10}c} 2D_{11} & P_{12} \\ P_{12}^{T}&P_{22} \end{array} \right )Q^{T} \in \mathcal{D}}$$

and \(\mathcal{D}\) is a face of \(\mathcal{P}^{{\ast}}\), we obtain that \(Q\left (\begin{array}{*{10}c} D_{11} & D_{12} \\ D_{12}^{T}&D_{22} \end{array} \right )Q^{T} \in \mathcal{D}\). Therefore, (5) holds.

Now we prove that \(\mathcal{F}\) is a face of \(\mathcal{S}_{+}^{r\times r}\). Let \(E_{11} \in \mathcal{S}_{+}^{r\times r}\) and \(F_{11} \in \mathcal{S}_{+}^{r\times r}\) such that \(E_{11} + F_{11} \in \mathcal{F}\). Then for any matrices \(G_{12} \in \mathcal{R}^{r\times (n-r)}\) and \(G_{22} \in \mathcal{S}^{(n-r)\times (n-r)}\), we know that \(Q\left (\begin{array}{*{10}c} E_{11} + F_{11} & G_{12} \\ G_{12}^{T} &G_{22} \end{array} \right )Q^{T} \in \mathcal{D}.\) Since

$$\displaystyle{Q\left (\begin{array}{*{10}c} E_{11} & \frac{G_{12}} {2} \\ \frac{G_{12}^{T}} {2} & \frac{G_{22}} {2} \end{array} \right )Q^{T}+Q\left (\begin{array}{*{10}c} F_{11} & \frac{G_{12}} {2} \\ \frac{G_{12}^{T}} {2} & \frac{G_{22}} {2} \end{array} \right )Q^{T} = Q\left (\begin{array}{*{10}c} E_{11} + F_{11} & G_{12} \\ G_{12}^{T} &G_{22} \end{array} \right )Q^{T} \in \mathcal{D},}$$

and \(Q\left (\begin{array}{*{10}c} E_{11} & \frac{G_{12}} {2} \\ \frac{G_{12}^{T}} {2} & \frac{G_{22}} {2} \end{array} \right )Q^{T} \in \mathcal{P}^{{\ast}}\) and \(Q\left (\begin{array}{*{10}c} F_{11} & \frac{G_{12}} {2} \\ \frac{G_{12}^{T}} {2} & \frac{G_{22}} {2} \end{array} \right )Q^{T} \in \mathcal{P}^{{\ast}}\), we obtain that \(Q\left (\begin{array}{*{10}c} E_{11} & \frac{G_{12}} {2} \\ \frac{G_{12}^{T}} {2} & \frac{G_{22}} {2} \end{array} \right )Q^{T} \in \mathcal{D}\) and \(Q\left (\begin{array}{*{10}c} F_{11} & \frac{G_{12}} {2} \\ \frac{G_{12}^{T}} {2} & \frac{G_{22}} {2} \end{array} \right )Q^{T} \in \mathcal{D}\) due to the assumption that \(\mathcal{D}\) is a face of \(\mathcal{P}^{{\ast}}\). Therefore, \(E_{11} \in \mathcal{F}\) and \(F_{11} \in \mathcal{F}\), which implies that \(\mathcal{F}\) is a face of \(\mathcal{S}_{+}^{r\times r}\).

Now, we are ready to give an expression of the orthogonal complement of a face of a cone, which is the dual cone of a face of the cone of positive semidefinite matrices.

Theorem 1.

Let \(\mathcal{P}\) be a face of \(\mathcal{S}_{+}^{n\times n}\) . Then \(\mathcal{P}^{{\ast}}\) is a cone that contains \(\mathcal{S}_{+}^{n\times n}\) . Let \(\mathcal{C}\) be a subcone of \(\mathcal{P}^{{\ast}}\) . \(F(\mathcal{C},\mathcal{P}^{{\ast}})\) represents the minimal face of \(\mathcal{P}^{{\ast}}\) which contains \(\mathcal{C}\) . \(F(\mathcal{C},\mathcal{P}^{{\ast}})^{c} = \mathcal{P}\cap F(\mathcal{C},\mathcal{P}^{{\ast}})^{\perp }\) is the complementary face of \(F(\mathcal{C},\mathcal{P}^{{\ast}})\) . Then \(F(\mathcal{C},\mathcal{P}^{{\ast}})^{c\perp } = \left \{W + W^{T}\ \vert \ W \in \mathcal{R}^{n\times n}\mbox{ and }U\succeq _{\mathcal{P}^{{\ast}}}WW^{T}\mbox{ for some }U \in \mathcal{C}\right \}.\)

Proof.

By Lemma 3, there is a Q and \(r \in \mathcal{N}\) such that

$$\displaystyle\begin{array}{rcl} & & \mathcal{P}^{{\ast}} = \left \{Q\left (\begin{array}{*{10}c} B_{11} & B_{12} \\ B_{12}^{T}&B_{22} \end{array} \right )Q^{T}\ \left \vert \ B_{ 11} \in \mathcal{S}_{+}^{r\times r},B_{ 12} \in \mathcal{R}^{r\times (n-r)},\right.\right. {}\\ & & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \left.\mbox{ and }B_{22} \in \mathcal{S}^{(n-r)\times (n-r)}\right \}. {}\\ \end{array}$$

Let

$$\displaystyle\begin{array}{rcl} & & \mathcal{C}_{11} = \left \{C_{11}\ \left \vert \ Q\left (\begin{array}{*{10}c} C_{11} & C_{12} \\ C_{12}^{T}&C_{22} \end{array} \right )Q^{T} \in \mathcal{C}\right.\right. \\ & & \qquad \qquad \qquad \qquad \qquad \left.\mbox{ for some }C_{12} \in \mathcal{R}^{r\times (n-r)}\mbox{ and }C_{ 22} \in \mathcal{S}^{(n-r)\times (n-r)}\right \}. {}\end{array}$$
(7)

Then \(\mathcal{C}_{11} \subseteq \mathcal{S}_{+}^{r\times r}\). By Lemma 4, we know there is a face \(\mathcal{E}\) of \(\mathcal{S}_{+}^{r\times r}\) such that

$$\displaystyle\begin{array}{rcl} & & F(\mathcal{C},\mathcal{P}^{{\ast}}) = \left \{Q\left (\begin{array}{*{10}c} B_{11} & B_{12} \\ B_{12}^{T}&B_{22} \end{array} \right )Q^{T}\ \left \vert \ B_{ 11} \in \mathcal{E},B_{12} \in \mathcal{R}^{r\times (n-r)},\right.\right. \\ & & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \left.\mbox{ and }B_{22} \in \mathcal{S}^{(n-r)\times (n-r)}\right \}. {}\end{array}$$
(8)

Because \(F(\mathcal{C},\mathcal{P}^{{\ast}})\) is the minimal face of \(\mathcal{P}^{{\ast}}\) containing \(\mathcal{C}\), we further obtain that \(\mathcal{E} = F(\mathcal{C}_{11},\mathcal{S}_{+}^{r\times r})\). Therefore, we obtain \(F(\mathcal{C},\mathcal{P}^{{\ast}})^{c} = \mathcal{P}\cap F(\mathcal{C},\mathcal{P}^{{\ast}})^{\perp } = Q\left (\begin{array}{*{10}c} F(\mathcal{C}_{11},\mathcal{S}_{+}^{r\times r})^{c}&0 \\ 0 &0 \end{array} \right )Q^{T}\). Hence

$$\displaystyle\begin{array}{rcl} & & F(\mathcal{C},\mathcal{P}^{{\ast}})^{c\perp } = \left \{Q\left (\begin{array}{*{10}c} B_{11} & B_{12} \\ B_{12}^{T}&B_{22} \end{array} \right )Q^{T}\ \left \vert \ B_{ 12} \in \mathcal{R}^{r\times (n-r)},\right.\right. \\ & & \qquad \qquad \qquad \qquad \qquad \left.B_{22} \in \mathcal{S}^{(n-r)\times (n-r)},\mbox{ and $B_{ 11} \in F(\mathcal{C}_{11},\mathcal{S}_{+}^{r\times r})^{c\perp }$}\right \}. {}\end{array}$$
(9)

Since by Lemma 1 \(F(\mathcal{C}_{11},\mathcal{S}_{+}^{r\times r})^{c\perp } =\{ W_{1} +W_{1}^{T}\ \vert \ W_{1} \in \mathcal{R}^{r\times r}\mbox{ and }U_{11}\succeq W_{1}W_{1}^{T}\mbox{ for some }U_{11} \in \mathcal{C}_{11}\}\), for any element in \(F(\mathcal{C},\mathcal{P}^{{\ast}})^{c\perp }\), it can be written as \(Q\left (\begin{array}{*{10}c} W_{1} + W_{1}^{T}&B_{12} \\ B_{12}^{T} &B_{22} \end{array} \right )Q^{T}\), where \(B_{12} \in \mathcal{R}^{r\times (n-r)}\) and \(B_{22} \in \mathcal{S}^{(n-r)\times (n-r)}\). Therefore,

$$\displaystyle{Q\left (\begin{array}{*{10}c} W_{1} & 0 \\ B_{12}^{T}& \frac{B_{22}} {2} \end{array} \right )Q^{T}+Q\left (\begin{array}{*{10}c} W_{1} & 0 \\ B_{12}^{T}& \frac{B_{22}} {2} \end{array} \right )^{T}Q^{T} = W+W^{T},}$$

where \(W = Q\left (\begin{array}{*{10}c} W_{1} & 0 \\ B_{12}^{T}& \frac{B_{22}} {2} \end{array} \right )Q^{T}\).

Since \(U_{11} \in \mathcal{C}_{11}\), so there is U 12 and U 22 such that \(U = Q\left (\begin{array}{*{10}c} U_{11} & U_{12} \\ U_{12}^{T}&U_{22} \end{array} \right )Q^{T} \in \mathcal{C}\). Because \(WW^{T} = Q\left (\begin{array}{*{10}c} W_{1}W_{1}^{T} & W_{1}B_{12} \\ B_{12}^{T}W_{1}^{T}&B_{12}^{T}B_{12} + \frac{B_{22}^{2}} {4} \end{array} \right )Q^{T}\) and \(U_{11}\succeq W_{1}W_{1}^{T}\), we obtain that \(U = Q\left (\begin{array}{*{10}c} U_{11} & U_{12} \\ U_{12}^{T}&U_{22} \end{array} \right )Q^{T}\succeq _{\mathcal{P}^{{\ast}}}WW^{T}\).

Remark 1.

Theorem 1 was used in [10]. But a proof was not given in [10]. Here we provide a complete proof of this result.

Now we briefly discuss an expression of the orthogonal complement of a face of a cone that is a face of the cone of positive semidefinite matrices. As in the discussion above, we let \(\mathcal{P}\) be a face of \(\mathcal{S}_{+}^{n\times n}\). \(\mathcal{P}\) itself is a cone. Let \(\mathcal{C}\) be a subcone of \(\mathcal{P}\). Then \(F(\mathcal{C},\mathcal{P})\) represents the minimal face of \(\mathcal{P}\) containing \(\mathcal{C}\) and \(F(\mathcal{C},\mathcal{S}_{+}^{n\times n})\) represents the minimal face of \(\mathcal{S}_{+}^{n\times n}\) containing \(\mathcal{C}\). Since \(\mathcal{P}\) is a face of \(\mathcal{S}_{+}^{n\times n}\), we can easily prove that \(F(\mathcal{C},\mathcal{P}) = F(\mathcal{C},\mathcal{S}_{+}^{n\times n})\). Therefore, \(F(\mathcal{C},\mathcal{P})^{c} = \mathcal{P}^{{\ast}}\cap F(\mathcal{C},\mathcal{P})^{\perp }\supseteq \mathcal{S}_{+}^{n\times n} \cap F(\mathcal{C},\mathcal{S}_{+}^{n\times n})^{\perp } = F(\mathcal{C},\mathcal{S}_{+}^{n\times n})^{c}\), which further implies that \(F(\mathcal{C},\mathcal{P})^{c\perp }\subseteq F(\mathcal{C},\mathcal{S}_{+}^{n\times n})^{c\perp }\). By Lemma 1, we obtain that \(F(\mathcal{C},\mathcal{S}_{+}^{n\times n})^{c\perp } = \mathcal{K}\equiv \{ W + W^{T}\ \vert \ W \in \mathcal{R}^{n\times n}\mbox{ and }U\succeq WW^{T}\mbox{ for some }U \in \mathcal{C}\}\). Therefore, \(F(\mathcal{C},\mathcal{P})^{c\perp }\subseteq \{ W + W^{T}\ \vert \ W \in \mathcal{R}^{n\times n}\mbox{ and }U\succeq WW^{T}\mbox{ for some }U \in \mathcal{C}\}\). The converse inclusion may not be true. However, in a similar way we can prove the following theorem which gives an expression of the orthogonal complement of a face of \(\mathcal{P}\).

Theorem 2.

\(F(\mathcal{C},\mathcal{P})^{c\perp }=\{W + W^{T}\ \vert \ W\in \mathcal{R}^{n\times n}\mbox{ and }U\succeq _{\mathcal{P}}WW^{T}\mbox{ for some }U\in \mathcal{C}\}.\)

Proof.

The proof is similar to that of Theorem 1.

3 Conclusion Remarks

An expression in terms of a system of semidefinite inequalities for the orthogonal complement of a face of the cone of positive semidefinite matrices plays an important role in formulating a dual of a polynomial size with a strong duality property for a semidefinite optimization problem. In this paper, we have extended this expression to the orthogonal complement of a face of cones, which are either a face of the cone of positive semidefinite matrices or the dual cone of a face of the cone of positive semidefinite matrices.