1 Introduction

There is considerable difficulty in the interpretation of properties of halides of group IIB transition-metals MeX2 (Me = Zn, Cd and Hg) and usually they are treated separately from other 2:1 type electrolytes in textbooks of electrochemistry [1–4]. Since in aqueous solutions of these salts, the series of mononuclear complexes, \( {\text{MeX}}_{n}^{2 - n} \), n = 1, 2, 3 and 4 are formed, these solutions are often named as solutions with “complex ions”. Davies [5] defined complex ions as “ions that can dissociate into a neutral part together with one or more simple ions”. This means that the ion-pair formation is followed by further association into neutral molecules and negatively highly charged ions [6–15]. In very dilute solutions, it was also found that the possibility of hydrolysis reactions with cation ions can not be excluded, but determined equilibrium constants are rather small (values of pK for principal reactions lie in −10 to −9 range) [16–20].

Solutions with complex ions found a special attention in the literature owing to anomalous changes observed in colligative and dynamic properties (e.g. vapor pressure lowering, transference numbers, diffusion coefficients) when the concentration of dissolved electrolyte is changed. It was observed that the presence of complex and intermediate ions made considerable difficulties in the interpretation of transference number experiments. In the middle of the twentieth century, many experimental techniques (potentiometric titration, polarographic, calorimetric, solubility, partition between two liquid phases, ion-exchange and others [21–29]) were applied to study the distribution of metal-containing species and their corresponding formation constants. Usually, concentrated or moderately concentrated aqueous solutions were studied, frequently with a rather large amount of added supporting electrolyte.

Based on available experimental data, it was generally concluded that in very dilute solutions the Me2+ ion exists almost exclusively, i.e. the electrolyte is completely dissociated, but with increasing concentration, the amount of the ion MeX+ rises to a maximum and then decreases again. Simultaneously, the undissociated molecules MeX2 and negatively charged complex ions \( {\text{MeX}}_{3}^{ - } \) and MeX2− become present.

Considering conductivity measurements, from the vast bulk of precise conductance determinations only a small fraction has been devoted to associated unsymmetrical electrolytes and fewer to solutions with complex ions. At that time, there were two main reasons for such a situation, the absence of suitable conductance equations and considerable mathematical difficulties arising from convergence problems in optimization procedures [4, 30]. Only after 1978 could conductances of unsymmetrical electrolytes of any type be treated rigorously by replacing the Debye–Hückel–Onsager [31], Davies [32], and Fuoss and Edelson [33] approaches with the Lee–Wheaton (L–W) and the Quint–Viallard (Q–V) conductance equations [34–39].

From unsymmetrical electrolytes of the type 2:1, the attention was mainly directed to alkaline earth halides and not to solutions with complex ions. The mathematical side of the problem, in the context of the Lee–Wheaton conductance equation, was discussed by Pethybridge [30]. He found that satisfactory agreement between experimental and calculated conductances needs introduction of a large number of pre-selected and adjustable parameters. These parameters are the closest distances of approach of ions a i , the limiting ionic conductances λ°(MeX+) and λ°(Me2+) and the equilibrium constants K. In the optimization procedures, the limiting conductance of the intermediate ion λ°(MeX+) plays the decisive role but, unfortunately, it can not be determined directly in an independent conductivity experiment. The ratio r = λ°(MeX+)/λ°(Me2+) has been first suggested to be r = 0.6 by Chandler [40], Pethybridge proposed r = 0.8 but other values from 0.5 to 0.9 can also be found in the literature.

Historically, the first determinations of conductivity of cadmium salts (CdCl2, CdBr2, CdI2 and CdSO4) were performed in 1883 by Wershoven and they are presented in 1898 in the classical book of Kohlrausch and Holborn [41]. Measurements were executed at 18 °C in the 0.002–0.7 mol·dm−3 concentration range. Systematic determinations of conductivity of cadmium halides solutions have been reported in 1912, by Jones [42] in the 0.00024–0.25 mol·dm−3 concentration range and from 0 to 65 °C, and by Noyes and Falk [43] at 18 °C, in the 0.001–0.005 mol·dm−3 concentration range. The Jones conductivities were actually performed by West and Winston. In the case of cadmium chloride, there are also conductivities of Fedotov from 1978 [44], determined in the 0.0005–0.0025 mol·dm−3 concentration range, from 25 to 80 °C. However, as has be recently demonstrated by Apelblat et al. [45], these conductivities are incorrect. There are a number of investigations dealing with transference numbers of cadmium halides, but unfortunately they are not accompanied by simultaneous determination of corresponding conductivities [21, 46–48].

There are two factors which limit the ability to analyze conductivities over an entire range of concentrations. The lower limit in conductance measurements depends on the quality of water which is used in experiments, and usually it is close to 1 × 10−4 mol·dm−3. The upper limit (about 0.01 mol·dm−3 for 1:1 electrolytes and strongly decreases for more highly charged ions) is associated with restrictions posed on the Quint–Viallard theory. Thus, these limitations mean that the molecular model presented here covers aqueous solutions where only Me2+ and MeX+ ions exist. The mathematical representation of extensions to much lower and much higher concentration ranges is given in the Appendix.

Using the conductances of cadmium bromide and cadmium iodide reported here, the molar limiting conductances of λ°(CdX+; T) ions were evaluated in the 15–35 °C temperature range. For the applied molecular model, the equilibrium constants K(T) and the standard thermodynamic functions of the CdX+ formation were also determined.

2 Experimental

Cadmium bromide tetrahydrate and cadmium iodide (purum. p.a., all better than 0.98 mass fraction) were purchased from Sigma–Aldrich and used without further purification. Solutions were prepared by weight by dissolving these reagents in doubly distilled water. Conversion from molal to molar units was performed by using densities of pure water [2]. Detailed description of procedure and equipment has been presented elsewhere [49]. Considering the sources of error (calibration, measurements, impurities), the specific conductivities are estimated to be accurate within 0.6 %.

3 Data Analysis

3.1 Chemical Equilibria and Conductivity Equations

As pointed out above, in dilute aqueous solutions of cadmium halides only the Me2+ and MeX+ ions predominantly exist. In such case, the chemical equilibria are represented by:

$$ \begin{aligned} {\text{MeX}}_{ 2} \to {\text{Me}}^{{ 2 { + }}} + 2 {\text{X}}^{ - } \hfill \\ {\text{Me}}^{{ 2 { + }}} + {\text{X}}^{ - } \mathop \rightleftharpoons \limits^{K} {\text{MeX}}^{ + } \hfill \\ \end{aligned} $$
(1)

and in the term of the mass-action law:

$$ \begin{aligned} K = \frac{{\left[ {{\text{MeX}}^{ + } } \right]}}{{\left[ {{\text{Me}}^{{ 2 { + }}} } \right]\left[ {{\text{X}}^{ - } } \right]}}F(c) \hfill \\ F(c) = \frac{{f_{{{\text{MeX}}^{ + } }} }}{{f_{{{\text{Me}}^{{ 2 { + }}} }} f_{{{\text{X}}^{ - } }} }}. \hfill \\ \end{aligned} $$
(2)

If α denotes the concentration fraction of Me2+ ions in the solution, the concentration fractions of MeX+ and X− ions can be obtained from the charge and material balance as:

$$ \begin{aligned} \left[ {{\text{Me}}^{{ 2 { + }}} } \right] &= c\alpha \hfill \\ \left[ {{\text{MeX}}^{ + } } \right]& = c\beta = c(1 - \alpha ) \hfill \\ \left[ {{\text{X}}^{ - } } \right] &= c(2\alpha + \beta ) = c(1 + \alpha ) \hfill \\ I& = c(3\alpha + \beta ) = c(1 + 2\alpha ). \hfill \\ \end{aligned} $$
(3)

Introducing Eq. 3 into Eq. 2, the concentration fraction α for a given c, comes from

$$ \begin{aligned} K = \frac{1 - \alpha }{{c{\kern 1pt} {\kern 1pt} \alpha (1 + \alpha )}}F(c) \hfill \\ F(c) = \frac{{f_{{{\text{MeX}}^{ + } }} }}{{f_{{{\text{Me}}^{{ 2 { + }}} }} f_{{{\text{X}}^{ - } }} }} \hfill \\ \end{aligned} $$
(4)

and

$$ \begin{aligned} \alpha & = \frac{{ - {\kern 1pt} {\kern 1pt} [1 + Q(c)] + \sqrt {{\kern 1pt} {\kern 1pt} [1 + Q(c)]^{2} + 4Q(c)} }}{2Q(c)} \hfill \\ Q(c)& = \frac{{K{\kern 1pt} {\kern 1pt} c}}{F(c)}. \hfill \\ \end{aligned} $$
(5)

This quadratic equation should be solved by an iterative procedure by considering that the quotient of activity coefficients F(c) depends on the value of α the concentration fraction of Me2+ ions. In dilute solutions, the activity coefficients of individual ions can be calculated by the Debye–Hückel expressions:

$$ \begin{aligned} \log_{10} [f_{j} (c,T)] &= - \frac{{z_{j}^{2} A(T)\sqrt I }}{{1 + a_{j} B(T)\sqrt I }} \hfill \\ I &= c(1 + 2\alpha ) \hfill \\ \end{aligned} $$
(6)

where the constants A(T) and B(T) depend on dielectric constant of pure water, D(T):

$$ \begin{aligned} A(T) = \frac{{1.8246 \times 10^{6} }}{{[D(T)T]^{3/2} }} \hfill \\ B(T) = \frac{{50.29 \times 10^{8} }}{{[D(T)T]^{1/2} }}. \hfill \\ \end{aligned} $$
(7)

The pre-selected sizes of ions, the distance parameters a j , were taken as recommended by Kielland [50] and they are: a(Cd2+) = 4.5 Å, a(CdX+) = 4.0 Å and a(X−) = 3.0 Å (X = Br and I). These parameters are assumed to be independent of temperature T.

Molar conductance of electrolyte \( \varLambda \)(c, T) is the sum of ionic contributions λ j (c, T):

$$ \varLambda (c,T) = \frac{1000\kappa }{c} = \sum\limits_{j} {\frac{{\left| {z_{j} } \right|c_{j} \lambda_{j} (c,T)}}{c}} $$
(8)

where κ is the measured specific conductance in solution of formal analytical concentration c, z j are the corresponding charges of cations and anions and c j are their molar concentrations. The ionic conductances λ j (c, T) are represented by:

$$ \begin{aligned} \lambda_{j} (c,T) &= \lambda_{j}^{0} (T) - S_{j} (T)\sqrt I + E_{j} (T)I\ln I + J_{1j} (T)I - J_{2j} (T)I^{3/2} \hfill \\ I &= \frac{1}{2}\sum\limits_{j} {z_{j}^{2} c_{j} } \hfill \\ \end{aligned} $$
(9)

where the coefficients S j , E j , J 1j and J 2j are complex functions of the limiting equivalent ionic conductances λ°(T), the distance parameters a j and the dielectric constant D(T) and viscosity η(T) of pure water. These coefficients are available from the Quint–Viallard theory [39] (for explicit expressions of these coefficients see also [51]).

In terms of concentration fractions α, the molar conductances Λ(c, T) are:

$$ \varLambda (c,T) = 2\alpha {\kern 1pt} \lambda_{{{\text{Cd}}^{{ 2 { + }}} }} (c,T) + (1 - \alpha ){\kern 1pt} {\kern 1pt} \lambda_{{{\text{CdX}}^{ + } }} (c,T) + (1 + \alpha ){\kern 1pt} {\kern 1pt} \lambda_{{{\text{X}}^{ - } }} (c,T). $$
(10)

The ionic conductances should be arranged in the pairs of ions in order to use the Quint–Viallard conductance equation and therefore:

$$ \begin{aligned} \varLambda (c,T) = 2\alpha {\kern 1pt} \varLambda_{1} (c,T) + (1 - \alpha ){\kern 1pt} {\kern 1pt} \varLambda_{2} (c,T) \hfill \\ \varLambda_{1} (c,T) = \left[ {\lambda_{{{\text{Cd}}^{{ 2 { + }}} }} (c,T) + \lambda_{{{\text{X}}^{ - } }} (c,T)} \right] \hfill \\ \varLambda_{2} (c,T) = \left[ {{\kern 1pt} \lambda_{{{\text{CdX}}^{ + } }} (c,T) + {\kern 1pt} {\kern 1pt} \lambda_{{{\text{X}}^{ - } }} (c,T)} \right]. \hfill \\ \end{aligned} $$
(11)

At each concentration c and temperature T, if the concentration fraction α is known, the experimental sets of conductances can formally be written in the following functional form \( \left( {\varLambda ,c} \right) \, = f\left[ {K,\lambda^\circ \left( {1/2{\text{Cd}}^{2 + } } \right),\lambda^\circ \left( {Cd{\text{X}}^{ + } } \right),\lambda^\circ \left( {{\text{X}}^{ - } } \right),a_{j} ,D,\eta , \, c} \right] \). Dielectric constants and viscosities of pure water are known [2], the distance parameters are prefixed and the molar limiting conductances of Cd2+, Br− and I− ions can be taken from the literature [2] (Table 1). In the optimization procedure, which included the iterative simultaneous solution of Eqs. 5, 6 and 10, two adjustable parameters K(T) and \( \lambda \)°(CdCl+, T) were determined to ensure the best fitting between experimental Λ exp and calculated Λ calc conductances.

Table 1 Densities, d, viscosities, η, dielectric constants, D, of pure water and limiting ionic conductances of ions, λ 0, at temperatures from T = (288.15–308.15) K
Full size table

4 Results and Discussion

4.1 Conductances of Cadmium Bromide and Cadmium Iodide in Aqueous Solutions

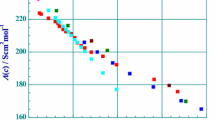
Experimental conductances of cadmium bromide and cadmium iodide solutions are presented in Table 2. They can only be compared with the old determinations performed by the Jones group [42] (old conductances should be multiplied by the factor 1.066 [52]). As can be observed in Figs. 1 and 2, the conductances at 25 °C are consistent. If calculated from Eq. 11 conductances are compared with experimental conductances, it is evident that the chosen molecular model (the mixture of two 1:1 and 2:1 type electrolytes, CdX+ + X− and Cd2+ + 2X−) is valid only for concentrations lower than about 0.003 mol·dm−3 for CdBr2 and about 0.001 mol·dm−3 for CdI2. As expected at higher concentrations, due to increasing formation of CdX2, the over-all number of ions decreases and therefore the calculated conductances are higher than experimental conductances (Figs. 1, 2). With increasing values of the equilibrium constants K(T), the number of Cd2+ ions in solution decreases and therefore the concentration range of the applied molecular model (CdX+ + X− and Cd2+ + 2X−) is shorter. Since K(CdCl2) < K(CdBr2) < K(CdI2), by considering that the limiting conductances of anions λ°(X−) are nearly the same for all halides (Table 1), it is expected also that Λ(c; CdCl2) > Λ(c; CdBr2) > Λ(c; CdI2), which is actually observed. Detailed results of calculations at 25 °C are presented Table 3 and they include Λ exp and Λ calc values, the concentration fractions of α and β = 1 − α of Cd2+ and CdX+ ions and their contributions Λ 1(c) and Λ 2(c) to the calculated conductances Λ calc(c). As can be predicted, Λ 1(c) is the predominant term and Λ 2(c) initially is very small but increases rapidly with increasing concentration c. Coefficients of the Quint–Viallard conductance equations for the (1/2Cd2+ + X−) and (CdX+ + X−) pair ions and the standard thermodynamic functions of CdCl+ formation are reported in Table 4.

Table 2 Experimental molar conductances of aqueous solutions of cadmium bromide and cadmium iodide as a function of concentration c and temperature T
Full size table
Fig. 1
figure 1

Experimental and calculated molar conductances of cadmium bromide solutions at 298.15 K. Green square Jones [42], blue square this work experimental, red square this work calculated, pink square fully dissociated 2:1 electrolyte (Color figure online)

Full size image
Fig. 2
figure 2

Experimental and calculated molar conductances of cadmium bromide solutions at 298.15 K. Green square Jones [42], blue square this work experimental, red square this work calculated, pink square fully dissociated 2:1 electrolyte (Color figure online)

Full size image
Table 3 Experimental Λ exp and calculated Λ calc molar conductances of aqueous solutions of cadmium bromide and cadmium iodide at 298.15 K, concentration fractions α and β and the corresponding contributions Λ 1 and Λ 2 to the calculated conductance as a function of concentration c
Full size table
Table 4 Coefficients of the Quint–Viallard conductance equations for (1/2Cd2+ + X−) and (CdX+ + X−) pair ions and the standard thermodynamic functions of CdX+ formation
Full size table

As has been observed, conductances of cadmium halides depend strongly on the value of dielectric constant D of solutions. This can be illustrated if water is mixed for example with ethanol. In Fig. 3 are compared conductances of cadmium bromide in pure water with those in two ethanol + water mixtures (in the 25 % w/w ethanol + water solution, the dielectric constant is 64.39, in the 10 % w/w ethanol + water solution is 73.14 and in pure water 78.41).

Fig. 3
figure 3

Experimental molar conductances of cadmium iodide at 298.15 K in pure water (a), in aqueous 10 % w/w ethanol solution (b) and in aqueous 25 % w/w ethanol solution (c) (Color figure online)

Full size image

Temperature dependence of the limiting conductances can be expressed in terms of the Walden products or using the Eyring theory [53]:

$$ \ln [\lambda_{j}^{0} (T){\kern 1pt} {\kern 1pt} d_{ 0}^{ 2 / 3} (T)] = - \frac{{\Delta H_{\lambda }^{\dag } (T)}}{RT} + {\text{const}} . $$
(12)

where d 0(T) is density of pure water and \( \Delta H_{\lambda }^{\dag } (T) \) is the partial molar enthalpy associated with the movement of ions and its value is assumed to be independent of temperature. In the case of investigated cadmium bromide and cadmium iodide we have:

$$ \begin{aligned} \ln [\lambda^{0} ({\text{CdBr}}^{ + } ,T){\kern 1pt} {\kern 1pt} d_{ 0}^{ 2 / 3} (T)] = - \frac{2020.1}{T} + 10.4823;\quad {\text{R}}^{2} = 0.9995 \hfill \\ \ln [\lambda^{0} ({\text{CdI}}^{ + } ,T){\kern 1pt} {\kern 1pt} d_{ 0}^{ 2 / 3} (T)] = - \frac{2019.3}{T} + 10.3178;\quad {\text{R}}^{2} = 0.9995 \hfill \\ \ln [\lambda^{0} (1/2{\text{Cd}}^{{ 2 { + }}} ,T){\kern 1pt} {\kern 1pt} d_{ 0}^{ 2 / 3} (T)] = - \frac{2047.5}{T} + 10.8267 ;\quad {\text{R}}^{2} = 0.9977 \hfill \\ \end{aligned} $$
(13)

which gives practically the same value of the enthalpy, \( \Delta H_{\lambda }^{\dag } \) = 16 kJ·mol−1 for both cadmium halides.

The formation constants of CdX+ complexes K(T) are nearly linearly dependent on temperature:

$$ \begin{aligned} K({\text{CdCl}}^{ + } ;T)/{\text{mol}}^{ - 1}\cdot{\text{dm}}^{ 3} = - 117.6 + 0.823{\kern 1pt} {\kern 1pt} (T/{\text{K}});\quad {\text{R}}^{2} = 0.9941 \hfill \\ K({\text{CdBr}}^{ + } ;T)/{\text{mol}}^{ - 1}\cdot{\text{dm}}^{ 3} = 577.7 - 1.46{\kern 1pt} {\kern 1pt} (T/{\text{K}});\quad {\text{R}}^{2} = 0.9994 \hfill \\ K({\text{CdI}}^{ + } ;T)/{\text{mol}}^{ - 1}\cdot{\text{dm}}^{3} = 1171.0 - 2.92{\kern 1pt} {\kern 1pt} (T/{\text{K}});\quad {\text{R}}^{2} = 0.9992. \hfill \\ \end{aligned} $$
(14)

They decrease with temperature in the case of CdBr+ and CdI+ formation, but increase with temperature for CdCl+ complexes. The values of formation constants are highest for CdI+ and lowest for CdCl+, i.e. K(CdI+) > K(CdBr+) > K(CdCl+) and the differences between them are large.

The standard thermodynamic functions of CdX+ formation:

$$ \begin{aligned} \Delta G^{0} (T) = \Delta H^{0} (T) - T\Delta S^{0} (T) \hfill \\ \Delta S^{0} (T) = - \left( {\frac{{\partial \Delta G^{0} (T)}}{\partial T}} \right)_{P} \hfill \\ \Delta G^{0} = - RT\ln [K(T)] \hfill \\ \end{aligned} $$
(15)

as can be observed in Table 4 behave differently for different ions. In the case of CdBr+ we have |\( \Delta \) G 0(T)| > |∆H 0(T)| > T∆S0(T) > 0 and for CdBr+, |∆G 0(T)| > T∆S 0(T) > |∆H 0(T)| > 0 as compared with CdCl+, T∆S 0(T) > |∆G 0(T)| > |∆H 0(T)| > 0 [45]. Thus in all cases we have ∆G 0(T) < 0 and ∆S 0(T) > 0, but the compensation in the entropy–enthalpy balance depends on the formed complex. The change of thermodynamic functions with temperature for all cadmium halides is small (Table 4).

5 Conclusions

Precise and systematic determinations of conductivities in dilute aqueous solutions of cadmium bromide and cadmium iodide were performed over a wide temperature range. Measured conductances clearly indicated a considerable deviation from fully dissociated 2:1 type unsymmetrical electrolyte. Thus, following an idea of stepwise formation of complex ions, it was proposed to treat dilute solutions of cadmium halides as a mixture of two 1:1 and 2:1 type electrolytes (CdX+ + X− and Cd2+ + 2X−). In a suitable optimization procedure, by using the Quint–Viallard conductance equations for representation of conductances, the Debye–Hückel equations for activity coefficients and the mass-action equation for the formation of CdX+ ions, the conductances were calculated and compared with the measured values. The chosen molecular model is valid for limited range of concentrations and basing on it, it was possible to evaluate the molar limiting conductances of ions, the equilibrium constants and the standard thermodynamic function of the complex formation process.