A hybrid scheduling approach for a two-stage flexible flow shop with batch processing machines

Abstract

In this paper, we discuss a flexible flow shop scheduling problem with batch processing machines at each stage and with jobs that have unequal ready times. Scheduling problems of this type can be found in semiconductor wafer fabrication facilities (wafer fabs). We are interested in minimizing the total weighted tardiness of the jobs. We present a mixed integer programming formulation. The batch scheduling problem is NP-hard. Therefore, an iterative stage-based decomposition approach is proposed that is hybridized with neighborhood search techniques. The decomposition scheme provides internal due dates and ready times for the jobs on the first and second stage, respectively. Each of the resulting parallel machine batch scheduling problems is solved by variable neighborhood search in each iteration. Based on the schedules of the subproblems, the internal due dates and ready times are updated. We present the results of designed computational experiments that also consider the number of machines assigned to each stage as a design factor. It turns out that the proposed hybrid approach outperforms an iterative decomposition scheme where a fairly simple heuristic based on time window decomposition and the apparent tardiness cost dispatching rule is used to solve the subproblems. Recommendations for the design of the two stages with respect to the number of parallel machines on each stage are given.

1 Introduction

The electronics industry has become one of the world’s largest industries over the last three decades. A key aspect of this industry is the manufacturing of integrated circuits (chips). Every semiconductor process starts with raw wafers, thin disks made of silicon. Lots of 25 or 50 wafers, called jobs to be consistent with the scheduling literature, are the moving entities in wafer fabs. A diverse product mix, a large number of jobs, and machines groups (i.e., parallel machines) are typical for semiconductor manufacturing (cf. Uzsoy et al. 1992). In addition, a mix of different process types including single-wafer processes and batch processes are characteristic of wafer fabs. A batch is a set of jobs that have to be processed jointly. Two types of batching are differentiated, namely serial batching (s-batch) and parallel batching (p-batch). In the serial batching case, the processing time of a batch is the sum of the processing times of all the jobs that form the batch, while in the parallel batching case the processing time of a batch is given by the maximum processing time of the jobs that are included in the batch. In the present paper, we consider a parallel batching problem, i.e., the jobs of the batch are processed at the same time on a single machine, a so-called batch processing machine. Each batch processing machine has a capacity that is given as the maximum number of jobs that can be batched together (cf. Mönch et al. 2011). It is well known that often one third of all operations in a wafer fab are performed on batch processing machines. Furthermore, the processing times of jobs are long, up to 20 h per job, compared to processing times on non-batching machines which are often less than 1 h. As a consequence of these two facts, an appropriate scheduling of jobs on batch processing machines has a large impact on the performance of wafer fabs (cf. Mönch et al. 2013).

Single and parallel batch processing machine scheduling models have been extensively studied in the last two decades (cf. Mathirajan and Sivakumar 2006 for a survey related to semiconductor batching). Despite the fact that these scheduling models provide many useful insights, it seems to be more desirable to study flow shop scheduling problems where batch processing machines are involved on at least one stage. This is justified by the fact that according to Robinson et al. (1995) batch processing machines heavily impact downstream machine groups, while information on jobs of upstream machine groups are useful to make scheduling decisions on batch processing machines. Two consecutive batch diffusion processes of oxidation and nitration occur in recent wafer fabs and this situation can be modeled as a flexible flow shop.

In the present paper, we propose an iterative decomposition method for a two-stage flexible flow shop where batch processing machines can be found at each stage. The decomposition approach is hybridized with VNS to solve the two parallel batch processing machine subproblems that are the result of each iteration. This paper extends the scheduling model of a two-stage flow shop with batch processing machines proposed by the present authors in Tan et al. (2014) toward parallel machines on each stage. The assumption of parallel machines at the two stages is crucial to increase the real-world fit of the scheduling model at hand. A preliminary version of the new scheduling model was presented in the Tan et al. (2015) extended abstract. However, this paper contains a complete description and a rigorous computational assessment of the proposed heuristics.

The paper is organized as follows. The problem is described in Sect. 2. This includes a MIP formulation. Related work is discussed in Sect. 3. The iterative decomposition heuristic is proposed in Sect. 4. Moreover, a time window decomposition approach and a VNS-based scheme to solve the resulting subproblems are discussed in this section. Computational results are presented in Sect. 5. Finally, conclusions and future research directions are discussed in Sect. 6.

2 Scheduling problem

We start by defining the problem in Subsect. 2.1. We then discuss a corresponding MIP formulation in Subsect. 2.2.

2.1 Problem setting

A two-stage flexible flow shop is considered where stage s contains $m_s$ identical parallel machines with a maximum batch size of $B_s$. No preemption is allowed, i.e., after a batch is started on a batch processing machine it cannot be interrupted. In addition, we assume that the buffer between the two stages is unlimited. We consider n jobs that have to be scheduled on the machines of the flow shop. We assume that each job j belongs to family $f_s \left( j \right) \in \left\{ {1,\ldots ,F_s } \right\}$ at stage s where $F_s$ is the number of incompatible families at stage s. The number of jobs in family $1\le f\le F_s$ is $n_f$. There are $n=\sum _{f=1}^{F_s } {n_f}$ jobs. Only jobs of the same family can be batched together due to the different nature of the chemical processes when the jobs belong to different families. The common processing time of all jobs of family f at stage s is given by $p_{fs}$. Each job j has a due date $d_j$, a ready time $r_j$, and a weight $w_j$. The completion time of the operation of job j at stage s is denoted by $C_{js}$. The performance measure TWT is the summation of the weighted tardiness $w_j T_j$ over all jobs $j=1,\ldots ,n$, where $T_j :=\left( {C_{j2} -d_j } \right) ^{+}$, i.e., we have $\hbox {TWT}=\sum _{j=1}^n {w_j T_j }$. Here, we use $x^{+}:=\max \left( {x,0} \right)$ for abbreviation in the rest of the paper. Using the $\alpha |\beta \hbox {|}\gamma$ notation from scheduling theory (cf. Graham et al. 1979), the researched problem can be represented as follows:

$$\begin{aligned} {\hbox {FF}}2|r_j ,{\textit{p-batch,incompatible}}|\mathrm{{TWT}}, \end{aligned}$$

(1)

where we denote by FF2 a two-stage flexible flow shop with identical parallel machines at each stage. The notation ${\textit{p-batch,incompatible}}$ refers to parallel batching with incompatible job families.

Next, we study the computational complexity of problem (1). Therefore, we prove the following slightly more general proposition.

Proposition 1

The scheduling problem

$$\begin{aligned} \hbox {F2}|{\textit{p-batch,incompatible}}|\mathrm{{TT}} \end{aligned}$$

(2)

is NP-hard. Here, F2 is a two-stage flow shop, and TT denotes the total tardiness of the jobs, i.e., TT $=\,\sum {T_j}$.

Proof

We know from Mehta and Uzsoy (1998) that $1|{\textit{p-batch,}}{\textit{incompatible}}|\mathrm{{TT}}$ is NP-hard. We can consider instances of problem (2) where the processing times of the jobs for all families on the second stage are zero. Therefore, we obtain all the instances of $1|{\textit{p-batch,incompatible}}|\mathrm{{TT}}$ and the NP-hardness of problem (2) follows. $\square$

Since problem (2) is a special case of problem (1), we obtain that problem (1) is also NP-hard.

Fig. 1

Exemplified two-stage flexible flow shop with batch processing machines

Therefore, we have to look for efficient heuristics to solve large-size problem instances in a reasonable amount of time.

The following three decisions have to be made at each of the two stages:

• 1. How to form batches.

• 2. How to assign each batch to one of the machines that belong to the stage.

• 3. How to sequence the batches on each of the machines of a single stage.

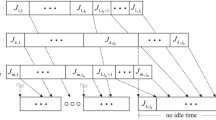
A fairly simple example is shown in Fig. 1. There are two batch processing machines on the first stage, while the second stage has four machines. There is a single waiting room for jobs in front of the machines of each stage. The maximum batch size of the machines on the first stage is $B_1 =4$, whereas the maximum batch size of the machines on the second stage is $B_2 =3$. The jobs belong to different families on the two stages. This is indicated by different colors. Only jobs of the same family are processed together in a batch. Moreover, we see that due to unequal ready times batches that contain less than the maximum batch size are formed in some situations. For instance, a batch that contains only a single job is processed on the first machine of the second stage.

2.2 MIP formulation

We formulate a MIP for problem (1) in this subsection. We start by introducing the set of indices, parameters, and decision variables.

Indices and sets

• $j=1,\ldots ,n:$ set of jobs

• $f=1,\ldots ,F_s :$ set of families of stage s

• $b=1,\ldots ,b_{sm} :$ set of batches on machine m of stage s

• $m=1,\ldots ,m_s :$ set of machines at stage s

Parameters

$B_s :$ :

maximum batch size of a machine on stage s

$p_{{ fs}} :$ :

processing time of family f jobs on the stage s machines

$d_j :$ :

due date of job j

$w_j :$ :

weight of job j

$r_j :$ :

ready time of job j

$e_{jfs} = \left\{ {{\begin{array}{ll} {1,}&{}\hbox {if job }j\hbox { belongs to family }f\;\hbox {at stage}\;s \\ 0,&{}\hbox {otherwise} \\ \end{array} }} \right.$

M : :

big number

Main decision variables

$$\begin{aligned} x_{jbsm}:= & {} \left\{ {{\begin{array}{ll} 1,\quad \text {if job }j \text { belongs to batch } b \text { on machine }m\\ \qquad \,\text {at stage }s \\ 0,\quad \hbox {otherwise} \\ \end{array} }} \right. \\ y_{bfsm}:= & {} \left\{ {{\begin{array}{ll} 1,&{}\quad \text {if batch} \;b \text { on machine }m\;\text {at stage } s \text {belongs}\\ &{}\quad \text {to family } f \\ 0,&{}\quad \hbox {otherwise} \\ \end{array} }} \right. \end{aligned}$$

Resultant variables

$C_{js}:$ :

completion time of job j at stage s

$T_j :$ :

tardiness of job j

$s_{bsm}:$ :

start time of batch b on machine m at stage s

Next, the MIP model can be formulated as follows:

$$\begin{aligned}&\hbox {min}\sum _{j=1}^n {w_j T_j }\\&\text {subject to}\nonumber \end{aligned}$$

(3)

$$\begin{aligned}&\sum _{b=1}^{b_{{\textit{sm}}} } {\sum _{m=1}^{m_s } {x_{{\textit{jbsm}}} =1,} \;j=1,\ldots ,n,\;s=1,2} \end{aligned}$$

(4)

$$\begin{aligned}&\sum _{j=1}^n {x_{{\textit{jbsm}}} \le B_s } ,\;s=1,2,\;m=1,..,m_{s } , b=1,\ldots ,b_{{\textit{sm}}} \end{aligned}$$

(5)

$$\begin{aligned}&\sum _{f=1}^F {y_{{\textit{bfsm}}} =1} , s=1,2, b=1,\ldots ,b_{{\textit{sm}}} , m=1,..,m_s \end{aligned}$$

(6)

$$\begin{aligned}&e_{{\textit{jfs}}} x_{{\textit{jbsm}}} \le y_{{\textit{bfsm}}} ,\;j=1,\ldots ,n, s=1,2,\nonumber \;\\&f=1,\ldots ,F_s , m=1,..,m_s , b=1,\ldots ,b_{{\textit{sm}}} \end{aligned}$$

(7)

$$\begin{aligned}&r_j x_{jb1m} \le s_{b1m} , j=1,\ldots ,n, b=1,\ldots ,b_{1m} ,\nonumber \\&m=1,..,m_s \end{aligned}$$

(8)

$$\begin{aligned}&s_{{\textit{bsm}}} +e_{jfs} p_{fs} x_{jbsm} \le s_{b+1,sm} , s=1,2, j=1,\ldots ,n,\nonumber \\&b=1,\ldots ,b_{{\textit{sm}}} ,f=1,\ldots ,F_s ,m=1,..,m_s \end{aligned}$$

(9)

$$\begin{aligned}&s_{{\textit{bsm}}} +e_{jfs} p_{fs} \le C_{js} +M\left( {1-x_{{\textit{jbsm}}} } \right) , j=1,\ldots ,n,\nonumber \\&s=1,2, b=1,\ldots ,b_{{\textit{sm}}} , f=1,\ldots ,F_s , \;m=1,..,m_s \end{aligned}$$

(10)

$$\begin{aligned}&C_{j1} \le M\left( {1-x_{jb2m} } \right) +s_{b2m} , j=1,\ldots ,n,\nonumber \\&b=1,\ldots ,b_{2m} ,\;m=1,\ldots ,m_s \end{aligned}$$

(11)

$$\begin{aligned}&C_{j2} -T_j \le d_j , j=1,\ldots ,n \end{aligned}$$

(12)

$$\begin{aligned}&x_{{\textit{jbsm}}} ,y_{{\textit{bfms}}} \in \left\{ {0,1} \right\} ,C_{js} ,T_j ,s_{{\textit{bsm}}} \ge 0, j=1,\ldots ,n,\nonumber \\&s=1,2, f=1,\ldots ,F_s , b=1,\ldots ,b_{{\textit{sm}}} , \;m=1,\ldots ,m_s .\nonumber \\ \end{aligned}$$

(13)

Our aim is to minimize the TWT value of the jobs. This is expressed by the objective function (3). Constraints (4) ensure that each job belongs to exactly one batch. The inequalities (5) model the fact that the number of jobs in each batch is not larger than the maximum batch size on a given stage. Constraints (6) make sure that each batch belongs to exactly one family. Constraints (7) ensure that all the jobs in a batch on a given stage belong to the same family. Constraints (8) model the fact that a given job cannot start on the first stage before its ready time. The sequencing of the batches on a given stage is represented by constraints (9). Constraints (10) relate the start time of a given batch to its completion time, while constraints (11) ensure that a batch on the second stage can only start if all the jobs that form this batch are completed on the first stage. Constraints (12) express the tardiness of each job, while constraints (13) model the fact that the decision variables are binary or nonnegative, respectively.

The MIP formulation (3)–(13) can be solved by a commercial solver. However, due to the NP-hardness of problem (1), only small-size problem instances can be solved to optimality, even with a large amount of computing time. These optimal solutions to small-size instances can be used to ensure that the proposed heuristics are correctly implemented and to determine the efficacy of the heuristics.

3 Related work

In this section, we discuss related work with respect to decomposition approaches for flow shop scheduling problems with due date-related objectives and with respect to flow shop scheduling problems that include batch processing machines.

We refer to Emmons and Vairaktarakis (2013) for a discussion of deterministic flow shop scheduling problems. Scheduling approaches for flexible flow shops are surveyed by Ruiz and Vázquez-Rodríguez (2010).

It is shown by Demirkol et al. (1997) and Jain and Meeran (2002) that the shifting bottleneck heuristic (SBH) works well for job shops, but is not particularly effective in flow shop settings. An efficient decomposition heuristic is proposed for the problem $\hbox {F2}||\mathrm{{TT}}$ by Koulamas (1998). The proposed heuristic exploits the relationship to the single-machine scheduling problem $1||\mathrm{{TT}}$. It is demonstrated by Mukherjee and Chatterjee (2006) that the SBH often fails to optimally solve problem instances of $\hbox {F2}||C_{\max }$ where $C_{\max }$ denotes the makespan. An alternative decomposition heuristic is designed that is based on a Schrage-type heuristic.

The problem $\mathrm{{FFc}}||\mathrm{{TWT}}$ is discussed by Yang et al. (2000). Here, FFc refers to a flexible flow shop with c stages. Several decomposition approaches based on the disjunctive graph representation, the SBH, and local search techniques are proposed. Demirkol and Uzsoy (2000) consider the problem ${\textit{Fm}}|s_{{\textit{jk}}} ,{\textit{recrc}}|L_{\max }$ where Fm refers to an m-stage flow shop, $s_{{\textit{jk}}}$ is used for sequence-dependent setup times, and ${\textit{recrc}}$ refers to reentrant flows. The maximum lateness criterion $L_{\max }$ is the objective to be minimized. Efficient decomposition heuristics are proposed; however, batching is not taken into account.

A bottleneck-focused scheduling approach is proposed by Lee et al. (2004) for the problem $\mathrm{{FFc}}||\mathrm{{TT}}$. In a first step, the operations are scheduled on the machines of the bottleneck stage using list scheduling. Then, the operations on the remaining stages are scheduled using the schedule for the bottleneck. The ready times of operations at the bottleneck stage are iteratively updated using information on the schedules obtained in previous iterations. Within each iteration, the ready time of a single job is fixed. However, in the present paper, we consider batching problems. Therefore, an insertion of single jobs is not possible, i.e., an extension of this approach toward problem (1) is not straightforward. Chen and Chen (2008) study the problem $\mathrm{{FFc}}||\sum {U_j}$ where $\sum {U_j}$ is the number of tardy jobs. They propose several heuristics that are based on the idea to schedule first the jobs at the machines of the bottleneck stage by a heuristic inspired by Moore’s algorithm. The heuristic schedules the jobs independently on the upstream stages to obtain the ready times at the bottleneck. The downstream machines are scheduled using list scheduling. A similar approach is proposed for $\mathrm{{FFc}}||\mathrm{{TT}}$ by Chen and Chen (2009). The bottleneck-focused approach outperforms list scheduling approaches and a tabu search heuristic. Liao and Huang (2010) propose a tabu search approach to solve the problem $\mathrm{{FFc}}||\mathrm{{TT}}$.

Next, we discuss work related to flow shop scheduling with batch processing machines. Sung et al. (2000) discuss a permutation flow shop scheduling problem where batch processing machines can be found on each stage. Based on structural properties of optimal solutions, a problem reduction approach is proposed that removes dominated machines. The makespan and the total completion time are considered as objectives. The problem $\hbox {F2}|{\textit{p-batch}},r_j |C_{\max }$ is discussed by Sung and Kim (2002). An efficient heuristic is provided and a worst-case error bound is derived. The same authors study in Sung and Kim (2003) a two-stage flow shop scheduling problem where each of the two machines is a batch processing machine. The processing time of a batch depends on the machine, but not on the jobs in the batch, i.e., only one incompatible family is assumed at each stage. It is shown that for the maximum tardiness, the maximum number of tardy jobs, and the TT measure, efficient polynomial time algorithms exist. A two-stage flow shop scheduling problem with a batch processing machine on the first stage and makespan objective is considered by Su (2003). A time constraint between the first and the second stage is assumed. A MIP formulation and heuristics are proposed for this problem.

MIP formulations for $\hbox {F2}|{\textit{p-batch}}|C_{\max }$ are presented by Damodaran and Srihari (2004). Liao and Liao (2008) study the same problem. Improved MIP formulations and several heuristics are proposed. A scheduling problem for a two-machine flow shop with batch processing and makespan objective is discussed in Manjeshwar et al. (2009). Simulated annealing is used to tackle this problem that is motivated by a real-world situation in a printed circuit assembly line. A two-stage flow shop scheduling problem with a parallel batch processing machine on the first stage and makespan objective is discussed in Oulamara (2012). A s-batching machine is on the second stage. A no-wait constraint is between processing jobs on the first and the second machine. An approximation algorithm is designed for this problem.

A flexible flow shop scheduling problem with batch processing machines at some stages and makespan objective is studied by Amin-Naseri and Beheshti-Nia (2009). The machines on each stage are uniform. Several heuristics, among them a genetic algorithm, are proposed. Bellanger and Oulamara (2009) consider a two-stage flexible flow shop where p-batching takes place on the second stage. Only compatible jobs can be batched together. The makespan objective is considered. Several heuristics are proposed. A polynomial time approximation scheme is proposed for the case of equal processing times.

The problem ${\textit{Fm}}|{\textit{p-batch,perm}}|C$ is investigated by Lei and Guo (2011). The maximum tardiness, the weighted number of tardy jobs, and the TT objective are considered as objective C, respectively. The notation ${\textit{perm}}$ is used to indicate that only permutation schedules are considered, i.e., the batches that are formed for the first machine and their sequence cannot change on the remaining machines. A VNS approach is applied to tackle this problem. A two-stage flow shop is studied by Fu et al. (2012) where the machine on the second stage is a batch processing machine. Incompatible families are considered on the first machine. There is a finite buffer between the machines. The mean completion time is the performance measure to be minimized. Several heuristics are used to form the batches, whereas the batches are sequenced by a differential evolution algorithm. Yugma et al. (2012) discuss a real-world flexible job shop scheduling problem where each machine group can consist of batch processing machines. Minimizing the waiting time of jobs, maximizing the number of performed operations, and maximizing the fullness of batches are considered. The scheduling problem is modeled by a disjunctive graph. An iterative sampling procedure and a simulated annealing procedure are proposed. However, problem (1) is different since we consider the TWT performance measure.

Wang et al. (2012) consider a two-stage flexible flow shop scheduling problem with makespan objective where batch processing machines are on the first stage. Ready times and machine dedications are assumed. Heuristics solution approaches are proposed. A genetic algorithm is proposed by Li et al. (2015) to solve a scheduling problem for a flexible flow shop where batch processing machines are allowed only at a single stage. Setup times are taken into account. The makespan and the TWT performance measure are considered, respectively. However, our problem is different since we allow for batching on both stages.

Overall, to the best of our knowledge, problem (1) has not been addressed so far with the exception of Tan et al. (2015) where only preliminary computational results are presented. In this paper, an iterative decomposition approach is proposed that can be interpreted in terms of the lead time iteration scheme of Vepsalainen and Morton (1988) to obtain waiting time estimates for the operations of the jobs. The resulting subproblems for identical parallel batch processing machines are solved by the time window decomposition procedure (cf. Mönch et al. 2005) and the VNS scheme proposed by Bilyk et al. (2014).

4 Hybrid heuristics

In this section, we start by describing the proposed iterative decomposition scheme in Subsect. 4.1. The time window decomposition heuristic is summarized in Subsect. 4.2, and a VNS scheme is discussed in Subsect. 4.3.

4.1 Iterative decomposition approach

In this subsection, we describe an iterative procedure to decompose the overall scheduling problem. In contrast to somewhat similar approaches proposed in the literature (cf. Lee et al. 2004; Chen and Chen 2008, 2009), we cannot consider scheduling one job after another since the scheduling entities in problem (1) are batches. Therefore, internal due dates and ready times for the first and second stage, respectively, are required to formulate the corresponding parallel machine subproblems. The main idea of the proposed iterative procedure consists of using the completion times of the operations on the first stage as ready times for the operations of the second stage. Note that a more direct application of the SBH based on disjunctive graphs seems not to be appropriate because we have only two stages and because of the deficiencies of the SBH for flow shops (cf. the discussion in Sect. 3).

We introduce the following additional notation to present the iterative decomposition approach:

l : :

iteration number

$d_{j1}^{(l)} :$ :

(internal) due date of job j at stage 1 in iteration l

$r_{j2}^{(l)} :$ :

(internal) ready time of job j at stage 2 in iteration l

$s_{j2}^{(l)} :$ :

start time of job j at stage 2 in iteration l

$w_{j2}^{(l)} :$ :

waiting time of job j at stage 2 that is a result of the scheduling decisions made in iteration l

$p_{js} :$ :

processing time of job j at stage s, i.e., $p_{js} :=p_{f\left( j \right) s}$

$C_{j1}^{(l)} :$ :

completion time of job j at stage 1 in iteration l

$\alpha :$ :

parameter of the iterative decomposition approach

$\beta :$ :

parameter of the iterative decomposition approach.

Now, we describe the iterative decomposition approach (IDA) as follows:

Algorithm IDA

• 1. Initialize $l:=1$. Set the parameter values $\alpha ,\beta$ (discussed below). Moreover, choose initial internal due dates as follows:

  $$\begin{aligned} d_{j1}^{\left( 1 \right) } :=\frac{1}{2}\left( {r_j +p_{j1} +d_j -p_{j2} } \right) . \end{aligned}$$

  (14)

• 2. If $l\ge 2$ set $d_{j1}^{\left( l \right) }, j=1,\ldots ,n$ using the waiting time information of the jobs obtained from the schedule computed in iteration $l-1,l\ge 2$ as follows:

  $$\begin{aligned} d_{j1}^{\left( 1 \right) } :=\left( {1-\alpha } \right) \; r_{j2}^{\left( {l-1} \right) } +\alpha \left( {d_j -p_{j2} -w_{j2}^{\left( {l-1} \right) } } \right) +\beta w_{j2}^{\left( {l-1} \right) } . \end{aligned}$$

  (15)

• 3. Solve the resulting scheduling problem for the first stage using $r_j$ and $d_{j1}^{\left( l \right) }, j=1,\ldots ,n$.

• 4. Using the solution of the first stage scheduling problem in iteration l, set $r_{j2}^{\left( l \right) } :=C_{j1}^{\left( l \right) }, j=1,\ldots ,n.$

• 5. Solve the resulting scheduling problem for the second stage using $r_{j2}^{\left( l \right) }$ and $d_j, j=1,\ldots ,n$.

• 6. Calculate the TWT value of the schedule x obtained in iteration l. If $l=1$ then initialize $x^{*}:=x$, otherwise update $x^{*}:=x$ if $\mathrm{{TWT}}( x )<\mathrm{{TWT}}( {x^{*}} )$. Here, $x^{*}$ is the best schedule found so far.

• 7. When the termination criterion is fulfilled then stop, otherwise increase the iteration number by $l:=l+1$ and go to Step 2.

The overall information flow between two consecutive iterations $l-1$ and l is depicted in Fig. 2. The parallel rectangles on each stage indicate the parallel machines. We see from this figure that the due dates for the first stage subproblem in iteration l are determined based on the ready time and waiting time of the jobs obtained from the solution of the second stage subproblem in iteration $l-1$ [based on expression (15)]. This information flow is indicated by an arrow across the two iterations and stages. The gray-colored boxes contain the information obtained from a schedule, while white-colored boxes are used to represent input information for a scheduling instance. Moreover, the completion times of the jobs in a schedule for the first stage subproblem in iteration l are used to determine the ready times for the jobs in the second stage subproblem in iteration l (see Step 4 in the IDA algorithm). Again an arrow is used to show this information flow.

Fig. 2

Information flow between two iterations of IDA

Note that we have to solve 2l subproblems of type

$$\begin{aligned} {\textit{Pm}}|r_j ,{\textit{p-batch,incompatible}}|\mathrm{{TWT}} \end{aligned}$$

(16)

in Step 3 and Step 5 when l iterations of IDA are performed. Here, Pm is used to refer to identical parallel machines. We continue with several remarks related to expressions (14), (15), and IDA:

• 1. The earliest possible completion of job j at the first stage is $r_j +p_{j1}$. The maximum possible slack of job j is then $d_j -p_{j2} -\left( {p_{j1} +r_j } \right)$. We add half of this slack to the earliest possible completion time of the first stage to set the internal due date for the first stage. We obtain $d_{j1}^{\left( 1 \right) } :=r_j +p_{j1} +\frac{1}{2}\left( {d_j -p_{j1} -p_{j2} -r_j } \right) =\frac{1}{2}\left( {r_j +p_{j1} +d_j -p_{j2} } \right)$. This motivates expression (14).

• 2. In the general case, we have for the waiting time at the second stage $w_{j2}^{\left( {l-1} \right) } :=s_{j2}^{\left( {l-1} \right) } -r_{j2}^{\left( {l-1} \right) }$. After some algebra, the following representation can be obtained from expression (15):

  $$\begin{aligned} d_{j1}^{\left( l \right) } :=\left( {1-\alpha } \right) s_{j2}^{\left( {l-1} \right) } +\alpha \left( {d_j -p_{j2} } \right) +\left( {\beta -1} \right) w_{j2}^{\left( {l-1} \right) } . \end{aligned}$$

  (17)

  We see from expression (17) that the internal due date for the first stage in iteration l is a linear combination of the second stage starting time in iteration $l-1$ and the latest possible starting time that does not lead to a tardy job j and a correction term that takes into account the amount of waiting time for job j at stage 2 in iteration $l-1$. The correction term can be positive, negative, or zero depending on the choice of the $\beta$ value. The overall situation is shown in Fig. 3. We see the potential place for the first stage due dates in iteration l according to expression (17). The corresponding section on the time axis is marked with crosses. The ready time for the second stage in iteration l is set according to the scheduling result for the first stage in iteration l. The corresponding possible values are also depicted in Fig. 3. As shown in Fig. 3, the ready times for the second stage in iteration l can be eventually before or after the ready times in iteration $l-1$.

  It becomes clear that the IDA scheme is similar to iterative simulation procedures such as the lead time iteration method proposed by Vepsalainen and Morton (1988). The evaluation of the schedule can be interpreted as a deterministic forward simulation.

• 3. At the first glance it seems that

  $$\begin{aligned} d_{j1}^{\left( l \right) } :=s_{j2}^{\left( {l-1} \right) } , \end{aligned}$$

  (18)

  is a natural choice for the internal due date for the first stage in iteration l. However, since all the operations at the first stage in iteration $l-1$ are completed before $s_{j2}^{\left( {l-1} \right) }$ it is fairly easy to obtain a small TWT value for the first stage in iteration l. Hence, it is reasonable to add waiting time as done in expression (15) or (17).

• 4. We will select the parameter values for $\alpha ,\beta$ from an equidistant grid over $[0,2]\times [0,2]$. The setting $\beta >1$ is useful in situations when the waiting time is small. Therefore, tighter due dates are possible. If $d_j -p_{j2} <s_{j2}^{\left( {l-1} \right) }$ then $\alpha >1$ leads to internal due dates that are smaller than $d_j -p_{j2}$.

• 5. We terminate IDA when either the same schedule is computed a second time or when a prescribed maximum number of iterations abbreviated by $iter_{\max }$ is reached.

In the next two subsections, we will describe the methods we use to solve the resulting parallel batch processing machine subproblems.

Fig. 3

Placing the internal due date within the different iterations of IDA

4.2 Time window decomposition

The first subproblem solution procedure is based on the time window decomposition (TWD) scheme proposed by Mönch et al. (2005). For the sake of completeness, we briefly summarize the decisions made by TWD to choose the batch to be processed next. In order to simplify the notation, we do not differentiate between the two stages. We simply assume that job j has a due date $\tilde{d}_j$, a processing time $\tilde{p}_j$, a weight $\tilde{w}_j$, and a ready time $\tilde{r}_j$. The maximum batch size is $\tilde{B}$, whereas $\tilde{F}$ is the number of incompatible families.

When a batch processing machine k becomes available at decision time t, we form for each family $f\in \tilde{F}$ the set

$$\begin{aligned} J_f \left( t \right) :=\left\{ {j|\tilde{r}_j \le t+\Delta t,f\left( j \right) =f} \right\} , \end{aligned}$$

(19)

i.e., we consider only the jobs of family f that are ready for processing before or at $t+\Delta t$. We sort all the jobs from $J_f \left( t \right)$ in non-increasing order with respect to the Apparent Tardiness Cost (ATC) index (cf. Vepsalainen and Morton 1987):

$$\begin{aligned} I_j \left( t \right) :=\frac{\tilde{w}_j }{\tilde{p}_j }\exp \left( {-\frac{\left( {\tilde{d}_j -\tilde{p}_j -\left( {\tilde{r}_j -t} \right) ^{+}} \right) }{\kappa \bar{{p}}}^{+}} \right) . \end{aligned}$$

(20)

The look-ahead parameter $\kappa$ is used for scaling in expression (20), whereas the quantity $\bar{{p}}$ is the average processing time of the remaining jobs. Due to the computational burden, we consider only the first thresh jobs from the list sorted according to ATC to form batches. The resulting set is called $\tilde{J}\left( t \right)$. In a next step, we consider all batches that can be formed using jobs from $\tilde{J}\left( t \right)$. Each of these potential batches b for each family f is evaluated based on the Batched ATC (BATC)-II index (cf. Mönch et al. 2005):

$$\begin{aligned} I_b \left( t \right) :=\sum _{j\in b} {{\tilde{w}_j }/{\tilde{p}}_j \exp \left( {-{\left( {\tilde{d}_j -\tilde{p}_j -t+\left( {r_b -t} \right) ^{+}} \right) ^{+}}\big /{\left( {\kappa \bar{{p}}} \right) }} \right) } \frac{\left| b \right| }{\tilde{B}}. \end{aligned}$$

(21)

Here, $\left| b \right|$ is the number of jobs in batch b. In addition, the ready time of batch b is given by $r_b :=\max \left\{ {\tilde{r}_j |j\in b} \right\}$. The batch with the largest BATC-II index is selected among all families $f\in \tilde{F}$ and processed on machine k. The entire procedure is repeated if a machine becomes available or a new job arrives at a new decision time $t^{{*}}$. The resulting iterative decomposition scheme for $iter_{\max }$ iterations that is based on the TWD approach is abbreviated by $\mathrm{{IDA}}( {{\mathrm{TWD},\textit{iter}}_{\max } } )$ in the rest of the paper.

An alternative TWD approach is considered that is based on the weighted earliest due date (WEDD) dispatching rule in combination with a full batch policy. Here, we replace the index (20) by $I_j :={\tilde{w}_j }/{\tilde{d}_j }$. Moreover, batches are formed by considering the first $\hbox {min}\left( {\tilde{B},l} \right)$ batches from the sorted list of unscheduled jobs of a given family. Here, we denote by l the number of jobs in the list of the corresponding family. Each formed batch b is assessed by the batch index $I_b :=\sum _{j\in b} {I_j }$. The resulting scheme is called $\mathrm{{IDA}}( {{\mathrm{BWEDD},\textit{iter}}_{\max } } )$ in the rest of the paper.

4.3 VNS scheme

We know from Mönch et al. (2005) and Bilyk et al. (2014) that the TWD scheme can be improved by metaheuristics. Therefore, we recall next the main ingredients of a VNS approach proposed by Bilyk et al. (2014) for a slightly more general situation, i.e., for precedence constraints among the jobs.

VNS is a local search-based metaheuristic that is based on the idea of using several neighborhood structures. The main ingredients of VNS are shaking and local search (cf. Hansen and Mladenovic 2001). The main purpose of shaking is to restart the local search when it gets stuck in a local optimum. We use the following five classes of neighborhood structures in this research:

• 1. MoveBatch(k) Randomly choose a batch on a randomly chosen machine. Remove this batch and insert it in a randomly chosen position of a randomly chosen machine that is different from the first one. Repeat this procedure k times.

• 2. SwapBatch(k) Randomly choose two batches from two different, randomly chosen machines at that stage. Exchange these batches. Repeat this procedure k times.

• 3. MoveSeq(k) This neighborhood structure is similar to MoveBatch(k); however, instead of moving single batches, sequences of batches are considered.

• 4. SwapSeq(k) This neighborhood structure is similar to SwapBatch(k); however, instead of swapping pairs of batches, sequences of batches are considered.

• 5. SplitBatch(k) Randomly choose a batch. Split this batch into two batches where the content of the first batch is randomly chosen. The first resulting batch does not change its position, while the second one is inserted in a randomly chosen position of a different, randomly chosen machine. Repeat the entire procedure k times.

While the proposed neighborhood structures work on the final solution representation, i.e., on batches that are assigned to single machines and sequenced there, the local search procedure is based on job insertion, job swap, and batch swap (cf. Bilyk et al. 2014 for more details). The used VNS scheme can be summarized as follows:

Algorithm VNS

• 1. Initialization Choose the neighborhood structures $N_k$, $k=1,\ldots ,25$. Compute initial solutions $x\left( \kappa \right)$ based on the TWD approach where we test the values $\kappa =0.5l,l=1,\ldots ,10$. Choose an initial solution $x\left( {\kappa ^{{*}}} \right)$ that has the smallest TWT values among the different initial solutions.

• 2. Main Loop

  • a. Shaking Choose randomly a solution $x{\prime }\in N_k \left( x \right)$.

  • b. Local Search Balance the solution $x{\prime }$, i.e., unify the workload on the different machines by the following procedure. If the last batch of the machine with the maximum completion time starts later than the completion time of the machine with the smallest workload, the batch is moved to that machine. This step is repeated until no batch can be moved anymore. The resulting solution is abbreviated by $\hat{{x}}$. Apply the local search procedure to $\hat{{x}}$ to obtain $x''$.

  • c. Acceptance Decision If $\mathrm{{TWT}}\left( {x''} \right) <\mathrm{{TWT}}\left( x \right)$ then set $x:=x''$ and $k:=1$, otherwise set $k:=k\bmod k_{\max } +1$.

• 3 Termination If a maximum computing time is reached then stop. Otherwise repeat Step 2.

The resulting iterative decomposition scheme including ${\textit{iter}}_{\max }$ iterations that is based on this VNS scheme is abbreviated by $\mathrm{{IDA}}( {{\mathrm{VNS},\textit{iter}}_{\max } } )$ in the rest of the paper.

For the sake of completeness, we summarize the hybrid approach in one place as follows:

• 1. The approach is based on an iterative decomposition scheme that uses scheduling results from the previous iteration, namely waiting times and ready times of the jobs in the second stage subproblem, to set the internal due dates for the first stage subproblem of the current iteration.

• 2. After the first stage subproblem is solved in the current iteration, the completion times of the jobs from the corresponding schedule are used as ready times for the second stage subproblem.

• 3. The resulting subproblems are solved either by TWD or by VNS. Since we combine iterative decomposition techniques with metaheuristic approaches, namely VNS, the proposed approach is hybrid.

The hybrid approach based on the IDA algorithm can be visualized as shown in Fig. 4.

Fig. 4

Overall flow of the hybrid approach

5 Computational experiments

In this section, we start by presenting the design of experiments. We then discuss how the various parameters of the heuristics are chosen in Subsect. 5.2, and we also describe implementation details. The computational results are presented in Subsect. 5.3. The obtained results are analyzed and discussed in Subsect. 5.4.

5.1 Design of experiments

We expect that the performance of the proposed heuristics depends on the number of jobs per family, on the number of families, the maximum batch size at each stage, the number of machines at each stage, and the ready time and due date setting. We generate ready times by using crude makespan estimates for each stage, i.e.,

$$\begin{aligned} r_j \sim U\left( {0,a\left( {\frac{1}{B_1 m_1 }\sum _{j=1}^n {p_{j1} +\frac{1}{B_2 m_2 }\sum _{j=1}^n {p_{j2}} } } \right) } \right) , \end{aligned}$$

(22)

where we denote by $X\sim U\left( {a,b} \right)$ a random variable X that is uniformly distributed over the interval $\left( {a,b} \right)$. The parameter a determines how widespread the ready times are. Based on the ready times, we are able to generate due dates according to

$$\begin{aligned} d_j :=r_j +\mathrm{{FF}}\left( {p_{j1} +p_{j2}} \right) , \end{aligned}$$

(23)

where we denote by $\mathrm{{FF}}\ge 1$ a flow factor that is used to represent the waiting time that occurs in the two-stage flow shop. Each first stage family will become either one or two families with equal probability at the second stage. This situation is typical for the two consecutive batch diffusion processes of oxidation and nitration that occur in modern wafer fabs.

Important design factors are the number of machines at each stage and the maximum batch size per stage since they directly influence the offered capacity at the two stages. We are interested in assessing the performance of the proposed algorithms in the situation when the number of machines at each stage is also a design factor. Therefore, the two stages can have a different bottleneck behavior. We measure the workload of stage s as follows:

$$\begin{aligned} \mathrm{{WL}}_s =\frac{1}{B_s m_s }\sum _{j=1}^n {p_{js}} , s=1, 2. \end{aligned}$$

(24)

We use the following algorithm to define the bottleneck behavior of the flow shop:

Algorithm bottleneck configuration (BC)

• 1. Initialization Start from the total number of machines in the two-stage flow shop. This number is denoted by m. Initialize $\Delta _{\min }$ with a large value.

• 2. Loop Repeat for each pair $\left( {m_1 ,m-m_1 } \right)$ with $m_1 =1,\ldots ,m-1$:

  • a. Compute the value $\Delta \left( {m_1 ,m-m_1 } \right) :=| \mathrm{{WL}}_1 -\mathrm{{WL}}_2 |$.

  • b. If $\Delta \left( {m_1 ,m-m_1 } \right) <\Delta _{\min }$ then set $m_1^*:=m_1$ and $m_2^*:=m-m_1$. Update $\Delta _{\min } :=\Delta \left( {m_1 ,m-m_1 } \right)$.

• 3. Output The pair $\left( {m_1^{*} ,m_2^{*} } \right)$ leads to the most balanced machine configuration of the flow shop. If possible, consider the configurations $\left( {m_1^{*} -1,m_2^{*} +1} \right)$ and $\left( {m_1^{*} +1,m_2^{*} -1} \right)$. They indicate a situation where the bottleneck is on the first and second stage, respectively.

The computational experiments are performed with the three different machine configurations that are the result of the BC algorithm. The design of experiments is summarized in Table 1.

Table 1 Design of experiments

Table 2 Settings for exploring the number of iterations versus computing time

Note that we have 384 problem instances in total. But we have only 128 unique sets of jobs. From each set of jobs, we obtain three different instances that have different bottleneck configurations.

In another experiment, we are interested in investigating the situation where the second stage has non-batching machines. This situation is also important in real-world situations found in wafer fabs (cf. Robinson et al. 1995). Therefore, we generate 16 additional problem instances that follow the design of experiments summarized in Table 1 with the exception that we consider only 16 machines, i.e., one level for the total number of machines, one level for the maximum batch size, i.e., we use $B_1 =4$ and $B_2 =1$, and only the balanced configuration.

Moreover, we are interested in assessing the correctness of the implementation and the efficacy of the heuristics by using the MIP model (3)–(13) for eight small-size instances. The design characteristics are similar to the one found in Table 1. We consider $n=12$ jobs. The maximum batch size at both stages is $B_1 =B_2 =2$. In total, $m=12$ machines are considered. The number of machines at each stage is selected in such a way that a balanced configuration is obtained from the BC algorithm. The jobs belong to two families at the first stage, whereas up to four families are possible at the second stage using the same family split as for the design of experiments summarized in Table 1.

In addition, we want to understand the importance of the number of iterations vs. the amount of computing time for the subproblems in $\mathrm{{IDA}}( {{\mathrm{VNS},\textit{iter}}_{\max } } )$. Therefore, we consider 20 randomly selected problem instances with six job families and 360 jobs. For these instances, we vary the number of iterations and the amount of computing time per subproblem in such a way that the overall computing time per instance is the same. We consider $\mathrm{{IDA}}( {{{\mathrm{VNS}}},40} )$ in addition to $\mathrm{{IDA}}( {{\mathrm{VNS}},20} )$, i.e., we use more iterations. At the same time, we use only a computing time of 5 s per subproblem in case of $\mathrm{{IDA}}( {{{\mathrm{VNS}}},40} )$. This variant is abbreviated by $\mathrm{{IDA}}( {\mathrm{{{ VNS},MI}}} )$. The second variant uses a computing time of 5 s in the first ten iterations. However, the computing time is 15 s from iteration 11–20, i.e., a longer computing time is allowed. This variant is called $\mathrm{{IDA}}({\mathrm{{{VNS},LT}}})$. Overall, we have an average computing time of around 400  s per problem instance for the two settings. The settings of the two variants are summarized in Table 2.

We are interested in assessing the performance of IDA-type heuristics. Therefore, we consider the ratio of the TWT value obtained by $\mathrm{{IDA}}( {{\mathrm{VNS},\textit{iter}}_{\max } } )$ and by $\mathrm{{IDA}}( {\mathrm{{TWD}},1} )$, i.e., we compute the quantity:

$$\begin{aligned} {\textit{Imp}}\left( {{\mathrm{VNS},\textit{iter}}_{\max } } \right):= & {} {\mathrm{{TWT}}( {\mathrm{{IDA}}\left( {{\mathrm{VNS},\textit{iter}}_{\max } } \right) } )}/\nonumber \\&\quad {{\mathrm{TWT}}}( {{\mathrm{IDA}}\left( {{\mathrm{TWD}},1} \right) } ) \end{aligned}$$

(25)

for each single instance. Note that it is reasonable to compare the performance relative to $\mathrm{{IDA}}( {\mathrm{{TWD}},1} )$ because we know for the problem $\hbox {F2}|r_j ,{\textit{p-batch,incompatible}}|\mathrm{{TWT}}$ that the improvement obtained by $\mathrm{{IDA}}({{\mathrm{TWD},\textit{iter}}_{\max } })$ compared to $\mathrm{{IDA}}({\mathrm{{TWD}},1})$ is fairly small (cf. Tan et al. 2014). Based on experiments for the problem instances of Table 1, we observe a similar behavior for problem (1). Moreover, we do not separately assess the performance of $\mathrm{{IDA}}( {\mathrm{{VNS}},1} )$ since we know from Bilyk et al. (2014) that up to 20% TWT reduction for the VNS scheme compared to TWD is possible for a single stage. This result carries over to the two-stage flexible flow shop setting as observed by experiments for the instances in Table 1.

Each problem instance is solved three times with different random number seeds to obtain statistically meaningful results. The average value of the corresponding ${\textit{Imp}}({\mathrm{VNS},\textit{iter}}_{\max } )$ values of the independent replications is presented.

Table 3 Summary of the computational experiments

5.2 Implementation issues and parameter setting

All the algorithms are coded using the C++ programming language. ILOG CPLEX 12.1 is applied to implement the MIP (3)–(13). The computational tests are performed on an Intel Xeon E5-2620 2.00 GHz, 32 GB computer with Windows Server 2008 R2 Standard operating system. The computer has two E5-2620 processors and a total of 12 cores. The grid search for appropriate $\left( {\alpha ,\beta } \right)$ pairs can be parallelized. Twelve processes of each of the heuristics are created and deployed on the multi-core computer in our experiments. The smallest TWT value and the longest computing time obtained from these twelve processes are recorded.

Next, we discuss the parameter setting for the different heuristics. The TWD scheme is parameterized by $\Delta t=4h$ and ${\textit{thresh}}=15$ since we know from (Mönch et al. 2005) that these settings lead to small TWT values. The BATC-II rule is applied for sequencing batches with appropriate values for the look-ahead parameter $\kappa$. The $\kappa$ values are taken from the grid $\left\{ {0.5l|l=1,\ldots ,10} \right\}$. The $\kappa$ value that leads to the smallest TWT value is recorded.

Table 4 Computational results for small-size problem instances

We consider $k_{\max } =25$ different neighborhood structures in the VNS-based subproblem solution procedure. These neighborhood structures are obtained by varying the k values in the five basic neighborhood structures described in Subsect. 4.3. The concrete k values and the sequence of the neighborhood structures can be found in Bilyk et al. (2014).

We use ${\textit{iter}}_{\max } =20$ iterations in the majority of the computational experiments with IDA-type heuristics. The computing time for the VNS-based subproblem solution procedure is 20  s per parallel machine problem instance. Therefore, the overall computing time per instance for problem (1) is around 400  s for a given $\left( {\alpha ,\beta } \right)$ pair. This amount is often still small enough to allow scheduling decisions in a real-world environment. Based on some preliminary tests using a small number of instances, we confirm that using a larger number of iterations does not lead to significant performance improvements.

In some situations, we use a different number of iterations and a different amount of computing time per subproblem. For the eight small-size problem instances, a maximum computing time of 4 h is allowed for CPLEX per problem instance. Moreover, we use a computing time of 6 s per subproblem for $\mathrm{{IDA}}( {{{\mathrm{VNS}}},15} )$ in this situation. This leads to an overall computing time of 180 s per problem instance. The number of iterations and the computing times for the problem instances that are used to look at the importance of the number of iterations vs. the amount of computing time for the subproblems are already specified in Subsect. 5.1.

We know from some preliminary computational experiments that the iterative decomposition scheme is sensitive to an appropriate selection of the parameters $\alpha$ and $\beta$. Therefore, in our computational experiments we use $\alpha \in \left\{ {{0.0, 0.33, 0.66, 1.0, 1.33, 1.66, 2.0}} \right\}$ and $\beta \in \left\{ {{0.0, 0.33, 0.66, 1.0, 1.33, 1.66, 2.0}} \right\}$, i.e., we consider 49 different pairs in total. Hence, carrying out the computations on a multi-core computer is reasonable to reduce the computational burden. In the last experiment where we are interested in exploring the impact of the number of iterations vs. the amount of computing time per subproblem, we consider only $\alpha =0.66$ and $\beta =1.66$ to reduce the computational burden. Preliminary experiments were used to determine this specific setting.

The main characteristics of the different experiments are summarized in Table 3. Note that the first experiment refers to the eight small-sized instances to check the correctness of the implementation. The second experiment is for the instances specified in Table 1, whereas the third and fourth experiments are related to the impact of non-batching machines on the second stage and to a different amount of computing time for the subproblems, respectively.

5.3 Computational results

5.3.1 Results for small-size problem instances

We start by presenting results for the eight small-size problem instances described in Subsect. 5.1 (experiment 1 in Table 3). The corresponding computational results are summarized in Table 4.

We see from Table 4 that $\mathrm{{IDA}}( {\mathrm{{VNS}},15} )$ is always able to find the same TWT value as CPLEX. As expected, CPLEX was only able to prove the optimality of the solution for one problem instance. For this instance, a computing time of around 23 minutes is observed. For the remaining seven instances, the maximum computation time of 4 h was used. In Table 4, we mark the best TWT value for each instance in bold.

5.3.2 Results for large-size problem instances

We present the computational results for the 384 problem instances that are specified by the design of experiments summarized in Table 1 (experiment 2 from Table 3). In a first step, we compare the performance of $\hbox {IDA}( {\mathrm{TWD},1})$ with $\mathrm{{IDA}}({\mathrm{{BWEDD}},1})$. However, since the average TWT values of $\mathrm{{IDA}}( {\mathrm{{BWEDD}},1} )$ are around 25% larger than the corresponding values obtained by $\mathrm{{IDA}}({\mathrm{{TWD}},1})$, we decided not to perform additional experiments with the WEDD-based TWD scheme.

Next, we show the absolute average TWT values for the different bottleneck configurations in Table 5. Instead of comparing all problem instances individually, the instances are grouped according to factor levels such as number of jobs, number of families, etc. For example, results for $F_1 =6$ imply that all other factors have been varied, but the number of families for the first stage has been kept constant at 6.

In Table 5, we abbreviate the balanced machine situation by BL, while the situation where the bottleneck is at the first or at the second stage is abbreviated by BN1 and BN2, respectively. In addition, for the content of the column “Best” we first collect for each unique set of jobs that belongs to a factor level the TWT values of the corresponding problem instance with the best performance. The average of these values is taken for each factor level. This allows us to compare the different bottleneck configurations.

Table 5 Results for different bottleneck configurations and large-size problem instances

Note that the best performing bottleneck configuration for each group is marked in bold in Table 5 for $\mathrm{{IDA}}({\mathrm{{VNS}},20} )$ and $\mathrm{{IDA}}( {\mathrm{{TWD}},1} )$, respectively.

We show the corresponding results for ${\textit{Imp}}(\mathrm{{VNS}},20)$ in Table 6. Again, the largest improvements are marked in bold.

The difference between Tables 5 and 6 is that Table 6 better represents the improvements of $\mathrm{{IDA}}( {\mathrm{{VNS}},20} )$ compared to $\mathrm{{IDA}}( {\mathrm{{TWD}},1} )$ for a given bottleneck configuration. The average computing time of $\mathrm{{IDA}}( {\mathrm{{VNS}},20} )$ per problem instance is 422 s whereas the corresponding time for $\mathrm{{IDA}}( {\mathrm{{TWD}},1} )$ is only around 0.09 s.

Improvements of up to 21% on average are possible when $\mathrm{{IDA}}( {\mathrm{{TWD}},20} )$ is considered. We observe a similar behavior of the $\mathrm{{IDA}}( {\mathrm{{TWD}},20} )$ values with respect to the bottleneck configuration. It is interesting to see that the average computing time for 20 iterations is less than 2 s. Due to space limitations, we do not present the detailed results.

Table 6 ${\textit{Imp}}({ VNS},20)$ Values for large-size problem instances

5.3.3 Results for a flow shop with non-batching machines on the second stage

We continue by showing computational results for the 16 additional problem instances where non-batching machines are at the second stage (experiment 3 in Table 3). The corresponding ${\textit{Imp}}(\textit{VNS},20)$ values are presented in Table 7.

Table 7 ${\textit{Imp}}({ VNS},20)$ values for non-batching machines on the second stage

Again, best results are marked in bold. The average computing time for $\mathrm{{IDA}}( {\mathrm{{VNS}},20} )$ is around 431  s, while the corresponding time for $\mathrm{{IDA}}( {\mathrm{{TWD}},1} )$ is only 0.16 s.

5.3.4 Results for a varying amount of computing time for the subproblems

In experiment 4 from Table 3, we are interested in understanding the importance of the number of iterations for $\mathrm{{IDA}}({\mathrm{{VNS}},20})$ vs. the amount of computing time per subproblem. The values for ${ Imp}( {\mathrm{{IDA}}( {\mathrm{{VNS,MI}}})})$ and ${\textit{Imp}}( {\mathrm{{IDA}}( {\mathrm{{VNS,LT}}})} )$ obtained in a specific iteration are plotted as a function of the number of iterations in Fig. 5.

Fig. 5

${\textit{Imp}}\left( {\mathrm{{IDA}}\left( {\mathrm{{VNS,MI}}} \right) } \right)$ and ${\textit{Imp}}\left( {\mathrm{{IDA}}\left( {\mathrm{{VNS,LT}}} \right) } \right)$ values depending on the number of iterations

Note that the blue line corresponds to ${\textit{Imp}}( \mathrm{{IDA}}( \mathrm{VNS,}\mathrm{MI} ) )$, whereas the red line is used to represent ${\textit{Imp}}( \mathrm{IDA}( \mathrm{VNS,}\mathrm{LT} ) )$. The average improvement of MI is 34%, while we observe 32% for LT.

5.4 Analysis and discussion of the computational results

We know from Table 4 that the MIP approach and $\mathrm{IDA}( \mathrm{VNS},15 )$ obtain the same results. This indicates that $\mathrm{IDA}(\mathrm{VNS,}\mathrm{iter}_{\max } )$ is correctly implemented and leads to high-quality solutions (at least) for small-size problem instances. We also see from Table 4 that $\mathrm{{IDA}}( {\mathrm{{TWD}},1} )$ is clearly outperformed by $\mathrm{{IDA}}( {\mathrm{{VNS}},15} )$. The average improvement is 15%. As expected, CPLEX was generally not able to prove the optimality for the solutions within 4 h of computing time.

The results presented in Table 5 clearly show that the balanced bottleneck configuration BL leads to the smallest average TWT values. This is also confirmed by the results collected in the columns with the Best label. We also see that the $\mathrm{{IDA}}( {\mathrm{{VNS}},20} )$ scheme clearly outperforms the $\mathrm{{IDA}}( {\mathrm{{TWD}},1} )$ approach. This statement is also supported by Table 6 where the relative improvements of $\mathrm{{IDA}}( {\mathrm{{VNS}},20} )$ compared to $\mathrm{{IDA}}( {\mathrm{{TWD}},1} )$ are shown.

Up to 60% improvement can be observed by $\mathrm{IDA}(\mathrm{VNS},20 )$ in the a = 0.75 case (widespread ready times). The largest average improvement is obtained for the balanced bottleneck configuration. We observe an improvement of around 40% in this situation. Note that the $\mathrm{{IDA}}( {\mathrm{{TWD}},20} )$ approach leads only up to 21% improvement on average (not shown). The largest improvements are obtained in the case of a small number of families and jobs, widespread ready times, and tight due dates. This behavior is expected because widespread ready times and tight due dates make the decomposition approach more important. When the number of families or the number of jobs is large, the scheduling problem is harder to solve.

We also see from Table 6 that the largest improvements are often obtained for the balanced bottleneck configuration because there is much room for optimization in this situation. A different behavior is observed in the situation where the first stage is the bottleneck and $\left( {B_1 ,B_2 } \right) =\left( {2,4} \right)$. It seems that $\mathrm{{IDA}}({\mathrm{{VNS}},20})$ is able to make better batching decisions in case of tight offered capacity. A similar behavior can be observed for the situation where the bottleneck is on the second stage and we have $\left( {B_1 ,B_2 } \right) =\left( {4,2} \right)$.

We see from Table 7 that the importance of the different factors is much smaller when the second stage consists of non-batching machines, i.e., if we have $\left( {B_1 ,B_2 } \right) =\left( {4,1} \right)$. In contrast to the results obtained for the general case, the improvements are fairly small, i.e., around 19% while we have around 40% in the general setting.

When we compare the impact of the number of iterations vs. the amount of computing time, we see from Fig. 5 that MI is slightly outperformed by LT from iteration 11–18. But for iteration 19 and 20, MI performs slightly better. This behavior is also confirmed by the improvements of around 34% for MI and only 32% for LT. In addition, we observe from Fig. 5 that using more than 20 iterations does not offer any advantage in case of MI.

We can summarize our insights from the computational experiments as follows:

• 1. A balanced bottleneck configuration is preferable since the TWT values are smaller than in the two other situations, and the largest improvements are possible for the iterative decomposition schemes.

• 2. If there are bottleneck stages for batch processing machines then a small maximum batch size offers some advantage in this situation. This observation is supported by the common practice in real-world wafer fabs to prescribe a minimum batch size in cases where there is a large maximum batch size to avoid poor performance because of undesirable batching decisions.

• 3. Performing a lot of iterations does not generally pay off. Using 20 iterations is enough. A fairly small amount of computing time is enough to solve the subproblems using the proposed VNS scheme.

• 4. The performance of the proposed iterative decomposition scheme is sensitive to its appropriate parameterization. From a computing point of view, the use of the iterative decomposition heuristic with VNS-based subsolution procedures with many $\left( {\alpha ,\beta } \right)$ pairs from a grid is only possible if multi-core computers are applied to solve the scheduling problem.

• 5. If the time for decision making is crucial, then the iterative decomposition variant with TWD-type subproblem solution procedures should be used. In this situation even, a grid search for appropriate $\left( {\alpha ,\beta } \right)$ pairs is possible without using multi-core machines.

6 Conclusions and future research

In this paper, we discussed a scheduling problem for a two-stage flexible flow shop that includes batch processing machines on each stage. Problems of this type arise in wafer fabs. An iterative decomposition approach was proposed. It is based on the idea to select internal due dates and ready times for the jobs at the first and second stage, respectively. Based on these internal due dates and ready times, the overall scheduling problem is decomposed in a series of scheduling problems for parallel batch processing machines. A time window decomposition scheme and a VNS approach are used to solve these scheduling problems. Extensive computational experiments on randomly generated problem instances are used to demonstrate that the proposed iterative decomposition approach leads to high-quality solutions in a short amount of computing time. A fairly small amount of iterations within the decomposition scheme is enough. Comparing the results of the iterative scheme including VNS-based subproblem solution procedures with the results obtained after the first iteration and the TWD approach for solving the two subproblems, we clearly see the advantage of performing more than a single iteration. The iterative update scheme is easier to implement than conventional SBH-type approaches since specific additional batching nodes are not required. We observed that it is worthwhile to consider machine configurations that lead to a balanced workload of the two stages. If bottleneck configurations cannot be avoided, then a small maximum batch size at the bottleneck stage offers some advantage.

Note that the iterative decomposition approach with VNS-based subproblem solution procedures tends to be time-consuming since appropriate parameter values for the iterations are required. To deal with this problem, multi-core computers can be applied. If no such computers are available and the time for decision making is a constraint, then the iterative decomposition scheme with subproblem solution procedures based on the time window decomposition can be applied. However, the performance improvement of this heuristic is much smaller.

There are several directions for future research. First of all, we are interested in extending the researched problem by modeling more real-world details such as unrelated parallel machines on each stage, machine dedications (i.e., only certain job families are allowed on specific machines), and machine-specific maximum batch sizes. Another avenue for fruitful research is given by including time constraints between the first and the second stage, i.e., the start of an operation on the second stage has to be completed within a prescribed time window; otherwise, the job will be scraped due to contamination effects (cf. Klemmt and Mönch 2012 for a more general discussion of time constraints in semiconductor manufacturing).

It is also interesting to spend more effort to parallelize the scheduling heuristics. We believe that it is worthwhile to apply graphics processing unit (GPU) computing techniques to tackle problem (1). This direction is especially important to reduce the effort to select instance-specific $\left( {\alpha ,\beta } \right)$ parameters in combination with using VNS to solve the subproblems. It seems that another fruitful application of parallelization approaches is sampling techniques that are used to deal with uncertain data (cf. Shahnaghi et al. 2016) because of the huge computational burden in this situation. Another interesting direction is to avoid the grid search approach for choosing instance-specific $\left( {\alpha ,\beta } \right)$ parameters. We believe that it is possible to extend the machine learning approaches proposed in Mönch et al. (2006) to select parameters of BATC-type rules to the present situation. Moreover, we are interested in designing a VNS scheme that avoids the stage-based decomposition. We expect that is possible to extend the approach from Liao and Huang (2010) to the situation of batch processing machines.

As a last research direction, we expect that it is possible to apply the proposed iterative decomposition approach also for flexible flow shops with serial batching machines and batch availability when due date-oriented performance measures are considered (cf. Shen et al. 2013, 2014 for corresponding parallel machine scheduling problems).