A simultaneous and iterative approach for parallel machine scheduling with sequence-dependent family setups

Abstract

In this paper, we address a parallel machine scheduling problem to minimize the total weighted completion time, where product families are involved. Major setups occur when processing jobs of different families, and sequence dependencies are also taken into account. Considering its high practical relevance, we focus on the special case where all jobs of the same family have identical processing times. In order to avoid redundant setups, batching jobs of the same family can be performed. We first develop a variable neighborhood search algorithm (VNS) to solve the interrelated subproblems in a simultaneous manner. To further reduce computing time, we also propose an iterative scheme which alternates between a specific heuristic to form batches and a VNS scheme to schedule entire batches. Computational experiments are conducted which confirm the benefits of batching. Test results also show that both simultaneous and iterative approach outperform heuristics based on a fixed batch size and list scheduling. Furthermore, the iterative procedure succeeds in balancing solution quality and computing time.

1 Introduction

1.1 Problem description

In this study, we address an identical parallel machine scheduling problem where product families are involved. The objective is to minimize the total weighted completion time (TWC). Each product family contains jobs with similar requirements in tooling and operation sequences. As a result, major setup times are inevitable whenever a machine switches from processing jobs in one family to those in another family.

Furthermore, we take into account sequence dependencies, which are commonly deemed as one of the most difficult aspects in scheduling (Laguna 1999). The length of setup times depends on the similarity in technological requirements for the two consecutive families. Typically, the greater the dissimilarities, the larger is the setup time required. Applications are frequently encountered, especially in printing, food processing, textile industries, as well as in container manufacturing (Barnes and Vanston 1981; White and Wilson 1977). It is generally assumed that sequence-dependent setup times are subject to the triangular inequality:

$$\begin{aligned} s_{fg}\le s_{ff^{\prime }}+s_{f^{\prime }g}\quad \forall f\ne g, \end{aligned}$$

(1)

where $s_{fg}$ denotes the sequence-dependent family setup time between jobs of families $f$ and $g$. This condition indicates that a switch of processing from jobs in family $f$ through $f^{\prime }$ to jobs in another family $g$ causes longer delay than a direct changeover between families $f$ and $g$.

In order to balance setup times and completion times, it is beneficial to divide a product family into separate batches. Jobs belonging to the same batch are then processed in a consecutive manner. Here we assume batch availability requiring that a job is not available until the entire batch to which it belongs is completed. Therefore, all jobs of the same batch have the same completion time, and the processing time of a batch is equal to the sum of the processing times of its jobs. Practical applications arise when, for example, the jobs in a batch are placed on pallets, containers, or boxes which can only be removed upon the completion of the last job (Potts and Kovalyov 2000).

In addition, we focus on the special case of identical jobs, i.e., jobs of the same family have identical processing times. Moreover, a distinct weight is assigned to each job in a family. From a practical point of view, this is a reasonable assumption. Since product families are formed based on technological similarities, the difference in the processing times of jobs belonging to the same family is negligible. In fact, this case is known to be highly relevant in manufacturing industries (Mosheiov et al. 2004), such as repetitive production of similar items and heating process of chemical purification. On the other hand, priorities differ among jobs of the same family. In this context, customized components and models produced according to specific customer requirements represent typical examples.

We have proved in Shen et al. (2012) that the specific parallel machine problem outlined here is NP-hard even in the unweighted case. To solve this scheduling problem, three subproblems—batch sizing, batch assignment, and batch sequencing—are to be synchronized. On the other hand, an iterative procedure is also desirable with respect to computing time.

1.2 Literature review

A comprehensive survey of scheduling research involving setup times can be found in Allahverdi et al. (1999); Cheng et al. (2000), and Allahverdi et al. (2008). While sequence independent setup times are widely studied, problems involving sequence-dependent setup times received comparatively less attention. (cf. Aldowaisan and Allahverdi (1998); Allahverdi (2000); Allahverdi and Aldowaisan (1998); Gupta and Tunc (1994) for two-machine flow-shop scheduling with sequence independent setup times, and Han and Dejax (1994); Rajendran and Ziegler (1997) for a flow-shop with $m$ stages.) By considering sequence-dependent setup times in scheduling problems, one of the objectives must attempt, either implicitly or explicitly, to minimize the total setup time. This makes these scheduling problems resemble the classical traveling salesman problems to varying extents. There is extensive literature on TSPs and their extensions. These methodologies are directly applicable to the single-stage problems by suitably modifying them to process a dummy job at the start and at the end of the sequence (Srikar and Ghosh 1986).

Regarding the scheduling problem with batch availability assumption, a significant body of existing literature in this area focuses on single-machine problems. Coffman et al. (1990) prove that for the problem with one family and the total completion time objective, an optimal schedule exists where jobs are sequenced in SPT order. The authors also show that the problem is solvable in $O(n\log n)$ time. Alternatively, van Hoesel et al. (1994) provide the complexity of $O(n)$ by using geometric techniques. For a given job sequence, Albers and Brucker (1993) show that a dynamic program solves the problem with the TWC objective in $O(n)$ time. Cheng et al. (1994) address the problem with an arbitrary number of families and the total completion time (TC) objective. They show that there is an optimal schedule in which the jobs within each family are sequenced in SPT order. Based on the studies of Monma and Potts (1989) and Coffman et al. (1990); Cheng et al. (1994) also propose a backward dynamic programming algorithm with batch insertion that requires $O\left( n^F\right)$ time, where $F$ denotes the number of families. Hurink (1998) compares various tabu search algorithms for the problem with alternative objective TWC. Whereas two adjacent jobs are interchanged for the transpose neighborhood, a job is reinserted into a distant new position in the restricted insert neighborhood. Computational results for instances with up to 200 jobs show that these two methods perform similarly well. Moreover, the best quality solutions are obtained with a combined approach iterating between the two neighborhoods.

Another stream of research concerns family scheduling in manufacturing cells. However, these studies are exclusively subject to job availability (cf. Reddy and Narendran 2003; Franca et al. 2005; Logendran et al. 2006; Hendizadeh et al. 2008). In order to reduce the scheduling difficulty, the group technology assumption is also imposed, where a batch must contain an entire family.

Concerning solution methods, metaheuristics have been widely applied to various scheduling problems. Among them variable neighborhood search (VNS) approaches belong to the most promising ones (cf. Almeder and Mönch 2011; Wang and Tang 2009; Rocha et al. 2007; Driessel and Mönch 2011). Therefore, we develop our algorithm using the structure of VNS.

To the best of our knowledge, the problem researched in this paper has not been discussed in the literature. In Shen et al. (2012), we only addressed the unweighted case. This paper is an extended version of Shen et al. (2011). It contains a new VNS scheme and extensive computational experiments.

The remainder of the paper is organized as follows: We describe the problem settings in the next section, where a MIP formulation is also presented. Section 3 proposes a variable neighborhood search algorithm to solve the problem simultaneously. In order to save computing time, we develop an iterative procedure consisting of a specific heuristic for batch formation and a VNS for scheduling batches in Sect. 4. Detailed computational results are reported in Sect. 5. This paper concludes with Sect. 6.

2 Problem formulation

2.1 Problem setting

Indices

• $i, j = 1,\ldots , n$              Job indices

• $b,b^{\prime },c,d = 1,\ldots , B$   Batch indices

• $f,g, h = 1,\ldots , F$        Family indices

• $k,k^{\prime },l = 1,\ldots , m$        Machine indices

Parameters

$\mathcal{B }_{bk}$ :

The $b$th batch on machine $k$

$\mathcal{F }_f$ :

Family $f$

$n_f$ :

Total number of jobs in family $f$

$M$ :

Sufficient large number

$p_f$ :

Processing times of jobs in family $f$

$s_{0f}$ :

Initial setup of family $f$

$s_{fg}$ :

Sequence-dependent family setup time

$w_j$ :

Weight of job $j$

$W_{bk}$ :

Aggregate weight of all jobs included in batch $b$ on machine $k$

$B_k$ :

Total number of batches assigned to machine $k$

$\beta _{jf}$ :

Parameter, equals 1 if job $j$ belongs to family $f$ and 0 otherwise

Decision variables

$C_j$ :

Completion time of job $j$

$t_{bk}$ :

Start time of the $b$th batch on machine $k$

$x_{jbk}$ :

Binary variable, equals 1 if job $j$ is assigned to batch $b$ on machine $k$

Assume that a set of $n$ jobs and a set of $m$ identical parallel machines are given. All jobs are simultaneously available. The jobs are partitioned into $F$ families according to their similarities. The processing times of all jobs of the same family $f$ are identical and denoted by $p_{f}$. There are sequence- dependent family setup times $s_{fg}>0$, when a job of family $g$ is immediately preceded by a job of family $f$ with $f \ne g$. Furthermore, we assume that $s_{ff}$ takes a small positive value instead of being 0, if two consecutive jobs of the same family are grouped into different batches. Otherwise, batch availability becomes a restrictive assumption, and item availability is desirable for any batch size greater than 1. This setting is also motivated by practical applications since a moderate time is often inevitable for preparing batch processing. In this context, rearranging tools, repositioning work-in-process material, or restocking component inventories, for instance, becomes necessary regardless of the family of batches. When a job of family $f$ is the first one processed on a certain machine, then the family setup time is denoted by $s_{0f}$. Pre-emption of the processing of batches is not allowed, i.e., once one job of a batch is started on a certain machine then all jobs of this batch have to be processed on this machine without interruption.

The problem can be represented using the $\alpha |\beta |\gamma$ notation from scheduling theory (cf. Graham et al. 1979) as follows:

$$\begin{aligned} P|s-{\text{ batch}},F,s_{fg}|{\text{ TWC}}, \end{aligned}$$

(2)

where $P$ refers to identical parallel machines and $s-batch$ to serial batching with batch availability. Under the $\beta$-field, we also have product families denoted by $F$, and the setup times $s_{fg}$. Finally, the performance measure is the total weighted completion time $\mathrm{TWC}:=\sum _{j=1}^{n} w_jC_{j}$.

2.2 MIP formulation

The specific scheduling problem (2) can be formulated as follows:

Objective:

$$\begin{aligned} \min \sum \limits ^n_{j=1}w_jC_{j} \end{aligned}$$

(3)

Subject to:

$$\begin{aligned}&\sum \limits ^B_{b=1}\sum \limits ^m_{k=1}x_{jbk}=1\quad \forall j \end{aligned}$$

(4)

$$\begin{aligned}&x_{ibk}\le \beta _{if}-\beta _{jf}-x_{jbk}+2\quad \forall i < j, b, k, f \end{aligned}$$

(5)

$$\begin{aligned}&t_{bk}\ge s_{0f}\quad \forall b \subseteq \mathcal{F }_f, k \end{aligned}$$

(6)

$$\begin{aligned}&t_{ck}\ge t_{bk}+s_{fg}x_{jbk}+\sum \limits ^n_{j=1}x_{jbk}p_f \nonumber \\&\forall b \subseteq \mathcal{F }_f, c \subseteq \mathcal{F }_g, b<c,j, k \end{aligned}$$

(7)

$$\begin{aligned}&C_{j}\ge t_{bk}+\sum \limits _{i=1}^n x_{ibk}p_f-(1-x_{jbk})M\quad \forall b \subseteq \mathcal{F }_f, j, k.\nonumber \\ \end{aligned}$$

(8)

The objective is to minimize the total weighted completion time (3). Constraints (4) require that each job is grouped into one and only one batch. Note that $B$ defines the maximum number of batches. This parameter does not restrict the formulation when we set $B=n$.

Constraints (5) ensure that a batch contains only jobs of the same family. For illustrating these constraints, concrete cases are given as follows:

$$\begin{aligned} \beta _{if}\!-\!\beta _{jf}\!-\!x_{jbk}\!+\!2\!=\! \left\{ \begin{array}{l@{\quad \text{ for}\quad }l} 1&i, j\in \mathcal{F }_{f}, j\in \mathcal{B }_{bk}\\ 2&i, j\in \mathcal{F }_{f}, j\not \in \mathcal{B }_{bk}\\ 2&i\in \mathcal{F }_{f}, j\not \in \mathcal{F }_{f},j\in \mathcal{B }_{bk}\\ 3&i\in \mathcal{F }_{f}, j\not \in \mathcal{F }_{f}, j\not \in \mathcal{B }_{bk}\\ 0&i\not \in \mathcal{F }_{f}, j\in \mathcal{F }_{f}, j\in \mathcal{B }_{bk}\\ 1&i\not \in \mathcal{F }_{f}, j\in \mathcal{F }_{f}, j\not \in \mathcal{B }_{bk}\\ 1&i, j\not \in \mathcal{F }_{f},j\in \mathcal{B }_{bk}\\ 2&i, j\not \in \mathcal{F }_{f}, j\not \in \mathcal{B }_{bk}.\\ \end{array}\right. \end{aligned}$$

Obviously, these constraints are only relevant to the case where jobs $i$ and $j$ belong to different families and $j$ is grouped into batch $b$ (that is, $\beta _{if}-\beta _{jf}-x_{jbk}+2=0$). As a result, job $i$ must not be assigned to the same batch as $j$ (that is, $x_{ibk}=0$). In all other cases, the value of $x_{ibk}$ is not decidable and constraints (5) are not violated.

Constraints (6) indicate that an initial setup time is incurred before processing the first batch on each machine. If $b=1$ holds, inequality $t_{bk}\ge s_{0f}$ for $b\in \mathcal{F }_f$ must be satisfied. For the case with $b\ne 1$, we assume that the batches processed before $b$ on machine $k$ belong to families $g, g^{\prime },\ldots ,f^{\prime }$ in that order. Thus,

$$\begin{aligned} t_{bk}\ge s_{0g} + s_{gg^{\prime }}+\cdots +s_{f^{\prime }f}, \end{aligned}$$

where only setup times are considered, and processing times of batches are not included. According to the triangular inequality, it follows

$$\begin{aligned} t_{bk}\ge s_{0g^{\prime }} +\cdots +s_{f^{\prime }f}. \end{aligned}$$

Applying the triangular inequalities repeatedly leads to

$$\begin{aligned} t_{bk}\ge s_{0f}. \end{aligned}$$

Therefore, the constraints concerning initial setup times can be generalized as written in expression (6).

Constraints (7) are then incorporated to determine batch sequences regarding setup times. It should be pointed out that batches are ordered according to their indices. Since batch compositions can be inconsistent on machines ($x_{jbk}\ne x_{jbk^{\prime }}$), a batch here is merely a symbol containing certain jobs. Thus, the predetermination of batch sequences does not limit the flexibility of the formulation.

Furthermore, batch completion time is determined by batch start time ($t_{bk}$) and the aggregate processing time of jobs. According to the expression $\sum \nolimits ^n_{j=1} x_{jbk}p_f$, only the processing times of the jobs grouped into the corresponding batch are taken into account, since $x_{jbk}$ is equal to 0 otherwise. We note that an empty batch does not affect the start time of other batches since neither setup time nor processing time of empty batches is considered ($x_{jbk}=0$ for all $j$).

According to constraints (8), the completion time of each job is determined by the start time and the processing time of the batch to which it belongs.

We implement this MIP formulation using Lingo 10.0 to solve small-sized problem instances, which is elaborated in Sect. 5.

3 Simultaneous approach

In this section, we start by describing a simple list scheduling approach that provides reference schedules. A VNS algorithm is then presented which solves the batch sizing, batch assignment, and batch sequencing problem simultaneously.

3.1 List scheduling approach

Our list scheduling heuristic is motivated by the fact that the SWPT dispatching rule is widely applied and provides fair performance for P||TWC. We first assume that all batches have the same maximum batch size $B_\mathrm{max}$ and that all batches consist of $B_\mathrm{max}$ jobs, except that the last batch of each family may contain a smaller number of jobs. We call the resulting procedure SWPT for abbreviation. Note that SWPT does not make any decisions with respect to the number of jobs within a batch. Furthermore, setup aspects are not taken into account either. The heuristic can be described as follows.

	SWPT Algorithm
(1)	Sort all jobs with respect to non-decreasing values of the index $I^0_{j}\!:=\!\!p_f/w_j,\, j\!\in \!\mathcal{F }_f$.
(2)	Select an unscheduled job $j$ with smallest $I^0_{j}$ value for the machine with the smallest availability time.
(3)	Form the batch by adding the next $min(B_{max},\tilde{n}_{f})$ jobs of family $f$ from the list obtained in Step (1), where $\tilde{n}_{f}$ denotes the number of jobs of family $f$ that are unscheduled. Update machine availability.
(4)	Start with Step (2) as long as there are jobs left unscheduled.

In order to integrate family setup times, we present three additional variants for calculating the index $I_j$. Except for the determination of $I_j$, the modified list scheduling follows the same procedure as the original SWPT.

• 1. In the first modification, the index is determined by

  $$\begin{aligned} I^1_j = \frac{\bar{s}_{f}+p_f}{w_j},\, j\in \mathcal{F }_f, \end{aligned}$$

  (9)

  where $\bar{s}_{f}$, also known as effective family setup time, can be written as:

  $$\begin{aligned} \bar{s}_{f}=\frac{1}{F}\sum \limits ^{F}_{g=1}s_{gf}. \end{aligned}$$

  (10)

  We refer to this modified list scheduling as LS-M1.

• 2. For the second variant (LS-M2), the index is calculated as

  $$\begin{aligned} I^2_j=\frac{s_{gf} + p_f}{w_j},\, j\in \mathcal{F }_f, \end{aligned}$$

  (11)

  where the batch scheduled directly before job $j$ belongs to family $g$. The corresponding setup time $s_{gf}$ is thus included in the calculation. For this variant, the index $I^2_j$ is to be adjusted after sequencing each new batch, and calculated again according to the current partial schedule.

• 3. The third variant (LS-M3) combines the previous two methods, where the index can be expressed as

  $$\begin{aligned} I^3_j=\left( \frac{p_f}{w_j}\right) \exp \left( {\frac{s_{gf}}{\bar{s}_{f}}}\right) \, j\in \mathcal{F }_f \end{aligned}$$

  (12)

  with $s_{gf}$ and $\bar{s}_{f}$ similarly defined as in LS-M1 and LS-M2.

• 4. Furthermore, we apply another modified list scheduling (LS-M4) to dynamically determine batch sizes, instead of using $B_\mathrm{max}$. Jobs are first sorted according to index $I^0_j$ as in SWPT. We then select an unscheduled job with smallest index and form a new batch $\mathcal{B }$. Afterwards, the next job of the same family in the list is added to the batch as long as the parameter $T$ does not exceed a prescribed value $T_\mathrm{max}$. In this context, $T$ is determined by

  $$\begin{aligned} T=\frac{s_{gf}+\sum \limits _{j\in \mathcal{B }}p_j}{\sum \limits _{j\in \mathcal{B }}w_j}, \, j\in \mathcal{F }_f. \end{aligned}$$

  (13)

  It is obvious that the $T$ value is to be updated according to the current batch composition. We repeat this procedure until no job is left unscheduled. Due to the different values of $p_f$ and $w_j$, the resulting batch sizes can vary widely.

3.2 Variable neighborhood search algorithm

VNS is a local-search-based metaheuristic (cf. Mladenovic and Hansen 1997; Hansen and Mladenovic 2001). The basic idea is to enrich a simple local-search method to enable it escaping from local optima. This is done by restarting the local search from a randomly chosen neighbor of the incumbent solution. This restarting step, so-called shaking, is performed using different neighborhoods of increasing sizes. There are many different variations of that VNS idea, such as variable neighborhood descent (VND) or reduced VNS (RVNS). In this paper, we will apply basic VNS (BVNS).

The VNS algorithm designed for scheduling problem (2) operates on the final solution representation, i.e., each job is assigned to a batch and each batch is assigned to a certain position on a machine. Batches are formed according to simple heuristics or the scheme described in the previous section.

The proposed local-search method used for BVNS consists of two different steps. The first step is balancing the workload of the machines. If the last batch of the machine with the maximum completion time starts later than the completion time of the machine with the smallest workload, the batch is moved to that machine. This step is repeated until no batch can be moved. We will call this improvement step balancing.

The second step is the application of a single-machine decomposition heuristic of Mehta and Uzsoy (1998). Since job sequences of each batch are not relevant, we focus only on batch sequences. From an initial sequence of batches for each machine, a sub-sequence of size $\lambda$ is solved to an optimal sequence using complete enumeration. We consider all the $\lambda !$ different subsequences. The first $\alpha$ batches of the optimal sub-sequence are fixed into the final sequence, and the next $\lambda$ unscheduled batches are considered. This process is repeated until all batches are scheduled and no improvement is made in the TWC value of the final sequence. A maximum number of $iter$ iterations are allowed. The larger the value of $\lambda$, the higher is the computation time and the better the solution quality. We call the local-search procedure based on the decomposition heuristic $DH(\lambda ,\alpha ,iter)$.

Next, we define seven classes of neighborhood structures $\mathcal{N }_{a}$, which concern individual jobs as well as entire batches:

• 1. $MoveBatch(n)$: Randomly select a batch from a machine and remove it. Insert it in a random position on another randomly selected machine. Repeat this step $n$ times.

• 2. $SwapBatch(n)$: Randomly select two batches from different machines and exchange their positions. Repeat this step $n$ times.

• 3. $SwapSeq(n)$: Randomly select two positions on different machines and exchange the batch sequences starting from that position of at most length $n$ ($n$ or all remaining batches).

• 4. $MoveJob1(n)$: Randomly select a job of a batch and remove it. Insert it in a randomly selected batch of the same family. Repeat this step $n$ times.

• 5. $MoveJob2(n)$: For batches with more than one job, randomly select two jobs of the same batch and remove them. Insert them in two randomly selected batches of the same family. Repeat this step $n$ times.

• 6. $MoveJob3(n)$: For batches with more than two jobs, randomly select three jobs of the same batch and remove them. Insert them in three randomly selected batches of the same family. Repeat this step $n$ times.

• 7. $SwapJob(n)$: Randomly select two jobs from different batches of the same family and exchange their positions. Repeat this step $n$ times.

Note that to obtain a new solution/neighbor, the move defined for each neighborhood is implemented $n$ times. The search then proceeds with a neighbor randomly selected from an entire neighborhood. Whereas the first three neighborhood functions consider batch sequences, the last four functions focus on varying batch sizes and batch compositions. More specifically, neighborhoods 1–3 also change the current assignment of batches. Neighborhoods 4–6, in principle, define the same type of moves. Since batches of the same family can be processed on different machines, such moves are also able to re-allocate jobs besides varying batch sizes. Therefore, we allow a simultaneous removal of up to three jobs in the same batch, each of them is then inserted in an individual position.

Finally, we select the sequence in which the neighborhood structures are applied. We determine the sequence as shown in Table 1 based on several pilot runs. Note that move and swap operations are different and one is not a special case of the other. Combined neighborhood structures containing move and swap operations are thus not nested.

Table 1 Sequence of neighborhood structures used for BVNS

The tailored BVNS (TBVNS) approach used in this research can be summarized as follows:

	TBVNS Algorithm
	Initialization:
(1)	Define the neighborhood structures $\mathcal{N }_{a},a=1,\ldots ,29$.
(2)	Generate an initial solution $y$ using SWPT.
(3)	Set $a=1$.
(4)	Repeat until stopping criterion is met:
	Loop:
(a)	Shaking: Select randomly $y^{\prime } \in \mathcal{N }_{a}(y)$.
(b)	Local search: Improve $y^{\prime }$ by balancing and $DH(5,2,10)$.
(c)	Accept? If $y^{\prime }$ is better than $y$, then $y \leftarrow y^{\prime }$ and $a \leftarrow 1$. Otherwise set $a \leftarrow (a \mod \! 29)+1$.

4 Iterative approach

Note that the VNS algorithm activates the embedded local search repeatedly which can be computationally expensive. In order to solve larger instances within less computing time, we also develop an iterative procedure for the same problem. A so-called batch variation procedure (BVP) is proposed to form batches for each product family. Afterwards, we adjust our VNS approach to sequence batches on machines. Finally, the two procedures are combined within an iterative scheme.

4.1 Batch variation procedure

4.1.1 Variation on a single machine

In order to justify the batch variation procedure, we first present some properties and observations regarding batch variation and objective value. Let $W_{bk}$ and $C_{bk}$ be the aggregate weight of all jobs included in $\mathcal{B }_{bk}$ and the completion time of $\mathcal{B }_{bk}$, respectively.

Theorem 1

Moving a job $i$ from $\mathcal{B }_{ck}\in \mathcal{F }_f$ to a batch $\mathcal{B }_{dk}$ of the same family improves the current total weighted completion time if $\Delta C> 0$ holds, where

$$\begin{aligned} \Delta C=\left\{ \begin{array}{l@{\quad \text{ for}\quad }l} \sum \limits ^{d-1}_{b=c} W_{bk}p_f-w_{i}(C_{dk}-C_{ck}+p_f)&c<d,\\ w_i(C_{ck}-C_{dk}-p_f)-\sum \limits ^{c-1}_{b=d}W_{bk}p_f&c>d.\\ \end{array}\right. \end{aligned}$$

Proof

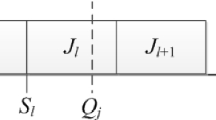
First of all, it is obvious that the schedules on machines $l\ne k$ remain unchanged. Two-related cases are illustrated in Figure 1.

• Case 1. By removing job $i$ from batch $\mathcal{B }_{ck}$, the completion time of the batches $\mathcal{B }_{ck}, \,\mathcal{B }_{(c+1)k}, \,\ldots , \,\mathcal{B }_{(d-1)k}$ is improved by $p_f$. Note that if $i$ is a single job in the batch, then $\mathcal{B }_{ck}$ does not exist after the removal. Assume that the batches preceding and following $\mathcal{B }_{ck}$ belong to families $g$ and $g^{\prime }$, respectively. The variation of setup time can be expressed as $s_{gf}+s_{fg^{\prime }}-s_{gg^{\prime }}$, which is not negative due to the triangular inequality. In case there are no preceding or/and following batches, this result holds as well. Therefore, the completion time can be further reduced by the difference of family setup times if $i$ is the only job in batch $\mathcal{B }_{ck}$. Thus, the reduction of TWC must not be smaller than

  $$\begin{aligned}&\qquad \sum \limits ^{d-1}_{b=c+1}W_{bk}p_f+ (W_{ck}-w_i)p_f+w_iC_{ck}\\&\qquad \qquad =\sum \limits ^{d-1}_{b=c} W_{bk}p_f-w_{i}(-C_{ck}+p_f). \end{aligned}$$

  Concerning job $i$, its new weighted completion time is not greater than $w_iC_{dk}$. Combining both derived terms, the total weighted completion time improves if

  $$\begin{aligned} \qquad \Delta C=\sum \limits ^{d-1}_{b=c} W_{bk}p_f-w_{i}(C_{dk}-C_{ck}+p_f)>0 \end{aligned}$$

  holds.

  Fig. 1

  

  Illustration of Theorem 1

• Case 2. Similarly, moving job $i$ in this case indicates that all jobs in batches $\mathcal{B }_{dk}, \,\mathcal{B }_{(d+1)k}, \,\ldots , \,\mathcal{B }_{(c-1)k}$ are delayed by $p_f$. If $\mathcal{B }_{ck}$ does not exist after removing $i$, then the completion time of all the following jobs on the same machine can be improved due to the reduced family setup time. Therefore, the decrease in the total weighted completion time is greater than

  $$\begin{aligned} \qquad \Delta C = w_i(C_{ck}-C_{dk}-p_f)-\sum \limits ^{c-1}_{b=d}W_{bk}p_f. \end{aligned}$$

$\square$

Lemma 1

Moving a job $i\in \mathcal{B }_{ck}\in \mathcal{F }_f$ to any batch $\mathcal{B }_{dk}$ of the same family can be beneficial.

According to Theorem 1, the variation of the total weighted completion time is actually a trade-off between the current completion times of the two-related batches ($C_{ck}, C_{dk}$) and the aggregate weight of all affected batches. The latter increases with the distance between batches $c$ and $d$. For instance, the further they are apart in the case with $c<d$, the larger is the increase in the completion time for $i$. On the other hand, the number of as well as the aggregate weight of jobs/batches scheduled in between grow accordingly. Therefore, moving a job to another batch of the same family can be beneficial in general.

Lemma 2

Moving a job in $\mathcal{B }_{ck}$ to $\mathcal{B }_{dk}$ of the same family with $c<d$ cannot improve the current total weighted completion time if moving the job with smallest weight in $\mathcal{B }_{ck}$ leads to $\Delta C\le 0$.

Given that batches $c$ and $d$ are scheduled on the same machine $k$, then the completion times $C_{ck}, C_{dk}$ and the aggregate weight of associated jobs are known as well. According to the expression $-w_{i}(C_{dk}-C_{ck}+p_f)$ stated in Theorem 1, the remaining jobs need not be examined since moving the job with smallest weight imposes least negative effect on the objective value. Similarly, we have the next lemma.

Lemma 3

Moving a job in $\mathcal{B }_{ck}$ to $\mathcal{B }_{dk}$ of the same family with $c>d$ cannot improve the current total weighted completion time if moving the job with largest weight in $\mathcal{B }_{ck}$ leads to $\Delta C\le 0$.

To summarize, Lemma 1 indicates that each and every batch of the same family deserves examination after removing a job from its original batch. Lemmas 2 and 3 imply that the most promising candidates are jobs with smallest and largest weights, respectively. Accordingly, we define the following moves for batch variation on a single machine.

• Move 1a. For a given batch $\mathcal{B }_{bk}\in \mathcal{F }_f$, remove the job with smallest weight and add it at the end of each following batch of the same family $f$ on the same machine $k$.

• Move 1b. For a given batch $\mathcal{B }_{bk}\in \mathcal{F }_f$, remove the job with largest weight and add it at the end of each previous batch of the same family $f$ on the same machine $k$.

• Move 1c. For a given batch $\mathcal{B }_{bk}\in \mathcal{F }_f$, remove the job with smallest weight and add it at the end of machine $k$.

According to Lemmas 2 and 3, jobs to be considered first are the ones with extreme weights in the corresponding batch. The placements are also divided into two groups (Move 1a and Move 1b). If moving these jobs does not improve TWC, the remaining jobs need not be examined. Furthermore, note that the job sequence inside a batch is irrelevant. Consequently, the removed jobs are then added at the end of a batch of the same family.

In addition, jobs with smallest weight are also placed at the end of each machine (Move 1c). This advances certain batches at the costs of delaying a single job. It also changes the total number of batches since the current number of batches may not be optimal and further splitting of batches can be advantageous.

In Shen et al. (2012), we used a separate splitting approach for solving a similar scheduling problem to minimze total completion time. However, in the presence of different weights, a general splitting strategy does not work. Therefore, we emphasize weights here and implement Move 1c.

Each type of move is performed repeatedly as long as an improvement occurs during the process. A detailed description of the procedure on a single machine is given below.

	BVP on a single machine
	Initialization:
(1)	Sort jobs $j$ in each batch according to non-increasing value of $w_j$.
(2)	Set $b=1, f=1$, and $k=1$.
(3)	If the number of batches of family $f$ on machine $k$ is greater than 1, repeat for all batches $b$:
	Loop:
(a)	Perform Move 1a and calculate $\Delta C$.
(b)	Perform Move 1b and calculate $\Delta C$.
(c)	Perform Move 1c and calculate $\Delta C$.
(d)	Accept? If $\Delta C>0$, then save the current TWC value and batch variation. Consider the next job with extreme weight in batch $b$ (job with smallest weight for Moves 1a and 1c, job with largest weight for Move 1b). Otherwise, perform the move with greatest improvement, and consider the next batch $b+1$.
(4)	Set $f\leftarrow f+1$ and repeat.
(5)	Set $k\leftarrow k+1$ and repeat.

4.1.2 Variation concerning two machines

In addition, we can derive the following property in a similar manner if batches $c$ and $d$ of the same family are scheduled on different machines. Let $B_k$ be the total number of batches assigned to machine $k$.

Theorem 2

Moving a job $i\in \mathcal{B }_{ck}\in \mathcal{F }_f$ to a batch $\mathcal{B }_{dl}$ of the same family with $l\ne k$ improves the current total weighted completion time if $\Delta C> 0$ holds, where

$$\begin{aligned} \Delta C= \left( \sum \limits ^{B_k}_{b=c} W_{bk}\!-\!\sum \limits ^{B_l}_{b=d}W_{bl}\right) p_f+w_{i}\left( C_{ck}-C_{dl}-2p_f\right) . \end{aligned}$$

Similarly, a reduction of the total weighted completion time again depends on the current completion times of the two-related batches ($C_{ck}, C_{dl}$) and the aggregate weight of all affected batches. Therefore, possible variations concerning all batches of the same family can be examined for improvement. Based on Theorem 2 and previous calculations, the following lemma is straightforward.

Lemma 4

Moving a job in $\mathcal{B }_{ck}$ to $\mathcal{B }_{dl}$ of the same family cannot improve the current total weighted completion time,

• 1. if moving the job with smallest weight in $\mathcal{B }_{ck}$ leads to $\Delta C\le 0$ for $C_{ck}\le C_{dl}$.

• 2. if moving the job with largest weight in $\mathcal{B }_{ck}$ leads to $\Delta C\le 0$ for $C_{ck}> C_{dl}$.

The procedure concerning two machines includes the following moves.

• Move 2a. For a given batch $\mathcal{B }_{bk}\in \mathcal{F }_f$, remove the job with the smallest weight and add it at the end of each batch of the same family $f$ on machine $l$.

• Move 2b. For a given batch $\mathcal{B }_{bk}\in \mathcal{F }_f$, remove the job with the largest weight and add it at the end of each batch of the same family $f$ on machine $l$.

• Move 2c. For a given batch $\mathcal{B }_{bk}\in \mathcal{F }_f$, remove the job with the smallest weight and add it at the end of machine $l$.

Regarding batches on different machines, jobs with either the smallest or largest weight are identified and moved into an arbitrary batch of the same family on another machine. Note that such moves concern not only batch sizing but also the assignment problem, and have higher improvement potential. Therefore, the completion times $C_{ck}$ and $C_{dl}$ are not explicitly considered here. More importantly, a greater number of moves are applied accordingly.

In addition to a process similar to that for single machines, we apply a procedure to balance machine load. There is a trivial property in this context: Moving the last jobs of a heavily loaded machine to another machine improves the completion time, as long as the removed jobs are not further delayed afterwards. Therefore, machines are to be sorted in a non-ascending order of the completion times of the last jobs processed on them. Batches on bottleneck machines thus have higher priority and are examined first to relieve bottlenecks. Removed jobs are then to be re-allocated on machines with smaller completion times. The entire procedure concerning two machines is summarized as follows.

	BVP on two machines
	Initialization:
(1)	Sort jobs $j$ in each batch according to non-increasing value of $w_j$.
(2)	Sort machines according to non-increasing completion times. (Machine $k=1$ is thus the bottleneck machine and Machine $k=m$ has the smallest completion time.)
(3)	Set $b=1, f=1 , k=1$, and $l= m$.
(4)	If the number of batches of family $f$ is greater than 1, repeat for all batches $b$:
	Loop:
(a)	Perform Move 2a and calculate $\Delta C$.
(b)	Perform Move 2b and calculate $\Delta C$.
(c)	Perform Move 2c and calculate $\Delta C$.
(d)	Accept? If $\Delta C>0$, then save the current TWC value and batch variation. Consider the next job with extreme weight in batch $b$ (job with smallest weight for Moves 2a and 2c, job with largest weight for Move 2b). Otherwise, perform the move with greatest improvement, and consider the next batch $b+1$.
(5)	Set $l\leftarrow l -1$ and repeat.
(6)	Set $f\leftarrow f+1$ and repeat.
(7)	Set $k\leftarrow k+1$ and repeat.

4.2 Scheduling batches based on VNS

Since the BVP performs a systematic and detailed variation on batch sizes, we adjust our VNS algorithm to focus solely on sequencing batches. As described in Sect. 3.2, neighborhood functions 1–3 are responsible for batch sequencing and batch assignment, which are then utilized in the iterative procedure. We sequence the reduced neighborhoods 1–11 as specified in Table 1.

4.3 Overall scheme

Starting with a solution determined by SWPT, VNS is first activated to improve the initial schedule by altering batch sequences. The current solution is then transferred to BVP once the stopping criterion of VNS is met. Based on the resulting batch sequence, BVP conducts a thorough batch size variation. Afterwards, batch formation is updated and VNS starts again with improved batch sizes. The entire iterative procedure is repeated until a prescribed maximum number of iterations ($MaxItr$) are reached. The overall procedure is called BVP–VNS for abbreviation.

	BVP–VNS Algorithm
	Initialization:
(1)	Generate an initial solution using SWPT.
(2)	Set $Itr=1$.
(3)	Repeat until $Itr=MaxItr$.
	Loop:
(a)	Run VNS until stopping criterion is met and update current batch sequence.
(b)	Run BVP until stopping criterion is met and update current batch size.
(c)	Set $Itr\leftarrow Itr + 1$.

5 Computational experiments

In this section, we first describe the design of our computational experiments. Then, we present the test results based on randomly generated problem instances. To the best of our knowledge, this specific parallel machine scheduling problem has not been addressed so far. Although similar problems can be found in Yalaoui and Chu (2003) and Tahar et al. (2006), both papers allow non-integer batch/lot-sizes to minimize makespan. Therefore, test results are not comparable. Considering the frequent application, especially the fair performance of list scheduling with SWPT rule, we use the best results provided by SWPT for comparison.

5.1 Design of experiments

The problem instances generated contain a varying number of families, and are tested on different number $m$ of parallel machines. A family is assigned to each job randomly. Hence, each family is allowed to contain a different number of jobs. An additional parameter $\mu$ is used here to regulate the total number of jobs $n$ with $n=\mu m$. The design of experiments is summarized in Table 2. Regarding setup times, we specify their values as given in Table 2 which also ensure that the triangular inequality is satisfied. Based on the defined intervals, $s_{ff}$ can sometimes be greater than small family setup times.

Table 2 Design of experiments

5.2 Results of the computational experiments

5.2.1 MIP formulation for small instances

First, we implement the MIP formulation in Lingo 10.0. However, only instances containing fewer than 10 jobs can be solved optimally within reasonable computing time (less than 20 s). When the problem size is slightly increased, such instances cannot be solved within 4 hours. Table 3 describes the resulting model size for increasing problem sizes, in terms of the number of variables, integer variables, constraints, and non-zeros.

Table 3 The model size with increasing problem sizes

Therefore, we use the MIP model to verify solutions obtained with our heuristics. For such very small-sized problem instances, both the simultaneous procedure TBVNS and the iterative approach BVP–VNS were able to reach optima.

5.2.2 Comparison of list scheduling procedures

The proposed list scheduling procedures SWPT, LS-M1, LS-M2, LS-M3, and LS-M4, as well as TBVNS and BVP–VNS are implemented using the C++ programming language. All the computational experiments are performed on an Intel Pentium 4, 3.40 GHz computer with 2 GB RAM.

To determine the value for $B_\mathrm{max}$, we ran some preliminary tests and decided on the values of 1, 2, and 4. The performance of the list scheduling heuristics strongly depends on the $B_\mathrm{max}$ value. Hence, $B_\mathrm{max}$ is a parameter of the heuristics. In general, the quality of the solutions for large instances improves with a slightly increased value for $B_\mathrm{max}$. Using $B_\mathrm{max}=4$ yields the best solutions on average. A further increase of $B_\mathrm{max}$, however, does not provide better TWC values. For SWPT, LS-M1, LS-M2, and LS-M3, we thus set $B_\mathrm{max}=1, 2$ and $4$. The best solutions of each approach are then chosen for comparison.

As for the selection of $T_\mathrm{max}$ in LS-M4, we have also run several tests which basically allow a batch size to range from 1 to $n_f$. Based on these tests, we set the maximum value as $T_\mathrm{max}=n\cdot \delta$ with $\delta \in \{1,3,5,7\}$. Again, the best solutions obtained from the four different $T_\mathrm{max}$ values are used as the results of LS-M4. The experiment is conducted on all 1440 instances.

Table 4 reports the performance of the list scheduling approaches in terms of relative percentage error which is determined by

$$\begin{aligned} \frac{{\text{ TWC}}_\mathrm{LS}-{\text{ TWC}}_{\min }}{{\text{ TWC}}_{\min }}\times 100, \end{aligned}$$

(14)

where TWC$_\mathrm{LS}$ denotes the best solution obtained using a specific approach and TWC$_{\min }$ the minimum value of all five applied list scheduling variants, respectively.

Table 4 Comparison of various list scheduling approaches

Obviously, the basic list scheduling approach SWPT outperforms the other variants. It implies that focusing on just processing time and weights $(p_f/w_j)$ can still yield satisfying solutions. This can be due to the fact that only one setup occurs for several jobs after forming batches. Moreover, considering sequence dependencies, the actual values of setup times are unpredictable. In comparison, specifying the setup times according to a concrete partial sequence, as in LS-M2, overly stresses the role of setup times. This may explain the difference in the performance of SWPT and LS-M2. Using the effective setup time $\bar{s}_{f}$ in LS-M1, on the other hand, provides better results than LS-M2. LS-M3 adopts both current setup $s_{gf}$ and the effective setup $\bar{s}_{f}$, and thus performs slightly better than LS-M1. As for LS-M4, a single $T_\mathrm{max}$ may be suitable for a given combination of $p_f$ and $w_j$, it can also lead to unfavorable large batches which then cause delays for the jobs included. The performance of LS-M4 is rather unstable and very poor on average.

Based on the overall good performance of SWPT, we use its solutions as references for comparison.

5.2.3 Comparison of TBVNS and BVP–VNS

Next, we compare the performance of the simultaneous approach (TBVNS) to the iterative procedure (BVP–VNS). Each problem instance is solved three times with different seeds and the average TWC values are taken.

As pointed out earlier, computing time plays a crucial role in this context, different amounts of computing time are therefore given for both TBVNS and BVP–VNS. We select one problem instance for each factor combination, and the algorithms are tested on 144 instances.

Compared to list scheduling approaches, BVP–VNS and TBVNS are relatively insensitive to a prescribed $B_\mathrm{max}$ value. Preliminary tests show that $B_\mathrm{max}=1$ is suitable for problem sizes of up to 60 jobs. For problem instances with 180 and 240 jobs, the best solutions are almost always found when using $B_\mathrm{max}=4$. Also note that, given the same amount of computing time, the TWC values for $B_\mathrm{max}>4$ cannot compete with the solutions from a smaller $B_\mathrm{max}$ value. Here, we again set $B_\mathrm{max}=1, 2$ and $4$.

Initially, experiments are performed when a small amount of computing time is given for TBVNS and BVP–VNS. More specifically, for instances with fewer than 60 jobs, 20 s are given for TBVNS while four iterations for BVP–VNS with 5 s per iteration are performed. For the larger problem instances, 40 s are given for TBVNS and $4\cdot 10$ s for BVP–VNS. In the next step, we doubled the computing time to 40 and 80 s, respectively. Whereas Table 5 shows detailed test results with 20/40 s, results with 40/80 s are summarized according to $n$ in Table 6. The columns with $B_\mathrm{max}=1, 2$ and $4$ indicate that the improvement is achieved using an initial solution with the parameter $B_\mathrm{max}=1, 2$ and $4$, respectively.

Table 5 Comparison of TWC improvement (%) for TBVNS and BVP–VNS regarding SWPT with 20/40 s

Table 6 Comparison of TWC improvement (%) for TBVNS and BVP–VNS regarding SWPT with 40/80 s

The TWC improvement in percent is calculated regarding the best reference solution obtained with SWPT. In the column for BVP–VNS, we determine the improvement as follows:

$$\begin{aligned} \frac{{\text{ TWC}}_\mathrm{SWPT}-{\text{ TWC}}_\mathrm{BVP-VNS}}{{\text{ TWC}}_\mathrm{SWPT}}\times 100, \end{aligned}$$

where TWC$_\mathrm{SWPT}$ denotes the best results obtained with SWPT by using $B_\mathrm{max}=1, 2$ and $4$, and TWC$_\mathrm{BVP-VNS}$ is the average objective value of BVP–VNS after three runs.

Column TBVNS is given for comparing the performance of TBVNS and BVP–VNS. The improvement in percent is calculated by

$$\begin{aligned} \frac{{\text{ TWC}}_\mathrm{TBVNS}-{\text{ TWC}}_\mathrm{BVP-VNS}}{{\text{ TWC}}_\mathrm{SWPT}}\times 100. \end{aligned}$$

It is clear that both BVP–VNS and TBVNS perform remarkably better than SWPT. Moreover, BVP–VNS outperforms TBVNS for different settings (see the positive values in the columns of TBVNS). These results confirm that the iterative procedure is able to reach better solutions using a smaller amount of computing time. This fact is especially obvious when the problem size increases.

To thoroughly examine the effect of computing time, we conduct the same tests with further increased computing time. For TBVNS, 120 s are allowed for instances with fewer than 60 jobs and 240 s for the remaining instances. For BVP–VNS, four iterations are performed and each iteration uses 30 (resp. 60) s. Finally, we also allow doubled time for TBVNS, that is, 240 and 480 s, respectively.

Table 7 summarizes the results with respect to the number of jobs. Both BVP–VNS and TBVNS perform similarly well. Starting from the same initial solution with $B_\mathrm{max}=1, 2$ and $4$, the iterative procedure BVP–VNS generally finds better solutions than the simultaneous approach TBVNS (again, see the positive values in the columns of TBVNS). Note that TBVNS cannot effectively change the number of batches due to the random selection of neighbors. The results thus strongly depend on the quality of initial solutions. It is also noteworthy (columns TBVNS 240/480 s) that doubled computing time achieved only marginal improvement. The negative entry indicates that TBVNS outperforms BVP–VNS in this case.

Table 7 Comparison of TWC improvement (%) for TBVNS and BVP–VNS with further increased computing time

In addition, we compare the overall best solutions obtained by SWPT, TBVNS, and BVP–VNS using 120/240 s. In Table 8, the TWC improvement is similarly determined except that we use the best solution of each heuristic for the calculation, which is chosen among solutions with $B_\mathrm{max}=1, 2$ and $4$. Standard deviations ($\sigma$) of the solutions with the three different settings $B_\mathrm{max}=1, 2,$ and $4$ of TBVNS (resp. BVP–VNS) are given as well, which are calculated according to:

$$\begin{aligned} \sigma&= \sqrt{\frac{1}{2}\sum \limits _{B_\mathrm{max}\in \{1,2,4\}} \left( {\text{ TWC}}_{B_\mathrm{max}}-\mu \right) ^2}\nonumber \\&\text{ with}\quad \mu =\frac{1}{3}\sum \limits _{B_\mathrm{max}\in \{1,2,4\}}{\text{ TWC}}_{B_\mathrm{max}}. \end{aligned}$$

(15)

From Table 8, we see that BVP–VNS provides slightly better solutions (less than 0.6 % on average). Moreover, the larger value of standard deviation for TBVNS also implies that its performance depends on the initial solutions used.

Table 8 Comparison of overall best solutions of TBVNS and BVP–VNS

To summarize, Fig. 2 depicts the performance of TBVNS and BVP–VNS regarding different computing time.

Fig. 2

Performance of TBVNS and BVP–VNS regarding computing time

We can see that the solution quality of TBVNS gradually improves with the amount of computing time given. However, good solutions can only be expected when sufficient computing time is available.

Particular attention should be paid to the performance of BVP–VNS. When solving smaller instances, BVP–VNS with less computing time actually performs similarly well. We conjecture that the heuristic BVP plays an important role here. With limited computing time, VNS generates a comparatively poor solution. This, on the other hand, can provide more possibilities for BVP to improve the current solution. Meanwhile, BVP requires far less computing time due to the integrated structural properties. Therefore, major improvement can be quickly achieved after a few iterations.

In comparison to TBVNS, BVP–VNS is less dependent on computing time. Additional computing time contributes to a further reduction of TWC. No significant improvement can be observed using excessive computing time. As a result, we can benefit from the iterative procedure BVP–VNS to gain good solutions with limited computational resources.

5.2.4 Results of BVP–VNS

As mentioned earlier, in comparison to TBVNS, BVP–VNS performs well and stably. Therefore, we focus on BVP–VNS in the following experiments.

Concerning computing time, 60 s are allowed for each single VNS step within BVP–VNS for $n>60$, while 30 s are considered for smaller values of $n$. Executing BVP requires only fractions of a second. We use $MaxItr = 4$ for all problem instances. In fact, most improvement is achieved after two iterations. In order to exploit the improvement potential, we allow two additional iterations. For $MaxItr > 4$ further improvement is hardly observed.

Table 9 summarizes the computational results according to the number of families, machines, jobs as well as setup values. The improvement in percent is again compared to the best solutions of SWPT.

Table 9 Improvement grouped according to different factor levels

In general, BVP–VNS performs stably regarding different factor combinations. These results also suggest a slight upward tendency with growing number of $F, m,$ and $n$. On the other hand, improvement clearly increases with the value of setup times. Remarkable reduction of TWC is achieved for problem instances with large setup times. Nevertheless, benefits of batching are still obvious even in the presence of small family setups. Regarding the total number of jobs, significant improvement is observed especially for large problem instances.

To examine the iterative procedure more closely, Table 10 shows the improvement while using $B_\mathrm{max}=2$. Detailed results after the first, second, third, and finally fourth iteration are given in this table. Note that the improvement in percent is calculated according to the best solution of SWPT instead of the initial solution with $B_\mathrm{max}=2$. Even by running VNS in an isolated manner, noticeable improvement has already been achieved. The BVP, on the other hand, often fails to improve the best results of SWPT. Nevertheless, the iterative procedure outperforms SWPT and offers considerable reduction in TWC values. Note that the major improvement is already obtained after two iterations. More iterations can then exhaust the improvement potential.

Table 10 Improvement of TWC for an initial solution found by $B_\mathrm{max}=2$

In order to evaluate the overall performance of BVP–VNS, we consider total setup times, and the total number of batches in addition to the TWC value. Table 11 reports the reduction of total setup times as well as the variation of total number of batches. Note that the value of $B_{\mathrm{max}}$ relates to the resulting total setup times and the number of batches in the start solution. The larger the value of $B_{\mathrm{max}}$, fewer batches are formed initially, which in turn leads to fewer setups. With $B_{\mathrm{max}}=1$ indicating a large number of batches, BVP–VNS achieves about 60% reduction in setup times, the number of batches in the final solution is also reduced accordingly. In contrast, the reduction of setup times is smaller for $B_{\mathrm{max}}=4$, and the number of batches is increased by around 30 %. These observations suggest that BVP–VNS is able to reach a similar solution quality regardless of the initial solution.

Table 11 Reduction of other objectives

6 Conclusions and future research

In this paper, we discussed a scheduling problem for identical parallel machines and identical jobs in product families. Due to sequence-dependent setup times incurred among jobs of different families, forming serial batches can effectively reduce TWC. Subject to the batch availability assumption, we first derived a MIP that allowed us to solve small-sized problem instances optimally. A VNS algorithm is then proposed for solving the three interrelated subproblems—batch sizing, batch assignment, and batch sequencing—in a simultaneous manner. To further reduce computing time, we develop a specific batch variation procedure to determine batch sizes while a VNS algorithm alters batch sequences for improvement. We also combine the heuristics by iterating the two phases. No major changes were observed after only a few iterations. Computational results show that our simultaneous and iterative approach outperform a list scheduling approach with fixed batch sizes. Furthermore, the iterative procedure succeeds in balancing solution quality and computing time.

For future research, we are interested in considering ready times of the jobs. This condition is often found in real-world settings. Alternative objectives, such as tardiness and lateness, can be taken into consideration. It seems also fruitful to study corresponding problems with non-identical jobs, as well as for unrelated parallel machines.