Stochastic Scheduling for a Network of Flexible Job Shops

Abstract

In this chapter, we address the problem of optimally routing and sequencing a set of jobs over a network of flexible machines for the objective of minimizing the sum of completion times and the cost incurred, assuming stochastic job processing times. This problem is of particular interest for the production control in high investment, low volume manufacturing environments, such as pilot-fabrication of microelectromechanical systems (MEMS) devices. We model this problem as a two-stage stochastic program with recourse, where the first-stage decision variables are binary and the second-stage variables are continuous. This basic formulation lacks relatively complete recourse due to infeasibilities that are caused by the presence of re-entrant flows in the processing routes, and also because of potential deadlocks that result from the first-stage routing and sequencing decisions. We use the expected processing times of operations to enhance the formulation of the first-stage problem, resulting in good linear programming bounds and inducing feasibility for the second-stage problem. In addition, we develop valid inequalities for the first-stage problem to further tighten its formulation. Experimental results are presented to demonstrate the effectiveness of using these strategies within a decomposition algorithm (the L-shaped method) to solve the underlying stochastic program. In addition, we present heuristic methods to handle large-sized instances of this problem and provide related computational results.

3.1 Introduction: Problem Statement and Related Literature

The production in high investment, low volume manufacturing environments, such as pilot-fabrication of microelectromechanical systems (MEMS) devices, gives rise to several special features of the underlying scheduling problem. Due to high prices of the processing equipments and complicated fabrication processes, it is impractical to assign dedicated equipment to each processing step. The relatively low volume of production during the pilot stage also implies that machine flexibility is highly desirable so that multiple product types can share processing equipments. Hence, each manufacturing facility is organized as a flexible job shop, serving multiple processing routes with flexible machines. Furthermore, due to novelty of the products and fabrication processes, a single facility often lacks the capability of performing all the required processing steps for a product from start to finish. To satisfy these special requirements, multiple manufacturing facilities are usually organized into a distributed fabrication network, where a central service provider coordinates production activities across facilities and directly deals with customers’ requirements. Products are shipped from one facility to another until all processing requirements are met. For a given processing step, there may be multiple facilities that can provide the required service. The flexibility of cross-facility routing not only provides more pricing and quality options for the customers, but also makes transportation time and cost an important aspect of the scheduling problem. We designate this type of distributed fabrication network as the Network of Flexible Job Shops (NFJS).

The management of operations for an NFJS involves two types of decisions: (1) choosing a facility for each job operation (i.e., processing step) and assigning it to a compatible machine within the facility (i.e., routing) and (2) stipulating a processing sequence for the operations assigned to any given machine (i.e., sequencing). The routing decisions need to take transportation time and cost into consideration, as they can be quite significant between geographically dispersed facilities. On the other hand, sequencing decisions need to account for the fact that sequence-dependent set-up times are required to prepare for the processing of operations of different jobs on the same machine. In view of the pricing and quality options that are available in an NFJS, the customer specifies for each job a fixed budget, which can only be exceeded under a given penalty rate. The job arrival times, number of operations for each job, machines capable of processing each operation, transportation times and transportation costs between facilities, sequence-dependent set-up times, and customer budgets are assumed to be known (and thus, deterministic). On the other hand, since exact values of processing times are expected to vary due to the novelty of fabrication technologies, they are assumed to be stochastic. The problem that we address in this chapter can be succinctly stated as follows:

Given a set of jobs and a network of flexible job shops, where operation processing times are uncertain but the sequence in which to process the operations of each job is known a priori, determine an allocation of job operations to facilities and a sequence in which to process these operations on the machines in the facility so as to minimize a function of the completion times and the transportation and processing costs incurred.

The NFJS problem combines the characteristics of three well-known problems: the multi-site planning and scheduling problem, the flexible job shop scheduling problem, and the stochastic job shop scheduling problem. Multi-site planning problems are extensions of capacitated lot-sizing problems, with emphasis on transportation requirements and site-specific holding cost. Production is assigned to machines at multiple sites to satisfy demands during each period of the time horizon. The multi-site scheduling problem further addresses underlying production issues, such as inventory interdependency and change-over setup. To deal with the integrated multi-site planning and scheduling problem, iterative methods have been applied that alternate between solving the long-term planning problem and solving the short-term scheduling problem (see, for example, Roux et al. 1999; Guinet 2001; Gnoni et al. 2003). Others have considered the monolithic approach, either using the approach of variable time scale (Timpe and Kallrath 2000; Lin and Chen 2006), or relying on heuristic methods (Gascon et al. 1998; Sauer etal. 2000; Jia et al. 2003) to handle the resulting complexity. Lee and Chen (2001) provided a comprehensive study on scheduling with transportation considerations for the single facility environment. They considered two particular cases pertaining to transportation within a flow shop environment and transportation during final product distribution. To the best of our knowledge, no previous research in the multi-site planning and scheduling area has considered routing flexibility and stochastic processing times, both of which are very pertinent to the NFJS problem.

In a flexible job shop environment, for each processing step of a job, there are multiple alternative machines that are capable of providing the required service. Various methods have been applied to solve problems of this type. For example, Iwata et al. (1980) and Kim (1990) have considered dispatching rules; Nasr and Elsayed (1990) have applied greedy heuristic methods, Hutchison et al. (1991) have devised a hierarchical decomposition method that determines the assignment of operations to machines and then generates sequences. With regard to iterative local search methods, Brandimarte (1993) considered re-assignment and re-sequencing as two different types of moves, while Dauzère-Pérès and Paulli (1997) and Mastrolilli and Gambardella (2000) did not explicitly treat them as different. Subramaniam etal. (2000) have performed a simulation study with dynamic job arrival and machine break downs. One can also find applications of meta-heuristic methods to solve this problem including, but not limited to, particle swam optimization (Xia and Wu 2005) and genetic algorithms (Pezzella et al. 2008 and Wang et al 2005). The routing flexibility that characterizes the flexible job shop problem is also present in the NFJS problem, but with an important distinction that the alternative machines may be located at different facilities (sites), thereby requiring consideration of transportation time and cost into the scheduling problem.

The stochastic scheduling problem has been addressed in the literature in the classical flow shop and job shop environments. Optimal policies, dominance relations, and dispatching rules for two- and three-machine flow shop scheduling problems having stochastic processing times have been developed by Ku and Niu (1986), Weiss (1982), Mittal and Bagga (1977), Cunningham and Dutta (1973), Bagga (1970), Talwar (1967), Makino (1965), Prasad (1981), Forst (1983), Pinedo (1982), Jia (1998), Elmaghraby and Thoney (1999), and Kamburowski (1999, 2000). These studies vary either in the distribution of the processing times used, or in the objective function, or in the amount of intermediate storage available between machines. Optimal rules have also been developed by Foley and Suresh (1984) and Pinedo (1982) to minimize the expected makespan for the m-machine flow shop problem with stochasticity in processing times. For work in stochastic job shops, see Golenko-Ginzburg et al. (1995, 1997, 2002), Singer (2000), Luh etal. (1999), Kutanoglu and Sabuncuoglu (2001), Yoshitomi (2002), Lai et al. (2004), and Tavakkoli-Moghaddam et al. (2005).

The remainder of this chapter is organized as follows. In Sect. 3.2, we model the NFJS problem as a two-stage stochastic program and present the L-shaped method for its solution. Besides developing the pertinent feasibility and optimality cuts, we also introduce an alternative approach to induce second-stage feasibility. In Sect. 3.3, the formulation of the first-stage problem is further tightened by using three types of valid inequalities, all of which rely upon the special structure of the NFJS problem. Computational results are provided in Sect. 3.4 to demonstrate the efficacy of our model formulation and solution approach. For even large-sized problem instances, we present heuristic methods and the results on their performances in Sect. 3.5. Concluding remarks are made in Sect. 3.6.

3.2 Stochastic Model for a Network of Flexible Job Shops

We model the stochastic NFJS problem as a two-stage stochastic program with recourse, where the first-stage variables are binary and pertain to the assignment of job operations to machines and to the sequencing of job operations for processing on these machines, while the second-stage variables are continuous and relate to the completion times and budget over-runs of the jobs, and where the uncertainty in processing time durations influences the job completion times. Multiple facilities are incorporated in our formulation by assigning to each machine a unique identification number that distinguishes it from the other machines in all the facilities, and by appropriately considering the inter-machine transportation times and costs. Stochastic processing times are modeled by a finite set of scenarios for the entire problem, and each of these scenarios assigns durations to every possible processing step and has an associated probability value.

We present the overall problem formulation and decompose it into two stages using Benders’ decomposition (Benders 1962). Besides constructing the feasibility cuts and optimality cuts, we further reinforce the first-stage problem by including additional valid inequalities that induce feasibility in the second stage.

3.2.1 Model Formulation for the NFJS Problem

Notation

Indices:

• Job index: i = 1, …, N

• Operation index for job i: j = 1, …, J _i

• Machine index: m = 1, …, $\left|M\right|$ (where M is the set of machines)

• Scenario index: s = 1, …, S

Decision Variables

• x ^m_(i,j)  = $\left\{\begin{array}{l}1,\ \mathrm{if}\ \mathrm{o}\mathrm{peration}\ j\ \mathrm{o}\mathrm{f}\ \mathrm{job}\ i\ \mathrm{is}\ \mathrm{assigned}\ \mathrm{t}\mathrm{o}\ \mathrm{machine}\ m,\hfill \\ {}0,\ \mathrm{o}\mathrm{t}\mathrm{herwise}.\hfill \end{array}\right.$

• y ^m_(i,j,k,l)  = $\left\{\begin{array}{l}\begin{array}{l}1,\ \mathrm{if}\ \mathrm{operation}\ j\ \mathrm{of}\ \mathrm{job}\ i\ \mathrm{directly}\ \mathrm{precedes}\ \mathrm{operation}\ l\ \mathrm{of}\\ {}\kern1em \mathrm{job}\ k\ \mathrm{on}\ \mathrm{machine}\ m,\end{array}\hfill \\ {}0,\ \mathrm{otherwise}.\hfill \end{array}\right.$

• ${v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}$ = $\left\{\begin{array}{l}\begin{array}{l}1,\ \mathrm{if}\ \mathrm{operation}\ j\ \mathrm{of}\ \mathrm{job}\ i\ \mathrm{is}\ \mathrm{performed}\ \mathrm{on}\ \mathrm{machine}\ e\ \mathrm{and}\\ {}\kern1em \mathrm{operation}\ j + 1\ \mathrm{of}\ \mathrm{job}\ i\ \mathrm{is}\ \mathrm{performed}\ \mathrm{on}\ \mathrm{machine}\ f,\end{array}\hfill \\ {}0,\ \mathrm{otherwise}.\hfill \end{array}\right.$

• t ^s_(i,j)  = completion time of operation j of job i under scenario s.

• Δ ^s _i  = budget over-run for job i under scenario s.

Parameters

• H ^(m,s)_(i,j,k,l)  = an appropriately large positive number; its value is specified in (3.16) below.

• w _i  = number of parts in job i.

• M = set of all the machines.

• ϕ _s  = probability of occurrence for scenario s.

• c ^m_(i,j)  = cost per unit processing time of operation j of job i on machine m.

• p ^(m,s)_(i,j)  = processing time of operation j of job i on machine m under scenario s.

• Z _m  = set of job operations that can be processed on machine m.

• M _(i,j) = set of machines capable of processing operation j of job i.

• u ^m_(i,j,k,l)  = changeover time to switch from operation j of job i to operation l of job k on machine m.

• b _i  = budget for job i.

• r _i  = ready time for the first operation of job i.

• d _(e,f) = transportation time between machines e and f.

• q _(e,f) = per part transportation cost between machines e and f.

• α _i  = cost coefficient for job i that is ascribed to its completion time.

• β _i  = penalty coefficient for job i corresponding to its budget over-run.

Formulation NFJSP

$$ \begin{array}{llll}[b]\mathrm{Minimize}\;z&={\displaystyle \sum_{i=1}^N{\alpha}_i}\left({\displaystyle \sum_{s=1}^S{\phi}_s}{t}_{\left(i,{J}_i\right)}^s\right)+{\displaystyle \sum_{i=1}^N{\beta}_i}\left({\displaystyle \sum_{s=1}^S{\phi}_s}{\varDelta}_i^s\right)\\&\quad+{\displaystyle \sum_{s=1}^S{\phi}_s}{\displaystyle \sum_{i=1}^N\kern0.5em {\displaystyle \sum_{j=1}^{J_i}\kern0.5em {\displaystyle \sum_{m\in {M}_{\left(i,j\right)}}{p}_{\left(i,j\right)}^{\left(m,s\right)}{x}_{\left(i,j\right)}^m}}}\\&\quad+{\displaystyle \sum_{m\in M}{\displaystyle \sum_{\left(i,j\right)\in {Z}_m}{\displaystyle \sum_{\begin{array}{l}\left(k,l\right)\in {Z}_m\\ {}\left(k,l\right)\ne \left(i,j\right)\end{array}}{u}_{\left(i,j,k,l\right)}^m{y}_{\left(i,j,k,l\right)}^m}}}\\ &\quad+{\displaystyle \sum_{i=1}^N{\displaystyle \sum_{j=1}^{J_i-1}\kern0.5em {\displaystyle \sum_{e\in {M}_{\left(i,j\right)}}{\displaystyle \sum_{f\in {M}_{\left(i,j+1\right)}}{d}_{\left(e,f\right)}{v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}}}}}\end{array} $$

(3.1)

subject to:

$$ \begin{array}{l}{t}_{\left(i,j\right)}^s+{\displaystyle \sum_{m\in {M}_{\left(i,j+1\right)}}\left({p}_{\left(i,j+1\right)}^{\left(m,s\right)}{x}_{\left(i,j+1\right)}^m\right)}+{\displaystyle \sum_{e\in {M}_{\left(i,j\right)}}{\displaystyle \sum_{f\in {M}_{\left(i,j+1\right)}}{d}_{\left(e,f\right)}{v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}}}\\ {}\kern1em \le {t}_{\left(i,j+1\right)}^s,\kern1em \forall i=1,\dots, N,\kern0.5em j=1,\dots, {J}_i-1,\kern0.5em s=1,\dots, S\end{array} $$

(3.2)

$$ {r}_i+{\displaystyle \sum_{m\in {M}_{\left(i,1\right)}}\left({p}_{\left(i,1\right)}^{\left(m,s\right)}{x}_{\left(i,1\right)}^m\right)}\le {t}_{\left(i,1\right)}^s,\kern1em \forall i=1,\dots, N,\kern0.5em s=1,\dots, S $$

(3.3)

$$ \begin{array}{llll}[b] {t}_{\left(i,j\right)}^s+{p}_{\left(k,l\right)}^{\left(m,s\right)}+{u}_{\left(i,j,k,l\right)}^m&\le {t}_{\left(k,l\right)}^s+\left(1-{y}_{\left(i,j,k,l\right)}^m\right){H}_{\left(i,j,k,l\right)}^{\left(m,s\right)},\\ &\quad\forall m\in M,\forall \left(i,j\right)\ne \left(k,l\right)\in {Z}_m,\kern0.5em \forall s=1,\dots, S \end{array} $$

(3.4)

$$ {\displaystyle \sum_{m\in {M}_{\left(i,j\right)}}{x}_{\left(i,j\right)}^m}=1,\kern1em \forall i=1,\dots, N,\kern0.5em j=1,\dots, {J}_i\forall i=1,\dots, N,\kern0.5em j=1,\dots, {J}_i $$

(3.5)

$$ {\displaystyle \sum_{\begin{array}{l}\left(i,j\right)\in {Z}_m\\ {}\left(i,j\right)\ne \left(k,l\right)\end{array}}{y}_{\left(i,j,k,l\right)}^m}\le {x}_{\left(k,l\right)}^m,\kern1em \forall k=1,\dots, N,\kern0.5em l=1,\dots, {J}_k,\kern0.5em m\in {M}_{\left(k,l\right)} $$

(3.6)

$$ {\displaystyle \sum_{\begin{array}{l}\left(i,j\right)\in {Z}_m\\ {}\left(i,j\right)\ne \left(k,l\right)\end{array}}{y}_{\left(k,l,i,j\right)}^m}\le {x}_{\left(k,l\right)}^m,\kern1em \forall k=1,\dots, N,\kern0.5em l=1,\dots, {J}_k,\kern0.5em m\in {M}_{\left(k,l\right)} $$

(3.7)

$$ {\displaystyle \sum_{\left(i,j\right)\in {Z}_m}{\displaystyle \sum_{\begin{array}{l}\left(k,l\right)\in {Z}_m\\ {}\left(k,l\right)\ne \left(i,j\right)\end{array}}{y}_{\left(i,j,k,l\right)}^m}}\ge {\displaystyle \sum_{\left(i,j\right)\in {Z}_m}{x}_{\left(i,j\right)}^m}-1,\kern1em \forall \kern0.5em m\in M $$

(3.8)

$$ \begin{array}{llll}[b]&{\displaystyle \sum_{j=1}^{J_i}{\displaystyle \sum_{m\in {M}_{\left(i,j\right)}}{c}_{\left(i,j\right)}^m}{p}_{\left(i,j\right)}^{\left(m,s\right)}{x}_{\left(i,j\right)}^m}\\ &\quad+\left({\displaystyle \sum_{j=1}^{J_i-1}\kern0.5em {\displaystyle \sum_{e\in {M}_{\left(i,j\right)}}{\displaystyle \sum_{\kern0.5em f\in {M}_{\left(i,j+1\right)}}{q}_{\left(e,f\right)}{\displaystyle {v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}}}}}\right){w}_i-{\varDelta}_i^s\le {b}_i,\\ &\quad\forall i=1,\dots, N,\kern0.5em s=1,\dots, S\end{array} $$

(3.9)

$$ \begin{array}{llll}[b] &{v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}\le {x}_{\left(i,j\right)}^e,{v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}\ge {x}_{\left(i,j\right)}^e+{x}_{\left(i,j+1\right)}^f-1,\\ &\quad\forall i=1,\dots, N,j=1,\dots, {J}_i-1,e\in {M}_{\left(i,j\right)},f\in {M}_{\left(i,j+1\right)} \end{array} $$

(3.10)

$$ {\varDelta}_i^s\ge 0,\kern1em \forall i=1,\dots, N,s=1,\dots, S $$

(3.11)

$$ {x}_{\left(i,j\right)}^m\in \left\{0,1\right\},\kern1em \forall i=1,\dots, N,j=1,\dots, {J}_i,m\in {M}_{\left(i,j\right)} $$

(3.12)

$$ {y}_{\left(i,j,k,l\right)}^m\in \left\{0,1\right\},\kern1em \forall m=1,\dots, M,\forall \left(i,j\right)\ne \left(k,l\right)\in {Z}_m $$

(3.13)

$$ {v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}\in \left[0,1\right],\kern1em \forall i=1,\dots, N,j=1,\dots {J}_i-1,e\in {M}_{\left(i,j\right)},f\in {M}_{\left(i,j+1\right)}. $$

(3.14)

The objective function (3.1) is composed of five terms. The first and the second terms penalize the sum of job completion times and budget over-runs, respectively. The penalty coefficients reflect the customer’s emphasis on the lead-time and costs incurred, and they also scale the first two terms to be commensurate with the next three terms, which are time based. The third term represents expected processing time for the operations of all the jobs; the fourth term computes the total set-up time on the machines, and the final term determines the sum of travel times incurred by all the jobs. Note that the last three terms in the objective function support the first term by aiding the achievement of lower completion times, while at the same time, reflect costs incurred by consuming machine and transportation capacities of the system. Constraints (3.2) capture precedence relationships between operations of the same job. Specifically, they state that under each scenario s, the completion time of operation j + 1 of job i, ∀i = 1,…,N, must be at least equal to the completion time of operation j of that job plus the processing time of operation j + 1 and any travel time incurred between the two operations (set-up time is assumed to be job-detached, and hence, is not included here). Constraints (3.3) ensure (for each scenario) that each job does not commence its first operation earlier than its ready time. Constraints (3.4) establish relationships among the operations to be performed on the same machine. Given two distinct job-operations, say (i, j) and (k, l) in Z _m for a certain machine m, if (i, j) were to directly precede (k, l), (i.e., ${y}_{\left(i,j,k,l\right)}^m=1$), then the completion time of (k, l) under any scenario s must be at least equal to the completion time of (i, j) for that scenario, plus the processing time of (k, l) and the sequence-dependent set-up time between the two operations. Observe that when y ^m_(i,j,k,l)  = 0, i.e., (i, j) does not directly precede (k, l), the constraint becomes redundant by the choice of a suitably large value of H ^(m,s)_(i,j,k,l) (see (3.16) below). Constraints (3.5) ensure that each job-operation is assigned to exactly one machine out of the several alternative machines that can process it. Constraints (3.6) and (3.7) state that if a job-operation, say (k, l), is assigned to a machine m, it can be preceded (respectively succeeded) by at most one job-operation from the set of operations that the machine is capable of processing. Note that if (k, l) is the first operation to be processed on this machine, it will not be preceded by any other operation; and likewise if (k, l) is the last operation to be processed, it will not be succeeded by any other operation. In both of these cases, the left-hand sides of (3.6) and (3.7) will be zero, which trivially yield valid relationships. Also, if (k, l) is not assigned to machine m, then all the direct precedence y-variables that relate (k, l) to other operations on machine m are validly set equal to zero by (3.6) and (3.7). Constraints (3.8) guarantee that if a machine has some ${\displaystyle {\sum}_{\left(i,j\right)\in {Z}_m}{x}_{\left(i,j\right)}^m}$ operations assigned to it for processing, then there must exist one less than this number of direct precedence variables that are set equal to 1 for this machine. These constraints are written as inequalities rather than as equalities to account for the case where the number of operations assigned to a machine is actually zero. Also, together with (3.6) and (3.7), these constraints establish the definitional role of the y-variables. Constraints (3.9) enforce budgetary restrictions on each job i under every processing time scenario s. These constraints permit the sum of processing costs and travel costs for all operations of a job to exceed the budget by an amount of Δ ^s _i , but with a corresponding penalty in the objective function. Note that the travel cost for each job i is assumed to be proportional to the number of parts, w _i , in that job. Constraints (3.10) enforce the relationship between the x- and v-variables according to ${v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}={x}_{\left(i,j\right)}^e{x}_{\left(i,j+1\right)}^f$ using a standard linearization technique whereby ${v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}$ = 1 if and only if both x ^e_(i,j)  = 1 and ${x}_{\left(i,j+1\right)}^f$ = 1. Note that the v-variables account for the required transfer between the machines in the objective function (3.1) and in Constraints (3.2) and (3.9). As such, because of the positive coefficients associated with these variables in the objective function (3.1) and the less-than-or-equal-to ($\le$) relationships in (3.2) and (3.9), we could omit the first two sets of $\le$ restrictions in (3.10) and have them automatically hold true at optimality. Constraints (3.11), (3.12), (3.13), and (3.14) ascribe nonnegativity and binary restrictions on the decision variables, while the v-variables will automatically turn out to be binary-valued even though declared to be continuous on [0, 1]. Note also that the nonnegativity on the t -variables is implied by (3.2), (3.3), (3.12), and (3.13).

The value of H ^(m,s)_(i,j,k,l) used in (3.4) can be prescribed as follows. Note that, if ${y}_{\left(i,j,k,l\right)}^m=0$, then this constraint reduces to

$$ {t}_{\left(i,j\right)}^s+{p}_{\left(k,l\right)}^{\left(m,s\right)}+{u}_{\left(i,j,k,l\right)}^m-{t}_{\left(k,l\right)}^s\le {H}_{\left(i,j,k,l\right)}^{\left(m,s\right)}. $$

(3.15)

Hence, it is sufficient to assign to H ^(m,s)_(i,j,k,l) a valid upper bound on the left-hand side expression in (3.15). Given conservative bounds for t ^s_(i,j) such that ${\left({t}_{\left(i,j\right)}^s\right)}_{\min}\le {t}_{\left(i,j\right)}^s\le {\left({t}_{\left(i,j\right)}^s\right)}_{\max }$, we can set

$$ {H}_{\left(i,j,k,l\right)}^{\left(m,s\right)}={\left({t}_{\left(i,j\right)}^s\right)}_{\max }+{p}_{\left(k,l\right)}^{\left(m,s\right)}+{u}_{\left(i,j,k,l\right)}^m-{\left({t}_{\left(k,l\right)}^s\right)}_{\min }. $$

(3.16)

With respect to the bounds for t ^s_(i,j) , we take

$$ \begin{array}{llll}[b]{\left({t}_{\left(i,j\right)}^s\right)}_{\min }&={r}_i+{\displaystyle \sum_{j^{\prime}\le j}\underset{m\in M\left(i,{j}^{\prime}\right)}{ \min}\left\{{p}_{\left(i,{j}^{\prime}\right)}^{\left(m,s\right)}\right\}}+{\displaystyle \sum_{2\le {j}^{\prime}\le j}\underset{\begin{array}{l}e\in M\left(i,{j}^{\prime }-1\right)\\ {}f\in M\left(i,j\hbox{'}\right)\end{array}}{ \min}\left\{{d}_{\left(e,f\right)}\right\}},\\ {}\;{\left({t}_{\left(i,j\right)}^s\right)}_{\max }&={\tau}^s-{\displaystyle \sum_{j\hbox{'}>j}\underset{m\in M\left(i,j\hbox{'}\right)}{ \min}\left\{{p}_{\left(i,{j}^{\prime}\right)}^{\left(m,s\right)}\right\}}-{\displaystyle \sum_{j<{j}^{\prime}\le {J}_i}\underset{\begin{array}{l}e\in M\left(i,{j}^{\prime }-1\right)\\ {}f\in M\left(i,{j}^{\prime}\right)\end{array}}{ \min}\left\{{d}_{\left(e,f\right)}\right\}},\\ &\quad\forall i=1,\dots, N,j=1,\dots, {J}_i,s=1,\dots, S,\end{array} $$

(3.17)

where τ ^s is some conservative upper bound on the overall makespan of all the jobs under scenario s. We used the value of τ ^s to be the sum of the processing times of all the operations of the jobs.

3.2.2 The L-Shaped Method for the NFJS Problem

Formulation NFJSP can be decomposed into the following Stage-I (master) and Stage-II (recourse) problems:

Stage-I: Master Problem

MP: Minimize

$$ \begin{array}{l}{\displaystyle \sum_{s=1}^S{\phi}_s}\kern0.5em {\displaystyle \sum_{i=1}^N\kern0.5em {\displaystyle \sum_{j=1}^{J_i}{\displaystyle \sum_{m\in {M}_{\left(i,j\right)}}{p}_{\left(i,j\right)}^{\left(m,s\right)}}{x}_{\left(i,j\right)}^m+{\displaystyle \sum_{m\in M}{\displaystyle \sum_{\left(i,j\right)\in {Z}_m}{\displaystyle \sum_{\begin{array}{l}\left(k,l\right)\in {Z}_m\\ {}\left(i,j\right)\ne \left(k,l\right)\end{array}}{y}_{\left(i,j,k,l\right)}^m}{u}_{\left(i,j,k,l\right)}^m}}}}\\ {}\kern1em +{\displaystyle \sum_{i=1}^N{\displaystyle \sum_{j=1}^{J_i-1}{\displaystyle \sum_{e\in {M}_{\left(i,j\right)}}{\displaystyle \sum_{f\in {M}_{\left(i,j+1\right)}}{v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}{d}_{\left(e,f\right)}}+}{\displaystyle \sum_{s=1}^S{\phi}_s}\mathbf{Q}\left(\mathbf{x},\mathbf{y},\mathbf{v},s\right)}}\end{array} $$

(3.18)

subject to: (3.5), (3.6), (3.7), (3.8), (3.10), (3.12), (3.13), and (3.14), where Q(x, y, v, s) is the recourse function corresponding to the optimal value of the subproblem that minimizes the penalized sum of job completion times and budget over-runs for a given assignment vector x, sequencing vector y, tracking vector v, and for a processing time scenario s. The linear recourse subproblem for scenario s is given by:

Stage-II: Recourse Problem

$$ \mathbf{R}\mathbf{P}:\kern1em \mathbf{Q}\left(\mathbf{x},\mathbf{y},\mathbf{v},s\right)=\mathrm{M}\mathrm{i}\mathrm{n}\ {\displaystyle \sum_{i=1}^N{\alpha}_i}{t}_{\left(i,{J}_i\right)}^s+{\displaystyle \sum_{i=1}^N{\beta}_i}{\varDelta}_i^s $$

(3.19)

subject to: (3.2), (3.3), (3.4), (3.9), and (3.11).

We note that, in the decomposition outlined above for formulation NFJSP, the master problem could generate an assignment and sequencing solution that might not be feasible to the subproblem. There are three possible causes for such infeasibility. First, the Stage-I formulation does not exclude “subtours” while sequencing operations assigned to a particular machine. For example, suppose that operations (a, b), (c, d), and (e, f) are assigned to machine m, so that

$$ {x}_{\left(a,b\right)}^m={x}_{\left(c,d\right)}^m={x}_{\left(e,f\right)}^m=1. $$

One can verify that the following values of direct precedence variables are feasible to the Stage-I formulation (in particular, satisfies Constraint (3.8)):

$$ \begin{array}{l}\begin{array}{cc}\hfill {y}_{\left(a,b,c,d\right)}^m=1;\hfill & \hfill {y}_{\left(a,b,e,f\right)}^m=0;\hfill \end{array}\\ {}\begin{array}{cc}\hfill {y}_{\left(c,d,a,b\right)}^m=1;\hfill & \hfill {y}_{\left(c,d,e,f\right)}^m=0;\hfill \end{array}\\ {}\begin{array}{cc}\hfill {y}_{\left(e,f,a,b\right)}^m=0;\hfill & \hfill {y}_{\left(e,f,c,d\right)}^m=0.\hfill \end{array}\end{array} $$

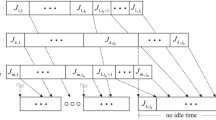
However, due to the subtour between (a, b) and (c, d), this solution does not represent a valid processing sequence. In the NFJSP formulation, this kind of subtour is eliminated by Constraints (3.4), which are not included in the master problem. Second, note that Constraints (3.2) in NFJSP, upon decomposition, become part of the subproblem and capture the fact that the completion time of a lower indexed operation of a job must be less than or equal to that for any higher indexed operations of the same job. In NFJSP, Constraints (3.2) in conjunction with other constraints that determine the value of the y -variables (Constraints (3.6), (3.7), and (3.8)) ensure that, in the case of re-entrant flow, where a job visits a machine for multiple operations, the lower indexed operations of a job are sequenced before a higher indexed operation of the same job. However, since Constraints (3.2) are no longer a part of the master problem, its absence may result in an assignment and sequencing vector that does not honor the re-entrant flow conditions. Third, the assignment and sequencing vectors from the master problem may cause a deadlock. This occurs in the face of a certain configuration of assignment and sequencing decisions that result in a circuit or a cycle wherein each operation in the cycle waits for another operation within the cycle to complete processing. This is illustrated in Fig. 3.1. Note that on machine M1, (c, d) waits for (a, b) to finish processing according to the sequencing decision. Operation (a, b) on machine M1 must follow (a, f) on machine M2 owing to operating precedence constraints. However, on machine M2, operation (a, f) follows (c, h), which, in turn, can begin only after (c, d) on machine M1 has been completed. Thus, none of the four operations can begin processing, resulting in a deadlock.

Fig. 3.1

A deadlock configuration involving two machines

As a result of this potential infeasibility, the above decomposition of NFJS problem does not possess the property of relatively complete recourse. In order to render the first-stage solution feasible to the second-stage, it is necessary to obviate the infeasibility due to subtours, re-entrant flows, and deadlocks. One way to achieve this is through the use of artificial variables as described by van Slyke and Wets (1969). These variables are inserted into the subproblems for every scenario and feasibility cuts are developed that become a part of the master problem, which in turn ultimately induce the master problem to generate solutions that are feasible to the subproblems. Accordingly, for a given output (x, y, v) from the master problem, the following augmented recourse problem (ARP) is solved, one for each scenarios:

ARP: Minimize

$$ {\displaystyle \sum_{i=1}^N{\displaystyle \sum_{j=1}^{J_i}{a}_{1\left(i,j\right)}^s}+}{\displaystyle \sum_{m\in M}{\displaystyle \sum_{\left(i,j\right)\in {Z}_m}{\displaystyle \sum_{\begin{array}{l}\left(k,l\right)\in {Z}_m\\ {}\left(k,l\right)\ne \left(i,j\right)\end{array}}{a}_{2\left(i,j,k,l\right)}^{\left(m,s\right)}}}} $$

(3.20)

subject to:

$$ \begin{array}{llll}[b] &{t}_{\left(i,j\right)}^s+{\displaystyle \sum_{m\in {M}_{\left(i,j+1\right)}}\left({p}_{\left(i,j+1\right)}^{\left(m,s\right)}{x}_{\left(i,j+1\right)}^m\right)}+{\displaystyle \sum_{e\in {M}_{\left(i,j\right)}}{\displaystyle \sum_{f\in {M}_{\left(i,j+1\right)}}{d}_{\left(e,f\right)}{v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}}}-{a}_{1\left(i,j+1\right)}^s\le {t}_{\left(i,j+1\right)}^s,\\ &\quad\forall i=1,\dots, N,j=1,\dots, {J}_i-1\end{array} $$

(3.21)

$$ {r}_i+{\displaystyle \sum_{m\in {M}_{\left(i,1\right)}}\left({p}_{\left(i,1\right)}^{\left(m,s\right)}{x}_{\left(i,1\right)}^m\right)}-{a}_{1\left(i,1\right)}^s\le {t}_{\left(i,1\right)}^s,\kern1em \forall i=1,\dots, N $$

(3.22)

$$ \begin{array}{llll}[b] &{t}_{\left(i,j\right)}^s+{p}_{\left(k,l\right)}^{\left(m,s\right)}+{u}_{\left(i,j,k,l\right)}^m-{a}_{2\left(i,j,k,l\right)}^{\left(m,s\right)}\le {t}_{\left(k,l\right)}^s+\left(1-{y}_{\left(i,j,k,l\right)}^m\right){H}_{\left(i,j,k,l\right)}^{\left(m,s\right)},\\ &\quad\forall m\in M,\forall \left(i,j\right)\ne \left(k,l\right)\ \mathrm{in}\ {Z}_m\end{array} $$

(3.23)

$$ \begin{array}{llll}[b] &\quad{\displaystyle \sum_{j=1}^{J_i}{\displaystyle \sum_{m\in {M}_{\left(i,j\right)}}{c}_{\left(i,j\right)}^m}{p}_{\left(i,j\right)}^{\left(m,s\right)}{x}_{\left(i,j\right)}^m}+\left({\displaystyle \sum_{j=1}^{J_i-1}{\displaystyle \sum_{\kern0.5em e\in {M}_{\left(i,j\right)}}{\displaystyle \sum_{f\in {M}_{\left(i,j+1\right)}}{q}_{\left(e,f\right)}{v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}}}}\right){w}_i-{\varDelta}_i^s\le {b}_i,\\ &\quad\forall i=1,\dots, N\end{array} $$

(3.24)

$$ {a}_{1\left(i,j\right)}^s\ge 0,\kern1em \forall i=1,\dots, N,j=1,\dots, {J}_i $$

(3.25)

$$ {a}_{2\left(i,j,k,l\right)}^{\left(m,s\right)}\ge 0,\kern1em \forall m\in M,\forall \left(i,j\right)\ne \left(k,l\right)\in {Z}_m $$

(3.26)

$$ {t}_{\left(i,j\right)}^s\ge 0,\kern1em \forall i=1,\dots, N,j=1,\dots, {J}_i $$

(3.27)

$$ {\varDelta}_i^s\ge 0,\kern1em \forall i=1,\dots, N. $$

(3.28)

Note that artificial variables are included in Constraints (3.2), (3.3), and (3.4), which now become (3.21), (3.22), and (3.23), respectively. Constraints (3.9) do not require any artificial variables because they can always be satisfied by virtue of the budget over-run variables Δ ^s _i , i = 1, …, N. Whereas the corresponding restrictions are included in (3.24), they can be effectively omitted from Problem ARP.

If the value of the objective function (3.20) in ARP equals zero for all the subproblems, then it indicates that the solution from the master program (first-stage) is feasible to the recourse (second-stage) problem. However, if there exists a scenario, say $\overline{s}$, such that the subproblem corresponding to this scenario has a positive optimal objective value, then a feasibility cut is generated so as to eliminate the corresponding solution from the master program, as follows. Rewriting Constraints (3.21), (3.22), and (3.23) as “≥” inequalities, we associate nonnegative dual variables ${\eta}_{\left(i,j\right)}^{\overline{s}}$, ${\eta}_i^{\overline{s}}$, ${\eta}_{\left(i,j,k,l\right)}^{\left(m,\overline{s}\right)}$ with these respective constraints. Note that (3.24) has been dropped from Problem ARP. Then, we derive the following feasibility cut for scenario $\overline{s}$:

$$ \begin{array}{llll}[b]&{\displaystyle \sum_{i=1}^N{\displaystyle \sum_{j=1}^{J_i-1}{\eta}_{\left(i,j\right)}^{\overline{s}}}\left({\displaystyle \sum_{m\in {M}_{\left(i,j+1\right)}}{p}_{\left(i,j+1\right)}^{\left(m,\overline{s}\right)}{x}_{\left(i,j+1\right)}^m+{\displaystyle \sum_{e\in {M}_{\left(i,j\right)}}{\displaystyle \sum_{f\in {M}_{\left(i,j+1\right)}}{d}_{\left(e,f\right)}{v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}}}}\right)}\;\\ &\quad+{\displaystyle \sum_{i=1}^N{\eta}_i^{\overline{s}}{\displaystyle \sum_{\kern0.5em m\in {M}_{\left(i,1\right)}}{p}_{\left(i,1\right)}^{\left(m,\overline{s}\right)}{x}_{\left(i,1\right)}^m}}+{\displaystyle \sum_{m\in M}{\displaystyle \sum_{\left(i,j\right)\in {Z}_m}{\displaystyle \sum_{\begin{array}{l}\left(k,l\right)\in {Z}_m\\ {}\left(k,l\right)\ne \left(i,j\right)\end{array}}{\eta}_{\left(i,j,k,l\right)}^{\left(m,\overline{s}\right)}{H}_{\left(i,j,k,l\right)}^{\left(m,\overline{s}\right)}{y}_{\left(i,j,k,l\right)}^m}}}\\ &\quad\le -{\displaystyle \sum_{i=1}^N{\eta}_i^{\overline{s}}{r}_i}+{\displaystyle \sum_{m\in M}{\displaystyle \sum_{\left(i,j\right)\in {Z}_m}{\displaystyle \sum_{\begin{array}{l}\left(k,l\right)\in {Z}_m\\ {}\left(k,l\right)\ne \left(i,j\right)\end{array}}{\eta}_{\left(i,j,k,l\right)}^{\left(m,\overline{s}\right)}}\left({H}_{\left(i,j,k,l\right)}^{\left(m,\overline{s}\right)}-{p}_{\left(k,l\right)}^{\left(m,\overline{s}\right)}-{u}_{\left(i,j,k,l\right)}^m\right)}}.\end{array} $$

(3.29)

This feasibility cut is appended to the master program. Whenever the objective function values for all the augmented subproblems equal zero, the Stage-I solution yields feasible Stage-II recourse problems, whence we either verify optimality or generate optimality cuts as described next.

3.2.3 Optimality Cuts

When a Stage-I solution ($\overline{\mathbf{x}},\overline{\mathbf{y}},\overline{\mathbf{v}}$) is feasible for the separable Stage-II problems, the latter effectively determine optimal values for the completion time and budget over-run variables for each scenario. This yields the expected recourse value of the Stage-II objective function as given by $\mathbf{Q}\left(\overline{\mathbf{x}},\overline{\mathbf{y}},\overline{\mathbf{v}}\right)\equiv {\displaystyle {\sum}_{s=1}^S{\phi}_s\mathbf{Q}\left(\overline{\mathbf{x}},\overline{\mathbf{y}},\overline{\mathbf{v}},s\right)}$. This value is then compared with the lower bound ($\overline{\theta}$ , say) on the recourse value as previously obtained by solving the master problem. Note that (3.18) evaluated for ($\overline{\mathbf{x}},\overline{\mathbf{y}},\overline{\mathbf{v}}$) provides an upper bound for the NFJS problem given the feasibility of ($\overline{\mathbf{x}},\overline{\mathbf{y}},\overline{\mathbf{v}}$), and can be used to update the incumbent objective function value. If $\overline{\theta}\ge \mathbf{Q}\left(\overline{\mathbf{x}},\overline{\mathbf{y}},\overline{\mathbf{v}}\right)$, we have that ($\overline{\mathbf{x}},\overline{\mathbf{y}},\overline{\mathbf{v}}$) is an optimal solution to the NFJS problem. Otherwise, if $\overline{\theta}<\mathbf{Q}\left(\overline{\mathbf{x}},\overline{\mathbf{y}},\overline{\mathbf{v}}\right)$, we generate an optimality cut to help close the gap between the two bounds. Letting ξ ^s_(i,j) , ξ ^s _i , ξ ^(m,s)_(i,j,k,l) , and ω ^s _i be the nonnegative dual variables associated with respect to Constraints (3.2), (3.3), (3.4), and (3.9) written as ≥ restrictions, the optimality cut is given as follows, where, as mentioned above, θ is used to represent the final term in the objective function (3.18) of the master program:

$$ \begin{array}{llll}[b]\theta &\ge {\displaystyle \sum_{s=1}^S{\phi}_s}\left\{{\displaystyle \sum_{i=1}^N{\displaystyle \sum_{j=1}^{J_i-1}{\xi}_{\left(i,j\right)}^s}\left({\displaystyle \sum_{m\in {M}_{\left(i,j+1\right)}}{p}_{\left(i,j+1\right)}^{\left(m,s\right)}{x}_{\left(i,j+1\right)}^m}+{\displaystyle \sum_{e\in {M}_{\left(i,j\right)}}{\displaystyle \sum_{f\in {M}_{\left(i,j+1\right)}}{d}_{\left(e,f\right)}{v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}}}\right)}\right.\\ &\quad+{\displaystyle \sum_{i=1}^N{\xi}_i^s{\displaystyle \sum_{m\in {M}_{\left(i,1\right)}}{p}_{\left(i,1\right)}^{\left(m,s\right)}{x}_{\left(i,1\right)}^m}}+{\displaystyle \sum_{m\in M}{\displaystyle \sum_{\left(i,j\right)\in {Z}_m}{\displaystyle \sum_{\begin{array}{l}\left(k,l\right)\in {Z}_m\\ {}\left(k,l\right)\ne \left(i,j\right)\end{array}}{\xi}_{\left(i,j,k,l\right)}^{\left(m,s\right)}{H}_{\left(i,j,k,l\right)}^{\left(m,s\right)}{y}_{\left(i,j,k,l\right)}^m}}}\\ &\quad+{\displaystyle \sum_{i=1}^N{\omega}_i^s\left[{\displaystyle \sum_{j=1}^{J_i}{\displaystyle \sum_{m\in {M}_{\left(i,j\right)}}{c}_{\left(i,j\right)}^m}}{p}_{\left(i,j\right)}^{\left(m,s\right)}{x}_{\left(i,j\right)}^m+\left({\displaystyle \sum_{j=1}^{J_i-1}{\displaystyle \sum_{\kern0.5em e\in {M}_{\left(i,j\right)}}{\displaystyle \sum_{f\in {M}_{\left(i,j+1\right)}}{q}_{\left(e,f\right)}{v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}}}}\right){w}_i\right]}\\ &\quad+{\displaystyle \sum_{i=1}^N{\xi}_i^s{r}_i}-{\displaystyle \sum_{m\in M}{\displaystyle \sum_{\left(i,j\right)\in {Z}_m}{\displaystyle \sum_{\begin{array}{l}\left(k,l\right)\in {Z}_m\\ {}\left(k,l\right)\ne \left(i,j\right)\end{array}}}}}\\&\qquad{\xi}_{\left(i,j,k,l\right)}^{\left(m,s\right)}\left({H}_{\left(i,j,k,l\right)}^{\left(m,s\right)}-{p}_{\left(k,l\right)}^{\left(m,s\right)}-{u}_{\left(i,j,k,l\right)}^m\right)-{\displaystyle \sum_{i=1}^N{\omega}_i^s{b}_i}.\end{array} $$

(3.30)

The optimality cut is appended to the MP and the revised MP is re-solved. The iterations continue in this fashion until the lower and upper bounds converge (or come within a desired optimality tolerance).

Note that the master problem and the linear programs corresponding to the subproblems need to be re-solved every time a new feasibility or optimality cut is added. This can lead to a lengthy process in case a large number of feasibility cuts are required to generate a feasible solution. Therefore, it is helpful to a priori include suitable valid inequalities in the master problem to induce second-stage feasibility. We present such inequalities next.

3.2.4 Alternative Valid Inequalities for Inducing Stage-II Feasibility That Also Provide a Stage-I Lower Bound

The alternative set of valid inequalities derived in this section relies on the fact that for any fixed value of (x, y, v), the feasibility of the Stage-II problem does not depend on a particular scenario. In other words, if the routing and sequencing decisions are feasible for a given scenario, then they are also feasible for any other scenario, because changes in job processing times can be accommodated by adjusting completion times while maintaining the feasibility of the subproblem constraints. Consequently, variables and constraints of the subproblem for a given scenario can be included in the master problem to induce feasibility of the subproblems for all the scenarios. The next result indicates that the particular scenario that use the expected values of processing times provides a lower bound on $\theta \equiv \mathbf{Q}\left(\mathbf{x},\mathbf{y},\mathbf{v}\right)$.

Proposition 1

The optimal objective value of the subproblem with expected processing times yields a lower bound on $\mathbf{Q}\left(\mathbf{x},\mathbf{y},\mathbf{v}\right)\equiv {\displaystyle {\sum}_{s=1}^S{\phi}_s\mathbf{Q}\left(\mathbf{x},\mathbf{y},\mathbf{v},s\right)}$.

Proof

For any fixed values of x, y, and v, the recourse function Q(x, y, v, s) is only a function of s. We rewrite this as Q(p ^s), where p ^s is the vector of operation processing times.

Let ${\boldsymbol{p}}^E={\displaystyle {\sum}_{s=1}^S{\phi}_s{\boldsymbol{p}}^s}$. The fact that $\mathbf{Q}\left({\boldsymbol{p}}^E\right)=\mathbf{Q}\left({\displaystyle {\sum}_{s=1}^S{\phi}_s{\boldsymbol{p}}^s}\right)\le {\displaystyle {\sum}_{s=1}^S{\phi}_s\mathbf{Q}\left({\boldsymbol{p}}^s\right)}$ is easily established because Q(p ^s) is a convex function of p ^s, due to fixed recourse (see Theorem 5 in Birge and Louveaux 2000, p. 89.) □

Accordingly, we define the following variables:

t ^E_(i,j)  = completion time of operation j of job i under expected processing times.

Δ ^E _i  = budget over-run for job i under expected processing times.

Then, by Proposition 1 and Constraints (3.2), (3.3), (3.4), and (3.9), we include the following set of restrictions in the Stage-I master program:

$$ \theta \ge\ {\displaystyle \sum_{i=1}^N{\alpha}_i}{t}_{\left(i,{J}_i\right)}^E+{\displaystyle \sum_{i=1}^N{\beta}_i}{\varDelta}_i^E $$

(3.31)

$$ \begin{array}{llll}[b] &{t}_{\left(i,j\right)}^E+{\displaystyle \sum_{m\in {M}_{\left(i,j+1\right)}}\left({p}_{\left(i,j+1\right)}^{\left(m,E\right)}{x}_{\left(i,j+1\right)}^m\right)}+{\displaystyle \sum_{e\in {M}_{\left(i,j\right)}}{\displaystyle \sum_{f\in {M}_{\left(i,j+1\right)}}{d}_{\left(e,f\right)}{v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}}}\le {t}_{\left(i,j+1\right)}^E,\\ &\quad\forall i=1,\dots, N,\kern0.5em j=1,\dots, {J}_i-1\end{array} $$

(3.32)

$$ {r}_i+{\displaystyle \sum_{m\in {M}_{\left(i,1\right)}}\left({p}_{\left(i,1\right)}^{\left(m,E\right)}{x}_{\left(i,1\right)}^m\right)}\le {t}_{\left(i,1\right)}^E,\kern1em \forall i=1,\dots, N $$

(3.33)

$$ \begin{array}{llll}[b]&{t}_{\left(i,j\right)}^E+{p}_{\left(k,l\right)}^{\left(m,E\right)}+{u}_{\left(i,j,k,l\right)}^m\le {t}_{\left(k,l\right)}^E+\left(1-{y}_{\left(i,j,k,l\right)}^m\right){H}_{\left(i,j,k,l\right)}^{\left(m,E\right)},\\ &\quad\forall m\in M,\forall \left(i,j\right)\ne \left(k,l\right)\in {Z}_m\end{array} $$

(3.34)

$$ \begin{array}{llll}[b]&{\displaystyle \sum_{j=1}^{J_i}{\displaystyle \sum_{m\in {M}_{\left(i,j\right)}}{c}_{\left(i,j\right)}^m}{p}_{\left(i,j\right)}^{\left(m,E\right)}{x}_{\left(i,j\right)}^m+\left({\displaystyle \sum_{j=1}^{J_i-1}{\displaystyle \sum_{e\in {M}_{\left(i,j\right)}}{\displaystyle \sum_{f\in {M}_{\left(i,j+1\right)}}{q}_{\left(e,f\right)}{v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}}}}\right)}{w}_i-{\varDelta}_i^E\le {b}_i,\\ &\quad\forall i=1,\dots, N\end{array} $$

(3.35)

$$ {t}_{\left(i,j\right)}^E\ge 0,{t}_{\left(i,j\right)}^E\ge 0,\kern1em \forall i=1,\dots, N,j=1,\dots, {J}_i $$

(3.36)

$$ {\varDelta}_i^E\ge 0,\kern1em \forall i=1,\dots, N. $$

(3.37)

Note that ${p}_{\left(i,j\right)}^{\left(m,E\right)}\equiv {\displaystyle {\sum}_{s=1}^S{\phi}_s{p}_{\left(i,j\right)}^{\left(m,s\right)}}$, and that H ^(m,E)_(i,j,k,l) is pre-calculated similar to that in (3.16) and (3.17), with p ^(m,E)_(i,j) replacing p ^(m,s)_(i,j) in the expressions.

Also note that the infeasibility caused by re-entrant flow will be eliminated by Constraints (3.32), (3.33), and (3.34), since they enforce a proper ordering (via the t ^E_(i,j) -variables) among the operations of the same job. These constraints also prevent the occurrence of a deadlock as follows. Consider the situation depicted in Fig. 3.1, where we have ${x}_{\left(a,b\right)}^{M1}={x}_{\left(c,d\right)}^{M1}={x}_{\left(c,h\right)}^{M2}={x}_{\left(a,f\right)}^{M2}=1$ and ${y}_{\left(a,b,c,d\right)}^{M1}={y}_{\left(c,h,a,f\right)}^{M2}=1$. Since h > d and f < b, the constraint set (3.32) asserts that ${t}_{\left(c,h\right)}^E>{t}_{\left(c,d\right)}^E$ and ${t}_{\left(a,f\right)}^E<{t}_{\left(a,b\right)}^E$. On the other hand, the constraint set (3.34) enforces ${t}_{\left(a,b\right)}^E<{t}_{\left(c,d\right)}^E$ and ${t}_{\left(c,h\right)}^E<{t}_{\left(a,f\right)}^E$. Clearly, these four inequalities lead to a contradiction, and consequently, the corresponding values of the x- and y-variables would be infeasible to the master problem augmented with Constraints (3.32) and (3.34).

Note that (3.34) also serves to eliminate subtours among the operations processed on a machine. These are essentially the MTZ-type of subtour elimination constraints (Miller et al. 1960), and they can be weak in the sense that they lead to loose LP relaxations. However, they can potentially be strengthened through the use of flow-based valid inequalities as shown by Sherali et al. (2006).

3.3 Valid Inequalities for Further Tightening theModelFormulation

In this section, we develop three classes of valid inequalities by exploiting the inherent structure of the NFJS problem. These inequalities are added to the MP to tighten its continuous relaxation and provide better lower bounds for use in the branch-and-bound algorithm for solving NFJSP. The first type of inequalities arises from the flow balance-type constraints that capture the movement of operations among the machines. The other two types of inequalities are formulated to obviate infeasibility caused by re-entrant flow and deadlock, respectively. They are based on a new formulation for the asymmetric travelling salesman problem (ATSP) presented in Sarin et al. (2005).

3.3.1 Flow-Balance Constraints

In the NFJSP formulation, we used the variable ${v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}$ to represent the transfer of job i from machine e to machine f when performing the respective operations j and j + 1. This definitional role of ${v}_{\left(i,j,j+1\right)}^{\left(e,f\right)}$ is enforced by (3.10). We can further tighten the continuous relaxation of the model by introducing the following flow-balance constraints (FBC):

$$ {\displaystyle \sum_{f\in {M}_{\left(i,2\right)}}{v}_{\left(i,1,2\right)}^{\left(e,f\right)}}={x}_{\left(i,1\right)}^e,\kern1em \forall i=1,\dots, N,e\in {M}_{\left(i,1\right)} $$

(3.38)

$$ {\displaystyle \sum_{e\in {M}_{\left(i,j-1\right)}}{v}_{\left(i,j-1,j\right)}^{\left(e,f\right)}}={\displaystyle \sum_{g\in {M}_{\left(i,j+1\right)}}{v}_{\left(i,j,j+1\right)}^{\left(f,g\right)}},\kern1em \forall i=1,\dots, N,j=2,\dots, {J}_i-1,f\in {M}_{\left(i,j\right)} $$

(3.39)

$$ {\displaystyle \sum_{e\in {M}_{\left(i,{J}_i-1\right)}}{v}_{\left(i,{J}_i-1,{J}_i\right)}^{\left(e,f\right)}}={x}_{\left(i,{J}_i\right)}^f,\kern1em \forall i=1,\dots, N,f\in {M}_{\left(i,{J}_i\right)}. $$

(3.40)

Constraints (3.38) assert that if the first operation of job i is assigned to machine e, then job i must be transported from machine e to some machine f that is capable of processing the second operation of job i. Constraints (3.39) capture the fact that if machine f is chosen for processing the jth operation of job i, 1 < j < J _i , then job i is necessarily transferred from some previous machine, e, and is transported to a succeeding machine, g, while performing the respective operations j − 1 and j + 1. Similarly, Constraints (3.40) require job i to be transferred from some previous machine e in case its last operation is processed on machine f.

3.3.2 Re-Entrant Flow-Based Constraints

In the case of re-entrant flows, the lower indexed operations of any job must precede the higher indexed operations of that job for the sequence to be feasible. For the sake of convenience, we designate an order ord(i, j) for elements of ${Z}_m,\forall m\in M,$ such that the ordering of operations from the same job is maintained. For instance, if Z _m  = {(1, 1), (2, 2), (1, 2)}, we can assign ord(1, 1) = 1, ord(2, 2) = 2, and ord(1, 2) = 3. Based on this definition, we let

$$ {h}_{\left(i,j,k,l\right)}^m\equiv {x}_{\left(i,j\right)}^m{x}_{\left(k,l\right)}^m,\forall m\in M;\left(i,j\right),\left(k,l\right)\in {Z}_m: ord\left(i,j\right)< ord\left(k,l\right) $$

We can linearize the foregoing relationship between the h- and the x -variables by using the following logical constraints:

$$ \begin{array}{lll}[b]&{h}_{\left(i,j,k,l\right)}^m\le {x}_{\left(i,j\right)}^m,\kern1em {h}_{\left(i,j,k,l\right)}^m\le {x}_{\left(k,l\right)}^m,\kern1em {h}_{\left(i,j,k,l\right)}^m\ge {x}_{\left(i,j\right)}^m+{x}_{\left(k,l\right)}^m-1,\\ &\quad\forall m\in M,\left(i,j\right),\left(k,l\right)\in {Z}_m: ord\left(i,j\right)< ord\left(k,l\right).\end{array} $$

(3.41)

We also define certain indirect precedence variables as follows:

$$ {g}_{\left(i,j,k,l\right)}^m=\left\{\begin{array}{l}1,\ \mathrm{if}\ \mathrm{operation}\ j\ \mathrm{of}\ \mathrm{job}\ i\ \mathrm{is}\ \mathrm{processed}\ \mathrm{sometime}\ \mathrm{before}\\ {}\kern1em \mathrm{operation}\ l\ \mathrm{of}\ \mathrm{job}\ k\ \mathrm{on}\ \mathrm{machine}\ m,\\ {}0,\ \mathrm{otherwise}.\end{array}\right. $$

Then, we have,

$$ {g}_{\left(i,j,k,l\right)}^m+{g}_{\left(k,l,i,j\right)}^m={h}_{\left(i,j,k,l\right)}^m,\kern1em \forall m\in M,\left(i,j\right),\left(k,l\right)\in {Z}_m: ord\left(i,j\right)< ord\left(k,l\right) $$

(3.42)

$$ {g}_{\left(i,j,\gamma, \eta \right)}^m\ge {g}_{\left(i,j,k,l\right)}^m+{g}_{\left(k,l,\gamma, \eta \right)}^m-1,\kern1em \forall m\in M,\forall \mathrm{distinct}\ \left(i,j\right),\left(k,l\right),\left(\gamma, \eta \right)\in {Z}_m $$

(3.43)

$$ {g}_{\left(i,j,i,l\right)}^m=0,\kern1em \forall m\in M,\left(i,j\right),\left(i,l\right)\in {Z}_m:\ j>l. $$

(3.44)

Constraints (3.42) state that given two job-operations on a machine, one of them must either precede or succeed the other. Constraints (3.43) represent the transitivity property; that is, for any triplet of job-operations (i, j), (k, l), and (γ, η) on machine m, if operation (i, j) is scheduled somewhere before operation (k, l) and operation (k, l) is scheduled somewhere before operation (γ, η), then operation (i, j) must necessarily be scheduled before operation (γ, η). Finally, the re-entrant flow Constraints (3.44) ensure that if two operations of the same job are assigned to a machine, then the lower indexed job operation precedes the higher indexed operation.

Also, we have the following logical constraints connecting the indirect and the direct precedence variables:

$$ {g}_{\left(i,j,k,l\right)}^m\ge {y}_{\left(i,j,k,l\right)}^m,\kern1em \forall m\in M,\forall \left(i,j\right)\ne \left(k,l\right)\kern0.5em \mathrm{in}\kern0.5em {Z}_m. $$

(3.45)

Hence, the re-entrant flow constraints that can be accommodated into the master (Stage-I) program are given by (3.41), (3.42), (3.43), (3.44), and (3.45). Note that by introducing the g ^m_(i,j,k,l) -variables, we also eliminate infeasibility caused by subtours in operation sequencing, since the indirect precedence enforced by the g ^m_(i,j,k,l) -variables precludes the occurrence of subtours.

3.3.3 Deadlock Prevention Constraints

Next, we develop valid inequalities to prevent the occurrence of a deadlock. For the sake of brevity, we only present inequalities for the prevention of 2-machine deadlocks and establish their validity. For a detailed development of the corresponding results for the general case of m-machine deadlocks, see Varadarajan (2006).

Consider the following situation in a job shop environment: operations (a, b) and (c, d) are assigned to machine m; and operations (a, f) and (c, h), where f < b and h > d, are assigned to machine n. If (a, b) precedes (c, d), then (a, f) must necessarily precede (c, h) to avoid a deadlock (see Fig. 3.1, where machines m and n are denoted by M1 and M2, respectively). Then, we have the following result:

Proposition 2

Two-machine deadlocks are prevented by including the following additional inequalities:

$$ \begin{array}{l}{g}_{\left(a,f,c,h\right)}^n\ge {g}_{\left(a,b,c,d\right)}^m+{h}_{\left(a,f,c,h\right)}^n-1,\\ {}\kern1em \forall\ m,n\in M,\left(a,b\right),\left(c,d\right)\in {Z}_m,\left(a,f\right),\left(c,h\right)\in {Z}_n,\\ {}\kern1em f<b\ \mathrm{and}\ h>d.\end{array} $$

(3.46)

Proof

If ${h}_{\left(a,f,c,h\right)}^n=0$, then ${g}_{\left(a,f,c,h\right)}^n=0$ by (3.42), and g ^m_(a,b,c,d) can be 1 without causing any deadlock. If ${h}_{\left(a,f,c,h\right)}^n=1$ and ${g}_{\left(a,b,c,d\right)}^m=0$, then ${g}_{\left(a,f,c,h\right)}^n\ge 0$, and the schedule is deadlock free. On the other hand, if both g ^m_(a,b,c,d) and h ⁿ_(a,f,c,h) are equal to 1, then (a, b) is processed sometime before (c, d) on machine m, and (a, f) and (c, h) are processed on the same machine n. To yield a deadlock-free schedule under this situation, (a, f) must be processed sometime before (c, h) on machine n, which is enforced by (3.46). □

Note that to apply the above deadlock prevention constraints to the master problem, we need to also include Constraints (3.41), (3.42), (3.43), and (3.44), so that g- and h-variables take their definitional roles in the model.

3.4 Computational Results

We now present results of computational experimentation to demonstrate the effectiveness of our feasibility-inducing and model-tightening inequalities within the framework of the L-shaped method for the solution of NFJS problem. In this method, the Stage-I master problem is solved using a branch-and-bound algorithm. Whenever an integer solution is obtained for a node problem’s LP relaxation, the Stage-II problem is solved to verify its feasibility and optimality. If any of these conditions are not met, a feasibility cut or an optimality cut is generated and added to the Stage-I problem, and the branch-and-bound process continues.

There are several ways in which the valid inequalities pertaining to the expected value scenario (EVS), the re-entrant flows (RF), and deadlock prevention (DP) (developed in Sects. 3.2.4, 3.3.2, and 3.3.3, respectively) can be applied. We can either use them separately, or we can apply the EVS inequalities in conjunction with selected members of the RF and DP inequalities in order to tighten the underlying relaxation. Our preliminary investigation has shown that the use of the EVS inequalities always leads to shorter CPU times. The question, then, is how (if at all) to apply the RF and DP inequalities in addition to the EVS inequalities. Note that, to achieve the full potential of the RF and DP inequalities, we need to consider re-entrant flows and deadlocks among all the machines, which would require a large number of extra variables and constraints that may overburden the master program and deteriorate its computational performance. Therefore, we choose to apply these inequalities to a proper subset of machines, as investigated in Sect. 3.4.2 below. Furthermore, we explore the optional addition of the flow-balance constraints FBC of Sect. 3.3.1.

3.4.1 Design of Test Problems

To represent routing flexibility, we group machines into work centers; operations assigned to a work center are allowed to be processed by any machine in that work center. Due to this feature, the manner in which workload is assigned to the machines within a work center is not determined until a solution is obtained. To indicate the potential workload on a machine, we define a load factor to be the total number of visits of all the jobs to that machine on average, assuming that all the machines within a work center equally share the workload. According to the load factor, we differentiate machines into two categories: low-number-of-visit (LNV) machines (with two potential visits on average), or high-number-of-visit (HNV) machines (with three potential visits on average). Consequently, three job-visiting patterns are considered, pertaining to different distributions of workload on the machines. These are: {“L⁺∙H⁻,” “L∙H,” “L⁻∙H⁺”}. The letters “L” and “H” refer to the LNV and HNV machines, respectively; the plus/minus signs in the superscript indicate that, relatively, there are higher or lower number of machines in a category than those in the other. We consider test problems of various sizes, involving 6, 8, or 10 machines. Their basic specifications are listed in Table 3.1.

Table 3.1 Specifications for various problem sizes

With respect to routing flexibility, three cases are considered. In Case ρ ₁, all HNV machines are grouped into one work center, while no routing flexibility exists among the LNV machines. In Case ρ ₂, all LNV machines are grouped into one work center; no routing flexibility exists among the HNV machines. In Case ρ ₃, no routing flexibility exists.

For each of the above 3 × 3 × 3 = 27 combinations of numbers of machines, job-visiting patterns, and routing flexibility, we constructed 20 test problems with randomly generated job routings and processing times. For the 6-machine problems, we considered the following numbers of scenarios: {100, 200, 300, 400}. The larger-sized problems (involving 8 and 10 machines) were solved using 400 scenarios to reveal the effectiveness of the proposed strategy.

All experimental runs were implemented using AMPL-CPLEX 10.1 and performed on a Pentium D 3.2 GHz CPU computer with 2 GB memory.

3.4.2 Experimental Results

We first compare the performance of solving NFJSP directly by AMPL-CPLEX (designated as Method I) with that of our decomposition approach (designated as Method II), which includes the EVS inequalities but not the RF and DP inequalities. Results of the L-shaped method without any additional inequalities, i.e., only with the standard feasibility and optimality cuts (3.29) and (3.30) (designated as Method III) are also provided for comparison. In addition, we considered the option of either adding or not adding the FBC inequalities of Sect. 3.3.1 to these three methods. The 6-machine problems were solved to optimality; the 8- and 10-machine problems were run until an integer solution was obtained within an optimality gap of 5 %. Since the superiority of Method II was observed in our preliminary study, we adopted the following approach to avoid excessive run times: Method II was used to solve the test problems first. Since there are two options (with or without the FBC inequalities), we record the CPU time as t ₂ ' and t ₂ '', respectively, for these options. Let t ₂ = max{t ₂ ', t ₂ ''}. For Methods I and III, we set an upper bound on the CPU time of max{1.2 × t ₂, t _c }, where the value of t _c is 1500, 2000, and 2500 s, respectively, for the 6-, 8-, and 10-machine problems. The first term (1.2 × t ₂) is used to provide a reasonable (20 %) margin to demonstrate the superiority of Method II over the other two methods. The second term (t _c ) is included to ensure that the effectiveness of adding the FBC inequalities is not obscured by stopping prematurely.

The results obtained are presented in Table 3.2. Note that the inclusion of the FBC inequalities results in shorter CPU times for Methods I and II in most cases. Therefore, in the following discussion, we only provide results for the case where the FBC inequalities have been added to the NFJSP formulation. From these results, it is also evident that Method II is substantially faster than Methods I and III.

Table 3.2 Computational results for Methods I, II, and III for 400 scenarios

To further illustrate how this dominance varies with an increasing number of scenarios, we present, in Fig. 3.2, the results for 6-machine problems with four different numbers of scenarios, namely, 100, 200, 300, and 400. The arrow and the number next to a data point indicate the percentage of test problems that consume CPU times more than the limit of 1500 s. Note that Method II substantially dominates the other methods as the number of scenarios increases from 100 to 400. This pattern is observed not only for the average values that are depicted in Fig. 3.2, but also for all combinations of job-visiting patterns and cases of routing flexibility. For the sake of brevity, we illustrate this behavior in Fig. 3.3 by using the combination “L∙H” × “ρ ₂”. Clearly, Method II dominates the other two methods for all numbers of scenarios considered. Moreover, as the number of scenarios increases, the CPU time required by Method II increases almost linearly, while that for Method I increases superlinearly. Although the CPU time for Method III also increases almost linearly, it does so at a much higher rate than that for Method II. Hence, the dominance of Method II becomes more prominent with an increase in the number of scenarios. Also, note that Method III begins to dominate Method I for larger number of scenarios.

Fig. 3.2

Average CPU times for 6-machine problems for various numbers of scenarios

Fig. 3.3

Average CPU times required by the combination “L∙H” × “(ii)” for 6-machine problems for various numbers of scenarios

Next, we investigated the impact of adding the RF and DP inequalities to MethodII. There are several options that we can consider. The default option is Method II with the FBC inequalities. We can either add to this default option the RF and DP inequalities separately, or we can add them both at the same time. Another aspect to consider is the set of machines to which these inequalities are applied. We considered two options in this respect, namely, their application to only the HNV machines, or to only the LNV machines. Our preliminary investigation showed that the application of the RF and DP inequalities to the HNV machines results in the addition of a large number of extra variables and constraints to the Stage-I master problem, which leads to greater CPU times in comparison with the default option. Therefore, in the following discussion, we only consider the addition of the RF and DP inequalities to the LNV machines. To compare the performances of different model configurations, we fixed the number of scenarios at 400. The average CPU times and the ratio between the values of the LP solution and the 1. best-found solution, under different job-visiting patterns and cases of routing flexibility, are summarized in Tables 3.3 and 3.4.

Table 3.3 Average CPU times and percentage improvements over Model A

Table 3.4 Comparing quality of LP relaxation

We highlight in bold, in Table 3.3, the CPU times that turn out to be shorter than that for the default model (A) for a given combination of job-visiting pattern and routing flexibility. For each such case, the percentage improvement in CPU time over the default model is also presented along with the CPU time. In view of these results, we can make the following observations: Simlarly a higher ratio between the values of the LP solution and the best-found solution obtained for a method over default is highlighted in Table 3.4

• 1. On average, the addition of the RF inequalities alone (Model B) and the addition of both types of inequalities (Model D) help in achieving a shorter CPU time. This is particularly true when routing flexibility occurs on the HNV machines (Case ρ ₁) because it leads to fewer conflicts for a large number of operations. This phenomenon appears to become more prominent with an increase in the number of machines, where savings of up to 58.1 % are achieved by Model B and up to 57.3 % by Model D for the 10-machine problems.

• 2. The benefit of adding the RF and DP inequalities is more evident for the harder problems, i.e., when the default model (Model A) takes a longer time to solve a problem, the addition of the RF and DP inequalities is more likely to help reduce the CPU time.

3.5 Heuristic Methods for the Solution of the NFJS Problem

Several heuristic methods can be used for the solution of the NFJSP that rely on work presented above. Six such viable procedures are described and investigated below.

1. Expected Value Problem Heuristic (EVP)

• 1. Assume processing times to be deterministic and equal to their expected values, and solve the model to optimality record the solution.

• 2. Evaluate solution using all scenarios.

2. Mixed Heuristic (Mixed)

Note that, even if all the scenarios are considered in the determination of budget over-runs, the resulting model is still relatively easy to solve (as the number of relevant constraints/variables is equal to NS). Hence, we can consider all scenarios in the determination of budget over-runs, while using expected processing times for the determination of job completion times. We call the resulting model a mixed-type model. Since this is a closer approximation of the original problem, we expect it to yield better solutions than the expected value heuristic.

For large-sized problem instances, even the mixed-type model becomes very difficult to solve. Therefore, we further relax the sequencing variables to be continuous and solve the mixed-type model to obtain assignment decisions. Then, we determine job sequences by considering the outcomes of all scenarios.

• 1. Solve the mixed-type model with sequencing variables relaxed as continuous; (assignment step).

• 2. Determine the processing sequences using the assignment decisions fixed in Step 1; (sequencing step).

3. Mixed + Shortest Processing Time (SPT)

The second step of the mixed heuristic is still difficult to solve for large-sized problems, hence we can apply the SPT dispatching rule to determine the job sequence. That is, whenever a machine is released by a previous operation, we choose the operation that has the shortest processing time on that machine from among the waiting operations. Note that, if an operation can be processed on multiple machines, it is considered to be waiting on all the compatible machines. Its assignment is determined based on which machine first chooses it as the next operation to be processed. Note that the SPT rule is based on the expected processing times.

4. Mixed + Least Work Remaining (LWKR)

This approach is similar to “Mixed + SPT,” except that we use the least-work-remaining-first rule to dispatch operations.

5 and 6. Mixed + Shifting Bottleneck Heuristic (SBN)

As a first step, we use Step 1 of the Mixed Heuristic to determine the assignment of operations to the machines. The remaining sequencing problem is modeled as a disjunctive graph. In the beginning, all disjunctive arcs are relaxed and job completion times are recorded and regarded as due dates. The ready time and due date of each operation are determined by following the forward and backward passes along the critical paths (for the completion time problem, there are usually multiple critical paths). Next, each machine is considered individually to fix its operation sequence using a heuristic rule. The machine that yields the largest change in the total completion time is chosen, and the corresponding sequence (set of disjunctive arcs) is fixed. The procedure continues until all the machines are sequenced. Note that after the sequence of operations on each machine is fixed, a re-sequencing step is implemented by adjusting the sequences of operations on previously fixed machines.

We employ the following two heuristic rules to determine the sequence in which to process the jobs on a machine:

5. SBN_ATC

Determine the following Apparent Tardiness Cost (ATC) priority index (Pinedo and Singer 1999):

$$ {I}_{ij}={\displaystyle \sum_{k=1}^N\frac{1}{p_{ij}} \exp \left(-\frac{d_{ij}^k-{p}_{ij}+{\left({r}_{ij}-t\right)}^{+}}{K\overline{p}}\right)},\kern1em \forall i\in M,j=1,\dots, N, $$

where t is the scheduling time, K = 2, and $\overline{p}$ is the average of the processing times of the jobs assigned to machine i, and ready time r _ij and local due date d ^k _ij of operation j of job k assigned to machine i are determined as explained in Pinedo and Singer (1999).

6. SBN_PRTT

Choose the operation that has the lowest value of Chu and Portmann (1992):

$$ PRT{T}_{ij}= \max \left({r}_{ij},\kern0.5em t\right)+ \max \left\{ \max \left\{{r}_{ij},\kern0.5em t\right\}+{p}_{ij},\kern1em { \min}_k\left\{{d}_{ij}^k\right\}\right\}, $$

$$ \forall i\in M,j=1,\dots, N. $$

This is a single machine sequencing rule, and we use the values of r _ij and d ^k _ij as determined above. Additionally, insert the earliest available operation, if the operation chosen by the above rule leaves enough idle time before itself.

The relative performances of these heuristic methods are presented in Tables 3.5 and 3.6 for 6 machines (with three jobs) and 10 machines (with 15 jobs), respectively. Optimal gap is determined with respect to the solution of mixed-method, which serves as a lower bound. Note that, although EVP gives the best results with the least CPU time for the first set of problems, it becomes impractical for larger-sized problems (second set) due to its large number of binary sequencing variables. Mixed + LWKR heuristic gives the best results on larger-sized problem instances.

Table 3.5 Results on 6-machine problems (with 3 jobs)

Table 3.6 Results on 10-machine problems (with 15 jobs)

3.6 Concluding Remarks

In this chapter, we have presented a stochastic programming approach for the NFJS (Network of Flexible Job Shops) problem. This problem arises in a distributed fabrication environment that has recently emerged to serve the evolving needs of the high investment, low volume MEMS industry. The problem is modeled as a two-stage stochastic program with recourse, where the uncertainty in processing times is captured using scenarios. The first-stage routing and sequencing variables are binary whereas the second-stage completion time and budget over-run variables are continuous. Since the NFJS problem lacks relatively complete recourse, the first-stage solution can be infeasible to the second-stage problem in that it might generate subtours, violate the re-entrant flow conditions, or create a deadlock. In the standard L-shaped method, feasibility cuts are iteratively added to the first-stage problem upon the discovery of these infeasibilities. As an alternative, we have provided certain expected-value-scenario-based inequalities to induce feasibility of the second-stage problem that greatly help reduce the effort required by the L-shaped method. To further tighten the first-stage problem formulation, we have also developed three types of valid inequalities: flow-balance constraints, re-entrant flow-based constraints, and deadlock prevention constraints. Our computational results reveal that: (a) our decomposition approach is substantially superior to the direct solution of the NFJSP using CPLEX; (b) the expected-value-scenario-based inequalities are significantly more effective than the use of standard feasibility cuts in the master problem; and (c) the judicious additional use of the re-entrant flow and deadlock prevention inequalities in conjunction with the expected-value-scenario-based inequalities further improves the overall algorithmic performance, particularly for more difficult problem instances. Furthermore, we have proposed heuristic methods for the solution relatively larger instances of NFJS and have presented results of their implementation.