A two-machine flowshop scheduling problem with precedence constraint on two jobs

Abstract

Job precedence can be found in some real-life situations. For the application in the scheduling of patients from multiple waiting lines or different physicians, patients in the same waiting line for scarce resources such as organs, or with the same physician often need to be treated on the first-come, first-served basis to avoid ethical or legal issues, and precedence constraints can restrict their treatment sequence. In view of this observation, this paper considers a two-machine flowshop scheduling problem with precedence constraint on two jobs with the goal to find a sequence that minimizes the total tardiness criterion. In searching solutions to this problem, we build a branch-and-bound method incorporating several dominances and a lower bound to find an optimal solution. In addition, we also develop a genetic and larger-order-value method to find a near-optimal solution. Finally, we conduct the computational experiments to evaluate the performances of all the proposed algorithms.

1 Introduction

In the classical scheduling models, most of works consider the scheduling problems without precedence constraints. In fact, the job precedence can be found in some real-life situations. For the application in the scheduling of patients from multiple waiting lines or with different physicians, Chandra et al. (2014) claimed that patients in the same waiting line for scarce resources such as organs, or with the same physician often need to be treated on the first-come, first-served basis to avoid ethical or legal issues, and precedence constraints can restrict their treatment sequence. Chandra et al. (2014) further examined a single machine scheduling problem of minimizing the maximum scheduling cost in which job release dates and precedence constraints are included. Panwalker and Iskander (1977) pointed out that flow time and tardiness are the most prominent measures. Essentially, minimizing the flow time keeps the work-in-process inventory at a low level while minimizing the tardiness reduces the penalties incurred for late jobs. The former represents internal efficiency, while the latter represents external efficiency. It is noted that Koulamas (1994) has proved that the flowshop scheduling problem with the objective to minimize total tardiness is an NP-hard one even for the two-machine case. It is also found that research with precedence constraints and flowshop settings has been relatively unexplored. In fact, the importance of the flowshop setting can be found in in many real production systems (French 1982; Pinedo 2008). As a result, both precedence constraints and flowshop settings have been taken into consideration in this paper.

As for the research concerning the two-machine flowshop scheduling problem with minimizing the mean tardiness or total tardiness criterion (the two measures are equivalent, namely, in choosing a schedule to minimize the mean tardiness, we are also minimizing the total tardiness). Sen et al. (1989) derived some rules of a pair of adjacent jobs used in a branch-and-bound solution procedure to reach an optimal solution and provided a simple and computationally efficient heuristic for the problem. Kim (1993) considered the two-machine flowshop scheduling problem with the objective to minimize mean tardiness. He presented several properties that are used to calculate lower bounds on total tardiness of jobs for a given partial sequence and to identify sequences dominated by others used in a branch-and-bound algorithm. Kim (1995) further considered the permutation flowshop scheduling problem with the objective to minimize total tardiness. He built a branch-and-bound method incorporated with several properties used to calculate lower bounds on total tardiness of jobs for a given partial sequence. Pan and Fan (1997) addressed the problem of sequencing jobs on a two-machine flowshop to minimize the total tardiness, and proposed a branch-and-bound algorithm incorporated with five dominance properties for the precedence relations between jobs in an optimal solution as well as a sharp lower bound on the total tardiness of a subproblem for the problem. Continued exploring the same problem, Pan et al. (2002) derived three dominance criteria to establish the precedence constraints between jobs in an optimal schedule and a lower bound on the total tardiness of the problem by constructing the sequence of jobs from front to back to simplify the bounding procedure. Schaller (2005) provided the improved versions of the three dominance conditions developed by Pan et al. (2002) and a new dominance condition.

Chung et al. (2006) used the branch-and-bound algorithms for minimizing the total tardiness in m-machine flowshop settings. Chen et al. (2006) addressed a bi-criteria two-machine flowshop scheduling problem with a learning effect to minimize a weighted sum of the total completion time and the maximum tardiness. Wu et al. (2007) studied a two-machine flowshop scheduling problem with a learning effect, with the goal to find a sequence that minimizes the maximum tardiness. They employed a branch-and-bound method and a simulated annealing (SA) method to search for the optimal solution and a near-optimal solution, respectively. Vallada et al. (2008) presented a review and comprehensive evaluation of heuristics and metaheuristics for the m-machine flowshop scheduling problem with the objective to minimize total tardiness. By contrast, Gelders (1978) developed some heuristic algorithms that are based on priority rules for minimizing the sum of weighted tardiness, and Ow (1985) applied a heuristic algorithm for a case in which processing times of the jobs on the machines depend on characteristics of the jobs such as order/processing quantities of the jobs.

As for some metaheuristics devised for flowshop problems with tardiness measures, the reader might refer to Parthasarathy and Rajendran (1997), who used a simulated annealing algorithm to minimize the weighted sum of tardiness, to Armentano and Ronconi (1999), who presented a tabu search method, and to Onwubolu and Mutingi (1999) and Gen and Lin (2012), who developed genetic algorithms for the same problem. For more recent works on two-machine flowshop settings, Bank et al. (2012) studied a two-machine scheduling problem with deteriorating jobs whose processing times depend on their waiting time. They developed a lower bound, several dominance properties and an initial upper bound derived from a heuristic algorithm that used a branch-and-bound algorithm to minimize the total tardiness criteria. Ta et al. (2013) proposed a Tabu search and a matheuristic algorithm and three upper bounds and a lower bound based on a partial relaxation of the MILP model. Kharbeche and Haouari (2013) proposed compact mixed-integer programming models for the NP-hard problem of minimizing tardiness in a two-machine flow shop. They also proposed valid inequalities that aim at tightening the models’ representations.

The remainder of this paper is organized as follows: In Sect. 2, we introduce some notation and formulate the problem. In Sect. 3, we derive several dominances and a lower bound to be used in a branch-and-bound algorithm. In Sect. 4, we develop a local search and genetic algorithm to find near-optimal solutions. In Sect. 5 we conduct some extensive computational experiments to determine the performance of all the proposed methods. We provide a conclusion and make some remarks for future research in the last section.

2 Problem definition

We introduce some notations which are used throughout in the contexts as follows;

• n—number of jobs.

• $M_{i}$—machine code, $i=1, 2$.

• $\sigma ,\sigma _1 ,\sigma _2$—denote job sequences.

• $\pi _1 ,\pi _2 ,\pi _3$—denote partial sequences of jobs.

• $t_i$—denotes the current completion time on machine $M_i$, $i=1, 2$.

• $p_{ij}$—denotes the job processing time of job j on machine i, $i=1,2,$ and $j=1,2, {\ldots }, n$.

• $C_{ij} (\sigma )$—denotes the completion time of job j on machine i in sequence $\sigma$, $i=1,2,$ and $j=1,2, {\ldots }, n$.

• $T_i (\sigma )$—denotes the tardiness of job i on machine $M_2$ in a sequence $\sigma$.

• $\sigma =({PS}, {US})$, where PS denotes the partial sequence with k scheduled jobs, and

• US denotes the partial sequence with $n-k$ unscheduled jobs.

The problem formulation is formally defined in the following. Consider a job set $N={\{} J_{1}, {\ldots }, J_{n} {\}}$ to be processed on machines $M_{1}$ and $M_{2}$. All the jobs have to follow the same route on each machine and the machines are assumed to be setup in series (see Baker 1974; Pinedo 2008). The jobs processing times of $J_{i}$ on $M_{1}$ and $M_{2}$ are all constant and fixed numbers, say $p_{1i}$ and $p_{2i}$, respectively. All jobs are ready at time zero. Assume that there are no set-up times and jobs are processed without interruption or preemption. Each job can be processed on one machine only. In the classical scheduling model, researchers consider there are no precedence constraints among operations of n jobs. However, the real application can be seen in the SQL Server Books Online that after a package contains multiple tasks or containers, one can link them into a sequenced workflow using precedence constraints. Each precedence constraint references two executables: two tasks, two containers, or one of each. They are known as the precedence executable and the constrained executable. The precedence executable is the task or container whose execution outcome (success or failure) can determine whether the next task or container, the constrained executable, runs. Motivated by this fact, we introduce precedence constraint into problem. Specifically, we consider a specific precedence constraints with only two jobs in a predetermined order. That is, $J_{u}$ must precede $J_{v}$, but not necessary immediately before, in a feasible sequence.

For a given sequence $\sigma$, the completion time of a job scheduled in the kth position on machines $M_{1}$ and $M_{2}$ are defined $C_{1[k]}(\sigma )$ and $C_{2[k]}(\sigma )$, where square brackets [ ] are used to signify the position of jobs in a sequence. Then, the completion times for the kth job in $\sigma$ on machines $M_{1}$ and $M_{2}$, respectively, are given by.

$$\begin{aligned} \begin{array}{l} C_{1[k]} (\sigma )=\sum \limits _{l=1}^k {p_{1[l]} } , \\ C_{2[k]} (\sigma )=\max \{C_{1[k]} (\sigma ),C_{2[k-1]} (\sigma )\}+p_{2[k]}, \\ \end{array} \end{aligned}$$

and its tardiness is given by

$$\begin{aligned} T_{[k]} (\sigma )=\max \{0, C_{2[k]} (\sigma )-d_{[k]} \}. \end{aligned}$$

The objective of this article is to find a schedule that minimizes total tardiness of n given jobs, which is a widely considered performance measure in literature.

3 Solution procedures

When the precedence constraint is not taken into consideration, the problem is an NP-hard one (Koulamas 1994; Lenstra et al. 1997; Garey et al. 1979). In view of the difficult problem, thus we will derive some dominance rules and a lower bound which are used in the branch-and-bound method. In the beginning, we develop a dominance rule for non-adjacent jobs to reduce the searching scope, then establish several dominance properties for adjacent jobs to further fathom the searching tree, and finally propose a property to determine the ordering of the remaining jobs.

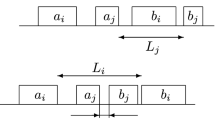
Let $\sigma _1$ be a sequence in which $J_{i}$ and $J_{j}$ are scheduled in the pth and the qth positions, where $p < q$. That is, $J_{i}$ is processed before $J_{j}$. Let $\sigma _2$ be the sequence obtained from $\sigma _1$ by interchanging the positions of $J_{i}$ and $J_{j}$. Thus, sequences $\sigma _1$ and $\sigma _2$ can be denoted as

$$\begin{aligned} \sigma _1 =( {\pi _1 J_i \pi _2 J_j \pi _3 }) \end{aligned}$$

and

$$\begin{aligned} \sigma _2 =( {\pi _1 J_j \pi _2 J_i \pi _3 }), \end{aligned}$$

where $\pi _1$, $\pi _2$, and $\pi _3$ are partial sequences. It is noted that once a node with a case of $J_{v}$ before $J_{u}$ is found, the node is deleted in the performing branch-and-bound algorithm. The cases of $N\backslash${$J_{u}$, $J_{v}$} are given as follows.

Theorem 1

Consider two jobs $J_{i}$, $J_{j}\in N\backslash${$J_{u}$, $J_{v}$}, if $p_{1i} <p_{1j}$, $p_{2i} =p_{2j}$, and $d_i \le d_j$, then there exists an optimal schedule in which $J_{i}$ is the predecessor of $J_{j}.$

Proof

Let $t_1$ and $t_2$ denote the completion times for the last job in $\pi _1$ on machines $M_{1}$ and $M_{2}$, respectively, and let the first job and last job in $\pi _2$ be $J_{k_1 }$and $J_{k_2 }$, respectively. Then, we have

$$\begin{aligned} C_{1i} (\sigma _1 )=t_1 +p_{1i}, \end{aligned}$$

$$\begin{aligned} C_{1k_1 } (\sigma _1 )=t_1 +p_{1i} +p_{1k_1 }, \end{aligned}$$

$$\begin{aligned} C_{1j} (\sigma _1 )=t_1 +p_{1i} +p_{1j} +\sum \limits _{J_l \in \pi _2 } {p_{1l} }, \end{aligned}$$

$$\begin{aligned} C_{2i} (\sigma _1 )=\max \{C_{1i} (\sigma _1 ),t_2 \}+p_{2i}, \end{aligned}$$

$$\begin{aligned} C_{2k_1 } (\sigma _1 )=\max \{C_{1k_1 } (\sigma _1 ),C_{2i} (\sigma _1 )\}+p_{2k_1 }, \end{aligned}$$

$$\begin{aligned} C_{2j} (\sigma _1 )=\max \{C_{1j} (\sigma _1 ),C_{2k} (\sigma _1 )\}+p_{2j}, \end{aligned}$$

$$\begin{aligned} C_{1j} (\sigma _2 )=t_1 +p_{1j}, \end{aligned}$$

$$\begin{aligned} C_{1k_1 } (\sigma _2 )=t_1 +p_{1j} +p_{1k_1 } \end{aligned}$$

$$\begin{aligned} C_{1i} (\sigma _2 )=t_1 +p_{1j} +p_{1i} +\sum \limits _{J_l \in \pi _2 } {p_{1l} }, \end{aligned}$$

$$\begin{aligned} C_{2j} (\sigma _2 )=\max \{C_{1j} (\sigma _2 ),t_2 \}+p_{2j}, \end{aligned}$$

$$\begin{aligned} C_{2k_1 } (\sigma _2 )=\max \{C_{1k_1 } (\sigma _1 ),C_{2j} (\sigma _2 )\}+p_{2k_1 }, \end{aligned}$$

and

$$\begin{aligned} C_{2i} (\sigma _2 )=\max \{C_{1i} (\sigma _2 ),C_{2k} (\sigma _2 )\}+p_{2i}. \end{aligned}$$

It follows from $p_{1i} <p_{1j}$ that $C_{1i} (\sigma _1 )<C_{1j} (\sigma _2 )$ and $C_{1k_1 } (\sigma _1 )<C_{1k_1 } (\sigma _2 )$, and hence $C_{2i} (\sigma _1 )=\max \{C_{1i} (\sigma _1 ),t_2 \}+p_{2i} \le \max \{C_{1j} (\sigma _2 ),t_2 \}+p_{2j} =C_{2j} (\sigma _2 )$ by $p_{2i} =p_{2j}$, implying that $C_{2k_1 } (\sigma _1 )<C_{2k_1 } (\sigma _2 )$. Combining $C_{1k_1 } (\sigma _1 )<C_{1k_1 } (\sigma _2 )$ and $C_{2k_1 } (\sigma _1 )<C_{2k_1 } (\sigma _2 )$, we have $C_{1k_2 } (\sigma _1 )<C_{1k_2 } (\sigma _2 )$ and $C_{2k_2 } (\sigma _1 )<C_{2k_2 } (\sigma _2 )$, and then it follows from $C_{1j} (\sigma _1 )=C_{1i} (\sigma _2 )$ that $C_{2j} (\sigma _1 )\le C_{2i} (\sigma _2 )$. Now, combining $C_{2i} (\sigma _1 )\le C_{2j} (\sigma _2 )$, $C_{2j} (\sigma _1 )\le C_{2i} (\sigma _2 )$ and $d_i \le d_j$, it is easy to see that $T_{2i} (\sigma _1 )+T_{2j} (\sigma _1 )=\max \{C_{2i} (\sigma _1 )-d_i ,0\}+\max \{C_{2j} (\sigma _1 )-d_j ,0\}$

$$\begin{aligned}&\le \max \{C_{2i} (\sigma _2 )-d_i ,0\}+\max \{C_{2j} (\sigma _2 )-d_j ,0\}\\&=T_{2i} (\sigma _2 )+T_{2j} (\sigma _2 ). \end{aligned}$$

Hence, the result holds. $\square$

In what follows, we propose several properties on the ordering criteria for a pair of adjacent jobs which are used in the branch-and-bound methods. Suppose that there are two schedules $\sigma _1 =(\pi _1 J_i J_j \pi _2 )$ and $\sigma _2 =(\pi _1 J_j J_i \pi _2 )$ in which $\pi _1$ and $\pi _2$ are two partial sequences of jobs. If both conditions $C_{2j} (\sigma _1 )\le C_{2i} (\sigma _2 )$ and $T_i (\sigma _1 )+T_j (\sigma _1 )<T_i (\sigma _2 )+T_j (\sigma _2 )$ hold, then it can be said that sequence $\sigma _1$ can dominate sequence $\sigma _2$. Furthermore, let $t_1$ and $t_2$ denote the completion times for the last job in $\pi _1$ on machines $M_{1}$ and $M_{2}$, respectively.

Property 1 Consider two adjacent jobs $J_{i}$, $J_{j}\in$ $N\backslash${J$_{u}$, $J_{v}$}, if $p_{1i} <\min \{p_{1j} ,p_{2j} ,p_{2i} ,p_{2i} +d_j -d_i \}$, $\max \{d_i ,d_j \}<t_1 +p_{1i} +p_{1j} +p_{2j}$, $p_{2i} <p_{1j}$, and $t_2 <t_1 +p_{1i}$, then $\sigma _1$ dominates $\sigma _2$.

Proof

By $p_{1i} <p_{1j}$ and $t_2 <t_1 +p_{1i}$, $C_{1i} (\sigma _1 )=t_1 +p_{1i} <C_{1j} (\sigma _2 )=t_1 +p_{1j}$,

$$\begin{aligned} C_{2i} (\sigma _1 )=\max \{C_{1i} (\sigma _1 ),t_2 \}+p_{2i} = t_1 +p_{1i} + p_{2i}, \end{aligned}$$

and

$$\begin{aligned} C_{2j} (\sigma _2 )=\max \{C_{1j} (\sigma _2 ),t_2 \}+p_{2j} = t_1 +p_{1j} + p_{2j}. \end{aligned}$$

In addition, it follows from $p_{2i} <p_{1j}$ and $p_{1i} <p_{2j}$ that $C_{2i} (\sigma _1 )<C_{2j} (\sigma _2 )$, and that

$$\begin{aligned} C_{1j} (\sigma _1 ) = t_1 +p_{1i} + p_{1j} > t_1 +p_{1i} + p_{2i} =C_{2i} (\sigma _1 ) \end{aligned}$$

and

$$\begin{aligned} C_{1i} (\sigma _2 ) = t_1 +p_{1j} + p_{1i} < t_1 +p_{1j} + p_{2j} =C_{2j} (\sigma _2 ), \end{aligned}$$

and hence we have

$$\begin{aligned} C_{2j} (\sigma _1 )&=\max \{C_{1j} (\sigma _1 ),C_{2i} (\sigma _1 )\}+p_{2j}\\&= t_1 +p_{1i} + p_{1j} +p_{2j} \end{aligned}$$

and

$$\begin{aligned} C_{2i} (\sigma _2 )&=\max \{C_{1i} (\sigma _2 ),C_{2j} (\sigma _2 )\}+p_{2i}\\&= t_1 +p_{1j} + p_{2j} +p_{2i}. \end{aligned}$$

Now, it follows from $p_{1i} <p_{2i}$ and $\max \{d_i ,d_j \}<t_1 +p_{1i} +p_{1j} +p_{2j}$ that

$T_{2j} (\sigma _1 )=t_1 +p_{1i} + p_{1j} +p_{2j} -d_j$ and $T_{2i} (\sigma _2 )=t_1 +p_{1j} + p_{2j} +p_{2i} -d_i$, and hence $T_{2j} (\sigma _1 ) - T_{2i} (\sigma _2 )=p_{1i} -d_j -p_{2i} +d_i <0$.

In what follows, we consider the following cases.

Case 1: $C_{2i} (\sigma _1 )\le d_i$.

It is clear that $T_{2i} (\sigma _1 )=0\le T_{2j} (\sigma _2 )$, and hence $T_{2i} (\sigma _1 ) + T_{2j} (\sigma _1 )<T_{2i} (\sigma _2 )+T_{2j} (\sigma _2 ).$

Case 2: $C_{2i} (\sigma _1 )>d_i$and $C_{2j} (\sigma _2 )>d_j$. In this case, we have

$$\begin{aligned} T_{2i} (\sigma _1 ) + T_{2j} (\sigma _1 )= & {} 2 t_1 +2p_{1i} + p_{2i} +p_{1j} +p_{2j}-(d_i +d_j )\\< & {} 2t_1 \,{+}\,2p_{1j} \,{+}\,2 p_{2j} \,{+}\,p_{2i} -(d_i \,{+}\,d_j )\\= & {} T_{2i} (\sigma _2 )\,{+}\,T_{2j} (\sigma _2 ). \end{aligned}$$

Case 3: $C_{2i} (\sigma _1 )>d_i$ and $C_{2j} (\sigma _2 )<d_j$.

In this case, $d_j >C_{2i} (\sigma _1 ) = t_1 +p_{1i} + p_{2i} >t_1 +2p_{1i}$, and hence we have

$$\begin{aligned} T_{2i} (\sigma _1 ) + T_{2j} (\sigma _1 )= & {} t_1 + p_{2i} +p_{1j} +p_{2j} -d_i\\&-(d_j -t_1 -2p_{1i} ) \end{aligned}$$

$$\begin{aligned} <t_1 +p_{1j} + p_{2j} +p_{2i} -d_i = T_{2i} (\sigma _2 )+T_{2j} (\sigma _2 ). \end{aligned}$$

Thus, in any case, we have $T_{2i} (\sigma _1 ) + T_{2j} (\sigma _1 )<T_{2i} (\sigma _2 )+T_{2j} (\sigma _2 )$, as required. $\square$

Property 2 Consider two adjacent jobs $J_{i}$, $J_{j}\in N\backslash${$J_{u}$, $J_{v}$}, if $t_2 <t_1 +p_{1i}$, $t_1 +p_{1j} +p_{2j} >\max \{d_j ,d_i -p_{2i} \}$, $p_{1i} <p_{1j} <p_{2i} <p_{2j}$, and $p_{2i} >d_i -d_j$, then $\sigma _1$ dominates $\sigma _2$.

Property 3 Consider two adjacent jobs $J_{i}$, $J_{j}\in N\backslash${$J_{u}$, $J_{v}$}, if $d_i -p_{2i} <t_2 +p_{2j} <d_j$, $p_{1i} <p_{1j}$, $p_{2i} <p_{2j}$, $t_1 +p_{1j} <\min \{t_2 ,t_2 +p_{2i} -p_{1i} \}$, and $d_i <d_j$, then $\sigma _1$ dominates $\sigma _2$.

Property 4 Consider two adjacent jobs $J_{i}$, $J_{j}\in N\backslash${$J_{u}$, $J_{v}$}, if $p_{2i} <p_{1j}$, $d_i <d_j$, $t_2 <t_1 +p_{1i}$, $p_{1i} <\min \{p_{1j} ,p_{2i} ,p_{2j} ,p_{2i} +d_j -d_i \}$, and, $d_i -p_{2i} <t_1 +p_{1j} +p_{2j} <d_j$ then $\sigma _1$ dominates $\sigma _2$.

Property 5 Consider two adjacent jobs $J_{i}$, $J_{j}{\in } N\backslash${$J_{u}$, $J_{v}$}, if, $d_i -p_{2i} <t_1 +p_{1j} +p_{2j} <d_j$, $p_{1i} <\min \{p_{2i} ,p_{2j} ,p_{2i} +d_j -d_i \}$, and $p_{1i} <t_2 -t_1 <p_{1j} +\min \{0,p_{1i} -p_{2i} ,p_{2j} -p_{2i} \}$, then $\sigma _1$ dominates $\sigma _2$.

Property 6 Consider two adjacent jobs $J_{i}$, $J_{j}{\in } N\backslash${$J_{u}$, $J_{v}$}, if $d_i -p_{2i} <t_1 +p_{1j} +p_{2j} <d_j$, $p_{1i} <p_{1j} <p_{2i} <p_{2j}$, $t_2 <t_1 +p_{1i}$ and $p_{1i} -d_j <p_{1j} -d_i$, then $\sigma _1$ dominates $\sigma _2$.

Apart that, let ($\pi _1$, $\pi _{US} )$ be a schedule of n jobs where $\pi _1$ denotes the determined part with k jobs and $\pi _{US}$ denotes the undetermined part with r jobs ($r=n-k$). The following property can be easily obtained due to the precedent constraint.

Property 7 Consider sequence $\sigma =(\pi _1 \mathrm{,} \pi _{US} )$ where $J_{v}$ is in $\pi _1$, while $J_{u}$ is in $\pi _{US}$, then $\sigma$ can be dominated.

Remark 1

We omit the proofs of Properties 2–7 since they are similar to those of Theorem 1 and Property 1.

In what follows, we describe a simple lower bound which is used in the branch-and-bound algorithm. Let $\sigma =({PS}, {US})$ be a sequence of jobs in which PS is the scheduled part and US is the unscheduled part. In addition, suppose that there are k jobs in US and we wish to derive a way to minimize the total tardiness of US. Note that the set of k jobs is excluded from job $J_{v}$ when $J_{v}$ is in US. Then, combining the values of the total tardiness of PS can be used to derive a lower bound for $\sigma$. The completion times and tardiness for the first r jobs in PS are

$$\begin{aligned} C_{2[r]} (PS)=\max \left\{ \sum \limits _{j=1}^r {p_{1[j]} ,C_{2[r-1]} (PS)} \right\} +p_{2[r]} \end{aligned}$$

(1)

and

$$\begin{aligned} T_{[r]} (PS)=\max \{0, C_{2[r]} (PS)-d_{[r]} \}, \quad r= 1, 2, {\ldots }, n-k.\nonumber \\ \end{aligned}$$

(2)

We further assume that the processing times of US on $M_{2 }$are ${p}'_{21}$, ${p}'_{22}$, ..., ${p}'_{2k}$. To derive the lower bound of the total tardiness for US, we first assume that all the processing times on $M_{1 }$are zero and have a common due date $d_{\max }$, which is the maximal due date among jobs in US. We then arrange job processing times on $M_{2 }$ according to the shortest processing time first (SPT) rule; that is, ${p}'_{2(1)} \le {p}'_{2(2)} \le \cdots \le {p}'_{2(k)}$. Thus, the completion time and the tardiness of pseudo jobs in US are

$$\begin{aligned} C_{2(i)} (US)=C_{2[r]} (PS)+{p}'_{2(i)} \end{aligned}$$

(3)

and

$$\begin{aligned} T_{(i)} (US)=\max \{0,C_{2(i)} (US)-d_{\max } \}, \quad i=1, 2, {\ldots }, k,\nonumber \\ \end{aligned}$$

(4)

Thus, based on Eqs. (2) and (4), the simple lower bound can be obtained as

$$\begin{aligned} \sum \limits _{i=1}^{n-k} {T_{(i)} (PS)} +\sum \limits _{i\in US\backslash \{J_v \}}^ {T_{(i)} (US)}. \end{aligned}$$

(5)

4 LH and GA algorithms

In this section, we further use a largest-order-value method (LH) in Sect. 4.1 and a genetic algorithm (GA) in Sect. 4.2 to solve this problem.

4.1 The details of LH

The differential evolution (DE) algorithm, proposed by Storn and Price (1997), is among the most commonly used metaheuristic methods for solving combinatorial optimization problems. Its major advantage is that this method requires few control variables, is robust and easy to use, and lends itself very well to parallel computation. Due to the parallel evolution framework of DE, local search is easy to embed in DE to develop effective hybrid algorithms. Tasgetiren et al. (2004) pointed out that there are possible two types of the local search used in DE algorithm. The first one is based on the neighbors of the parameter values, whereas the second one is based on the neighbors of job positions in the permutation schedule. Tasgetiren et al. (2004) claimed that the latter has a good property that the repair algorithm is only needed after evaluating all the neighbors in a permutation. Furthermore, Gao et al. (2010) adopted largest-order-value rule, based on the idea of work by Tasgetiren et al. (2004), successfully to solve a no-wait flow shop to minimize total flow time. In inspired by these successful cases, we use the similar idea to solve this problem. For the details of main equation of DE variant, the reader may refer to Storn and Price (1997) and Qian et al. (2009).

At the initial stage, a population of individuals is first constructed randomly and the largest-order-value method is adopted to decode a set of n initial populations to be used in problem under consideration. A simple illustrative instance is given to state the working of the lov method converting initial populations to job sequences. According to the example by Wang and Qian (2012), vector $X_i =(1.36,3.85,2.55,0.63,2.68,0.82)$ randomly generated is ranked by the descending order to get $\varphi _i =(4,1,3,6,2,5)$, then convert $\varphi _i =(4,1,3,6,2,5)$ to $\sigma _i =(2,5,3,1,6,4)$ using formula $J_{i,\varphi _{i,k} } =k$. In case we exchange job position 3 and job position 1 in sequence $\sigma _i$ to a new job sequence ${\sigma }'_i =(2,5,1,3,6,4)$, then $\varphi _i =(4,1,3,6,2,5)$ and $X_i =(1.36,3.85,2.55,0.63,2.68,0.82)$ should be repaired as ${\varphi }'_i =(3,1,4,6,2,5)$ and ${X}'_i =(2.55,3.85,1.63,0.63,2.68,0.82)$, respectively. For more detail, the reader may refer to Gao et al. (2010) and Wang and Qian (2012). It is also noted that once a job sequence with a case of $J_{v}$ before $J_{u}$ is generated, we regenerate another instance problem. The most important implementation details of the LH method are summarized as follows:

For i $=$ 1, 30

Randomly generate individuals X$_{1}$, X$_{2}$, ..., X$_{30}$, and convert them into job sequence$\sigma _1$, $\sigma _2$, ..., $\sigma _{30}$ using the largest-order-value method.

For j $=$ 1, 30

For k $=$ 1, $n\cdot (n-1)$

Randomly generate two integers p and q.

Swap positions p and q in $\sigma _j$ to yield a new job sequence ${\sigma }'_j$.

Determine if the objective function of ${\sigma }'_j$ is less than that of $\sigma _j$, then replace $\sigma _j ={\sigma }'_j$.

End do

Compare and update the temporary solution with the current best sequence to keep the best one that has the smaller objective function

End do

End do.

4.2 The details of GA

Genetic algorithm (GA) is intelligent random search method which has been successfully applied to find near-optimal solutions in many complex problems (Mati and Xie 2008; Li and Song 2013; Chen et al. 2014; Gong et al. 2014). A genetic algorithm starts with a set of feasible solutions (population) and iteratively replaces the current population with a new population. It requires a suitable encoding for the problem and a fitness function that represents a measure of the quality of each encoded solution (chromosome or individual). The reproduction mechanism selects the parents and recombines them using a crossover operator to generate offsprings that are submitted to a mutation operator to alter them locally (Essafi et al. 2008). Following Reeves (1995) and Etiler et al. (2004), the steps of the GA are summarized as follows.

*Representation of structure: The random number encoding method is used in this study. Its advantage is that all the chromosomes are feasible solutions (Bean 1994). For a problem instance with n jobs, a chromosome with n uniform random numbers (genes) is generated, where each gene corresponds to a job. The order of the random numbers represents the job sequence. All the jobs have to follow the same route on $M_{1}$ and $M_{2}$. It should be noted that once a job sequence with a case of $J_{v}$ before $J_{u}$ is generated, we regenerate another instance problem.

*Initial population: During the performing of GA algorithm, it can be seen that the larger the population size, the easier it can be to yield a good quality solution, but it takes more CPU time. On the other hand, the smaller the population size, the less CPU time is consumed, the easier it is to fall into local solution. In this study, when the parameters $n,\tau , R$, mutation rate, and generation size are set at 10, 0.25, 0.25, 0.25, and 100, we generate 100 instance problems to determine the size of initial population. The results indicated that all the mean error percentages of GA or GA with three improvements were less than 1 % when population size increases up 700 or more instances. Therefore, $70*n$ initial sequences are adopted in all the simulation case study (Fig. 1).

Fig. 1

The performance of all GAs’ algorithms when population size varies

*Fitness function: The fitness function of the strings can be calculated as follows:

$$\begin{aligned} f(\sigma _i (v))=\max _{1\le l\le \rho } \left\{ \sum \limits _{j=1}^{n} {T_j (\sigma _l (v))} \right\} -\sum \limits _{j=1}^{n} {T_j (\sigma _i (v))}, \end{aligned}$$

where $\rho =70*n$ denotes the populations or the string chromosomes, $\sigma _i (v)$ is the ith string chromosome in the v-th generation, $\sum \nolimits _{j=1}^n {T_j (\sigma _i (v))}$ is the total tardiness of $\sigma _i (v)$, and $f(\sigma _i (v))$ is the fitness function of $\sigma _i (v)$ of the jobs. Therefore, the probability, $P(\sigma _i (v))$, of selection for a schedule is to ensure that the probability of selection for a sequence with lower value of the objective function is higher. $P(\sigma _i (v))=f(\sigma _i (v))/\sum \nolimits _{l=1}^\rho {f(\sigma _l } (v))$. This is also the criterion used for the selection of parents for the reproduction of children.

*Crossover: Two-point crossover method is used in GA. For more details, the reader may refer to Ishibuchi and Murata (1998).

*Mutation can be applied to prevent premature convergence and fall into a local optimum in GA procedure. This operation can be viewed as a transition from a current solution to its neighborhood solution in a local search algorithm. Following the way by Ishibuchi and Murata (1998), in this study, we adopt shift mutation operator in GA. To illustrate the working of shift mutation, taking a job sequence (1, 2, 3, 4, 5), we generate two integers $p=2$ and $q=4$, then move the 4th job to insert between job 1 and job 2, and obtain the final sequence (1, 4, 2, 3, 5). Furthermore, when other parameters are fixed and set at $n=12$, we generate 840 instances to determine the value of shift mutation. The results indicated that with all the mean error percentages of GA or GA with three improvements declining at less than 2 % when shift mutation rate increases to 2.5, and GPI and GFW further down to a mean error percentage of less than 1 %. Therefore, the shift mutation rate is set at 0.25 in GA (Fig. 2).

Fig. 2

The performance of all GAs’ algorithms when mutation rate varies

*Selection: In GA, we exclude the best schedule which has the minimum total tardiness and generate the rest of the offsprings from the parent chromosomes by the roulette wheel method.

*Termination: In our pretests, when the parameters $n,\tau , R,$ and mutation rate are set to 10, 0.25, 0.25, and 0.25, we test seven different types of population sizes of 100, 200, ..., and 700 vs five types of generation sizes of 100, 500, ..., and 2000. We generate 100 instances for each case. Figure 3 releases that GA takes CPU time less than 1 s of CPU time even when the proposition size is up to 700 instances and the mean error percentage is less than 1 % at the case of 100 generation size. Therefore, we set 100 generations as the stopping rule for GA.

Fig. 3

The performance of GA over the population and generation vary

Furthermore, to get a good quality solution, we add some local search after the LH or GA process. There include pairwise interchange, backward-shifted reinsertion, and forward-shifted reinsertion. Given job sequence $\sigma _0 =(1,2,3,4,5,6)$, we do a pairwise interchange of jobs scheduled in the 2nd and the 5th positions to obtain $\sigma _1 =(1,5,3,4,2,6)$ for the pairwise interchange method; we extract the 5th position job and reinsert it just before the 2nd position job to produce $\sigma _1 =(1,5,2,3,4,6)$ for backward-shifted reinsertion, and we consider extracting the 2nd position job from its position and reinserting it just after the 5th position job to yield $\sigma _1 =(1,3,4,5,2,6)$ for forward-shifted reinsertion. For further details, the reader may refer to Della Croce et al. (1996). They are recorded as LH, LPI, LBW, and LFW for the larger-order-value; and GA, GPI, GBW, and GFW for the GA without improvement or with improving by pairwise interchange, backward-shifted reinsertion, and forward-shifted reinsertion, respectively.

Table 1 Experiment setup

Following LH and GA algorithms, we describe the steps of the branch-and-bound method which follows the designs of French (1982), Chen et al. (2006) and Wu et al. (2007). We apply the depth-first search in the branch-and-bound algorithm. Then, we scheduled n jobs in a forward manner from the first position to the last position for each active node. In the searching tree, once a branch is selected and it is systematically worked down the tree until either it is eliminated by virtue of the dominance properties or the lower bound, or it can be expanded to the final node, in which case the resulting sequence either replaces the initial incumbent solution or is eliminated. The details of branch-and-bound algorithm are summarized in the following:

• (i) Initialization Do LH and GA and then choose the best one between LH and GA to use an initial incumbent solution.

• (ii) Branching Perform the branching procedure using the depth-first search until all the nodes are visited or cut.

• (iii) Eliminating Determine whether the nodes are cut by applying Theorem 1, Properties 1–7 or not.

• (vi) Bounding Find a lower bound for each unfathomed partial sequence or the objective function for each completed sequence. If the lower bound for an active partial sequence is larger than the initial incumbent solution, then cut that node and all the nodes beyond it in the branch. If the objective function of the completed sequence is less than the incumbent solution, use the completed sequence as the new incumbent solution. Otherwise, eliminate it.

• (v) Termination condition Do (ii)–(vi) until all nodes are visited.

5 Computational results

In this section, we carry on two experimental parts to take measurements of the performances of proposed algorithms which consist of the branch-and-bound, LH and GA algorithms. All the proposed algorithms are coded in FORTRAN using Compaq Visual Fortran version 6.6 and the experiments are performed on a personal computer powered by an Intel Pentium(R) Dual-Core CPU E6300 @ 2.80GHz with 2GB RAM operating under Windows XP. Following the design of Chung et al. (2006), the job processing times are generated based on the six group data sets as follows, Type I: Neither correlation nor trend: $p_{1i} \sim U(1,100)$ and $p_{2i} \sim U(1,100)$; Type II: Correlation only: $p_{1i} \sim U(20r_i ,20r_i +20)$ and $p_{2i} \sim U(20r_i ,20r_i +20)$; Set III: Positive trend only: $p_{1i} \sim U(1,100)$ and $p_{2i} \sim U(12\frac{1}{2}+1,12\frac{1}{2}+100)$; Type IV: Correlation and positive trend: $p_{1i} \sim U(20r_i +1,20r_i +20)$ and $p_{2i} \sim U(\frac{5}{2}+20r_i +1,\frac{5}{2}+20r_i +20)$; Type V: Negative trend only: $p_{1i} \sim U(12\frac{1}{2}+1,12\frac{1}{2}+100)$ and $p_{2i} \sim U(1,100)$; and Type VI: Correlation and negative trend: $p_{1i} \sim U(\frac{5}{2}+20r_i +1,\frac{5}{2}+20r_i +20)$ and $p_{2i} \sim U(20r_i +1,20r_i +20)$, where $r_i$, $i=1, 2, {\ldots }, n,$ are randomly generated from {0, 1, 2, 3, 4}. Following Fisher’s (1971) design, the due dates are generated from another uniform distribution $T*(1-\tau -R/2, 1-\tau +R/2)$, where $T=\sum \nolimits _{i=1}^n {p_{1i} }$, and the due dates range R and tardiness factor $\tau$ are taken as recorded as (0.25, 0.25), (0.25, 0.5), (0.25, 0.75), (0.5, 0.25), (0.5, 0.5), and (0.5, 0.75). It is noted that once an instance generated is not feasible or $J_{v}$ placed before $J_{u}$, we regenerate another instance problem. For each case, we generate 100 instances tested. In addition, an experiment set table containing used of all control parameters of both LH and GA is also provided in Table 1.

In the first part, we evaluate the performance of the branch-and-bound algorithm over the impacts of the $\tau , R,$ and data class. The number of jobs was set at $n=10, 12,$ and 14. We only recorded the average number of nodes and the average execution time (in seconds) for the branch-and-bound algorithm. The results were summarized in Tables 2, 3, and 4.

Table 2 The performance of B&B when $\tau$ varies

As shown in Table 2, it can be seen that the branch-and- bound algorithm took few nodes or less time at $\tau =0.5$ than at $\tau =0.25$ when n is 10 and 12, but the trend is opposite when n is 14. The reason is that the instances at $\tau =0.25$ has a longer due date and this case causes to yield an optimal solution of 0. Table 3 released that the branch-and-bound algorithm took few nodes or less CPU time as the value of R increases. The instance with a bigger range of R easily yielded an optimal solution of 0 than that with a smaller one. Table 4 reports that the instances can be easily solved out and be located at type I at $n=10$, type IV at $n=12$, and type VI at $n=14$, respectively. On average, the most easily instances, which can be solved out, are located at type VI. It is noted in Table 4 that the bigger mean of node numbers should take the longer CPU time, however, there exists some opposite cases. The reason is that the increments of node numbers and CPU time are not linear.

Table 3 The performance of B&B when R varies

In the second part, we measure the performances of eight proposed heuristics when compared with an optimal solution obtained from the branch-and-bound algorithm. The number of jobs was set at $n=10$, 12, and 14. The logarithmic error percentage (LRE) is defined as follows

$$\begin{aligned} \mathrm{LRE}=\left\{ {{\begin{array}{ll} {-\log _{10} \left| {\frac{H_i -H^*}{H^*}} \right| } , &{} \quad \mathrm{if} \quad {H^*\ne 0} \\ {-\log _{10} \left| {H_i -H^*} \right| }, &{}\quad \mathrm{if}\quad {H^*=0} \\ \end{array} }} \right. , \end{aligned}$$

where $H_i$ is the objective value obtained by algorithm $H_{i}$ and $H^*$ is the optimal solution obtained by the branch-and-bound method. For smooth discussion, when $H_{i}$ is equal to $H^*$, we set $H_i -H^*=0.1$ since both $H_{i}$ and $H^*$ are integers. It is remarked that the resulting values are roughly interpretable as the number of significant digits of agreement between $H^*$ and $H_{i}$. Larger values of LREs indicate that $H_{i}$ is a relatively more accurate approximation of $H^*$. For each case, we only recorded the average LRE. The results are summarized in Tables 5, 6 and 7.

Table 4 The performance of B&B among six different data types

Table 5 The performance of heuristic algorithms for small jobs when $\tau$ varies

Table 6 The performance of heuristic algorithms for small jobs when R varies

Table 7 The performance of heuristics over different data types for small-size jobs

Table 8 The performance of heuristics for large number of jobs when $\tau$ varies

Table 9 The performance of heuristics for large number of jobs when R varies

Table 10 The performance of heuristics over different data types for large number of jobs

To measure the impact of varying $\tau$, it can be seen in Table 5 that the mean LREs of LH and GA stay at about 0.90–2.23 % and 1.22–2.74 %. On average, the mean LREs of LH and GA are 1.51 % and 2.01 %. GA performs slightly better than LH. When three local improvements are added to GA and LH, it can be observed that LFW with a LRE of staying at about 1.93–3.05 is better than LBW of staying at about 1.45–2.84 % and LPE of staying at about 1.76–3.04 %, while GFW and GPI with a LRE of staying at about 2.33–3.21 % and 2.27–3.24 % is better than GBW of staying at about 1.18–3.10 %. It is also noted that GA performs better located at the instance cases with a smaller value of $\tau$, while LH does not. The trend disappears when GA or LH is added three local searches. For the impact of the R, Table 6 indicates that LRE decreases as the value of R increases among all 8 proposed heuristics, i.e., all proposed algorithms perform better located at the smaller value of R than those at the bigger value of R. This trend released that all proposed algorithms have a good quality solution in solving the instances with a narrow width of range R. For the impact of data types, when further summing all three job sizes for each data type, we observed that both LH and GA perform best located at type II with the LREs of 4.94 and 6.45 %, but GA does better than LH. After adding the improvements, The LRE of LH increases from 4.94 to 6.45 % located at type II by the LBW, to 7.82 % located at type VI by LFW, and to 7.15 % located at type I by LPI, while The LRE of GA increases from 4.94 to 7.62 % located at type II by the GBW, to 8.45 % located at type VI by GFW, and to 8.17 % located at type I by GPI. On an average, all three improved GAs are better than those of LH.

In the third part, we evaluate the performances of proposed eight algorithms at the large number of jobs in which we set the number of jobs to $n = 40$ and 80. We measure the performance of a heuristic algorithm in terms of the logarithmic relative percentage deviation (LRPD), defined as

$$\begin{aligned} \mathrm{LRPD}=\left\{ {{\begin{array}{ll} {-\log _{10} \left| {\frac{H_i -H_m }{H_m }} \right| } , &{}\quad \mathrm{if} \quad {H_m \ne 0} \\ {-\log _{10} H_i }, &{} \quad \mathrm{if} \quad {H_m =0} \\ \end{array} }} \right. \end{aligned}$$

where $H_i$ is the objective value obtained by one of eight algorithms and $H_m$ is the best solution among eight algorithms. A total of 7200 instances are tested. For each case, we only recorded the average LRPD. All the results are further summarized in Tables 8, 9 and 10.

It can be seen in Table 8 that either LH or GA performs better at a bigger value of $\tau$ and GA with a mean LRPD of 0.01 % does better than LH with a mean LRPD of $-$0.59 %. When adding the proposed improved method, the mean LRPDs of LBW, LFW, and LPI increase to 0.30, 1.53, and 1.71 %, while those of GBW, GFW, and GPI become 0.58, 1.84, and 2.28 %, respectively. In addition, all three improved GAs perform better than the corresponding SAs. Table 9 shows that LRPD decreases as the value of R increases among most of eight proposed heuristics, but LFW and GFW. This also implied that most proposed algorithms perform better located at the smaller value of R than those at the bigger value of R for the larger number cases. For the impact of data types over the big number of jobs, we further sum up two job sizes for each data type, it can be observed that both LH and GA perform best located at type III with the LRPDs of $-$0.98 and 0.29 %, and GA still performs well than LH. After adding the improvements, the LRPD of LH increases from $-$0.98 to 0.65 % located at types II, III, and VI by the LBW, to 3.32 % located at type VI by LFW, and to 3.77 % located at type III by LPI, while the LRPD of GA increases from 0.29 to 1.47 % located at type VI by the GBW, to 4.04 % located at type VI by GFW, and to 5.15 % located at type III by GPI. On average, each improved GA is still better than its corresponding one of LH. There is no clearly trend found in data types.

Based on the above observations, it is recommended that GPI can be used for finding a near-optimal solution for this problem in terms of the short CPU time and good solution quality. It is noted that the CPU time of SA or GA is omitted here because it is very fast to get a solution.

6 Conclusion

In this paper, we considered a two-machine flowshop scheduling problem with precedence constraint on two jobs to minimize the total tardiness criterion. The contributions of this paper are as follows. First, we derive several dominances and a lower bound to be used in a branch-and-bound algorithm to find an optimal solution. Besides, we also develop a genetic and a larger-order-value method to find a near-optimal solution. Finally, after conducting the computational experiments, we recommend that GPI can be used for finding a near-optimal solution for this problem in terms of the short CPU time and good solution quality. Future research may consider studying the m-machine flowshop problem with more general precedence constraint.