The Generalized Tensor Decomposition with Heterogeneous Tensor Product for Third-Order Tensors

Abstract

Recently, tensor decompositions have attracted increasing attention and shown promising performance in processing multi-dimensional data. However, the existing tensor decompositions assume that the correlation along one mode is homogeneous and thus cannot characterize the multiple types of correlations (i.e., heterogeneous correlation) along the mode in real data. To address this issue, we propose a heterogeneous tensor product that allows us to explore this heterogeneous correlation, which can degenerate into the classic tensor products (e.g., mode product and tensor–tensor product). Equipped with this heterogeneous tensor product, we develop a generalized tensor decomposition (GTD) framework for third-order tensors, which not only induces many novel tensor decompositions but also helps us to better understand the interrelationships between the new tensor decompositions and the existing tensor decompositions. Especially, under the GTD framework, we find that new tensor decompositions can faithfully characterize the multiple types of correlations along the mode. To examine the effectiveness of the new tensor decomposition, we evaluate its performance on a representative data compression task. Extensive experimental results on multispectral images, light field images, and videos compression demonstrate the superior performance of our developed tensor decomposition compared to other existing tensor decompositions.

1 Introduction

Tensors [6, 10, 41], as multi-dimensional extensions of matrices, can naturally represent the complex intrinsic structures of high-order data. This characteristic has drawn significant attention in recent years, making tensor analysis increasingly important in various fields, such as numerical linear algebra [4, 24, 28, 30], graph analysis [11, 15], image processing [14, 16, 25, 42, 45], and computer vision [7, 12, 34]. Within these literatures, the processing and analysis of multi-dimensional data primarily rely on a powerful tool, i.e., tensor decomposition.

Fig. 1

The illustration of heterogeneous correlation of the light field image dishes along mode-3

Recently, various tensor decompositions, generalized from the matrix singular value decomposition (SVD), have been widely studied and applied. As is well-known, the SVD can represent a matrix as the sum of a series of rank-1 matrices. Analogously, the CANDECOMP/PARAFAC (CP) decomposition [5, 13, 21] aims to represent a tensor as the sum of a finite number of rank-1 tensors. Another convincing multi-linear generalization of the SVD is the higher-order singular value decomposition (HOSVD), which expresses a tensor as a core tensor multiplied by a factor matrix along each mode. The key point of departure is that the mode product treats the vector (i.e., one column of the factor matrix) in a similar way as the SVD does for the left and the right singular vectors. Furthermore, HOSVD is also commonly referred to as Tucker decomposition [36, 37]. Subsequently, the tensor singular value decomposition (T-SVD) [18, 19] is proposed, which regards a third-order tensor as a matrix with each element being a tube. This tube-based strategy enables T-SVD to take a similar form to the matrix SVD by decomposing a third-order tensor into the tensor-tensor product (T-product) of three third-order tensors, with two of them being orthogonal tensors and one being the diagonal tensor[23, 31, 32]. Later, $\text {T}_k$-product and generalized T-SVD (see Definitions 2 and 4) are proposed, which allows us to handle interactions flexibly among slices of different modes [40, 46].

More recently, tensor network (TN)-based decompositions, inspired by the graph representation, have garnered significant interest. The most well-known one is the tensor train (TT) decomposition [3, 27, 43], which breaks down a tensor into sequential multi-linear products over a sequence of factors with matrices as the first and last factors and third-order tensors as the intermediate factors. TT decomposition can serve as the building block for other complex tensor networks (e.g., tensor ring (TR) decomposition [29, 44] and fully-connected tensor network (FCTN) decomposition [47]) due to its simple form. In the quantum physics community, the TT format is frequently referred to as the matrix product state representation [33, 38].

The existing tensor decompositions only consider a single type of correlation (i.e., homogeneous correlation) along one mode. However, real data typically exhibit multiple types of correlations (i.e., heterogeneous correlation) along one mode. Taking a light field image dishes as an example, we illustrate its heterogeneous correlation along mode-3 in Fig. 1. Figure 1a displays the singular value curve of the mode-3 unfolding matrix of data $\mathcal {X} \in \mathbb {R}^{128 \times 128 \times 243}$, which reveals the correlation along mode-3. This type of correlation can be characterized by the mode-3 product, i.e., $\mathcal {X} = \mathcal {Y} \times _3 \varvec{H}$. Moreover, the factor $\mathcal {Y} \in \mathbb {R}^{128 \times 128 \times 40}$ exhibits another type of correlation along mode-3, as shown in Fig. 1b. The more faithful characterization of the heterogeneous correlation can lead to better performance of multi-dimensional data processing. Therefore, a natural question is can we construct new tensor product and tensor decomposition that more accurately capture this heterogeneous correlation along the mode of multi-dimensional data?

Table 1 Notations

To address this challenge, we define a heterogeneous tensor product that allows us to better characterize the heterogeneous correlation. Leveraging this product, we develop a generalized tensor decomposition (GTD) framework. More specifically, the main contributions of this work are twofold.

• To faithfully characterize the heterogeneous correlation along one mode, we establish a heterogeneous tensor product, which can degenerate into the mode product and the $\text {T}_k$-product. Based on this product, we develop a GTD framework that not only delivers many novel tensor decompositions but also helps us to better understand the interconnections between these new tensor decompositions and the classic tensor decompositions.

• To verify the effectiveness of the new tensor decomposition within the GTD framework, we examine its performance on the representative data compression task. We propose a corresponding algorithm for the decomposition and conduct extensive compression experiments on multispectral images, light field images, and videos. The results demonstrate the superior compression performance of our developed new tensor decomposition as compared to the existing tensor decompositions.

The outline of this paper is as follows. We begin by summarizing the notations and preliminaries in Sect. 2. Then, we define the heterogeneous tensor product and analyze the relationship between this product and two classic tensor products in Sect. 3. Based on the proposed heterogeneous tensor product, we develop a GTD framework in Sect. 4. We consider a data compression task to examine the new tensor decomposition within the GTD framework in Sect. 5. We conduct extensive numerical experiments to evaluate the performance of the new tensor decomposition in Sect. 6. Finally, we conclude this paper in Sect. 7.

2 Tensor Preliminaries

Before presenting the main body of this paper, we summarize the notations in Table 1 and provide preliminaries about tensor products and tensor decompositions.

2.1 Two Classic Tensor Products

In this subsection, we review two classic tensor products, including mode product and $\text {T}_k$-product.

Definition 1

(Mode product [8]) The mode product of a tensor $\mathcal {X} \in \mathbb {R}^{I_1 \times I_2 \times \cdots \times I_M}$ by a matrix $\varvec{Y} \in \mathbb {R}^{J_m \times I_m}$ $(m \in \{1,2,\ldots ,M\})$, denoted by $\mathcal {X} \times _m \varvec{Y}$, is a tensor of size $I_1 \times I_2 \times \cdots \times I_{m-1} \times J_m \times I_{m+1} \times \cdots \times I_M$, whose elements are defined as

$$\begin{aligned} (\mathcal {X} \times _m \varvec{Y})_{i_1 i_2 \cdots i_{m-1} j_m i_{m+1} \cdots i_M} = \sum _{i_m=1}^{I_m}\mathcal {X}_{i_1 i_2 \cdots i_{m-1} i_m i_{m+1} \cdots i_M}\varvec{Y}_{j_m i_m}. \end{aligned}$$

(1)

Definition 2

($\hbox {T}_k$-product [40]) The ${\textbf {T}}_\mathbf{{1}}$-product of a tensor $\mathcal {X} \in \mathbb {R}^{I_1 \times I_2 \times R_1}$ and a tensor $\mathcal {Y} \in \mathbb {R}^{I_1 \times R_1 \times I_3}$, denoted by $\mathcal {X} *_1 \mathcal {Y}$, is a tensor of size $I_1 \times I_2 \times I_3$, whose mode-1 fibers are defined as

$$\begin{aligned} (\mathcal {X} *_1 \mathcal {Y})(:,i_2,i_3)= \sum _{r_1=1}^{R_1} \mathcal {X}(:,i_2,r_1)\star _L \mathcal {Y}(:,r_1,i_3). \end{aligned}$$

(2)

The ${\textbf {T}}_\mathbf{{2}}$-product of a tensor $\mathcal {X} \in \mathbb {R}^{I_1 \times I_2 \times R_2}$ and a tensor $\mathcal {Y} \in \mathbb {R}^{R_2 \times I_2 \times I_3}$, denoted by $\mathcal {X} *_2 \mathcal {Y}$, is a tensor of size $I_1 \times I_2 \times I_3$, whose mode-2 fibers are defined as

$$\begin{aligned} (\mathcal {X} *_2 \mathcal {Y})(i_1,:,i_3)= \sum _{r_2=1}^{R_2} \mathcal {X}(i_1,:,r_2)\star _L \mathcal {Y}(r_2,:,i_3). \end{aligned}$$

(3)

The $\hbox {T}_\mathbf{{3}}$-product of a tensor $\mathcal {X} \in \mathbb {R}^{I_1 \times R_3 \times I_3}$ and a tensor $\mathcal {Y} \in \mathbb {R}^{R_3 \times I_2 \times I_3}$, denoted by $\mathcal {X} *_3 \mathcal {Y}$, is a tensor of size $I_1 \times I_2 \times I_3$, whose mode-3 fibers are defined as

$$\begin{aligned} (\mathcal {X} *_3 \mathcal {Y})(i_1,i_2,:)= \sum _{r_3=1}^{R_3} \mathcal {X}(i_1,r_3,:) \star _L \mathcal {Y}(r_3,i_2,:), \end{aligned}$$

(4)

where the T-product of two fibers is $\varvec{x} \star _L \varvec{y}=\varvec{L}^{-1}((\varvec{L}\varvec{x})\odot (\varvec{L}\varvec{y}))$, $\varvec{L}$ is an invertible matrix, and $\odot$ denotes Hadamard product.

Recently, some structured invertible matrices $\varvec{L}$ have been studied, such as discrete Fourier transform (DFT) matrix [19], discrete cosine transform (DCT) matrix [17], and wavelet transform matrix [35].

2.2 Three Classic Tensor Decompositions

In this subsection, we review three classic tensor decompositions, including HOSVD, generalized T-SVD, and TT decomposition. To facilitate understanding, this paper mainly focuses on the third-order tensors.

Definition 3

(HOSVD [9]) A tensor $\mathcal {X} \in \mathbb {R}^{I_1 \times I_2 \times I_3}$ can be factored as the mode product

$$\begin{aligned} \mathcal {X} = \mathcal {C} \times _1 \varvec{F} \times _2 \varvec{G} \times _3 \varvec{H}, \end{aligned}$$

(5)

where $\varvec{F} \in \mathbb {R}^{I_1 \times R_1}$, $\varvec{G} \in \mathbb {R}^{I_2 \times R_2}$, and $\varvec{H} \in \mathbb {R}^{I_3 \times R_3}$ are column-orthogonal matrices, and $\mathcal {C} \in \mathbb {R}^{R_1 \times R_2 \times R_3}$ is the core factor.

Definition 4

(Generalized T-SVD [40]) A tensor $\mathcal {X} \in \mathbb {R}^{I_1 \times I_2 \times I_3}$ can be factored as the generalized $\text {T}_k$-product

$$\begin{aligned} \mathcal {X} = \mathcal {U}_k *_k \mathcal {S}_k *_k \mathcal {V}_k^{T_k}, ~~k=1,2,3, \end{aligned}$$

(6)

in which

• 1. $\mathcal {U}_k$ and $\mathcal {V}_k$ are mode-k orthogonal tensors,

• 2. $\mathcal {S}_k$ is mode-k diagonal tensor that each of its mode-k slices is a diagonal matrix.

  • (i) mode-k conjugate transpose: The mode-k conjugate transpose of $\mathcal {X}$, denote by $\mathcal {X}^{T_k}$, is obtained by conjugate transposing each of the mode-k slices and then reversing the order of transposed mode-k slices 2 through $N_k$.

  • (ii) orthogonality: tensor $\mathcal {X}$ is mode-k orthogonal if

    $$\begin{aligned} \mathcal {X} *_k \mathcal {X}^{T_k} = \mathcal {X}^{T_k} *_k \mathcal {X} = \mathcal {I}_k, \end{aligned}$$

    (7)

    where $\mathcal {I}_k$ is identity tensor that its first mode-k slice is an identity matrix and other mode-k slices are all zeros.

Definition 5

(TT decomposition [27]) A tensor $\mathcal {X} \in \mathbb {R}^{I_1 \times I_2 \times I_3}$ can be factored as

$$\begin{aligned} \mathcal {X} = \mathcal {C} \times _1 \varvec{F} \times _3 \varvec{H}, \end{aligned}$$

(8)

where $\varvec{F} \in \mathbb {R}^{I_1 \times R_1}$, $\mathcal {C} \in \mathbb {R}^{R_1 \times I_2 \times R_2}$, and $\varvec{H} \in \mathbb {R}^{I_3 \times R_2}$ are called canonical factors.

The forms of tensor products and tensor decompositions introduced above are quite distinct. This gives rise to two intriguing questions: (i) Can we devise a tensor product and decomposition that encompasses the aforementioned tensor products and decompositions? (ii) In the framework of this newly constructed tensor product and decomposition, is it possible to analyze the relationships between the classic tensor products as well as the relationships among the classic tensor decompositions?

3 The Heterogeneous Tensor Product

To address the above problems, we define a heterogeneous tensor product that can degenerate into the classic tensor products. Additionally, we detailedly analyze the relationships between this heterogeneous tensor product and the classic tensor products.

We first introduce the heterogeneous tensor product that extends the classic mode product and $\text {T}_k$-product.

Definition 6

(Mode permutation) The m-mode permutation $(m \in \{1,2,\ldots ,M\})$ of an Mth-order tensor $\mathcal {X} \in \mathbb {R}^{I_1 \times \cdots \times I_{m-1} \times I_{m+1} \times \cdots \times I_M \times I_m}$ is defined as tensor $\overrightarrow{\mathcal {X}}^m$ with size $I_1 \times \cdots \times I_{m-1} \times I_m \times I_{m+1} \times \cdots \times I_M$, whose elements obey

$$\begin{aligned} \overrightarrow{\mathcal {X}}^m_{i_1 \cdots i_{m-1} i_m i_{m+1} \cdots i_M} =\mathcal {X}_{i_1 \cdots i_{m-1} i_{m+1} \cdots i_M i_m}. \end{aligned}$$

(9)

Definition 7

(Heterogeneous tensor product) Given an Mth-order tensor $\mathcal {X} \in \mathbb {R}^{I_1 \times I_2 \times \cdots \times I_M}$ and an Nth-order tensor $\mathcal {Y} \in \mathbb {R}^{J_1 \times J_2 \times \cdots \times J_N}$ with d common modes $(1 \le d \le min (M,N)$, $d \in \mathbb {Z})$. Assume that two vectors $\varvec{m} = (\varvec{m}_1,\varvec{m}_2,\ldots ,\varvec{m}_M)$ and $\varvec{n} = (\varvec{n}_1,\varvec{n}_2,\ldots ,\varvec{n}_N)$ respectively indicate the recording of vectors $(1,2,\ldots ,M)$ and $(1,2,\ldots ,N)$, satisfying $I_{\varvec{m}_l}=J_{\varvec{n}_l}$ for $l=1,2,\ldots ,d$, $\varvec{m}_{d+1}< \varvec{m}_{d+2}< \cdots < \varvec{m}_{M}$, and $\varvec{n}_{d+1}< \varvec{n}_{d+2}< \cdots < \varvec{n}_{N}$. Then the heterogeneous tensor product between $\mathcal {X}$ and $\mathcal {Y}$, denoted as $\mathcal {X} \boxtimes \mathcal {Y}$,¹ is defined as

$$\begin{aligned} \begin{aligned} \mathcal {X} \boxtimes \mathcal {Y}&= \overrightarrow{\mathcal {Z}}^{\varvec{m}_{d-1}}, \mathcal {Z}(i_{\varvec{m}_{d+1}},\ldots , i_{\varvec{m}_M}, j_{\varvec{n}_{d+1}},\ldots ,j_{\varvec{n}_N},:) \\&\quad = \sum _{i_{\varvec{m}_d}=1}^{I_{\varvec{m}_d}} \Phi \left( \hat{\mathcal {X}}(i_{\varvec{m}_d},i_{\varvec{m}_{d+1}},\ldots ,i_{\varvec{m}_M},:)~,~\hat{\mathcal {Y}}(i_{\varvec{m}_d},j_{\varvec{n}_{d+1}},\ldots ,j_{\varvec{n}_N},:) \right) , \end{aligned} \end{aligned}$$

(10)

where $\hat{\mathcal {X}}(i_{\varvec{m}_d},i_{\varvec{m}_{d+1}},\ldots ,i_{\varvec{m}_M},:)$ is a fiber of tensor $\hat{\mathcal {X}}$ with size $I_{\varvec{m}_1} I_{\varvec{m}_2} \cdots I_{\varvec{m}_{d-1}}$, $\hat{\mathcal {X}}$ denotes the permutation of $\mathcal {X}$ satisfying $\hat{\mathcal {X}}_{i_{\varvec{m}_d} i_{\varvec{m}_{d+1}} \cdots i_{\varvec{m}_M} i_{\varvec{m}_1} \cdots i_{\varvec{m}_{d-1}}}=\mathcal {X}_{i_d i_{d+1} \cdots i_M i_1 \cdots i_{d-1}}$, and $\Phi (\varvec{x},\varvec{y})$ denotes the product of fibers $\varvec{x}$ and $\varvec{y}$.

Considering different vector products (i.e., $\Phi (\varvec{x},\varvec{y})$) in Definition 7 delivers various tensor products. In the following, we detailedly show how the heterogeneous tensor product degenerates into the classic tensor products. The following lemmas present our conclusions.

Lemma 1

The heterogeneous tensor product can degenerate into the mode product.

Proof

Given an Mth-order tensor $\mathcal {X} \in \mathbb {R}^{I_1 \times I_2 \times \cdots \times I_M}$ and a second-order tensor $\mathcal {Y} \in \mathbb {R}^{J_m \times I_m}$ with one common mode (i.e., $d=1$). Assume that $\varvec{m} = (m,1,2,\ldots ,m-1,m+1,\ldots ,M)$, $\varvec{n}=(2,1)$, and $\Phi (\varvec{x},\varvec{y})$ denotes the inner product of vectors $\varvec{x}$ and $\varvec{y}$, then the heterogeneous tensor product between $\mathcal {X}$ and $\mathcal {Y}$ is

$$\begin{aligned} \begin{aligned}&(\mathcal {X} \boxtimes \mathcal {Y})_{i_1 i_2 \cdots i_{m-1} j_m i_{m+1} \cdots i_M} = \overrightarrow{\mathcal {Z}}^m _{i_1 i_2 \cdots i_{m-1} j_m i_{m+1} \cdots i_M} \\&\quad =\mathcal {Z}_{i_1 \cdots i_{m-1} i_{m+1} \cdots i_M j_m}= \sum _{i_m=1}^{I_m} \Phi (\hat{\mathcal {X}}_{i_m i_1 \cdots i_{m-1} i_{m+1} \cdots i_M}~,~\hat{\mathcal {Y}}_{i_m j_m})\\&\quad = \sum _{i_m=1}^{I_m} \hat{\mathcal {X}}_{i_m i_1 \cdots i_{m-1} i_{m+1} \cdots i_M} \hat{\mathcal {Y}}_{i_m j_m}= \sum _{i_m=1}^{I_m} \mathcal {X}_{i_1 i_2 \cdots i_{m-1} i_m i_{m+1} \cdots i_M}\varvec{Y}_{j_m i_m}\\&\quad =(\mathcal {X} \times _m \mathcal {Y})_{i_1 i_2 \cdots i_{m-1} j_m i_{m+1} \cdots i_M}. \end{aligned} \end{aligned}$$

(11)

Equation (11) verifies that the heterogeneous tensor product and the mode product are consistent when $\Phi (\varvec{x},\varvec{y})$ is the inner product of vectors $\varvec{x}$ and $\varvec{y}$. $\square$

Lemma 2

The heterogeneous tensor product can degenerate into the generalized $\text {T}_k$-product.

Proof

The proof is divided into three parts, in which we demonstrate that the heterogeneous tensor product can respectively degenerate into $\text {T}_1$-product, $\text {T}_2$-product, and $\text {T}_3$-product.

(i) The heterogeneous tensor product can degenerate into the $\text {T}_1$-product:

Given a third-order tensor $\mathcal {X} \in \mathbb {R}^{I_1 \times I_2 \times R_1}$ and a third-order tensor $\mathcal {Y} \in \mathbb {R}^{I_1 \times R_1 \times I_3}$ with two common modes (i.e., $d=2$). Assume that $\varvec{m} = (1,3,2)$, $\varvec{n}=(1,2,3)$, and $\Phi (\varvec{x},\varvec{y})$ denotes the $\text {T}$-product of vectors $\varvec{x}$ and $\varvec{y}$, then the heterogeneous tensor product between $\mathcal {X}$ and $\mathcal {Y}$ is

$$\begin{aligned} \begin{aligned}&(\mathcal {X} \boxtimes \mathcal {Y})(:,i_2,i_3) = \overrightarrow{\mathcal {Z}}^1(:,i_2,i_3)=\mathcal {Z}(i_2,i_3,:)\\&\quad = \sum _{r_1=1}^{R_1} \Phi (\hat{\mathcal {X}}(r_1,i_2,:)~,~\hat{\mathcal {Y}}(r_1,i_3,:)) =\sum _{r_1=1}^{R_1} \mathcal {X}(:,i_2,r_1) \star _L \mathcal {Y}(:,r_1,i_3) \\&\quad =(\mathcal {X} *_1 \mathcal {Y})(:,i_2,i_3). \end{aligned} \end{aligned}$$

(12)

(ii) The heterogeneous tensor product can degenerate into the $\text {T}_2$-product:

Given a third-order tensor $\mathcal {X} \in \mathbb {R}^{I_1 \times I_2 \times R_2}$ and a third-order tensor $\mathcal {Y} \in \mathbb {R}^{R_2 \times I_2 \times I_3}$ with two common modes (i.e., $d=2$). Assume $\varvec{m} = (2,3,1)$, $\varvec{n}=(2,1,3)$, and $\Phi (\varvec{x},\varvec{y})$ denotes the $\text {T}$-product of vectors $\varvec{x}$ and $\varvec{y}$, then the heterogeneous tensor product between $\mathcal {X}$ and $\mathcal {Y}$ is

$$\begin{aligned} \begin{aligned}&(\mathcal {X} \boxtimes \mathcal {Y}) (i_1,:,i_3) = \overrightarrow{\mathcal {Z}}^2 (i_1,:,i_3) = \mathcal {Z}(i_1,i_3,:)\\&\quad = \sum _{r_2=1}^{R_2} \Phi (\hat{\mathcal {X}}(r_2,i_1,:)~,~\hat{\mathcal {Y}}(r_2,i_3,:)) =\sum _{r_2=1}^{R_2} \mathcal {X}(i_1,:,r_2) \star _L \mathcal {Y}(r_2,:,i_3)\\&\quad = (\mathcal {X} *_2 \mathcal {Y})(i_1,:,i_3). \end{aligned} \end{aligned}$$

(13)

(iii) The heterogeneous tensor product can degenerate into the $\text {T}_3$-product:

Given a third-order tensor $\mathcal {X} \in \mathbb {R}^{I_1 \times R_3 \times I_3}$ and a third-order tensor $\mathcal {Y} \in \mathbb {R}^{R_3 \times I_2 \times I_3}$ with two common modes (i.e., $d=2$). Assume $\varvec{m} = (3,2,1)$, $\varvec{n}=(3,1,2)$, and $\Phi (\varvec{x},\varvec{y})$ denotes the $\text {T}$-product of vectors $\varvec{x}$ and $\varvec{y}$, then the heterogeneous tensor product between $\mathcal {X}$ and $\mathcal {Y}$ is

$$\begin{aligned} \begin{aligned}&(\mathcal {X} \boxtimes \mathcal {Y}) (i_1,i_2,:) = \overrightarrow{\mathcal {Z}}^3 (i_1,i_2,:) = \mathcal {Z}(i_1,i_2,:)\\&\quad = \sum _{r_3=1}^{R_3} \Phi (\hat{\mathcal {X}}(r_3,i_1,:)~,~\hat{\mathcal {Y}}(r_3,i_2,:)) =\sum _{r_3=1}^{R_3} \mathcal {X}(i_1,r_3,:) \star _L \mathcal {Y}(r_3,i_2,:)\\&\quad =(\mathcal {X} *_3 \mathcal {Y})(i_1,i_2,:). \end{aligned} \end{aligned}$$

(14)

Equations (12)–(14) verify that the heterogeneous tensor product and the $\text {T}_k$-product are consistent when $\Phi (\varvec{x},\varvec{y})$ is the T-product of vectors $\varvec{x}$ and $\varvec{y}$. $\square$

Now, we restate the relationship between the $\text {T}_k$-product and the mode product [40], which helps us better understand the relationship between tensor decompositions within the proposed GTD framework, as discussed in the subsequent section.

Lemma 3

The $\text {T}_k$-product can degenerate into the mode product.

Proof

Suppose that $\mathcal {C}\in \mathbb {R}^{R_1 \times R_2 \times R_3}$, $\varvec{F} \in \mathbb {R}^{I_1 \times R_1}$, $\mathcal {F}\in \mathbb {R}^{I_1 \times R_2 \times R_1}$, $\hat{\mathcal {F}}\in \mathbb {R}^{I_1 \times R_1 \times R_3}$, $\varvec{G} \in \mathbb {R}^{I_2 \times R_2}$, $\mathcal {G}\in \mathbb {R}^{R_2 \times I_2 \times R_3}$, $\hat{\mathcal {G}}\in \mathbb {R}^{R_1 \times I_2 \times R_2}$, $\varvec{H} \in \mathbb {R}^{I_3 \times R_3}$, $\mathcal {H}\in \mathbb {R}^{R_1 \times R_3 \times I_3}$, $\hat{\mathcal {H}}\in \mathbb {R}^{R_3 \times R_2 \times I_3}$, if the following constraints

$$\begin{aligned}&\varvec{F}_2^{(1)} = \varvec{F}, \varvec{F}_2^{(2)} = \cdots = \varvec{F}_2^{(R_2)} = \varvec{0}, ~~~ \hat{\varvec{F}}_3^{(1)} =\varvec{F}, \hat{\varvec{F}}_3^{(2)}=\cdots =\hat{\varvec{F}}_3^{(R_3)}=\varvec{0}, \end{aligned}$$

(15)

$$\begin{aligned}&\varvec{G}_3^{(1)}=\varvec{G}^T, \varvec{G}_3^{(2)} = \cdots = \varvec{G}_3^{(R_3)}= \varvec{0}, ~~~ \hat{\varvec{G}}_1^{(1)} =\varvec{G}, \hat{\varvec{G}}_1^{(2)} =\cdots =\hat{\varvec{G}}_1^{(R_1)}=\varvec{0}, \end{aligned}$$

(16)

$$\begin{aligned}&\varvec{H}_1^{(1)}=\varvec{H}^T,\varvec{H}_1^{(2)}=\cdots = \varvec{H}_1^{(R_1)}= \varvec{0}, ~~~ \hat{\varvec{H}}_2^{(1)}=\varvec{H}^T, \hat{\varvec{H}}_2^{(2)}=\cdots = \hat{\varvec{H}}_2^{(R_2)}=\varvec{0}, \end{aligned}$$

(17)

are satisfied, the $\text {T}_k$-product can degenerate into the mode product

$$\begin{aligned} \left\{ \begin{aligned} \mathcal {F}*_2 \mathcal {C}= \mathcal {C} \times _1 \varvec{F}, \\ \hat{\mathcal {F}}*_3 \mathcal {C}= \mathcal {C} \times _1 \varvec{F}, \end{aligned} \right. ~~~~~~~~~~~~~~ \left\{ \begin{aligned} \mathcal {C}*_3 \mathcal {G}= \mathcal {C} \times _2 \varvec{G}, \\ \hat{\mathcal {G}}*_1 \mathcal {C}= \mathcal {C} \times _2 \varvec{G}, \end{aligned} \right. ~~~~~~~~~~~~~~ \left\{ \begin{aligned} \mathcal {C}*_1 \mathcal {H}= \mathcal {C} \times _3 \varvec{H}, \\ \mathcal {C}*_2 \hat{\mathcal {H}}= \mathcal {C} \times _3 \varvec{H}. \end{aligned} \right. \end{aligned}$$

(18)

where $\varvec{F}_1^{(i)}$, $\varvec{F}_2^{(i)}$, and $\varvec{F}_3^{(i)}$ denote the ith horizontal slice, lateral slice, and frontal slice of tensor $\mathcal {F}$, respectively. $\square$

These lemmas possess significant values. Specifically, they serve three purposes: (i) They can inspire some new forms of tensor decomposition. For instance, in HOSVD (i.e., $\mathcal {C} \times _1 \varvec{F} \times _2 \varvec{G} \times _3 \varvec{H}$), we can replace $\mathcal {C} \times _1 \varvec{F}$ with $\mathcal {F}*_2 \mathcal {C}$, resulting in a novel tensor decomposition $\mathcal {F}*_2 \mathcal {C}\times _2 \varvec{G} \times _3 \varvec{H}$; (ii) Additionally, by establishing the connections among these tensor products, we can explore the relationships between tensor decompositions based on different tensor products; (iii) By inserting inner product or T-product of vectors, this heterogeneous tensor product degenerates into the mode product and the $\text {T}_k$-product, which inspires us to consider other suitable vector products to design new tensor products.

4 The GTD Framework

With the heterogeneous tensor product, we develop a GTD framework. For easier analysis, the GTD framework is mainly established on third-order tensors. This framework not only encompasses the classic tensor decompositions as special cases but also induces numerous novel tensor decompositions. Furthermore, this framework helps us to understand the relationships among these tensor decompositions, including the classic and novel tensor decompositions.

Definition 8

(GTD framework) A tensor $\mathcal {X} \in \mathbb {R}^{I_1 \times I_2 \times I_3}$ can be factored as

$$\begin{aligned} \mathcal {X} = \mathcal {G}_1 \boxtimes \mathcal {G}_2 \boxtimes \cdots \boxtimes \mathcal {G}_K, \end{aligned}$$

(19)

where $\mathcal {G}_k$ $(k=1,2,\ldots ,K)$ are the factors. These factors can be third-order tensors or matrices with matched dimensions.

Remark 1

We can further impose constraints on certain factors, such as requiring the factors to be orthogonal, sparse, or diagonal.

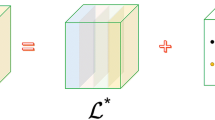
For simplicity, we focus on the GTD framework containing four factors, i.e., $\mathcal {X} = \mathcal {F} \boxtimes \mathcal {C} \boxtimes \mathcal {G} \boxtimes \mathcal {H}$. Among these factors, $\mathcal {C} \in \mathbb {R}^{R_1 \times R_2 \times R_3}$ is referred to as the core factor. The GTD framework with four factors is illustrated in Fig. 2.

Figure 2 shows how the GTD framework degenerates into the classic tensor decompositions. For example, when the four factors are all third-order tensors, the heterogeneous tensor products degenerate into $\text {T}_3$-product, and $\mathcal {C}$ and $\mathcal {H}$ are f-diagonal tensor and identity tensor respectively, the decomposition $\mathcal {X} = \mathcal {F} \boxtimes \mathcal {C} \boxtimes \mathcal {G} \boxtimes \mathcal {H}$ degenerates into T-SVD.

Furthermore, this GTD framework allows us to explore many new tensor decompositions. We systematically consider the new tensor decompositions from $three$ $aspects$ according to the relationships between heterogeneous tensor product, $\text {T}_k$-product, and mode product revealed by Lemmas 2 and 3.

(i) All heterogeneous tensor products in GTD framework $\mathcal {X} = \mathcal {F} \boxtimes \mathcal {C} \boxtimes \mathcal {G} \boxtimes \mathcal {H}$ degenerate into the $\text {T}_k$-product. In this context, there are some implicit constraints, such as the requirement that the two tensors involved in the $\text {T}_k$-product must have two common dimensions and the size requirement of the core factor (i.e., $\mathcal {C} \in \mathbb {R}^{R_1 \times R_2 \times R_3}$). Therefore, it is difficult to directly consider these tensor decompositions. But fortunately, by applying the inverse process of Lemma 3, which extends the mode product in the Tucker decomposition into the $\text {T}_k$-product, we can quickly derive these new tensor decompositions:

$$\begin{aligned} \begin{aligned}&\mathcal {X}=\mathcal {F}*_2 \mathcal {C} *_3 \mathcal {G} *_1 \mathcal {H},~~~~~~~~~~ \mathcal {X}=\mathcal {F}*_2 \mathcal {C} *_3 \mathcal {G} *_2 \mathcal {H},\\&\mathcal {X}=\mathcal {F}*_2 \mathcal {C} *_2 \mathcal {G} *_3 \mathcal {H},~~~~~~~~~~ \mathcal {X}=\mathcal {F}*_2 \mathcal {C} *_1 \mathcal {G} *_3 \mathcal {H},\\&\mathcal {X}=\mathcal {F}*_3 \mathcal {C} *_3 \mathcal {G} *_1 \mathcal {H},~~~~~~~~~~ \mathcal {X}=\mathcal {F}*_3 \mathcal {C} *_3 \mathcal {G} *_2 \mathcal {H},\\&\mathcal {X}=\mathcal {F}*_3 \mathcal {C} *_2 \mathcal {G} *_3 \mathcal {H},~~~~~~~~~~ \mathcal {X}=\mathcal {F}*_3 \mathcal {C} *_1 \mathcal {G} *_3 \mathcal {H}. \end{aligned} \end{aligned}$$

(20)

We see that there are only eight forms of tensor decomposition rather than twenty seven ($3^3$).

Fig. 2

The illustration of GTD framework

(ii) Based on (i), some but not all $\text {T}_k$-product degenerate into mode product. According to Lemma 3, each decomposition in Eq. (20) can induce many degenerated forms. For instance, $\mathcal {X}=\mathcal {F}*_3 \mathcal {C} *_3 \mathcal {G} *_1 \mathcal {H}$ can degenerate into:

$$\begin{aligned} \mathcal {X}=\mathcal {C} \times _1 \varvec{F} *_3 \mathcal {G} *_1 \mathcal {H},~~~~~ \mathcal {X}=\mathcal {F}*_3 \mathcal {C} \times _2 \varvec{G} *_1 \mathcal {H},~~~~~ \mathcal {X}=\mathcal {F}*_3 \mathcal {C} *_3 \mathcal {G} \times _3 \varvec{H}. \end{aligned}$$

(21)

By applying Lemma 1 once more, the decompositions in Eq. (21) then degenerate into:

$$\begin{aligned} \mathcal {X}=\mathcal {F}*_3 \mathcal {C} \times _2 \varvec{G} \times _3 \varvec{H},~~~~~ \mathcal {X}=\mathcal {C} \times _1 \varvec{F} *_3 \mathcal {G} \times _3 \varvec{H},~~~~~ \mathcal {X}=\mathcal {C} \times _1 \varvec{F}\times _2 \varvec{G} *_1 \mathcal {H}. \end{aligned}$$

(22)

(iii) Based on (ii), all $\text {T}_k$-product degenerates into mode product. Then the decomposition is classic Tucker decomposition.

Under the GTD framework, we can obtain many new tensor decompositions with three factors by simply multiplying the first two factors of the tensor decompositions containing four factors. For example, $\mathcal {X}=\mathcal {F}*_3 \mathcal {C} *_1 \mathcal {G} *_3 \mathcal {H}$ can be rewritten as $\mathcal {X}=\hat{\mathcal {F}} *_1 \mathcal {G} *_3 \mathcal {H}$ with $\hat{\mathcal {F}} = \mathcal {F}*_3 \mathcal {C}$; $\mathcal {X}=\mathcal {F}*_3 \mathcal {C} *_3 \mathcal {G} \times _3 \varvec{H}$ can be rewritten as $\mathcal {X}=\hat{\mathcal {F}} *_3 \mathcal {G} \times _3 \varvec{H}$ with $\hat{\mathcal {F}} = \mathcal {F}*_3 \mathcal {C}$; and $\mathcal {X}=\mathcal {C} \times _1 \varvec{F}\times _2 \varvec{G} \times _3 \varvec{H}$ can be rewritten as $\mathcal {X}=\hat{\mathcal {C}} \times _2 \varvec{G} \times _3 \varvec{H}$ with $\hat{\mathcal {C}} = \mathcal {C} \times _1 \varvec{F}$.

Remark 2

For real data, it is crucial to find a suitable or optimal GTD within the GTD framework. We can determine a suitable or optimal GTD using heuristic algorithms (e.g., genetic algorithm [2, 22]). For example, by employing genetic algorithm, we can encode different tensor products into binary strings and search for an optimal GTD that achieves the highest compression ratio or recovered PSNR value on Hamming space.

5 Representative Application

This GTD framework not only helps us to better understand the interconnection between the separated tensor decompositions but also delivers new tensor decompositions for different tasks (e.g., data compression and recovery).

Algorithm 1

The data compression algorithm

Table 2 The compression ratio and computational complexity of different decomposition algorithms for $\mathcal {X} \in \mathbb {R}^{I_1 \times I_2 \times I_3}$

Fig. 3

The compression ratio with respect to relative error of the reconstructed results by different methods on the multispectral images

Here, we consider the multi-dimensional data compression task as an example. For multi-dimensional data, such as multispectral image, light field image, and video, it has significant low-rankness along the third mode. We mainly exploit this feature to compress data. As shown in Fig. 1, the multi-dimensional data typically exhibits multiple types of correlations along the third mode, where the correlation shown in Fig. 1a can be characterized by the mode-3 product, i.e., $\mathcal {X}=\mathcal {Y} \times _3 \varvec{H}$ and the correlation shown in Fig. 1b can be characterized by the $\text {T}_3$-product, i.e., $\mathcal {Y}=\mathcal {F} *_3 \mathcal {G}$. Therefore, this work empirically utilizes the GTD $\mathcal {X}=\mathcal {F} *_3 \mathcal {G} \times _3 \varvec{H}$ within the GTD framework to compress multi-dimensional data, especially for data with obvious low-rankness in the third mode. To solve this decomposition, we design a corresponding algorithm. The algorithm can be divided into two steps: the first step is to decompose the data as follows: $\mathcal {X} \approx \hat{\mathcal {X}} \times _3 \varvec{H}$; the second step is to perform T-SVD on $\hat{\mathcal {X}}$. The accompanying data compression algorithm is summarized in Algorithm 1.

Fig. 4

Reconstructed results of multispectral images by different methods under compression ratio 0.8. From top to bottom: the odd-numbered rows are the visual results of $toy$, $cloth$, and $feather$, respectively; the even-numbered rows are the corresponding residual images average over three color channels

Fig. 5

The compression ratio with respect to relative error of the reconstructed results by different methods on the light field images

6 Numerical Experiment

In this section, we conduct extensive numerical experiments to verify the effectiveness of the proposed data compression algorithm. To objectively evaluate the compression performance of the algorithm, we consider four classic tensor decompositions-based compression algorithms for comparison: HOSVD (Section 3 in [9]), T-SVD (Algorithm T-Compress in [18]), TT-SVD (Algorithm 2 in [27]), and TR-SVD (Algorithm 1 in [44]). It should be noted that all the compared algorithms and the suggested algorithm have no parameters. By inputting the prescribed relative error $\epsilon$, we can obtain the final compression ratios of the corresponding algorithms. The peak signal-to-noise ratio (PSNR) and the structural similarity index (SSIM) [39] are employed to measure the quality of reconstruction. In addition, the compression ratio is defined as

$$\begin{aligned} \text {compression ratio} (\uparrow ) = \text {1} - \dfrac{\text {numel(Stored factors)}}{\text {numel(Whole data)}}, \end{aligned}$$

(23)

where numel($\cdot$) denotes the number of elements. Moreover, we theoretically analyze the compression ratio and computational complexity of different decomposition algorithms in Table 2 for comparison.

The experiments for the HOSVD and the T-SVD are based on Matlab Tensor Toolbox, version 3.0 [20]. Additionally, all data is normalized into [0,1] band-by-band. All computations are performed in MATLAB (R2019a) on a computer of 64Gb RAM and Intel(R) Core(TM) i9-10900KF CPU: @3.60 GHz.

6.1 Multispectral Images Compression

We conduct experiments on three multispectral images,² each with a size of $256 \times 256 \times 31$, to evaluate the performance of the proposed method.

Figure 3 shows the compression ratio with respect to relative error of the reconstructed results by different methods. It is evident that the proposed compression algorithm outperforms the compared methods for overall relative errors. The T-SVD method achieves a higher compression rate than other comparison methods when the relative error is low, and the compression rate is lower than other comparison methods when the relative error is high. T-SVD utilizes T-product to characterize the correlation in the third mode, while HOSVD and TT decomposition use mode product to characterize the correlation in the third mode. However, these decompositions cannot faithfully capture this multiple types of correlations in the third mode. Tensor decomposition $\mathcal {X}=\mathcal {F}*_3 \mathcal {C} *_3 \mathcal {G} \times _3 \varvec{H}$ can compensate for the defect of these methods, significantly improving the compression ratio.

Furthermore, Fig. 4 shows the reconstructed results (the first, third, and fifth rows), their corresponding residual images (the second, fourth, and sixth rows), and their corresponding PSNR and SSIM values of the multispectral images $toy$, $cloth$, and $feather$. From Fig. 4, especially for the residual images, it is evident that the proposed method yields better reconstructed results compared to the other methods.

6.2 Light Field Images Compression

We then consider three light field images,³ each with a size of $128 \times 128 \times 243$, to verify the effectiveness of the proposed method.

Fig. 6

Reconstructed results of light field images by different methods under compression ratio 0.9. From top to bottom: the odd-numbered rows are the visual results of $greek$, $dishes$, and $table$, respectively; the even-numbered rows are the corresponding residual images average over three color channels

Fig. 7

The compression ratio versus relative error of the reconstructed results by different methods on three videos

Table 3 The adjusted tensor ranks for three multispectral images under different SRs

Figure 5 shows the compression ratio with respect to relative error of the reconstructed results by different methods. For overall relative errors, the suggested algorithm performs better than the compared methods. Additionally, compared to the other three methods (HOSVD, T-SVD, and TR-SVD), the TT-SVD method typically achieves a higher compression rate in the case of equal relative error. The reason is that it fully utilizes the low-rankness of the spatial and spectral dimensions. Although HOSVD method and TR-SVD method also take advantage of the correlation of all dimensions, truncating different dimensions with the same relative error (e.g., the HOSVD method truncates singular values in each dimension using the same relative error $\epsilon /\sqrt{3}$) cannot achieve satisfied compression performance. Note that the TT-SVD method has produced positive results, the suggested new tensor decomposition $\mathcal {X}=\mathcal {F}*_3 \mathcal {C} *_3 \mathcal {G} \times _3 \varvec{H}$ can significantly benefit from it.

Additionally, Fig. 6 shows the reconstructed results (the odd-numbered rows), their corresponding residual images (the even-numbered rows), and their corresponding PSNR and SSIM values of the light field images $greek$, $dishes$, and $table$. As observed, the results obtained by the proposed method are significantly superior to those of the compared ones, especially for the recovery of objects in the images, such as statues in $greek$, bowls and spoons in $dishes$, cabinets and plants in $table$.

6.3 Videos Compression

We finally evaluate the performance of the proposed method on three widely used color videos sequence,⁴ each with a size of $144 \times 176 \times 150$.

Fig. 8

Reconstructed results of videos by different methods under compression ratio 0.95. From top to bottom: the odd-numbered rows are the visual results of $bunny$, $carphone$, and $news$, respectively; the even-numbered rows are the corresponding residual images average over three color channels

Figure 7 shows the compression ratio with respect to relative error of the reconstructed results by different methods. We observe that the proposed data compression algorithm outperforms the compared methods for overall relative errors. Notice that videos frequently feature moving objects and people, such as a flowing river in $bunny$, and a moving person in $carphone$ and $news$, which destroy the relevance of videos in spatial and temporal modes. Similar to light field image compression, HOSVD and TT-SVD methods still achieve positive results while T-SVD and TR-SVD methods do not deliver satisfactory results in video compression.

Additionally, Fig. 8 shows the reconstructed results (the odd-numbered rows), their corresponding residual images (the even-numbered rows), and their corresponding PSNR and SSIM values of the videos $bunny$, $carphone$, and $news$. It is evident that the results obtained by the proposed method are notably superior to those of the compared methods, particularly in the recovery of moving objects in the images, such as river in $bunny$, person in $carphone$ and $news$.

6.4 Discussion

To comprehensively evaluate the potential of our GTD, we investigate its performance on another representative task: tensor completion (TC). We conduct TC experiments on three multispectral images (i.e., Toy, Cloth, and Feather). All data are normalized to [0, 1]. Incomplete data are generated by randomly sampling elements of the data with three sampling rates (SRs): 1$\%$, 5$\%$, and 10$\%$.

Table 4 The PSNR and SSIM values of the recovered multispectral images by different methods under different sampling ratios

Four methods are selected as compared methods, including Tucker decomposition-based method HaLRTC [26], tensor singular value decomposition-based method TF-TC [48], TT decomposition-based method TT-TC [27], and TR decomposition-based method TR-TC [44]. For fairness, TF-TC, TT-TC, TR-TC, and our GTD-TC models are all solved using the proximal alternating minimization (PAM) algorithm [1]. The algorithm parameters are set as follows: proximal parameter $\rho =0.1$, maximum iteration number $t^{\text {max}}=1000$, and stopping criteria $\Vert \mathcal {X}^{t+1}-\mathcal {X}^t\Vert _F/ \Vert \mathcal {X}^t\Vert _F \le 10^{-5}$. Additionally, the parameters of HaLRTC are set to $(\frac{1}{3},\frac{1}{3},\frac{1}{3})$. The parameters of TF-TC, TT-TC, TR-TC, and GTD-TC are tubal rank (i.e., $R^{\text {Tub}}$), TT rank (i.e., ($R_1^{\text {TT}}, R_2^{\text {TT}}$)), TR rank (i.e., ($R_1^{\text {TR}}, R_2^{\text {TR}},R_3^{\text {TR}}$)), and GTD rank (i.e., ($R_1^{\text {GTD}}, R_2^{\text {GTD}}$)), respectively, which are manually adjusted to achieve the best performance. Specifically, the adjusted tensor ranks for the three multispectral images under different SRs are provided in Table 3.

Table 4 reports the PSNR and SSIM values of the recovered multispectral images by different recovered methods under different SRs. From Table 4, we can observe that our decomposition outperforms the classical tensor decompositions in most cases, which validates the superiority of the proposed tensor decomposition on TC task.

7 Conclusion

In this paper, we first define a heterogeneous tensor product that enables us to better characterize the heterogeneous correlation along the mode of the real-world data. In addition, this heterogeneous tensor product can degenerate into the mode product and the $\text {T}_k$-product. Based on this heterogeneous tensor product, we propose a GTD framework, which helps to discover numerous novel tensor decompositions. Subsequently, for the data compression problem, we flexibly choose a new tensor decomposition within the GTD framework and design the corresponding compression algorithm. Extensive experimental results verify the effectiveness of the developed tensor decomposition in comparison to other existing tensor decompositions.

We believe that our framework still offers significant potential for exploration. In the future, we will explore simple and efficient methods that can find a suitable GTD under the GDT framework for different types of data and applications.