Abstract
Many kinds of real-world multi-way signal, like color images, videos, etc., are represented in tensor form and may often be corrupted by outliers. To recover an unknown signal tensor corrupted by outliers, tensor robust principal component analysis (TRPCA) serves as a robust tensorial modification of the fundamental PCA. Recently, a successful TRPCA model based on the tubal nuclear norm (TNN) (Lu et al. in IEEE Trans Pattern Anal Mach Intell 42:925–938, 2019) has attracted much attention thanks to its superiority in many applications. However, TNN is computationally expensive due to the requirement of full singular value decompositions, seriously limiting its scalability to large tensors. To address this issue, we propose a new TRPCA model which adopts a factorization strategy. Algorithmically, an algorithm based on the non-convex augmented Lagrangian method is developed with convergence guarantee. Theoretically, we rigorously establish the sub-optimality of the proposed algorithm. We also extend the proposed model to the robust tensor completion problem. Both the effectiveness and efficiency of the proposed algorithm is demonstrated through extensive experiments on both synthetic and real data sets.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
PCA is arguably the most broadly applied statistical approach for high-dimensional data analysis and dimension reduction. However, it regards each data instance as a vector, ignoring the rich intra-mode and inter-mode information in the emerging multi-way data (tensor data). One the other hand, it is sensitive to outliers which are ubiquitous in real applications. By manipulating the tensor instance in its original multi-way form and attempting to work well against outliers, tensor robust PCA [7, 23] is a powerful extension of PCA which can overcome the above issues. TRPCA finds many real life applications likes image/video restoration, video surveillance, face recognition, to name a few [7, 23].
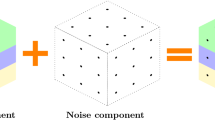
As shown in Fig. 1, an idealized version of TRPCA aims to recover an underlying tensor \({\mathcal {L}}^*\) from measurements \({\mathcal {M}}\) corrupted by outliers represented by tensor \({\mathcal {S}}^*\), that is,
Obviously, the decomposition in Model (1) is impossible without additional assumptions on the underlying tensor \({\mathcal {L}}^*\) and the outlier tensor \({\mathcal {S}}^*\). Thus, TRPCA further assumes \({\mathcal {L}}^*\) is “low-rank” and \({\mathcal {S}}^*\) sparse. Mathematically, TRPCA tries to solve a minimization problem as follows
where \({{\,\mathrm{\text {rank}}\,}}(\cdot )\) denotes the “rank function” of a tensor, \( \Vert {\cdot } \Vert _{0}\) is the tensor \(l_0\)-norm (used as a sparsity measure), and \(\lambda >0\) is a regularization parameter. Problem (2) is numerically very challenging, since both the tensor rank function and the tensor \(l_0\)-norm are neither continuous nor convex, even in their simplest matrix versions.
A mainstream approach for tackling the numerical hardness of Problem (2) is to respectively replace the rank function and \(l_0\)-norm with their convex surrogates \(\text {conv-rank}(\cdot )\) and \(l_1\)-norm, leading to the following convex version of Problem (2)
The \(l_1\)-norm \( \Vert {\cdot } \Vert _{\text {1}}\) in Problem (3) is widely used as a convex envelop of the \(l_0\)-norm in compressive sensing and sparse representation to impose sparsity [5, 14, 27, 41].
In the 2-way version of Problem (3) where \({\mathcal {L}},{\mathcal {S}}\) and \({\mathcal {M}}\) are matrices, tensor Robust PCA degenerates to the Robust PCA [2]. In RPCA, the matrix nuclear norm \(\Vert {\cdot }\Vert _{*}\) [4] is often chosen as the convex surrogate of matrix rank. However, for general \(K-\)way \((K\ge 3)\) tensors, one may have multiple choices of \(\text {conv-rank}(\cdot )\), since a tensor has many definitions of rank function due to different extensions of the matrix singular value decomposition. The most direct tensor extension of matrix rank is the tensor CP rank [8, 13] which is the smallest number of rank-one tensors that a tensor can be decomposed into. Nevertheless, both the CP rank and its corresponding version of nuclear norm are NP hard to compute [6, 9]. Thanks to its computational tractability, the Tucker rank [29] defined as a vector of ranks of the unfolding matrices along each mode, is the most widely used tensor rank. Its corresponding nuclear norm (denoted by SNN in this paper) [18] is defined as the (weighted) sum of nuclear norms of the unfolding matrices along each mode, and has been used in TRPCA [7]. However, SNN is not a tight convex relaxation of sum of the Tucker rank [28], and it models the underlying tensor as low Tucker rank, which maybe too strong for some real data tensors.
Recently, the low tubal rank models have achieved better performances than low Tucker rank models in many low rank tensor recovery tasks, like tensor completion [30, 33, 44], tensor RPCA [23, 44], sample outlier robust tensor PCA [45] and tensor low rank representation [36, 37], etc. At the core of these models is the tubal nuclear norm (TNN), a version of tensor nuclear norm defined within the framework of t-SVD [12]. Using TNN as the low-rank regularization in Problem (3), the recently proposed TNN-based TRPCA model has shown better performances than traditional models [23, 24, 44]. The rationality behind the superior performance of TNN-based models lies in that TNN is the tight convex relaxation of the tensor average rank, and the low average rank assumption is weaker than the low Tucker rank and low CP rank assumption [24].
Despite its broad use, TNN is computationally expensive since it requires full matrix singular value decompositions. The high computational complexity limits the application of TNN-based models to scale to emerging high-dimensional tensor data. By exploiting the orthogonal invariance of TNN, we come up with a factorization based model for TRPCA which can powerfully accelerate the original TNN-based TRPCA model. Extensive experiments show the superiority and efficiency of the proposed algorithm.
The main contributions of this paper are as follows:
-
1.
A new model for TRPCA named TriFac is proposed in Model (9) with an ALM algorithm (Algorithm 1) designed to efficiently solve it.
-
2.
Convergence of the proposed algorithm is shown in Theorem 1.
-
3.
Sub-optimality of the proposed algorithm is established in Theorems 2 and 3.
-
4.
We also extend the proposed model to the robust tensor completion problem.
The remaining of this paper is organized as follows. In Sect. 2, the notations, some preliminaries of t-SVD, and some related works are introduced. The problem formulation and the algorithm are shown in Sect. 3. Theoretical analysis of the proposed algorithm is given in Sect. 4. Experimental results are shown in Sect. 6. Finally, we conclude this work in Sect. 7.
2 Tensor SVD and related works
2.1 Notations and tensor SVD
The main notations and abbreviations are listed in Table 1 for convenience. For a 3-way tensor, a tube is a vector defined by fixing indices of the first two modes and varying the third one; A slice is a matrix defined by fixing all but two indices; \(\mathrm{fft}_3({\cdot })\) denotes the fast discrete Fourier transformation (FFT) along the third mode of a 3rd order tensor, i.e., the command \(\text {fft}(\cdot ,[],3)\) in Matlab; similarly, \(\mathrm{ifft}_3({\cdot })\) is defined. Let \(\lceil a \rceil \) denote the closest integer to \(a \in \mathbb {R}^{}\) that is not smaller than a, and \(\lfloor a \rfloor \) denotes the closest integer to \(a \in \mathbb {R}^{}\) that is not larger than a. Let \(\varvec{1}(\cdot )\) denote the indicator function which equals 1 if the condition is true and 0 otherwise. The spectral norm \(\Vert {\cdot }\Vert \) and nuclear norm \(\Vert {\cdot }\Vert _{*}\) of a matrix are the maximum and the sum of the singular values, respectively.
Then, we introduce the tensor SVD by defining some notions first.
Definition 1
(T-product [43]) Let \({\mathcal {T}}_1 \in {\mathbb {R}}^{d_1 \times d_2 \times d_3}\) and \({\mathcal {T}}_2 \in {\mathbb {R}}^{d_2\times d_4 \times d_3}\). The t-product of \({\mathcal {T}}_1\) and \({\mathcal {T}}_2\) is a tensor \({\mathcal {T}}\) of size \(d_1 \times d_4 \times d_3\):
whose \((i,j)_{th}\) tube is given by \({\mathcal {T}}(i,j,:)=\sum _{k=1}^{d_2} {\mathcal {T}}_1(i,k,:) \bullet {\mathcal {T}}_2(k,j,:)\), where \(\bullet \) denotes the circular convolution between two fibers [12].
T-Product and FFT The t-product of \({\mathcal {T}}_1\) and \({\mathcal {T}}_2\) can be computed efficiently by performing the fast Fourier transformation (FFT) along the tube fibers of \({\mathcal {T}}_1\) and \({\mathcal {T}}_2\) to get \(\widetilde{{\mathcal {T}}_1}\) and \(\widetilde{{\mathcal {T}}_2}\), multiplying the each pair of the frontal slices of \(\widetilde{{\mathcal {T}}_1}\) and \(\widetilde{{\mathcal {T}}_2}\) to obtain \(\widetilde{{\mathcal {T}}}\), and then taking the inverse FFT along the third mode to get the result. For details, please refer to [12].
Definition 2
(Tensor transpose [43]) Let \({\mathcal {T}}\) be a tensor of size \(d_1 \times d_2 \times d_3\), then \({\mathcal {T}}{}^\top \) is the \(d_2 \times d_1 \times d_3\) tensor obtained by transposing each of the frontal slices and then reversing the order of transposed frontal slices 2 through \(d_3\).
Definition 3
(Identity tensor [43]) The identity tensor \({\mathcal {I}} \in {\mathbb {R}}^{d_1 \times d_1 \times d_3}\) is a tensor whose first frontal slice is the \(d_1 \times d_1\) identity matrix and all other frontal slices are zero.
Definition 4
(F-diagonal tensor [43]) A tensor is called f-diagonal if each frontal slice of the tensor is a diagonal matrix.
Definition 5
(Orthogonal tensor [43]) A tensor \({\mathcal {Q}}\in {\mathbb {R}}^{d_1\times d_1\times d_3}\) is orthogonal if \({\mathcal {Q}} {}^\top * {\mathcal {Q}} = {\mathcal {Q}} * {\mathcal {Q}} {}^\top = {\mathcal {I}}\).
Based on the concepts of tensor transpose, f-diagonal tensor and orthogonal tensor, the tensor singular value decomposition (t-SVD) can be defined as follows. It is illustrated in Fig. 2.
Definition 6
(T-SVD, Tensor tubal-rank [43]) For any \({\mathcal {T}}\in {\mathbb {R}}^{d_1 \times d_2 \times d_3}\), the tensor singular value decomposition (t-SVD) of \({\mathcal {T}}\) is given as follows
where \({\mathcal {U}}\in {\mathbb {R}}^{d_1 \times d_1 \times d_3}\), \({\underline{\varSigma }}\in {\mathbb {R}}^{d_1 \times d_2 \times d_3}\), \({\mathcal {V}}\in {\mathbb {R}}^{d_2 \times d_2 \times d_3}\), \({\mathcal {U}}\) and \({\mathcal {V}}\) are orthogonal tensors, \({\underline{\varSigma }}\) is a rectangular f-diagonal tensor.
The tensor tubal rank of \({\mathcal {T}}\) is defined to be the number of non-zero tubes of \({\underline{\varSigma }}\) in the t-SVD factorization, i.e.,
Definition 7
(Block diagonal matrix [43]) For any \({\mathcal {T}}\in {\mathbb {R}}^{d_1 \times d_2 \times d_3}\), let \({\overline{{\mathcal {T}}}}\) (or \({\overline{{\mathbf{T}}}}\)) denote the block-diagonal matrix of the tensor \(\widetilde{{\mathcal {T}}}:=\mathrm{fft}_3({{\mathcal {T}}})\), i.e.,
According to the relationships between the tensor t-product and FFT, the inner product of two 3-D tensors \({\mathcal {T}}_1,{\mathcal {T}}_2 \in \mathbb {R}^{d_1\times d_2 \times d_3}\) and the inner product of their corresponding block diagonal matrices \({\overline{{\mathcal {T}}_1}},{\overline{{\mathcal {T}}_2}} \in \mathbb {C}^{d_1d_3\times d_2d_3}\) satisfy
When \({\mathcal {T}}_1={\mathcal {T}}_2={\mathcal {T}}\), one has
Definition 8
(Tensor average rank [43]) The tensor average rank \(r_{\mathrm{{a}}}({\mathcal {T}})\) of \({\mathcal {T}}\in \mathbb {R}^{d_1\times d_2 \times d_3}\) is the rescaled matrix rank of \({\overline{{\mathcal {T}}}}\), i.e.,
Definition 9
(Tensor operator norm [24, 43]) The tensor operator norm \( \Vert {{\mathcal {T}}} \Vert \) of a 3-D tensor \({\mathcal {T}}\in \mathbb {R}^{d_1\times d_2 \times d_3}\) is defined as follows
The relationship between t-product and FFT indicates that
Definition 10
(Tensor spectral norm [43]) The tensor spectral norm \( \Vert {{\mathcal {T}}} \Vert \) of a 3-D tensor \({\mathcal {T}}\) is defined as the matrix spectral norm (i.e. the largest singular value) of \({\overline{{\mathbf{T}}}}\), i.e.,
The tubal nuclear norm is further defined.
Definition 11
(Tubal nuclear norm [24]) For any \({\mathcal {T}}\in {\mathbb {R}}^{d_1 \times d_2 \times d_3}\) having t-SVD \({\mathcal {T}}= {\mathcal {U}}*{\underline{\varLambda }}*{\mathcal {V}}{}^\top \), the tubal nuclear norm of \({\mathcal {T}}\) is defined as
where \(r=r_{\text{ t }}({{\mathcal {T}}})\).
The property of FFT also indicates the relationship as follows
As can be seen from Eq. (4), TNN indeed models low-rankness in spectral domain.
As shown in [24], tensor spectral norm is the dual norm of TNN. Besides, TNN is the tightest convex relaxation of the average rank in the unit ball of tensor spectral norm \(\{{\mathcal {T}}\in \mathbb {R}^{d_1\times d_2 \times d_3}| \Vert {{\mathcal {T}}} \Vert \le 1\}\) [24].
2.2 Related works
In this subsection, only the most relevant works are introduced.Footnote 1 Limited to the focus of this paper, we only introduce related works of TRPCA based on different variants of tensor nuclear norms.
RPCA can be seen as TRPCA in the 2-way case. It tries to separate a low rank matrix \({\mathbf{L}}^*\in \mathbb {R}^{d_1 \times d_2}\) and a sparse matrix \({\mathbf{S}}^*\in \mathbb {R}^{d_1 \times d_2}\) from their sum \({\mathbf{M}}={\mathbf{L}}^*+{\mathbf{S}}^*\). As shown in [2], when the underlying tensor \({\mathbf{L}}^*\) satisfies the matrix incoherence conditions, the solution of the following problem
can exactly recover \({\mathbf{L}}^*\) and \({\mathbf{S}}^*\) with high probability with parameter \(\lambda =1/\sqrt{\max \{d_1,d_2\}}\). Problem (5) uses the matrix nuclear norm \(\Vert {\cdot }\Vert _{*}\) as the low rank regularization term \(\text {conv-rank}(\cdot )\) in Problem (3).
For general K-way tensors, many variants of tensor nuclear norms are proposed as the low rank term \(\text {conv-rank}(\cdot )\) in Problem (3). The most typical is the Tucker rank based tensor nuclear norm (SNN), defined as \( \Vert {{\mathcal {T}}}\Vert _{\text {SNN}}:=\sum \nolimits _{i=1}^{K}\lambda _k\Vert {{\mathbf{T}}_{(k)}}\Vert _{*},\) where \(\lambda _k>0\) and \({\mathbf{T}}_{(k)}\) is the mode-k unfolding of \({\mathcal {T}}\) [13]. The SNN-based TRPCA is given as follows
SNN inherently assumes the underlying tensor to be low Tucker rank, i.e., simultaneously low rank along each mode. However, this assumption may be too strong for some real tensor data. At the same time, the low average rank assumption has been shown to be weaker than low Tucker rank assumption [24]. As shown in Theorem 3.1 in [24], TNN is a convex envelop of the tensor average rank. The TNN-based TRPCA model adopts TNN as a low rank item in Problem 3, formulated as follows
In [23, 24], it is proved that when the underlying tensor \({\mathcal {L}}^*\) satisfy the tensor incoherent conditions, by solving Problem (7), one can exactly recover the underlying tensor \({\mathcal {L}}^*\) and \({\mathcal {S}}^*\) with high probability with parameter \(\lambda =1/\sqrt{\max \{d_1,d_2\}d_3}\).
3 TriFac for tensor robust PCA
3.1 Model formulation
To solve the TNN-based TRPCA in Eq. (7), an algorithm based on the alternating directions methods of multipliers (ADMM) is proposed [23]. In each iteration, it computes a proximity operator of TNN, which requires FFT/IFFT, and \(d_3\) full SVDs of \(d_1\)-by-\(d_2\) matrices when the observed tensor \({\mathcal {M}}\) is in \(\mathbb {R}^{d_1\times d_2 \times d_3}\). The one-iteration computation complexity of the ADMM-based algorithm is
which is very expensive for large tensors.
To reduce the cost of computing TNN in Problem (7), we come up with the following lemma, indicating that TNN is an orthogonal invariant norm.
Lemma 1
(Orthogonal invariance of TNN) Given a tensor \({\mathcal {X}}\in \mathbb {R}^{r\times r \times d_3}\), let \({\mathcal {P}}\in \mathbb {R}^{d_1\times r \times d_3}\) and \({\mathcal {Q}}\in \mathbb {R}^{d_2\times r \times d_3}\) be two semi-orthogonal tensors, i.e., \({\mathcal {P}}{}^\top *{\mathcal {P}}={\mathcal {I}}\in \mathbb {R}^{r\times r\times d_3}\) and \({\mathcal {Q}}{}^\top *{\mathcal {Q}}={\mathcal {I}}\in \mathbb {R}^{r\times r\times d_3}\), and \(r\le \min \{d_1,d_2\}\). Then, we have the following relationship:
Proof
Let the full t-SVD of \({\mathcal {X}}\) be \({\mathcal {X}}={\mathcal {U}}*{\underline{\varLambda }}*{\mathcal {V}}{}^\top \), where \({\mathcal {U}},{\mathcal {V}}\in \mathbb {R}^{r \times r \times d_3}\) are orthogonal tensors and \({\underline{\varLambda }}\in \mathbb {R}^{r\times r\times d_3}\) is f-diagonal. Then
Then \({\mathcal {P}}*{\mathcal {X}}*{\mathcal {Q}}{}^\top =({\mathcal {P}}*{\mathcal {U}})*{\underline{\varLambda }}*({\mathcal {Q}}*{\mathcal {V}}){}^\top \). Since
we obtain that
Thus, \( \Vert {{\mathcal {P}}*{\mathcal {X}}*{\mathcal {Q}}{}^\top } \Vert _{\star }= \Vert {{\mathcal {X}}} \Vert _{\star }\). \(\square \)
Equipped with Lemma 1, we decompose the low rank component in Problem 7 as follows:
where \({\mathcal {I}}_{r}\in \mathbb {R}^{r\times r\times d_3}\) is an identity tensor. Inspired by [17, 20], the tensors \({\mathcal {P}}\) and \({\mathcal {Q}}\) can be seen as “active tensor spaces”. Further, we propose the following model based on triple factorization (TriFac) for tensor robust PCA
where \({\mathcal {I}}_{r}:={\mathcal {I}}\in \mathbb {R}^{r\times r \times d_3}\), r is an upper estimate of the true tubal rank of the underlying tensor \(r^*=r_{\text{ t }}({{\mathcal {L}}^*})\) and we set parameter \(\lambda =1/\sqrt{\max \{d_1,d_2\}d_3}\) as suggested by [24]. Not that, different from Problem 7, the proposed TriFac is a non-convex model which may have many local minima.
3.2 Optimization algorithm
The partial augmented Lagrangian of Problem (9) is as follows:
where \(\mu >0\) is a penalty parameter, and \({\mathcal {Y}}\in \mathbb {R}^{d_1\times d_2 \times d_3}\) is the Lagrangian multiplier.
Based on the Lagrangian in Eq. (10), we update each variable by fixing others as follows:
Solutions to each sub-problem in Problem (11) will be given next. The algorithm is summarized in Algorithm 1.
The \({\mathcal {P}}\)-subproblem We update \({\mathcal {P}}\) by fixing other variables and minimize \(L_{\mu }(\cdot )\) as follows
where \({\mathcal {A}}={\mathcal {C}}_{t}*{\mathcal {Q}}{}^\top _{t}\) and \({\mathcal {B}}={\mathcal {M}}-{\mathcal {S}}_{t}-{\mathcal {Y}}_{t}/\mu _t\). We need the following lemma to solve Problem (12).
Lemma 2
Given any tensors \({\mathcal {A}}\in \mathbb {R}^{r\times d_2 \times d_3},{\mathcal {B}}\in \mathbb {R}^{d_1\times d_2 \times d_3}\), suppose tensor \({\mathcal {B}}*{\mathcal {A}}{}^\top \) has t-SVD \({\mathcal {B}}*{\mathcal {A}}{}^\top ={\mathcal {U}}*{\underline{\varLambda }}*{\mathcal {V}}{}^\top \), where \({\mathcal {U}}\in \mathbb {R}^{d_1\times r \times d_3}\) and \({\mathcal {V}}\in \mathbb {R}^{r\times r\times d_3}\). Then, the problem
has a closed-form solution as
Proof
Since \({\mathcal {P}}{}^\top *{\mathcal {P}}={\mathcal {I}}_{r}\), we have that
Also, we have
where \({\mathcal {X}}={\mathcal {B}}*{\mathcal {A}}{}^\top \) and \(\widetilde{{\mathcal {X}}}=\mathrm{fft}_3({{\mathcal {X}}})\).
According to the trace inequality of Von Neuman, the inequality reaches its maximum when matrices \(\widetilde{{\mathcal {P}}}^{(k)}\in \mathbb {C}^{d_1\times r}\) and \(\widetilde{{\mathcal {X}}}^{(k)}\in \mathbb {C}^{d_1\times r}\) have the same right and left singular vectors.
We perform SVD on its first \(\lceil \frac{d_3+1}{2}\rceil \) frontal slices \(\widetilde{{\mathcal {X}}}^{(k)}\in \mathbb {C}^{d_1\times }\) as follows
where \({{\mathbf{U}}}^{(k)}\in \mathbb {C}^{d_3\times r}\) is a column-orthogonal matrix,\({\mathbf{V}}^{(k)} \in \mathbb {C}^{r\times r}\) is an orthogonal matrix, \({\mathbf{S}}^{(k)}=\text {diag}(\sigma ^{(k)}_1,\ldots ,\sigma ^{(k)}_r)\), and \(\sigma ^{(k)}_1 \ge \sigma ^{(k)}_2\ge \cdots \ge \sigma ^{(k)}_r\ge 0\) are the singular values of \(\widetilde{{\mathcal {X}}}^{(k)}\). Using the relationships between FFT and t-SVD [24], we have that for all \(k>\lceil \frac{d_3+1}{2}\rceil \), the frontal slice \(\widetilde{{\mathcal {X}}}^{(k)}\) also has an SVD as
Then, we construct a semi-orthogonal tensor \({\mathcal {U}}\in \mathbb {R}^{d_1\times r\times d_3}\) and orthogonal tensor \({\mathcal {V}}\in \mathbb {R}^{r\times r\times d_3}\) as a pair of “singular vector tensors” of \({\mathcal {X}}\):
and
Further, we construct \({\mathcal {P}}\in \mathbb {R}^{d_1\times r\times d_3}\) by
Thus we have \({\mathcal {P}}{}^\top *{\mathcal {P}}={\mathcal {I}}\). Also, according to the trace inequality of Von Neuman, the left hand side of Eq. (16) get its maximum and thus Problem (13) get its minimum. \(\square \)
The \({\mathcal {Q}}\)-subproblem By fixing other variables, we update \({\mathcal {Q}}\) as follows
where \({\mathcal {A}}'={\mathcal {P}}_{t+1}*{\mathcal {C}}_{t}\) and \({\mathcal {B}}={\mathcal {M}}-{\mathcal {S}}_{t}-{\mathcal {Y}}_{t}/\mu _t\), and \({\mathfrak {P}}(\cdot )\) is defined in Lemma 2. The last equality holds because of Eq. (14) in Lemma 2.
The \({\mathcal {C}}\)-subproblem We update \({\mathcal {C}}\) as follows
where \(\mathfrak {S}_{\tau }(\cdot )\) is the proximity operator of TNN. In [30], a closed-form expression of \(\mathfrak {S}_{\tau }(\cdot )\) is given as follows:
Lemma 3
(Proximity operator of TNN [30]) For any 3D tensor\({\mathcal {A}}\in \mathbb {R}^{d_1\times d_2 \times d_3}\) with reduced t-SVD\({\mathcal {A}}={\mathcal {U}}*{\underline{\varLambda }}*{\mathcal {V}}{}^\top \), where\({\mathcal {U}}\in \mathbb {R}^{d_1 \times r \times d_3}\) and\({\mathcal {V}}\in \mathbb {R}^{d_2 \times r \times d_3}\) are orthogonal tensors and\({\underline{\varLambda }}\in \mathbb {R}^{r \times r \times d_3}\) is the f-diagonal tensor of singular tubes, the proximity operator \(\mathfrak {S}_{\tau }({\mathcal {A}})\) at \({\mathcal {A}}\) can be computed by:
The \({\mathcal {S}}\)-subproblem We update \({\mathcal {S}}\) as follows
where \({\mathcal {B}}'={\mathcal {P}}_{t+1}*{\mathcal {C}}_{t+1}*{\mathcal {Q}}{}^\top _{t+1}\), and \(\mathfrak {T}_{\tau }(\cdot )\) is the proximity operator of tensor \(l_1\)-norm whose closed-from solution is given as follows:
where \(\circledast \) denotes the element-wise tensor product.

Complexity analysis In a single iteration, the main cost of Algorithm 1 lies in updating the primal variables \({\mathcal {P}},{\mathcal {C}},{\mathcal {Q}},{\mathcal {S}}\) (using operators \({\mathfrak {P}}(\cdot )\), \(\mathfrak {S}_{\tau }(\cdot )\), \({\mathfrak {P}}(\cdot )\), \(\mathfrak {T}_{\tau }(\cdot )\) respectively) and the dual variables \({\mathcal {Y}},{\mathcal {Y}}^{i}, i\le 3\).
Note that, we have to compute many intermediate t-products like \({\mathcal {B}}*{\mathcal {A}}{}^\top \), \({\mathcal {P}}*{\mathcal {C}}*{\mathcal {Q}}{}^\top \) before directly updating the primal and dual variables. These t-products can be efficiently computed using FFT/IFFT with a total cost at most \(O(d_1d_2d_3\log d_3)\), since the intermediate tensors to conduct FFT/IFFT have sizes at most \(d_1\times d_2\times d_3\).
Then, the direct update of \({\mathcal {P}}\) using operator \({\mathfrak {P}}(\cdot )\) involves computing FFT, IFFT and \(d_3\) SVDs of \(r\times d_2\) matrices, having complexity \(O\big (rd_2d_3\log d_3 + r^2d_2d_3\big )\). Similarly, the direct update of \({\mathcal {Q}}\) using operator \({\mathfrak {P}}(\cdot )\) has complexity \(O\big ( rd_1d_3\log d_3 + r^2d_1d_3\big )\). Directly updating \({\mathcal {C}}\) using operator \(\mathfrak {S}_{\tau }(\cdot )\) involves complexity \(O\big ( r^2d_3(r+\log d_3)\big )\). Directly updating \({\mathcal {S}}\) using operator \(\mathfrak {T}_{\tau }(\cdot )\) costs \(O\big (d_1d_2d_3\big )\). Directly updating \({\mathcal {Y}},{\mathcal {Y}}^{i}, i\le 3\) costs \(O(d_1d_2d_3)\). Thus, the one iteration cost of Algorithm 1 is as follows
where \({\tilde{d}}=d_1+d_2.\) When \(r\ll \min \{d_1,d_2\}\), the above cost is significantly lower than the one-iteration cost of ADMM-based TRPCA [24] in Eq. (8).
Consider an extreme case in high dimensional settings where \(r_{\text{ t }}({{\mathcal {L}}^*})=O(1)\), that is the tubal rank of the underlying tensor \({\mathcal {L}}^*\) scales like a small constant. By choosing the initialized rank \(r=2r_{\text{ t }}({{\mathcal {L}}^*})=O(1)\), the one-iteration cost of Algorithm 1 scales like
much cheaper than \(O(d_1d_2d_3\min \{d_1,d_2\})\) of ADMM-based algorithm in high dimensional settings.
4 Theoretical analysis
In this section, some theoretical properties of Algorithm 1 is discussed. Specifically, we first analyze the convergence behavior of Algorithm 1, and then establish the sub-optimality of it.
4.1 Convergence analysis of Algorithm 1
We will show in the following theorem that Algorithm 1 is convergent.
Theorem 1
Letting \(({\mathcal {P}}_t,{\mathcal {C}}_t,{\mathcal {Q}}_t,{\mathcal {S}}_t)\) be any sequence generated by Algorithm 1, the following statements hold
-
(I).
The sequences \(({\mathcal {C}}_t,{\mathcal {P}}_t*{\mathcal {C}}_t*{\mathcal {Q}}_t{}^\top ,{\mathcal {S}}_{t})\) are Cauchy sequences respectively.
-
(II).
\(({\mathcal {P}}_t,{\mathcal {C}}_t,{\mathcal {Q}}_t,{\mathcal {S}}_t)\) is a feasible solution to Problem (9) in a sense that
$$\begin{aligned} \lim _{t\rightarrow \infty } \Vert {{\mathcal {P}}_t*{\mathcal {C}}_t*{\mathcal {Q}}{}^\top _t+{\mathcal {S}}_{t}-{\mathcal {M}}} \Vert _{\infty } \le \varepsilon . \end{aligned}$$
Before proving Theorem 1, we need the following lemmas.
Lemma 4
[16] Let \(\Vert {\cdot }\Vert \) denote any norm with dual norm \(\Vert {\cdot }\Vert ^*\). If \({\mathbf{y}}\in \partial \Vert {{\mathbf{x}}}\Vert \), then it holds that \(\Vert {{\mathbf{y}}}\Vert ^*\le 1\).
Lemma 5
The sequence \(\{{\mathcal {Y}}_{t}\},\{{\mathcal {Y}}^1_{t}\},\{{\mathcal {Y}}^2_{t+1}\},\{{\mathcal {Y}}^3_{t+1}\}\) in Algorithm 1 are bounded.
Proof
First, according to the optimality of \({\mathcal {S}}_{t+1}\) in Problem 19, we have that
which means
Thus, \(\{{\mathcal {Y}}_{t}\}\) is a bounded sequence.
Then, according to the optimality of \({\mathcal {Q}}_{t+1}\) to Problem 17, we obtain \( \Vert {{\mathcal {Y}}^2_{t+1}} \Vert _{\text {F}}\le \Vert {{\mathcal {Y}}^3_{t+1}} \Vert _{\text {F}}. \)
Next, the optimality of \({\mathcal {P}}_{t+1}\) to Problem (12) yields
Since the boundedness of \(\{{\mathcal {Y}}_{t}\}\) leads to the boundedness of \(\{{\mathcal {Y}}_{t}^3\}\). Then \(\{{\mathcal {Y}}_{t}^2\}\) is also bounded.
The optimality of \({\mathcal {C}}_{t+1}\) to Problem (18) yields
which means
Let \({\mathcal {P}}_{t+1}^{\perp }={\mathcal {I}}-{\mathcal {P}}_{t+1}\) and \({\mathcal {Q}}_{t+1}^{\perp }={\mathcal {I}}-{\mathcal {Q}}_{t+1}\). Then,
Thus, \(\{({\mathcal {P}}_{t+1}^{\perp }){}^\top {\mathcal {Y}}^1_{t+1}{\mathcal {Q}}_{t+1}\}\) is bounded. Similarly, sequences \(\{({\mathcal {P}}_{t+1}^{\perp }){}^\top {\mathcal {Y}}^1_{t+1}{\mathcal {Q}}_{t+1}^{\perp }\}\) and \(\{{\mathcal {P}}_{t+1}{}^\top {\mathcal {Y}}^1_{t+1}{\mathcal {Q}}_{t+1}^{\perp }\}\) are also bounded.
In this way, \(\{{\mathcal {Y}}_{t}^1\}\) is also bounded. \(\square \)
Equipped with the above two lemmas, we are able to prove Theorem 1.
Proof of Theorem 1
First, according to the process of Algorithm 1, we have the following chain of inequalities of the Lagrangian:
Note that the quantity \(\max _{s} \Vert {{\mathcal {Y}}_{s}-{\mathcal {Y}}_{s-1}} \Vert _{\text {F}}^2\) in the above inequality is bounded, since \(\{{\mathcal {Y}}_t\}\) is bounded. Recall the update of \(\mu _t\) in Algorithm 1 \(\mu _{t}=\rho \mu _{t-1}=\rho ^t\mu _{0}\), then we show the quantity \(\sum _{t=1}^{\infty }\frac{\mu _{t}+\mu _{t-1}}{2\mu _{t-1}^2}\) is also bounded, since
Thus, \(L_{\mu _{t-1}}({\mathcal {P}}_{t},{\mathcal {C}}_{t},{\mathcal {Q}}_{t},{\mathcal {S}}_{t},{\mathcal {Y}}_{t-1})\) is bounded. Note that
Then, the sequence \(\big \{ \Vert {{\mathcal {C}}_{t}} \Vert _{\star }+\lambda \Vert {{\mathcal {S}}_{t}} \Vert _{\text {1}}\big \}\) is bounded.
According to the orthogonal invariance of TNN given in Lemma 1, we have
Then, we obtain that \(({\mathcal {C}}_{t},{\mathcal {P}}_{t}*{\mathcal {C}}_{t}*{\mathcal {Q}}{}^\top _{t},{\mathcal {S}}_{t})\) is bounded.
According to the process of Algorithm 1, we have
and the following relationships
and
By the update of \(\mu _t=\rho \mu _{t-1}\) with \(\rho =1.1\) in Algorithm 1, we have the fact that \(\lim _{t\rightarrow \infty }\mu _{t}=+\infty \). Combing the above with the boundedness of \({\mathcal {Y}}_{t}\) and \({\mathcal {Y}}^i_{t},~i=1,2,3\), we have
Then \(\{{\mathcal {S}}_{t}\},\{{\mathcal {C}}_{t}\},\{{\mathcal {P}}_t*{\mathcal {C}}_t*{\mathcal {Q}}{}^\top _t\}\) are Cauchy sequences, and
\(\square \)
4.2 Sub-optimality of Algorithm 1
In this subsection, we will establish the sub-optimality of Algorithm 1 by upper bounding the gap in objective value produced by Algorithm 1 and the optimal value of TNN-based TRPCA [24] in Problem (7).
4.2.1 Connection between Algorithm 1 and TRPCA
We first build a connection between the proposed model TriFac in Problem (9) with the TNN-based TRPCA model [24] in Problem (7) in the following theorem.
Theorem 2
(Connection between TriFac and TRPCA) Let \(({\mathcal {P}}_{*},{\mathcal {C}}_{*},{\mathcal {Q}}_{*},{\mathcal {S}}_{*})\) be a global optimal solution to TriFac in Problem (9). And let \(({\mathcal {L}}^\star ,{\mathcal {S}}^\star ) \) be the solution to TRPCA in Problem (7), and \(r_{\text{ t }}({{\mathcal {L}}^\star })\le r\), where r is the initialized tubal rank. Then \(({\mathcal {P}}_{*}*{\mathcal {C}}_{*}*{\mathcal {Q}}{}^\top _{*},{\mathcal {S}}_{*})\) is also the optimal solution to Problem (7).
Theorem 2 asserts that the global optimal point of TriFac coincides with the solution of TNN-based TRPCA, which is guaranteed to exactly recover the underlying tensor \({\mathcal {L}}^*\) under certain conditions. That means that the accuracy of the proposed model cannot exceed TPRCA, which will be shown numerically in the experiment section. The proof of Theorem 2 is given as follows.
Proof of Theorem 2
Note that \(({\mathcal {P}}_{*}*{\mathcal {C}}_{*}*{\mathcal {Q}}{}^\top _{*},{\mathcal {S}}_{*})\) is a feasible point of Problem (7), then we have
By the assumption that \(r_{\text{ t }}({{\mathcal {L}}^\star })\le r\), there exists a decomposition \({\mathcal {L}}^\star ={\mathcal {P}}^\star *{\mathcal {C}}^\star *({\mathcal {Q}}^\star ){}^\top \), such that \(({\mathcal {P}}^\star ,{\mathcal {C}}^\star ,{\mathcal {Q}}^\star ,{\mathcal {S}}^\star )\) is also a feasible point of Problem (9).
Moreover, since \(({\mathcal {C}}_*,{\mathcal {S}}_*)\) is a global optimal solution to Problem (9), then we have that
By \({\mathcal {L}}^\star ={\mathcal {P}}^\star *{\mathcal {C}}^\star *({\mathcal {Q}}^\star ){}^\top \), we have
Thus, we deduce
According to Eqs. (21) and (22), we further have
In this way, \(({\mathcal {P}}_{*}*{\mathcal {C}}_{*}*{\mathcal {Q}}{}^\top _{*},{\mathcal {S}}_{*})\) is also the optimal solution to the TRPCA Problem (7). \(\square \)
Next, we further establish the sub-optimality of Algorithm 1. Let \(t^*\) be the iteration number that Algorithm 1 stops at, then we have the following result.
Theorem 3
(The sub-optimality of Algorithm 1 with respect to TriFac) Let \(({\mathcal {P}}_g,{\mathcal {C}}_g,{\mathcal {Q}}_g,{\mathcal {S}}_g)\) be a global optimal solution to Problem (9). Denote \(f_g= \Vert {{\mathcal {C}}_g} \Vert _{\star }+\lambda \Vert {{\mathcal {S}}_g} \Vert _{\text {1}}\) and \(f_{t^*+1}= \Vert {{\mathcal {C}}_{t^*+1}} \Vert _{\star }+\lambda \Vert {{\mathcal {S}}_{t^*+1}} \Vert _{\text {1}}\). Then, we have
where
Theorem 3 gives an upper bound on the gap between the global optimal value of TriFac and the objective value of Algorithm 1. Since TriFac shares the global optima with TRPCA, the gap between objective values of Algorithm 1 and TRPCA is upper bounded by
Now, we are in a position to give the proof of Theorem 3 in the following subsection.
4.2.2 Proof of Theorem 3
To prove Theorem 3, we should be equipped with the following lemmas.
Lemma 6
(Subgradient of TNN [23]) Let \({\mathcal {X}}\in \mathbb {R}^{m\times n \times k}\) with tubal rank r and its skinny t-SVD be \({\mathcal {X}}={\mathcal {U}}*{\mathcal {S}}*{\mathcal {V}}{}^\top \). The subdifferential (the set of subgradients) of \(\partial \Vert {{\mathcal {X}}} \Vert _{\star }\) is
Lemma 7
Let \({\mathcal {X}},{\mathcal {Y}}\) and \({\mathcal {Q}}\) are tensors of compatible dimensions. If \({\mathcal {P}},{\mathcal {Q}}\) obeys \({\mathcal {P}}{}^\top *{\mathcal {P}}={\mathcal {I}}_{r},{\mathcal {Q}}{}^\top *{\mathcal {Q}}={\mathcal {I}}_{r}\) and \({\mathcal {Y}}\in \partial \Vert {{\mathcal {X}}} \Vert _{\star }\), then
Proof
Let the skinny t-SVD of \({\mathcal {X}}\) be \({\mathcal {X}}={\mathcal {U}}*{\mathcal {S}}*{\mathcal {V}}{}^\top \). By \({\mathcal {Y}}\in \Vert {{\mathcal {X}}} \Vert _{\star }\) and Lemma 6, we have
where \({\mathcal {U}}{}^\top *{\mathcal {W}}={\mathbf{0}},{\mathcal {W}}*{\mathcal {V}}={\mathbf{0}}, \Vert {{\mathcal {W}}} \Vert \le 1\). Since \({\mathcal {P}}\) is column-orthogonal, then \({\mathcal {P}}*{\mathcal {X}}\) has a skinny t-SVD as
where \(({\mathcal {P}}*{\mathcal {U}}){}^\top *({\mathcal {P}}*{\mathcal {U}})={\mathcal {U}}{}^\top *{\mathcal {P}}{}^\top *{\mathcal {P}}*{\mathcal {U}}={\mathcal {I}}_{r}\). Then, it yields to
where \({\mathcal {U}}{}^\top *{\mathcal {P}}{}^\top *{\mathcal {W}}_1={\mathbf{0}},{\mathcal {W}}_1*{\mathcal {V}}={\mathbf{0}}, \Vert {{\mathcal {W}}_1} \Vert \le 1\). With the above notations, it can be verified that \({\mathcal {P}}*{\mathcal {Y}}\in \partial \Vert {{\mathcal {P}}*{\mathcal {X}}} \Vert _{\star }\). Similarly, the remaining two relationships can be proved. \(\square \)
Lemma 8
For any tensor \({\mathcal {X}}\), we have \( \Vert {{\mathcal {X}}} \Vert _{\infty }\le \Vert {{\mathcal {X}}} \Vert \).
Proof
It is obvious that \( \Vert {{\mathcal {X}}} \Vert _{\infty }=\Vert \text {bcirc}({\mathcal {X}})\Vert _{\infty }\), where \(\text {bcirc}(\cdot )\) is the block-circulant operator [24]. It is also known that \( \Vert {{\mathcal {X}}} \Vert =\Vert {{\overline{{\mathcal {X}}}}}\Vert =\Vert {\text {bcirc}({\mathcal {X}})}\Vert \). Note that for any matrix \({\mathbf{X}}\in \mathbb {R}^{m\times n}\), we have
Thus, we have the following relationship
\(\square \)
Based on the above three lemmas, we give the following proposition which is key to the proof of Theorem 3.
Proposition 1
Let \(({\mathcal {P}}_{t^*+1},{\mathcal {C}}_{t^*+1},{\mathcal {Q}}_{t^*+1},{\mathcal {S}}_{t^*+1})\) denote the the solution generated by Algorithm 1, we have that
for any feasible point \(({\mathcal {P}},{\mathcal {C}},{\mathcal {Q}},{\mathcal {S}})\) of Problem (9).
Proof
Recall the update of \({\mathcal {P}}_{t^*+1}\) that
Let the skinny t-SVD of \(({\mathcal {M}}-{\mathcal {S}}_{t^*}-{\mathcal {Y}}_{t^*}/\mu _{t^*})\) is \({\mathcal {U}}_t*{\underline{\varLambda }}_t*{\mathcal {V}}{}^\top _t\). Also let the full t-SVD of \({\underline{\varLambda }}_t*{\mathcal {V}}{}^\top _t*({\mathcal {C}}_{t^*}{\mathcal {Q}}{}^\top _{t^*}){}^\top \) be \({\mathcal {U}}*{\underline{\varLambda }}*{\mathcal {V}}{}^\top \), then we have
which further leads to
Similarly, one has
Recall the definition of \({\mathcal {Y}}^1_{t^*+1}\) in Algorithm 1 that
Performing left t-product of \({\mathcal {P}}_{t^*+1}*{\mathcal {P}}{}^\top _{t^*+1}\) and right t-product \({\mathcal {Q}}_{t^*+1}*{\mathcal {Q}}{}^\top _{t^*+1}\) on both sides of the above equation, we get
Thus, we have
The update of \({\mathcal {C}}_{t^*+1}\) indicates that
Then, we have the relationship \( {\mathcal {P}}_{t^*+1}*{\mathcal {P}}{}^\top _{t^*+1}*{\mathcal {Y}}^1_{t^*+1}*{\mathcal {Q}}_{t^*+1}*{\mathcal {Q}}{}^\top _{t^*+1} \in \partial \Vert {{\mathcal {P}}_{t^*+1}*{\mathcal {C}}_{t^*+1}*{\mathcal {Q}}{}^\top _{t^*+1}} \Vert _{\star }. \)
According to the update \({\mathcal {S}}_{t^*+1}\), we get \( \Vert {{\mathcal {Y}}_{t^*+1}} \Vert _{\text {1}}\le \lambda \). Then using the property of convex functions, we have for any feasible solution \(({\mathcal {P}},{\mathcal {C}},{\mathcal {Q}},{\mathcal {S}})\)
Note that the feasibility of \(({\mathcal {P}},{\mathcal {C}},{\mathcal {Q}},{\mathcal {S}})\) indicates \( {\mathcal {P}}*{\mathcal {C}}*{\mathcal {Q}}{}^\top +{\mathcal {S}}={\mathcal {M}}. \) Then, we have
Note that for any tensor \({\mathcal {X}}\), we have \( \Vert {{\mathcal {X}}} \Vert _{\infty }\le \Vert {{\mathcal {X}}} \Vert \) according to Lemma 8. Then, it holds that
Thus, the statement of this proposition is proved. \(\square \)
Then, we are able to prove Theorem 3 based on Proposition 1.
Proof of Theorem 3
Let \(({\mathcal {P}}_g,{\mathcal {C}}_g,{\mathcal {Q}}_g,{\mathcal {S}}_g)\) be a global solution to Problem (9). Since \(({\mathcal {P}}_{t^*+1},{\mathbf{0}},{\mathcal {Q}}_{t^*+1},{\mathcal {M}})\) is feasible to Problem (9). Then, we have
Also, we have
Since \( \Vert {{\mathcal {Y}}_t} \Vert _{\infty }\le \lambda ,\forall t\in {\mathbb {N}}_+\), we have
Thus we have \(\max _s \Vert {{\mathcal {Y}}_{s}-{\mathcal {Y}}_{s-1}} \Vert _{\text {F}}^2\le 4d_1d_2d_3\lambda ^2\) and \( \Vert {{\mathcal {Y}}_{t^*}} \Vert _{\text {F}}^2\le \lambda ^2\). Then, it yields
Hence,
where
Also note that \( \Vert {{\mathcal {Y}}_{t^*}-{\mathcal {Y}}^1_{t^*}} \Vert _{\infty }\le \Vert {{\mathcal {Y}}_{t^*}} \Vert _{\infty }+ \Vert {{\mathcal {Y}}^1_{t^*}} \Vert _{\infty }\le \Vert {{\mathcal {Y}}_{t^*}} \Vert _{\infty }+ \Vert {{\mathcal {Y}}^1_{t^*}} \Vert \le 1+\lambda \). Thus, we have
which completes the proof. \(\square \)
5 Extensions and differences with prior works
In this section, we first consider an extension where the observation also suffers from missing values, known as robust tensor completion [11], and then explain the differences from this work and prior works.
5.1 Extensions to robust tensor completion
Besides corruptions, the observation \({\mathcal {M}}\) may also suffer from missing entries in many scenarios [11]. Thus, it is also practical to consider robust tensor completion which aims to recover \({\mathcal {L}}^*\) against outliers \({\mathcal {S}}^*\) and missing entries shown in the following observation model
where tensor \({\mathcal {B}}\in \mathbb {R}^{d_1\times d_2 \times d_3}\) denote the missing mask where \({\mathcal {B}}_{ijk}=1\), if the (i, j, k)th entry of \({\mathcal {L}}\) is observed and \({\mathcal {B}}_{ijk}=0\) otherwise.
In [11], a TNN-based robust tensor completion model is proposed as follows
For Model (24), the ADMM algorithm proposed in [11] also requires full SVDs in each iteration, and thus can be accelerated by the factorized strategy in this paper. Taking into consideration of missing entries, we simply modify Model (9) as:
Model (25) can be optimized by ADMM [1] and we omit it due to the focus of this paper.
It is easy to build a connection between the proposed Model (25) with Model (24) in the following theorem.
Theorem 4
(Connection between Model (25) and Model (24)) Let \(({\mathcal {P}}_{*},{\mathcal {C}}_{*},{\mathcal {Q}}_{*},{\mathcal {S}}_{*})\) be a global optimal solution Problem (25). And let \(({\mathcal {L}}^\star ,{\mathcal {S}}^\star ) \) be the solution Problem (24), and \(r_{\text{ t }}({{\mathcal {L}}^\star })\le r\), where r is the initialized tubal rank. Then \(({\mathcal {P}}_{*}*{\mathcal {C}}_{*}*{\mathcal {Q}}{}^\top _{*},{\mathcal {S}}_{*})\) is also the optimal solution to Problem (24).
5.2 Differences with prior works
First, we explain the differences between this paper and the TNN-based TRPCA [24].
-
1.
[24] recovers the underlying tensor using a convex model whereas our factorization-based model is non-convex.
-
2.
The theoretical results in [24] guarantee exact recovery of the underlying tensor whereas our theoretical analysis focus on the sub-optimality of the proposed algorithm.
Then, since our work is motivated by the “active space” model [17], we compare them as follows.
-
1.
The objectives are different: Our method is for tensor recovery and [17] is for matrix RPCA. Our model is based on the algebraic framework t-SVD and it can be viewed as a non-trivial multi-linear extension of [17].
-
2.
In our model, we adopts a triple tensor factorization \({\mathcal {L}}={\mathcal {P}}*{\mathcal {C}}*{\mathcal {Q}}{}^\top \) whereas [17] considers bipartite matrix factorization \({\mathbf{L}}={\mathbf{P}}{\mathbf{C}}\). Thus, our results cannot be trivially obtained from the analysis of [17].
Finally, we extend the conference version of this work [32] in the following aspects.
-
1.
We analyze the sub-optimality of the proposed Algorithm which is a main technical contribution of this paper. Besides, all proofs of lemmas and theorems in the conference version can be found directly in this paper.
-
2.
We also extend the proposed model to the robust tensor completion problem [11] in this paper.
-
3.
A large number of additional experiments are performed in this paper.
6 Experiments
In this section, we experiment on both synthetic and real datasets to verify the effectiveness and the efficiency of the proposed algorithm. All codes are written in Matlab and all experiments are performed in Windows 10 based on Intel(R) Core(TM) i7-8565U 1.80-1.99 GHz CPU with 8G RAM.
6.1 Synthetic data experiments
In this subsection, we compare Algorithm 1 (TriFac) with the TNN-based TRPCA [23] in accuracy and speed on synthetic datasets. Given tensor size \(d_1\times d_2 \times d_3\) and tubal rank \(r^*\ll \min \{d_1,d_2\}\), we first generate a tensor \({\mathcal {L}}_0\in \mathbb {R}^{d_1\times d_2 \times d_3}\) by \( {\mathcal {L}}_0={\mathcal {A}}*{\mathcal {B}}, \) where the elements of tensors \({\mathcal {A}}\in \mathbb {R}^{d_1\times r^*\times d_3}\) and \({\mathcal {B}}\in \mathbb {R}^{r^*\times d_2\times d_3}\) are sampled from independent and identically distributed (i.i.d.) standard Gaussian distribution. We then form \({\mathcal {L}}^*\) by \({\mathcal {L}}^*=\sqrt{d_1d_2d_3}{\mathcal {L}}_0/ \Vert {{\mathcal {L}}_0} \Vert _{\text {F}}\). Next, the support of \({\mathcal {S}}^*\) is uniformly sampled at random. For any \((i,j,k)\in \mathrm {supp}\left( {\mathcal {S}}^*\right) \), we set \({\mathcal {S}}^*_{ijk} = {\mathcal {B}}_{ijk}\), where \({\mathcal {B}}\) is a tensor with independent Bernoulli \(\pm 1\) entries. Finally, we form the observation tensor \({\mathcal {M}}={\mathcal {L}}^*+{\mathcal {S}}^*\). In the experiments, we set parameter \(\lambda =1/\sqrt{d_3\max \{d_1,d_2\}}\). For an estimation \(\hat{{\mathcal {L}}}\) of the underlying tensor \({\mathcal {L}}^*\), the relative squared error (RSE) is used to evaluate the quality of \(\hat{{\mathcal {L}}}\), that is,
6.1.1 Effectiveness and efficiency of TriFac
We first show that TriFac can exactly recover the underlying tensor \({\mathcal {L}}^*\) from corruptions with fast speed than TRPCA. We first test the recovery performance of different tensor sizes by setting \(d_1=d_2\in \{100,160,200\}\) and \(d_3=30\), with \((r_{\text{ t }}({{\mathcal {L}}^*}), \Vert {{\mathcal {S}}^*} \Vert _{0})=(0.05d,0.05d^2d_3)\). Then, a more difficult setting \((r_{\text{ t }}({{\mathcal {L}}^*}), \Vert {{\mathcal {S}}^*} \Vert _{0})=(0.15d,0.1d^2d_3)\) is tested. The results are shown in Table 2. It can be seen that TriFac can perform as well as TRPCA in the sense that both of them can exactly recover the underlying tensor. However, TriFac is much faster than TRPCA.
To test whether the distribution of outliers affects the performance of TriFac. We also test the cases where elements of the outlier tensor \({\mathcal {S}}^*\) are drawn from i.i.d. Gaussian distribution \({\mathcal {N}}(0,1)\), or uniform distribution \({\mathcal {U}}[0,1]\). The corresponding results are shown in Tables 3 and 4, respectively. As can be seen, the performance and speed of TriFac and TRPCA has not been significantly affected by the distribution of outliers. This can be explained by Theorem 4.1 in [24] that the underlying tensor \({\mathcal {L}}^*\) can be exactly recovered by TRPCA under some mild conditions if the support of the outlier tensor \({\mathcal {S}}^*\) is uniformly distributed. For the outlier tensor \({\mathcal {S}}^*\), Theorem 4.1 in [24] only makes one assumption on the random location distribution, but no assumption about the magnitudes or signs of the nonzero entries. Since the proposed TriFac can well mimic TRPCA for low-tubal-rank tensors, it is not surprising that TriFac is robust to different outliers.
To further show the efficiency of the proposed TriFac, we consider a special case where the size of the underlying tensor \({\mathcal {L}}^*\) increases while the tubal rank is fixed as a constant. Specifically, we fix \(r_{\text{ t }}({{\mathcal {L}}^*})=5\), and vary \(d\in \{100,150,200,\ldots ,500\}\) with \(d_3=20\). We set the parameter of initialized rank r of TriFac in Algorithm 1 by \(r=30\). We test each setting 10 times and compute the averaged time. In all the runs, both TRPCA and TriFac can recover the underling tensor with RSE smaller than \(1{\text {e}}{-6}\). The plot of averaged time versus the tensor size (shown in d) is given in Fig. 3. We can see that the time cost of TRPCA scales super-linearly with respect to d, whereas the proposed TriFac has approximately linear scaling.
Computation time of TRPCA [24] and the proposed TriFac versus \(d\in \{100,150,200,\ldots ,500\}\) with \(d_3=20\), when the tubal rank of the underlying tensor is 5. The RSEs of TNN and TriFac in all the setting are smaller than \(1{\text {e}}{-6}\)
6.1.2 Effects of the initialized tubal rank r
The performance of TriFac heavily rely on the choice of initialized tubal rank r in Model (9). Here, we explore the effects of initialized tubal rank on the accuracy and speed of TriFac. Specifically, we consider tensors of size \(100\times 100\times 30\) with four different settings of tubal rank \(r^*=r_{\text{ t }}({{\mathcal {L}}^*})\) and sparsity \(s^*= \Vert {{\mathcal {S}}^*} \Vert _{0}\) as \((r^*,s^*)\in \{(10,1.5{\text {e}}{4}),(10,3{\text {e}}{4}),(15,1.5{\text {e}}{4}),(10,3{\text {e}}{4})\}\), where the elements outliers follow i.i.d. \({\mathcal {N}}(0,1)\). By varying the initialized \(r\in \{5,10,15,\ldots ,50\}\), we show the effects of the initialized tubal rank r on the accuracy and speed of TriFac.
We first report the effects of initialized tubal rank r on the recovery accuracy of the underlying tensor \({\mathcal {L}}^*\), in terms of RSE and tubal rank of the final solution \(\hat{{\mathcal {L}}}\). The results are shown in Fig. 4. As can be seen, there exists a phrase transition point \(r_{\mathrm{{pt}}}\) that once the initialized rank r is larger than it, the RSE of \(\hat{{\mathcal {L}}}\) will decrease rapidly.
Then, the effects of initialized tubal rank r on the estimation performance of the outlier tensor \({\mathcal {S}}^*\), in terms of RSE and \(l_0\)-norm of the final solution \(\hat{{\mathcal {S}}}\) are shown in Fig. 5. We can also see that when the initialized rank r gets larger than the same phrase transition point \(r_{\mathrm{{pt}}}\), the RSE of \(\hat{{\mathcal {S}}}\) will soon vanish.
Finally, we show the effects of initialized tubal rank r on the running time of TriFac in Fig. 6. We can see that the running time increases as the initialized rank r gets larger, the underlying tensor gets more complex (i.e., \(r^*\) gets higher), and the corruption gets heavier (i.e., \(s^*\) gets larger). That is consistent with our intuition.
6.2 Real data experiments
In this section, the efficiency of the proposed TriFac compared with TRPCA [24] is evaluated on real-world datasets. Specifically, we carry out tensor restoration experiments on point cloud data, color images and brain MRI data. For an estimation \(\hat{{\mathcal {L}}}\) of the underlying tensor \({\mathcal {L}}^*\), the peak signal-to-noise ratio (PSNR) is applied to evaluate the quality of \(\hat{{\mathcal {L}}}\), that is,
6.2.1 Robust recovery point cloud data
We conduct experiments on a point cloud data set acquired by a vehicle-mounted Velodyne HDL-64E LiDARFootnote 2 which is used for moving object tracking [25]. We extract the first 32 frames, transform and upsample the data to form two tensors in \(\mathbb {R}^{512\times 800 \times 32}\) representing the distance data and the intensity data, respectively. Given a data tensor, we uniformly choose its indices with probability \(\rho _s\in \{0.2,0.4\}\). We then corrupt the chosen positions with element-wise outliers from i.i.i. symmetric Bernoulli \(\text {Bin}(-1,+1)\) or \({\mathcal {N}}(0,1)\). The proposed algorithm is also compared with SNN [10] and RPCA [2]. RPCA works on each frontal slice individually. The parameters of RPCA is set by \(\lambda =1/\sqrt{\max \{d_1,d_2\}}\) [2]. The weight parameters \(\varvec{\lambda }\) of SNN are chosen by \(\lambda _k=\sqrt{\max \{d_k,\prod _{k'\ne k}d_{k'}\}}/3\). We set the parameter \(\lambda =1/\sqrt{d_3\max \{d_1,d_2\}}\) [23] for TRPCA and the proposed TriFac. We choose the initialized tubal rank \(r=196\).
We report the PSNR value and running time of each algorithm on the distance and intensity data in Fig. 7. It can be seen that TNN-based TRPCA has the highest PSNR values in all the settings, which is consistent with the results of tensor completion on this data that TNN outperforms SNN [33]. The proposed TriFac algorithm performs slightly worse than TNN, but it has the lowest running time. As is shown in Theorem 2, the proposed model in Eq. 9 can not outperform TNN-based RPCA model in Eq. (7) since they have the same global optimal solutions but the proposed model is non-convex. This explains why TriFac cannot achieve better performances than TRPCA.
Quantitative comparison of algorithms in PSNR and running time on point cloud data. a PSNR values of algorithms on the distance data; b running time of algorithms on the distance data; c PSNR values of algorithms on the intensity data; d running time of algorithms on the intensity data. (‘0.2,B’ means 20% of the positions are corrupted by Ber(\(-1,+1\)) outliers, and ‘0.4,G’ means 40% of the positions are corrupted by \({\mathcal {N}}(0,1)\) outliers)
6.2.2 Robust recovery of color images
We conduct image restoration on color images, which have natural 3-way tensor formats. The image restoration task aims at recovering an image from its corrupted observation. In this experiment, we test on 20 images of size \(512\times 512\times 3\) shown in Fig. 8. Given a color image \({\mathcal {M}}\in \mathbb {R}^{m \times m \times 3}\), we first choose \(10\%\) of is entries uniformly at random, and then corrupt them by i.i.d. outliers from \({\mathcal {U}}[0,1]\).
We also compare the proposed TriFac with SNN [10] and RPCA [2]. The weight parameters \(\varvec{\lambda }\) of SNN are set by two different choices \([\lambda _1,\lambda _2,\lambda _3]=[15,15,1.5]\) as suggested by [24] or \([\lambda _1,\lambda _2,\lambda _3]=[\sqrt{3m},\sqrt{3m},m]/3\), and we use the result with higher PSNR. The parameter \(\lambda \) of NN is set by \(\lambda =1/\sqrt{m}\) [2]. We set the parameter \(\lambda =1/\sqrt{3m}\) [23] for TRPCA and the proposed TriFac. We choose the initialized tubal rank \(r=226\). Given a color image and a corruption level, we test 10 times and report the averaged PSNR and time.
Qualitative comparison of algorithms for robust image recovery with \(10\%\) entries corrupted by i.i.d. \({\mathcal {U}}[0,1]\) outliers. a The corrupted image; b–e the images recovered by RPCA [2], SNN [10], TRPCA [24], and the proposed TriFac; e PSNR values of each algorithm. Best viewed in color pdf with 400% zooming-in
Examples of the recovered images are shown in Fig. 9 for qualitative comparison. For quantitative comparison, the PSNR values and running time are reported in Fig. 10. We can see that TRPCA also performs best in most cases, consistent with the results in [24]. The proposed TriFac algorithm has the shortest running time and only slightly lower PSNRs than TRPCA.
6.2.3 Robust recovery of brain MRI data
To show the efficiency of the proposed TriFac, we also use the 3-way MRI data set analyzed in [38] which has good low-rank property. We extract the first 15 slices, each having a size of \(181 \times 217\). To further show the efficiency of TriFac, we resize the data with scale parameter \(\kappa \in \{1,1.5,2,2.5,3\}\) to form tensors in \(\mathbb {R}^{\lceil 181\kappa \rceil \times \lceil 217\kappa \rceil \times 15}\). Then, we randomly choose 20% of the elements in the rescaled tensor, and corrupts them by elements from i.i.d. Bernoulli distribution \(\text {Bin}(-1,+1)\). We compare TriFac with TRPCA in both running time and recovery performance with respect to different sizes. The results are shown in Table 5. It can be seen that the proposed TriFac works almost as well as TRPCA but has faster speed.
6.2.4 Robust completion of color images
To evaluate the factorization strategy in its extension to robust tensor completion, we also conduct robust image completion on the test images in Fig. 8. In the experiment, we aim to restore a color image when 60% of its entries are missing uniformly at random and 10% of the observed entries are randomly corrupted by \(\text {Bin}(-1,+1)\) outliers. The SSIM (Structural Similarity Index) [35] is also used to measure the quality of a restored image. The higher the SSIM value is, the higher the quality of a restored image is.
The proposed model (RTC-Fac) is compared with robust image completion models based on matrix nuclear norm (NN), SNN, and TNN, respectively. We also compare with a double \(l_{1-2}\) metric based image completion model (DL1-2) inspired by [42]. The PSNR values, SSIM values, and running time are shown in Fig. 11. According to the results in Fig. 11, we can find that the proposed model has the least running time and achieves second highest PSNR and SSIM values in most cases.
7 Conclusion
In this paper, a factorization-based TRPCA model (TriFac) is first proposed to recover a 3-way data tensor from its observation corrupted by sparse outliers. Then, we come up with a non-convex ALM algorithm (Algorithm 1) to efficiently solve it. Further, the convergence and sub-optimality of the proposed algorithm are analyzed in Theorems 1 and 3, respectively. The effectiveness and efficiency of the proposed algorithm are demonstrated in experiments on both synthetic and real data sets.
It is interesting to study the statistical performance of the proposed model like [19, 31, 34], and consider sparse tensor discriminant analysis like [15, 21, 22, 26] as future works. It is also interesting to use non-convex tensor rank minimization [39, 40].
Notes
References
Boyd S, Parikh N, Chu E, Peleato B, Eckstein J (2011) Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends®. Mach Learn 3(1):1–122
Candès EJ, Li X, Ma Y, Wright J (2011) Robust principal component analysis? J ACM (JACM) 58(3):11
Candès EJ, Tao T (2010) The power of convex relaxation: near-optimal matrix completion. IEEE Trans Inf Theory 56(5):2053–2080
Fazel M (2002) Matrix rank minimization with applications. Ph.D. thesis, Stanford University
Foucart S, Rauhut H (2013) A mathematical introduction to compressive sensing, vol 1. Birkhäuser, Basel
Friedland S, Lim L (2017) Nuclear norm of higher-order tensors. Math Comput 87(311):1255–1281
Goldfarb D, Qin Z (2014) Robust low-rank tensor recovery: models and algorithms. SIAM J Matrix Anal Appl 35(1):225–253
Harshman RA (1970) Foundations of the parafac procedure: models and conditions for an “explanatory” multi-modal factor analysis
Hillar CJ, Lim L (2009) Most tensor problems are np-hard. J ACM 60(6):45
Huang B, Mu C, Goldfarb D, Wright J (2015) Provable models for robust low-rank tensor completion. Pac J Optim 11(2):339–364
Jiang Q, Ng M (2019) Robust low-tubal-rank tensor completion via convex optimization. In: Proceedings of the 28th international joint conference on artificial intelligence. AAAI Press, Macao, China, pp 2649–2655
Kilmer ME, Braman K, Hao N, Hoover RC (2013) Third-order tensors as operators on matrices: a theoretical and computational framework with applications in imaging. SIAM J Matrix Anal Appl 34(1):148–172
Kolda TG, Bader BW (2009) Tensor decompositions and applications. SIAM Rev 51(3):455–500
Lai Z, Xu Y, Chen Q, Yang J, Zhang D (2014) Multilinear sparse principal component analysis. IEEE Trans Neural Netw 25(10):1942–1950
Lai Z, Xu Y, Yang J, Tang J, Zhang D (2013) Sparse tensor discriminant analysis. IEEE Trans Image Process 22(10):3904–3915
Lin Z, Chen M, Ma Y (2010) The augmented Lagrange multiplier method for exact recovery of corrupted low-rank matrices. arXiv preprint arXiv:1009.5055
Liu G, Yan S (2012) Active subspace: toward scalable low-rank learning. Neural Comput 24(12):3371–3394
Liu J, Musialski P, Wonka P, Ye J (2013) Tensor completion for estimating missing values in visual data. IEEE Trans Pattern Anal Mach Intell 35(1):208–220
Liu X, Aeron S, Aggarwal V, Wang X (2020) Low-tubal-rank tensor completion using alternating minimization. IEEE Trans Inf Theory 66(3):1714–1737
Liu Y, Jiao L, Shang F (2013) A fast tri-factorization method for low-rank matrix recovery and completion. Pattern Recognit 46(1):163–173
Liu Z, Lai Z, Ou W, Zhang K, Zheng R (2020) Structured optimal graph based sparse feature extraction for semi-supervised learning. Signal Process 170:107456
Liu Z, Wang J, Liu G, Zhang L (2019) Discriminative low-rank preserving projection for dimensionality reduction. Appl Soft Comput 85:105768
Lu C, Feng J, Chen Y, Liu W, Lin Z, Yan S (2016) Tensor robust principal component analysis: Exact recovery of corrupted low-rank tensors via convex optimization. In: Proceedings of the IEEE conference on computer vision and pattern recognition. IEEE, Las Vegas, USA, pp 5249-5257
Lu C, Feng J, Liu W, Lin Z, Yan S et al (2019) Tensor robust principal component analysis with a new tensor nuclear norm. IEEE Trans Pattern Anal Mach Intell 42:925–938
Moosmann F, Stiller C (2013) Joint self-localization and tracking of generic objects in 3d range data. In: Proceedings of the IEEE international conference on robotics and automation. IEEE, Karlsruhe, Germany, pp 1138–1144
Peng Y, Lu BL (2017) Discriminative extreme learning machine with supervised sparsity preserving for image classification. Neurocomputing 261:242–252
Peng Y, Lu BL (2017) Robust structured sparse representation via half-quadratic optimization for face recognition. Multimed Tools Appl 76(6):8859–8880
Romera-Paredes B, Pontil M (2013) A new convex relaxation for tensor completion. In: Proceedings of advances in neural information processing systems. The Neural Information Processing Systems Foundation, Lake Tahoe, USA, pp 2967–2975
Tucker LR (1966) Some mathematical notes on three-mode factor analysis. Psychometrika 31(3):279–311
Wang A, Jin Z (2017) Near-optimal noisy low-tubal-rank tensor completion via singular tube thresholding. In: Proceedings of the IEEE international conference on data mining workshop (ICDMW). IEEE, New Orleans, USA, pp 553–560
Wang A, Jin Z, Tang G (2020) Robust tensor decomposition via t-SVD: near-optimal statistical guarantee and scalable algorithms. Signal Process 167:107319. https://doi.org/10.1016/j.sigpro.2019.107319
Wang A, Jin Z, Yang J (2019) A factorization strategy for tensor robust PCA. In: 2019 5th IAPR Asian conference on pattern recognition (ACPR). IAPR, Auckland, New Zealand, pp 424–437
Wang A, Lai Z, Jin Z (2019) Noisy low-tubal-rank tensor completion. Neurocomputing 330:267–279
Wang A, Li C, Jin Z, Zhao Q (2020) Robust tensor decomposition via orientation invariant tubal nuclear norms. In: Proceedings of AAAI conference on artiicial intelligence. AAAI Press, New York, USA, pp 6102–6109
Wang Z, Bovik AC, Sheikh HR, Simoncelli EP (2004) Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process 13(4):600–612
Wu T, Bajwa WU (2018) A low tensor-rank representation approach for clustering of imaging data. IEEE Signal Process Lett 25(8):1196–1200
Xie Y, Tao D, Zhang W, Liu Y, Zhang L, Qu Y (2018) On unifying multi-view self-representations for clustering by tensor multi-rank minimization. Int J Comput Vis 126(11):1157–1179
Xu Y, Hao R, Yin W, Su Z (2015) Parallel matrix factorization for low-rank tensor completion. Inverse Probl Imaging 9(2):601–624
Xue J, Zhao Y, Liao W, Chan JCW (2018) Total variation and rank-1 constraint rpca for background subtraction. IEEE Access 6:49955–49966
Xue J, Zhao Y, Liao W, Chan JCW (2019) Nonconvex tensor rank minimization and its applications to tensor recovery. Inf Sci 503:109–128
Xue J, Zhao Y, Liao W, Chan JCW, Kong SG (2020) Enhanced sparsity prior model for low-rank tensor completion. IEEE Trans Neural Netw Learn Syst. https://doi.org/10.1109/TNNLS.2019.2956153
Zhang F, Yang G, Yang Z, Wan M (2018) Robust recovery of corrupted image data based on \(l_{1-2}\) metric. IEEE Access 6:5848–5855
Zhang Z, Aeron S (2017) Exact tensor completion using t-SVD. IEEE Trans Signal Process 65(6):1511–1526
Zhang Z, Ely G, Aeron S, Hao N, Kilmer M (2014) Novel methods for multilinear data completion and de-noising based on tensor SVD. In: Proceedings of the IEEE conference on computer vision and pattern recognition. IEEE, Columbus, USA, pp 3842–3849
Zhou P, Feng J (2017) Outlier-robust tensor PCA. In: Proceedings of the IEEE conference on computer vision and pattern recognition. IEEE, Honolulu, USA, pp 3938–3946
Acknowledgements
The authors would like to thank Prof. Qibin Zhao, Ms. Jin Wang, Mr. Bo Wang and Dr. Dongxu Wei for their long time support. This work is partially supported by National Natural Science Foundation of China [Grant nos. 61872188, U1713208, 61972204, 61672287, 61861136011, 61773215, 61703209,61972212], by the Natural Science Foundation of Guangdong Province [Grant nos. 2020A1515010671, 2017A030313367], and by the Natural Science Foundation of Jiangsu Province [Grant no. BK20190089].
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Part of this work [32] has been presented in 5th IAPR Asian Conference on Pattern Recognition (ACPR), 26-29 November 2019, Auckland, New Zealand.
Rights and permissions
About this article
Cite this article
Wang, AD., Jin, Z. & Yang, JY. A faster tensor robust PCA via tensor factorization. Int. J. Mach. Learn. & Cyber. 11, 2771–2791 (2020). https://doi.org/10.1007/s13042-020-01150-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13042-020-01150-2