The Nonconvex Tensor Robust Principal Component Analysis Approximation Model via the Weighted $\ell _p$-Norm Regularization

Abstract

Tensor robust principal component analysis (TRPCA), which aims to recover the underlying low-rank multidimensional datasets from observations corrupted by noise and/or outliers, has been widely applied to various fields. The typical convex relaxation of TRPCA in literature is to minimize a weighted combination of the tensor nuclear norm (TNN) and the $\ell _1$-norm. However, owing to the gap between the tensor rank function and its lower convex envelop (i.e., TNN), the tensor rank approximation by using the TNN appears to be insufficient. Also, the $\ell _1$-norm generally is too relaxing as an estimator for the $\ell _0$-norm to obtain desirable results in terms of sparsity. Different from current approaches in literature, in this paper, we develop a new non-convex TRPCA model, which minimizes a weighted combination of non-convex tensor rank approximation function and the weighted $\ell _p$-norm to attain a tighter approximation. The resultant non-convex optimization model can be solved efficiently by the alternating direction method of multipliers (ADMM). We prove that the constructed iterative sequence generated by the proposed algorithm converges to a critical point of the proposed model. Numerical experiments for both image recovery and surveillance video background modeling demonstrate the effectiveness of the proposed method.

1 Introduction

With the rapid development of science and technology, more and more complex datasets are obtainable and appear to be multi-dimensional in nature [22, 39]. For example, a color image, consisting of three color channels (red, green, blue), is a three-dimensional data. A greyscale video consisted of two pixel variables and a time variable is modeled as a three-dimensional dataset, while a color video comprised of color images is characterized as a four-dimensional dataset. Mathematically, multi-dimensional data can be formulated as a tensor [22], which is a natural generalization of a matrix. Employing tensor models to handle various multi-dimensional datasets has become increasingly valuable since the tensor representation maintains the spatial structure information among individual entries and provides a more suitable characterization for datasets. Quite often, many real-world multi-dimensional datasets can be approximated by low dimensional subspaces due to the underlying correlation inside the datasets [34]. Low rank properties not only greatly simplify the data representation but also allow us to process multi-dimensional datasets more efficiently. Therefore, the study of low-rank optimization problems under the tensor framework becomes not only important but also critical in many applications.

As one of the important applications of the low-rank matrix optimization, robust principal component analysis (RPCA) [4] has been widely used in many areas including subspace clustering [24], machine learning [7], face recognition [13], etc. In the past, common approaches by using RPCA for multi-dimensional datasets are to directly restructure the datasets into matrices or vectors. However, such approaches result in the loss of structural information that may be critical in data characterization. Recently, tensor robust principal component analysis (TRPCA) has been developed [25, 31] to handle the multi-dimensional datasets. Suppose that we are given an observed tensor data ${\mathcal {X}} \in {\mathbb {R}}^{N_1\times N_2\times N_3}$ and know that it can be split as ${\mathcal {X}} ={\mathcal {L}}+{\mathcal {E}}$ , where ${\mathcal {L}}$ and ${\mathcal {E}}$ are low rank and sparse parts of ${\mathcal {X}}$, respectively. TRPCA is used to extract ${\mathcal {L}}$ and ${\mathcal {E}}$ from ${\mathcal {X}}$, its mathematical model can be formulated as

$$\begin{aligned} \min _{{\mathcal {L}},{\mathcal {E}}} \quad {\text {rank}} ({\mathcal {L}}) +\lambda \Vert {\mathcal {E}}\Vert _0, \quad \mathrm {s.t.} \quad {\mathcal {X}}={\mathcal {L}}+{\mathcal {E}}, \end{aligned}$$

(1.1)

where $\lambda$ is a positive regularization parameter used to balance the low rank and sparse terms, $\Vert {\mathcal {E}} \Vert _0$ denotes the number of nonzero entries of ${\mathcal {E}}$. The key to solve the above optimization problem is to use a suitable tensor rank characterization. However, one of the major challenges for the tensor lies in that the characterizations of the tensor rank are not always tractable. Based on problems at hand, many tensor rank definitions have been proposed [8, 15, 22, 36] and have led to different tensor rank minimization models while each has its limitation and applicable scope. For example, the CANDECOMP/PARAFAC (CP) rank [15] of a tensor ${\mathcal {X}}$, defined as the minimum number of rank-one tensors required to express ${\mathcal {X}}$, is generally NP-hard to compute [40, 53]. Although many approaches have successfully recovered some special low CP rank tensors (see e.g., [19]), it is often a challenge to determine the CP rank and its best convex relaxation. The Tucker rank of the Mth-order tensor ${\mathcal {X}}$ is defined to be an M-dimension vector whose i-th component is the rank of the mode-i unfolding matrix of ${\mathcal {X}}$ [8, 22]. Liu et al. [25] introduced a tractable convex method for the Tucker rank tensor completion problem by defining the sum of the nuclear norms (SNN) of all unfolding matrices of the tensor. Numerical experiments on TRPCA by using SNN was presented in [29] by Lu et al. However, the solution of the above model appears to be suboptimal since SNN is not the convex envelope of the sum of ranks of all those unfolding matrices. The tensor train (TT) rank [36] is composed by ranks of matrices formed by a well-balanced matricization scheme, i.e., matricize the tensor along one or a few modes. Bengua et al. [1] developed a TT rank tensor completion method for color images and videos. Yang et al. [45] applied the TT nuclear norm (TTNN) to the TRPCA problem with good numerical results. However, the performance of the TT-based methods is always unsatisfactory when the third-dimension of the data is large (such as for the hyperspectral images).

Recently, the tensor singular value decomposition (t-SVD) developed by Kilmer et al. [20] has attracted considerable interests. Based on the definition of tensor-tensor product (denoted as $``* "$) , t-SVD decomposes a tensor ${\mathcal {X}}$ into one f-diagonal tensor ${\mathcal {S}}$ multiplied by two orthogonal tensors ${\mathcal {U}}$ and ${\mathcal {V}}$: ${\mathcal {X}}={\mathcal {U}}*{\mathcal {S}}*{\mathcal {V}}^T$. By using the discrete Fourier transform (DFT), the t-SVD can be easily obtained by computing certain matrix SVDs in the Fourier domain. With the framework of the t-SVD, Kilmer et al. provided a new tensor rank definition named tubal rank [21]. Compared with other tensor decompositions, the t-SVD has been shown to be more robust in maintaining the intrinsic correlative structure of the multi-dimensional data [29]. Based on the t-SVD, Lu et al. [29] proposed the following TRPCA model by replacing the tensor tubal rank with the tensor nuclear norm (TNN) (see Sect. 2 for the definition) and the $\ell _0$-norm with the $\ell _1$-norm:

$$\begin{aligned} \min _{{\mathcal {L}},{\mathcal {E}}} \Vert {\mathcal {L}} \Vert _{*}+\lambda \Vert {\mathcal {E}}\Vert _{\ell _1}, \quad \mathrm {s.t.} \quad {\mathcal {X}}={\mathcal {L}}+{\mathcal {E}}, \end{aligned}$$

(1.2)

where $\Vert {\mathcal {L}} \Vert _{*}$ denotes the TNN of ${\mathcal {L}}$ . However, this model has some important issues needed to address in applications. First, the gap between the tensor rank function and its lower convex envelop (i.e., TNN) may be large, especially when some of the singular values of the original tensor are very large. The TNN minimization method (1.2) usually penalizes the large singular values and leads to the loss of main information [14]. Also, the $\ell _1$-norm is a coarse approximation of the $\ell _0$-norm, which usually leads to undesirable results.

Inspired by the success of the non-convex matrix rank minimization models [18, 37], many non-convex tensor rank minimization models have been proposed to improve the aforementioned approaches. For instance, Jiang et al. [16] proposed to use the partial sum of the tensor nuclear norm (PSTNN) as the approximation for the tensor tubal rank. Cai et al. [2] established a non-convex TRPCA model by introducing a t-Gamma tensor quasi-norm as a non-convex regularization to approximate the tensor tubal rank. Beyond TRPCA, many non-convex rank surrogates were proposed in the tensor completion (TC) problem, e.g., Laplace [43], Minimax Concave Penalty (MCP) [12, 49], Smoothly Clipped Absolute Deviation (SCAD) [12, 49], Exponential-Type Penalty (ETP) [12], and Logarithmic [42]. The advantage of non-convex approximation model is due to that it can capture the tensor rank more accurately than the convex setting and thus can obtain a more accurate result than convex approaches. For example, in [42], the logarithmic function based non-convex surrogate is shown to be a more accurate approximation for the Tucker rank. In [43], the laplace function based non-convex surrogate is shown to be a better measure of the tubal rank compared with TNN.

In this paper, we mainly focus on the non-convex approach for the TRPCA problem. Different from existing non-convex TRPCA models, we not only propose a non-convex approximation for the tensor tubal rank but also develop a new and suitable non-convex characterization for the sparse constraint term. The properties and advantages of the proposed two non-convex relaxations will be illustrated in Sect. 3 with more details. The main contributions of this paper are summarized as follows:

• (a) In this paper, we develop a feasible non-convex TRPCA model, in which a non-convex $e^{\gamma }$-type approximation rank function is established for a more accurate rank approximation under the tensor framework, while at the same time, a weighted $\ell _p$-norm is developed being better capture the sparsity of the noise term without requiring p to be too small.

• (b) The corresponding alternating direction method of multipliers (ADMM) is constructed to solve the optimization model, which can be divided into two sub-problems, in which two sub-problems can be solved effectively by the generalized soft-thresholding (GST) operator and local linearization minimization approach, respectively. We show that the sequence generated by the proposed algorithm converges to a KKT stationary point.

• (c) Extensive numerical experiments with several benchmark datasets are given to demonstrate the robustness and the efficiency of the proposed model, compared with some related existing approaches.

The rest of the paper is organized as follows. Related notations and definitions are given in Sect. 2. In Sect. 3, the proposed non-convex TRPCA model is presented. Meanwhile, based on the ADMM algorithm, we provide a detailed process for solving the proposed model. In Sect.  4, we analyze the convergence of the proposed algorithm. The numerical results are shown in Sect. 5. The paper ends with concluding remarks in Sect. 6.

2 Preliminaries

In this section, we first introduce some basic tensor notations used in this paper and then present the t-SVD algebraic framework. More details about tensors and the t-SVD can be found in [20, 38].

2.1 Notation

The fields of real numbers and complex numbers are denoted by ${\mathbb {R}}$ and ${\mathbb {C}}$, respectively. Throughout this paper, scalars, vectors, matrices, and tensors are denoted by lowercase letters (e.g., x), boldface lowercase letters (e.g., ${\mathbf {x}}$), boldface capital letters (e.g., ${\mathbf {X}}$), and boldface calligraphy letters (e.g., ${\mathcal {X}}$), respectively.

For a third-order tensor ${\mathcal {X}}$, its (i, j, k)-th entry is denoted by ${\mathcal {X}}(i,j,k)$ or ${\mathcal {X}}_{ijk}$. We use Matlab notations ${\mathcal {X}}(i, :, :)$, ${\mathcal {X}}(:, i, :)$, and ${\mathcal {X}}(:, :, i)$ to denote the i-th horizontal, lateral, and frontal slices of ${\mathcal {X}}$, respectively. For simplicity, ${\mathcal {X}}(:, :, i)$ is denoted by ${\mathbf {X}}_i$. The (i, j)-th tube of ${\mathcal {X}}$, denoted by the Matlab notation ${\mathcal {X}}(i,j,:)$, is a vector obtained by fixing the first two indices and varying the third one. The inner product of two same size tensors ${\mathcal {X}}, {\mathcal {Y}} \in {\mathbb {R}}^{N_1 \times N_2 \times N_3}$ is defined as $\left\langle {\mathcal {X}},{\mathcal {Y}} \right\rangle := \sum _{i=1}^{N_1} \sum _{j=1}^{N_2} \sum _{k=1}^{N_3} {\mathcal {X}}_{ijk} {\mathcal {Y}}_{ijk}$. The Frobenius norm, the $\ell _1$-norm, and the infinity norm of a third-order tensor ${\mathcal {X}}$ are defined as $\Vert {\mathcal {X}}\Vert _F :=(\sum _{i,j,k}|{\mathcal {X}}_{ijk}|^2)^{\frac{1}{2}}$, $\Vert {\mathcal {X}}\Vert _{\ell _1} :=\sum _{i,j,k}|{\mathcal {X}}_{ijk}|$, and $\Vert {\mathcal {X}} \Vert _\infty :=\max _{i,j,k}|{\mathcal {X}}_{ijk}|$, respectively.

For a third-order tensor ${\mathcal {X}}$, we use $\hat{{\mathcal {X}}} = \text{ fft } ({\mathcal {X}},[ \ ],3)$ to denote the DFT along the third dimension (by using the Matlab command fft).

It is noted that the $N_3 \times N_3$ DFT matrix ${\mathbf {F}}_{N_3}$ is not unitary, but $\tilde{{\mathbf {F}}}_{N_3} = \dfrac{1}{\sqrt{N_3}} {\mathbf {F}}_{N_3}$ is unitary. In later theoretical analysis we see that ${\mathbf {F}}_{N_3}$ may be replaced by the unitary matrix $\tilde{{\mathbf {F}}}_{N_3}$.

2.2 Review of the t-SVD

The t-SVD was first proposed by Kilmer et al. [20] and has been widely used in TC [17, 28, 35, 41, 43, 47,48,49, 51, 52], image multi-view subspace clustering [46] and TRPCA [2, 6, 29].

For a third-order tensor ${\mathcal {X}}\in {\mathbb {R}}^{N_1 \times N_2 \times N_3}$, five block-based operations bcirc($\cdot$), unfold($\cdot$), fold($\cdot$), bdiag($\cdot$) and unbdiag($\cdot$) are defined as follows:

$$\begin{aligned} {\text {bcirc}}({\mathcal {X}})= & {} \left[ \begin{array}{cccc}{\mathbf {X}}_1 &{} {\mathbf {X}}_{N_3} &{} \dots &{} {\mathbf {X}}_2 \\ {\mathbf {X}}_2 &{} {\mathbf {X}}_1 &{} \dots &{} {\mathbf {X}}_3 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {\mathbf {X}}_{N_3} &{} {\mathbf {X}}_{N_3-1} &{} \dots &{} {\mathbf {X}}_1\end{array}\right] , \\ \text{ unfold }({\mathcal {X}})= & {} \left[ \begin{array}{c}{\mathbf {X}}_1 \\ {\mathbf {X}}_2 \\ \vdots \\ {\mathbf {X}}_{N_3}\end{array}\right] , \quad \text{ fold } (\text{ unfold }({\mathcal {X}}))={\mathcal {X}}, \\ \text{ bdiag }({\mathcal {X}})= & {} \left[ \begin{array}{cccc} {\mathbf {X}}_1 &{} &{} &{} \\ &{} {\mathbf {X}}_2 &{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} {\mathbf {X}}_{N_3} \end{array}\right] , \quad \text{ unbdiag }(\text{ bdiag }({\mathcal {X}}))= {\mathcal {X}}. \end{aligned}$$

Definition 1

(t-product [20]) The t-product ${\mathcal {X}} * {\mathcal {Y}}$ of ${\mathcal {X}} \in {\mathbb {R}}^{N_1 \times N_2 \times N_3}$ and ${\mathcal {Y}} \in$ ${\mathbb {R}}^{N_2 \times N_4 \times N_3}$ is a tensor ${\mathcal {Z}} \in {\mathbb {R}}^{N_1 \times N_4 \times N_3}$ given by

$$\begin{aligned} {\mathcal {Z}}={\mathcal {X}} * {\mathcal {Y}}= {\text {fold}} ({\text {bcirc}}({\mathcal {X}}) {\text {unfold}}({\mathcal {Y}})). \end{aligned}$$

(2.1)

Remark 1

Different from direct unfolding the tensor ${\mathcal {X}}$ along the third mode, the block circulant matrix ${\text {bcirc}}({\mathcal {X}})$ of ${\mathcal {X}}$ keeps the order of frontal slices of ${\mathcal {X}}$ in a circulant way that maintains the structure of ${\mathcal {X}}$ in terms of the frontal direction.

It is well known that the circulant matrix can be diagonalized by DFT [20], Kilmer et al. gave a similar property for block-circulant matrix as follows.

Property 1

[20] For a tensor ${\mathcal {X}}\in {\mathbb {R}}^{N_1\times N_2 \times N_3}$, its block circulant matrix ${\text {bcirc}}({\mathcal {X}})$ can be block-diagonalized by DFT as follows:

$$\begin{aligned} {\text {bdiag}}(\hat{{\mathcal {X}}})=\left( \tilde{{\mathbf {F}}}_{N_3} \otimes {\mathbf {I}}_{N_1}\right) {\text {bcirc}}({\mathcal {X}}) \left( \tilde{{\mathbf {F}}}_{N_3}^{*} \otimes {\mathbf {I}}_{N_2}\right) , \end{aligned}$$

(2.2)

where $\tilde{{\mathbf {F}}}_{N_3} = \dfrac{1}{\sqrt{N_3}} {\mathbf {F}}_{N_3}$, ${\mathbf {F}}_{N_3}$ is an $N_3 \times N_3$ DFT matrix, ${\mathbf {F}}_{N_3}^{*}$ denotes its conjugate transpose, the notation $\otimes$ represents the Kronecker product, and ${\mathbf {I}}_{N}$ is an $N \times N$ identity matrix.

Remark 2

From Property 1, t-product ${\mathcal {Z}} = {\mathcal {X}} * {\mathcal {Y}}$ in (2.1) implies

$$\begin{aligned} \begin{aligned} {\text {unfold}}({\mathcal {Z}})&= {\text {bcirc}}({\mathcal {X}}) {\text {unfold}}({\mathcal {Y}}) \\&= (\tilde{{\mathbf {F}}}_{N_3}^{*} \otimes {\mathbf {I}}_{N_1}) \left( (\tilde{{\mathbf {F}}}_{N_3} \otimes {\mathbf {I}}_{N_1}) {\text {bcirc}}({\mathcal {X}}) (\tilde{{\mathbf {F}}}_{N_3}^{*} \otimes {\mathbf {I}}_{N_2})\right) \left( (\tilde{{\mathbf {F}}}_{N_3} \otimes {\mathbf {I}}_{N_2}) {\text {unfold}}({\mathcal {Y}}) \right) \\&= (\tilde{{\mathbf {F}}}_{N_3}^{*} \otimes {\mathbf {I}}_{N_1}) {\text {bdiag}}(\hat{{\mathcal {X}}}) {\text {unfold}}(\hat{{\mathcal {Y}}}). \end{aligned} \end{aligned}$$

(2.3)

Then left multiplying both sides of (2.3) by $\tilde{{\mathbf {F}}}_{N_3} \otimes {\mathbf {I}}_{N_1}$ gives

$$\begin{aligned} {\text {unfold}}(\hat{{\mathcal {Z}}}) = {\text {bdiag}}(\hat{{\mathcal {X}}}) {\text {unfold}}(\hat{{\mathcal {Y}}}). \end{aligned}$$

(2.4)

The equation (2.4) is equivalent to

$$\begin{aligned} \hat{{\mathbf {Z}}}_k = \hat{{\mathbf {X}}}_k \hat{{\mathbf {Y}}}_k, \quad k= 1, \ldots , N_3, \end{aligned}$$

(2.5)

which means the t-product (2.1) in the original domain can be computed by the matrix multiplication of the frontal slices in the Fourier domain. This greatly simplifies the computational procedure.

Remark 3

[29] Since $\tilde{{\mathbf {F}}}_{N_3} \otimes {\mathbf {I}}_{N_1}$ and $\tilde{{\mathbf {F}}}_{N_3}^{*} \otimes {\mathbf {I}}_{N_2}$ in (2.2) are unitary matrices, it follows from (2.2) that

$$\begin{aligned} \Vert {\mathcal {X}} \Vert _F^2 = \dfrac{1}{N_3} \Vert {\text {bdiag}} (\hat{{\mathcal {X}}}) \Vert _F^2. \end{aligned}$$

Definition 2

(Identity tensor and f-diagonal tensor [20]) The identity tensor ${\mathcal {I}}$ $\in$ ${\mathbb {R}}^{N_1 \times N_1 \times N_3}$ is the tensor whose first frontal slice is an identity matrix and other frontal slices are all zeros. A tensor is called f-diagonal if each frontal slice is a diagonal matrix.

Definition 3

(Tensor transpose and orthogonal tensor [20]) The transpose of a tensor ${\mathcal {X}} \in {\mathbb {R}}^{N_1 \times N_2 \times N_3}$ is the tensor ${\mathcal {X}}^T \in {\mathbb {R}}^{N_2 \times N_1 \times N_3}$ obtained by transposing each frontal slice of ${\mathcal {X}}$ and then reversing the order of transposed frontal slices 2 through $N_3$, i.e., ${\text {unfold}} ({\mathcal {X}}^T ) =[{\mathbf {X}}_1,{\mathbf {X}}_{N_3},\cdots ,{\mathbf {X}}_2]^T$. A tensor ${\mathcal {Q}} \in {\mathbb {R}}^{N_1 \times N_1 \times N_3}$ is orthogonal if it satisfies ${\mathcal {Q}} * {\mathcal {Q}}^{T}={\mathcal {Q}}^{T} * {\mathcal {Q}}={\mathcal {I}}$.

Based on the above definitions, we now restate the factorization strategy [20] for the third-order tensor.

Lemma 1

(t-SVD) For ${\mathcal {X}} \in {\mathbb {R}}^{N_1 \times N_2 \times N_3}$, the t-SVD of ${\mathcal {X}}$ is given by

$$\begin{aligned} {\mathcal {X}}={\mathcal {U}} * {\mathcal {S}} * {\mathcal {V}}^{T}, \end{aligned}$$

(2.6)

where ${\mathcal {U}} \in {\mathbb {R}}^{N_1 \times N_1 \times N_3}$, ${\mathcal {V}} \in {\mathbb {R}}^{N_2 \times N_2 \times N_3}$ are orthogonal tensors, and $S \in$ ${\mathbb {R}}^{N_1 \times N_2 \times N_3}$ is an f-diagonal tensor.

Remark 4

According to Remark 2, we have $\hat{{\mathbf {X}}}_k =\hat{{\mathbf {U}}}_k \hat{{\mathbf {S}}}_k \hat{{\mathbf {V}}}_k^T$ for $k = 1, \ldots , N_3$, where $\hat{{\mathbf {X}}}_k$, $\hat{{\mathbf {U}}}_k$, $\hat{{\mathbf {S}}}_k$ and $\hat{{\mathbf {V}}}_k$ are frontal slices of $\hat{{\mathcal {X}}}$, $\hat{{\mathcal {U}}}$, $\hat{{\mathcal {S}}}$ and $\hat{{\mathcal {V}}}$, respectively. This means the t-SVD can be obtained by computing several matrix SVDs in the Fourier domain.

Definition 4

(Tensor tubal rank [21]) Given a tensor ${\mathcal {X}} \in {\mathbb {R}}^{N_1 \times N_2 \times N_3}$, its tubal rank is defined as the number of nonzero singular tubes of the f-diagonal tensor ${\mathcal {S}}$, i.e.,

$$\begin{aligned} {\text {rank}}_t ({\mathcal {X}})= \# \left\{ i, {\mathcal {S}}(i,i,:) \ne 0 \right\} , \end{aligned}$$

(2.7)

where ${\mathcal {S}}$ comes from the t-SVD of ${\mathcal {X}} = {\mathcal {U}} * {\mathcal {S}} * {\mathcal {V}}^{T}$ and the notation “$\#$” denotes the cardinality of a set.

Definition 5

(T-SVD based TNN [29]) The TNN of ${\mathcal {X}}\in {\mathbb {R}}^{N_1 \times N_2 \times N_3}$ is given by

$$\begin{aligned} \begin{aligned} \Vert {\mathcal {X}}\Vert _{*} = \frac{1}{N_3}\sum _{k=1}^{N_3} \Vert \hat{{\mathbf {X}}}_{k}\Vert _{*} = \frac{1}{N_3}\sum _{k=1}^{N_3} \sum _{i=1}^{\min \left\{ N_1, N_2\right\} } \sigma _i (\hat{{\mathbf {X}}}_{k} ), \end{aligned} \end{aligned}$$

(2.8)

where $\sigma _i ( \hat{{\mathbf {X}}}_{k} )$ is the i-th singular value of matrix $\hat{{\mathbf {X}}}_{k}$ and $\sigma _1 (\hat{{\mathbf {X}}}_{k} ) \ge \cdots \ge \sigma _{\min \left\{ N_1, N_2\right\} } (\hat{{\mathbf {X}}}_{k} )$ for all $k = 1,\ldots , N_3$.

3 The TRPCA Model and Algorithms

In this section, we first give the motivation and then propose a non-convex TRPCA model based on some non-convex functions. Finally, an algorithm for solving the model is established.

3.1 Motivation

• Motivation for the low rank part:

In this paper, to overcome the disadvantages of the model (1.2), we propose to use a non-convex but smooth $e^{\gamma }$-type function to approximate the tensor tubal rank. The $e^{\gamma }$-type function used in [37] is for the matrix rank approximation, and we will adopt it under t-SVD framework for tensor rank approximation. The $e^{\gamma }$-type function is given by

$$\begin{aligned} \phi (x)= \dfrac{e^{\gamma }x}{\gamma +x}, \quad x \in [0,+\infty ), \end{aligned}$$

(3.1)

where $\gamma$ is a positive parameter. It can be seen that $\phi$ is a smooth, monotonously increasing and concave function. Using the $e^{\gamma }$-type function $\phi (x)$, a non-convex surrogate for an $M \times N$ matrix ${\mathbf {X}}$ is given by [37]:

$$\begin{aligned} \Vert {\mathbf {X}}\Vert _{e^{\gamma }}:= \sum _{i=1}^{\min \left\{ M,N\right\} } \phi ( \sigma _i({\mathbf {X}})), \quad \gamma > 0, \end{aligned}$$

(3.2)

where $\sigma _i({\mathbf {X}})$ is the i-th singular value of ${\mathbf {X}}$ and $\sigma _1({\mathbf {X}}) \ge \cdots \ge \sigma _{\min \left\{ M,N\right\} } ({\mathbf {X}})$. For a third-order tensor ${\mathcal {X}}\in {\mathbb {R}}^{N_1\times N_2 \times N_3}$, we define a non-convex surrogate for the tubal rank as

$$\begin{aligned} \Vert {\mathcal {X}}\Vert _{t-e^{\gamma }}:=\frac{1}{N_3}\sum _{k=1}^{N_3}\Vert \hat{{\mathbf {X}}}_{k}\Vert _{e^{\gamma }}, \quad \gamma >0, \end{aligned}$$

(3.3)

where $\hat{{\mathbf {X}}}_{k}$ is the k-th frontal slice of $\hat{{\mathcal {X}}}=\text {fft}({\mathcal {X}},[ \ ],3)=[\hat{{\mathbf {X}}}_{1}| \cdots | \hat{{\mathbf {X}}}_{N_3}]$ obtained by applying FFT on ${\mathcal {X}}$ along the third mode.

Now we explain why we adopt the $e^{\gamma }$-type function as the non-convex surrogate for the tubal rank. We randomly select twenty color images from Berkeley Segmentation Dataset (BSD) [33], the size of each image is $321 \times 481 \times 3$ or $481 \times 321 \times 3$. For each image, in Fig. 1a, we show the comparison of associated results coming from the tensor tubal rank given by (2.7), the TNN given by (2.8), and the $e^{\gamma }$-type approximation rank ($\gamma =1.1$) given by (3.3). We also illustrate the distance between $\Vert \cdot \Vert _{t-e^{\gamma }}$, $\Vert \cdot \Vert _{*}$ and the tubal rank for each image in Fig. 1b. It can be seen from Fig. 1 that the result obtained by (3.3) gives a tighter approximation to the tensor tubal rank than that obtained by the TNN for each image. The above comparison indicates that our proposed non-convex surrogate (3.3) is a more accurate approximation of the tensor tubal rank.

Fig. 1

Comparison (3.3) with (2.7) and (2.8)

The $e^{\gamma }$-type non-convex rank approximation function (3.3) has the following property.

Property 2

Let ${\mathcal {X}}\in {\mathbb {R}}^{N_1 \times N_2 \times N_3}$. The $e^{\gamma }$-type rank surrogate function (3.3) is unitarily invariant, i.e., $\Vert {\mathcal {U}}* {\mathcal {X}} * {\mathcal {V}}^T \Vert _{t-e^{\gamma }} = \Vert {\mathcal {X}}\Vert _{t-e^{\gamma }}$, where ${\mathcal {U}}\in {\mathbb {R}}^{N_1 \times N_1 \times N_3}$ and ${\mathcal {V}}\in {\mathbb {R}}^{N_2 \times N_2 \times N_3}$ are orthogonal tensors. In addition, $\lim _{\gamma \rightarrow 0} \Vert {\mathcal {X}}\Vert _{t-e^{\gamma }}= {\text {rank}}_t \left( {\mathcal {X}}\right)$.

Proof

The proof of $\lim _{\gamma \rightarrow 0} \Vert {\mathcal {X}}\Vert _{t-e^{\gamma }}= {\text {rank}}_t \left( {\mathcal {X}}\right)$ is straightforward, we omit it here. Now we show that the $e^{\gamma }$-type rank surrogate function (3.3) is unitarily invariant.

Let ${\mathcal {Z}} \in {\mathbb {R}}^{n\times n \times m}$ be an orthogonal tensor. We first show that all frontal slices $\hat{{\mathbf {Z}}}_k$ $(k = 1,\ldots ,m)$ of $\hat{{\mathcal {Z}}}$ are orthogonal matrices. Since ${\mathcal {Z}} * {\mathcal {Z}}^T = {\mathcal {Z}}^T * {\mathcal {Z}} = {\mathcal {I}},$ it follows from Remark 2 that $\hat{{\mathbf {Z}}}_k \hat{{\mathbf {Z}}}_k^T = \hat{{\mathbf {Z}}}_k^T \hat{{\mathbf {Z}}}_k = \hat{{\mathbf {I}}}_k$ for $k = 1,\ldots ,m$. Because ${\mathcal {I}}$ is an identity tensor, according to the property of the Fourier transform, it is easy to see that $\hat{{\mathbf {I}}}_k$ is an identity matrix for $k=1,\ldots ,m$. Hence, $\hat{{\mathbf {Z}}}_k$ is an orthogonal matrix for $k=1,\ldots ,m$.

According to Remark 2 and (3.3), we have

$$\begin{aligned} \Vert {\mathcal {U}}* {\mathcal {X}} * {\mathcal {V}}^T \Vert _{t-e^{\gamma }} = \frac{1}{N_3}\sum _{k=1}^{N_3} \Vert \hat{{\mathbf {U}}}_k \hat{{\mathbf {X}}}_k \hat{{\mathbf {V}}}_k^T \Vert _{e^{\gamma }}. \end{aligned}$$

(3.4)

Since ${\mathcal {U}}$ and ${\mathcal {V}}$ are orthogonal tensors, it follows that $\hat{{\mathbf {U}}}_k$ and $\hat{{\mathbf {V}}}_k$ are orthogonal matrices for $k = 1,\ldots , N_3$. Therefore, by (3.2) and (3.3) we have

$$\begin{aligned} \frac{1}{N_3}\sum _{k=1}^{N_3} \Vert \hat{{\mathbf {U}}}_k \hat{{\mathbf {X}}}_k \hat{{\mathbf {V}}}_k^T \Vert _{e^{\gamma }} = \frac{1}{N_3}\sum _{k=1}^{N_3} \Vert \hat{{\mathbf {X}}}_k \Vert _{e^{\gamma }} = \Vert {\mathcal {X}}\Vert _{t-e^{\gamma }}. \end{aligned}$$

This proves the conclusion. $\square$

• Motivation for the sparse constraint term:

It is well known that the $\ell _0$-norm in the sparse constraint term is usually relaxed by using the $\ell _1$-norm due to its simplicity. The obtained solution by the $\ell _1$-norm minimization is often suboptimal to the original $\ell _0$-norm minimization since the $\ell _1$-norm is a coarse approximation of the $\ell _0$-norm. Some non-convex surrogates of $\ell _0$-norm have been applied in the fields of signal and image processing to find the sparsest solution (see e.g., [5, 44]), but the non-convex surrogates of $\ell _0$-norm in the sparse constraint term in tensor case have not been well studied. Recently, $\ell _p$-norm ($0<p<1$) was proposed to as an approximation for the $\ell _0$-norm by using small positive p in TRPCA problem [6]. Numerical tests given by [6] showed that non-convex $\ell _p$-norm outperformed $\ell _1$-norm. However, small p will lead to the insensitivity to tensor elements, for example, $1000^p \approx 0.1^p$ when p is small enough, and larger elements will be misclassified as small entries in later optimization process (e.g., see Step 1 of (3.8)). Inspired by the idea that sparsity enhancement by using the weighted $\ell _1$-norm minimization in signal recovery [3, 50], we propose to use the weighted $\ell _p$-norm as the non-convex relaxation of the $\ell _0$-norm. Given a tensor ${\mathcal {X}} \in {\mathbb {R}}^{N_1 \times N_2 \times N_3}$, the weighted $\ell _p$-norm for ${\mathcal {X}}$ is given by

$$\begin{aligned} \Vert {\mathcal {X}} \Vert _{{\mathcal {W}},\ell _p} := \left( \sum _{i,j,k}\left( {\mathcal {W}}_{ijk} |{\mathcal {X}}_{ijk}|\right) ^p \right) ^{\frac{1}{p}}, \quad 0<p<1, \end{aligned}$$

(3.5)

where ${\mathcal {W}}$ is a nonnegative weight tensor. It is not difficult to see

$$\begin{aligned} \lim _{p \rightarrow 1} \lim _{\epsilon \rightarrow 0} \lim _{{\mathcal {W}}_{ijk} \rightarrow \frac{1}{|{\mathcal {X}}_{ijk}| +\epsilon } } \Vert {\mathcal {X}} \Vert _{{\mathcal {W}},\ell _p} = \Vert {\mathcal {X}}\Vert _0. \end{aligned}$$

This clearly implies that the introduction of the weighted $\ell _p$-norm (3.5) can allow p not necessarily to be too small but maintain the sparse characteristics.

3.2 The Proposed Model

Equipped with the two non-convex surrogates given by (3.3) and (3.5), we establish the following non-convex TRPCA model:

$$\begin{aligned} \begin{aligned} \min _{{\mathcal {L}},{\mathcal {E}}} \Vert {\mathcal {L}}\Vert _{t-e^{\gamma }} + \lambda \Vert {\mathcal {E}}\Vert _{{\mathcal {W}},\ell _p}^{p}, \quad \mathrm {s.t.} \quad {\mathcal {X}}={\mathcal {L}}+{\mathcal {E}}, \end{aligned} \end{aligned}$$

(3.6)

where the weight tensor ${\mathcal {W}}$ will be updated in each iteration and the (i, j, k)-th entry of ${\mathcal {W}}$ in the $(k+1)$-th iteration is $\dfrac{1}{|{\mathcal {E}}_{ijk}^{(k)}|+\epsilon }$, here ${\mathcal {E}}_{ijk}^{(k)}$ is the (i, j, k)-th entry of ${\mathcal {E}}$ in the k-th iteration and $\epsilon$ is a small positive constant.

We develop the ADMM to solve the proposed model (3.6). The augmented Lagrange function of (3.6) is given by

$$\begin{aligned} \begin{aligned} L_{\beta }({\mathcal {L}},{\mathcal {E}},{\mathcal {M}})&= \left\| {\mathcal {L}}\right\| _{t-e^{\gamma }} + \lambda \left\| {\mathcal {E}} \right\| _{{\mathcal {W}},\ell _p}^{p} -\left\langle {\mathcal {X}}-{\mathcal {L}}-{\mathcal {E}}, {\mathcal {M}} \right\rangle + \frac{\beta }{2} \left\| {\mathcal {X}}-{\mathcal {L}}-{\mathcal {E}}\right\| _{F}^{2}\\&= \left\| {\mathcal {L}}\right\| _{t-e^{\gamma }} + \lambda \left\| {\mathcal {E}}\right\| _{{\mathcal {W}},\ell _p}^{p}+\frac{\beta }{2}\Vert {\mathcal {X}}-{\mathcal {L}}-{\mathcal {E}}-\frac{{\mathcal {M}}}{\beta }\Vert _{F}^{2}-\frac{1}{2\beta }\left\langle {\mathcal {M}},{\mathcal {M}} \right\rangle , \end{aligned} \end{aligned}$$

(3.7)

where ${\mathcal {M}}$ is the Lagrange multiplier and $\beta$ is the penalty parameter. According to the framework of ADMM, ${\mathcal {L}}$, ${\mathcal {E}}$, and ${\mathcal {M}}$ are alternately updated as:

$$\begin{aligned} {\left\{ \begin{array}{ll} Step \ 1: {\mathcal {E}}_{k+1}=\underset{{\mathcal {E}}}{\arg \min } \lambda \Vert {\mathcal {E}}\Vert _{{\mathcal {W}}_k,\ell _p}^{p}+\dfrac{\beta _k}{2}\Vert {\mathcal {B}}_k-{\mathcal {E}}\Vert _{F}^{2} \quad \text {with} \quad {\mathcal {B}}_k = {\mathcal {X}}-{\mathcal {L}}_{k}-\dfrac{{\mathcal {M}}_k}{\beta _k},\\ Step \ 2: {\mathcal {L}}_{k+1} =\underset{{\mathcal {L}}}{\arg \min } \dfrac{1}{\beta _k} \Vert {\mathcal {L}} \Vert _{t-e^{\gamma }} +\dfrac{1}{2} \Vert {\mathcal {A}}_k -{\mathcal {L}} \Vert _{F}^{2} \quad \text {with} \quad {\mathcal {A}}_k = {\mathcal {X}}-{\mathcal {E}}_{k+1}-\dfrac{{\mathcal {M}}_k}{\beta _k}, \\ Step \ 3: {\mathcal {M}}_{k+1}={\mathcal {M}}_k + \beta _k ({\mathcal {L}}_{k+1}+{\mathcal {E}}_{k+1}-{\mathcal {X}}). \end{array}\right. } \end{aligned}$$

(3.8)

1) Update ${\mathcal {E}}$: Before giving the solution of Step 1, we take a look at the $\ell _p$-norm minimization problem for scalars which was given in [54].

Lemma 2

[54] For the given p $(0<p<1)$ and $\lambda >0$, an optimal solution of the following optimization problem

$$\begin{aligned} \underset{x}{\arg \min } \frac{1}{2}(y-x)^2+\lambda |x|^p \end{aligned}$$

(3.9)

is given by the generalized soft-thresholding (GST) operator, which is defined as

$$\begin{aligned} GST(y,\lambda ,p) = {\left\{ \begin{array}{ll} 0, &{} \text{ if } |y| \le \tau _p^{GST}(\lambda ), \\ {\text {sgn}}(y) \cdot S_p^{GST}(y,\lambda ), &{} \text{ if } |y|>\tau _p^{GST}(\lambda ), \end{array}\right. } \end{aligned}$$

where ${\text {sgn}}(y)$ denotes the signum function, $\tau _p^{GST}(\lambda )= \left( 2\lambda (1-p)\right) ^{\frac{1}{2-p}}+\lambda p \left( 2\lambda (1-p)\right) ^{\frac{p-1}{2-p}}$ is a threshold value, and $S_p^{GST}(y,\lambda )$ can be obtained by solving the following equation

$$\begin{aligned} S_p^{GST}(y,\lambda )-y+\lambda p (S_p^{GST}(y,\lambda ))^{p-1}=0. \end{aligned}$$

(3.10)

The iterative algorithm for solving (3.9) is summarized in Algorithm 1 [54].

According to Step 1, the $(k+1)$-th iteration is

$$\begin{aligned} {\mathcal {E}}_{ijk}^{(k+1)}=\underset{{\mathcal {E}}_{ijk}}{\arg \min } \lambda \left( {\mathcal {W}}_{ijk}^{(k)} |{\mathcal {E}}_{ijk}|\right) ^p +\dfrac{\beta _k}{2} \left( b_{ijk}^{(k)} -{\mathcal {E}}_{ijk} \right) ^2. \end{aligned}$$

From Lemma 2, the solution with respect to ${\mathcal {E}}_{k+1}$ is given by

$$\begin{aligned} \text{ GST } \left( {\mathcal {B}}_k, \dfrac{\lambda {\mathcal {W}}_k^p }{\beta _k},p \right) , \end{aligned}$$

(3.11)

where ${\mathcal {W}}_k^p$ is a weight tensor whose (i, j, k)-th entry is $\left( \dfrac{1}{|{\mathcal {E}}_{ijk}^{(k)}|+\epsilon } \right) ^p$, $\epsilon$ is a small positive constant.

2) Update ${\mathcal {L}}$: We first give the global convergence results for the descent algorithm [30], which will be used to analyze the convergence of the fixed point inner iteration in Theorem 1.

Lemma 3

(Global Convergent Theorem in Chapter 7.7 of [30]) Let A be an algorithm on a real finite-dimensional metric space X and suppose that, for a given $x_{0},$ the sequence $\left\{ x_{k}\right\} _{k=0}^{\infty }$ is generated by $x_{k+1} \in A\left( x_{k}\right) .$ Let a solution set $\Gamma \subset$ X be given and suppose

• (i) all points $x_{k}$ are contained in a compact set $S \subset X$,

• (ii) there is a continuous function Z on X such that if $x \notin \Gamma$ then $Z(y)<Z(x)$ for all $y \in A(x) ;$ if $x \in \Gamma$ then $Z(y) \le Z(x)$ for all $y \in A(x)$,

• (iii) the mapping A is closed at points outside $\Gamma$,

then the limit of any convergent subsequence of $x_{k}$ is a solution.

The solution of the ${\mathcal {L}}$-subproblem is given by the following theorem.

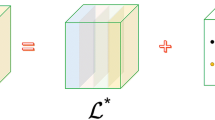
Theorem 1

Let ${\mathcal {A}}_k ={\mathcal {U}}_k*\Sigma _k * {\mathcal {V}}_k^{T}$ be the t-SVD of ${\mathcal {A}}_k \in {\mathbb {R}}^{N_1 \times N_2 \times N_3}$. Then an optimal solution of the following minimization

$$\begin{aligned} \underset{{\mathcal {L}}}{\arg \min } \frac{1}{2}\Vert {\mathcal {A}}_k-{\mathcal {L}}\Vert _{F}^{2}+\tau \Vert {\mathcal {L}}\Vert _{t-e^{\gamma }}, \end{aligned}$$

(3.12)

is given by $\mathcal {L^*}={\mathcal {U}}_k*{\mathcal {S}}_{k} * {\mathcal {V}}_{k}^{T}$, where ${\mathcal {S}}_{k} \in {\mathbb {R}}^{N_1 \times N_2 \times N_3}$ is an f-diagonal tensor and $\tau = \frac{1}{\beta _k}$. And let ${\hat{\Sigma }}_k=[{\hat{\Sigma }}_{n,n,i}^{(k)}]={\text {fft}}(\Sigma _k,[ \ ],3)$, $\hat{{\mathcal {S}}}_{k}= [{\hat{S}}_{n,n,i}^{(k)}] = {\text {fft}}({\mathcal {S}}_{k},[ \ ],3),$ $1\le n \le \min \left\{ N_1,N_2\right\} ,$ $1\le i \le N_3$. Then ${\hat{S}}_{n,n,i}^{(k)}$ is the limit point of the following fixed point inner iteration

$$\begin{aligned} {\hat{S}}_{n,n,i}^{(k,l+1)}=\left( {\hat{\Sigma }}_{n,n,i}^{(k)}-\tau \dfrac{\gamma e^{\gamma }}{(\gamma +{\hat{S}}_{n,n,i}^{(k,l)})^2} \right) _{+}, \end{aligned}$$

(3.13)

where $(x)_{+}=\max \left\{ x,0 \right\}$ and ${\hat{S}}_{n,n,i}^{(0,0)} = 0$.

Proof

According to the Remark 3 and (3.3), the optimization problem (3.12) is equivalent to

$$\begin{aligned} \begin{aligned}&\underset{\hat{{\mathbf {L}}}_{k,i}}{\arg \min } \dfrac{1}{N_3} \left( \sum _{i=1}^{N_3} \left( \frac{1}{2} \Vert \hat{{\mathbf {A}}}_{k,i}-\hat{{\mathbf {L}}}_{k,i}\Vert _F^2 + \tau \Vert \hat{{\mathbf {L}}}_{k,i} \Vert _{e^{\gamma }} \right) \right) \end{aligned} \end{aligned}$$

$$\begin{aligned} \Leftrightarrow \underset{\hat{{\mathbf {L}}}_{k,i}}{\arg \min } \frac{1}{2} \Vert \hat{{\mathbf {A}}}_{k,i}-\hat{{\mathbf {L}}}_{k,i}\Vert _F^2 + \tau \Vert \hat{{\mathbf {L}}}_{k,i}\Vert _{e^{\gamma }}, \quad i = 1,\ldots , N_3, \end{aligned}$$

(3.14)

where $\hat{{\mathbf {A}}}_{k,i}$ and $\hat{{\mathbf {L}}}_{k,i}$ denote the i-th frontal slice of $\hat{{\mathcal {A}}}_k$ and $\hat{{\mathcal {L}}}_k$, respectively. That is to say, the tensor optimization problem (3.12) in original domain is transformed to $N_3$ matrix optimization problems (3.14) in Fourier domain.

Since ${\mathcal {A}}_k = {\mathcal {U}}_k * \Sigma _k * {\mathcal {V}}_k^T$, by Remark 4, we have $\hat{{\mathbf {A}}}_{k,i} = \hat{{\mathbf {U}}}_{k,i} \hat{{\varvec{\Sigma }}}_{k,i} \hat{{\mathbf {V}}}_{k,i}^T$ for $i=1,\ldots ,N_3$. If $\hat{{\mathbf {L}}}_{i}^{*}$ minimize (3.14), by the von Neumann trace inequality for singular values (see Theorem 1 of [18]), we have

$$\begin{aligned} \hat{{\mathbf {L}}}_i^{*}=\hat{{\mathbf {U}}}_{k, i} \hat{{\mathbf {S}}}_{k, i} \hat{{\mathbf {V}}}_{k,i}^T, \quad i=1,\ldots ,N_3 , \end{aligned}$$

(3.15)

where $\hat{{\mathbf {S}}}_{k, i}= [{\hat{S}}_{n,n,i}^{(k)}]$ is the i-th frontal slice of $\hat{{\mathcal {S}}}_{k}$, and

$$\begin{aligned} {\hat{S}}_{n,n,i}^{(k)}=\underset{\sigma \ge 0}{\arg \min } \frac{1}{2}(\sigma -{\hat{\Sigma }}_{n,n,i}^{(k)})^2+\tau \dfrac{e^{\gamma }\sigma }{\gamma +\sigma }. \end{aligned}$$

(3.16)

Since the objective function in (3.16) is a combination of concave and convex functions, following the DC programming algorithm [10, 18], we use a local minimization method to solve it. That is to say, we iteratively optimize (3.16) by linearizing the concave term $\phi (\sigma )=\dfrac{e^{\gamma }\sigma }{\gamma +\sigma }$ at each iteration, i.e., for the l-th inner iteration, we use the following first-order Taylor expansion (with Big “O” truncation error) to approximate $\phi (\sigma )$:

$$\begin{aligned} \phi (\sigma )=\phi ({\hat{S}}_{n,n,i}^{(k,l)})+\dfrac{\gamma e^{\gamma }}{(\gamma +{\hat{S}}_{n,n,i}^{(k,l)})^2}(\sigma -{\hat{S}}_{n,n,i}^{(k,l)})+O((\sigma -{\hat{S}}_{n,n,i}^{(k,l)})^{2}), \end{aligned}$$

where ${\hat{S}}_{n,n,i}^{(k,l)}$ is the solution of (3.16) obtained in the l-th inner iteration and ${\hat{S}}_{n,n,i}^{(0,0)} = 0$. Therefore, (3.16) can be solved by iteratively solving the following optimization problem:

$$\begin{aligned} {\hat{S}}_{n,n,i}^{(k,l+1)}=\underset{\sigma >0}{\arg \min } \frac{1}{2}(\sigma -{\hat{\Sigma }}_{n,n,i}^{(k)})^2+\tau \dfrac{\gamma e^{\gamma }}{(\gamma +{\hat{S}}_{n,n,i}^{(k,l)})^2} |\sigma |. \end{aligned}$$

(3.17)

According to the soft-thresholding operator [9], (3.17) has a closed-form solution

$$\begin{aligned} {\hat{S}}_{n,n,i}^{(k,l+1)}=\left( {\hat{\Sigma }}_{n,n,i}^{(k)}-\tau \dfrac{\gamma e^{\gamma }}{(\gamma +{\hat{S}}_{n,n,i}^{(k,l)})^2} \right) _{+}. \end{aligned}$$

Let

$$\begin{aligned} g({\hat{S}}_{n,n,i}) = \left( {\hat{\Sigma }}_{n,n,i}^{(k)}-\tau \dfrac{\gamma e^{\gamma }}{(\gamma +{\hat{S}}_{n,n,i})^2} \right) _{+}, \quad 0\le {\hat{S}}_{n,n,i}<{\hat{\Sigma }}_{n,n,i}^{(k)}. \end{aligned}$$

Since $\phi (\sigma )$ is concave in $\sigma$, at each iteration its value decreases by an amount more than the decrease in the value of the linearized objective function. Following Lemma 3, the iteration ${\hat{S}}_{n,n,i}^{(k,l+1)} = g({\hat{S}}_{n,n,i}^{(k,l)} )$ converges to the local minimum ${\hat{S}}_{n,n,i}^{(k)}$ after a number of iterations. We thus complete the proof. $\square$

By summarizing the aforementioned solving process, we show the pseudocode of the developed ADMM algorithm for solving Model (3.6) in Algorithm 2.

3.3 Computational Complexity

Suppose that after finite iterations, we can get optimal solutions of the fixed point iterations (3.10) and (3.13), respectively. Then the computation cost of the proposed algorithm mainly lies in updating ${\mathcal {L}}$. To update ${\mathcal {L}}$, in each iteration, we need to compute the FFT along the third mode, calculate singular values of all frontal slices by using SVD, and compute the inverse FFT along the third mode.

As we all know, for an $M_1\times M_2$ matrix, the computational complexity of the SVD is $O(M_1M_2\min \left\{ M_1,M_2\right\} )$; the computational complexity of the FFT on an M-dimension vector is $O(M\log (M))$.

Given an observed tensor ${\mathcal {X}} \in {\mathbb {R}}^{N_1 \times N_2 \times N_3}$. To update ${\mathcal {L}}\in {\mathbb {R}}^{N_1 \times N_2 \times N_3}$, we first calculate $\hat{{\mathcal {L}}}= \text {fft}({\mathcal {L}},[ \ ], 3)$ along the third mode and the computational complexity of this process is $O(N_1N_2N_3\log (N_3))$; then we compute the SVD of matrices $\hat{{\mathbf {L}}}_i \in {\mathbb {R}}^{N_1 \times N_2} (i = 1, \ldots , N_3)$ in the Fourier domain and it will take $O(N_1N_2N_3\min \left\{ N_1,N_2\right\} )$; finally, calculating ${\mathcal {L}}= \text {ifft}(\hat{{\mathcal {L}}},[ \ ], 3)$ along the third mode will take $O(N_1N_2N_3\log (N_3))$. In summary, in each iteration, the total computational complexity of the proposed Algorithm is $O(2N_1N_2N_3\log (N_3)+N_1N_2N_3\min \left\{ N_1,N_2\right\} )$. For simplicity, if $N_1 \approx N_2 \approx N_3 = N$, the cost in each iteration is $O(N^4)$.

4 Convergence Analysis of the Proposed Algorithm

In this section, we provide a theoretical guarantee for the convergence of the developed ADMM Algorithm 2. Before giving the convergence analysis, we first show that the sequences $\{{\mathcal {L}}_k \}$, $\{{\mathcal {E}}_k \}$, $\{{\mathcal {M}}_k \}$ generated by Algorithm 2 are bounded.

Lemma 4

The sequence $\{{\mathcal {M}}_k \}$ generated by Algorithm 2 is bounded.

Proof

According to (3.8), at the $(k+1)$-th iteration, we have

$$\begin{aligned} \Vert {\mathcal {M}}_{k+1}\Vert _F^2&=\Vert {\mathcal {M}}_k+\beta _k\left( {\mathcal {L}}_{k+1}+{\mathcal {E}}_{k+1}-{\mathcal {X}}\right) \Vert _F^2 \nonumber \\&=\beta _k^2 \Vert \frac{1}{\beta _k}{\mathcal {M}}_k+{\mathcal {L}}_{k+1}+{\mathcal {E}}_{k+1}-{\mathcal {X}}\Vert _F^2 \nonumber \\&= \beta _k^2 \Vert {\mathcal {A}}_k-{\mathcal {L}}_{k+1}\Vert _F^2 \nonumber \\&= \frac{\beta _k^2}{N_3} \sum _{i=1}^{N_3} \Vert \hat{{\mathbf {A}}}_{k,i} - \hat{{\mathbf {L}}}_{k+1,i} \Vert _F^2 \nonumber \\&= \frac{\beta _k^2}{N_3} \sum _{i=1}^{N_3} \Vert \hat{{\mathbf {U}}}_{k,i} \left( \hat{{\varvec{\Sigma }}}_{k,i} - \hat{{\mathbf {S}}}_{k,i} \right) \hat{{\mathbf {V}}}_{k,i}^T \Vert _F^2\nonumber \\&= \frac{\beta _k^2}{N_3} \sum _{i=1}^{N_3} \Vert \hat{{\varvec{\Sigma }}}_{k,i} - \hat{{\mathbf {S}}}_{k,i}\Vert _F^2 \nonumber \\&= \frac{\beta _k^2}{N_3} \sum _{i=1}^{N_3} \sum _{n=1}^{\min \left\{ N_1,N_2\right\} } \left( {\hat{\Sigma }}_{n,n,i}^{(k)} - {\hat{S}}_{n,n,i}^{(k)}\right) ^2, \end{aligned}$$

(4.1)

where the fourth equality holds due to Remark 3, the fifth one follows from Theorem 1, the sixth one holds due to the unitary invariance of the Frobenius norm.

Recall (3.16) in Theorem 1

$$\begin{aligned} {\hat{S}}_{n,n,i}^{(k)}=\underset{\sigma \ge 0}{\arg \min } \frac{1}{2}(\sigma -{\hat{\Sigma }}_{n,n,i}^{(k)})^2+\tau \dfrac{e^{\gamma }\sigma }{\gamma +\sigma }, \end{aligned}$$

we thus get the following KKT conditions:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\left( {\hat{S}}_{n,n,i}^{(k)}-{\hat{\Sigma }}_{n,n,i}^{(k)} \right) +\tau \dfrac{e^{\gamma }\gamma }{\left( \gamma +{\hat{S}}_{n,n,i}^{(k)}\right) ^2}-\mu =0, \\ &{}\mu \cdot {\hat{S}}_{n,n,i}^{(k)} = 0,\\ &{} {\hat{S}}_{n,n,i}^{(k)} \ge 0, \\ &{} \mu \ge 0, \\ \end{array}\right. } \end{aligned}$$

(4.2)

where $\mu$ is the Lagrange multiplier.

If $\mu = {\hat{S}}_{n,n,i}^{(k)} =0$, we have

$$\begin{aligned} \left( {\hat{S}}_{n,n,i}^{(k)} - {\hat{\Sigma }}_{n,n,i}^{(k)} \right) ^2 = \left( {\hat{\Sigma }}_{n,n,i}^{(k)} \right) ^2 = \left( \tau \dfrac{e^{\gamma }\gamma }{\left( \gamma +{\hat{S}}_{n,n,i}^{(k)}\right) ^2} \right) ^2 \le \dfrac{(\tau e^{\gamma })^2}{\gamma ^2}. \end{aligned}$$

If $\mu = 0$, ${\hat{S}}_{n,n,i}^{(k)} \ne 0$, we have

$$\begin{aligned} \left( {\hat{S}}_{n,n,i}^{(k)} - {\hat{\Sigma }}_{n,n,i}^{(k)} \right) ^2 = \left( \tau \dfrac{e^{\gamma }\gamma }{\left( \gamma +{\hat{S}}_{n,n,i}^{(k)}\right) ^2} \right) ^2 \le \dfrac{(\tau e^{\gamma })^2}{\gamma ^2}. \end{aligned}$$

If $\mu \ne 0$, ${\hat{S}}_{n,n,i}^{(k)} = 0$, then $\left( -{\hat{\Sigma }}_{n,n,i}^{(k)} \right) +\tau \dfrac{e^{\gamma }}{\gamma }-\mu =0.$ This means ${\hat{\Sigma }}_{n,n,i}^{(k)} =\tau \dfrac{e^{\gamma }}{\gamma }-\mu \le \dfrac{\tau e^{\gamma }}{\gamma }$ due to $\gamma$, $\tau$, $\mu$ are positive numbers. Noting that ${\hat{\Sigma }}_{n,n,i}^{(k)}$ is the n-th singular value of $\hat{{\mathbf {A}}}_{k,i}$, then $0 \le {\hat{\Sigma }}_{n,n,i}^{(k)} \le \dfrac{\tau e^{\gamma }}{\gamma }$ holds for all $i=1,\ldots ,N_3$ and $n=1,\ldots , \min \left\{ N_1,N_2\right\}$. That is to say, in this case, $\left( {\hat{\Sigma }}_{n,n,i}^{(k)} \right) ^2$ has an upper bound $\dfrac{(\tau e^{\gamma })^2}{\gamma ^2}$.

As discussed above, we always have $\left( {\hat{\Sigma }}_{n,n,i}^{(k)}- {\hat{S}}_{n,n,i}^{(k)} \right) ^2 \le \dfrac{(\tau e^{\gamma })^2}{\gamma ^2}.$ This implies that (4.1) has an upper bound

$$\begin{aligned} \frac{\beta _k^2}{N_3} \sum _{i=1}^{N_3} \sum _{n=1}^{\min \left\{ N_1,N_2\right\} } \dfrac{(\tau e^{\gamma })^2}{\gamma ^2} = \min \left\{ N_1,N_2\right\} \cdot \dfrac{e^{2\gamma }}{\gamma ^2}, \end{aligned}$$

which proves the lemma. $\square$

Lemma 5

Both sequences $\{{\mathcal {L}}_k \}$ and $\{{\mathcal {E}}_k \}$ generated by Algorithm 2 are bounded.

Proof

According to (3.7) and Step 3 in (3.8), we have

$$\begin{aligned}&L_{\beta _{k}}\left( {\mathcal {L}}_{k}, {\mathcal {E}}_{k}, {\mathcal {M}}_{k}\right) \nonumber \\&\quad =L_{\beta _{k-1}}\left( {\mathcal {L}}_{k}, {\mathcal {E}}_{k}, {\mathcal {M}}_{k-1}\right) \nonumber \\&\quad \quad +\frac{\beta _{k}-\beta _{k-1}}{2}\Vert {\mathcal {L}}_{k}+{\mathcal {E}}_{k}-{\mathcal {X}}\Vert _{F}^{2}+ \beta _{k-1} \Vert {\mathcal {X}}-{\mathcal {L}}_{k}-{\mathcal {E}}_{k}\Vert _{F}^{2} \nonumber \\&\quad =L_{\beta _{k-1}}\left( {\mathcal {L}}_{k}, {\mathcal {E}}_{k}, {\mathcal {M}}_{k-1}\right) +\frac{\beta _{k}+\beta _{k-1}}{2\left( \beta _{k-1}\right) ^{2}}\Vert {\mathcal {M}}_{k}-{\mathcal {M}}_{k-1}\Vert _{F}^{2}. \end{aligned}$$

(4.3)

Since

$$\begin{aligned} {\mathcal {E}}_{k+1}= & {} \underset{{\mathcal {E}}}{\arg \min } L_{\beta _{k}}\left( {\mathcal {L}}_{k}, {\mathcal {E}}, {\mathcal {M}}_{k}\right) , \\ {\mathcal {L}}_{k+1}= & {} \underset{{\mathcal {L}}}{\arg \min } L_{\beta _{k}}\left( {\mathcal {L}}, {\mathcal {E}}_{k+1}, {\mathcal {M}}_{k}\right) , \end{aligned}$$

we have

$$\begin{aligned}&L_{\beta _{k}}\left( {\mathcal {L}}_{k+1}, {\mathcal {E}}_{k+1}, {\mathcal {M}}_{k}\right) \le L_{\beta _{k}}\left( {\mathcal {L}}_{k}, {\mathcal {E}}_{k+1}, {\mathcal {M}}_{k}\right) \le L_{\beta _{k}}\left( {\mathcal {L}}_{k}, {\mathcal {E}}_{k}, {\mathcal {M}}_{k}\right) \nonumber \\&\quad =L_{\beta _{k-1}}\left( {\mathcal {L}}_{k}, {\mathcal {E}}_{k}, {\mathcal {M}}_{k-1}\right) + \frac{\beta _{k}+\beta _{k-1}}{2\left( \beta _{k-1}\right) ^{2}}\Vert {\mathcal {M}}_{k}-{\mathcal {M}}_{k-1}\Vert _{F}^{2}. \end{aligned}$$

(4.4)

Iterating (4.4) k times, we can obtain

$$\begin{aligned} \begin{aligned} L_{\beta _{k}}\left( {\mathcal {L}}_{k+1}, {\mathcal {E}}_{k+1}, {\mathcal {M}}_{k}\right)&\le L_{\beta _{0}}\left( {\mathcal {L}}_{1}, {\mathcal {E}}_{1}, {\mathcal {M}}_{0}\right) +\sum _{i=1}^{k} \frac{\beta _{i}+\beta _{i-1}}{2\left( \beta _{i-1}\right) ^{2}}\Vert {\mathcal {M}}_{i}-{\mathcal {M}}_{i-1}\Vert _{F}^{2} \\&\le L_{\beta _{0}}\left( {\mathcal {L}}_{0}, {\mathcal {E}}_{1}, {\mathcal {M}}_{0}\right) +\sum _{i=1}^{k} \frac{\beta _{i}+\beta _{i-1}}{2\left( \beta _{i-1}\right) ^{2}}\Vert {\mathcal {M}}_{i}-{\mathcal {M}}_{i-1}\Vert _{F}^{2} \\&\le L_{\beta _{0}}\left( {\mathcal {L}}_{0}, {\mathcal {E}}_{0}, {\mathcal {M}}_{0}\right) +\sum _{i=1}^{k} \frac{\beta _{i}+\beta _{i-1}}{2\left( \beta _{i-1}\right) ^{2}}\Vert {\mathcal {M}}_{i}-{\mathcal {M}}_{i-1}\Vert _{F}^{2} \\&= \frac{\beta _0}{2} \Vert {\mathcal {X}} \Vert _F^{2} +\sum _{i=1}^{k} \frac{\beta _{i}+\beta _{i-1}}{2\left( \beta _{i-1}\right) ^{2}}\Vert {\mathcal {M}}_{i}-{\mathcal {M}}_{i-1}\Vert _{F}^{2} \\&\le \frac{\beta _0}{2} \Vert {\mathcal {X}} \Vert _F^{2} +\left( \max _i \Vert {\mathcal {M}}_{i}-{\mathcal {M}}_{i-1}\Vert _{F}^{2} \right) \cdot \sum _{i=1}^{k} \frac{\beta _{i}+\beta _{i-1}}{2\left( \beta _{i-1}\right) ^{2}}. \end{aligned} \end{aligned}$$

(4.5)

Since $\left\{ {\mathcal {M}}_k \right\}$ is bounded, it follows that the quantity $\max _i \Vert {\mathcal {M}}_{i}-{\mathcal {M}}_{i-1}\Vert _{F}^{2}$ is also bounded. Notice that $\beta _i = \eta \beta _{i-1} = \eta ^{i} \beta _0$, $\eta = 1.1$, $\beta _0 = 10^{-4}$, then

$$\begin{aligned} \sum _{i=1}^{\infty } \frac{\beta _{i}+\beta _{i-1}}{2\left( \beta _{i-1}\right) ^{2}} = \frac{\eta +1 }{2\beta _0} \sum _{i=1}^{\infty }\dfrac{1}{\eta ^{i-1}} = \dfrac{\eta (\eta +1)}{2\beta _0 (\eta -1)} \end{aligned}$$

is bounded, and hence $L_{\beta _{k}}\left( {\mathcal {L}}_{k+1}, {\mathcal {E}}_{k+1}, {\mathcal {M}}_{k}\right)$ has upper bound.

On the other hand, we have

$$\begin{aligned}&L_{\beta _{k}}\left( {\mathcal {L}}_{k+1}, {\mathcal {E}}_{k+1}, {\mathcal {M}}_{k}\right) +\frac{1}{2 \beta _{k}}\Vert {\mathcal {M}}_{k}\Vert _{F}^{2} \nonumber \\&\quad =\Vert {\mathcal {L}}_{k+1}\Vert _{t-e^{\gamma }}+\lambda \Vert {\mathcal {E}}_{k+1}\Vert _{{\mathcal {W}}_{k+1},\ell _{p}}^p+\frac{\beta _{k}}{2}\Vert {\mathcal {L}}_{k+1}-{\mathcal {X}}+{\mathcal {E}}_{k+1}+\frac{{\mathcal {M}}_{k}}{\beta _{k}}\Vert _{F}^{2}, \end{aligned}$$

(4.6)

and noting that each term on the right-hand side of the equation (4.6) is nonnegative, we thus obtain the sequences $\left\{ {\mathcal {L}}_{k+1} \right\}$ and $\left\{ {\mathcal {E}}_{k+1} \right\}$ are bounded. $\square$

Lemma 6

[23] Suppose $F: {\mathbb {R}}^{N_1\times N_2} \rightarrow {\mathbb {R}}$ is represented as $F({\mathbf {X}})= f \circ \sigma ({\mathbf {X}})$, where ${\mathbf {X}}\in {\mathbb {R}}^{N_1 \times N_2}$ with the SVD is ${\mathbf {X}}={\mathbf {U}} {\text {diag}} (\sigma ({\mathbf {X}})){\mathbf {V}}^T$, and f is differentiable. Then the gradient of $F({\mathbf {X}})$ at ${\mathbf {X}}$ is

$$\begin{aligned} \dfrac{\partial F({\mathbf {X}})}{\partial {\mathbf {X}}} = {\mathbf {U}} {\text {diag}}(\theta ) {\mathbf {V}}^T, \end{aligned}$$

where $\theta = \frac{\partial f(y)}{\partial y}|_{y=\sigma ({\mathbf {X}})}.$

Lemma 7

[32] For the $\ell _p$ regularized unconstrained nonlinear programming model

$$\begin{aligned} \min _{{\mathbf {x}} \in {\mathbb {R}}^{n}}\left\{ F({\mathbf {x}}):=f({\mathbf {x}})+\lambda \Vert {\mathbf {x}}\Vert _{p}^{p}\right\} , \end{aligned}$$

(4.7)

where $\lambda >0$, $p\in (0,1)$, $\Vert {\mathbf {x}}\Vert _p :=\left( \sum _{i=1}^{n} |x_i|^p \right) ^{1/p}$, f is a smooth function with $L_f$-Lipschitz continuous gradient in ${\mathbb {R}}^{n}$, that is

$$\begin{aligned} \Vert \nabla f({\mathbf {x}})-\nabla f({\mathbf {y}})\Vert _{2} \le L_{f}\Vert {\mathbf {x}}-{\mathbf {y}}\Vert _{2}, \quad \forall {\mathbf {x}}, {\mathbf {y}} \in {\mathbb {R}}^{n}, \end{aligned}$$

and f is bounded below in ${\mathbb {R}}^{n}$. Then the following statements and results hold:

• (i) Let ${\mathbf {x}}^{*}$ be a local minimizer of (4.7) and ${\mathbf {X}}^{*}={\text {diag}}\left( {\mathbf {x}}^{*}\right)$. Then ${\mathbf {x}}^{*}$ is a first-order stationary point, that is, ${\mathbf {X}}^{*} \nabla f\left( {\mathbf {x}}^{*}\right) +\lambda p\left| {\mathbf {x}}^{*}\right| ^{p}=0$ holds at ${\mathbf {x}}^{*}$, where $\left| {\mathbf {x}}^{*}\right| ^{p} =(|x_1^*|^p, \cdots ,|x_n^*|^p)^T$ is an n dimensional vector.

• (ii) Let ${\mathbf {x}}^{*}$ be a first-order stationary point of (4.7) satisfying $F\left( {\mathbf {x}}^{*}\right) \le F\left( {\mathbf {x}}^{0}\right) +\epsilon _1$ for some ${\mathbf {x}}^{0} \in {\mathbb {R}}^{n}$ and a tiny $\epsilon _1 > 0$. Defining ${\underline{f}} = \inf _{{\mathbf {x}} \in {\mathbb {R}}^n} f({\mathbf {x}})$ and ${\text {supp}} ({\mathbf {x}}^{*})=\left\{ i: x_{i}^{*} \ne 0\right\}$, then

  $$\begin{aligned} \left| x_{i}^{*}\right| \ge \left( \frac{\lambda p}{\sqrt{2 L_{f}\left[ F\left( {\mathbf {x}}^{0}\right) +\epsilon _1-{\underline{f}} \right] }}\right) ^{\frac{1}{1-p}}, \quad \forall i \in {\text {supp}} ({\mathbf {x}}^{*}). \end{aligned}$$

With the help of the preceding results, we can now present the convergence analysis of Algorithm 2.

Theorem 2

Let the sequence ${\mathcal {P}}_k=\left\{ {\mathcal {L}}_k,{\mathcal {E}}_k,{\mathcal {M}}_k \right\}$ be generated by Algorithm 2. Then the accumulation point ${\mathcal {P}}^{*} = \left\{ {\mathcal {L}}^*,{\mathcal {E}}^*,{\mathcal {M}}^* \right\}$ of ${\mathcal {P}}_k$ is a KKT stationary point, i.e., ${\mathcal {P}}^{*}$ satisfies the following KKT conditions:

$$\begin{aligned} 0 \in \partial \Vert {\mathcal {L}}^* \Vert _{t-e^{\gamma }} +{\mathcal {M}}^*, \quad \lambda \cdot p \cdot \Vert {\mathcal {E}}^*\Vert _{{\mathcal {W}},\ell _p}^p + \left\langle {\mathcal {E}}^*, {\mathcal {M}}^* \right\rangle =0, \quad {\mathcal {L}}^*+{\mathcal {E}}^*={\mathcal {X}}. \end{aligned}$$

Proof

From Lemmas 4 and 5, the sequence ${\mathcal {P}}_k = \left\{ {\mathcal {L}}_k, {\mathcal {E}}_k, {\mathcal {M}}_k \right\}$ generated by Algorithm 2 is bounded. According to the Bolzano-Weierstrass theorem, the sequence $\left\{ {\mathcal {P}}_k \right\}$ has at least one convergent subsequence, thus there must be at least one accumulation point ${\mathcal {P}}^* = \left\{ {\mathcal {L}}^*, {\mathcal {E}}^*, {\mathcal {M}}^* \right\}$ for the sequence ${\mathcal {P}}_k$. Without loss of generality, we assume that $\left\{ {\mathcal {P}}_k \right\}$ converges to ${\mathcal {P}}^*$.

By (3.8), we have

$$\begin{aligned} \left( {\mathcal {M}}_{k+1}-{\mathcal {M}}_{k}\right) / \beta _{k}={\mathcal {L}}_{k+1}+{\mathcal {E}}_{k+1}-{\mathcal {X}}. \end{aligned}$$

(4.8)

Taking the limit on both sides of the above formula gives:

$$\begin{aligned} \lim _{k \rightarrow \infty }\left( {\mathcal {L}}_{k+1}+{\mathcal {E}}_{k+1}-{\mathcal {X}}\right) =\lim _{k \rightarrow \infty }\left( {\mathcal {M}}_{k+1}-{\mathcal {M}}_{k}\right) / \beta _{k}=0, \end{aligned}$$

(4.9)

and hence we have

$$\begin{aligned} {\mathcal {L}}^{*}+{\mathcal {E}}^{*}={\mathcal {X}}. \end{aligned}$$

(4.10)

By

$$\begin{aligned} {\mathcal {L}}_{k+1} =\underset{{\mathcal {L}}}{\arg \min } L_{\beta _{k}}\left( {\mathcal {L}}, {\mathcal {E}}_{k+1}, {\mathcal {M}}_{k}\right) , \end{aligned}$$

we have

$$\begin{aligned} \begin{aligned}&\left. 0 \in \partial \Vert {\mathcal {L}}\Vert _{t-e^{\gamma }}\right| _{{\mathcal {L}}_{k+1}}+{\mathcal {M}}_{k}+\beta _{k}\left( {\mathcal {L}}_{k+1}+{\mathcal {E}}_{k+1}-{\mathcal {X}}\right) \\&\quad = \left. \partial \Vert {\mathcal {L}}\Vert _{t-e^{\gamma }}\right| _{{\mathcal {L}}_{k+1}}+{\mathcal {M}}_{k+1}. \end{aligned} \end{aligned}$$

(4.11)

From Lemma 6, we know

$$\begin{aligned} \frac{\partial \Vert \hat{{\mathbf {L}}}_{n_{3}}\Vert _{e^{\gamma }}}{\partial \hat{{\mathbf {L}}}_{n_{3} }} =\hat{{\mathbf {U}}}_{{\mathcal {L}}, n_{3}} {\text {diag}}\left( \frac{\gamma e^{\gamma }}{\left( \gamma +\sigma _1(\hat{{\mathbf {L}}}_{n_3})\right) ^{2}}, \cdots , \frac{\gamma e^{\gamma }}{\left( \gamma +\sigma _n(\hat{{\mathbf {L}}}_{n_3})\right) ^{2}} \right) ^T \hat{{\mathbf {V}}}_{{\mathcal {L}}, n_{3}}^{T} \end{aligned}$$

for all $n_3 = 1,\ldots , N_3$, where $n=\min \left\{ N_1,N_2\right\}$. Noting that $\dfrac{\gamma e^{\gamma }}{\left( \gamma +\sigma _i(\hat{{\mathbf {L}}}_{n_3}) \right) ^{2}} \le \dfrac{e^{\gamma }}{\gamma }$ holds for the given $\gamma >0$ and any $\sigma _i(\hat{{\mathbf {L}}}_{n_3})$ $(i=1,\ldots ,n)$. Thus

$$\begin{aligned} \Vert \dfrac{\partial \Vert \hat{{\mathbf {L}}}_{n_{3}}\Vert _{e^{\gamma }}}{\partial \hat{{\mathbf {L}}}_{n_{3} }} \Vert _F^2 \le n \cdot \dfrac{e^{\gamma }}{\gamma }, \quad n_3 = 1,\ldots ,N_3. \end{aligned}$$

Therefore, it is easily to see that

$$\begin{aligned} \frac{\partial \Vert {\mathcal {L}}\Vert _{t-e^{\gamma }}}{\partial \hat{{\mathcal {L}}}}= \left[ \frac{\partial \Vert \hat{{\mathbf {L}}}_{1} \Vert _{e^{\gamma }}}{\partial \hat{{\mathbf {L}}}_{1}} |\cdots | \frac{\partial \Vert \hat{{\mathbf {L}}}_{N_{3}} \Vert _{e^{\gamma }}}{\partial \hat{{\mathbf {L}}}_{N_{3}}} \right] \end{aligned}$$

is bounded. Using $\hat{{\mathcal {L}}}={\mathcal {L}} \times _{3} \widetilde{{\mathbf {F}}}_{N_{3}}$ and the chain rule [7] give

$$\begin{aligned} \Vert \dfrac{\partial \Vert {\mathcal {L}}\Vert _{t-e^{\gamma }}}{\partial {\mathcal {L}}} \Vert _F^2= \Vert \frac{ \partial \Vert {\mathcal {L}}\Vert _{t-e^{\gamma }} }{\partial \hat{{\mathcal {L}}}} \times _{3} \widetilde{{\mathbf {F}}}_{N_{3}}^{*} \Vert _F^2 \le n \cdot N_3 \cdot \dfrac{e^{\gamma }}{\gamma }. \end{aligned}$$

From (4.11), let $k \rightarrow \infty$, we have

$$\begin{aligned} 0 \in \partial \Vert {\mathcal {L}}^{*}\Vert _{t-e^{\gamma }} + {\mathcal {M}}^*. \end{aligned}$$

(4.12)

Similarly, since

$$\begin{aligned} {\mathcal {E}}_{k+1} =\underset{{\mathcal {E}}}{\arg \min } \ L_{\beta _{k}}\left( {\mathcal {L}}_k, {\mathcal {E}}, {\mathcal {M}}_{k}\right) , \end{aligned}$$

according to Lemma 7, we have the following first-order optimality condition

$$\begin{aligned} \lambda \cdot p \cdot \Vert {\mathcal {E}}_{k+1}\Vert _{{\mathcal {W}},\ell _{p}}^p + \left\langle {\mathcal {E}}_{k+1}, {\mathcal {M}}_{k+1} - \beta _{k} \left( {\mathcal {L}}_{k+1}-{\mathcal {L}}_{k} \right) \right\rangle =0. \end{aligned}$$

(4.13)

Noting that $\beta _k<\beta _{max}=10^{10}$, then when $k\rightarrow \infty$, we have $\beta _{k}\left( {\mathcal {L}}_{k+1}-{\mathcal {L}}_{k} \right) \rightarrow 0$. By (4.13), we have

$$\begin{aligned} \lambda \cdot p \cdot \Vert {\mathcal {E}}^*\Vert _{{\mathcal {W}},\ell _p}^p + \left\langle {\mathcal {E}}^*, {\mathcal {M}}^* \right\rangle =0, \end{aligned}$$

which together with (4.10) and (4.12) give the assertion. $\square$

Theorem 3

The series $\left\{ {\mathcal {L}}_k \right\}$ and $\left\{ {\mathcal {E}}_k \right\}$ generated by Algorithm 2 are Cauchy sequences, and converge to some critical points of $L_{\beta } \left( {\mathcal {L}}, {\mathcal {E}}, {\mathcal {M}} \right)$.

Proof

We first show that $\left\{ {\mathcal {E}}_k \right\}$ is a Cauchy sequence. From the third equation in (3.8), we have

$$\begin{aligned} {\mathcal {E}}_t = {\mathcal {X}}-{\mathcal {L}}_t+\dfrac{1}{\beta _{t-1}} \left( {\mathcal {M}}_t - {\mathcal {M}}_{t-1}\right) . \end{aligned}$$

Thus,

$$\begin{aligned} \begin{aligned}&\Vert {\mathcal {E}}_{t+1}-{\mathcal {E}}_t \Vert _F \\&\quad = \Vert {\mathcal {E}}_{t+1}- \left( {\mathcal {X}}- {\mathcal {L}}_t - \dfrac{1}{\beta _{t}} {\mathcal {M}}_t\right) -\dfrac{1}{\beta _{t}} {\mathcal {M}}_t - \dfrac{1}{\beta _{t-1}} \left( {\mathcal {M}}_t - {\mathcal {M}}_{t-1}\right) \Vert _F \\&\quad \le \Vert {\mathcal {E}}_{t+1}- {\mathcal {B}}_t \Vert _F +\Vert \dfrac{1}{\beta _{t}} {\mathcal {M}}_t + \dfrac{1}{\beta _{t-1}} \left( {\mathcal {M}}_t - {\mathcal {M}}_{t-1}\right) \Vert _F. \end{aligned} \end{aligned}$$

(4.14)

By (3.8), we have

$$\begin{aligned} {\mathcal {E}}_{ijk}^{(t+1)}=\underset{{\mathcal {E}}_{ijk}}{\arg \min } \lambda \left( {\mathcal {W}}_{ijk}^{(t)} |{\mathcal {E}}_{ijk}|\right) ^p +\dfrac{\beta _t}{2} \left( b_{ijk}^{(t)} -{\mathcal {E}}_{ijk} \right) ^2, \end{aligned}$$

(4.15)

it follows from Lemma 7 that

$$\begin{aligned} \lambda \cdot p \cdot \left( {\mathcal {W}}_{ijk}^{(t)} |{\mathcal {E}}_{ijk}^{(t+1)}| \right) ^p + \beta _{t} \cdot {\mathcal {E}}_{ijk}^{(t+1)} \cdot \left( {\mathcal {E}}_{ijk}^{(t+1)} - b_{ijk}^{(t)} \right) =0. \end{aligned}$$

(4.16)

From (4.15) and (4.16), it is easy to see that ${\mathcal {E}}_{ijk}^{(t+1)}=0$ if and only if $b_{ijk}^{(t)}=0$.

If ${\mathcal {E}}_{ijk}^{(t+1)}\ne 0$, we have

$$\begin{aligned} \left( {\mathcal {E}}_{ijk}^{(t+1)} - b_{ijk}^{(t)} \right) ^2 = \left( \dfrac{ \lambda \cdot p \cdot \left( {\mathcal {W}}_{ijk}^{(t)} |{\mathcal {E}}_{ijk}^{(t+1)}| \right) ^p }{\beta _t \cdot {\mathcal {E}}_{ijk}^{(t+1)} } \right) ^2 \le \left( \dfrac{ \lambda \cdot \left( {\mathcal {W}}_{ijk}^{(t)} \right) ^p \cdot |{\mathcal {E}}_{ijk}^{(t+1)}|^{p-1} }{\beta _t} \right) ^2 \end{aligned}$$

since $0<p<1$. Noting that ${\mathcal {W}}_{ijk}^{(t)} = \dfrac{1}{|{\mathcal {E}}_{ijk}^{(t)}|+\epsilon }$, $\epsilon$ is a given constant. Thus we have

$$\begin{aligned} \left( {\mathcal {W}}_{ijk}^{(t)} \right) ^{2p} \le \left( \dfrac{1}{\epsilon } \right) ^{2p}. \end{aligned}$$

(4.17)

On the other hand, according to the second result of Lemma 7, ${\mathcal {E}}_{ijk}^{(t+1)} \ne 0$ has a lower bound, which is denoted by $\delta$. Thus we can obtain the following inequality

$$\begin{aligned} \left( |{\mathcal {E}}_{ijk}^{(t+1)}|\right) ^{2p-2} \le \left( \delta \right) ^{2p-2}. \end{aligned}$$

(4.18)

Denoting the upper bounds in inequalities (4.17) and (4.18) by $M_1$ and $M_2$, respectively. Therefore,

$$\begin{aligned} \left( {\mathcal {E}}_{ijk}^{(t+1)} - b_{ijk}^{(t)} \right) ^2 \le \dfrac{\lambda ^2 \cdot M_1 \cdot M_2}{\beta _t^2} \quad \text {if} \quad {\mathcal {E}}_{ijk}^{(t+1)}\ne 0. \end{aligned}$$

If ${\mathcal {E}}_{ijk}^{(t+1)} = 0$, we also have $b_{ijk}^{(t)} = 0$. And thus we have

$$\begin{aligned} \left( {\mathcal {E}}_{ijk}^{(t+1)} - b_{ijk}^{(t)} \right) ^2 = 0 \le \dfrac{\lambda ^2 \cdot M_1 \cdot M_2}{\beta _t^2}. \end{aligned}$$

In conclude, we have

$$\begin{aligned} \begin{aligned} \Vert {\mathcal {E}}_{t+1}-{\mathcal {E}}_t \Vert _F \le&\dfrac{\lambda \cdot \sqrt{ (N_1N_2N_3) \cdot M_1 \cdot M_2}}{\beta _t} + \dfrac{1}{\beta _{t}} \Vert {\mathcal {M}}_t \Vert _F \\&+ \dfrac{1}{\beta _{t-1}} \Vert {\mathcal {M}}_t \Vert _F + \dfrac{1}{\beta _{t-1}} \Vert {\mathcal {M}}_{t-1} \Vert _F, \end{aligned} \end{aligned}$$

where $N_1 \times N_2 \times N_3$ is the size of the tensor ${\mathcal {X}}$. Noting that $\left\{ {\mathcal {M}}_t\right\}$ is a bounded sequence and $\beta _{t+1} = \eta \beta _t$, $\eta =1.1$, $\beta _0 = 10^{-4}$, we thus have

$$\begin{aligned} \lim _{m,n \rightarrow \infty }\Vert {\mathcal {E}}_m-{\mathcal {E}}_n \Vert _F \le \lim _{m,n \rightarrow \infty } \sum _{t=n}^{m} \Vert {\mathcal {E}}_{t+1}-{\mathcal {E}}_t \Vert _F = 0 \end{aligned}$$

for any $n<m$. We thus proved $\left\{ {\mathcal {E}}_t \right\}$ is a Cauchy sequence.

Next, we prove that $\left\{ {\mathcal {L}}_t \right\}$ is a Cauchy sequence. From the third equation in (3.8), we have

$$\begin{aligned} {\mathcal {L}}_{t+1} = {\mathcal {X}}-{\mathcal {E}}_{t+1}+\dfrac{1}{\beta _{t}} \left( {\mathcal {M}}_{t+1} - {\mathcal {M}}_{t}\right) . \end{aligned}$$

Thus,

$$\begin{aligned}&\Vert {\mathcal {L}}_{t+1}-{\mathcal {L}}_t \Vert _F \\&\quad =\Vert {\mathcal {X}}-{\mathcal {E}}_{t+1}+\dfrac{1}{\beta _{t}} \left( {\mathcal {M}}_{t+1} - {\mathcal {M}}_{t}\right) -{\mathcal {L}}_t + \left( {\mathcal {E}}_t +\frac{1}{\beta _{t-1}} {\mathcal {M}}_{t-1} \right) \\&\qquad -\left( {\mathcal {E}}_t +\frac{1}{\beta _{t-1}} {\mathcal {M}}_{t-1} \right) \Vert _F \\&\quad =\Vert \left( {\mathcal {X}}-{\mathcal {E}}_t-\dfrac{1}{\beta _{t-1}}{\mathcal {M}}_{t-1}\right) -{\mathcal {L}}_t+{\mathcal {E}}_t-{\mathcal {E}}_{t+1}\\&\qquad +\dfrac{1}{\beta _{t}} \left( {\mathcal {M}}_{t+1} - {\mathcal {M}}_{t}\right) +\frac{1}{\beta _{t-1}}{\mathcal {M}}_{t-1} \Vert _F \\&\quad \le \Vert {\mathcal {A}}_{t-1}-{\mathcal {L}}_t \Vert _F+ \Vert {\mathcal {E}}_t-{\mathcal {E}}_{t+1} \Vert _F \\&\qquad + \frac{1}{\beta _t}\Vert {\mathcal {M}}_{t+1}\Vert _F+\frac{1}{\beta _t}\Vert {\mathcal {M}}_t\Vert _F+\frac{1}{\beta _{t-1}}\Vert {\mathcal {M}}_{t-1} \Vert _F. \end{aligned}$$

Proceeding as in the proof of Lemma 4, we can easily obtain the following inequality

$$\begin{aligned} \Vert {\mathcal {A}}_{t-1}-{\mathcal {L}}_t \Vert _F^2 \le \dfrac{1}{\beta _t^2} \cdot \dfrac{\min \left\{ N_1,N_2\right\} \cdot e^{2\gamma }}{\gamma ^2}. \end{aligned}$$

Since $\left\{ {\mathcal {E}}_t\right\}$ is a Cauchy sequence, $\left\{ {\mathcal {M}}_t\right\}$ is a bounded sequence, it yields that

$$\begin{aligned} \lim _{m,n\rightarrow \infty } \Vert {\mathcal {L}}_m-{\mathcal {L}}_n \Vert _F \le \lim _{m,n\rightarrow \infty }\sum _{t=n}^{m} \Vert {\mathcal {L}}_{t+1}-{\mathcal {L}}_t \Vert _F = 0 \end{aligned}$$

for any $n<m$. We thus proved $\left\{ {\mathcal {L}}_k\right\}$ is a Cauchy sequence.

It follows from Theorem 2 that the limit points of sequences $\left\{ {\mathcal {L}}_k\right\}$ and $\left\{ {\mathcal {E}}_k\right\}$ converge to some critical points of $L_{\beta } \left( {\mathcal {L}}, {\mathcal {E}}, {\mathcal {M}} \right)$. This completes the proof. $\square$

5 Numerical Experiments

In this section, to verify the efficiency of the proposed model, we will report the experiment results on two kinds of problems, i.e., image recovery from observations corrupted by random noise and background modeling for surveillance video, where image recovery including color image, brain magnetic resonance image (brain MRI) and gray video sequence. We compare the proposed model (3.6) (denoted by “t-$e^{\gamma }$-${\mathcal {W}}$”) with four existing models: the sum of the nuclear norms of all unfolding matrices of the tensor based model (denoted by “SNN”) [25], the t-SVD based nuclear norm model (denoted by “TNN”) [29], the t-SVD based partial sum of the nuclear norm model (denoted by “PSTNN”) [16], the t-SVD based t-Gamma tensor quasi-norm model (denoted by “t-$\gamma$”) [2]. Besides, to show the effectiveness of the weighted $\ell _p$-norm, we also compare the proposed model (3.6) with the following $\ell _p$-norm based model

$$\begin{aligned} \begin{aligned} \min _{{\mathcal {L}},{\mathcal {E}}} \Vert {\mathcal {L}}\Vert _{t-e^{\gamma }} + \lambda \Vert {\mathcal {E}}\Vert _{\ell _p}^{p}, \quad \mathrm {s.t.} \quad {\mathcal {X}}={\mathcal {L}}+{\mathcal {E}}, \end{aligned} \end{aligned}$$

(5.1)

where $\Vert {\mathcal {E}}\Vert _{\ell _p}^{p} = \left( \sum _{i,j,k} |{\mathcal {E}}_{i,j,k}|^p\right) ^\frac{1}{p}$ and $0<p<1$. For simplicity, we denote the model (5.1) by “t-$e^{\gamma }$”.

We first normalize the gray-scale value of the tested tensor to [0, 1]. The observed tensor is then obtained by randomly setting some pixels into random values in the range [0, 1]. All experiments are implemented in the Matlab R2019a Windows 10 environment and run on a desktop computer (AMD Ryzen 7-3750H, @ 2.3GHz, 16G RAM).

5.1 Parameter Setting

The ADMM has been widely used to solve the problems of tensor completion and TRPCA [2, 11, 16, 26, 27, 41]. There are different choices for initialization parameters in different models. For the TNN, PSTNN, and t-$\gamma$ models, parameters will be adjusted according to the authors’ suggestions [2, 16, 29]. For SNN, numerical experiments on TRPCA by using SNN was performed by Lu et al. [29]. Thus, parameter setting for the SNN will be adjusted according to [29]. For the proposed t-$e^{\gamma }$-${\mathcal {W}}$ model (3.6) and the competing t-$e^{\gamma }$ model (5.1), the parameters are tuned according to the parameter analysis given below.

The proposed t-$e^{\gamma }$-${\mathcal {W}}$ model involves seven parameters: $\lambda$ is the regularization parameter, which is used to balance the low rank and the sparse parts, respectively; $\beta$ is the Lagrange penalty parameter; tol is the error tolerance; K is the maximum permission iterative number of times; $\gamma$ is a positive parameter in the proposed non-convex rank approximation function; $0<p < 1$ and $\epsilon > 0$ are two parameters in the weighted $\ell _p$-norm. The t-$e^{\gamma }$ model involves six parameters: $\lambda$, $\beta$, tol, K, $\gamma$, p. For these two models, parameters $\beta$, tol and K are set consistent with [2] for a fair comparison, i.e., $\beta$ is initialized to $10^{-4}$ and iteratively increased by $\beta _{k+1}=\eta \beta _k$ with $\eta =1.1$; tol and K are set as $tol=10^{-8}$ and $K=500$, respectively. For other parameters ($\lambda$, $\gamma$, p, $\epsilon$ for the t-$e^{\gamma }$-${\mathcal {W}}$ model and $\lambda$, $\gamma$, p for the t-$e^{\gamma }$ model), we illustrate their effect on image restoration by using two color images Bear and Horse (they are randomly selected from the BSD [33]).

• The regularization parameter $\lambda$ has been studied in many literatures. For the TNN model (1.2), when the low rank and sparse components satisfy certain assumptions, regularization parameter is $\lambda _{TNN} = 1/\sqrt{\max (N_1, N_2) N_3}$ in theory to guarantee correct recovery (more details can be found in Theorem 4.1 of [29]). Therefore, $\lambda _{TNN}$ is as a good rule of thumb, which can then be adjusted to obtain the best possible results in different models.

  • For the task of color image recovery in our experiments, the size of each color image is $481 \times 321 \times 3$ or $321 \times 481 \times 3$. According to [29], $\lambda _{TNN} = 0.0263$. Therefore, we search for the best value of $\lambda$ nearby 0.0263 for the t-$e^{\gamma }$ and t-$e^{\gamma }$-${\mathcal {W}}$ models. The effect of the parameter $\lambda$ on image restoration (Bear) with respect to PSNR, SSIM and RSE values (see Sect. 5.3 for the definitions) are shown in Fig. 2. We can see that the noise levels and the best parameter value of $\lambda$ are in inverse proportion, i.e., the higher the noise level, the smaller $\lambda$ is the better choice. Meanwhile, we can see that the best parameter value of $\lambda$ in the t-$e^{\gamma }$-${\mathcal {W}}$ model is smaller than that in the t-$e^{\gamma }$ model. Therefore, in the experiment of color image recovery, $\lambda$ is selected from [0.01, 0.06] and [0.01, 0.03] with increment of 0.002 for the t-$e^{\gamma }$ and t-$e^{\gamma }$-${\mathcal {W}}$ models, respectively.

  • When the third-dimension of the data is large (such as brain MRI data, video data, hyperspectral data), $\lambda _{TNN}$ is usually very small. And thus a small $\lambda$ would be better. In our experiments, both brain MRI and video data are medium sizes and $\lambda _{TNN}<0.01$, thus the parameter $\lambda$ is selected from [0.001, 0.01] with increment of 0.001 for the t-$e^{\gamma }$ and t-$e^{\gamma }$-${\mathcal {W}}$ models when we conduct the experiments on brain MRI and videos.

• The effect of the parameter p on image restoration (Bear) with respect to PSNR, SSIM, RSE values are shown in Fig. 3. It can be seen from Fig. 3 that the best parameter value of p for t-$e^{\gamma }$ and t-$e^{\gamma }$-${\mathcal {W}}$ models are bigger than 0.5. Therefore, in the experiments, p is selected from [0.5, 1] with increment of 0.1 for the two models.

• For different noise levels, the effect of the parameter $\gamma$ on image restoration (Bear) with respect to PSNR are shown in Fig. 4. For the t-$e^{\gamma }$ model, when $\gamma >2$, the curves begin to decline. Therefore, [0.1, 2] can be as a reference range for $\gamma$ in the t-$e^{\gamma }$ model. For the t-$e^{\gamma }$-${\mathcal {W}}$ model, the curves reach their peaks at 1.5, 1.8 and 2.2, respectively. And after reaching the peaks, the curves begin to decline slowly. Therefore, [1.5, 3] can be as a reference range for $\gamma$ in the t-$e^{\gamma }$-${\mathcal {W}}$ model. Therefore, in the experiments, $\gamma$ is selected from [0.1, 2] and [1.5, 3] with increment of 0.1 for the t-$e^{\gamma }$ and t-$e^{\gamma }$-${\mathcal {W}}$ models, respectively.

• For the t-$e^{\gamma }$-${\mathcal {W}}$ model, the influence of the parameter $\epsilon$ on image restoration (Bear and Horse) with respect to PSNR are plotted in Fig. 5. It can be observed that when $\epsilon =0.1$, the curves get their peaks; when $\epsilon > 0.1$, the curves gradually tend to be stable. Therefore, in the experiments, we fixed $\epsilon$ to 0.1.

Since our experiments involve different applications associated with various datasets, we thus adjust the above parameters slightly to obtain the best performance results. For the sake of readability, we list all parameter settings for different models and different datasets in tables in the corresponding section.

Fig. 2

The effect of the parameter $\lambda$ on image restoration (Bear) with respect to PSNR, SSIM and RSE values. The first row is for the t-$e^{\gamma }$ model, the second row is for the t-$e^{\gamma }$-${\mathcal {W}}$ model

Fig. 3

The effect of the parameter p on image restoration (Bear) with respect to PSNR, SSIM and RSE values. The first row is for the t-$e^{\gamma }$ model, the second row is for the t-$e^{\gamma }$-${\mathcal {W}}$ model

Fig. 4

The effect of the parameter $\gamma$ on image restoration (Bear) with respect to PSNR values. The first row is for the t-$e^{\gamma }$ model, the second row is for the t-$e^{\gamma }$-${\mathcal {W}}$ model

Fig. 5

The effect of the parameter $\epsilon$ on image restoration (Bear and Horse) with respect to PSNR values for the t-$e^{\gamma }$-${\mathcal {W}}$ model

5.2 Convergence Test

In this subsection, we perform the convergence test for the proposed t-$e^{\gamma }$-${\mathcal {W}}$ model and the competing t-$e^{\gamma }$ model with the application to color Tiger image recovery (the Tiger image can be seen in Fig. 9). Figure 6 shows the curve of PSNR versus outer iteration numbers, residual (given by (3.18)) versus outer iteration numbers, and RSE (given by (5.2)) versus outer iteration numbers, respectively. It can be observed that as the number of iterations increases, the curves gradually tend to be stable. This clearly demonstrates the convergence of the proposed t-$e^{\gamma }$-${\mathcal {W}}$ and the competing t-$e^{\gamma }$ models as shown in Theorem 3.

Fig. 6

Convergence test on color Tiger image with different noise levels by PSNR values, residual, and RSE, respectively. The first and second rows are the convergence test for the t-$e^{\gamma }$ and t-$e^{\gamma }$-${\mathcal {W}}$ models, respectively (Color figure online)

5.3 Image Recovery

In this subsection, we conduct numerical experiments on image recovery including color image, brain MRI and gray video sequence. The results are illustrated in Sects. 5.3.1, 5.3.2 and 5.3.3, respectively.

Some quantitative assessment indexes including the relative square error (RSE), peak signal-to-noise ratio (PSNR), structural similarity index (SSIM) are adopted to evaluate the quality of the recovered images. The RSE and PSNR between the recovered tensor $\tilde{{\mathcal {L}}}\in {\mathbb {R}}^{N_1 \times N_2 \times N_3}$ and the original tensor ${\mathcal {L}}\in {\mathbb {R}}^{N_1 \times N_2 \times N_3}$ are defined as follows:

$$\begin{aligned} {\text {RSE}}(\tilde{\mathcal {L}},{\mathcal {L}}):= & {} \dfrac{\Vert \tilde{\mathcal {L}}-{\mathcal {L}}\Vert _F}{\Vert {\mathcal {L}}\Vert _F}, \end{aligned}$$

(5.2)

$$\begin{aligned} {\text {PSNR}}(\tilde{\mathcal {L}},{\mathcal {L}}):= & {} 10 {\text {log}}_{10} \left( \dfrac{N_1N_2N_3\Vert {\mathcal {L}}\Vert _\infty ^2}{\Vert \tilde{\mathcal {L}}-{\mathcal {L}}\Vert _F^2} \right) . \end{aligned}$$

(5.3)

SSIM measures the similarity of two images in luminance, contrast and structure, which is defined as

$$\begin{aligned} {\text {SSIM}}(\tilde{{\mathbf {L}}},{\mathbf {L}}) := \dfrac{\left( 2\mu _{{\mathbf {L}}} \mu _{\tilde{{\mathbf {L}}}} +c_1\right) \left( 2\sigma _{{\mathbf {L}} \tilde{{\mathbf {L}}}}+c_2\right) }{ \left( \mu _{{\mathbf {L}}}^2+\mu _{\tilde{{\mathbf {L}}}}^2 +c_1\right) \left( \sigma _{{\mathbf {L}}}^2+\sigma _{\tilde{{\mathbf {L}}}}^2 +c_2\right) }, \end{aligned}$$

(5.4)

where $\mu _{{\mathbf {L}}}$ and $\mu _{\tilde{{\mathbf {L}}}}$ represent the mean values of the original data matrix ${\mathbf {L}}$ and the recovered data matrix $\tilde{{\mathbf {L}}}$, respectively, $\sigma _{{\mathbf {L}}}^2$ and $\sigma _{\tilde{{\mathbf {L}}}}^2$ represent the standard variances of ${\mathbf {L}}$ and $\tilde{{\mathbf {L}}}$, respectively, $\sigma _{{\mathbf {L}}\tilde{{\mathbf {L}}}}$ represents the covariance of ${\mathbf {L}}$ and $\tilde{{\mathbf {L}}}$, $c_1,c_2 > 0$ are two constants to stabilize the division with weak denominator. For tensor data, the SSIM value is obtained by calculating the average SSIM values for all frontal slices. As we can see, lower RSE value, higher PSNR and SSIM values mean better image quality.

5.3.1 Color Image

In this section, we select thirty color images from the Berkeley Segmentation Dataset (BSD) [33] for the test. These images are different natural scenes and objects in real life and all have size $321 \times 481 \times 3$ or $481 \times 321 \times 3$. For each image, we test three different noise levels: $30\%$, $20\%$, $10\%$. The parameter setting for color image recovery is listed in Table 1.

In Table 2, we list the average PSNR, SSIM, RSE values of the results recovered by different models for thirty color images. From the quantitative assessment results, we can see that the t-$e^{\gamma }$-${\mathcal {W}}$ model always achieves the best recovery performance for different noise levels. For each image, the PSNR, SSIM and RSE obtained by different models are shown in Figs. 7 and 8, respectively. It can be seen that the results obtained by the proposed t-$e^{\gamma }$-${\mathcal {W}}$ model reaches higher PSNR, SSIM and lower RSE values in most cases.

Table 1 The parameter setting for color image recovery

Table 2 The average PSNR, SSIM and RSE values for restoring results of different models for thirty color images corrupted by different noise levels

Fig. 7

The PSNR values obtained by different models for thirty color images with different noise levels. From top to bottom: the noise levels are $30\%$, $20\%$ and $10\%$, respectively (Color figure online)

Fig. 8

The SSIM and RSE values obtained by different models for thirty color images with different noise levels. From top to bottom: the noise levels are $30\%$, $20\%$ and $10\%$, respectively (Color figure online)

Fig. 9

The recovered results on three sample color images with the noise level is $30\%$

Figure 9 further exhibits the visual results on three sample color images, where only noise level $30\%$ is shown exemplarily. From Fig. 9, we can see that the proposed t-$e^{\gamma }$-${\mathcal {W}}$ model preserves image details (such as animal’s eyes, the edge of the pyramid) better than other models.

Based on the above comparison, we have the following conclusions: First, among all competing models, the Tucker rank based SNN shows the worst recovery performance because the SNN is a loose convex relaxation of the sum of the Tucker rank. Second, the t-SVD based models can obtain better results because the t-SVD framework make more efficient use of the spatial structure of the tensor data. Third, among all competing non-convex models, t-$e^{\gamma }$ and t-$e^{\gamma }$-${\mathcal {W}}$ can achieve better recovery performance compared with PSTNN and t-$\gamma$. The reason is that both the tensor rank and the sparse constraint term in the t-$e^{\gamma }$ and t-$e^{\gamma }$-${\mathcal {W}}$ models are measured by the non-convex functions. This demonstrates the superiority of the non-convex models. Finally, the proposed t-$e^{\gamma }$-${\mathcal {W}}$ can achieve the best performance and recover more details because the weighted $\ell _p$-norm is a more accurate relaxation of the $\ell _0$-norm compared with the $\ell _p$-norm. This shows the effectiveness of the proposed model.

Table 3 The parameter setting for brain MRI recovery

Table 4 The PSNR, SSIM and RSE values for restoring results of different models for MRI corrupted by different noise levels

5.3.2 Brain MRI

In this section, we conduct experiments on brain MRI¹, whose size is $181\times 217 \times 181$. The noise levels are set to be $40\%$, $30\%$, $20\%$ and $10\%$, respectively. The parameter setting for brain MRI recovery is listed in Table 3.

Table 4 shows the numerical results obtained by six models for recovering the brain MRI. It can be seen that when the noise level is $40\%$, PSTNN and t-$\gamma$ always yield unsatisfactory results. With the decrease of the noise levels, although the performance of SNN and TNN are increase steadily, they do not perform well for the lower noise levels (such as $10\%$). In contrast, t-$e^{\gamma }$ and t-$e^{\gamma }$-${\mathcal {W}}$ always have powerful recovery performance for different noise levels. In particular, the proposed t-$e^{\gamma }$-${\mathcal {W}}$ model always achieves the best in terms of three assessment indexes for different noise levels, which further shows the robustness and unbiasedness of the proposed non-convex model.

Apart from quantitative assessment, we also show the visual comparison of one slice of the brain MRI recovered by different models in Fig. 10, where only noise levels $40\%$ and $30\%$ are shown exemplarily. Obviously, when the noise level is high, both the PSTNN and the t-$\gamma$ fail to remove the noise. Although the SNN and TNN can remove most of the noise, the images obtained by them are very fuzzy. In contrast, the t-$e^{\gamma }$ and t-$e^{\gamma }$-${\mathcal {W}}$ can recover most information of the images while the images obtained by t-$e^{\gamma }$-${\mathcal {W}}$ are almost the same as the original ones.

Fig. 10

The recovered results on brain MRI with the noise levels are $40\%$ and $30\%$, respectively. The first two rows: noise level is $40\%$. The last two rows: noise level is $30\%$

5.3.3 Gray Video Sequence

In this section, two gray videos² Grandma ($144 \times 176 \times 150$) and MotherDaughter ($144 \times 176 \times 150$) are chosen for the test. For each video, we test three different noise levels: $40\%$, $30\%$, $10\%$. The parameter setting for gray video recovery is listed in Table 5.

In Table 6, we report the PSNR, SSIM, and RSE values obtained by six models for the two gray videos in different noise levels. Figure 11 also exhibits the visual comparison on one frame for the two gray videos, where only noise level $40\%$ is shown exemplarily. For different noise levels and the two videos, it can be observed from Table 6 that the t-$e^{\gamma }$-${\mathcal {W}}$ always achieve best in terms of three assessment indexes. From Fig. 11, we can see that the recovery images by the SNN, TNN, PSTNN, and t-$\gamma$ are very fuzzy while the t-$e^{\gamma }$ and t-$e^{\gamma }$-${\mathcal {W}}$ can obtain clear recovery images. In particular, owing to the two non-convex relaxations, the t-$e^{\gamma }$-${\mathcal {W}}$ perfectly preserves more detailes such as the eyes and the mouth. The above comparison shows the feasibility and effectiveness of the proposed model.

Table 5 The parameter setting for gray video recovery

Table 6 The PSNR, SSIM and RSE values for restoring results of different models for gray videos corrupted by different noise levels

Fig. 11

The recovered results on gray videos with noise levels is $40\%$. The first two rows: Grandma. The last two rows: MotherDaughter

5.4 Video Background Modeling

In this subsection, the proposed model is applied to solve the background modeling problem. The task of background modeling aims to separate the foreground objects from the background. This is the pre-process step in many vision applications such as surveillance video processing, moving target detection and segmentation [33]. Surveillance videos from a fixed camera can be naturally modeled by TRPCA since the frames of the background are highly correlated and thus can be considered as a low rank tensor and the moving foreground objects occupy only a small part of the image pixels and thus can be regarded as sparse errors. In our work, we select three color video sequences: highway ($240 \times 360$), pedestrians ($240 \times 360$) and PETS2006 ($576 \times 720$) from CD.net dataset³ in the baseline category, where the numbers in the parentheses denote the frame size. We only choose the frames from 900 to 1000 for these video sequences to reduce the computational time. For each sequence with color frame size $h \times w \times 3$ and frame number k, we reshape it to the $(hw) \times k \times 3$ tensor for the test. The parameter setting for video background modeling is listed in Table 7.

Table 7 The parameter setting for Video Background Modeling

The F-Measure is used to assess the performance of the results of the background modeling, which is defined by

$$\begin{aligned} \text {F-Measure} = 2 \frac{\text {Precision} \cdot \text {Recall} }{\text {Precision} + \text {Recall}}, \end{aligned}$$

where

$$\begin{aligned} \text {Recall}= & {} \frac{\text {the number of correctly classified foreground pixels}}{\text {the number of foreground pixels in ground truth}}, \\ \text {Precision}= & {} \frac{\text {the number of correctly classified foreground pixels}}{\text {the number of pixels classified as foreground}}. \end{aligned}$$

In Table 8, we report the F-Measure obtained by different models for video background modeling. Obviously, compared with the SNN, the F-Measures of other competing models are high, which indicates that the t-SVD has a better performance in maintaining the spatial structure of the multi-dimensional data.

Figure 12 displays the background images and the foreground images separated by different models. We can see that the background images obtained by the SNN, TNN and PSTNN always have obvious foreground ghosting. It indicates that these models can not remove the sparse foreground component effectively. Although the t-$\gamma$ model can get the clean background images in the highway and pedestrians videos, a twisted foreground image can be found in the PETS2006 video. In addition, we can see that the results obtained by the t-$e^{\gamma }$ and t-$e^{\gamma }$-${\mathcal {W}}$ models are almost same. But from Table 8, the background modeling results obtained by the t-$e^{\gamma }$-${\mathcal {W}}$ model outperform those obtained by the t-$e^{\gamma }$ model in terms of F-Measure.

In summary, the proposed model shows strong background modeling capability, producing satisfying results both in visualization and in quantitative assessment.

Table 8 The F-Measure of the results of the background modeling obtained by different models

Fig. 12

The background modeling results obtained by different models. From left to right: original frames, the background modeling results obtained by the SNN, TNN, PSTNN, t-$\gamma$, t-$e^{\gamma }$, and t-$e^{\gamma }$-${\mathcal {W}}$, respectively. Rows 1 and 2 are samples of highway; rows 3 and 4 are samples of pedestrians; rows 5 and 6 are samples of PETS2006

6 Concluding Remarks

In this paper, we present a new non-convex approach for the TRPCA problem. Different from existing non-convex TRPCA models, we not only propose a novel non-convex relaxation for the tensor tubal rank but also introduce a new and suitable non-convex sparsity measuration for the sparse constraint term rather than by the $\ell _1$-norm commonly used in literature. It is well known that convergence analysis of the non-convex optimization algorithm is a challenging problem, and we are able to show that the sequence generated by the proposed algorithm always converges to a KKT stationary point. The numerical experiments for practical applications are given to demonstrate that the proposed non-convex model outperforms the existing approaches.