A New Discontinuous Galerkin Method for Elastic Waves with Physically Motivated Numerical Fluxes

Abstract

The discontinuous Galerkin (DG) method is an established method for computing approximate solutions of partial differential equations in many applications. Unlike continuous finite elements, in DG methods numerical fluxes are used to enforce inter-element conditions, and internal/external physical boundary conditions. For elastic wave propagation in complex media several wave types, including dissipative surface and interface waves, are simultaneously supported. The presence of multiple wave types and different physical phenomena pose a significant challenge for numerical fluxes. When modelling surface or interface waves an incompatibility of the numerical flux with the physical boundary condition leads to numerical artefacts. We present a stable and arbitrary order accurate DG method for elastic waves with a physically motivated numerical flux. Our numerical flux is compatible with all well-posed, internal and external, boundary conditions, including linear and nonlinear frictional constitutive equations for modelling spontaneously propagating shear ruptures in elastic solids and dynamic earthquake rupture processes. By construction our choice of penalty parameters yield an upwind scheme and a discrete energy estimate analogous to the continuous energy estimate. We derive a priori error estimate for the DG method proving optimal convergence to discontinuous and nearly singular exact solutions. The spectral radius of the resulting spatial operator has an upper bound which is independent of the boundary and interface conditions, thus it is suitable for efficient explicit time integration. We present numerical experiments in one and two space dimensions verifying high order accuracy and asymptotic numerical stability. We demonstrate the potential of the method for modelling complex nonlinear frictional problems in elastic solids with 2D dynamically adaptive meshes and non-planar topography with 2D curvilinear elements.

1 Introduction

High order accurate and explicit time-stable solvers are well suited for hyperbolic wave propagation problems. See, for example, the pioneering work by Kreiss and Oliger [31]. However, because of the complexities of real geometries, internal interfaces, nonlinear boundary/interface conditions and the presence of disparate spatial and temporal scales present in real media and sources, discontinuities and sharp wave fronts become fundamental features of the solutions. Thus, in addition to high order accuracy, geometrically flexible and adaptive numerical algorithms are critical for high fidelity and efficient simulations of wave phenomena in many applications.

Since its introduction [39], the discontinuous Galerkin method (DG method) method has been extensively applied to hyperbolic partial differential equations (PDEs), see for example [8, 9, 24, 25] and references therein. It has been applied in particular to computational fluid dynamics problems [14, 28, e.g.,] and to simulate wave and fracture phenomena occurring in geometrically complex and heterogeneous media [6, 18, 45, 53, e.g.,]. Powerful advantages of the DG method are the local nature of the discrete high order accurate spatial operators and the possibility to use unstructured or boundary conforming curvilinear meshes [12, 29, 49]. Due to the spatial locality of the operators, the DG method lends itself to efficient parallel numerical algorithms on modern high performance computing platforms [4, 23, 48, 52].

Wave propagation problems often appear with nontrivial boundary conditions. Examples include nonlocal transparent boundary conditions, local absorbing boundary conditions, and other dynamic boundary conditions that result from local or nonlocal coupling with differential equations on the boundary. Here we focus on seismological application of the DG method accounting for heterogeneous and geometrically complex solid Earth models as well as linear and nonlinear friction laws to describe earthquake rupture physics. Exploration seismology and natural earthquake hazard mitigation increasingly rely on multi-scale (0–20 Hz) and multi-physics (non-linear rheology, fluid and heat transport, dynamic rupture sources) simulations. Seismic waves propagate over hundreds to thousands of kilometres interacting with complicated geological structure and topography and are generated by seismic source processes acting on scales down to centimetres. Dynamic earthquake sources modelled as non-linear frictional failure on a pre-defined fault can be treated as an internal boundary condition [11, 15, 22, 27]. Non-linear boundary conditions and material behavior may lead to very large gradients in the numerical solution. In particular, for spontaneously propagating shear ruptures in elastic solids, the particle velocity can be discontinuous and the shear stress nearly singular at the rupture tip. Accurate and efficient numerical simulation of these problems require carefully designed and provably stable numerical methods.

A crucial component of any DG method is the numerical flux [10, 26] which is inherited from finite volume and finite difference methods [20, 43], and exchanges information across element boundaries based on approximate or exact solutions of the Riemann problem. Due to its simplicity and robustness, the Rusanov flux [43] (also called local Lax–Friedrichs flux) is widely used. Other established numerical fluxes include the centred flux, Godunov flux, Roe flux, and the Engquist–Osher flux. The choice of a numerical flux is critical for accuracy and stability of the DG method [28, 30, 36]. For example, including nonlinear frictional failure in elastodynamic wave propagation solvers by direct adaption of a Godunov flux introduces a very selective numerical dissipation avoiding spurious high-frequency oscillations [35] due to the favourable upwind property of the Godunov flux for first order hyperbolic problems [7, 30, 51]. However, issues of numerical instability may arise when interesting linear or nonlinear physical phenomena occur at internal and external boundaries motivating the development of numerical fluxes consistent with the underlying physics.

In this study we develop a new DG flux incorporating the physical boundary conditions acting at element boundaries. The new physically motivated numerical flux is designed to be compatible with all well-posed and energy stable physical boundary conditions, including linear and nonlinear friction laws. Elastic wave propagation problems in complex media include surface and interface waves, thus several wave types and wave speeds are simultaneously present. In such applications, we confirm in preliminary numerical studies that the Rusanov flux [43] can lead to numerical instabilities, for example, when Rayleigh surface waves need to be captured. Such incompatibility can lead to (longtime) numerical instabilities which will eventually destroy numerical accuracy.

We present a novel approach to couple DG elements in elastic solids in a provably stable manner. All DG inter-element interfaces are treated as frictional interfaces with associated frictional strength. Classical inter-element interfaces where slip is not permitted have infinite frictional strength, and can never be broken by any load of finite magnitude. Other interfaces have finite frictional strength and are governed by a generic friction law [2, 3, 41, 42, 44]. An analogous method has been proposed to model rupture dynamics in a finite difference framework [15]. However, static and dynamic adaptive mesh refinement, natural to DG methods, is challenging with finite difference methods. More importantly, we extend their approach by using physical conditions, such as friction, to couple locally adjacent DG elements within the global domain. External boundaries of the domain are closed with general linear energy-stable boundary conditions. We design a numerical flux obeying the eigen-structure of the PDE and the underlying physics at the internal and external DG element boundaries. This work initialises the development of a unified provably stable and robust adaptive DG framework for the numerical treatment of (1) nonlinear frictional sliding in elastic solids, (2) coupling classical DG inter-element interfaces in elastic solids where slip is not permitted, and (3) numerical enforcement of external well-posed boundary conditions modeling various geophysical phenomena.

For clarity, we will focus on the one space dimensional (1D) problem. We remark that most of the difficulties we hope to alleviate often appear in higher (2D and 3D) space dimensions. While the 1D problem is sufficient to demonstrate the fundamentals of our idea, the analysis and implementation can be readily extended as we here demonstrate in numerical experiments in 1D and 2D. We note, that the proposed physics based flux is formulated using derived quantities such as tractions and particle velocities rotated into local orthogonal coordinates. The numerical flux construction, in 2D and 3D, completely avoids the eigen-decomposition of coefficient matrices. We refer the reader to [17, 40] for further discussion on extension to multiple dimensions.

Since the elastic wave equation is hyperbolic it can be decomposed into characteristics as natural carriers of information. The holy grail of prescribing well-posed boundary conditions is to ensure that boundary data preserve the amplitude of the outgoing characteristics. Boundary conditions can then be enforced by modifying the amplitude of the incoming characteristics [21].

In order to generate boundary and interface data, we solve a Riemann-like problem and constrain the solution such that the amplitude of the outgoing characteristics is preserved and that the solution satisfies physical boundary and interface conditions (eg., a force balance and friction law). The solution is exact and unique. To communicate data across internal and external element boundaries, we penalize the numerical boundary/interface data against incoming characteristics only. Next we construct a flux fluctuation vector obeying the structure of the underlying PDE. Finally, we append the flux fluctuation vector to the discretized PDE. By construction our choice of penalty parameters yield an upwind scheme and a discrete energy estimate analogous to the continuous energy estimate. Furthermore, we derive a priori error estimates for the presented DG method proving optimal convergence. Under certain conditions our numerical flux is equivalent to the classical Godunov flux [20] which is used in previous work on elasticity [13, 51, e.g.,] and frictional shear motion [34]. For example, in 1D and in the absence of slip and external boundary conditions the physics based interface data matches the exact solution of the Riemann problem for a hyperbolic PDE. However, since dynamic boundary conditions dissipate energy, the coupled initial-boundary value problem (IBVP) is no longer purely hyperbolic and the proposed numerical flux fluctuation differs completely from the Godunov flux.

We present numerical experiments corroborating the continuous accuracy and stability analysis using a Lagrange basis with Gauss–Legendre–Lobatto (GLL) quadrature nodes and Gauss–Legendre (GL) quadrature nodes, respectively. We verify in 2D numerical experiments the extension of our method to multiple spatial dimensions as well as high order accuracy for a Rayleigh surface wave. We also simulate dynamic earthquake rupture in 1D and 2D to demonstrate the robustness and versatility of the method.

This paper is structured as follows. In Sect. 2 we define the problem and derive continuous energy estimates. Boundary and interface data are constructed in Sect. 3. In Sect. 4, we present the new DG boundary and inter-element procedures from the integral formulation to numerical approximations. Numerical stability is proven in Sect. 5. In Sect. 6, we derive an error equation and a priori error estimate, proving optimal convergence. In Sect. 7, we present 1D and 2D numerical examples. We draw conclusions and suggest future work in Sect. 8.

2 Model Problem

Consider the elastic wave equation in a heterogeneous one space dimensional domain

$$\begin{aligned} \begin{aligned} \rho (x) \frac{\partial v}{\partial t}&= \frac{\partial \sigma }{\partial x}, \quad \frac{1}{\mu (x)} \frac{\partial \sigma }{\partial t} = \frac{\partial v}{\partial x}, \quad x \in [0, L], \quad t \ge 0. \end{aligned} \end{aligned}$$

(1)

The unknowns are v(x, t), the particle velocity, and $\sigma (x,t)$, the stress field. The material parameter $\rho (x)$ is the mass density and $\mu (x)$ is the shear modulus. Define the shear wave-speed by $c_s = \sqrt{\mu /\rho }$.

For real functions u(x), v(x), define the $L^2$-inner product, the corresponding norm

$$\begin{aligned} \left( u, v\right) _{\varOmega } = \int _{\varOmega } u(x)v(x) dx, \quad \Vert u\Vert ^2_{\varOmega }= \left( u, u\right) _{\varOmega }, \end{aligned}$$

(2)

and the function space

$$\begin{aligned} {\mathbb {L}}^2\left( \varOmega \right) = \{u(x): \quad \Vert u\Vert _{\varOmega } < \infty , \quad \forall x \in \varOmega \}. \end{aligned}$$

(3)

The subscript $\varOmega$ in (2) and (3) denote the spatial domain, and will sometimes be omitted when the context is clear.

In order to complete the statement of the problem (1), and define a well-posed IBVP, we will need initial conditions at $t = 0$ and boundary conditions at $x = 0, L$. We prescribe the initial condition

$$\begin{aligned} (v(x, 0), \sigma (x, 0)) = (v_0(x), \sigma _0(x)) \in {\mathbb {L}}^2(0, L). \end{aligned}$$

(4)

Now we introduce the shear impedance $Z_s$, the left-going characteristic p, and the right-going characteristic q defined by

$$\begin{aligned} p = \frac{1}{2}\left( Z_sv + \sigma \right) , \quad q = \frac{1}{2}\left( Z_s v - \sigma \right) , \quad Z_s = \rho c_s. \end{aligned}$$

(5)

Note that at the left boundary, $x = 0$, p is the outgoing characteristic and q is the incoming characteristic. Conversely, at the right boundary, $x = L$, q is the outgoing characteristic and p is the incoming characteristic.

2.1 Boundary Conditions

In prescribing well-posed boundary conditions, we aim to ensure that all boundary data preserve the amplitude of the outgoing characteristics. Boundary conditions can then be enforced by modifying the amplitude of the incoming characteristics. In general, boundary data for the incoming characteristics can be expressed as a linear combination of the outgoing characteristics [21]. We consider the general linear well-posed boundary conditions

$$\begin{aligned} q = r_0 p, \quad \text {at} \quad x = 0, \quad \text {and} \quad p = r_L q, \quad \text {at} \quad x = L, \end{aligned}$$

(6)

with the reflection coefficients $r_0$, $r_L$ being real numbers and $|r_0|, |r_L| \le 1$. Note that at $x = 0$, $r_0 = -1$ yields a clamped boundary condition, $r_0 = 0$ yields an absorbing boundary, and with $r_0 = 1$ we have a free-surface boundary condition. Similarly, at $x = L$, $r_L = -1$ yields a clamped wall, $r_L = 0$ yields an absorbing boundary, and $r_L = 1$ gives a free-surface boundary condition. We have tacitly considered homogeneous boundary forcing, however, the analysis carries over to the case of inhomogeneous boundary forcing. By rearranging and collecting terms together, the boundary condition (6) can be rewritten in terms of the primitive variables, $v, \sigma$, having

$$\begin{aligned} \begin{aligned} B_0(v, \sigma , Z_{s}, r_0)&: =\frac{Z_{s}}{2}\left( {1-r_0}\right) {v} -\frac{1+r_0}{2} {\sigma } = 0, \quad \text {at} \quad x = 0, \\ B_L(v, \sigma , Z_{s}, r_L)&: =\frac{Z_{s}}{2} \left( {1-r_L}\right) {v} + \frac{1+r_L}{2}{\sigma } = 0, \quad \text {at} \quad x = L. \end{aligned} \end{aligned}$$

(7)

To see that the IBVP, (1) with (6) or (7), is well-posed we seek an integral form of the PDE (1) by multiplying the elastic wave equation by a set of arbitrary test functions $(\phi _v(x), \phi _\sigma (x)) \in {\mathbb {L}}^2(\varOmega )$ and integrate over the whole domain. We have

$$\begin{aligned}&\left( \phi _v, {\rho } \frac{\partial v}{\partial t}\right) _{\varOmega } - \left( \phi _v, \frac{\partial \sigma }{\partial x} \right) _{\varOmega } = 0, \end{aligned}$$

(8)

$$\begin{aligned}&\left( \phi _{\sigma }, \frac{1}{\mu }\frac{\partial \sigma }{\partial t}\right) _{\varOmega } - \left( \phi _{\sigma }, \frac{\partial v}{\partial x} \right) _{\varOmega } = 0. \end{aligned}$$

(9)

We introduce the weighted $L^2$-norm $\Vert Q\Vert _{\varOmega P}$, $Q = (v, \sigma )^T$ and mechanical energy defined by

$$\begin{aligned} \Vert Q\Vert _{\varOmega P}^2 :=E(t) = \frac{1}{2}\left( v, \rho v \right) _{\varOmega }+ \frac{1}{2}\left( \sigma , \frac{1}{\mu } \sigma \right) _{\varOmega } > 0, \end{aligned}$$

(10)

where E(t) is the sum of the kinetic energy and the strain energy. The mechanical energy is the weighted $L_2$ norm of the unknown fields $Q = (v, \sigma )^T$. The weighted $L^2$-norm $\Vert Q\Vert _{\varOmega P}$ is equivalent to the classical $L^2$-norm $\Vert Q\Vert _{\varOmega }$, that is for all $Q \in {\mathbb {L}}^2(\varOmega )$ we have

$$\begin{aligned} C_1\Vert Q\Vert _{\varOmega } \le \Vert Q\Vert _{\varOmega P} \le C_2 \Vert Q\Vert _{\varOmega }, \end{aligned}$$

(11)

with $C_1 = \min \left( \sqrt{\rho /2}, 1/\sqrt{2\mu }\right)$ and $C_2 = \max \left( \sqrt{\rho /2}, 1/\sqrt{2\mu }\right)$.

Now, replace $\phi _v(x)$ with v(x, t) in (8) and $\phi _{\sigma }(x)$ with ${\sigma }(x,t)$ in (9). Integrating the second term in (8) by parts, and summing Eqs. (8)–(9), we find that the spatial derivatives vanish. We have

$$\begin{aligned} \frac{d E(t)}{dt} = -v(0, t)\sigma (0, t) + v(L, t)\sigma (L, t). \end{aligned}$$

(12)

From the boundary conditions (7), it is easy to check that $v(0, t)\sigma (0, t) \ge 0$ and $v(L, t)\sigma (L, t) \le 0$, for all $|r_0|, |r_L| \le 1$. The boundary terms in (12) are negative semi-definite, $-v(0, t)\sigma (0, t) + v(L, t)\sigma (L, t) \le 0$, and dissipative. Since boundary terms are negative semi-definite, we therefore have

$$\begin{aligned} \frac{d E(t)}{dt} \le 0. \end{aligned}$$

(13)

Thus, the mechanical energy is bounded by the initial mechanical energy for all times, $E(t) \le E(0)$. This energy loss through the boundaries is what the numerical method should mimic.

2.2 Interface Conditions

In this section we define physical interface conditions that must be satisfied when elastic blocks are in contact. A main idea of this study is to use friction to couple DG elements to the global domain. Therefore, we consider a generic nonlinear friction law, accommodating frictional slip motion.

Fig. 1

Distribution of fields across a slidding frictional interface in a 1D elastic solid. At the interface $x = x_0$, the particle velocity is discontinuous $[\![{v} ]\!]\ne 0$, the stress is continuous $\sigma ^- = \sigma ^+=\sigma$ but nearly singular

To begin, we consider the domain $\varOmega = \varOmega _{-}\cup \varOmega _{+}$, with $\varOmega _{-}:= [0, x_0]$, $\varOmega _{+}:= [x_0, L]$, $0<x_0< L$, see Fig. 1. We denote field variables and material parameters in the sub-domains $\varOmega _{\pm }$ with the superscripts ±: $v^{\pm }$, $\sigma ^{\pm }$, $\rho ^{\pm }$, $\mu ^{\pm }$, $Z_s^{\pm }$. Since there are two characteristics going in and out of the interface we need exactly two interface conditions coupling the elastic subdomains. Define tractions $T^- = \sigma ^-$, $T^{+} = - \sigma ^{+}$, acting on the interface. We begin with the force balance:

$$\begin{aligned} T^- = -T^+ \iff \sigma ^{-} = \sigma ^{+} = \sigma . \end{aligned}$$

(14)

To complete the interface condition we introduce the discontinuity in particle velocity: $\llbracket v \rrbracket := v^{+} - v^{-}$, and define the absolute slip-rate $V: = \left| \llbracket v \rrbracket \right|$. We introduce the compressive normal stress $\sigma _n > 0$ and define the frictional constitutive relation such that

$$\begin{aligned} \sigma = \alpha \llbracket v \rrbracket , \quad \alpha = \sigma _n\frac{f(V)}{V} \ge 0 . \end{aligned}$$

(15)

Here f(V) is the nonlinear friction coefficient and takes the sign of its argument V. Thus for all $V\ge 0$ we have $f(V) \ge 0$ with $f(0)=0$ and $f^{\prime }(V) \ge 0$. Note that

$$\begin{aligned} \alpha \rightarrow \infty \implies {V} \rightarrow 0 . \end{aligned}$$

(16)

For later use, we summarise the interface condition:

$$\begin{aligned} \begin{aligned} \text {force balance:} \quad&\sigma ^{-} = \sigma ^{+} = \sigma , \\ \text {friction law:} \quad&\sigma =\alpha \llbracket v \rrbracket , \quad \alpha = \sigma _n\frac{f(V)}{V}\ge 0. \end{aligned} \end{aligned}$$

(17)

Tractions on the interface are related to particle velocities via $\sigma = \alpha \llbracket v \rrbracket$, with $\alpha \ge 0$. The parameter $\alpha \ge 0$ is related to the nonlinear frictional strength of the interface. Note that there are two limiting values, a locked interface: $\alpha \rightarrow \infty \implies [\![{v} ]\!]\rightarrow 0$, and a frictionless interface: $\alpha \rightarrow 0 \iff \sigma \rightarrow 0$. These limiting cases are degenerate but physically feasible.

Since $\alpha \rightarrow \infty \implies [\![{v} ]\!]\rightarrow 0$, the limit $\alpha \rightarrow \infty$ in (17) is an alternative way of expressing the continuity of particle velocities across an interface, thus gives the natural condition to be used to patch DG elements together, when slip motion is not present. However, we can model nonlinear frictional slip motion by replacing f(V) in (17) with an appropriate friction law [2, 41, 42, 44].

Remark 1

We also remark that $V\rightarrow 0 \implies \alpha \rightarrow \sigma _n f^{\prime }(0)>0$. For realistic friction laws [41, 42, 44] the magnitude of $\alpha >0$ can attain very large values ranging between $10^2$ and $10^{20}$. This parameter is grid independent, makes the problem stiff and can severely limit the time-step of an explicit scheme.

We define the mechanical energy in each subdomain by

$$\begin{aligned} E^{\pm }(t) = \frac{1}{2}\left( v^{\pm }, \rho ^{\pm } v^{\pm } \right) _{\varOmega ^{\pm }}+ \frac{1}{2}\left( \sigma ^{\pm }, \frac{1}{\mu ^{\pm }} \sigma ^{\pm } \right) _{\varOmega ^{\pm }} > 0. \end{aligned}$$

(18)

The elastic wave equation with the physical interface condition (17), satisfies the energy equation

$$\begin{aligned} \frac{d E(t)}{dt} = -\sigma \llbracket v \rrbracket -v^-(0, t)\sigma ^-(0, t) + v^+(L, t)\sigma ^+(L, t), \end{aligned}$$

(19)

with $E(t) = E^{-}(t) + E^{+}(t)$. The interior term $-\sigma \llbracket v \rrbracket$ is the rate of work done by friction during frictional slip, which is dissipated as heat. We note the negative work rate and for $\alpha \ge 0$ we have $\sigma \llbracket v \rrbracket = \alpha \llbracket v \rrbracket ^2 = \frac{1}{\alpha } \sigma ^2 \ge 0$. At the limit $\alpha \rightarrow \infty \implies [\![{v} ]\!]\rightarrow 0$ or $\alpha \rightarrow 0 \iff \sigma \rightarrow 0$, the interior term vanishes, ${\sigma } {[\![{v} ]\!]} \rightarrow 0$. Thus, at $\alpha \rightarrow \infty$ or $\alpha \rightarrow 0$, the energy Eq. (19) is completely equivalent to (12).

3 Hat-Variables

We now reformulate the boundary condition (6) and interface condition (17) by introducing transformed (hat-) variables such that we can simultaneously construct (numerical) boundary/interface data for particle velocities and tractions. Our objective is to formulate an inter-element procedure incorporating the physical interface condition (17) and the boundary condition (7), such that a discrete energy equation analogous to (19) can be derived. The procedure should be formulated in a unified manner such that numerical flux functions are compatible with the general linear boundary condition (6) or (7). Furthermore, the procedure should be efficient for explicit time stepping schemes, thus avoiding numerical stiffness for all $0\le \alpha \le \infty$. The numerical treatment should be applicable to higher space dimensions (2D and 3D). The hat-variables, commonly referred to as the flux states, encode the solution of the IBVP on the boundary/interface and are solutions of the Riemann problem constrained against physical boundary/interface conditions (7) and (17).

3.1 Boundary Data

We will construct boundary data which satisfy the physical boundary conditions (7) exactly and preserve the amplitude of the outgoing characteristic p at $x = 0$, and q at $x = L$. To begin, we define the hat-variables preserving the amplitude of outgoing characteristics

$$\begin{aligned} \frac{1}{2}\left( Z_{s}(0){\widehat{v}}_0 + {\widehat{\sigma }}_0\right) = p_0, \quad \frac{1}{2}\left( {Z_{s}(L)}{\widehat{v}}_L - {\widehat{\sigma }}_L \right) = q_L, \end{aligned}$$

(20)

with

$$\begin{aligned} p_0 = \frac{1}{2}\left( Z_s(0)v(0,t) + \sigma (0,t)\right) , \quad q_L = \frac{1}{2}\left( Z_s(L) v(L,t) - \sigma (L,t)\right) . \end{aligned}$$

(21)

Since hat-variables also satisfy the physical boundary condition, we must have

$$\begin{aligned} \frac{Z_{s}(0)}{2}\left( {1-r_0}\right) {\widehat{v}}_0 -\frac{1+r_0}{2} {\widehat{\sigma }}_0 = 0, \quad \frac{Z_{s}(L)}{2} \left( {1-r_L}\right) {\widehat{v}} _L+ \frac{1+r_L}{2}{\widehat{\sigma }}_L = 0. \end{aligned}$$

(22)

The algebraic problem for the hat-variables, defined by Eqs. (20) and (22), has a unique solution, namely

$$\begin{aligned} {\widehat{v}}_0&= \frac{(1+r_0)}{Z_{s}(0)}p_0, \quad {\widehat{\sigma }}_0 = {(1-r_0)}p_0, \nonumber \\ {\widehat{v}}_L&= \frac{(1+r_L)}{Z_{s}(L)}q_L, \quad {\widehat{\sigma }}_L = {-(1-r_L)}q_L. \end{aligned}$$

(23)

The expressions in (23) define a rule to update particle velocities and tractions on the external boundaries $x = 0, L$,

$$\begin{aligned} v(x, t)&= {\widehat{v}}_0(x, t) , \quad {\sigma }(x, t) = {\widehat{\sigma }}_0(x, t) , \quad \text {at} \quad x = 0, \nonumber \\ v(x, t)&= {\widehat{v}}_L(x, t) , \quad {\sigma }(x, t) = {\widehat{\sigma }}_L(x, t) , \quad \text {at} \quad x = L. \end{aligned}$$

(24)

It is particularly important to note that the boundary procedure (24) is equivalent to the original boundary condition (6). To verify this, we consider a free-surface boundary condition at $x = 0$, with $r_0 = 1$. From (23) and (24) we have ${\sigma }(0, t) = {\widehat{\sigma }}_0(0, t) = 0,$ and ${v}(0, t) = {\widehat{v}}_0(0, t) = v(0,t).$ The traction on the boundary, at $x = 0$, vanishes and the particle velocity on the boundary, at $x = 0$, is not altered by the boundary procedure (24).

By construction, the hat-variables ${\widehat{v}}_0, {\widehat{\sigma }}_0$, ${\widehat{v}}_L, {\widehat{\sigma }}_L$ satisfy the following algebraic identities:

(25a)

(25b)

(25c)

The first identity (25a) holds by definition (20). Using (25a) in $\left( p_0\right) ^2-\left( {\widehat{q}}_0\right) ^2$ and $\left( q_L\right) ^2 -\left( {\widehat{p}}_L\right) ^2$ gives the second identity (25b). From the solutions of the hat-variables in (23) it is clear that (25c) holds. The algebraic identities (25a)–(25c) will be crucial in proving numerical stability.

3.2 Interface Data

Similarly, for the interface we define the outgoing characteristics

$$\begin{aligned} q^{-}:= \frac{1}{2}\left( Z_{s}^{-} v^{-} - \sigma ^{-}\right) , \quad p^{+}:= \frac{1}{2}\left( Z_{s}^{+} v^{+} + \sigma ^{+}\right) , \end{aligned}$$

(26)

that must be preserved by the interface data. By combining (26) with force balance, $\sigma ^{-} = \sigma ^{+} = \sigma$, we obtain

$$\begin{aligned} {\sigma } = \varPhi - \eta \llbracket {v} \rrbracket , \end{aligned}$$

(27)

where

$$\begin{aligned} \varPhi = \eta \left( \frac{2}{Z_{s}^{+}}p^{+} - \frac{2}{Z_{s}^{-}} q^{-}\right) , \quad \eta = \frac{Z_{s}^{-}Z_{s}^{+}}{Z_{s}^{+}+Z_{s}^{-}} > 0. \end{aligned}$$

Note that $\varPhi$ is the stress transfer functional and $\eta \llbracket {v} \rrbracket$ is the radiation damping term [15, 19]. Equation (27) arises naturally in the boundary integral formulation of linear elasticity [19]. In particular, ${\sigma } = \varPhi$ is the traction on a locked interface, $\llbracket {v} \rrbracket = 0$. When the interface is slipping, $\llbracket {v} \rrbracket \ne 0$, traction is altered by wave radiation according to (27).

We want to construct interface data ${\widehat{v}}^{-}, {\widehat{\sigma }}^{-}$, ${\widehat{v}}^{+}, {\widehat{\sigma }}^{+}$, and the absolute slip-rate ${\widehat{V}} = |{[\![{\widehat{v}} ]\!]}| \ge 0$, such that the data satisfy the physical interface conditions (force balance + friction law)

$$\begin{aligned} \text {force balance:} \quad&{ {\widehat{\sigma }}^{-} = {\widehat{\sigma }}^{+} = {\widehat{\sigma }}}, \nonumber \\ \text {friction law:} \quad&{\widehat{\sigma }} = \alpha {[\![{\widehat{v}} ]\!]}, \quad \alpha = \sigma _n\frac{f({\widehat{V}})}{{\widehat{V}}}\ge 0, \end{aligned}$$

(28)

and preserve the amplitude of the outgoing characteristics

$$\begin{aligned} {\widehat{q}}^{-}:=\frac{1}{2}\left( Z_{s}^{-} {\widehat{v}}^{-} - {\widehat{\sigma }}^{-}\right) = q^{-}, \quad {\widehat{p}}^{+}:= \frac{1}{2}\left( Z_{s}^{+} {\widehat{v}}^{+} + {\widehat{\sigma }}^{+}\right) = p^{+}. \end{aligned}$$

(29)

As before, combining both equations in (29) and enforcing force balance, ${ {\widehat{\sigma }}^{-} = {\widehat{\sigma }}^{+} = {\widehat{\sigma }}}$, defined in (28), we obtain

$$\begin{aligned} {\widehat{\sigma }} = \varPhi - \eta \llbracket {\widehat{v}} \rrbracket . \end{aligned}$$

Thus, we obtain the nonlinear algebraic problem for tractions and the slip-rate,

$$\begin{aligned} {\widehat{\sigma }} = \varPhi - \eta \llbracket {\widehat{v}} \rrbracket , \quad {\widehat{\sigma }} = \alpha \llbracket {\widehat{v}} \rrbracket , \quad \alpha = \sigma _n\frac{f({\widehat{V}})}{{\widehat{V}}}\ge 0. \end{aligned}$$

(30)

However, if the friction coefficient $f({\widehat{V}})$ is linear the corresponding algebraic problems in (30) will be linear.

We combine the two equations in (30) to

$$\begin{aligned} \sigma _n{f({\widehat{V}})} + \eta {\widehat{V}} = |\varPhi |, \end{aligned}$$

(31)

which is a nonlinear algebraic equation for the absolute slip-rate ${\widehat{V}}\ge 0$. We can now solve (31) for the absolute slip-rate ${\widehat{V}}$ using any root finding algorithm, and compute $\alpha \ge 0$. The above algebraic problem (30) has a unique solution which is solved exactly,

$$\begin{aligned} {\widehat{\sigma }} = \frac{\alpha }{\eta + \alpha }\varPhi , \quad \llbracket {\widehat{v}} \rrbracket = \frac{1}{\eta + \alpha }\varPhi , \quad \alpha = \sigma _n\frac{f({\widehat{V}})}{{\widehat{V}}}\ge 0. \end{aligned}$$

(32)

We therefore have

$$\begin{aligned} {\widehat{\sigma }}^{-} = {\widehat{\sigma }}^{+} = {\widehat{\sigma }}, \end{aligned}$$

and

$$\begin{aligned} {\widehat{v}}^{-} = \frac{1}{Z_{s}^{+} }\left( 2p^{+} - {\widehat{\sigma }}^{+}\right) - \llbracket {\widehat{v}} \rrbracket , \quad {\widehat{v}}^{+} = \frac{1}{Z_{s}^{-} }\left( 2q^{-} + {\widehat{\sigma }}^{-}\right) + \llbracket {\widehat{v}} \rrbracket . \end{aligned}$$

We have constructed a rule to update tractions and particle velocities on the interface, $x = x_0$,

$$\begin{aligned} {\sigma }^{-}&= {\widehat{\sigma }}^{-}, \quad {\sigma }^{+} = {\widehat{\sigma }}^{+},\nonumber \\ {v}^{-}&= {\widehat{v}}^{-}, \quad {v}^{+} = {\widehat{v}}^{+}. \end{aligned}$$

(33)

In (33), we have equivalently redefined the physical interface condition (17).

By construction, the hat-variables ${\widehat{v}}^{-}, {\widehat{\sigma }}^{-}$, ${\widehat{v}}^{+}, {\widehat{\sigma }}^{+}$ satisfy the following algebraic identities:

$$\begin{aligned}&{\widehat{p}}^+ = p^+, \quad {\widehat{q}}^- = q^-, \end{aligned}$$

(34a)

$$\begin{aligned}&\left( p^+\right) ^2-\left( {\widehat{q}}^+\right) ^2 = Z_s^+{\widehat{\sigma }}{\widehat{v}}^+, \quad \left( q^-\right) ^2 -\left( {\widehat{p}}^-\right) ^2 = -Z_s^-{\widehat{\sigma }}{\widehat{v}}^-, \end{aligned}$$

(34b)

$$\begin{aligned}&\frac{1}{Z_s^+}\left( \left( p^+\right) ^2-\left( {\widehat{q}}^+\right) ^2\right) + \frac{1}{Z_s^-}\left( \left( q^-\right) ^2 -\left( {\widehat{p}}^-\right) ^2\right) = {\widehat{\sigma }} \llbracket {\widehat{v}} \rrbracket = \frac{\alpha }{(\eta + \alpha )^2}|\varPhi |^2, \end{aligned}$$

(34c)

where

$$\begin{aligned} {\widehat{p}}^{-}:=\frac{1}{2}\left( Z_{s}^{-} {\widehat{v}}^{-} +{\widehat{\sigma }}^{-}\right) , \quad {\widehat{q}}^{+}:= \frac{1}{2}\left( Z_{s}^{+} {\widehat{v}}^{+} - {\widehat{\sigma }}^{+}\right) . \end{aligned}$$

The first identity (34a) holds by the definition (29). Using (34a) in $\left( p^+\right) ^2-\left( {\widehat{q}}^+\right) ^2$ and $\left( q^-\right) ^2 -\left( {\widehat{p}}^-\right) ^2$ gives the second identity (34b). The third identity (34c) follows directly from (34b) with ${\widehat{\sigma }} = \frac{\alpha }{\eta + \alpha }\varPhi$, ${\widehat{v}}^+ - {\widehat{v}}^- := \llbracket {\widehat{v}} \rrbracket = \frac{1}{\eta + \alpha }\varPhi$. The data is unique and exact. Note the consistency at the limits: $\alpha \rightarrow \infty \implies [\![{\widehat{v}} ]\!]\rightarrow 0$, ${\widehat{\sigma }}[\![{\widehat{v}} ]\!]\rightarrow 0$, and $\alpha \rightarrow 0 \implies {\widehat{\sigma }} \rightarrow 0$, ${\widehat{\sigma }} [\![{\widehat{v}} ]\!]\rightarrow 0$. As before, the identities defined in (34a)–(34c) will be crucial in proving numerical stability.

4 The Discontinuous Galerkin Method

We begin by discretizing the domain $x \in \varOmega = [0, L]$ into K elements denoting the k-th element by $\varOmega _k = [x_k, x_{k+1}]$, where $k = 1, 2, \dots , K$, with $x_1 = 0$ and $x_{K+1} = L$. Next, we map the element $\varOmega _k$ to a reference element $\xi \in {\widetilde{\varOmega }} = [-1, 1]$ by the linear transformation

$$\begin{aligned} x(\xi ) = x_k + \frac{\varDelta {x}_k}{2}\left( 1 + \xi \right) , \quad \varDelta {x}_k = x_{k+1} - x_k. \end{aligned}$$

(35)

In the reference element, ${\widetilde{\varOmega }} = [-1, 1]$, the $L^2$-scalar product and norm are given by

$$\begin{aligned} \left( u, v\right) = \int _{-1}^{1} uvd\xi , \quad \Vert u\Vert ^2 = \left( u, u\right) . \end{aligned}$$

(36)

Note that for the reference element ${\widetilde{\varOmega }}$, we have omitted the subscript ${\widetilde{\varOmega }}$ in the scalar product and denoted $\left( u, v\right) : = \left( u, v\right) _{{\widetilde{\varOmega }}}.$ Therefore, the integral form (8)–(9) yield

$$\begin{aligned}&\sum _{k = 1}^{K} \left( \frac{\varDelta _k}{2}\left( \phi _v, {\rho } \frac{\partial v}{\partial t}\right) - \left( \phi _v, \frac{\partial \sigma }{\partial \xi } \right) \right) = 0, \end{aligned}$$

(37)

$$\begin{aligned}&\sum _{k = 1}^{K} \left( \frac{\varDelta _k}{2}\left( \phi _{\sigma }, \frac{1}{\mu }\frac{\partial \sigma }{\partial t}\right) - \left( \phi _{\sigma }, \frac{\partial v}{\partial \xi } \right) \right) = 0. \end{aligned}$$

(38)

4.1 Inter-element and Boundary Procedure, and Energy Identity

We will begin the development and construction of the inter-element and boundary procedure for the continuous integral form (37)–(38). As we will see later the procedure and analysis will naturally carry over when numerical approximations are introduced. We will end the discussion with the derivation of an energy equation analogous to (12).

We consider the element boundaries, $\xi = -1, 1$, and generate boundary and interface data ${\widehat{v}}(\xi , t)$, ${\widehat{\sigma }} (\xi , t)$. Note that the characteristics p, q are the natural carrier of information in the system. For an element $x \in \varOmega _k \rightarrow \xi \in {\widetilde{\varOmega }}$, we construct flux fluctuations by penalizing data against incoming characteristics p and q,

$$\begin{aligned} \begin{aligned}&F^k(-1, t):=q-{\widehat{q}} =\frac{Z_{s}(-1)}{2} \left( v(-1, t)-{\widehat{v}}(-1, t) \right) - \frac{1}{2}\left( \sigma (-1, t)- {\widehat{\sigma }} (-1, t)\right) ,\\&G^k(1, t) := p-{\widehat{p}} = \frac{Z_{s}(1) }{2} \left( v(1, t) -{\widehat{v}}(1, t) \right) + \frac{1}{2}\left( \sigma (1, t) - {\widehat{\sigma }}(1, t) \right) . \end{aligned} \end{aligned}$$

(39)

Note that q is the incoming characteristic at the left element boundary $\xi = -1$ and p is incoming characteristic at right element boundary $\xi = 1$. Therefore, $F^k(-1, t)$ penalizes data against the incoming characteristic at $\xi = -1$ and $G^k(1, t)$ penalizes data against the incoming characteristic at $\xi = 1$.

Remark 2

Note the uniform treatment of all DG element boundaries $\xi = -1, 1$, by the flux fluctuations $F^k(-1, t)$ and $G^k(1, t)$. The difference between external element boundaries $x = 0$, $x =L$ and internal element boundaries $0<x<L$, is determined by the algebraic problem yielding the corresponding hat-variables ${\widehat{v}}$, ${\widehat{\sigma }}$.

Since no approximations were introduced yet, we must have $v(\xi , t) \equiv {\widehat{v}}(\xi , t)$, $\sigma (\xi , t) \equiv {\widehat{\sigma }}(\xi , t)$ for $\xi = \pm 1$. Thus, at the external boundaries, $x = 0$, $x = L$, the fluctuations satisfy

$$\begin{aligned} \begin{aligned}&F^1(-1, t)\equiv B_0\left( v(0, t), \sigma (0, t), Z_{s}(0), r_0\right) =0, \quad x = 0,\\&G^K(1, t)\equiv B_L\left( v(L, t), \sigma (L, t), Z_{s}(L), r_L\right) =0, \quad x = L. \end{aligned} \end{aligned}$$

(40)

Next, we append the flux fluctuations, $F^k(-1, t) \rightarrow 0$, $G^k(1, t) \rightarrow 0$, to the integral form (37)–(38) with specifically chosen penalty weights, having

$$\begin{aligned}&\frac{\varDelta _k}{2}\left( \phi _v, {\rho } \frac{\partial v}{\partial t}\right) - \left( \phi _v, \frac{\partial \sigma }{\partial \xi } \right) + {\phi _v(-1) F^k(-1, t) + \phi _v(1)G^k(1, t)} = 0, \end{aligned}$$

(41)

$$\begin{aligned}&\frac{\varDelta _k}{2}\left( \phi _{\sigma }, \frac{1}{\mu }\frac{\partial \sigma }{\partial t}\right) - \left( \phi _{\sigma }, \frac{\partial v}{\partial \xi } \right) - \frac{\phi _{\sigma }(-1)}{Z_s(-1)}F^k(-1, t) + \frac{\phi _{\sigma }(1)}{Z_s(1)}G^k(1, t) = 0. \end{aligned}$$

(42)

The flux fluctuations vanish identically for the exact solutions that satisfy the IBVP, that is $G^k(1, t) = F^k(-1, t) = 0$. However, when numerical approximations are introduced the flux fluctuations will be proportional to the truncation error.

The penalty weights have been chosen such that the physical dimensions of all terms in Eqs. (41)–(42) match. For instance in the stress Eq. (42), we have penalized the flux functions by the shear admittance, $1/Z_s(\xi )$. This is motivated by a dimensional analysis. As we will see later, this physically motivated penalty weight is also critical for numerical stability.

Again we note that at infinite frictional strength $\alpha \rightarrow \infty \implies \llbracket {v} \rrbracket = 0$, the hat-variable match the exact solutions of the Riemann problem for the hyperbolic PDE, and the numerical flux in (41)–(42) is equivalent to the Godunov flux [20].

Remark 3

The following remarks summarise the inter-element and boundary procedure:

• 1. All DG inter-element faces are held together by a frictional strength, $\alpha \ge 0$.

• 2. Classical internal element faces where slip is not permitted have infinite frictional strength, $\alpha \rightarrow \infty$.

• 3. Weak interfaces have finite frictional strength, $\alpha \ge 0$, the slip motion is governed by a friction law.

• 4. External DG element faces, $x = 0, L$, are closed with the linear well-posed boundary conditions (6).

• 5. We construct transformed (hat-) variables that encode the solutions of the IBVP at element faces.

• 6. By construction the DG flux fluctuations, $G^k(1, t)$, $F^k(-1, t)$, have been designed to satisfy the boundary condition (6) and the frictional interface condition (17) exactly.

We can now state our first main result.

Theorem 1

The weak form (41)–(42) satisfies the energy identity

$$\begin{aligned} \begin{aligned} \frac{d}{dt} {E}(t)&= -\sum _{k=1}^{K}\left( \frac{1}{Z_{s}(-1)}|F^k(-1, t)|^2 + \frac{1}{Z_{s}(1)}|G^k(1, t)|^2 \right) \\&\quad - \sum _{k=2}^{K}\frac{\alpha ^k(\xi )}{\left( \eta ^k(\xi ) + \alpha ^k(\xi )\right) ^2}|\varPhi ^k(\xi )|^2 - \frac{1-r_0^2}{Z_{s}(0)}|p_0|^2 -\frac{1-r_L^2}{Z_{s}(L)}|q_L |^2. \end{aligned} \end{aligned}$$

(43)

Proof

As above, we replace $\phi _v(\xi )$ with $v(\xi ,t)$ in (41) and $\phi _{\sigma }(\xi )$ with ${\sigma }(\xi ,t)$ in (42), integrate by parts the spatial derivative term in (41) and sum the equations. We have

$$\begin{aligned} \begin{aligned} \frac{d}{dt}E^k(t)&= {v(1, t)\sigma (1, t) - v(-1, t)\sigma (-1, t) } -{v(-1, t) F^k(-1, t) - v(1, t)G^k(1, t) } \\&\quad +\left( \frac{{\sigma }(-1, t)}{Z_s(-1)}F^k(-1, t) - \frac{{\sigma }(1, t)}{Z_s(1)}G^k(1, t)\right) , \end{aligned} \end{aligned}$$

(44)

where

$$\begin{aligned} E^k(t) = \frac{\varDelta {x}_k}{2}\left( v, \rho v \right) + \frac{\varDelta {x}_k}{2}\left( \sigma , \frac{1}{\mu } \sigma \right) > 0. \end{aligned}$$

(45)

Introducing $E(t) = \sum _{k=1}^{K}E^k(t)$ and summing contributions from all elements yields

$$\begin{aligned} \begin{aligned} \frac{d}{dt} E(t)&= -\sum _{k = 1}^{K}{\left( \frac{1}{Z_s(-1) }\left( |F^k(-1,t)|^2 + |p^k(-1,t)|^2 - |{\widehat{q}}^k(-1,t)|^2\right) \right) } \\&\quad -\sum _{k = 1}^{K}{\left( \frac{1}{Z_s(1) }\left( |G^k(1, t)|^2 + |q^k(1, t)|^2 - |{\widehat{p}}^k(1, t)|^2\right) \right) }. \end{aligned} \end{aligned}$$

(46)

Using the identities (25a)–(25c) and (34a)–(34c), with

$$\begin{aligned} {\widehat{\sigma }}(\xi )= \frac{\alpha ^k(\xi ) }{\eta ^k(\xi ) + \alpha ^k(\xi ) }\varPhi ^k(\xi ) , \quad \llbracket {\widehat{v}}(\xi ) \rrbracket = \frac{1}{\eta ^k(\xi ) + \alpha ^k(\xi )}\varPhi ^k(\xi ), \end{aligned}$$

in the right hand side of (46) gives the energy identity (43). $\square$

Since $|r_0|\le 1$, $|r_L|\le 1$ and ${\widehat{\sigma }} \llbracket {\widehat{v}} \rrbracket = \frac{\alpha ^k}{(\eta ^k + \alpha ^k)^2}\varPhi ^2 \ge 0$, then the boundary terms in the right hand side of (43) are negative semi-definite. The term $-{\widehat{\sigma }} \llbracket {\widehat{v}} \rrbracket = -\frac{\alpha ^k}{(\eta ^k + \alpha ^k)^2}\varPhi ^2 \le 0$ represents the rate of work done by friction at the interface, which is dissipated as heat. For exact solutions of the IBVP the flux fluctuations vanish identically $G^k(1, t) \equiv 0$, $F^k(-1, t) \equiv 0$ and the energy equation (43) is identical to (19). In the limit $\alpha _k \rightarrow \infty \implies {\widehat{\sigma }}(\xi )\llbracket {\widehat{v}}(\xi ) \rrbracket \rightarrow 0$, we obtain the energy identity (12). Numerical approximations will introduce truncation errors and $G^k(1, t) \ne 0$, $F^k(-1, t) \ne 0$. The numerical flux fluctuations $G^k(1, t)$, $F^k(-1, t)$ will be proportional to the truncation error and will introduce some numerical dissipation. However, the numerical dissipation will vanish in the limit of mesh refinement, $\varDelta {x}_k \rightarrow 0$ with $\varDelta {x}_k = x_{k+1} - x_k$, and the remaining terms in the right hand side of (43) match exactly the physical energy rate given by the boundary condition (7) and interface condition (17).

4.2 The Galerkin Approximation

Inside the transformed element $\xi \in [-1, 1]$, we approximate the solution by a polynomial interpolant, and write

$$\begin{aligned} v^k(\xi , t) = \sum _{j = 1}^{N+1}v_j^k(t) {\mathscr {L}}_j(\xi ), \quad \sigma ^k(\xi , t) = \sum _{j = 1}^{N+1}\sigma _j^k(t) {\mathscr {L}}_j(\xi ), \end{aligned}$$

(47)

where $v_j^k(t)$, $\sigma _j^k(t)$ are evolving degrees of freedom to be determined and ${\mathscr {L}}_j\in {\mathbb {P}}^N$ is the jth interpolating polynomial of degree N. Here ${\mathbb {P}}^N$ is the space of degree $N\ge 0$ polynomials. If we consider nodal basis then the interpolating polynomials satisfy ${\mathscr {L}}_j(\xi _i) = \delta _{ij}$, where $\delta _{ij}$ is the Kronecker delta. The interpolating nodes $\xi _i$, $i = 1, 2, \dots , N+1$ are the nodes of a Gauss-type quadrature with

$$\begin{aligned} \sum _{i = 1}^{N+1} f(\xi _i)w_i \approx \int _{-1}^{1}f(\xi ) d\xi , \end{aligned}$$

(48)

where $w_i$ are quadrature weights. We will only use quadrature rules that are exact for all polynomial integrand $f(\xi )$ of degree $\le 2N-1$. Admissible candidates are the Gauss–Lobatto quadrature rule with the GLL nodes and the Gauss–Legendre quadrature rule with the GL nodes. Note that, boundary nodes $\xi = -1, 1$ belong to the GLL quadrature nodes but not to the GL quadrature nodes.

The $L^2$-scalar products and norm (36) are approximated by

$$\begin{aligned} \left( u, v\right) _N = \sum _{i = 1}^{N+1} u(\xi _i)v(\xi _i)w_i, \quad \Vert v\Vert ^2_N = \left( v, v\right) _N. \end{aligned}$$

(49)

The discrete norm $\Vert v\Vert _N$ is equivalent to the continuous norm $\Vert v\Vert$ (see [5], after (5.3.2)), that is for all $v\in {\mathbb {P}}^N$ we have

$$\begin{aligned} \Vert v\Vert \le \Vert v\Vert _N \le \sqrt{3}\Vert v\Vert . \end{aligned}$$

(50)

We now make a classical Galerkin approximation by choosing test functions $(\phi _v(\xi ), \phi _\sigma (\xi )) \in {\mathbb {P}}^N$ in the same space as the basis functions, so that the residual is orthogonal to the approximation space. We obtain the DG approximation of the IBVP, (1) with (7) and (17)

$$\begin{aligned}&\frac{\varDelta _k}{2}\left( \phi _v, {\rho } \frac{\partial v^k}{\partial t}\right) _N - \left( \phi _v, \frac{\partial \sigma ^k}{\partial \xi } \right) _N+ {\phi _v(-1) F^k(-1, t) + \phi _v(1)G^k(1, t)} = 0, \end{aligned}$$

(51)

$$\begin{aligned}&\frac{\varDelta _k}{2}\left( \phi _{\sigma }, \frac{1}{\mu }\frac{\partial \sigma ^k}{\partial t}\right) _N - \left( \phi _{\sigma }, \frac{\partial v^k}{\partial \xi } \right) _N - \frac{\phi _{\sigma }(-1)}{Z_s(-1)}F^k(-1, t) + \frac{\phi _{\sigma }(1)}{Z_s(1)}G^k(1, t) = 0, \qquad \end{aligned}$$

(52)

where

$$\begin{aligned} G^k(1, t)&:= \frac{Z_{s}^{k}(1)}{2} \left( v^{k}(1, t)-{\widehat{v}}^{k}(1, t) \right) + \frac{1}{2}\left( \sigma ^{k}(1, t)- {\widehat{\sigma }}^{k}(1, t)\right) , \\ F^{k}(-1, t)&:= \frac{Z_{s}^{k}(-1)}{2} \left( v^{k}(-1, t)-{\widehat{v}}^{k}(-1, t) \right) - \frac{1}{2}\left( \sigma ^{k}(-1, t)- {\widehat{\sigma }}^{k}(-1, t)\right) . \end{aligned}$$

Note that the discrete scalar product for the terms involving spatial derivatives are exact and allows discrete integration by parts, that is

$$\begin{aligned} \left( \phi _v, \frac{\partial \sigma ^k}{\partial \xi } \right) _N =&\left( \phi _v, \frac{\partial \sigma ^k}{\partial \xi } \right) , \quad \left( \phi _v, \frac{\partial \sigma ^k}{\partial \xi } \right) _N = -\left( \frac{\partial \phi _v}{\partial \xi } , \sigma ^k\right) _N \nonumber \\&+ \phi _v(1)\sigma ^k(1,t)-\phi _v(-1)\sigma ^k(-1,t). \end{aligned}$$

(53)

The hat-variables, at the element boundaries, $\xi = -1, 1$, are computed as outlined in Sects. 3.1 and 3.2. The only difference is that instead of the exact continuous solutions used in Sect. 3.1 and 3.2, the numerical boundary/interface data for the characteristics are generated using the elemental polynomial approximations, $v^k (\xi , t), \sigma ^k(\xi , t)$, defined in (47) and evaluated at the boundaries, at $\xi = -1, 1$. However, as before, the discrete hat-variables satisfy the same algebraic identities, (25a)–(25c) and (34a)–(34c), as the continuous exact counterparts.

5 Stability

In this section, we will prove that the semi-discrete approximation (51)–(52) is asymptotically stable. We will derive a discrete energy equation analogous to the continuous energy equation (43). To begin, define the elemental discrete energy

$$\begin{aligned} {\mathscr {E}}^k(t) = \frac{\varDelta {x}_k}{2}\left( v^k, \rho v^k \right) _N+ \frac{\varDelta {x}_k}{2}\left( \sigma ^k, \frac{1}{\mu } \sigma ^k \right) _N > 0. \end{aligned}$$

(54)

Definition 1

Let ${\mathscr {E}}(t) = \sum _{k=1}^{K} {\mathscr {E}}^k(t)$ denote the global semi-discrete energy. The semi-discrete approximation (51)–(52) is asymptotically stable if

$$\begin{aligned} \frac{d}{dt} {\mathscr {E}}(t) \le 0, \quad \forall \varDelta {x} > 0. \end{aligned}$$

(55)

Our second main result is the following theorem:

Theorem 2

The semi-discrete approximation (51)–(52) satisfies the energy equation

$$\begin{aligned} \begin{aligned} \frac{d}{dt}{\mathscr {E}}(t)&= -\sum _{k=1}^{K}\left( \frac{1}{Z_{s}^k(-1)}|F^k(-1, t)|^2 + \frac{1}{Z_{s}^k(1)}|G^k(1, t)|^2\right) -\sum _{k=2}^{K} \frac{\alpha ^k}{\left( \eta ^k + \alpha ^k\right) ^2}|\varPhi ^k|^2 \\&\quad - \frac{1-r_0^2}{Z_{s}^1(-1)}|p_0|^2 -\frac{1-r_L^2}{Z_{s}^K(1)}|q_L|^2, \end{aligned} \end{aligned}$$

(56)

with ${\mathscr {E}}(t) = \sum _{k=1}^{K} {\mathscr {E}}^k(t)$, and

$$\begin{aligned} p_0 = \frac{1}{2}\left( Z_s^1(-1)v^1(-1, t) + \sigma ^1(-1, t)\right) , \quad q_L = \frac{1}{2}\left( Z_s^K(1) v^K(1, t) - \sigma ^K(1, t)\right) . \end{aligned}$$

Proof

As above, we replace $\phi _v(\xi )$ with $v^k(\xi ,t)$ in (51) and $\phi _{\sigma }(\xi )$ with ${\sigma }^k(\xi ,t)$ in (52), integrate by parts, that is we replace the spatial derivative term in (51) by (53) and sum the equations. We have

$$\begin{aligned} \begin{aligned} \frac{d}{dt}{\mathscr {E}}^k(t)&= -{v}^k(-1, t){\sigma }^k(-1, t) + {v}^k(1, t){\sigma }^k(1, t) \\&\quad - {v}^k(-1, t)F^k(-1, t)- {v}^k(1, t)G^k(1, t)\\&\quad + \frac{1}{Z_{s}(-1)}{\sigma }^k( -1, t)F^k(-1, t)- \frac{1}{Z_{s}(1)}{\sigma }^k( 1, t)G^k(1, t). \end{aligned} \end{aligned}$$

(57)

Introducing the global energy ${\mathscr {E}}(t) = \sum _{k=1}^{K}{\mathscr {E}}^k(t)$ and summing contributions from all elements yields

$$\begin{aligned} \begin{aligned} \frac{d}{dt} {\mathscr {E}}(t)&= -\sum _{k = 1}^{K}{\left( \frac{1}{Z_s(-1) }\left( |F^k(-1,t)|^2 + |p^k(-1,t)|^2 - |{\widehat{q}}^k(-1,t)|^2\right) \right) } \\&\quad -\sum _{k = 1}^{K}{\left( \frac{1}{Z_s(1) }\left( |G^k(1, t)|^2 + |q^k(1, t)|^2 - |{\widehat{p}}^k(1, t)|^2\right) \right) }. \end{aligned} \end{aligned}$$

(58)

Using the identities (25a)–(25c) and (34a)–(34c), with

$$\begin{aligned} {\widehat{\sigma }}^k(\xi )= \frac{\alpha ^k(\xi ) }{\eta ^k(\xi ) + \alpha ^k(\xi ) }\varPhi ^k(\xi ) , \quad \llbracket {\widehat{v}}(\xi ) \rrbracket = \frac{1}{\eta ^k(\xi ) + \alpha ^k(\xi )}\varPhi ^k(\xi ), \end{aligned}$$

in the right hand side of (58) gives the energy identity (56). $\square$

The energy equation (56) is completely analogous to the continuous equation (43) and (19).

Note that the quantity in the right hand side of (56) are surface terms, and their units match the energy-rate per surface area. Note that ${\widehat{\sigma }}^k {[\![{\widehat{v}}^k ]\!]} = \frac{\alpha ^k}{(\eta ^k + \alpha ^k)^2}|\varPhi ^k|^2 \rightarrow 0$, for $\alpha ^k \rightarrow \infty$ or $\alpha ^k \rightarrow 0$. This implies that the spectral radius of the discrete operator has an upper bound which is independent of $\alpha ^k \ge 0$. If we had used characteristics to directly enforce the physical condition (17), we will have $\sigma ^k [\![{v}^k ]\!]= \alpha ^k [\![{v}^k ]\!]^2\ge 0$, which yields an energy estimate. However it will potentially introduce artificial numerical stiffness, for $\alpha ^k \gg 1$, which will require implicit time integration, for practical problems. The energy equation (56) is valid for both nodal and modal polynomial basis, and for Gauss–Lobatto–Legendre nodes, with boundary points as quadrature nodes, and Gauss–Legendre nodes, where boundary points are not quadrature nodes.

Remark 4

Theorems 1 and 2 prove the asymptotic stability and robustness of the method. Here, all internal DG element faces are frictional interfaces. In principle, we can allow all adjacent elements to slide governed by a nonlinear friction law. While this will not affect stability, the energy decay rate will increase due to heat dissipation.

The analysis here focuses on a 1D model problem, however with limited modifications the results can be extended to multidimensional (2D and 3D) tensor product DG method approximations of the elastic wave equation on quadrilateral and hexahedral meshes, and also on triangular and tetrahedral meshes.

6 The Error Equation and Error Estimate

We will now derive the error equation and the error estimate for the derived DG method (51)–(52). We will demonstrate that the physics based numerical flux designed in this study allows to prove convergence for discontinuous and nearly singular exact solutions and in particular when the interface is sliding, $\llbracket {v} \rrbracket \ne 0$.

Let $v(\xi , t), \sigma (\xi , t)$ denote the elemental exact solutions that satisfy (41)–(42), where $\xi \in {\widetilde{\varOmega }} = [-1, 1]$ and $x(\xi ) \in \varOmega _k = [x_k, x_{k+1}]$. We define the function space

$$\begin{aligned} H^m\left( {\widetilde{\varOmega }}\right) = \left\{ v(\xi ): \quad \left\| \frac{\partial ^m v}{\partial \xi ^m}\right\| ^2< \infty , \quad \forall \xi \in {\widetilde{\varOmega }} \right\} . \end{aligned}$$

(59)

Within the element $\xi \in {\widetilde{\varOmega }}$, we seek exact solutions $(v, \sigma ) \in H^m\left( {\widetilde{\varOmega }}\right)$, $m \ge 1$. This ensures the exact solutions are at the least weakly differentiable within the element. Conditions across the inter-element boundaries are given by (17). As in Fig. 1, note in particular that the particle velocity $v(\xi , t)$ can be discontinuous across the elements and the stress $\sigma (\xi , t)$ nearly singular at the rupture tip. Define the error in the particle velocity and the stress by

$$\begin{aligned} e_v(\xi , t)=v(\xi , t)-v^k(\xi , t), \quad e_\sigma (\xi , t)=\sigma (\xi , t)-\sigma ^k(\xi , t), \end{aligned}$$

where $v(\xi , t), \sigma (\xi , t)$ are the exact solutions satisfying (41)–(42) and $v^k(\xi , t), \sigma ^k(\xi , t)$ are the numerical solutions satisfying (51)–(52).

Now denote $\pi ^N\left( v\right) \in {\mathbb {P}}^N$ a degree N polynomial interpolant of $v(\xi , t)$. We split the errors into

$$\begin{aligned}&e_v(\xi , t) = \underbrace{\left( \pi ^N\left( v\right) -v^k(\xi , t)\right) }_{e_v^k(\xi , t)} + \underbrace{\left( v(\xi , t) - \pi ^N\left( v\right) \right) }_{e_v^p(\xi , t) } \equiv e_v^k(\xi , t) + e_v^p(\xi , t),\nonumber \\&e_\sigma (\xi , t) = \underbrace{\left( \pi ^N\left( \sigma \right) -\sigma ^k(\xi , t)\right) }_{e_\sigma ^k(\xi , t)} + \underbrace{\left( \sigma (\xi , t) - \pi ^N\left( \sigma \right) \right) }_{e_\sigma ^p(\xi , t) } \equiv e_\sigma ^k(\xi , t) + e_\sigma ^p(\xi , t). \end{aligned}$$

(60)

Here $e_v^k(\xi , t)$, $e_\sigma ^k(\xi , t)$ are the numerical errors and $e_v^p(\xi , t)$, $e_\sigma ^p(\xi , t)$ are the interpolation errors. The interpolation errors $e_v^p(\xi , t), e_\sigma ^p(\xi , t)$ are independent of the approximate solutions $v^k(\xi , t), \sigma ^k(\xi , t)$ and is the sum of the series truncation error and the aliasing error. The norm of the interpolation error converges to zero spectrally fast as [5] (5.4.33)

$$\begin{aligned} \Vert e_v^p\Vert _{L^2\left( {\widetilde{\varOmega }}\right) } \le C N^{-m} |v|_{H^{m;N}\left( {\widetilde{\varOmega }}\right) }, \end{aligned}$$

(61)

where

$$\begin{aligned} |v|_{H^{m;N}\left( {\widetilde{\varOmega }}\right) }^2 = \sum _{n = \min \left( m, N+1\right) }^{m} \left\| \frac{\partial ^n v}{\partial \xi ^n}\right\| ^2. \end{aligned}$$

(62)

The generalisation of (61) for $\Vert \cdot \Vert _{H^n\left( {\widetilde{\varOmega }}\right) }$, $1 \le n \le m$ is [5] (5.4.34)

$$\begin{aligned} \Vert e_v^p\Vert _{H^n\left( {\widetilde{\varOmega }}\right) } \le C N^{\gamma _{mn}} |v|_{H^{m;N}\left( {\widetilde{\varOmega }}\right) }, \end{aligned}$$

(63)

where $\gamma _{mn} = {2n-m-1/2}$ for GL nodes and $\gamma _{mn} = {n-m}$ for GLL nodes. On a physical element $\varOmega _k = [x_k, x_{k+1}]$, as opposed to a reference element $\xi \in {\widetilde{\varOmega }} = [-1, 1]$, the interpolation error is bounded by [5] (5.4.42)

$$\begin{aligned} \Vert e_v^p\Vert _{H^n\left( {\varOmega _k}\right) } \le C\varDelta {x}_k^{\min \left( m, N\right) -n} N^{\gamma _{mn}} |v|_{H^{m;N}\left( {\varOmega _k}\right) }, \end{aligned}$$

(64)

for $n =0, 1$.

We write $v = \pi ^N\left( v\right) + e_v^p$, $\sigma = \pi ^N\left( \sigma \right) + e_\sigma ^p$, from (41)–(42) we have

$$\begin{aligned} \frac{\varDelta {x}_k}{2}\left( \phi _v, {\rho } \frac{\partial \pi ^N\left( v\right) }{\partial t} \right)&= -\left( \frac{\partial \phi _v}{\partial \xi }, \pi ^N\left( \sigma \right) \right) - \frac{\varDelta {x}_k}{2}\left( \phi _{v}, {\rho } \frac{\partial e_v^p}{\partial t} \right) + \frac{\varDelta {x}_k}{2}\left( \phi _{v}, \frac{\partial e_\sigma ^p}{\partial x} \right) \nonumber \\&\quad - \phi _v\left( -1\right) \left( \sigma \left( -1, t\right) +F^k\left( -1, t\right) \right) \nonumber \\&\quad - \phi _v\left( 1\right) \left( G^k\left( 1, t\right) -\sigma \left( 1, t\right) \right) , \end{aligned}$$

(65)

$$\begin{aligned} \frac{\varDelta {x}_k}{2}\left( \phi _{\sigma }, \frac{1}{\mu }\frac{\partial \pi ^N\left( \sigma \right) }{\partial t}\right)&= \left( \phi _{\sigma }, \frac{\partial \pi ^N\left( v\right) }{\partial \xi } \right) - \frac{\varDelta {x}_k}{2}\left( \phi _{\sigma }, \frac{1}{\mu }\frac{\partial e_\sigma ^p}{\partial t} \right) + \frac{\varDelta {x}_k}{2}\left( \phi _{\sigma }, \frac{\partial e_\sigma ^p}{\partial x}\right) \nonumber \\&\quad + \frac{\phi _{\sigma }(-1)}{Z_s(-1)}F^k(-1, t) - \frac{\phi _{\sigma }(1)}{Z_s(1)}G^k(1, t). \end{aligned}$$

(66)

Through (64), the gradients of the interpolation errors are bounded and spectrally small, namely

$$\begin{aligned} \begin{aligned}&\left\| \frac{\partial e_v^p}{\partial x} \right\| _{\varOmega _k} \le C\varDelta {x}_k^{\min \left( m, N\right) -1} N^{\gamma _{m1}} |v|_{H^{m;N}\left( {\varOmega _k}\right) },\\&\left\| \frac{\partial e_\sigma ^p}{\partial x} \right\| _{\varOmega _k} \le C\varDelta {x}_k^{\min \left( m, N\right) -1} N^{\gamma _{m1}} |\sigma |_{H^{m;N}\left( {\varOmega _k}\right) }. \end{aligned} \end{aligned}$$

(67)

The time derivatives of the interpolation errors are also bounded by (67) through (1).

Restrict $\phi _{v}, \phi _{\sigma } \in {\mathbb {P}}^N$ we have

$$\begin{aligned}&\frac{\varDelta {x}_k}{2}\left( \phi _v, {\rho } \frac{\partial \pi ^N\left( v\right) }{\partial t} \right) _N = -\left( \frac{\partial \phi _v}{\partial \xi }, \pi ^N\left( \sigma \right) \right) _N - \phi _v\left( -1\right) \left( \pi ^N\left( \sigma \right) \left( -1, t\right) +F^k\left( -1, t\right) \right) \nonumber \\&\quad - \phi _v\left( 1\right) \left( G^k\left( 1, t\right) -\pi ^N\left( \sigma \right) \left( 1, t\right) \right) \nonumber \\&\quad + \frac{\varDelta {x}_k}{2} \left( \phi _v, \rho \left( \frac{\partial e_v^p(\xi , t)}{\partial t} + {\mathbb {I}}_{v}^k\right) \right) - \frac{\varDelta {x}_k}{2}\left( \phi _v, \rho {\mathbb {I}}_{v}^k\right) _N + \frac{\varDelta {x}_k}{2}\left( \phi _{v}, \frac{\partial e_\sigma ^p(x, t)}{\partial x}\right) , \end{aligned}$$

(68)

$$\begin{aligned}&\frac{\varDelta {x}_k}{2}\left( \phi _{\sigma }, \frac{1}{\mu }\frac{\partial \pi ^N\left( \sigma \right) }{\partial t}\right) _N = \left( \phi _{\sigma }, \frac{\partial \pi ^N\left( v\right) }{\partial \xi } \right) _N + \frac{\phi _{\sigma }(-1)}{Z_s(-1)}F^k(-1, t) - \frac{\phi _{\sigma }(1)}{Z_s(1)}G^k(1, t) \nonumber \\&\quad + \frac{\varDelta {x}_k}{2} \left( \phi _\sigma , \frac{1}{\mu }\left( \frac{\partial e_\sigma ^p(\xi , t)}{\partial t} + {\mathbb {I}}_{\sigma }^k\right) \right) - \frac{\varDelta {x}_k}{2}\left( \phi _\sigma , \frac{1}{\mu }{\mathbb {I}}_{\sigma }^k\right) _N\nonumber \\&\quad + \frac{\varDelta {x}_k}{2}\left( \phi _{\sigma }, \frac{\partial e_v^p(x, t)}{\partial x}\right) , \end{aligned}$$

(69)

where

$$\begin{aligned} {\mathbb {I}}_v^k= & {} \frac{\partial }{\partial t} \left( \pi ^N\left( v\right) -\pi ^{N-1}\left( \pi ^N\left( v\right) \right) \right) , \\ {\mathbb {I}}_{\sigma }^k= & {} \frac{\partial }{\partial t} \left( \pi ^N\left( \sigma \right) -\pi ^{N-1}\left( \pi ^N\left( \sigma \right) \right) \right) . \end{aligned}$$

Here, $\pi ^{N-1}\left( \pi ^N\left( v\right) \right)$ is the $L^2$-projection of $\pi ^N\left( v\right) \in {\mathbb {P}}^N$ onto ${\mathbb {P}}^{N-1}$, the space of polynomials of degree $N-1$. For quadrature rules, such as Gauss–Legendre or Gauss–Lobatto quadrature, that are exact for polynomial integrands of degree $2N-1$, using $N+1$ nodes, we have the identity

$$\begin{aligned} \left( \phi _v, {\rho } \frac{\partial \pi ^N\left( v\right) }{\partial t} \right) - \left( \phi _v, {\rho } \frac{\partial \pi ^N\left( v\right) }{\partial t} \right) _N = \left( \phi _v, {\rho } {\mathbb {I}}_v^k \right) - \left( \phi _v, {\rho } {\mathbb {I}}_v^k \right) _N. \end{aligned}$$

Thus, ${\mathbb {I}}_v$ and ${\mathbb {I}}_{\sigma }$ are spectrally small through [5] (5.5.29)

$$\begin{aligned} \left| \left( \phi _v, {\rho } v \right) - \left( \phi _v, {\rho } v\right) _N\right|&\le C N^{-m} |v|_{H_{\rho }^{m;N}\left( {\widetilde{\varOmega }}\right) } \Vert \phi _v\Vert _{L_{\rho }^2\left( {\widetilde{\varOmega }}\right) }\\&= C N^{-m} |v|_{H^{m;N}\left( {\widetilde{\varOmega }}\right) } \Vert \phi _v\Vert _{L^2\left( {\widetilde{\varOmega }}\right) }. \end{aligned}$$

The equality follows from the equivalence of weighted norms.

Subtracting (51)–(52) from (68)–(69) gives the error equation

$$\begin{aligned} \frac{\varDelta {x}_k}{2}\left( \phi _v, {\rho } \frac{\partial e_v^k}{\partial t} \right) _N&= -\left( \frac{\partial \phi _v}{\partial \xi }, e_\sigma ^k\right) _N + \frac{\varDelta {x}_k}{2} \left( \phi _v, \rho {\mathbb {T}}_{v}^k\right) \nonumber \\&\quad - \frac{\varDelta {x}_k}{2}\left( \phi _v, \rho {\mathbb {I}}_{v}^k\right) _N + \frac{\varDelta {x}_k}{2}\left( \phi _{v}, {\tau }_v^k \right) \nonumber \\&\quad - \phi _v\left( -1\right) \left( e_\sigma ^k\left( -1, t\right) +F_k^k\left( -1, t\right) \right) \nonumber \\&\quad - \phi _v\left( 1\right) \left( G_k^k\left( 1, t\right) -e_\sigma ^k\left( 1, t\right) \right) , \end{aligned}$$

(70)

$$\begin{aligned} \frac{\varDelta {x}_k}{2}\left( \phi _{\sigma }, \frac{1}{\mu }\frac{\partial e_\sigma ^k}{\partial t}\right) _N&= \left( \phi _{\sigma }, \frac{\partial e_v^k}{\partial \xi } \right) _N + \frac{\phi _{\sigma }(-1)}{Z_s(-1)}F_k^k(-1, t) - \frac{\phi _{\sigma }(1)}{Z_s(1)}G_k^k(1, t) \nonumber \\&\quad + \frac{\varDelta {x}_k}{2} \left( \phi _\sigma , \frac{1}{\mu } {\mathbb {T}}_{\sigma }^k\right) - \frac{\varDelta {x}_k}{2}\left( \phi _\sigma , \frac{1}{\mu }{\mathbb {I}}_{\sigma }^k\right) _N + \frac{\varDelta {x}_k}{2}\left( \phi _{\sigma }, {\tau }_\sigma ^k \right) , \end{aligned}$$

(71)

with

$$\begin{aligned} {\mathbb {T}}_{v}= & {} \frac{\partial e_v^p}{\partial t} + {\mathbb {I}}_{v}, \quad {\tau }_v^k = \frac{\partial e_\sigma ^p}{\partial x}, \quad {\mathbb {T}}_{\sigma } = \frac{\partial e_\sigma ^p}{\partial t} + {\mathbb {I}}_{\sigma }, \quad {\tau }_\sigma ^k = \frac{\partial e_v^p}{\partial x}, \\ G^k(1, t)= & {} G_k^k(1, t) + G_p^k(1, t), \quad F^k(-1, t) = F_k^k(-1, t) + F_p^k(-1, t), \end{aligned}$$

where

$$\begin{aligned}&G_k^k(1, t):= \left( \frac{Z_{s}}{2} \left( e_v^k-{\widehat{e}}_v^k\right) + \frac{1}{2} \left( e_\sigma ^k-{\widehat{e}}_\sigma ^k\right) \right) \Big |_{\xi = 1}, \quad \\&G_p^k(1, t):= \left( \frac{Z_{s}}{2} \left( e_v^p-{\widehat{e}}_v^p\right) + \frac{1}{2} \left( e_\sigma ^p-{\widehat{e}}_\sigma ^p\right) \right) \Big |_{\xi = 1}, \\&F_k^k(-1, t):= \left( \frac{Z_{s}}{2} \left( e_v^k-{\widehat{e}}_v^k\right) - \frac{1}{2} \left( e_\sigma ^k-{\widehat{e}}_\sigma ^k\right) \right) \Big |_{\xi = -1},\quad \\&F_p^k(-1, t):= \left( \frac{Z_{s}}{2} \left( e_v^p-{\widehat{e}}_v^p\right) - \frac{1}{2} \left( e_\sigma ^p-{\widehat{e}}_\sigma ^p\right) \right) \Big |_{\xi = -1}. \end{aligned}$$

Here $F_k^k(-1, t), G_k^k(1, t)$ are flux fluctuations for the numerical error and $F_p^k(-1, t)$, $G_p^k(1, t)$ are flux fluctuations for the interpolation error. Note that $F_p^k(-1, t)$, $G_p^k(1, t)$ are independent of the numerical solution with $e_v^p= {\widehat{e}}_v^p$, $e_\sigma ^p={\widehat{e}}_\sigma ^p$ and vanish identically $F_p^k(-1, t)\equiv 0$, $G_p^k(1, t) \equiv 0$.

At the external boundaries $x = 0, L$ the errors $e_v^k, {\widehat{e}}_v^k$ and $e_\sigma ^k,{\widehat{e}}_\sigma ^k$ satisfy the algebraic identities (25a)–(25c). Similarly, at the internal interfaces $0< x_k < L$, the errors $e_v^k, {\widehat{e}}_v^k$ and $e_\sigma ^k, {\widehat{e}}_\sigma ^k$ satisfy the identities defined in (34a)–(34c) with

$$\begin{aligned} \alpha := {\bar{\alpha }}^k = f^{\prime }\left( \theta ^k\right) \ge 0, \quad 0\le \theta ^k \le |\llbracket {\widehat{e}}_v^k \rrbracket |, \end{aligned}$$

for a generic friction law. The case of a locked interface is obtained with ${\bar{\alpha }}^k \rightarrow +\infty$.

Now introduce the discrete energy for the numerical error

$$\begin{aligned} \Vert e^k(t)\Vert ^2_{NP} \equiv {\mathscr {E}}_e^k(t) = \frac{\varDelta {x}_k}{2}\left( \left( e_v^k, \rho e_v^k\right) _N + \left( e_\sigma ^k, \frac{1}{\mu }e_\sigma ^k\right) _N \right) , \end{aligned}$$

(72)

and the energy for the truncation error

$$\begin{aligned} \Vert \tau ^k(t)\Vert ^2_{NP^{-1}} \equiv {\mathscr {E}}_\tau ^k(t) = \frac{\varDelta {x}_k}{2}\left( \left( \tau _v^k, \frac{1}{\rho } \tau _v^k\right) _N + \left( \tau _\sigma ^k, {\mu }\tau _\sigma ^k\right) _N \right) . \end{aligned}$$

(73)

Our third main result is the following theorem:

Theorem 3

The semi-discrete error Eqs. (70)–(71) satisfy the energy estimate

$$\begin{aligned} \begin{aligned} \frac{d}{dt}\Vert e(t)\Vert ^2_{NP} + \mathrm {BT}_e \le \left\{ \Vert {\mathbb {T}}(t)\Vert _{NP} + \Vert {\mathbb {I}}(t)\Vert _{NP} + \Vert {\tau }(t)\Vert _{NP^{-1}} \right\} \Vert e(t)\Vert _{NP}, \end{aligned} \end{aligned}$$

(74)

with $\Vert e(t)\Vert ^2_{NP} = \sum _{k=1}^{K} \Vert e^k(t)\Vert ^2_{NP}$, $\Vert \tau (t)\Vert ^2_{NP^{-1}} = \sum _{k=1}^{K} \Vert \tau ^k(t)\Vert ^2_{NP^{-1}}$ and

$$\begin{aligned} \mathrm {BT}_e&= \sum _{k=1}^{K}\left( \frac{1}{Z_{s}^k(-1)}|F_k^k(-1, t)|^2 + \frac{1}{Z_{s}^k(1)}|G_k^k(1, t)|^2\right) + \sum _{k=2}^{K} \frac{ {\bar{\alpha }}^k}{\left( \eta ^k + {\bar{\alpha }}^k\right) ^2}|\varPhi ^k|^2 \\&\quad + \frac{1-r_0^2}{Z_{s}^1(-1)}|p_0|^2 + \frac{1-r_L^2}{Z_{s}^K(1)}|q_L|^2,\\ p_0&= \frac{1}{2}\left( Z_s(-1)e_v^1(-1, t) + e_\sigma ^1(-1, t)\right) , \quad q_L = \frac{1}{2}\left( Z_s^K(1) e_v^K(1, t) - e_\sigma ^K(1, t)\right) , \\ {\bar{\alpha }}^k&= f^{\prime }\left( \theta ^k\right) , \quad 0\le \theta ^k \le |\llbracket {\widehat{e}}_v^k \rrbracket |. \end{aligned}$$

Proof

Similarly as above, by replacing $\phi _v(\xi )$ with $e_v^k(\xi ,t)$ in (70) and $\phi _{\sigma }(\xi )$ with $e_{\sigma }^k(\xi ,t)$ in (71) and sum the equations together, we have

$$\begin{aligned} \begin{aligned} \frac{d}{dt}\Vert e^k(t)\Vert ^2_{NP}&= -e_{v}^k(-1, t)e_{\sigma }^k(-1, t) + e_{v}^k(1, t)e_{\sigma }^k(1, t) - e_{v}^k(-1, t)F^k_k(-1, t)\\&\quad - e_{v}^k(1, t)G_k^k(1, t)\\&\quad + \frac{1}{Z_{s}^{k}(-1)}e_{\sigma }^k( -1, t)F^k_k(-1, t)- \frac{1}{Z_{s}^{k}(1)}e_{\sigma }^k( 1, t)G_k^k(1, t)\\&\quad + \frac{\varDelta {x}_k}{2} \left( e_{v}^k, \rho {\mathbb {T}}_{v}^k\right) - \frac{\varDelta {x}_k}{2}\left( e_{v}^k, \rho {\mathbb {I}}_{v}^k\right) _N + \frac{\varDelta {x}_k}{2}\left( e_{v}^k, {\tau }_v^k \right) \\&\quad + \frac{\varDelta {x}_k}{2} \left( e_{\sigma }^k, \frac{1}{\mu } {\mathbb {T}}_{\sigma }^k\right) - \frac{\varDelta {x}_k}{2}\left( e_{\sigma }^k, \frac{1}{\mu }{\mathbb {I}}_{\sigma }^k\right) _N + \frac{\varDelta {x}_k}{2}\left( e_{\sigma }^k, {\tau }_\sigma ^k \right) . \end{aligned} \end{aligned}$$

(75)

Introducing $\Vert e(t)\Vert ^2_{NP} = \sum _{k=1}^{K} \Vert e^k(t)\Vert ^2_{NP}$, summing contributions from all elements and using the Cauchy-Schwarz inequality yield

$$\begin{aligned} \begin{aligned} \frac{d}{dt} \Vert e(t)\Vert ^2_{NP}&\le -\sum _{k = 1}^{K}{\left( \frac{1}{Z^k_s(-1) }\left( |F_k^k(-1,t)|^2 + |p^k(-1,t)|^2 - |{\widehat{q}}^k(-1,t)|^2\right) \right) } \\&\quad -\sum _{k = 1}^{K}{\left( \frac{1}{Z^k_s(1) }\left( |G_k^k(1, t)|^2 + |q^k(1, t)|^2 - |{\widehat{p}}^k(1, t)|^2\right) \right) }\\&\quad + \sum _{k=1}^{K}{\left( \Vert e^k(t)\Vert _{P}\Vert {\mathbb {T}}^k(t)\Vert _{P} + \Vert e^k(t)\Vert _{NP}\Vert {\mathbb {I}}^k(t)\Vert _{NP} + \Vert e^k(t)\Vert _{P}\Vert {\tau }^k(t)\Vert _{P^{-1}}\right) }. \end{aligned} \end{aligned}$$

(76)

Using the equivalence of norms (50) and the identities (25a)–(25c), (34a)–(34c), with

$$\begin{aligned} {\widehat{e}}_{\sigma }^k(\xi )&= \frac{{\bar{\alpha }}^k(\xi ) }{\eta ^k(\xi ) + {\bar{\alpha }}^k(\xi ) }\varPhi ^k(\xi ) , \quad \llbracket {\widehat{v}}(\xi ) \rrbracket = \frac{1}{\eta ^k(\xi ) + {\bar{\alpha }}^k(\xi )}\varPhi ^k(\xi ), \quad \sum _{k=1}^{K}|a_k| |b_k|\\&\le \sqrt{\sum _{k=1}^{K}{|a_k|^2}} \sqrt{\sum _{k=1}^{K}{|b_k|^2}}, \end{aligned}$$

in the right hand side of (76) give the energy estimate (74). $\square$

As suggested in [30], one should not throw away the dissipation contributed by the boundary and interface terms. Advancing the arguments as in [30] using Theorem 3 with $\mathrm {BT}_e \ge 0$ proves that the numerical method is error bounded. Note that the “truncation” error $\left\{ \Vert {\mathbb {T}}(t)\Vert _{NP} + \Vert {\mathbb {I}}(t)\Vert _{NP} + \Vert {\tau }(t)\Vert _{NP^{-1}} \right\}$ is spectrally small, and for GLL nodes it is of the same asymptotic order with the truncation error obtained in [30]. For exact solutions that are sufficiently smooth locally, we expect the optimal convergence of the error to zero.

Finally, the physics based numerical flux designed in this study allows us to prove convergence for smooth solutions, and for discontinuous and nearly singular exact solutions, in particular when the interface is slidding, $\llbracket {v} \rrbracket \ne 0$.

7 Numerical Experiments

We will perform 1D and 2D numerical experiments to verify numerical stability and accuracy. Lagrange polynomial bases are used with GLL and GL quadrature nodes, respectively. Numerical solutions are evolved using the explicit one-step ADER (arbitrary high-order derivative) time-stepping scheme [11, 14, 34, 46] reaching locally the same order of accuracy as the spatial discretization. For polynomial approximation of degree N we expect an optimal asymptotic convergence rate of $N+1$. We will proceed later to 2D verifying the accuracy of the method for Raleigh surface waves. We will demonstrate the extension of our method to 2D curvilinear elements and 2D dynamically adaptive meshes for dynamic earthquake rupture propagation. Some presented examples use the high performance computing toolkit ExaHyPE [40], which combines the ADER-DG method with space time adaptive Cartesian meshes (AMR, [50]).

7.1 One Space Dimension

We will now present numerical examples in 1D. First, we show an example of wave propagation in a heterogeneous medium with material properties varying within each element for which we lock all interior element boundaries, $\alpha \rightarrow \infty$. Second, we model dynamic earthquake rupture across a nonlinear frictional fault and wave propagation emitted by the sliding elastic solids.

7.1.1 Wave Propagation in a Heterogeneous Medium

We consider a 1D domain, $0 \le x \le L = 10$ km, with the heterogeneous shear wave velocity profile $c_s = c_0 + c_{\epsilon }(x)$. The component $c_0$ is a mean velocity and the perturbation component $c_{\epsilon }(x)$ models small scale heterogeneity. We use the mean shear wave velocity $c_0 = 3343$ m/s, density $\rho = 2700$ kg/m$^{3}$, typical for crustal rocks, and set $c_{\epsilon }(x) = \epsilon \sin (n\pi x/L)$. The velocity perturbation oscillates $n=20$ times in the domain, with the amplitude $\epsilon =0.1$ km/s.

We have chosen the initial and boundary conditions to match the exact solution

$$\begin{aligned} v_e(x,t) = \cos \left( {k\pi }t\right) \sin \left( \frac{n}{L}\pi x + a_0\right) , \quad \sigma _e(x,t) = \frac{n}{Lk}\sin \left( {k\pi }t\right) \cos \left( \frac{n}{L}\pi x + a_0\right) . \end{aligned}$$

(77)

We chose the phase shift $a_0 = 10$, temporal wave number $k = 2$ s$^{-1}$, and the spatial wave number $n/L = 2$ km$^{-1}$, such that the wavelength is in consonance with that of the small scale heterogeneity. At the left boundary, $x = 0$, we set a traction boundary condition $\sigma (0, t) = \sigma _e(0, t)$, and at the right boundary $x = L$, we set a velocity boundary condition $v(L, t) = v_e(L, t)$.

We discretize the domain with uniform elements of size $\varDelta {x} = {L}/{K}$ km, where K is the number of elements used. Material parameters vary within each element. We set the time step to

$$\begin{aligned} \varDelta {t} = \frac{CFL}{\max _{ {x}}(c_s( {x} ))(2N+1)}\varDelta {x} , \quad \text {with}~\ {CFL} = 0.5. \end{aligned}$$

(78)

We use polynomial degree $N = 4$ and $K = 80$ elements, resulting in 400 degrees of freedom (DoF) for each unknown field. The spatial resolution equates to 8 elements per wavelength. We evolve the solutions until $t = 100$ s. The numerical relative error at $t = t_n$ is defined by

$$\begin{aligned} \mathrm {error}(t_n) =\frac{\sqrt{\sum _i\left( |v_i^n-v_e(x_i, t_n)|^2 + |\sigma _i^n-\sigma _e(x_i, t_n)|^2\right) }}{\max _{t_n}\sqrt{\left( \sum _i\left( |v_e(x_i, t_n)|^2 + |\sigma _e(x_i, t_n)|^2\right) \right) }}, \end{aligned}$$

(79)

where $v_i^n, \sigma _i^n$ is the numerical solution and $v_e(x_i, t_n), \sigma _e(x_i, t_n)$ is the exact solution at $x = x_i$, $t = t_n$. Here $x_i$ are given by GLL nodes or GL nodes. The numerical solution (at $t = 100$ s) superimposed with the analytical solution, and the respective errors are shown in Fig. 2. The errors remain bounded throughout the simulation time, with GLL node errors differing from GL node errors by a factor 4. The error bound can be related to the discrete error estimate (74), consistent to the 1D scalar advection analysis in [30].

Fig. 2

1D wave propagation simulation in a heterogeneous medium using GL and GLL nodes. Particle velocity at $t = 100$ s and time history of the numerical error using ${N = 4}$ (polynomial degree) and $K = 80$ number of elements

Table 1 1D wave propagation simulation in a heterogeneous medium using GL and GLL nodes varying resolution (DoFs). Numerical errors and convergence rate at $t = 100$ s

For various resolutions (DoF) of the same model, Table 1 reports the numerical errors and shows optimal ${N+1}$ convergence rates. For a fixed number of elements, $K = 80$, and various polynomial degrees $N = 2, 4, 6, 8, 10$ we find spectral convergence of the discretization error as shown in Fig. 3.

Fig. 3

1D wave propagation in a heterogeneous medium using GL and GLL nodes. Spectral convergence rate at $t= 100$ s

7.1.2 Dynamic Rupture in 1D

We will now model the dynamic earthquake rupture process in 1D and the emitted seismic waves. The domain is $0 \le x \le L = 60$ km, with homogeneous material properties, $c_s = 3464$ m/s, $\rho = 2670$ $\mathrm {kg/m^3}$, and ${\mu } = \rho c_s^2 = 32.0381$ GPa.

We prescribe an embedded fault with finite but high static frictional resistance.

The evolving friction coefficient is governed by a linear slip-weakening friction law [3] which is widely used, e.g., to model megathrust earthquake dynamics [37, 47],

$$\begin{aligned} \begin{aligned}&f\left( S\right) = \left\{ \begin{array}{ll} f_s -\left( f_s-f_d\right) \frac{ {S}}{d_c}, &{}\quad \text {if} \quad {S} \le d_c,\\ f_d, &{}\quad \text {if} \quad {S} \ge d_c, \end{array} \right. \end{aligned} \end{aligned}$$

(80)

where $f_s$ and $f_d$ are the static and dynamic friction coefficients, $d_c$ is the critical slip-distance. The slip S evolves according to

$$\begin{aligned} \frac{dS}{dt} = V, \end{aligned}$$

(81)

where $V = |\llbracket {v} \rrbracket |$ is the slip-rate. We introduce the peak frictional strength on the fault $\tau _p = f_s \sigma _n$ and the residual frictional strength on the fault $\tau _r = f_d \sigma _n$, where $\sigma _n > 0$ is the compressive normal stress. By (80), as soon as the load on the fault exceeds the peak strength $\tau _p$, the fault will begin to slip and the strength on the fault will weaken linearly with slip S, until slip reaches the critical slip-distance $S = d_c$. When the fault is fully weakened its residual strength is $\tau _r$. Here, no mechanism arrests rupture and the fault will continue to slip after yielding.

Our friction parameters (Table 2) follow [22] assuming $\tau _0 = 81.6$ MPa as the initial load, and $\tau _p = f_s \sigma _n = 81.24$ MPa and $\tau _r = f_d \sigma _n = 63$ MPa. Since $\tau _0 > \tau _p$, the initiation of rupture will be instantaneous.

Table 2 Friction parameters for the 1D dynamic rupture problem following [22]

We discretize the 1D domain [0, L] into 400 DG elements with $N = 3$ polynomial degree approximation on GL nodes. The effective sub-cell grid spacing is $h = \varDelta {x}/(N+1) = L/1600$. We define a frictional interface at $x = 30$ km governed by the slip-weakening friction law (80) with the parameters (Table 2). All other DG interfaces remain locked at infinite frictional strength, $\alpha \rightarrow \infty$. We use the time-step (78) to simulate for $t = 8$ s. Snapshots of 1D particle velocity and stress (Fig. 4) illustrate that the particle velocity is discontinuous across the fault interface, with the discontinuity corresponding to slip-rate V, while the stress field is continuous but nearly singular for $t \le 0.45$ s. This is comparable to the hypothetical field distribution in Fig. 1. At future times $t > 0.45$ s the stress drop $\varDelta {\tau } = \tau _0-\tau _r$ propagates from the fault into the adjacent elastic solids carried by radiated elastic waves.

Fig. 4

Snapshots of 1D velocity and stress fields for the dynamic rupture example using the DG method

We compare our DG scheme to an SBP finite difference scheme with uniform grid spacing $h = L/1600$. The SBP operator is 6th order accurate in the interior with 3rd order accurate boundary closure, yielding a 4th order accurate scheme, globally. In the finite difference scheme friction is only used at the fault.

In Fig. 5, we display the evolution of slip-rate V, shear stress $\tau$ and slip S at the fault. Both schemes agree well, in particular in terms of accumulated slip. During instantaneous rupture initiation shear stress weakens and slip-rate increases exponentially, respectively. When the fault is fully weakened, $\tau = \tau _r$, slip-rate saturates at $V \sim 4$ m/s, which governs rupture until the simulation is terminated.

Fig. 5

1D dynamic rupture comparing the DG scheme to an SBP finite difference scheme. Evolution of slip-rate V, shear stress $\tau$ and slip S at the fault

The corresponding wave fields of the DG method and SBP method agree equally well (Fig. 6). However, the SBP method exhibits high frequency oscillations trailing the discontinuities. In 2D and 3D such spurious oscillations will not only appear within the medium but also across the fault surface due to large (temporal and spatial) gradients in the slip-rate and stress fields.

Fig. 6

1D dynamic rupture comparing the DG scheme to an SBP finite difference scheme. Snapshots of the velocity and stress fields at $t = 8$ s

7.2 Two Space Dimensions

This section presents 2D numerical experiments including accuracy verification for Rayleigh surface waves, using curvilinear meshing for non-planar free surface topography and dynamic earthquake rupture on a dynamically adaptive Cartesian mesh.

7.2.1 Accuracy of Rayleigh Surface Waves

Here we demonstrate the effectiveness of the method for computing surface waves in an elastic medium. The 2D elastic wave equation in a half-plane $-\infty< x <\infty$, $0 \le y < \infty$, with the free-surface boundary condition at $y = 0$, $\sigma _{xy}(x, 0, t) = 0$, $\sigma _{yy}(x, 0, t) = 0$, can support surface waves. We consider specifically Rayleigh surface waves, see [1, 16, 32, 38]. For a constant coefficients x-periodic problem with the free-surface boundary condition at $y = 0$, the displacement field satisfies the Rayleigh wave solution

$$\begin{aligned} \begin{aligned}&\begin{pmatrix} u_x(x,y,t)\\ u_y(x,y,t)\\ \end{pmatrix} = e^{-\omega \sqrt{1-{\tilde{\xi }}^2} y} \begin{pmatrix} \cos {\left( \omega \left( x + c_r t\right) \right) }\\ \sqrt{1-{\tilde{\xi }}^2}\sin {\left( \omega \left( x + c_r t\right) \right) }\\ \end{pmatrix} \\&\quad + \left( \frac{{\tilde{\xi }}^2}{2}-1\right) e^{-\omega \sqrt{1-{\tilde{\xi }}^2\mu /\left( 2\mu + \lambda \right) }y} \begin{pmatrix} \cos {\left( \omega \left( x + c_r t\right) \right) }\\ \sin {\left( \omega \left( x + c_r t\right) \right) }/\sqrt{1-{\tilde{\xi }}^2\mu /\left( 2\mu + \lambda \right) }\\ \end{pmatrix}. \end{aligned} \end{aligned}$$

(82)

Here $\omega > 0,$ $c_r = {\tilde{\xi }}\sqrt{\mu }$ is the Rayleigh phase velocity, and ${\tilde{\xi }}$ satisfies the Rayleigh dispersion relation

$$\begin{aligned} \begin{aligned} \sqrt{1-{\tilde{\xi }}^2}\sqrt{1-\frac{{\tilde{\xi }}^2\mu }{\left( 2\mu + \lambda \right) }} - \left( \frac{{\tilde{\xi }}^2}{2}-1\right) ^2 = 0. \end{aligned} \end{aligned}$$

(83)

Note that for all $\mu > 0$ and $\lambda \ge 0$ we must have $0.763< {\tilde{\xi }}^2< 0.913$. Thus, the Rayleigh surface wave propagates in the x-direction and decays exponentially in the y-direction. The velocity field can be extracted from (82), by taking the time derivative of the displacement field, giving

$$\begin{aligned} \begin{aligned} {v}_x(x,y,t) = \frac{\partial {u}_x(x,y,t) }{\partial t}, \quad {v}_y(x,y,t) = \frac{\partial {u}_y(x,y,t) }{\partial t}. \end{aligned} \end{aligned}$$

(84)

The stress field can be obtain from (82), by combining the spatial gradients of the displacement field with the stiffness tensor of elastic material, as prescribed by Hooke’s law.

We consider the x-periodic rectangular domain, $0\le x \le 1$ km, $0 \le y \le 10$ km, with $\omega = 2 \pi$. The solution is 1-periodic in the x-direction, at $y = 0$ we have the free-surface boundary condition and at $y = 10$ km we prescribe a Dirichlet condition for the velocity fields.

We use the $N = 4$ degree polynomial approximation on GL and GLL nodes separately, and evaluate numerical accuracy, on a sequence of uniformly refined meshes. We consider the relative $L^2$-norm error of the particle velocity vector and the stress vector, separately. First we consider a Poisson solid with $\rho = 1000$ kg/$\hbox {m}^3$, $\lambda = 1000$ MPa, $\mu = 1000$ MPa, with $\lambda /\mu =1$. Numerical errors are at the final time $t = 1$ s are shown in Tables 3 and 4 for the particle velocity and the stress field respectively. In the asymptotic regime the errors converge optimally (at the rate $N+1$).

Table 3 Relative $L^2$-norm numerical errors of the particle velocity and convergence rate at $t = 1.0$ s with $\lambda /\mu = 1$

Table 4 Relative $L^2$-norm numerical errors of the stress field and convergence rate at $t = 1.0$ s with $\lambda /\mu = 1$

High-order accuracy becomes essential for surface wave propagation in almost incompressible elastic materials, that is when $\lambda /\mu \gg 1$, as shown in [16, 32]. Thus, we next increase $\lambda /\mu = 100$, with $\rho = 1000$ kg/$\hbox {m}^3$, $\lambda = 100{,}000$ MPa, $\mu = 1000$ MPa. The relative $L^2$-norm errors (Tables 5 and 6) reveal that the particle velocity error amplitudes seem unaffected, while stress field error amplitudes increase by a factor of 4. As in the case of $\lambda /\mu = 1$ also $\lambda /\mu = 100$ leads to optimal convergence in the asymptotic regime.

Table 5 Relative $L^2$-norm numerical errors of the particle velocity and convergence rate at $t = 1.0$ s with $\lambda /\mu = 100$

Table 6 Relative $L^2$-norm numerical errors of the stress field and convergence rate at $t = 1.0$ s with $\lambda /\mu = 100$

7.2.2 2D Curvilinear Non-planar Free-Surface Topography

We demonstrate potential of the method for including geometrically complex free surface topography using curvilinear mesh and coordinate transformation. Consider the 2D isotropic elastic medium, with $-10 \le x \le 10$ km, $0 \le y \le {\widetilde{y}}(x)$ km, and

$$\begin{aligned} {\widetilde{y}}(x) = 10 + 0.1x + \sin \left( 4\pi x/20 + 3.34\right) \cos \left( 2\pi \left( x/20 -0.5\right) + 3.34\right) . \end{aligned}$$

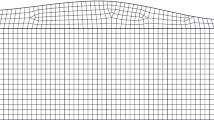
We use transfinite interpolation to propagate points from the boundaries into the domain, resulting in a curvilinear mesh obeying the topography. To ensure efficient numerical treatment, we map the mesh and the PDE to a regular Cartesian mesh. We discretise the transformed domain into a tensor-product of DG elements, and discretise each element using GLL nodes. In the physical space the DG elements are curved (Fig. 7).

We consider homogeneous crustal rock material properties with $\rho = 2700$ kg/$\hbox {m}^3$, $c_p = 6000$ m/s, and $c_s = 3343$ m/s. In the transformed domain, however, the medium is heterogeneous and anisotropic. At the top boundary $y = {\widetilde{y}}(x)$ we set a free-surface boundary condition, while at all other boundaries we set the incoming characteristic to zero. We initialize the normal stress ($\sigma _{xx}$, $\sigma _{yy}$) with a Gaussian perturbation centered at $x = 0$ km, $y = 6$ km, while the shear stress ($\sigma _{xy}$) and the particle velocity vector ($v_x$, $v_y$) are initially set to zero. The initial condition generates pressure wave perturbation only.

Snapshots of the absolute divergence: $\left| \frac{\partial v_x}{\partial x} + \frac{\partial v_y}{\partial y}\right|$, and the absolute curl: $\left| \frac{\partial v_y}{\partial x} - \frac{\partial v_x}{\partial y}\right|$, of the particle velocity vector (Fig. 8) show the evolution of the wave field as well as its interaction with the non-planar topography. Initially, for $t \le 2.3$ s, the absence of shear wave perturbation in the initial data implies that the curl of the velocity vector vanishes identically. However, as time progresses and waves increasingly interact with the free-surface topography, shear waves are generated due to mode conversions (Fig. 8 for $t \ge 0.62$ s). We evolve the wave field for a sufficiently long time, $t \le 100$ s, without observing instabilities.

Fig. 7

2D curvilinear free-surface topography example. Graphical representations of the physical and curvilinear transformed computational meshes

Fig. 8

Complex topography. Snapshots of the wave field, from left to right, at $t = 0.23$, 0.62, 1.01, 1.40 s. The top panel is the absolute divergence of the particle velocity vector and the lower panel is the absolute curl of the particle velocity vector

7.2.3 Dynamic Earthquake Ruptures on a Dynamically Adaptive Mesh

Our final 2D numerical experiment models dynamic earthquake rupture following an adaptive mesh refinement strategy and demonstrates the robustness of the method. The domain spans $(x, y) \in [0, 30~\text {km}] \times [0, 20\,\text {km}]$. The fault is a vertical line, at $x = 15~\text {km}$, subdividing two isotropic, homogeneous elastic solids with material properties of $c_p=6000$ m/s, $c_s=3464$ m/s, $\rho =2670$ kg/$\hbox {m}^3$. It is governed by a slip-weakening friction law, (80), with $f_s = 0.677$, $f_d = 0.525$, and $d_c= 0.40$ m. We assign uniform initial prestress as $\sigma _{xy}^0 = 70$ MPa, $\sigma _{yy}^0 = 0$ MPa, $\sigma _{xx}^0= 120$ MPa.

At $t =0$ we discretize the domain uniformly with the element size $\varDelta {x} = 30/21$ km, $\varDelta {y} = 20/14$ km, and consider degree $N = 5$ polynomial approximation on GL nodes. The peak frictional strength on the fault is $\tau _p = f_s \sigma _n = 81.24~\ \text {MPa}$. We initiate rupture by over-stressing ($\tau _0= 81.6$ MPa) the element located at $y = 7.5$ km depth.

Fig. 9

2D dynamic earthquake rupture on a dynamically adaptive mesh. The snapshots of the particle velocity $v_y$ are taken at $t = 0.1$, 1, 2, 3, 4, 5 s. Initially, the two elements closest the hypocenter are refined, then adaptive mesh refinement tracks the rupture front and the accompanying elastic waves

The root mean square of the particle velocity, $v = \sqrt{v_x^2 + v_y^2}$, defines the mesh refinement criterion for seismic wave fields in the domain. Whenever v exceeds 50 cm/s the mesh is refined in one level, leading to 3 times smaller elements than the original coarse mesh (Fig. 9). On the fault, we define an adaptive mesh refinement criterion based on monitoring the slip rate V. Once slip-rates at any point exceed a threshold of $V = 1$ cm/s we activate dynamic, two-level mesh refinement (Fig. 10) resulting in 9 times smaller fault elements than in the initial coarse mesh.

Fig. 10

2D dynamic earthquake rupture on a dynamically adaptive mesh. A zoom-in snapshot of the particle velocity vy at t $=$ 1 s, showing multiple levels of mesh refinement

8 Summary and Outlook

We present a provably stable DG method for the linear elastic wave equation incorporating physical interface and boundary conditions acting at element boundaries. All DG element interfaces are treated as frictional interfaces with an associated frictional strength. Classical element interfaces are assigned infinite frictional strength and can thus never be broken by any load of finite magnitude. Weak interfaces where frictional slip can be accommodated can be assigned a finite nonlinear frictional strength governed by generic nonlinear friction laws. External boundaries of the domain are closed with general linear well-posed and energy-stable boundary conditions.

We derive a physics based numerical flux that is compatible with all well-posed boundary and interface conditions. By construction, our flux implementation is upwind and yields energy identity analogous to the continuous energy estimate. We present 1D numerical experiments to demonstrate stability, higher-order accuracy and optimal convergence for polynomial degrees $N\le 10$. In 2D numerical examples we demonstrate our method in various challenging seismological applications.

We provide the 1D numerical implementation as a Jupyter Python Notebook which is publicly available at Seismolive [33] (http://seismo-live.org/), an online educational collection for computational seismology. The method has been recently extended to 3D [17], and is implemented in ExaHyPE [40], a simulation engine for hyperbolic PDEs on adaptive Cartesian meshes. ExaHyPE is open source: https://exahype.eu/exahype-engine.