1 Introduction

To compute long time behavior of hyperbolic wave propagation problems accurately, the error should not grow large over time. Stability of a numerical scheme ensures that the solution remains bounded in some norm for fixed time, but the equation that describes the time variation of the error includes a forcing term generated by the approximation or truncation errors. That forcing term can lead to unbounded growth in the error for long times even though the solution remains bounded.

Examples of both linear and bounded temporal error growth are observed in computations presented in the literature. Linear growth of the error in approximations of hyperbolic systems has been noted for both finite difference [5, 11] and discontinuous Galerkin [4, 7] approximations. In [7], the authors prove linear growth of the error and note that the bound is sharp, meaning that slower than linear growth cannot be guaranteed, though the growth rate is controlled by the order of the approximation. On the other hand, bounded error behavior is observed for some finite difference approximations, e.g. [1, 2], and [8].

An explanation for when the error is bounded or not was presented in [10]. Linear growth is observed when waves are trapped in cavities or in periodic geometries, which is what was studied in [7]. Bounded growth occurs when waves are present in the domain for finite amounts of time, as in an inflow-outflow problem. The idea was explained at the partial differential equation (PDE) level in [10] in terms of a model problem with forcing. The analysis of SBP-SAT (Summation-By-Parts/Simultaneous-Approximation-Term) finite difference approximations in that paper predicted the same behavior. The conclusion was that the error is bounded if a sufficiently dissipative boundary procedure is used. It is not bounded due to the internal discretization. The error levels were significantly lower using characteristic boundary conditions versus noncharacteristic ones. Since the error is bounded, arbitrarily high order accuracy can be found at any time.

In this paper we examine the long time behavior of the error for discontinuous Galerkin spectral element methods (DGSEM). We show that although the bounded error property is a result of dissipative boundary conditions as was shown in [10], the behavior of the error and its bound are influenced by the internal approximation. In particular, we show that the choice of the numerical flux at interior element interfaces affects both the rate at which the error grows and the asymptotic value it attains. The presence of inter-element dissipation introduced by the numerical flux is a feature of the DGSEM not found in single domain SBP finite difference approximations. The results, however, apply to multidomain or multiblock versions of those methods.

2 The Model Problem in One Space Dimension

To show the boundedness of the energy when characteristic boundary conditions are applied, we study the error equation for the DGSEM approximation of the scalar constant coefficient initial boundary value problem with a non-periodic boundary condition

$$\begin{aligned} \left\{ \begin{aligned}&{u_t} + {u_x} = 0\quad x \in [0,L] \\&u(0,t) = g(t) \\&u(x,0) = {u_0}(x). \\ \end{aligned} \right. \end{aligned}$$
(1)

For truncation errors of the approximation to be bounded in time we assume that the initial and boundary values are constructed so that \(u(x,t) \in H^{m}(0,L)\) for \(m> 1\) and that its norm \(\left\| u\right\| _{H^{m}}\) is uniformly bounded in time. Such conditions are physically meaningful and describe problems where the boundary input is, for example, sinusoidal.

The energy of the solution of the initial boundary value problem, measured by the \(\mathbb {L}^{2}\) norm \({\left\| u \right\| ^2} = (u,u) = \int _0^L {{u^2}dx}\), is increased through the addition of energy at the left boundary, and dissipated as waves move out through the boundary at the right. To see this, construct a weak form of the equation by multiplying it with a test function \(\phi \in \mathbb {L}^{2}(0,L)\) and integrating over the domain

$$\begin{aligned} \int _0^L {{u_t}\phi dx} + \int _0^L {{u_x}\phi dx} = 0. \end{aligned}$$
(2)

Replacing \(\phi \) with u yields

$$\begin{aligned} \frac{1}{2}\frac{d}{{dt}}{\left\| u \right\| ^2} = - \left( {u,{u_x}} \right) . \end{aligned}$$
(3)

Integration by parts implies that when the boundary condition at the left is applied,

$$\begin{aligned} \frac{d}{{dt}}{\left\| u \right\| ^2} = {g^2}\left( t \right) - {u^2}(L,t). \end{aligned}$$
(4)

Integrating in time over an interval [0, T] leads to

$$\begin{aligned} {\left\| {u\left( T \right) } \right\| ^2} + \int _0^T {{u^2}(L,t)dt} = {\left\| {u_{0}} \right\| ^2} + \int _0^T {{g^2}(t)dt}. \end{aligned}$$
(5)

Thus, the energy at time T is the initial energy, plus energy added at the left through the boundary condition minus the energy lost through the right boundary. It is this behavior that the numerical approximation should emulate.

3 The DGSEM Approximation of the Model Problem

To construct the DGSEM, we subdivide the interval into elements \(e^{k}=\left[ x_{k-1},x_{k}\right] \), \(k=1,2,\ldots ,K\), where the \(x_{k},\;k=0,1,\ldots ,K\) are the element boundaries with \(x_{0}=0\) and \(x_{K}=L\). Then

$$\begin{aligned} \sum \limits _{k = 1}^K {\int _{{x_{k - 1}}}^{{x_k}} {\left\{ {{u_t} + {u_x}} \right\} \phi dx} } = 0. \end{aligned}$$
(6)

Since \(\phi \in \mathbb {L}^{2}\), we can choose \(\phi \) to be nonzero selectively in each element, which tells us that on each element the solution satisfies

$$\begin{aligned} \int _{{x_{k - 1}}}^{{x_k}} {\left\{ {{u_t} + {u_x}} \right\} \phi dx} = 0. \end{aligned}$$
(7)

To allow us to use a Legendre polynomial approximation of the solution, we map the element \(\left[ x_{k-1},x_{k}\right] \) onto the reference element \(E=[-1,1]\) by the linear transformation

$$\begin{aligned} x = {x_{k - 1}} + \Delta {x_k}\frac{{\xi + 1}}{2}, \end{aligned}$$
(8)

where \(\Delta x_{k} = x_{k}-x_{k-1}\) is the length of the element. Under this transformation, \(u_{x}= 2u_{\xi }/\Delta x_{k}\) so the elemental contribution is

$$\begin{aligned} \frac{{\Delta {x_k}}}{2}\int _{ - 1}^1 {{u_t}\phi d\xi } + \int _{ - 1}^1 {{u_\xi }\phi d\xi } = 0. \end{aligned}$$
(9)

We then integrate the term with the space derivative by parts to get the elemental weak form

$$\begin{aligned} \frac{{\Delta {x_k}}}{2}\int _{ - 1}^1 {{u_t}\phi d\xi } + \left. {u\phi } \right| _{-1}^{1} - \int _{ - 1}^1 {u{\phi _\xi }d\xi } = 0. \end{aligned}$$
(10)

Finally, we define the elemental inner product and norm by

$$\begin{aligned} {\left( {u,\phi } \right) _E} = \int _{ - 1}^1 {u\phi d\xi }, \quad \left\| u \right\| _E^2 = {\left( {u,u} \right) _E} \end{aligned}$$
(11)

and write the elemental contribution as

$$\begin{aligned} \frac{{\Delta {x_k}}}{2}\left( {{u_t},\phi } \right) _{E} + \left. {u\phi } \right| _{ - 1}^1 - \left( {u,{\phi _\xi }} \right) _{E} = 0. \end{aligned}$$
(12)

Since it is unlikely to cause confusion, we will typically drop the subscript E.

We are now ready to construct the DGSEM approximation. Let \(\mathbb {P}^{N}\) be the space of polynomials of degree \(\le N\) and let \(\mathbb {I}^{N}:\mathbb {L}^{2}(-1,1)\rightarrow \mathbb {P}^{N}(-1,1)\) be the interpolation operator. We approximate the solution by a polynomial interpolant, \(u\approx U\in \mathbb {P}^{N}\), which we write in Lagrange (nodal) form

$$\begin{aligned} U^{k} = \sum \limits _{j = 0}^N {{U^{k}_j}(t){\ell _j}} (\xi ), \end{aligned}$$
(13)

where \(\ell _{j}(\xi )\in \mathbb {P}^{N}\) is the jth Lagrange interpolating polynomial that satisfies \(\ell _{j}\left( \xi _{i}\right) = \delta _{ij}\). The interpolation nodes, \(\xi _{j},\; j=0,1,\ldots ,N\) are the nodes of the Gauss-Lobatto quadrature

$$\begin{aligned} \int _N {ud\xi } \equiv \sum \limits _{j = 0}^N {u\left( {{\xi _j}} \right) {w_j}} \approx \int _{ - 1}^1 {ud\xi }. \end{aligned}$$
(14)

Then we can define the discrete inner product and norm in terms of the Legendre–Gauss–Lobatto quadrature as

$$\begin{aligned} {\left( {u,v} \right) _N} \equiv \int _N {uvd\xi }, \quad \left\| u \right\| _N^2 = {\left( {u,u} \right) _N}. \end{aligned}$$
(15)

We choose the Gauss–Lobatto points here because they allow for the derivation of provably stable approximations in multiple dimensions and on curved elements [9]. The discrete norm is equivalent to the continuous norm ([3], after (5.3.2)) in that for all \(U\in \mathbb {P}^{N}\),

$$\begin{aligned} 1 \leqslant \frac{{{{\left\| U \right\| }_N}}}{{{{\left\| U \right\| }_{{L^2}( - 1,1)}}}} = \sqrt{2 + \frac{1}{N}} \le \sqrt{3} . \end{aligned}$$
(16)

The Gauss–Lobatto quadrature has the property [3] that

$$\begin{aligned} {\left( {U,V} \right) _N} = \left( {U,V} \right) \quad \forall \; UV \in \mathbb {P}^{2N - 1}. \end{aligned}$$
(17)

Furthermore, with the interpolation property \(\mathbb {I}^{N}(u)\left( \xi _{j}\right) = u\left( \xi _{j}\right) = u_{j}\),

$$\begin{aligned} {\left( {u,V} \right) _N} = \sum \limits _{j = 0}^N {{u\left( \xi _{j}\right) }{V_j}{w_j}} = \sum \limits _{j = 0}^N {{u_{j}}{V_j}{w_j}} = {\left( {{\mathbb {I}^N}\left( u \right) ,V} \right) _N}\quad \forall \; V \in {\mathbb {P}^N} \end{aligned}$$
(18)

which says that the interpolation operator is the orthogonal projection of \(\mathbb {L}^{2}\) onto the space of polynomials with respect to the discrete inner product \(\left( \cdot ,\cdot \right) _{N}\).

In addition to the solution, three more quantities need to be approximated. We use the Gauss-Lobatto quadrature to approximate the inner products in (12). We restrict the test function to be \(\phi ^{k}\in \mathbb {P}^{N}\subset \mathbb {L}^{2}\). Finally, we introduce the continuous numerical “flux” \(U^{*}=U^{*}\left( U^{L},U^{R}\right) \) to couple the elements at the boundaries to create the weak form of the DGSEM

$$\begin{aligned} \begin{aligned}&\frac{{\Delta {x_k}}}{2}{\left( {U_t^k,\phi ^{k} } \right) _N} + \left\{ {{U^*}\left( {{U^k}(1),{U^{k + 1}}( - 1}) \right) \phi ^{k} (1) - {U^*}\left( {{U^{k - 1}}(1),{U^k}( - 1}) \right) \phi ^{k} ( - 1)} \right\} \\&\qquad - {\left( {{U^k},{\phi ^{k}_\xi }} \right) _N} = 0. \end{aligned} \end{aligned}$$
(19)

In this work we will choose the numerical flux to have the form

$$\begin{aligned} {U^*}\left( {{U^L},{U^R}} \right) = \frac{{{U^L} + {U^R}}}{2} - \frac{\sigma }{2}\left( {{U^R} - {U^L}} \right) , \end{aligned}$$
(20)

where \(U^{L,R}\) are the states on the left and the right and \(\sigma \in [0,1]\). The numerical flux includes both the upwind (\(\sigma =1\)) and central (\(\sigma =0\)) fluxes

$$\begin{aligned} {U^*}\left( {{U^L},{U^R}} \right) = \left\{ \begin{aligned} {U^L},\quad \quad \quad \quad \sigma = 1, \\ \frac{{{U^L} + {U^R}}}{2},\quad \; \sigma = 0. \\ \end{aligned} \right. \end{aligned}$$
(21)

In shorthand, the approximation on the \(k^{th}\) element satisfies

$$\begin{aligned} \frac{{\Delta x_{k}}}{2}{\left( {{U^{k}_t},\phi ^{k} } \right) _N} + \left. {{U^{*}}\phi ^{k} } \right| _{ - 1}^1 - {\left( {U^{k},{\phi ^{k} _\xi }} \right) _N} = 0. \end{aligned}$$
(22)

3.1 Stability of the DGSEM

The DGSEM is stable in the sense that the energy of the approximate solution approximates (5) if the upwind numerical flux is used at the physical boundaries. To show this, we let \(\phi ^{k} = U^{k}\) to get the energy equation on an element

$$\begin{aligned} \frac{1}{2}\frac{{\Delta {x_k}}}{2}\frac{d}{{dt}}{\left\| {{U^k}} \right\| ^2_{N}} = \frac{{\Delta {x_k}}}{2}{\left( {U_t^k,{U^k}} \right) _N} = - \left. {{U^{*}}{U^k}} \right| _{ - 1}^1 + {\left( {{U^k},{U^{k}_\xi }} \right) _N}. \end{aligned}$$
(23)

The quadrature in the discrete inner product on the right is exact. Alternatively, we can say that the discrete inner product satisfies the summation by parts rule [9]

$$\begin{aligned} {\left( {{U^k},U_\xi ^k} \right) _N} = \left. {{{\left( {{U^k}} \right) }^2}} \right| _{ - 1}^1 - {\left( {U_\xi ^k,{U^k}} \right) _N} \Rightarrow {\left( {{U^k},U_\xi ^k} \right) _N} = \frac{1}{2}\left. {{{\left( {{U^k}} \right) }^2}} \right| _{ - 1}^1. \end{aligned}$$
(24)

Therefore, the elemental contribution to the energy is

$$\begin{aligned} \frac{1}{2}\frac{{\Delta {x_k}}}{2}\frac{d}{{dt}}{\left\| {{U^k}} \right\| ^2_{N}} = - \left. {\left\{ {{U^{*}}{U^k} - \frac{1}{2}{{\left( {{U^k}} \right) }^2}} \right\} } \right| _{ - 1}^1. \end{aligned}$$
(25)

Summing over all the elements gives the time rate of change of the total energy

$$\begin{aligned} \frac{1}{2}\frac{d}{{dt}}\sum \limits _{k = 1}^K {\frac{{\Delta {x_k}}}{2}{{\left\| {{U^k}} \right\| }^2_{N}}} = - \sum \limits _{k = 1}^K {\left. {\left\{ {{U^{*}}{U^k} - \frac{1}{2}{{\left( {{U^k}} \right) }^2}} \right\} } \right| _{ - 1}^1} . \end{aligned}$$
(26)

The sum over the element endpoints splits into three parts: One for the left physical boundary, one for the right physical boundary and a sum over the internal element endpoints. The internal term has contributions from the elements to the left and the right of the interface and uses the fact that the numerical flux \(U^{*}\) is unique at the interface. Therefore,

$$\begin{aligned} \begin{aligned}&\sum \limits _{k = 1}^K {\left. {\left\{ {{U ^*} - \frac{1}{2}U^{k} } \right\} U^{k} } \right| _{ - 1}^1} = -\left\{ {{U^*}\left( {g,{U ^1}( - 1)} \right) - \frac{1}{2}{U ^1}( - 1)} \right\} {U ^1}( - 1) \\&\quad + \sum \limits _{k = 2}^K {\left\{ {{U^*}\left( {{U ^{k - 1}}(1),{U ^k}( - 1)} \right) - \frac{1}{2}\left[ {{U ^{k - 1}}(1) + {U ^k}( - 1)} \right] } \right\} \left[ {{U ^{k - 1}}(1) - {U ^k}( - 1)} \right] } \\&\quad + \left\{ {{U^*}\left( {{U ^K}(1),U_{ext}} \right) - \frac{1}{2}{U ^K}(1)} \right\} {U ^K}(1), \end{aligned} \end{aligned}$$
(27)

where \(U_{ext}\) is some external state required by the numerical flux function.

Using the central solver at the boundaries does not give conditions that match those of the PDE seen in (5). On the other hand, when the upwind flux is used,

$$\begin{aligned} \begin{aligned}&\left\{ {{U^*}\left( {g,{U^1}( - 1)} \right) - \frac{1}{2}{U^1}( - 1)} \right\} {U^1}( - 1) = \frac{1}{2}{g^2} - \frac{1}{2}{\left( {{U^1}( - 1) - g} \right) ^2} \\&\left\{ {{U^*}\left( {{U^K}(1),{U_{ext}}} \right) - \frac{1}{2}{U^K}(1)} \right\} {U^K}(1) = \frac{1}{2}{\left( {{U^K}(1)} \right) ^2}. \\ \end{aligned} \end{aligned}$$
(28)

The terms in the sum over the internal faces are each of the form

$$\begin{aligned} {U^*}\left( {{V^L},{V^R}} \right) \llbracket V \rrbracket - \frac{1}{2}{\llbracket V^{2} \rrbracket }, \end{aligned}$$
(29)

where \(\llbracket V\rrbracket = {V^L} - {V^R}\) is the jump in the argument. This quantity is non-negative for either the upwind or central numerical flux. Direct calculation shows that

$$\begin{aligned} {U^*}\left( {{V^L},{V^R}} \right) \llbracket V\rrbracket - \frac{1}{2}{\llbracket V^2\rrbracket } = \frac{\sigma }{2}{\llbracket V\rrbracket }^2 \geqslant 0. \end{aligned}$$
(30)

Therefore,

$$\begin{aligned} \frac{1}{2}\frac{d}{{dt}}\sum \limits _{k = 1}^K {\frac{{\Delta {x_k}}}{2}{{\left\| {{U^k}} \right\| }^2_{N}}} = \frac{1}{2}{g^2} - \frac{1}{2}{\left( {{U^1}( - 1,t) - g(t)} \right) ^2} - \frac{1}{2}{\left( {{U^K}(1,t)} \right) ^2} -\frac{\sigma }{2}\sum \limits _{k = 2}^K \llbracket {U^k}\rrbracket ^2. \end{aligned}$$
(31)

Let us now define the global norm by

$$\begin{aligned} \left\| U \right\| _N^2 = \sum \limits _{k = 1}^K {\frac{{\Delta {x_k}}}{2}\left\| {{U ^k}} \right\| _N^2}. \end{aligned}$$
(32)

Then, if we define U(0) as the interpolant of the initial condition \(u_{0}\) on the element,

$$\begin{aligned} \begin{aligned} {\left\| {U(T)} \right\| ^2_{N}}&+ \int _0^T {{{\left( {{U^K}(1,t)} \right) }^2}dt} + \int _0^T {{{\left( {{U^1}( - 1,t) - g(t)} \right) }^2}dt} + \sigma \int _0^T {\sum \limits _{k = 2}^K {\llbracket {U^k}\rrbracket ^2} dt} \\ {}&= {\left\| {U(0)} \right\| ^2_{N}} + \int _0^T {{g^2}(t)dt} , \end{aligned} \end{aligned}$$
(33)

which also satisfies

$$\begin{aligned} {\left\| {U(T)} \right\| ^2_{N}} + \int _0^T {{{\left( {{U^K}(1,t)} \right) }^2}dt} \leqslant {\left\| {U(0)} \right\| ^2_{N}} + \int _0^T {{g^2}(t)dt}. \end{aligned}$$
(34)

Equation (33) matches (5) except for the additional dissipation that comes from the weak imposition of the boundary condition, and dissipation from the jumps in the solution at the element interfaces if the upwind flux (\(\sigma =1\)) is used. Therefore, the DGSEM for the (constant coefficient) problem is strongly stable and the energy at any time T is bounded by the initial energy plus the energy added at the left boundary minus the energy lost from the right if the upwind flux (i.e. characteristic boundary condition) is used at the endpoints of the domain.

4 The Error Equation

We now study the time behavior of the error, whose elemental contribution is \(E^{k}=u\left( x\left( \xi \right) ,t\right) - U^{k}\left( \xi ,t \right) \). For a more general derivation and for multidimensional problems, although with exact integration, see [7] and [12].

We compute the error in two parts as

$$\begin{aligned} E^{k} = \left( {{\mathbb {I}^N}(u) - U^{k}} \right) + \left( {u - {\mathbb {I}^N}(u)} \right) \equiv \varepsilon ^{k} + {\varepsilon ^{k} _p}, \end{aligned}$$
(35)

so that \(\varepsilon ^{k}\in \mathbb {P}^{N}\). The triangle inequality allows us to bound the two parts separately

$$\begin{aligned} \left\| E^{k} \right\| _N^2 \le \left\| \varepsilon ^{k} \right\| _N^2 + \left\| {{\varepsilon ^{k} _p}} \right\| _N^2. \end{aligned}$$
(36)

The interpolation error, \(\varepsilon ^{k}_{p}\), is independent of the approximate solution and is the sum of the series truncation error and the aliasing error. Its continuous norm converges spectrally fast as [3] (5.4.33)

$$\begin{aligned} {\left\| {{\varepsilon ^{k}_p}} \right\| _{{L^2}( - 1,1)}} = {\left\| {u - {\mathbb {I}^N}u} \right\| _{{L^2}( - 1,1)}} \leqslant C{N^{ - m}}{\left| u \right| _{{H^{m;N}}( - 1,1)}}, \end{aligned}$$
(37)

where

$$\begin{aligned} \left| u \right| _{{H^{m;N}}( - 1,1)}^2 = \sum \limits _{n = \min (m,N + 1)}^m {\left\| {\frac{{{\partial ^n}u}}{{\partial {\xi ^n}}}} \right\| _{{L^2}( - 1,1)}^2} . \end{aligned}$$
(38)

On an element itself (as opposed to the reference element), the interpolation error is bounded by [3] (5.4.42)

$$\begin{aligned} {\left\| {{\varepsilon ^{k}_p}} \right\| _{{H^n}(e^{k})}} = {\left\| {u - {\mathbb {I}^N}(u)} \right\| _{{H^n}(e^{k})}} \leqslant C{\Delta x_{k}^{\min (m,N)-n}}{N^{ n- m}}{\left| u \right| _{{H^{m;N}}(e^{k})}}, \end{aligned}$$
(39)

for \(n=0,1\). Equivalence of the discrete and continuous norms allows us to bound the discrete norm in terms of the continuous one, so the contribution of \(\varepsilon ^{k}_{p}\) in (36) decays spectrally fast.

The part of the error that depends on U, namely \(\varepsilon ^{k}\), depends on the spatial approximation. To find the equation that \(\varepsilon ^{k}\) satisfies, note that u satisfies the continuous equation (12) and that \(u=\mathbb {I}^{N}(u) + \varepsilon ^{k}_{p}\). Then when we replace u by this decomposition and restrict \(\phi \) to \(\mathbb {P}^{N}\subset \mathbb {L}^{2}\),

$$\begin{aligned} \begin{aligned}&\frac{{\Delta x_{k}}}{2}\left( {\frac{\partial }{{\partial t}}{\mathbb {I}^N}(u),\phi ^{k} } \right) + \left. {{\mathbb {I}^N}(u)\phi ^{k} } \right| _{ - 1}^1 - {\left( {{\mathbb {I}^N}(u),{\phi ^{k} _\xi }} \right) } \\&\quad = - \frac{{\Delta x_{k}}}{2}\left( {\frac{{\partial {\varepsilon ^{k} _p}}}{{\partial t}},\phi ^{k} } \right) - \left. {{\varepsilon ^{k} _p}\phi ^{k} } \right| _{ - 1}^1 + {\left( {{\varepsilon ^{k} _p},{\phi ^{k} _\xi }} \right) }. \end{aligned} \end{aligned}$$
(40)

Note that the endpoints of the interval are Gauss-Lobatto points, so the interpolant equals the solution there and \(\varepsilon ^{k}_{p}=0\) at the endpoints. Also, we can integrate the last term by parts so the boundary terms on the right vanish and

$$\begin{aligned} \begin{aligned}&\frac{{\Delta x_k}}{2}\left( {\frac{\partial }{{\partial t}}{\mathbb {I}^N}(u),\phi ^{k} } \right) + \left. {{\mathbb {I}^N}(u)\phi ^{k} } \right| _{ - 1}^1 - \left( {{\mathbb {I}^N}(u),{\phi ^{k} _\xi }} \right) \\&\quad = - \frac{{\Delta x_k}}{2}\left( {\frac{{\partial {\varepsilon ^{k} _p}}}{{\partial t}},\phi ^{k}} \right) - \left( {\left( {\varepsilon ^{k} _p}\right) _\xi ,{\phi ^{k}}} \right) . \end{aligned} \end{aligned}$$
(41)

Next,

$$\begin{aligned} \left( {\frac{\partial }{{\partial t}}{\mathbb {I}^N}(u),\phi ^{k}} \right) = {\left( {\frac{\partial }{{\partial t}}{\mathbb {I}^N}(u),\phi ^{k}} \right) _N} + \left\{ {\left( {\frac{\partial }{{\partial t}}{\mathbb {I}^N}(u),\phi ^{k}} \right) - {{\left( {\frac{\partial }{{\partial t}}{\mathbb {I}^N}(u),\phi ^{k}} \right) }_N}} \right\} , \end{aligned}$$
(42)

where the term in the braces is the error associated with the Gauss-Lobatto quadrature, which is spectrally small through [3] (5.4.38)

$$\begin{aligned} \left| {\left( {u,\phi } \right) - {{\left( {u,\phi } \right) }_N}} \right| \leqslant C{N^{ - m}}{\left| u \right| _{{H^{m;N - 1}}( - 1,1)}}{\left\| \phi \right\| _{{L^2}( - 1,1)}} \end{aligned}$$
(43)

for all \(\phi \in \mathbb {P}^{N}\) and \(m\ge 1\) and some C independent of m and u. The error bound (43) comes from applying the Cauchy–Schwarz inequality, the interpolation error estimate, exactness of the quadrature and the norm equivalence to

$$\begin{aligned} \begin{aligned} \left( {u,\phi } \right) - {\left( {u,\phi } \right) _N}&= \left( {u,\phi } \right) - \left( {{\varPi ^{N - 1}}(u),\phi } \right) + \left( {{\varPi ^{N - 1}}(u),\phi } \right) - {\left( {u,\phi } \right) _N} \\&=\left( {u - {\varPi ^{N - 1}}(u),\phi } \right) - {\left( {u - {\varPi ^{N - 1}}(u),\phi } \right) _N}, \end{aligned} \end{aligned}$$
(44)

where \(\varPi ^{N}:\mathbb {L}^{2}\rightarrow \mathbb {P}^{N}\) is the \(\mathbb {L}^{2}\) orthogonal projection (series truncation) operator.

Also when \(\phi \) is restricted to \(\mathbb {P}^{N}\), the volume term in (41) is equal to the quadrature

$$\begin{aligned} \left( {{\mathbb {I}^N}(u),{\phi _\xi }} \right) = {\left( {{\mathbb {I}^N}(u),{\phi _\xi }} \right) _N}. \end{aligned}$$
(45)

Finally, the value of the interpolant at a point can be represented in terms of the limits from the left, \({\mathbb {I}^N}{{(u)}^ - }\), and the right, \({\mathbb {I}^N}{{(u)}^ + }\) as

$$\begin{aligned} {\mathbb {I}^N}(u) = {U^*}\left( {{\mathbb {I}^N}{{(u)}^ - },{\mathbb {I}^N}{{(u)}^ + }} \right) + \left\{ {{\mathbb {I}^N}(u) - {U^*}\left( {{\mathbb {I}^N}{{(u)}^ - },{\mathbb {I}^N}{{(u)}^ + }} \right) } \right\} . \end{aligned}$$
(46)

At the element interfaces, u is continuous (\(m>1\)), so that the error term in the braces is zero. Thus, at \(\xi =\pm 1\), \({\mathbb {I}^N}(u) = {U^*}\left( {{\mathbb {I}^N}{{(u)}^ - },{\mathbb {I}^N}{{(u)}^ + }} \right) \).

Making these substitutions,

$$\begin{aligned} \begin{aligned} \frac{{\Delta x_k}}{2}{\left( {\frac{\partial }{{\partial t}}{\mathbb {I}^N}(u),\phi ^{k} } \right) _N}&+ \left. {{U^*}\left( {{\mathbb {I}^N}{{(u)}^ - },{\mathbb {I}^N}{{(u)}^ + }} \right) \phi ^{k} } \right| _{ - 1}^1 - {\left( {{\mathbb {I}^N}(u),{\phi ^{k} _\xi }} \right) _N} = \\&-\frac{{\Delta x_k}}{2}\left( {\frac{{\partial {\varepsilon ^{k} _p}}}{{\partial t}},\phi ^{k} } \right) - \left( {\left( {\varepsilon ^{k} _p}\right) _\xi ,{\phi ^{k} }} \right) \\&-\frac{{\Delta x_k}}{2}\left\{ {\left( {\frac{\partial }{{\partial t}}{\mathbb {I}^N}(u),\phi ^{k} } \right) - {{\left( {\frac{\partial }{{\partial t}}{\mathbb {I}^N}(u),\phi ^{k} } \right) }_N}} \right\} \end{aligned} \end{aligned}$$
(47)

The right hand side of (47) is the amount by which the exact solution u fails to satisfy the approximation (22), in other words it is the spectrally small “truncation error”. Therefore, we use (44) and write

$$\begin{aligned} \begin{aligned}&\frac{{\Delta x_k}}{2}{\left( {\frac{\partial }{{\partial t}}{\mathbb {I}^N}(u),\phi ^{k} } \right) _N} + \left. {{U^*}\left( {{\mathbb {I}^N}{{(u)}^ - },{\mathbb {I}^N}{{(u)}^ + }} \right) \phi ^{k}} \right| _{ - 1}^1 - {\left( {{\mathbb {I}^N}(u),{\phi ^{k} _\xi }} \right) _N}\\&\quad = \frac{{\Delta x_k}}{2}\left( \mathbb {T}^{k}(u),\phi ^{k}\right) + \frac{{\Delta x_k}}{2}\left( \mathbb {Q}^{k}(u),\phi ^{k}\right) _{N}, \end{aligned} \end{aligned}$$
(48)

where

$$\begin{aligned} \mathbb {Q}^{k}(u) = \frac{\partial }{{\partial t}}\left( {{\mathbb {I}^N}(u) - {\varPi ^{N - 1}}\left( {\mathbb {I}^N}(u)\right) } \right) = \mathbb I^{N}\left( u_{t}\right) - \varPi ^{N-1}\left( {\mathbb {I}^N}(u_{t})\right) , \end{aligned}$$
(49)

and

$$\begin{aligned} \mathbb {T}^{k} = - \left\{ {\frac{{\partial {\varepsilon ^{k} _p}}}{{\partial t}} + \frac{{{\partial {\varepsilon ^{k} _p}}} }{\partial x}} +\mathbb {Q}^{k}(u)\right\} . \end{aligned}$$
(50)

The quantity \(\mathbb Q\) measures the projection error of a polynomial of degree N onto a polynomial of degree \(N-1\). It is bounded under the assumptions on the boundedness of u. The remaining parts of \(\mathbb T\) satisfy bounds determined by (39). Specifically,

$$\begin{aligned} \left\| {\frac{{\partial \varepsilon _p^k}}{{\partial x}}} \right\| \leqslant C\Delta x_k^{\min \left( {m,k} \right) -1}{N^{1 - m}}{\left| u \right| _{{H^{m;N}}\left( {{e^k}} \right) }}, \end{aligned}$$
(51)

which is convergent in N when \(m>1\) and the Sobolev norm of the solution is uniformly bounded in time. (It is for this reason the initial and boundary conditions for (1) have the specified smoothness.) The norm of the time derivative term is similarly bounded in time since \(u_{t}=-u_{x}\).

When we subtract (22) from (48), we get an equation for the error, \(\varepsilon ^{k}\)

$$\begin{aligned} \frac{{\Delta x_k}}{2}{\left( {{\varepsilon ^{k} _t},\phi ^{k} } \right) _N} + \left. {{\varepsilon ^{*} }\phi ^{k} } \right| _{ - 1}^1 - {\left( {\varepsilon ^{k} ,{\phi ^{k} _\xi }} \right) _N} = \frac{{\Delta x_k}}{2}(\mathbb {T}^{k},\phi ^{k})+\frac{{\Delta x_k}}{2}\left( \mathbb {Q}^{k},\phi ^{k}\right) _{N}, \end{aligned}$$
(52)

where by linearity of the numerical flux,

$$\begin{aligned} \varepsilon ^{*} = U^{*}\left( \varepsilon ^{L},\varepsilon ^{R}\right) . \end{aligned}$$
(53)

We get the energy equation for the error by letting \(\phi ^{k} = \varepsilon ^{k}\). Then

$$\begin{aligned} \frac{1}{2}\frac{{\Delta x_k}}{2}\frac{d}{{dt}}\left\| \varepsilon ^{k} \right\| _N^2 + \left. {{\varepsilon ^{*}}\varepsilon ^{k} } \right| _{ - 1}^1 - {\left( {\varepsilon ^{k} ,{\varepsilon ^{k} _\xi }} \right) _N} = \frac{{\Delta x_k}}{2}(\mathbb {T}^{k},\varepsilon ^{k} ) + \frac{{\Delta x_k}}{2}\left( \mathbb {Q}^{k},\varepsilon ^{k} \right) _{N}. \end{aligned}$$
(54)

As before, summation by parts says that

$$\begin{aligned} {\left( {\varepsilon ^{k} ,{\varepsilon ^{k} _\xi }} \right) _N} = \frac{1}{2}\left. {{(\varepsilon ^{k}) ^2}} \right| _{ - 1}^1. \end{aligned}$$
(55)

Therefore,

$$\begin{aligned} \frac{1}{2} \frac{{\Delta x_k}}{2}\frac{d}{{dt}}\left\| \varepsilon ^{k} \right\| _N^2 + \left. {\left\{ {{\varepsilon ^{*}} - \frac{1}{2}\varepsilon ^{k} } \right\} \varepsilon ^{k} } \right| _{ - 1}^1 = \frac{{\Delta x_k}}{2}(\mathbb {T}^{k},\varepsilon ^{k} ) + \frac{{\Delta x_k}}{2}\left( \mathbb {Q}^{k},\varepsilon ^{k} \right) _{N}, \end{aligned}$$
(56)

We now sum over all of the elements

$$\begin{aligned} \begin{aligned}&\frac{1}{2}\frac{d}{{dt}}\sum \limits _{k = 1}^K {\frac{{\Delta {x_k}}}{2}\left\| {{\varepsilon ^k}} \right\| _N^2} + \sum \limits _{k = 1}^K {\left. {\left\{ {{\varepsilon ^*} - \frac{1}{2}\varepsilon ^{k} } \right\} \varepsilon ^{k} } \right| _{ - 1}^1} \\&\quad = \sum \limits _{k = 1}^K {\frac{{\Delta {x_k}}}{2}\left\{ {\left( {\mathbb {T}^{k},\varepsilon ^{k} } \right) + \left( \mathbb {Q}^{k},\varepsilon ^{k} \right) _{N}} \right\} } , \end{aligned} \end{aligned}$$
(57)

to get the global energy equation

$$\begin{aligned} \frac{1}{2}\frac{d}{{dt}}\left\| \varepsilon \right\| _N^2 + \sum \limits _{k = 1}^K {\left. {\left\{ {{\varepsilon ^*} - \frac{1}{2}\varepsilon ^{k} } \right\} \varepsilon ^{k} } \right| _{ - 1}^1} = \sum \limits _{k = 1}^K {\frac{{\Delta {x_k}}}{2}\left\{ {\left( {\mathbb {T}^{k},\varepsilon ^{k} } \right) + \left( \mathbb {Q},\varepsilon ^{k} \right) _{N}} \right\} }, \end{aligned}$$
(58)

which is of the same form as (26) except for the right hand side generated by the approximation errors.

We now bound the right hand side of (58). We re-write it as

$$\begin{aligned} R = \sum \limits _{k = 1}^K {\left\{ {\left( {\sqrt{\frac{{\Delta {x_k}}}{2}} \mathbb {T}^{k},\sqrt{\frac{{\Delta {x_k}}}{2}} \varepsilon ^{k} } \right) + \left( {\sqrt{\frac{{\Delta {x_k}}}{2}} \mathbb {Q}^{k},\sqrt{\frac{{\Delta {x_k}}}{2}} \varepsilon ^{k} } \right) _{N}} \right\} }, \end{aligned}$$
(59)

and use the Cauchy–Schwarz inequality on the inner products to get the bound

$$\begin{aligned} R \leqslant \sum \limits _{k = 1}^K {\left\{ {\left\| {\sqrt{\frac{{\Delta {x_k}}}{2}} {\mathbb {T}^k}} \right\| \left\| {\sqrt{\frac{{\Delta {x_k}}}{2}} {\varepsilon ^k}} \right\| } \right\} } + \sum \limits _{k = 1}^K {\left\{ {{{\left\| {\sqrt{\frac{{\Delta {x_k}}}{2}} {\mathbb {Q}^k}} \right\| }_N}{{\left\| {\sqrt{\frac{{\Delta {x_k}}}{2}} {\varepsilon ^k}} \right\| }_N}} \right\} }. \end{aligned}$$
(60)

We then use the Cauchy–Schwarz inequality

$$\begin{aligned} \sum \limits _{k = 1}^K {{a_k}{b_k}} \leqslant \sqrt{\sum \limits _{k = 1}^K {a_k^2} } \sqrt{\sum \limits _{k = 1}^K {b_k^2} } \end{aligned}$$
(61)

to see that

$$\begin{aligned} R \leqslant \sqrt{\sum \limits _{k = 1}^K {\frac{{\Delta {x_k}}}{2}{{\left\| {{\mathbb {T}^k}} \right\| }^2}} } \sqrt{\sum \limits _{k = 1}^K {\frac{{\Delta {x_k}}}{2}{{\left\| {{\varepsilon ^k}} \right\| }^2}} } + \sqrt{\sum \limits _{k = 1}^K {\frac{{\Delta {x_k}}}{2}\left\| {{\mathbb {Q}^k}} \right\| _N^2} } \sqrt{\sum \limits _{k = 1}^K {\frac{{\Delta {x_k}}}{2}\left\| {{\varepsilon ^k}} \right\| _N^2} } .\end{aligned}$$
(62)

Using the definition of the global norm (32) and the equivalence between the continuous and discrete norms, (16),

$$\begin{aligned} R \leqslant \left\{ {\left\| \mathbb {T} \right\| + \left\| \mathbb {Q} \right\| _{N}} \right\} {\left\| \varepsilon \right\| _N}\equiv \mathbb {E}(t){\left\| \varepsilon \right\| _N}. \end{aligned}$$
(63)

Therefore, the global error equation is

$$\begin{aligned} \frac{1}{2}\frac{d}{{dt}}\left\| \varepsilon \right\| _N^2 + \sum \limits _{k = 1}^K {\left. {\left\{ {{\varepsilon ^*} - \frac{1}{2}\varepsilon ^{k} } \right\} \varepsilon ^{k} } \right| _{ - 1}^1} \leqslant {\mathbb {E}}(t){\left\| \varepsilon \right\| _N}. \end{aligned}$$
(64)

Again, the sum over the element endpoints splits into three parts: One for the left physical boundary, one for the right physical boundary and a sum over the internal element endpoints. The last has contributions from the elements to the left and the right of the interface

$$\begin{aligned} \sum \limits _{k = 1}^K {\left. {\left\{ {{\varepsilon ^*} - \frac{1}{2}\varepsilon } \right\} \varepsilon } \right| _{ - 1}^1}&= -\left\{ {{U^*}\left( {0,{\varepsilon ^1}( - 1)} \right) - \frac{1}{2}{\varepsilon ^1}( - 1)} \right\} {\varepsilon ^1}( - 1)\nonumber \\&\qquad + \sum \limits _{k = 2}^K \left\{ {{U^*}\left( {{\varepsilon ^{k - 1}}(1),{\varepsilon ^k}( - 1)} \right) - \frac{1}{2}\left[ {{\varepsilon ^{k - 1}}(1) + {\varepsilon ^k}( - 1)} \right] } \right\} \left[ {{\varepsilon ^{k - 1}}(1) - {\varepsilon ^k}( - 1)} \right] \nonumber \\&\qquad + \left\{ {{U^*}\left( {{\varepsilon ^K}(1),0} \right) - \frac{1}{2}{\varepsilon ^K}(1)} \right\} {\varepsilon ^K}(1). \end{aligned}$$
(65)

The external states for the physical boundary contributions are zero because \(\mathbb {I}^{N}(u)=g\) at the left boundary and the external state for \(U^{1}\) is set to g. At the right boundary, where the upwind numerical flux is used, it doesn’t matter what we set for the external state, since its coefficient in the numerical flux is zero.

The inner element boundaries contribute as in the stability proof

$$\begin{aligned} \begin{aligned}&\sum \limits _{k = 2}^K {\left\{ {{U^*}\left( {{\varepsilon ^{k - 1}}(1),{\varepsilon ^k}( - 1)} \right) - \frac{1}{2}\left[ {{\varepsilon ^{k - 1}}(1) - {\varepsilon ^k}( - 1)} \right] } \right\} \left[ {{\varepsilon ^{k - 1}}(1) - {\varepsilon ^k}( - 1)} \right] } \\&= \frac{\sigma }{2}{\left[ {{\varepsilon ^{k - 1}}(1) - {\varepsilon ^k}( - 1)} \right] ^2}\ge 0. \end{aligned} \end{aligned}$$
(66)

At the left boundary, let \(e\leftarrow {\varepsilon ^0}( - 1)\) to simplify the notation. Then

$$\begin{aligned} - \left\{ {{U^*}\left( {0,e} \right) - \frac{1}{2}e} \right\} e = - \left\{ {\left( {\frac{{0 + e}}{2} - \frac{\sigma e}{2}} \right) - \frac{1}{2}e} \right\} e = \frac{\sigma }{2}e^{2}. \end{aligned}$$
(67)

At the right, with \(e\leftarrow {\varepsilon ^K}( 1)\),

$$\begin{aligned} \left\{ {{U^*}\left( {e,0} \right) - \frac{1}{2}e} \right\} e = \left\{ {\left( {\frac{{0 + e}}{2} + \frac{1}{2}\sigma e} \right) - \frac{1}{2}e} \right\} e = \frac{\sigma }{2}e^{2}. \end{aligned}$$
(68)

Therefore, the energy growth rate is bounded by

$$\begin{aligned} \frac{1}{2}\frac{d}{{dt}}\left\| \varepsilon \right\| _N^2 + \frac{\sigma }{2}\left\{ {{{\left( {{\varepsilon ^0}( - 1)} \right) }^2} + {{\left( {{\varepsilon ^K}(1)} \right) }^2}} \right\} + \frac{\sigma }{2}\sum \limits _{k = 2}^K {{{\llbracket \varepsilon ^{k}\rrbracket }^2}} \leqslant {\mathbb {E}}(t)\left\| \varepsilon \right\| _{N}. \end{aligned}$$
(69)

Grouping the boundary and interface terms,

$$\begin{aligned} \frac{1}{2}\frac{d}{{dt}}\left\| \varepsilon \right\| _N^2 + BTs \leqslant {\mathbb {E}}(t){\left\| \varepsilon \right\| _N}, \end{aligned}$$
(70)

where

$$\begin{aligned} BTs = \frac{\sigma }{2}\left\{ {{{\left( {{\varepsilon ^0}( - 1)} \right) }^2} + {{\left( {{\varepsilon ^K}(1)} \right) }^2}} \right\} + \frac{\sigma }{2}\sum \limits _{k = 2}^K {{{\llbracket \varepsilon ^{k}\rrbracket }^2}}. \end{aligned}$$
(71)

Note that \(BTs\ge 0\). We also note that (69) is the same kind of estimate found for summation by parts finite difference approximations [10] except for the additional sum over the squares of the element endpoint jumps, which represents additional damping (when \(\sigma >0\)) that does not exist in the single block finite difference approximation. However, in the multi-block version, it does, see Remark 2 below.

5 Bounded Error in Time for the DGSEM

Using the product rule, we write (70) as

$$\begin{aligned} \frac{d}{{dt}}{\left\| \varepsilon \right\| _N} + \frac{{BTs}}{{\left\| \varepsilon \right\| _N^2}}{\left\| \varepsilon \right\| _N} \leqslant {\mathbb {E}}(t). \end{aligned}$$
(72)

As noted in [10], one should not throw away the dissipation contributed by the boundary terms. So we leave them in and write

$$\begin{aligned} \frac{d}{{dt}}{\left\| \varepsilon \right\| _N} + \eta (t){\left\| \varepsilon \right\| _N} \leqslant {\mathbb {E}}(t). \end{aligned}$$
(73)

In [10], it is argued that the mean value of \(\eta (t)\) over any finite time interval, \(\bar{\eta }\), is bounded from below by a positive constant, i.e., \(\bar{\eta }\geqslant {\delta _0} > 0\). Furthermore, the truncation and quadrature errors are bounded in time under the assumption that u and its time and space derivatives are bounded in time. An integrating factor allows one to integrate (73) to get a bound on the error at any time t

$$\begin{aligned} {\left\| {\varepsilon (t)} \right\| _N} \leqslant \frac{{1 - {e^{-{\delta _0}t}}}}{{{\delta _0}}}{{M}}, \end{aligned}$$
(74)

where by the boundedness assumption on the exact solution, \(M = \mathop {\max }\limits _{s \in [0,\infty )} \mathbb E(s)<\infty \) is bounded.

Equation (74) says that for bounded truncation error the dissipative boundary conditions keep the error bounded for large time.

We now make four predictions from (74) about the behavior of the error, which come from the fact that \(\delta _{0}\) is a lower bound on the average of \(\eta (t)\), which in turn depends on the size of the contributions of the element boundaries. Before doing so, we modify the boundary terms to explicitly incorporate the upwind flux (\(\sigma = 1\)) at the physical boundaries. We now write

$$\begin{aligned} BTs=\frac{1 }{2}\left\{ {{{\left( {{\varepsilon ^0}( - 1)} \right) }^2} + {{\left( {{\varepsilon ^K}(1)} \right) }^2}} \right\} + \frac{\sigma }{2}\sum \limits _{k = 2}^K {{{\llbracket \varepsilon ^{k}\rrbracket }^2}}. \end{aligned}$$
(75)

The model (74) predicts:

  1. P1

    Using the upwind flux at the physical boundaries and either the upwind flux or the central flux at the interior element interfaces, the error growth is bounded asymptotically in time.

    Under these conditions, \(BTs\ne 0\) for all time, leading to (74). For large time, the error \({\left\| {\varepsilon (t)} \right\| _N}\rightarrow M/\delta _{0}\). Equivalence of the norms implies that the same holds true in the continuous norm.

  2. P2

    Using the upwind flux \(\sigma = 1\) in the interior will lead to a smaller asymptotic error than using the central flux, \(\sigma = 0\). This will be especially true for under-resolved approximations.

    As time increases the error approaches \(M/\delta _{0}\), so the larger \(\delta _{0}\) is the smaller the asymptotic error. Using the upwind flux in the interior, \(\sigma =1\), increases the contribution of the boundary terms, BTs, and hence the size of the mean, \(\bar{\eta }\). The interface jumps in (75) are larger when the resolution is low, so the effect will be more pronounced at low resolution.

  3. P3

    As the resolution increases, the difference between the asymptotic error from the central and upwind fluxes should decrease.

    Following the argument of prediction P2, the size of the jumps decreases as the solution converges, therefore decreasing the effects of the inter-element jump terms in BTs so that \(\delta _{0}\) approaches the same value.

  4. P4

    The error growth rate will be larger when the upwind flux is used compared to when the central flux is used. Equivalently, the upwind flux solution should approach its asymptotic value faster than the central flux solution.

    The rate at which the error approaches the asymptotic value depends on \(\delta _{0}\), which is larger with the upwind flux due to the presence of the jump terms in the interior.

Remark 1

The fundamental bounded error behavior P1 was shown to hold for SBP-SAT finite difference approximations in [10]. The predictions P2–P4 are new.

Remark 2

We have also revisited [10], and derived the error bounds for the multi-block finite difference approximation. The relations (73),(74) and (75) also hold, i.e. an almost identical result. The bound M now corresponds to the maximum truncation error and \(\varepsilon \) represents the difference between the numerical solution and the exact one at each grid-point. The main difference between the DGSEM and SBP-SAT result is that in practice the number of interfaces used in the DGSEM is larger in a typical application due to the differences in the types of meshes used, unstructured vs block structured.

6 Numerical Examples

In this section we present numerical examples to illustrate the bounded error properties of the DGSEM for the boundary value problem (1) as predicted by the model, (74). We also present a two dimensional example to show that the same behaviors appear for systems of equations in multiple space dimensions.

6.1 Error Behavior in One Space Dimension

We illustrate the behavior of the error for \(L=2\pi \) and the initial condition \(u_{0}=\sin (12(x-0.1))\), with the boundary condition g(t) chosen so that the exact solution is \(u(x,t) = \sin (12(x - t - 0.1))\). We approximate the PDE with the DGSEM in space, and integrate in time with a low storage third order Runge-Kutta method, with the time step chosen so that the time integration error is negligible. In all the one dimensional tests, the elements will be of uniform size.

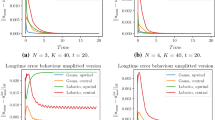
Figure 1 shows the error as a function of time for 50 elements with a fourth order polynomial approximation. The error is bounded as time increases for both the upwind and central fluxes (P1) and the error bound for the central flux is larger than that of the upwind flux (P2). The upwind flux error also reaches its asymptotic value much sooner (\(t \lesssim 1/2\) vs. \(t \approx 3\)) than the central flux error (P4).

We observe in Fig. 1 that the central flux error is significantly noisier than the upwind flux error. This observation is typical for all of the meshes and polynomial orders tested. We interpret that as due to the fact that when using the central flux in the interior, the only dissipation comes from the upwind flux at the physical boundaries, as observed in the plot on the left of Fig. 2 showing the eigenvalues of the discrete spatial operator. The eigenvalues of the upwind flux shown on the right of Fig. 2 all have negative real parts, indicating dissipation in all modes.

Fig. 1
figure 1

Error behavior as a function of time for \(N=4\), \(K=50\). Right Closeup of the early time behavior. The dashed horizontal lines mark the mean time-asymptotic value of the error

Full size image
Fig. 2
figure 2

Eigenvalues of the spatial operator with the central flux (Left) and the upwind flux (Right) for \(N=4\), \(K=50\)

Full size image

At better resolution, P3 suggests that the difference between the asymptotic errors from the upwind and central fluxes should decrease. Figure 3 on the left shows the time behavior of the error for \(N=7\) and \(K=50\), where the polynomial order is increased but the number of elements stays fixed. The asymptotic error has decreased and the central flux still gives a larger error. There is also much less difference between the time it takes for the two approximations to reach the error bound, which is consistent with the argument leading to P4. Using the same number of degrees of freedom but lower order and more elements also supports P3. The asymptotic errors are closer than for \(N=4\), \(K=50\), but more elements means more jumps to dissipate energy and the dissipation effect is stronger at the lower order [6].

Fig. 3
figure 3

Error behavior as a function of time for \(N=7\), \(K=50\) (Left) and \(N=4\),\(K=80\) (Right)

Full size image

In general, we would expect spectral convergence of the error for a spectral element method. Indeed, we’ve seen that the quantity \(\mathbb {E}\) depends only on the smoothness of the solution, u. However, we expect the time asymptotic error to be bounded by \(\mathbb {E}/\delta _{0}\) where \(\delta _{0}\) depends on the size of the jumps at the element interfaces. So the question is whether \(1/\delta _{0}\) increases faster or slower than the approximation errors in \(\mathbb {E}\). The arguments in [10] leading to the estimate (74) are not precise enough to answer that question. Experimentally, Fig. 4 shows that the upper bound of the error for the upwind flux (which is less noisy and hence more easily measured) as a function of polynomial order is clearly spectral. This suggests that the approximation errors decay faster than \(1/\delta _{0}\) grows.

Fig. 4
figure 4

Convergence of the time asymptotic error for the upwind flux as a function of N for \(K=50\)

Full size image

6.2 Error Behavior in Two Space Dimensions

To see that the conclusions derived from the one dimensional approximation extend to multiple space dimensions, we compute solutions to the symmetric linear wave equation in first order system form

$$\begin{aligned} {\left[ {\begin{array}{c} p \\ u \\ v \end{array}} \right] _t} + \left[ {\begin{array}{ccc} 0&{}c&{}0 \\ c&{}0&{}0 \\ 0&{}0&{}0 \end{array}} \right] {\left[ {\begin{array}{c} p \\ u \\ v \end{array}} \right] _x} + \left[ {\begin{array}{ccc} 0&{}0&{}c \\ 0&{}0&{}0 \\ c&{}0&{}0 \end{array}} \right] {\left[ {\begin{array}{c} p \\ u \\ v \end{array}} \right] _x} = 0, \end{aligned}$$
(76)

with wavespeed \(c=1\) on the circular domain with a hole shown in Fig. 5.

Fig. 5
figure 5

Circular mesh with a hole showing internal degrees of freedom for \(N=4\)

Full size image

We choose the initial and boundary conditions so that the exact solution is the sinusoidal plane wave

$$\begin{aligned} \left[ {\begin{array}{c} p \\ u \\ v \end{array}} \right] = \left[ {\begin{array}{c} 1 \\ {\frac{{{k_x}}}{c}} \\ {\frac{{{k_y}}}{c}} \end{array}} \right] \sin \left( {2\left( {{k_x}x + {k_y}y - ct} \right) } \right) \end{aligned}$$
(77)

with wavevector \(\left( k_{x},k_{y}\right) =\left( \sqrt{3}/2,1/2\right) \). The computed solution contours at \(t=10\) are shown in Fig. 6.

Fig. 6
figure 6

Contours of p for the plane wave solution of the symmetric wave equation for \(N=4\)

Full size image
Fig. 7
figure 7

Time history of the error for the two dimensional wave propagation problem. The dashed horizontal guidelines mark the limits of the time asymptotic states. Arrows mark the approximate times where the time asymptotic state is reached

Full size image

Since the element boundaries are curved in this test problem, the metric terms associated with the transformations from the elements to the reference element \([-1,1]^{2}\) are not constant. To ensure that the approximation is stable, we use the skew-symmetric DGSEM approximation developed in [9]. With the skew-symmetric approximation, the volume terms for the constant coefficient problem vanish in the stability and error proofs leaving only the boundary terms, just as in one space dimension. For the time integration, we again use a third order low storage Runge–Kutta method with the time step chosen so that the time integration error is negligible.

The time history of the error for the two-dimensional example is shown in Fig. 7. The features predicted by the one dimensional analysis still hold: For both the upwind and central fluxes, the error is bounded in time (P1), rather than growing linearly. The error bound for the central flux is once again larger than that of the upwind flux (P2). Finally, it takes longer for the central flux to reach its time asymptotic state where the pattern starts repeating than does the upwind flux, \(T\approx 8\) vs. \(T\approx 2\) (P3).

7 Conclusions

We have shown that when characteristic boundary conditions are implemented through the numerical flux, the discontinuous Galerkin spectral element method exhibits bounded error growth, just as has been observed in the past for finite difference approximations. The numerical flux used at element interfaces affects the speed at which the asymptotic error is reached and the magnitude of that error. The use of the upwind flux leads to a shorter time to, and a smaller value of, the asymptotic error. This effect decreases as the resolution increases and the jumps at the interfaces decreases. Numerical experiments in both one and two space dimensions show this behavior predicted by the error growth model.