1 Introduction

Discontinuous Galerkin methods [4, 6] have emerged as one of the most popular discretization techniques for simulating physical and engineering phenomena including various linear and nonlinear wave models. Discontinuous Galerkin methods have excellent dispersive properties, are geometrically flexible, do not have a global mass matrix, can be implemented at any order of accuracy, and, being Galerkin methods, have robust stability properties.

Although discontinuous Galerkin methods are spectrally convergent with the order q of the approximation, very high order methods, say \(q>6\), are seldom used in practice. The primary reason for this is that the spectral radius of the discrete spatial derivative operator grows as \(q^2/h\), where h is an element length scale. This rapidly growing numerical stiffness forces the use of excessively small time steps, effectively prohibiting the use of very high order methods. The source of this numerical stiffness is the approximation by polynomials which must be sampled throughout an element. Heuristically this can be understood by comparing a wave \(w=e^{i q x}\) and its q times larger derivative \(w_x = iq w\) with a typical orthogonal polynomial, say a Chebyshev polynomial, \(T_q(x) =\cos (q \cos ^{-1}(x))\) and its derivative \(T_q'(x)\). Clearly \(| T_q(x) | \le 1,\) for \( |x| \le 1\) and for all q, as for the wave, but the derivative \(|T_q'(\pm 1)| = q^2\), is q times larger at the edges.

This numerical stiffness is particularly troublesome for linear wave propagation problems where solutions typically remain smooth throughout the computation and thus favor very high order spatial discretizations. Fortunately this numerical stiffness can be circumvented in several ways, for example by allowing the polynomial approximations to the solution to spread out over many elements as in the traditional finite difference methods or as in the more recent Galerkin difference methods [3], or by only sampling the derivatives at the cell center as in Hermite methods [2].

It is also possible to remove this numerical stiffness within the discontinuous Galerkin framework either by co-volume filtering as proposed in [13] or by carrying two approximate solutions on staggered grids as in central discontinuous Galerkin methods [10]. Central discontinuous Galerkin methods combine features of discontinuous Galerkin methods and central schemes [11], and they are shown in [10], via Fourier analysis, to allow a larger time step size than standard upwind discontinuous Galerkin methods when applied to the linear advection equation. In [12] these results were established quantitatively for upwind discontinuous Galerkin methods and central discontinuous Galerkin methods by estimating the dependence of the operator bound of the respective spatial discretizations on the approximation order. A serious drawback with the co-volume approach [13] and the central discontinuous Galerkin approach [10] is that they must carry two copies of the solution hence with memory usage and computational cost per right hand side evaluation doubled.

In this paper we present an alternative method that can be time-marched at very high order of accuracy and with an explicit time discretization and \(\mathscr {O}(1)\) CFL. Our method is a staggered version of the energy-based discontinuous Galerkin method [1]. Our method does not require any additional copies of the solution vector and thus has the same memory cost as the original method in [1] but can take much larger timesteps.

With our method being staggered, some polynomial approximations are only sampled in a mesh element away from its edges. This allows us to prove, in one dimension and with periodic boundary conditions, that this staggered energy-based discontinuous Galerkin method results in a semi-discrete-in-space operator whose norm grows linearly with the order of the method. Precisely, in Theorem 2 we establish a bound for the spatial operator \(\mathscr {L}_c\):

$$\begin{aligned} \Vert \mathscr {L}_c \Vert \le C \frac{q}{h}, \end{aligned}$$

where h is the element width and q is the polynomial degree. This, in combination with the Kreiss-Wu theory [9], indicates that the Courant-Friedrich-Levy (CFL) number is constant independent of order of accuracy as long as high order locally stable time stepping methods with large stability domains are applied. Such time-stepping methods can be constructed at arbitrary order by adding additional stages to enhance the stability of standard methods; see, for example, [7] where stability-enhanced leap-frog schemes are proven to exist at all orders and optimized at orders up to sixteen.

At physical boundaries it is no longer possible to stagger the mesh and the CFL constraint becomes order dependent again. As long as the bulk of the problem can be meshed by a rectilinear mesh this can easily be remedied in any dimension by the use of local timestepping in elements near the boundary. Here we use the local timestepping methods of Diaz and Grote [5] and show in numerical experiments in one and two dimensions that this approach allows us to retain the large time steps in the interior. The resulting method, while having some additional computational overhead near boundaries, asymptotically has the same computational complexity as the staggered method for the periodic case.

Fig. 1
figure 1

The method presented here can handle problems on meshes as the one above

Full size image

The two dimensional examples we consider below are proof-of-concept computations in square geometries but we emphasize that a more sophisticated (than the one we have used for the results in this paper) implementation could be very efficient for meshes of the type that is displayed in Fig. 1, and that extensions to three spatial dimensions are straightforward. An example of problems of this type is the simulation of underwater acoustics with bathymetry.

The rest of the paper is organized as follows. In Sect. 2 we review the formulation of energy-based DG methods for the scalar wave equation and extend them to staggered, structured meshes. In Sect.  3 we establish bounds on the norm of the spatial operator in one space dimension and with periodic boundary conditions. In Sect.  4 we briefly discuss our time-stepping schemes and the corrections needed to maintain large time steps in the presence of boundaries. Lastly, in Sect. 5 we demonstrate the accuracy and stability of the method in one and two space dimensions by means of numerical experiments.

2 Energy-based discontinuous Galerkin method for the wave equation

We consider the scalar wave equation written as a first order system in time

$$\begin{aligned}{} & {} \frac{\partial u(x,t)}{\partial t} = v(x,t), \end{aligned}$$
(2.1)
$$\begin{aligned}{} & {} \quad \frac{\partial v(x,t)}{\partial t}= \nabla \cdot (c^2(x) \nabla u(x,t)) + f(x,t), \end{aligned}$$
(2.2)

on the domain

$$\begin{aligned} x = (x_1,\ldots ,x_d) \in \Omega \subset \mathbb {R}^d, \, t>0, \end{aligned}$$

with initial conditions

$$\begin{aligned} u(x,0) = g(x), \ \ \frac{\partial u}{\partial t }(x,0) = v(x,0) = h(x), \end{aligned}$$
(2.3)

and boundary conditions

$$\begin{aligned} \gamma \frac{\partial u}{\partial t } + \kappa c \, \vec {n} \cdot \nabla u = 0, \ \ x \in \partial \Omega . \end{aligned}$$
(2.4)

Here \(c=c(x)\) is the speed of sound and \(\vec {n}\) is the outward pointing unit normal. For the boundary conditions we assume the normalization \(\gamma ^2+\kappa ^2 = 1\) and that \(\gamma ,\kappa \ge 0\). Then the choice \(\kappa = 0\) corresponds to a homogeneous Dirichlet boundary condition on \(\frac{\partial u}{\partial t }\) and \(\gamma = 0\) corresponds to a homogeneous Neumann boundary condition. Any choice with \(\gamma \kappa \) being positive will dissipate the energy of the system and can be thought of as a low order non-reflecting boundary condition.

The energy associated with the scalar wave equation is

$$\begin{aligned} \mathscr {E}(t) = \frac{1}{2} \int _\Omega \left( \frac{\partial u}{\partial t}\right) ^2 + c^2(x) |\nabla u|^2 {dx,} \end{aligned}$$
(2.5)

and it is a discrete version of this energy that our energy-based discontinuous Galerkin method is built from.

We now present the non-staggered and staggered formulations of the method. A more thorough analysis of the non-staggered method can be found in [1], but we include it here to illustrate the differences between the two formulations. The essential new idea in the energy-based method is to enforce Eq. (2.1) weakly with a nonstandard test function; see Eqs. (2.6a) and (2.12a) below. With this choice we can establish energy estimates without the need for mesh-dependent penalty parameters.

2.1 Non-staggered formulation

Let the finite element mesh, \(\Omega ^h=\{ \Omega _j \}\), with

$$\begin{aligned} {\Omega } = \bigcup _j {\Omega }_j, \end{aligned}$$

be a discretization of \(\Omega \) consisting of geometry-conforming and non-overlapping (possibly curved) elements with piecewise smooth boundaries.

On each element \({\Omega }_j\), the approximation to the displacement, \(u^h\), and the approximation to the velocity, \(v^h\), are elements of some finite dimensional spaces \(U^h\) and \(V^h\) respectively. Then, the non-staggered energy-based discontinuous Galerkin method can be stated as follows. On each element \({\Omega }_j\), require that for all test functions

$$\begin{aligned} \phi \in U^h, \ \ \psi \in V^h, \end{aligned}$$

the following variational formulation holds:

$$\begin{aligned}{} & {} \int _{{\Omega }_j} c^2 \nabla \phi \cdot \left( \frac{\partial \nabla u^h}{\partial t} - \nabla v^h \right) {dx} = \int _{\partial {\Omega }_j} (c^2 \nabla \phi \cdot \vec {n}) \left( v^{*} - v^h \right) ds, \end{aligned}$$
(2.6a)
$$\begin{aligned}{} & {} \int _{{\Omega }_j} \psi \frac{\partial v^h}{\partial t} + \nabla \psi \cdot (c^2\nabla u^h) - \psi f dx = \int _{\partial {\Omega }_j} \psi ( (c^2 \nabla u ) \cdot \vec {n})^{*}ds. \end{aligned}$$
(2.6b)

As described in [1] the energy is invariant to constants and this necessitates an additional equation complementing (2.6a)

$$\begin{aligned} \int _{{\Omega }_j} \left( \frac{\partial u^h}{\partial t} - v^h\right) dx = 0,\quad \forall j. \end{aligned}$$
(2.7)

Here \(v^*\) and \(( (c^2 \nabla u ) \cdot \vec {n})^{*}\) are numerical fluxes computed from the averages and jumps of function values and derivatives. Arbitrarily labeling values from adjacent elements 1 and 2 we recall the standard notation:

$$\begin{aligned} \{\{v^h \}\}_{\alpha }= & {} \frac{1}{2} \left( \alpha v^{h,1} + (1- \alpha ) v^{h,2} \right) \nonumber \\ [[v^h ]]= & {} v^{h,1} \vec {n}^1 + v^{h,2} \vec {n}^2, \end{aligned}$$
(2.8)
$$\begin{aligned} \{\{c^2 \nabla u^h \}\}_{\alpha }= & {} \frac{1}{2} \left( \alpha c^2 \nabla u^{h,1} + (1- \alpha ) c^2 \nabla u^{h,2} \right) , \nonumber \\ [[c^2 \nabla u^h ]]= & {} c^2 \nabla u^{h,1} \cdot \vec {n}^1 + c^2 \nabla u^{h,2} \cdot \vec {n}^2. \end{aligned}$$
(2.9)

We then set

$$\begin{aligned} v^{*}= & {} \{\{v^h \}\}_{\alpha } - \beta [[c^2 \nabla u^h ]], \end{aligned}$$
(2.10)
$$\begin{aligned} \left( c^2 \nabla u \cdot \vec {n} \right) ^{*}= & {} \{\{c^2 \nabla u^h \}\}_{1-\alpha } \cdot \vec {n} - \tau [[v^h ]]\cdot \vec {n}. \end{aligned}$$
(2.11)

Here \(\beta \ge 0\) is an upwinding parameter with units of \(c^{-1}\) and \(\tau \ge 0\) is an upwinding parameter with units of c. When \(\beta =\tau =0\), one can recover the commonly used central fluxes by choosing \(\alpha =1/2\), and alternating fluxes with \(\alpha =0\) or 1.

2.2 Staggered formulation

We now consider two structured finite element meshes, \(\Omega ^h=\{ \Omega _j \}\) and \(\Omega ^{\diamond ,h}=\{ \Omega _k^{\diamond } \}\)

$$\begin{aligned} \Omega = \bigcup _j\Omega _j = \bigcup _k\Omega _k^\diamond . \end{aligned}$$

We assume each mesh consists of geometry-conforming and non-overlapping (possibly curved) quadrilaterals (or hexahedra) with piecewise smooth boundaries. We assume that the meshes are staggered. More precisely, away from non-periodic boundaries we assume that all quadrilaterals (hexahedra) are straight sided and convex and that all vertices have valence 4 (6). By staggering we mean that, away from boundaries, the vertices of the mesh \(\Omega ^{\diamond ,h}\) coincide with the centers (defined as the vertex, side or area/volume centroid) of the elements in \(\Omega ^h\). An example of a periodic staggered mesh is presented in Fig. 2.

For consistency with the theoretical and computational results to follow, we take the approximation to the velocity, \(v^h\), restricted to an element \({\Omega }^\diamond _k\) in \(\Omega ^{\diamond ,h}\), to be a tensor product polynomial in \((\mathbb {Q}^{q_v} ({\Omega }^\diamond _k))^d\) while the approximation to the displacement, \(u^h\), restricted to an element \({\Omega }_j\) in \(\Omega ^h\), is taken to be a tensor product polynomial in \((\mathbb {Q}^{q_u} ({\Omega }_j))^d\). Here \(q_u\in \mathbb {N}\), \(q_v\in \mathbb {N}\cup \{0\}\).

The staggered energy-based discontinuous Galerkin method then can be stated as follows. On each element \(\Omega _j\) and \(\Omega _k^\diamond \), require that for all test functions

$$\begin{aligned} \phi \in (\mathbb {Q}^{q_u} ({\Omega }_j) )^d, \ \ \psi \in (\mathbb {Q}^{q_v} ({\Omega }_k^\diamond ))^d, \end{aligned}$$

the following variational formulation holds:

$$\begin{aligned} \int _{{\Omega }_j} \left( c^2 \nabla \phi \cdot \frac{\partial \nabla u^h}{\partial t} + \nabla \cdot (c^2 \nabla \phi ) v^h \right) dx= & {} \int _{\partial {\Omega }_j} (c^2 \nabla \phi \cdot \vec {n}) v^{*} ds, \end{aligned}$$
(2.12a)
$$\begin{aligned} \int _{{\Omega }_k^\diamond } \psi \frac{\partial v^h}{\partial t} + \nabla \psi \cdot (c^2 \nabla u^h) - \psi f dx= & {} \int _{\partial {\Omega }_k^\diamond } \psi ( (c^2 \nabla u ) \cdot \textbf{n})^{*}ds. \end{aligned}$$
(2.12b)

As with the non-staggered formulation we must complement (2.12a) with the equation

$$\begin{aligned} \int _{{\Omega }_j} \left( \frac{\partial u^h}{\partial t} - v^h \right) dx = 0,\quad \forall j. \end{aligned}$$
(2.13)

Again, here \(v^*\) and \(( (c^2 \nabla u ) \cdot \vec {n})^{*}\) are numerical fluxes as in (2.10)–(2.11). However, taking account of the staggering, we note that \(v^h\) is single valued at \(\partial \Omega _j\) and \(c^2 \nabla u\) is single valued at \(\partial \Omega _k^{\diamond }\) so the choice of \(\alpha \) is not relevant. Lastly we note that the integrals of gradients in the variational form as well as in the calculations below are understood to be piecewise-defined in subdomains where the functions are smooth. For example, the integral in (2.12b) includes boundaries of elements in \(\Omega ^h\) across which \(u^h\) is discontinuous. We do not, here, interpret \(\nabla u^h\) in a distributional sense and so no additional boundary terms are implied.

We note the difference between (2.6a) and (2.12a). If the term \(\nabla \cdot (c^2 \nabla \phi ) v^h\) is integrated by parts in (2.12a), terms involving the jump in \(v^h\) across boundaries of dual mesh elements will appear. These play a role in the energy estimate we now derive. For the subsequent analysis we set \(f=0\) for simplicity as the source function plays no role in determining time step stability constraints.

Define the discrete energy to be

$$\begin{aligned} \mathscr {E}^h (t) = \frac{1}{2} \sum _k \int _{\Omega _k^{\diamond }} \left( v^h \right) ^2\ dx + \frac{1}{2} \sum _j \int _{\Omega _j} c^2 \arrowvert \nabla u^h \arrowvert ^2\ dx. \end{aligned}$$
(2.14)

To start, we assume periodic boundary conditions. Choosing \(\phi = u^h\) in (2.12a), integrating by parts, and using the fact that \(v^h\) is single valued on \(\partial \Omega _j\) we find

$$\begin{aligned} \frac{1}{2} \frac{d}{dt} \sum _j \int _{\Omega _j} c^2 \arrowvert \nabla u^h \arrowvert ^2\ dx= & {} \sum _j \int _{\Omega _j} c^2 \nabla u^h \cdot \nabla v^h \ dx - \sum _k \int _{\partial \Omega _k^\diamond } c^2 \nabla u^h \cdot [[v^h ]]\ ds \\{} & {} - \;\beta \sum _j \int _{\partial \Omega _j} [[c^2 \nabla u^h ]]^2 \ ds, \end{aligned}$$

Similarly we find

$$\begin{aligned} \frac{1}{2} \frac{d}{dt} \sum _k \int _{\Omega _k^{\diamond }} \left( v^h \right) ^2\ dx= & {} - \sum _k \int _{\Omega _k^{\diamond }} c^2 \nabla u^h \cdot \nabla v^h \ dx + \sum _k \int _{\partial \Omega _k^{\diamond }} c^2 \nabla u^h \cdot [[v^h ]]\ ds\\{} & {} - \;\tau \sum _k \int _{\partial \Omega _k^{\diamond }} \arrowvert [[v^h ]]\arrowvert ^2 \ ds. \end{aligned}$$

Summing these equations, we see that the left-hand side is the time derivative of the discrete energy. Since \(\bigcup _j \Omega _j = \bigcup _k \Omega _k^{\diamond }\) and recalling the piecewise definition of the integrals we conclude that the terms involving \(c^2 \nabla u^h \cdot \nabla v^h\) cancel. Thus we conclude:

$$\begin{aligned} \frac{d \mathscr {E}^h}{dt} = - \beta \sum _j \int _{\partial \Omega _j} [[c^2 \nabla u^h ]]^2 \ ds - \tau \sum _k \int _{\partial \Omega _k^{\diamond }} \arrowvert [[v^h ]]\arrowvert ^2 \ ds. \end{aligned}$$
(2.15)

At nonperiodic boundaries we alter the staggered mesh so that elements from both \(\Omega ^h\) and \(\Omega ^{\diamond ,h}\) conform to \(\partial \Omega \). Now the imposition of the boundary conditions is the same as for the non-staggered formulation. For example, recalling (2.4) we may set

$$\begin{aligned} v^{*}= & {} \frac{\kappa }{\gamma + \kappa } \left( v^h - c \nabla u^h \cdot \vec {n} \right) , \end{aligned}$$
(2.16)
$$\begin{aligned} \left( c^2 \nabla u^h \cdot \vec {n} \right) ^{*}= & {} \frac{\gamma }{\gamma + \kappa } \left( c^2 \nabla u^h \cdot \vec {n} - c v^h \right) . \end{aligned}$$
(2.17)

Then the contribution of the nonperiodic boundaries to the energy derivative can be shown to be nonpositive. The mesh modification at these boundaries will preclude taking global large time steps. To maintain the efficiency of the staggered scheme we will then use local time stepping in the vicinity of the boundaries; see Sect.  4 for details.

3 Operator bounds on periodic domains in one space dimension

In this section we use the techniques from [12, 13] to establish bounds for the energy-based DG and the staggered energy-based DG spatial operator for the second-order wave Eqs. (3.1) and (3.2) in one space dimension. This allows us to invoke the Kreiss-Wu theory [9] combined with the energy estimates to establish the stability of fully discrete locally stable explicit time-stepping schemes.

We restrict the analysis to uniform grids, periodic boundary conditions, and constant coefficients. The key ingredient to taming the CFL condition is to evaluate certain terms with derivatives only near the element centers, and this is made possible by the proposed staggered formulation. We expect that the analysis can be extended to smoothly varying grids and to variable coefficients. The numerical experiments demonstrate the efficiency of the method for a variable coefficient problem. It may also be possible to extend the analysis to problems with Dirichlet or Neumann boundary conditions by using the image principle. However, we don’t pursue this here.

3.1 Operator bounds for the non-staggered formulation

Now, consider the one dimensional wave equation in a uniform medium

$$\begin{aligned} u_t= & {} v, \end{aligned}$$
(3.1)
$$\begin{aligned} v_t= & {} c^2 u_{xx}, \end{aligned}$$
(3.2)

on the domain \(x\in [x_\textrm{L}, x_\textrm{R}] \equiv \Omega \). Let the domain be discretized by a grid \(x_j = x_\textrm{L} + j h,\) \(j = 0,\ldots ,N,\, h = (x_\textrm{R}-x_\textrm{L}) / N\), and \(I_j=[x_j, x_{j+1}]\). Associated with the grid, we define two broken finite element spaces

$$\begin{aligned} U_h^{q_u} = \{ w: w|_{I_j} \in \mathbb {Q}^{q_u}(I_j)\;\forall j\}, \ \ \ \ V_h^{q_v} = \{ w: w|_{I_j} \in \mathbb {Q}^{q_v}(I_j)\;\forall j\}. \end{aligned}$$

Here and below \(\mathbb {Q}^{q_u}(I_j)\) is the space of polynomials of degree up to \(q_u\) in \(I_j\), \(q_u\in \mathbb {N}\), and \(q_v\in \mathbb {N}\cup \{0\}\). In addition, we denote \(\phi ^\pm (x) = \lim _{\varepsilon \rightarrow 0\pm } \phi (x+ \varepsilon )\).

The energy-based DG scheme then consists of finding \(u^h(\cdot ,t) \in U_h^{q_u}\) and \(v^h(\cdot ,t) \in V_h^{q_v}\) such that for any \(\phi \in U_h^{q_u}\) and \(\psi \in V_h^{q_v}\) and for all j

$$\begin{aligned} \int _{x_j}^{x_{j+1}} c^2 \phi _x\left( \frac{\partial u^h_x}{\partial t}-v^h_x\right) dx= & {} c^2 \phi _x^-(v^*-v^{h,-})\Big |_{x_{j+1}}- c^2 \phi _x^+(v^*-v^{h,+})\Big |_{x_j},\nonumber \\ \end{aligned}$$
(3.3a)
$$\begin{aligned} \int _{x_j}^{x_{j+1}}\psi \frac{\partial v^h}{\partial t} + c^2 \psi _x u^h_x dx= & {} c^2 \psi ^- u_x^*\Big |_{x_{j+1}}- c^2 \psi ^+ u_x^*\Big |_{x_j}, \end{aligned}$$
(3.3b)
$$\begin{aligned} \int _{x_j}^{x_{j+1}} \frac{\partial u^h}{\partial t}-v^h dx= & {} 0. \end{aligned}$$
(3.3c)

Assuming periodic boundary conditions we may add up the Eqs. (3.3a) and (3.3b) in j to find

$$\begin{aligned} \int _{\Omega } c^2 \phi _x\frac{\partial u^h_x}{\partial t} + \psi \frac{\partial v^h}{\partial t} dx =&\int _\Omega c^2 \phi _x v^h_x - c^2 \psi _x u^h_x dx \nonumber \\&+ \sum _j c^2 \left( \phi _x^-(v^*-v^{h,-})\Big |_{x_{j+1}}- \phi _x^+(v^*-v^{h,+})\Big |_{x_j} \right. \nonumber \\&\left. +\;\psi ^- u_x^*\Big |_{x_{j+1}}-\psi ^+ u_x^*\Big |_{x_j}\right) . \end{aligned}$$
(3.4)

Throughout, the spatial derivative of functions in any broken finite element space shall be understood as being defined element by element. To connect the element solutions in a stable fashion we use the numerical fluxes defined in (2.10)–(2.11) and introduce the notation

$$\begin{aligned} v^*= & {} \mathscr {H} ({v}^h, u_x^h)= \{\{v^h\}\}_\alpha - \beta c^2 (u_{x}^{h,-} - u_{x}^{h,+}), \end{aligned}$$
(3.5a)
$$\begin{aligned} u_{x}^*= & {} \mathscr {G}(u_x^h, v^h)= \{\{u_{x}^{h}\}\}_{1-\alpha } - \frac{\tau }{c^2} (v^{h,-}-v^{h,+}). \end{aligned}$$
(3.5b)

Then the energy estimate (2.15) holds. We note that it can also be used to establish error estimates for different choices of \(\alpha \), \(\beta \) and \(\tau \); see [1] for details.

We now establish bounds on the spatial operators which constrain the allowable time step sizes for explicit marching schemes. In particular we are interested in the dependence of these bounds on the approximation orders, \(q_u\) and \(q_v\) and will follow a similar analysis as in [12, 13]. With the choice of the numerical fluxes in (2.10)–(2.11), an important observation is that the first two equations in (3.3) are coupled with (3.3c) in a one-way manner. That is, (3.3a)–(3.3b) will uniquely determine \(w^h=u_x^h\in U_h^{q_u-1}\) and \(v^h\in V_h^{q_v}\). Once \(w^h\), \(v^h\) are available, one can further recover the missing constant in \(u^h\) on \([x_j, x_{j+1}]\) (i.e. in the form of the cell average of \(u^h\)) through (3.3c) for all j. As this last step is simply an integration in time it can not affect the numerical stability; see also the discussion in Sect.  4.

These considerations motivate us to define the operator \({\mathscr {L}}: U_h^{q_u-1}\times V_h^{q_v}\mapsto U_h^{q_u-1}\times V_h^{q_v}\),

$$\begin{aligned}&\int _{\Omega }\mathscr {L}(cw,v)(c\varphi ,\psi )dx = \;c^2 \int _\Omega \varphi v_x - \psi _x w dx \nonumber \\&\quad +\; c^2 \sum _j \left( \psi ^- \mathscr {G}(w,v) \Big |_{x_{j+1}}-\psi ^+ \mathscr {G}(w,v) \Big |_{x_j}\right) \nonumber \\&\quad +\; c^2 \sum _j \left( \varphi ^-(\mathscr {H}(v,w)-v^{-})\Big |_{x_{j+1}}- \varphi ^+(\mathscr {H}(v,w)-v^{+})\Big |_{x_j}\right) \end{aligned}$$
(3.6)

for any \(\varphi \in U_h^{q_u-1}\) and \( \psi \in V_h^{q_v},\) with the operator norm as

$$\begin{aligned}{} & {} \left\| \mathscr {L} \right\| \equiv \sup _{\begin{array}{c} w,\varphi \in U_h^{q_u-1},\, v, \psi \in V_h^{q_v}\\ (w,v)\ne (0,0), (\varphi , \psi )\ne (0,0) \end{array}}\nonumber \\{} & {} \frac{\int _{\Omega }\mathscr {L}(cw,v)(c\varphi ,\psi )dx}{\left( \Vert cw \Vert _{L^2(\Omega )}^2+\Vert v \Vert _{L^2(\Omega )}^2 \right) ^{1/2}\left( \Vert c\varphi \Vert _{L^2(\Omega )}^2 + \Vert \psi \Vert _{L^2(\Omega )}^2 \right) ^{1/2}}. \end{aligned}$$
(3.7)

Once the bound is established for \(\left\| \mathcal L\right\| \), time step condition, \(\Delta t \left\| \mathscr {L} \right\| \le \mathscr {R}\), for method of lines discretization combined with locally stable one-step temporal methods will follow from Kreiss-Wu theory [9]. Here \(\mathscr {R}\) is defined as the radius of the largest semidisk in the closed left half complex plane contained in the stability domain of the method. It is well known [8], that one-step methods based on Taylor expansion with \(q_\textrm{T} = 3,4,7,8,11,12,15,16,\ldots \) terms are locally stable. For \(q_\textrm{T}\) of moderate size they have stability domains which grow with order. Thus, if we can establish a bound on \(\left\| \mathscr {L} \right\| \) that grows linearly in \(q_u\) and \(q_v\), we should expect that the fully discrete method can time-march at a CFL condition of \(\mathscr {O}(1)\) when the spatial and temporal orders are matched. As the order increases this does not hold, but, as discussed in Sect. 4, with the introduction of additional stages the size of the stability domain can be greatly increased. In what follows we will see that such a bound can be established for the staggered method with suitably chosen numerical fluxes but not for the non-staggered method. For the non-staggered method, the bound on \(\left\| \mathscr {L} \right\| \) is quadratic in \(q_u\) and \(q_v\), and this will be proved next. We note that the quadratic dependence on the degrees is sharp as demonstrated numerically in [1].

Theorem 1

Let the energy-based DG spatial operator \(\mathscr {L}\) be defined as in (3.6) with periodic boundary conditions and with numerical fluxes defined by (2.10)–(2.11). Then the following estimate holds:

$$\begin{aligned} \Vert \mathcal L\Vert\le & {} C_1 \frac{c}{h}\max \{(q_u-1)^2, q_v^2\} \nonumber \\{} & {} + \;C_2 \frac{c}{h} \left( 2\max \left\{ c \beta q_u^2,\frac{\tau }{c} (q_v+1)^2\right\} +(|\alpha |+|1-\alpha |)(q_v+1)q_u\right) . \nonumber \\ \end{aligned}$$
(3.8)

Here \(C_1\le 2 \sqrt{3}\) and \(C_2 \le 2\) are two universal positive constants, independent of \(q_u\), \(q_v\), h, and \(\alpha ,\beta , \tau \).

Proof

Consider any \(w,\varphi \in U_h^{q_u-1}\) and \(v,\psi \in V_h^{q_v}\). Applying element-wise integration by parts and the triangle inequality, we have

$$\begin{aligned} \int _{\Omega }\mathscr {L}(cw,v)(c\varphi ,\psi )dx =&-\;c^2 \int _\Omega \varphi _{x} v +\psi _x w dx \nonumber \\&+\; c^2 \sum _j \left( \varphi ^-\mathscr {H}(v,w)\Big |_{x_{j+1}}-\varphi ^+\mathscr {H}(v,w)\Big |_{x_j}\right) \nonumber \\&+\; c^2 \sum _j \left( \psi ^- \mathscr {G}(w,v) \Big |_{x_{j+1}}-\psi ^+ \mathscr {G}(w,v) \Big |_{x_j}\right) \nonumber \\ \le&\; \Lambda _1+\Lambda _2+\Lambda _3, \end{aligned}$$
(3.9)

with

$$\begin{aligned} \Lambda _1= & {} c^2 \sum _j\int _{x_j}^{x_{j+1}} \left| \varphi _{x} v \right| dx+\int _{x_j}^{x_{j+1}}\left| \psi _x w\right| dx,\\ \Lambda _2= & {} c^2 \sum _j \left| \varphi ^-\mathscr {H}(v,w)\right| \Big |_{x_{j+1}}+ \left| \varphi ^+\mathscr {H}(v,w)\right| \Big |_{x_j},\\ \Lambda _3= & {} c^2 \sum _j \left| \psi ^- \mathscr {G}(w,v)\right| \Big |_{x_{j+1}}+\left| \psi ^+ \mathscr {G}(w,v)\right| \Big |_{x_j}. \end{aligned}$$

We now bound each of the terms, starting with the volume term \(\Lambda _1\). By applying the Cauchy-Schwarz inequality, we have

$$\begin{aligned} \Lambda _1 \le c \sum _j\Vert c\varphi _{x}\Vert _{L^2(I_j)}\Vert v\Vert _{L^2(I_j)} + \Vert \psi _x\Vert _{L^2(I_j)}\Vert cw\Vert _{L^2(I_j)}. \end{aligned}$$

For \(\Lambda _2\) and \(\Lambda _3\), we use the definitions of \(\mathscr {H}(v, w)\) and \(\mathscr {G}(w, v)\) as well as the triangle inequality, and arrive at

$$\begin{aligned} \Lambda _2 \le&\; c \sum _j \left| c \varphi ^-\right| \left( |\alpha |\left| v^{-}\right| + |1-\alpha | \left| v^{+}\right| + c \beta \left| c w^{-}\right| + c \beta \left| c w^{+}\right| \right) \Big |_{x_{j+1}}\\&+\;\left| c \varphi ^+\right| \left( |\alpha |\left| v^{-}\right| + |1-\alpha | \left| v^{+}\right| + c \beta \left| c w^{-}\right| + c \beta \left| cw^{+}\right| \right) \Big |_{x_j},\\ \Lambda _3 \le&\; c \sum _j \left| \psi ^-\right| \left( |1-\alpha |\left| c w^{-}\right| +|\alpha | \left| c w^{+}\right| + \frac{\tau }{c} \left| v^{-}\right| +\frac{\tau }{c}\left| v^{+}\right| \right) \Big |_{x_{j+1}} \\&+\; \left| \psi ^+\right| \left( |1-\alpha |\left| c w^{-}\right| +|\alpha |\left| c w^{+}\right| + \frac{\tau }{c} \left| v^{-}\right| +\frac{\tau }{c}\left| v^{+}\right| \right) \Big |_{x_j}. \end{aligned}$$

Now we recall some standard inverse inequalities for polynomials spaces [12]; there exist positive constants \(\hat{C}_1\le \sqrt{3}\), \(\hat{C}_2\le \frac{\sqrt{2}}{2}\), such that \(\forall p\in \mathbb {Q}^k([-1,1])\),

$$\begin{aligned} \Vert p_x\Vert _{L^2([-1,1])}\le \hat{C}_1 k^2\Vert p\Vert _{L^2([-1,1])}, \, p(x) \le \hat{C}_2 (k+1)\Vert p\Vert _{L^2([-1,1])}\; \forall x\in [-1,1].\nonumber \\ \end{aligned}$$
(3.10)

By applying these inverse inequalities, with a linear scaling from \([-1, 1]\) to \(I_j\), and Cauchy-Schwarz inequality, we find that

$$\begin{aligned} \Lambda _1 \le&\;2 \hat{C}_1 \frac{c}{h} \sum _j \left( (q_u-1)^2 \Vert c \varphi \Vert _{L^2(I_j)}\Vert v\Vert _{L^2(I_j)} +q_v^2 \Vert \psi \Vert _{L^2(I_j)}\Vert cw \Vert _{L^2(I_j)}\right) \\ \le&\;C_1 \frac{c}{h}\max \{(q_u-1)^2, q_v^2\}\left( \Vert cw\Vert ^2_{L^2(\Omega )}+\Vert v\Vert ^2_{L^2(\Omega )}\right) ^{1/2}\\&\;\left( \Vert c\varphi \Vert _{L^2(\Omega )}^2+\Vert \psi \Vert _{L^2(\Omega )}^2\right) ^{1/2}, \end{aligned}$$

and similarly, using a linear scaling from \([-1, 1]\) to \(I_s\) (with \(s=j,j\pm 1\)), we have

$$\begin{aligned} \Lambda _2\le&\;2 \hat{C}_2^2 \frac{c}{h} \sum _j \Big ( q_u(q_v+1) \Vert c \varphi \Vert _{L^2(I_j)}\left( |\alpha |\Vert v\Vert _{L^2(I_{j-1}\cup I_{j})}+|1-\alpha |\Vert v\Vert _{L^2(I_j\cup I_{j+1})}\right) \\&+\; c \beta q_u^2 \Vert c \varphi \Vert _{L^2(I_j)}\left( 2\Vert cw\Vert _{L^2(I_j)}+\Vert cw\Vert _{L^2(I_{j-1}\cup I_{j+1})}\right) \Big ), \\ \Lambda _3\le&\;2 \hat{C}_2^2 \frac{c}{h} \sum _j \Big ( q_u(q_v+1)\Vert \psi \Vert _{L^2( I_j)}\left( |1-\alpha |\Vert cw\Vert _{L^2(I_{j-1}\cup I_j)}+|\alpha |\Vert cw\Vert _{L^2(I_{j}\cup I_{j+1})}\right) \\&+\;\frac{\tau (q_v+1)^2}{c}\Vert \psi \Vert _{L^2(I_j)}\left( 2\Vert v\Vert _{L^2(I_j)}+\Vert v\Vert _{L^2(I_{j-1}\cup I_{j+1})}\right) \Big ), \end{aligned}$$

and hence

$$\begin{aligned} \Lambda _2+\Lambda _3\le&\;C_2 \frac{c}{h} \left( 2\max \left\{ c \beta q_u^2, \frac{\tau }{c} (q_v+1)^2\right\} +(|\alpha |+ |1-\alpha |)(q_v+1)q_u\right) \\&\;\;\;\; \left( \Vert cw\Vert ^2_{L^2(\Omega )}+\Vert v\Vert ^2_{L^2(\Omega )}\right) ^{1/2} \left( \Vert c \varphi \Vert _{L^2(\Omega )}^2+\Vert \psi \Vert _{L^2(\Omega )}^2\right) ^{1/2}. \end{aligned}$$

Finally by adding up \(\Lambda _j, j=1, 2, 3\), and based on the operator norm \(\Vert \mathcal L\Vert \) in (3.7), we reach the bound in (3.8). \(\square \)

Fig. 2
figure 2

An example of a periodic staggered mesh in one dimension. When physical boundaries are enforced at \(x_0\) and \(x_n\) the approximations of both \(u^h\) and \(\tilde{v}^h\) would contain a break at those vertices and the mild growth with polynomial degree would no longer be guaranteed (color figure online)

Full size image

3.2 Operator bounds for the staggered formulation

For the staggered version of the method we introduce element centers \(\rho _j = x_{j+\frac{1}{2}} = (x_j+x_{j+1})/2\) as well as the staggered grid composed of the elements \(I_{j+\frac{1}{2}} = [\rho _{j},\rho _{j+1}] \; \forall j\). Associated with both grids, we define two broken finite element spaces

$$\begin{aligned} U_h^{q_u} = \{ w: w|_{I_j} \in \mathbb {Q}^{q_u}(I_j)\; \forall j\}, \ \ \ \ \widetilde{V}_h^{q_v} = \{ w: w|_{I_{j+\frac{1}{2}}} \in \mathbb {Q}^{q_v}(I_{j+\frac{1}{2}}) \; \forall j\}. \end{aligned}$$

Figure 2 displays a staggered grid on a periodic mesh. Note how \(\tilde{v}^h\) is continuous at the breaks of \(u^h\) and vice versa.

The staggered energy-based DG scheme then consists of finding \(u^h(\cdot ,t) \in U_h^{q_u}\) and \(\tilde{v}^h(\cdot ,t) \in \widetilde{V}_h^{q_v}\) such that for any \(\phi \in U_h^{q_u}\) and \(\psi \in \widetilde{V}_h^{q_v}\) and for all j

$$\begin{aligned}&\int _{x_j}^{x_{j+1}} c^2 \phi _x \frac{\partial u_x^h}{\partial t}dx +\underbrace{\int _{x_j}^{\rho _j} c^2 \phi _{xx} \tilde{v}^{h} dx + \int _{\rho _j}^{x_{j+1}} c^2 \phi _{xx} \tilde{v}^h dx}_{\int _{x_j}^{x_{j+1}}c^2\phi _{xx} \tilde{v}^{h} dx } \nonumber \\&\quad =c^2 \phi ^-_x v^*\big |_{x_{j+1}}- c^2 \phi ^+_x v^*\big |_{x_j}, \end{aligned}$$
(3.11a)
$$\begin{aligned}&\int _{\rho _j}^{\rho _{j+1}} \psi \frac{\partial \tilde{v}^{h}}{\partial t}dx +\underbrace{\int _{\rho _j}^{x_{j+1}} c^2 \psi _x u_x^h dx + \int _{x_{j+1}}^{\rho _{j+1}} c^2 \psi _x u_x^{h}dx}_{\int _{\rho _j}^{\rho _{j+1}} c^2\psi _x u_x^{h}dx} \nonumber \\&\quad =c^2 \psi ^- u_x^*\big |_{\rho _{j+1}}- c^2 \psi ^+ u_x^*\big |_{\rho _j}, \end{aligned}$$
(3.11b)
$$\begin{aligned}&\int _{x_j}^{x_{j+1}} \left( \frac{\partial u^h}{\partial t}-\tilde{v}^h\right) dx=0. \end{aligned}$$
(3.11c)

Note that the second and third integrals in (3.11a) (resp. in (3.11b)) are against \(\tilde{v}^h\) (resp. \(u^h\)) from two elements.

Explicitly we write the flux terms

$$\begin{aligned} v^*= & {} H(\tilde{v}^h, u_x^h)= \tilde{v}^{h} - \beta c^2 (u_{x}^{h,-} - u_{x}^{h,+}), \end{aligned}$$
(3.12a)
$$\begin{aligned} u_{x}^*= & {} G(u_x^h, \tilde{v}^h)= u_{x}^{h} - \frac{\tau }{c^2} (\tilde{v}^{h,-}-\tilde{v}^{h,+}), \end{aligned}$$
(3.12b)

noting that there is no ambiguity for \(\tilde{v}^h\) in (3.12a) and \(u_x^h\) in (3.12b) since they are evaluated at the element centers and are uniquely defined.

Assuming periodic boundary conditions, we apply integration by parts to (3.11a) and (3.11b), add them up in j and reach the equality

$$\begin{aligned} \int _{\Omega } c^2 \phi _x\frac{\partial u^h_x}{\partial t} + \psi \frac{\partial \tilde{v}^h}{\partial t}dx =&\; c^2 \sum _j \int _{x_j}^{x_{j+1}} \left( \phi _{x} \tilde{v}^h_x -\psi _x u_x^h\right) dx \nonumber \\&+\; c^2 \sum _j \left( \phi _x^-(v^*-\tilde{v}^h)\big |_{x_{j+1}}- \phi _x^+(v^*-\tilde{v}^h)\big |_{x_{j}} \right. \nonumber \\&\left. +\;\phi _x(\tilde{v}^{h,+}-\tilde{v}^{h,-}) \big |_{\rho _j}\right) \nonumber \\&+\; c^2 \sum _j\left( \psi ^- u_x^*\big |_{\rho _{j+1}}- \psi ^+ u_x^*\big |_{\rho _j}\right) , \end{aligned}$$
(3.13)

with semi-discrete stability of the method following directly from (2.15).

As for the non-staggered scheme, the first two Eqs. (3.11a)–(3.11b) will determine \(w^h=u^h_x\in U_h^{q_u-1}\) and \(\tilde{v}^h\in \widetilde{V}_h^{q_v}\), and hence we define the operator \({\mathcal L}_c: U_h^{q_u-1}\times \widetilde{V}_h^{q_v}\mapsto U_h^{q_u-1}\times \widetilde{V}_h^{q_v}\), satisfying

$$\begin{aligned}{} & {} \int _{\Omega }\mathscr {L}_c(cw,v)(c\varphi ,\psi ) dx\nonumber \\{} & {} \quad = -\; c^2 \sum _j\left( \int _{x_j} ^{x_{j+1}} \varphi _{x} v dx -\varphi ^-H(v, w)|_{x_{j+1}}+ \varphi ^+H(v, w)|_{x_j}\right) \nonumber \\{} & {} \qquad -\; c^2 \sum _j\left( \int _{\rho _j} ^{\rho _{j+1}} \psi _x wdx -\psi ^- G(w, v)|_{\rho _{j+1}}+ \psi ^+ G(w, v)|_{\rho _j}\right) \end{aligned}$$
(3.14)

for any \(\varphi \in U_h^{q_u-1}\) and \( \psi \in \widetilde{V}_h^{q_v},\) with the operator norm as

$$\begin{aligned}{} & {} \left\| \mathscr {L}_c \right\| \equiv \sup _{\begin{array}{c} w,\varphi \in U_h^{q_u-1},\, v, \psi \in \widetilde{V}_h^{q_v}\\ (w,v)\ne (0,0), (\varphi , \psi )\ne (0,0) \end{array}}\\{} & {} \frac{\int _{\Omega }\mathscr {L}_c(cw,v)(c\varphi ,\psi )dx}{\left( \Vert cw\Vert _{L^2(\Omega )}^2+\Vert v\Vert _{L^2(\Omega )}^2\right) ^{1/2}\left( \Vert c\varphi \Vert _{L^2(\Omega )}^2+\Vert \psi \Vert _{L^2(\Omega )}^2\right) ^{1/2}}. \end{aligned}$$

The theorem governing the bound on the operator \(\mathcal L_c\) has a similar form as the non-staggered case, namely, with the quadratic dependence on \(q_u\) and \(q_v\). But when the upwinding parameters \(\beta \) and \(\tau \) are set to zero and the numerical fluxes become purely central, or when \(\beta \) and \(\tau \) are chosen to be order-dependent, the result is significantly stronger. We now state and prove this theorem.

Theorem 2

Let the staggered energy-based DG spatial operator \(\mathscr {L}_c\) be defined as in (3.14), with numerical fluxes defined by (3.12) and periodic boundary conditions. Then the following estimate holds:

$$\begin{aligned} \Vert \mathscr {L}_c\Vert \le{} & {} \frac{c}{h}C_{3,\frac{1}{2}} (q_u+q_v-1)\nonumber \\{} & {} +\frac{c}{h}C_{4,\frac{1}{2}} \sqrt{q_u(q_v+1)}+\frac{c}{h}C_5 \max \left\{ c\beta q_u^2, \frac{\tau }{c} (q_v+1)^2\right\} . \end{aligned}$$
(3.15)

In particular, when \(\beta =\tau = 0\), or when \(\beta = \frac{\hat{\beta }}{q_u c}\), \(\tau =\frac{c \hat{\tau }}{q_v+1}\) with fixed dimensionless constants \(\hat{\beta }\), \(\hat{\tau }\), the result is strengthened in that \(\Vert \mathscr {L}_c\Vert \) is bounded linearly in \(q_u\) and \(q_v\). Here \(C_{3,\frac{1}{2}}\le \frac{8\sqrt{3}+4}{3}\), \(C_{4,\frac{1}{2}}\le \frac{128}{\sqrt{3}\pi }\), and \(C_5 \le 4\) are universal positive constants, independent of \(q_u\), \(q_v\), h, and \(\beta \), \(\tau \).

Proof

What set apart the proof below from the proof of Theorem 1 are the following inverse inequalities for polynomials spaces (e.g. see Lemmas 3-4 in [12]): there exist positive constants \(\hat{C}_{3,\frac{1}{2}}\le \frac{4\sqrt{3}+2}{3}\), \(\hat{C}_{4,\frac{1}{2}}\le 4\sqrt{\frac{3}{\pi }}(\frac{3}{4})^{-1/4}=\sqrt{\frac{32}{\sqrt{3}\pi }}\), such that \(\forall p\in \mathbb {Q}^k([-1,1])\),

$$\begin{aligned} \Vert p_x\Vert _{L^2([-\frac{1}{2},\frac{1}{2}])}\le \hat{C}_{3,\frac{1}{2}} k\Vert p\Vert _{L^2([-1,1])}, \quad p\left( \pm \frac{1}{2}\right) \le \hat{C}_{4,\frac{1}{2}} \sqrt{k+1}\Vert p\Vert _{L^2([-1,1])}. \nonumber \\ \end{aligned}$$
(3.16)

With \(p_x\) (resp. p) evaluated away from the edges of the domain \([-1,1]\), these inverse inequalities display different, and indeed milder, dependence on polynomial degree k than those in (3.10), and they will play a key role for our estimate with the desired dependence on the approximation order \(q_u\), \(q_v\).

In order to utilize the opportunity provided by the inequalities in (3.16), we proceed to analyze the terms in the operator \(\mathcal L_c\) on each \(I_j\) and \(I_{j+\frac{1}{2}}\) by examining their behavior on sub-intervals away or near the element edges. By partitioning \(I_j\) into \((x_j, x_{j+\frac{1}{4}})\), \((x_{j+\frac{1}{4}}, x_{j+\frac{3}{4}})\), \((x_{j+\frac{3}{4}}, x_{j+1})\), partitioning \(I_{j+\frac{1}{2}}\) into \((x_{j+\frac{1}{2}},x_{j+\frac{3}{4}})\), \((x_{j+\frac{3}{4}},x_{j+\frac{5}{4}})\), \((x_{j+\frac{5}{4}},x_{j+\frac{3}{2}})\), and performing integration by parts on those sub-intervals of length h/4, we find for any \(w,\varphi \in U^{q_u-1}_h\) and \(v,\psi \in \tilde{V}^{q_v}_h\),

$$\begin{aligned}&\int _{\Omega }\mathscr {L}_c(cw,v)(c\varphi ,\psi ) dx \\&\quad = c^2 \sum _j\left( \int _{x_j}^{x_{j+\frac{1}{4}}}\varphi v_xdx-\int _{x_{j+\frac{1}{4}}}^{x_{j+\frac{3}{4}}}\varphi _{x}vdx+\int _{x_{j+\frac{3}{4}}}^{x_{j+1}}\varphi v_xdx\right) \\&\qquad + c^2 \sum _j\left( \int _{x_{j+\frac{1}{2}}}^{x_{j+\frac{3}{4}}}\psi w_{x}dx - \int _{x_{j+\frac{3}{4}}}^{x_{j+\frac{5}{4}}}\psi _x wdx+\int _{x_{j+\frac{5}{4}}}^{x_{j+\frac{3}{2}}}\psi w_{x}dx\right) \\&\qquad + c^2 \sum _j\left( -\beta c^2 \varphi ^+\left( w^+-w^-\right) \big |_{x_j} + \beta c^2 \varphi ^-\left( w^+-w^-\right) \big |_{x_{j+1}} \right) \\&\qquad + c^2 \sum _j\left( -\frac{\tau }{c^2}\psi ^{+}\left( v^{+}-v^{-}\right) \big |_{x_{j+\frac{1}{2}}}+\frac{\tau }{c^2}\psi ^{-}\left( v^{+}-v^{-}\right) \big |_{x_{j+\frac{3}{2}}}\right) \\&\qquad +c^2\sum _j\left( -\psi w\big |_{x_{j+\frac{3}{4}}}+\psi w\big |_{x_{j+\frac{5}{4}}}-\varphi v\big |_{x_{j+\frac{1}{4}}} + \varphi v\big |_{x_{j+\frac{3}{4}}}\right) . \end{aligned}$$

Then by the triangle inequality and \(\sum _j \int _{x_j}^{x_{j+\frac{1}{4}}}= \sum _{j} \int _{x_{j+1}}^{x_{j+\frac{5}{4}}}\), \(\sum _j\int _{x_{j+\frac{5}{4}}}^{x_{j+\frac{3}{2}}}=\sum _j\int _{x_{j+\frac{1}{4}}}^{x_{j+\frac{1}{2}}}\), we have

$$\begin{aligned} \int _{\Omega }\mathscr {L}_c(cw,v)(c\varphi ,\psi ) dx\le \sum _{k=1}^3 \Theta _{u,k}+ \sum _{k=1}^3 \Theta _{v,k}, \end{aligned}$$
(3.17)

where

$$\begin{aligned} \Theta _{u,1}= & {} c \sum _j\left( \int _{x_{j+\frac{3}{4}}}^{x_{j+\frac{5}{4}}}\big |c \varphi v_x\big |dx+\int _{x_{j+\frac{1}{4}}}^{x_{j+\frac{3}{4}}}\big | c \varphi _{x}v\big |dx\right) , \\ \Theta _{u,2}= & {} c \sum _j\left( \big |c \varphi \big |\big |v\big |\Big |_{x_{j+\frac{1}{4}}} + \big | c \varphi \big |\big |v\big |\Big |_{x_{j+\frac{3}{4}}}\right) ,\\ \Theta _{u,3}= & {} \beta c^2 \sum _j\left( \big |c \varphi ^+\big |\big | c w^+\big |\Big |_{x_j}+\big | c \varphi ^+\big |\big | c w^{-}\big |\Big |_{x_j} + \big | c \varphi ^{-}\big |\big | c w^{+}\big |\Big |_{x_{j+1}}+\big | c \varphi ^-\big |\big | c w^-\big |\Big |_{x_{j+1}}\right) ,\\ \Theta _{v,1}= & {} c \sum _j\left( \int _{x_{j+\frac{1}{4}}}^{x_{j+\frac{3}{4}}}\big |\psi cw_{x}\big |dx + \int _{x_{j+\frac{3}{4}}}^{x_{j+\frac{5}{4}}}\big |\psi _x cw\big |dx\right) , \\ \Theta _{v,2}= & {} c \sum _j\left( \big |\psi \big |\big | c w\big |\Big |_{x_{j+\frac{3}{4}}}+\big |\psi \big |\big | cw \big |\Big |_{x_{j+\frac{5}{4}}}\right) ,\\ \Theta _{v,3}= & {} \tau \sum _j\left( \big |\psi ^{+}\big |\big |v^{+}\big |\Big |_{x_{j+\frac{1}{2}}}+\big |\psi ^{+}\big |\big |v^{-}\big |\Big |_{x_{j+\frac{1}{2}}} +\big |\psi ^{-}\big |\big |v^{+}\big |\Big |_{x_{j+\frac{3}{2}}}+\big |\psi ^{-}\big |\big |v^{-}\big |\Big |_{x_{j+\frac{3}{2}}}\right) . \end{aligned}$$

We start by bounding the volume integral terms \(\Theta _{u,1}\), \(\Theta _{v,1}\). By using the Cauchy-Schwarz inequality, and the first inverse inequality in (3.16) with a linear scaling from \([-1, 1]\) to \(I_j\) (or to \(I_{j-\frac{1}{2}}=[x_{j-\frac{1}{2}},x_{j+\frac{1}{2}}]\)), we get

$$\begin{aligned} \Theta _{u,1} \le&\;c \sum _j \Vert c \varphi \Vert _{L^2 ([x_{j+\frac{3}{4}},x_{j+\frac{5}{4}}])}\Vert v_x\Vert _{L^2 ([x_{j+\frac{3}{4}},x_{j+\frac{5}{4}}])}\\&+ \Vert c \varphi _{x}\Vert _{L^2 ([x_{j+\frac{1}{4}},x_{j+\frac{3}{4}}])}\Vert v\Vert _{L^2 ([x_{j+\frac{1}{4}},x_{j+\frac{3}{4}}])}\\ \le&\; \frac{c}{h} 2 \hat{C}_{3,\frac{1}{2}} \sum _j \left( q_v\Vert c \varphi \Vert _{L^2(I_{j+\frac{1}{2}})}\Vert v\Vert _{L^2(I_{j+\frac{1}{2}})}+(q_u-1)\Vert c \varphi \Vert _{L^2(I_j)}\Vert v\Vert _{L^2(I_j)}\right) \\&\times \left( q_v\Vert \varphi \Vert _{L^2([x_{j+\frac{3}{4}},x_{j+\frac{5}{4}}])}\Vert v\Vert _{L^2(I_{j+\frac{1}{2}})}+(q_u-1)\Vert \varphi \Vert _{L^2(I_j)}\Vert v\Vert _{L^2([x_{j+\frac{1}{4}},x_{j+\frac{3}{4}}])}\right) . \end{aligned}$$

Similarly, we obtain

$$\begin{aligned} \Theta _{v,1} \le \frac{c}{h} 2 \hat{C}_{3,\frac{1}{2}} \sum _j \left( (q_u-1)\Vert cw \Vert _{L^2(I_j)}\Vert \psi \Vert _{L^2(I_j)} + q_v\Vert cw \Vert _{L^2(I_{j+\frac{1}{2}})} \Vert \psi \Vert _{L^2(I_{j+\frac{1}{2}})}\right) . \end{aligned}$$

By applying the Cauchy-Schwarz inequality, we have

$$\begin{aligned} \Theta _{u,1}+\Theta _{v,1} \le&\;\frac{c}{h} C_{3,\frac{1}{2}} (q_u+q_v-1) \nonumber \\&\left( \Vert cw \Vert _{L^2(\Omega )}^2+\Vert v\Vert _{L^2(\Omega )}^2\right) ^{1/2}\left( \Vert c \varphi \Vert _{L^2(\Omega )}^2+\Vert \psi \Vert _{L^2(\Omega )}^2\right) ^{1/2}. \end{aligned}$$
(3.18)

Next, we bound the boundary terms \(\Theta _{u,2},\Theta _{v,2}\). By using the second inverse inequality in (3.16) with a linear scaling from \([-1, 1]\) to \(I_j\) (or to \(I_{j-\frac{1}{2}}\)), we reach

$$\begin{aligned} \Theta _{u,2}&\le \frac{c}{h} 2 \hat{C}_{4,\frac{1}{2}}^2\sqrt{q_u(q_v+1)}\sum _j\Vert c \varphi \Vert _{L^2(I_j)}\Big (\Vert v\Vert _{L^2(I_{j-\frac{1}{2}})}+ \Vert v\Vert _{L^2(I_{j+\frac{1}{2}})}\Big ),\\ \Theta _{v,2}&\le \frac{c}{h} 2 \hat{C}_{4,\frac{1}{2}}^2\sqrt{q_u(q_v+1)} \sum _j \Big (\Vert cw \Vert _{L^2(I_j)}\Vert + \Vert cw \Vert _{L^2(I_{j+1})}\Big )\Vert \psi \Vert _{L^2(I_{j+\frac{1}{2}})}, \end{aligned}$$

and hence

$$\begin{aligned} \Theta _{u,2}+\Theta _{v,2} \le&\; \frac{c}{h}C_{4,\frac{1}{2}}\sqrt{q_u(q_v+1)}\nonumber \\&\left( \Vert cw \Vert _{L^2(\Omega )}^2+\Vert v\Vert _{L^2(\Omega )}^2\right) ^{1/2}\left( \Vert c \varphi \Vert _{L^2(\Omega )}^2+\Vert \psi \Vert _{L^2(\Omega )}^2\right) ^{1/2}. \end{aligned}$$
(3.19)

For \(\Theta _{u,3}\) and \(\Theta _{v,3}\), using the inverse inequality in (3.10) with a linear scaling from \([-1, 1]\) to \(I_s\) (with \(s=j, j\pm 1, j\pm \frac{1}{2}, j+\frac{2}{3}\)),

$$\begin{aligned} \Theta _{u,3}&\le \frac{c}{h} 2 \hat{C}_2^2 c \beta q_u^2 \sum _j \Vert c \varphi \Vert _{L^2(I_j)} \Big (2\Vert cw \Vert _{L^2(I_j)} + \Vert cw \Vert _{L^2(I_{j-1})} + \Vert cw \Vert _{L^2(I_{j+1})}\Big ),\\ \Theta _{v,3}&\le \frac{c}{h} 2 \hat{C}_2^2 \frac{\tau }{c} (q_v+1)^2 \sum _j\Vert \psi \Vert _{L^2(I_{j+\frac{1}{2}})} \Big (2\Vert v\Vert _{L^2(I_{j+\frac{1}{2}})} + \Vert v\Vert _{L^2(I_{j-\frac{1}{2}})} + \Vert v\Vert _{L^2(I_{j+\frac{3}{2}})}\Big ), \end{aligned}$$

and hence

$$\begin{aligned} \Theta _{u,3}+\Theta _{v,3} \le&\; \frac{c}{h} C_5 \max \{c \beta q_u^2, \frac{\tau }{c} (q_v+1)^2\} \nonumber \\&\left( \Vert cw\Vert _{L^2(\Omega )}^2+\Vert v\Vert _{L^2(\Omega )}^2\right) ^{1/2}\left( \Vert c \varphi \Vert _{L^2(\Omega )}^2+\Vert \psi \Vert _{L^2(\Omega )}^2\right) ^{1/2}. \end{aligned}$$
(3.20)

Finally, we combine (3.17), (3.18)-(3.20), and conclude

$$\begin{aligned} \Vert \mathscr {L}_c\Vert \le \frac{c}{h}C_{3,\frac{1}{2}} (q_u+q_v-1) +\frac{c}{h}C_{4,\frac{1}{2}} \sqrt{q_u(q_v+1)}+\frac{c}{h}C_5\max \left\{ c \beta q_u^2, \frac{\tau }{c} (q_v+1)^2\right\} . \end{aligned}$$

\(\square \)

4 Timestepping

After the spatial semi-discretization, we are faced with evolving the linear system of equations

$$\begin{aligned} M \frac{d W^h}{dt} = AW^h + F^h. \end{aligned}$$
(4.1)

Here M and A are the mass and stiffness matrices corresponding to the spatial discretizations at hand and \(W^h\) is a vector containing all degrees of freedom. To exploit the operator bounds (3.15) we note that we can partition \(W^h\),

$$\begin{aligned} W^h = \left( \begin{array}{c} W_1^h \\ W_0^h \end{array} \right) , \end{aligned}$$

where \(W_0^h\) is the vector containing all the degrees of freedom representing the cell averages of \(u^h\) and \(W_1^h\) contains all other degrees of freedom for both the velocity and displacement. In other words, if in each element we write

$$\begin{aligned} u^h = u_1^h + u_0^h, \ \ \int _{\Omega _j} u_1^h dx =0, \end{aligned}$$

then \(W_0^h\) contains all the \(u_0^h\) and \(W_1^h\) contains the degrees of freedom representing \(u_1^h\) and \(v^h\). Similarly partitioning the test functions we see that the semi-discrete system is of the form

$$\begin{aligned} \left( \begin{array}{cc} M_1 &{} 0 \\ 0 &{} M_0 \end{array} \right) \frac{d}{dt} \left( \begin{array}{c} W_1^h \\ W_0^h \end{array} \right) = \left( \begin{array}{cc} A_{11} &{} 0 \\ A_{01} &{} 0 \end{array} \right) \left( \begin{array}{c} W_1^h \\ W_0^h \end{array} \right) + \left( \begin{array}{c} F_1^h \\ F_0^h \end{array} \right) . \end{aligned}$$
(4.2)

This structure implies that stability is determined by the time stepping scheme applied to the \(W_1^h\) subsystem; \(W_0^h\) can be computed independently via an integration in time, though in practice we have used the same scheme for all degrees-of-freedom. In addition, as the \(W_0^h\) subsystem is simply the discrete form of (2.13), the matrix \(M_0^{-1} A_{01}\) will be uniformly bounded in both h and the polynomial degrees. The operator bounds derived in Sect. 3 directly apply to the \(W_1^h\) subsystem under the restrictions given there (one space dimension and periodic boundary conditions). In particular as the norm induced by \(M_1\) is simply the sum of the \(L^2\) norms of \(v^h\) and \(\frac{\partial u^h}{\partial x}\) we have:

$$\begin{aligned} \Vert |a\Vert |&=\text {sup}_{0\ne g, \phi \in F_h}\frac{a(g,\phi )}{\Vert g\Vert _{L^2(\Omega )}\Vert \phi \Vert _{L^2(\Omega )}}\nonumber \\&=\text {sup}_{\textbf{x}, \textbf{y}\ne 0}\frac{\textbf{x}^T A_{11} \textbf{y}}{\Vert \textbf{x}\Vert _{M_1}\Vert \textbf{y}\Vert _{M_1}} =\text {sup}_{\textbf{x}, \textbf{y} \ne 0}\frac{\langle \textbf{x}, M_1^{-1} A_{11} \textbf{y}\rangle _{M_1}}{\Vert \textbf{x}\Vert _{M_1}\Vert \textbf{y}\Vert _{M_1}}=\Vert M_1^{-1} A_{11}\Vert _{M_1}. \end{aligned}$$
(4.3)

Here \(F_h=U_h^{q_u-1}\times \tilde{V}_h^{q_v}\), and the staggered method for the unknowns \(f^h=(u_x^h, \tilde{v}^h)\in F_h\) can be written as \((\frac{d f^h}{dt}, \phi )=a(f^h, \phi ) \; \forall \phi \in F_h\). The simplest application of this result is in the case of central fluxes, which is what we use in the numerical experiments. Then \(A_{11}\) is skew-symmetric and therefore the generalized eigenvalue problem \(i \alpha _j M_{11} \phi _j = A_{11} \phi _j\) has orthonormal eigenvectors in the induced inner product; thus a simple von Neumann analysis applies. In fact for the central fluxes we can prove that stability-enhanced leap-frog schemes as constructed in [7] of the same order as the spatial discretization and a number of stages proportional to the order can always be used with a CFL number \(\mathscr {O}(1)\). We note that optimized schemes are constructed in [7] and in Fig. 4 we display time step stability limits based on these.

Theorem 3

Under the assumptions of Theorem 2 and using central fluxes, there exist constants \(C_1\) and \(C_2\) independent of \(q_u\) and \(q_v\) and time stepping schemes with order \(q_T \ge \max (q_u,q_v)\) and a number of stages bounded by \(C_2 q_T\) such that the fully discrete method is stable under the CFL condition \(c \Delta t \le C_1 h\).

Proof

The results in [7] may be directly applied to the second order equation \(M_1 \frac{d^2 W_1^h}{dt^2}=A_{11}M_1^{-1} A_{11} W_1^h\). In particular they show that order \(q_T\) leap-frog schemes with \(q_T\) stages (applications of the spatial operator) can be constructed which are stable for \(\Delta t^2 \le \frac{q_T^2}{e^2 \rho ^2(M_1^{-1} A_{11})}\) with \(\rho \) denoting the spectral radius. This establishes the result. It is possible to adapt their arguments to leap-frog schemes applied to the first order case, leading to the analogous inequality \(\Delta t \le \frac{q_T}{e \ \rho (M_1^{-1} A_{11})}\), but we omit the algebraic details. \(\square \)

More generally, we can invoke the Kreiss-Wu theory [9] to relate the time step stability limits to the local stability radius of any locally stable time stepping we employ. This theory is based on energy estimates which we have derived above. In particular if the local stability radius is R the fully discrete method is stable if \(\Delta t < \frac{R}{\Vert M_1^{-1} A_{11} \Vert _{M_1}} = O( h/\max (q_u,q_v))\). In our numerical experiments we simply use Taylor time stepping. Given the value of \(W^h\) at time t

$$\begin{aligned} W^h(t) \approx \sum _{j=0}^{q_\textrm{T}} \frac{(t-t_n)^j}{j!} \frac{d^j W^h}{dt^j} \end{aligned}$$
(4.4)

This expansion can easily be computed as time derivatives of \(W^h\) at \(t = t_n\), and can be obtained sequentially by (4.1) and the time step is completed by setting \(t=t_n + \Delta t\). As is well-known, the Taylor methods are locally stable for orders \(q_\textrm{T}=3,4,7,8,11,12, \ldots \). However, for \(q_\textrm{T}\) large they satisfy \(R \sim \pi \) for \(q_T\) a multiple of 4 and \(R \sim \pi /2\) for \(q_\textrm{T}\) one less than a multiple of 4 [8]. Thus we cannot use them with an order-independent CFL number. (We conjecture that stability-enhanced schemes can be built off of the Taylor methods and have some preliminary examples, but they are not used here.) Despite this we find that if the spatial discretization order is bounded by 16 we can march at the same or greater order with a CFL number bounded by 0.1. We emphasize that the method is not restricted to the stability-enhanced leap-frog schemes or the Taylor-based methods used in the experiments. Any standard locally-stable scheme can be used for all our choices of numerical flux and reversible schemes can be applied for the energy-conserving fluxes.

On the other hand, when physical boundaries are present the mesh cannot be staggered and the time steps must be reduced to maintain stability. Fortunately this step size reduction can be localized to a few elements near the boundary. Following the local time stepping method by Diaz and Grote [5] we advance the solution for one time step \(\Delta t\), starting with \(W^h(t_n)\), as follows.

  1. 1.

    Partition \(W^h\) into two parts, \(W^h_B\) consisting of degrees-of-freedom associated with elements near the boundary, and \(W^h_I\).

  2. 2.

    Compute all terms \(\frac{d^{\ell } W^h (t_n)}{dt^{\ell }}\), \(\ell =1, \ldots , q_\textrm{T}\). These can be used to update \(W^h_I (t_n+\Delta t)\).

  3. 3.

    To update \(W_B^h\) take p sub-steps with step size \(\delta t = \Delta t / p\) using (4.1)–(4.4) with \(W^h\) replaced by \(W_B^h\). Here flux terms associated with the interface between elements assigned to the near boundary group and the interior group give rise to a forcing function \(F_B^h\). We evaluate \(F_B^h\) and all necessary derivatives at any intermediate time step using (4.4).

5 Numerical experiments

In this section, we present numerical experiments that illustrate the properties of our staggered method. In all cases we use a modal formulation with tensor product Legendre polynomials and we use exact integration (through the use of quadrature of sufficiently high order) to compute the integrals in the variational formulation. For all tests, we use purely central fluxes, i.e. we set \(\tau ,\beta = 0\).

5.1 Computed rates of convergence

Here we evolve the exact solution

$$\begin{aligned} u(x,t) = \sin (\omega (x+t)), \ \ v(x,t) = \omega \cos (\omega (x+t)), \end{aligned}$$

on the periodic domain \(\Omega =[-1,1]\) until \(T = 2.2\). We discretize using the staggered scheme with \(q_u = 2,3,6,7,10,11,14,15,18,19,22,23,26,27\) and \(q_v = q_u-1\). In order to make it possible to observe the rates of convergence we set \(\omega = 2 q_u \pi \) for \(q_u = 2,3,6,7,10,11,14,15\) and \(\omega = 4 q_u \pi \) for \(q_u = 18,19,22,23,26,27\).

To evolve in time we use Taylor series time stepping with \(q_\textrm{T}=q_u+1\) (the stability domains of all of these Taylor series methods contain the imaginary axis) and throughout we keep the ratio \(\frac{\Delta t}{h} = 0.1\). The \(L_2\)-errors in the solution \(u^h\) as a function of the element size h are displayed in Fig. 3. As can be seen from the figure the rates of convergence (as indicated by the dashed lines) appear to be optimal, i.e. \(q_u+1\), when \(q_u = 3,7,\ldots \) and suboptimal by one, i.e. \(q_u\) when \(q_u = 2,6,\ldots \). This is consistent with the analysis and numerical experiments for the non-staggered scheme and central fluxes; see [1].

5.2 Spectral radii of periodic semi-discretization

Consider now the matrix, A, in the semi-discretization (4.1). With purely central fluxes, the eigenvalues of A will be imaginary and based on the estimates on the operator norm of \(\mathscr {L}_c\) we expect them to grow linearly with \(q_u\). In this experiment we set \(q_v = q_u\) and consider a computational domain \(\Omega = [-1,1]\).

Fig. 3
figure 3

To the left are the \(L_2\)-errors in \(u^h\) for \(q_u = 2, 3, 6,7,10,11,14,15\) and to the right for \(q_u = 18,19,22,23,26,27\). The dashed lines have slope \(q_u\) when \(q_u\) is even and \(q_u+1\) when \(q_u\) is odd corresponding to the expected rates of convergence for central fluxes

Full size image
Fig. 4
figure 4

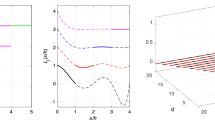
The left figure displays the spectral radii of the time stepping matrix A scaled by the element size h and the reciprocal of \(q_u\) as a function of \(q_u\). The right figure displays the ratio of the square root of the diagonal entries in Fig. 2 in [7] and the spectral radii of the time stepping matrix A scaled by the element size h. We note that the black dot, red circle, and blue cross overlap with each other, which indicates that the spectral radii of the time stepping matrix A are independent of the element size h. See the text for details (color figure online)

Full size image

In Fig. 4 we display the spectral radii of the matrix A, i.e. the eigenvalue of A with the largest magnitude, \(\lambda _\infty \), scaled by \((h/q_u)\) for three different element sizes \(h = 2/5, 2/10, 2/20\). As can be seen the growth of the spectral radii appears to be asymptotically linear in \(q_u\) (i.e. constant when scaled by \(q_u^{-1}\)). The right figure displays ratio of the square root of the diagonal entries in Fig. 2 in [7] (the square root of those numbers corresponds to optimal CFL numbers for optimized modified equation timestepping methods of order \(\mathscr {O}(2m)\)) and the spectral radii of the time stepping matrix A scaled by the element size h. Note that the enhanced stability limits (\(\sqrt{\alpha _{m,k}}, k = m-1\)) given in [7] are only available for even orders so for \(q_u = 3\) we use the 4th order limit and for \(q_u=5\) we use the 6th order limit, etc. From the figure we see that the ratio (which corresponds to the CFL number) is at least 0.6 for all orders considered.

5.2.1 Numerical investigation of stability of the local timestepping

Fig. 5
figure 5

On the left \(1-\arrowvert \lambda _j \arrowvert \), \(\{ \lambda _j \}\) the eigenvalues of B from (5.1) for \(q_u = 14\) and \(q_v = 13\) with \(m = 2\); to the right \(1-\arrowvert \lambda _j \arrowvert \) for \(q_u = 14\) with \(m = 3\)

Full size image

In this section, the computational domain is chosen to be \([-1,1.5]\). We impose a homogeneous Neumann boundary condition at the left boundary and a homogeneous Dirichlet boundary condition at the right boundary. The discretization is carried out on a staggered uniform mesh with mesh size h. The process of evolving the solution a full timestep by the local timestepping procedure described above can be expressed as a matrix multiplication

$$\begin{aligned} W^h(t_{n+1}) = BW^h(t_{n}). \end{aligned}$$
(5.1)

Here, again, \(W^h\) is a vector containing the modes describing the element-wise expansions of the displacement and the velocity. The eigenvalues \(\lambda \) of the matrix B reveal if a particular discretization is stable. As we use a central flux all the eigenvalues should satisfy \(|\lambda | = 1\). In practice, the accuracy of the eigenvalue computation can make it difficult to distinguish if the eigenvalues are strictly smaller than one, equal to one, or slightly larger than one. If the largest eigenvalue is slightly larger than one, say \(|\lambda | = 1+\delta \), this may be an indication of an unstable method. However, if \(\delta \) is very small and does not change as the mesh is refined the method may still be considered useful even though it cannot be claimed to be stable in a mathematically strict sense.

We have found that for very high degrees and when the local timestepping is used, the thickness, m, of the layer where the local timestepping is used can impact the size of \(\delta \). In this experiment we always set the parameters of the local timestepping as \(q_\textrm{T} = p = q_u + 1\).

We first fix the number of DG elements for u to be 10, i.e., \(h = 2.5/10\), and the number of DG elements for v is 11. The degrees of the approximation spaces for u and v are chosen to be \(q_u = 14\) and \(q_v = 13\), respectively. The ratio between time step size \(\Delta t\) and the mesh size h are fixed as \(\frac{\Delta t}{h} = 0.1\).

In Fig. 5 we display \(1-|\lambda | = - \delta \) as a function of the eigenvalue index. The left figure is for an overlap with \(m=2\). We observe that the modulus of the largest eigenvalue is larger than 1 by about \(6\cdot 10^{-4}\). This would correspond to a magnification of about 2 of an unstable mode after about 1400 time steps, indicating a fast growing instability. In our simulations, we also observed that \((q_u,q_v) = (10,9)\) is the highest degree we can have to guarantee \(|\delta | \le 10^{-7}\) when the thickness of the overlap is \(m = 2\) and the number of DG elements equals 10. The right figure displays the same method except that the overlap is now increased to \(m= 3\). Now we find that the modulus of the largest eigenvalue is larger than 1 by about \(10^{-7}\). As this means that it will take around 7 million time steps before this mode is doubled in amplitude it is unlikely that it would show up in any practical computation.

Importantly, \(\delta \) appears to be robust to grid refinement. In Fig. 6, we fix the \(m = 3\) and increase the number of DG elements for u from 20 to 40 and 80. Again we find that the modulus of the largest eigenvalue is larger than 1 by about \(10^{-7}\) for all three discretizations.

Fig. 6
figure 6

We plot \(1-|\lambda |\), \(\{ \lambda _j \}\) the eigenvalues of B in (5.1), as a function of the eigenvalue index j when \(q_u = 14\), \(q_v = 13\) and \(m = 3\). Specifically, from left to right are the results with the number of elements in \(\Omega _h\) being \(n = 20,40,80\), respectively

Full size image

5.3 Convergence in two dimensions with Dirichlet boundary condition

In this section, we investigate the convergence of the staggered energy-based DG scheme with the local time stepping of Sect.  4 and variable sound wave speed c(x, y) in two space dimensions. Precisely we solve

$$\begin{aligned} \frac{\partial ^2 u}{\partial t^2} = \nabla \cdot (c^2(x,y) \nabla u) + f(x,y,t), \ \ \ (x,y)\in [-1,1]\times [-1,1],\ \ \ t>0, \end{aligned}$$

where \(c(x,y) = 1 + x^2 + y^2\). Further, we construct a manufactured solution so that

$$\begin{aligned} u(x,y,t)&= \sin \left( \sqrt{k_1^2+k_2^2}\pi t \right) \sin (k_1\pi x)\sin (k_2\pi y), \\ v(x,y,t)&= \sqrt{k_1^2+k_2^2}\pi \cos \left( \sqrt{k_1^2+k_2^2}\pi t \right) \sin (k_1\pi x)\sin (k_2\pi y). \end{aligned}$$

That is, the initial condition and the external forcing function f(x, y, t) are determined by this manufactured solution. The boundary conditions are homogeneous Dirichlet conditions. To allow for sufficient range to compute the errors we set \(k_1 = k_2 = q = 2\) for \(q_u = q_v = q = 2,3\), and \(k_1 = k_2 = 2q\) for \(q_u = q_v = q = 6,7\) with q being the degree of the approximation space for both u and v (Fig. 7).

Fig. 7
figure 7

The \(L^2\) errors for u, from left to right, are for \(q_u = q_v = 2,3\) and \(q_u = q_v = 6,7\), respectively

Full size image

The discretization is performed with staggered elements. The mesh \(\Omega ^h\) corresponding to the piecewise polynomial approximation to u is Cartesian with vertices given by \(x_i = ih\), \(y_j = jh\), \(i, j = 0,1,\ldots ,n\) with \(h = 2/n\). In the interior the elements of \(\Omega ^{\diamond ,h}\) corresponding to the piecewise polynomial approximation to v are staggered with respect to \(\Omega ^h\); its vertices are \(x_{i+1/2}=(i+1/2)h\), \(y_{j+1/2}=(j+1/2)h\). Near the boundaries the elements for v are reduced in size by a factor of 1/2 or 1/4. Then we have \(n^2\) elements in \(\Omega ^h\) and \((n+1)^2\) elements in \(\Omega ^{\diamond ,h}\). Figure 8 gives an illustration of the staggered grids with \(n = 3\).

Fig. 8
figure 8

A staggered grid in two dimensions. Blue boxes are elements of \(\Omega ^h\) corresponding to the piecewise approximation to u and non-blue boxes are elements of \(\Omega ^{\diamond ,h}\) corresponding to the piecewise approximation to v. Here, we have \(3\times 3 = 9\) elements in \(\Omega ^h\) and 4 interior (red boxes), 8 edge (magenta boxes) and 4 corner (green boxes) elements in \(\Omega ^{\diamond ,h}\) (color figure online)

Full size image

Here we use the central flux, \(\beta =\tau =0\). We evolve the solution by the local Taylor time stepping described in Sect.  4 with \(p=q_\textrm{T} = q+1\) and \(m = 3\) until the final time \(T = 0.5\). The ratios of the time step size \(\Delta t\) and mesh size h are set to be \(\frac{\Delta t}{h} = 0.1\).

Table 1 Linear regression estimates of the convergence rate for u with central flux in two dimensions
Full size table

The \(L^2\) errors for u are plotted against the mesh size h in Fig. 7. Table 1 presents the linear regression estimates of the convergence rate for u based on the data in Fig. 7. From Table 1, we observe an optimal convergence rate of \(q + 1\) when \(q = 3,6,7\) and a suboptimal convergence by one for \(q = 2\).

5.4 Numerical investigation of the stability of the local time stepping in two dimensions

In this section, we investigate the stability of the full discretization with the local time stepping in two dimensions with homogeneous Dirichlet boundary conditions. The computational domain is chosen to be the same as above, so is the spatial discretization. Here, we set \(n = 10\). Then, the number of elements in \(\Omega ^h\) is 100 and in \(\Omega ^{\diamond ,h}\) is 121. The degree of the approximation space for u and v is q for both. The parameters p, \(q_\textrm{T}\) in the local Taylor time stepping are set to be \(p = q_\textrm{T} = q+1\) and the overlap is set to \(m = 3\).

In Fig. 9, we display \(1- | \lambda |\) for the fully discrete method with different values of q. The top panel, from left to right, displays the results for \(q = 2,3\) and the bottom panel, from left to right displays the results for \(q = 6,7\). Here, we observe that \(1- | \lambda |>0\) for all q indicating that these particular discretizations are stable.

Fig. 9
figure 9

The top panel, from left to right are \( 1- \arrowvert \lambda _j \arrowvert \), \(\{ \lambda _j \}\) the eigenvalues of B in (5.1), for the two-dimensional case with \(q_u = q_v=2,3\), respectively. The bottom panel displays the same results for \(q_u=q_v=6,7\), respectively

Full size image

6 Conclusion

We have shown that, away from boundaries, the use of staggered meshes and suitably chosen numerical fluxes leads to energy-based DG methods for the wave equation with favorable time step stability bounds at high order. In particular, using explicit single step methods built from Taylor polynomials with degrees \(q_\textrm{T}=4s\), or \(q_\textrm{T}=4s-1\) and spatial approximations of comparable order we can stably march in time at a fixed, order-independent CFL number. A large global time step can be maintained if local time stepping is used near boundaries. Here we only consider simple geometries, but with local time stepping the proposed method should be applicable in more complex domains containing a sufficiently large volume separated from boundaries.