Maximum-Principle-Satisfying and Positivity-Preserving High Order Central DG Methods on Unstructured Overlapping Meshes for Two-Dimensional Hyperbolic Conservation Laws

Abstract

In this paper, we first present a family of high order central discontinuous Galerkin methods defined on unstructured overlapping meshes for the two-dimensional conservation laws. The primal mesh is a triangulation of the computational domain, while the dual mesh is a quadrangular partition which is formed by connecting an interior point and the three vertexes of each triangle on the primal mesh. We prove the $L^2$ stability of the present method for linear equation. Then we design and analyze high order maximum-principle-satisfying central discontinuous Galerkin methods for two-dimensional scalar conservation law, and high order positivity-preserving central discontinuous Galerkin methods for two-dimensional compressible Euler systems. The performance of the proposed methods is finally demonstrated through a set of numerical experiments.

1 Introduction

Many problems in science and engineering fields can be governed by a scalar conservation law or a system of hyperbolic conservation laws. Various numerical methods have been developed for solving such conservation laws, such as the finite difference methods [13, 29, 32], the finite volume methods [35], the discontinuous Galerkin (DG) methods [6, 7, 31] and the central DG methods [11, 24].

The DG method is a class of high order finite element methods, which was originally introduced in 1973 by Reed and Hill [27]. Since the basis functions can be discontinuous, the DG method is very flexible to achieve any order of accuracy and handle complicated geometry and boundary conditions. It is also a very compact numerical scheme due to the extremely local data structure. Therefore, it has been successfully developed for solving various linear and nonlinear problems [3, 4, 6, 7, 9, 26].

As a variant of the DG method, the central DG method is also one of popular high order numerical methods for hyperbolic conservation laws, which was originally presented by Liu et al. [24]. By evolving two sets of numerical solutions defined on overlapping meshes, the central DG method does not rely on any exact or approximate Riemann solver at element interfaces as in DG methods. Therefore, the central DG method is widely applied to various problems, such as diffusion equations [25], Hamilton–Jacobi equations [15], ideal MHD equations [16, 17, 34], the Camassa–Holm equation [19] and the shallow water equations [10, 18, 21, 22].

However, most of works on the central DG methods mentioned above are built on structured overlapping meshes. Therefore, they are only applied to some problems defined on simple domains, such as rectangle, L-shape domain. In order to extend the central DG methods to problems on more complex geometry domains, Xu and Liu [34] first presented a central DG method defined on unstructured overlapping meshes. In their work, the primal mesh is triangulation of the computational domain, and then they define the dual mesh according to nodes in the primal mesh, one node is related to one cell in the dual mesh. Thus the cells in the dual mesh are polygons with different numbers of edges, and more complex than the cells in the primal mesh.

In this paper, in order to simplify the dual mesh, we define the dual mesh by a different way, which is according to the edges in the primal mesh, one edge is related to one cell in the dual mesh. Specifically, we first define the primal mesh by a triangulation of the computational domain as any kind of finite element methods, then we take an interior point in each triangle and connect the point to the three vertices of the triangle, this operation forms a quadrangular partition of the computational domain which is used as the dual mesh. Compared with the one in [34], the presented dual mesh is simpler. This idea comes from the staggered discontinuous Galerkin method [14]. The central DG method is defined on the presented unstructured overlapping meshes and is used to solve the two-dimensional conservation laws.

The second objective of this paper is to design high order maximum-principle-satisfying central DG methods on the presented unstructured overlapping meshes for the two-dimensional scaler conservation law:

$$\begin{aligned} {U}_t+\nabla \cdot \mathbf {F}(U)=0,\quad U(x,y,0)=U_0(x,y) \end{aligned}$$

(1)

with $M=\max _{x,y} U_0(x,y)$ and $m=\min _{x,y} U_0(x,y)$.

The unique entropy solution to (1) satisfies a strict maximum principle [8]. That is the entropy solution $U(x,y,t)\in [m,M]$ for any x, y and t. This property is also desired for numerical schemes solving (1), for instance in some applications where U represents a volume ratio, and it should always be in the range of [0, 1].

Many high order numerical schemes, which can be used to solve the conservation law (1), do not in general satisfy the strict maximum principle. Therefore, much effort has been devoted to this issue. Various maximum-principle-satisfying numerical methods have been presented for solving the conservation law (1). One important breakthrough was made in [35], where the authors proposed a very general framework to achieve maximum principle especially for high order methods. There a sufficient condition was first given to ensure that the cell averages of the numerical solution, which is from a high order finite volume WENO method or a DG method on structured meshes with the Euler forward method in time, satisfy the maximum principle. A linear scaling limiter was then designed and applied to enforce this condition without destroying the local conservation and accuracy. For higher order temporal accuracy, strong stability preserving (SSP) time discretizations were used, and they can be expressed as a convex combination of the first order Euler forward method and therefore keep the maximum principle property. Then, the scheme is extended to the high order finite volume WENO method and the DG method on unstructured meshes in [37]. Based on the work in [35], two authors of the present paper have designed a maximum-principle-satisfying central DG method on structured overlapping meshes in [20]. Therefore, we will extend the method to unstructured overlapping meshes in this paper, based on the works in [20, 37].

Thirdly, we are interested in the high order positivity-preserving scheme for the compressible Euler equations. For this conservation law system, the entropy solution in general does not satisfy any maximum principle, but physically, the density and the pressure of the fluids should be positive. Such property is important for the well-posedness of the equations, and the violation of numerical schemes can lead to instability and the breakdown of the simulation. With the success in [35], the authors further developed high order positivity-preserving DG methods on structured meshes to compressible Euler equations in [36], which preserve the positivity of density and pressure. A simpler and more robust strategy was later proposed in [33]. Then the authors extended the high order positivity-preserving DG methods to unstructured meshes in [37]. In [20], two authors of the present paper extended the positivity-preserving techniques in [33, 36] to compressible Euler equations by using the central DG method on structured overlapping meshes. Our development with the central DG methods in [20], together with the successful analysis in [37], motivates us to examine both theoretically and numerically the central DG methods on unstructured overlapping meshes in this paper for solving compressible Euler equations while preserving positivity of density and pressure.

This paper is organized as follows. In Sect. 2, we present the central DG methods defined on unstructured overlapping meshes for the conservation laws, and prove the $L^2$ stability of the present method for a linear hyperbolic equation. Then, we develop a maximum-principle-satisfying high order central DG method for the two-dimensional scalar conservation laws in Sect. 3. In Sect. 4, we construct and analyze positivity-preserving central DG methods for two-dimensional compressible Euler equations, employing the positivity-preserving limiting techniques similar to those in [5, 20, 33]. In Sect. 5, numerical experiments are presented, which are followed by some concluding remarks in Sect. 6.

2 Central DG Methods on Unstructured Overlapping Meshes

In this section, we extend the central DG methods on structured overlapping meshes in [24] to unstructured overlapping meshes for solving the two-dimensional conservation laws:

$$\begin{aligned} \mathbf {U}_t+\nabla \cdot \mathbf {F}(\mathbf {U})=0, \end{aligned}$$

(2)

where $\mathbf {U} \in R^{m \times 1}$ is a conservative variable, $m \ge 1$ is an integer, the flux function $\mathbf {F}(\mathbf {U})$ and its divergence are defined by

$$\begin{aligned} \mathbf {F}(\mathbf {U})=\left( \begin{array}{c} \mathbf {F}_1(\mathbf {U}) \\ \mathbf {F}_2(\mathbf {U}) \\ \cdot \\ \cdot \\ \cdot \\ \mathbf {F}_m(\mathbf {U}) \end{array} \right) ,\quad \nabla \cdot \mathbf {F}(\mathbf {U})=\left( \begin{array}{c} \nabla \cdot \mathbf {F}_1(\mathbf {U}) \\ \nabla \cdot \mathbf {F}_2(\mathbf {U}) \\ \cdot \\ \cdot \\ \cdot \\ \nabla \cdot \mathbf {F}_m(\mathbf {U}) \end{array} \right) =\left( \begin{array}{c} \frac{\partial f_{11}(\mathbf {U})}{\partial x}+\frac{\partial f_{12}(\mathbf {U})}{\partial y} \\ \frac{\partial f_{21}(\mathbf {U})}{\partial x}+\frac{\partial f_{22}(\mathbf {U})}{\partial y} \\ \cdot \\ \cdot \\ \cdot \\ \frac{\partial f_{m1}(\mathbf {U})}{\partial x}+\frac{\partial f_{m2}(\mathbf {U})}{\partial y} \end{array} \right) \end{aligned}$$

with $\mathbf {F}_i(\mathbf {U})=(f_{i1}(\mathbf {U}),f_{i2}(\mathbf {U})) \in R^{1 \times 2}, i=1,2, \ldots ,m$.

2.1 Unstructured Overlapping Meshes

Since the central DG methods evolve two copies of numerical solutions on unstructured overlapping meshes, we first define the unstructured overlapping meshes. The primal mesh (denoted by $\mathcal {T}^C$) is a triangulation of the computational domain $\varOmega$. Then we take an interior node in each triangle and connect the node to the three vertices of the triangle. Noting that we have chosen some points outside the domain to make sure all cells on the dual mesh are quadrangle. This is to simplify the dual mesh. This operation generates the dual mesh (denoted by $\mathcal {T}^D$). Like the DG method, a few ghost cells (triangles) have been added along the boundary of the domain in order to impose the boundary conditions. Those chosen points outside the domain actually are the interior points of the ghost cells. The solutions on these ghost cells are given according to the boundary conditions. Although parts of elements in the dual mesh are outside of the computational domain, all elements in the dual mesh are covered by the primal mesh together with the ghost cells. Thus the numerical solution on all elements in the dual mesh can be directly obtained from the central DG scheme without any special treatment provided that the solutions in all ghost cells are given according to the boundary conditions. To avoid too small cells generated in the dual mesh, the interior node should be chosen as far away from the edges of the triangle as possible. In general, the geometric center of the triangle or the center of the inscribed circle of the triangle can be chosen as the interior node. In the simulation, the geometric center of the triangle in the primal is chosen as the interior node in order to generate the dual mesh.

For sake of understanding the unstructured overlapping meshes more clearly, a simple illustration has been shown in Fig. 1, where the computational domain $\varOmega$ is the triangle $A_1A_2A_3$ and is partitioned into 4 small triangles: $A_1A_6A_5$, $A_6A_2A_4$, $A_4A_3A_5$ and $A_4A_5A_6$. The primal mesh is given by

$$\begin{aligned} \mathcal {T}^C= & {} \{A_1A_6A_5, A_6A_2A_4, A_4A_3A_5, A_4A_5A_6\}. \end{aligned}$$

In Fig. 1, points $B_1,B_2,B_3,B_4$ are the interior nodes of the four triangles in the primal mesh, points $C_1,C_2, \ldots ,C_6$ are the chosen nodes outside the domain, these points are used to generate the dual mesh $\mathcal {T}^D$, which includes 9 quadrangles, namely,

$$\begin{aligned} \mathcal {T}^D= & {} \{A_1C_1A_6B_1, B_1A_6B_4A_5, A_1B_1A_5C_6, A_6C_2A_2B_2, B_2A_2C_3A_4, \\&~~ B_2A_4B_4A_6, B_4A_4B_3A_5, B_3A_4C_3A_3, B_3A_3C_5A_5 \} \end{aligned}$$

The triangles $G_1A_6A_1$, $G_2A_2A_6$, $G_3A_4A_2$, $G_4A_3A_4$, $G_5A_5A_3$ and $G_6A_1A_5$ are the ghost cells used to impose the boundary conditions. Noting that points $C_1,C_2, \ldots ,C_6$ are the interior nodes of the six ghost cells, respectively.

Fig. 1

Unstructured overlapping meshes for the central DG methods. Solid line: primal mesh; dashed line: dual mesh

Associated with each mesh, we define the following discrete spaces:

$$\begin{aligned} \mathbf{W}^C= & {} \{\mathbf{v}=(v_1,v_2, \ldots ,v_m)^\top : {v_i}|_{K^C}\in P^k(K^C), i=1,2, \ldots ,m, \forall K^C \in \mathcal {T}^C \},\\ \mathbf{W}^D= & {} \{\mathbf{v}=(v_1,v_2, \ldots ,v_m)^\top :{v_i}|_{K^D}\in P^k(K^D), i=1,2, \ldots ,m, \forall K^D \in \mathcal {T}^D \}. \end{aligned}$$

Two copies of numerical solutions are assumed to be available at $t=t_n$, denoted by $\mathbf {U}^{n,\star } \in \mathbf{W}^\star$, and we want to find the solutions at $t=t_{n+1}=t_n+\varDelta t$, the superscript $` \star \hbox {'}$ denotes C and D throughout this paper. For simplicity, we present the schemes in the case of the forward Euler method for time discretization. High order time discretizations will be discussed afterward.

2.2 Central DG Methods for Conservation Laws

For the conservation laws (2), the fully discretized central DG method with the forward Euler method for time discretization is to look for $\mathbf {U}^{n+1,\star }\in \mathbf{W}^{\star }$ such that for any $\mathbf {V}^{\star } \in \mathbf{W}^{\star }|_{K^{\star }}$ with any $K^{\star } \in \mathcal {T}^{\star }$,

$$\begin{aligned} \int _{K^C} \mathbf {U}^{n+1,C}\cdot {\mathbf {V}}^C dxdy= & {} \int _{K^C}\left( \theta \mathbf {U}^{n,D} + (1-\theta ) \mathbf {U}^{n,C}\right) \cdot {\mathbf {V}}^C dxdy \nonumber \\&+\,\varDelta t \int _{K^C} \left[ {\mathbf {F}}(\mathbf {U}^{n,D})\cdot \nabla {\mathbf {V}}^C \right] dxdy \nonumber \\&-\,\varDelta t \int _{ \partial K^C} \left[ ({\mathbf {F}}(\mathbf {U}^{n,D}) \cdot {\mathbf {n}}_{K^C}) \cdot {\mathbf {V}}^C \right] ds. \end{aligned}$$

(3)

$$\begin{aligned} \int _{K^D} \mathbf {U}^{n+1,D}\cdot {\mathbf {V}}^D dxdy= & {} \int _{K^D}\left( \theta \mathbf {U}^{n,C} + (1-\theta ) \mathbf {U}^{n,D}\right) \cdot {\mathbf {V}}^D dxdy \nonumber \\&+\,\varDelta t \int _{K^D} \left[ {\mathbf {F}}(\mathbf {U}^{n,C})\cdot \nabla {\mathbf {V}}^D \right] dxdy \nonumber \\&-\,\varDelta t \int _{ \partial K^D} \left[ ({\mathbf {F}}(\mathbf {U}^{n,C}) \cdot {\mathbf {n}}_{K^D}) \cdot {\mathbf {V}}^D \right] ds. \end{aligned}$$

(4)

where ${\mathbf {n}}_{K^{\star }}=(n_{1K^{\star }},n_{2K^{\star }})$ denotes the outward unit normal vector of cell $K^{\star }$, $\theta =\varDelta t/\tau _{max} \in [0, 1]$ with $\tau _{max}$ being the maximal time step allowed by the CFL restriction. The product “$\cdot$” is defined by $\mathbf {U} \cdot \mathbf {V}= \sum _{i=1}^{m}U_iV_i$, ${\mathbf {F}} \cdot \nabla {\mathbf {V}} = \sum _{i=1}^{m}({\mathbf {F}}_i \cdot \nabla {V}_i)=\sum _{i=1}^{m}(f_{i1}\frac{\partial {V}_i}{\partial x}+f_{i2}\frac{\partial {V}_i}{\partial y})$, $({\mathbf {F}} \cdot {\mathbf {n}}) \cdot {\mathbf {V}}=\sum _{i=1}^{m}({\mathbf {F}}_i \cdot {\mathbf {n}})V_i=\sum _{i=1}^{m}(f_{i1} n_1+f_{i2} n_2)V_i$.

2.3 High Order Time Discretization

In order to match with high order accuracy in space, strong stability preserving (SSP) high order time discretizations will be used [12] in the numerical tests. In this paper, we use the third order Runge–Kutta method

$$\begin{aligned} U^{(1)}= & {} U^{n} + \varDelta t \mathcal {L} (U^{n}) \nonumber \\ U^{(2)}= & {} \frac{3}{4} U^{n} + \frac{1}{4} ( U^{(1)}+ \varDelta t \mathcal {L} (U^{(1)})) \nonumber \\ U^{n+1}= & {} \frac{1}{3} U^{n} + \frac{2}{3} ( U^{(2)}+ \varDelta t \mathcal {L} (U^{(2)})). \end{aligned}$$

(5)

Here $\mathcal {L}(U)$ denotes the spatial operator.

When central DG methods are applied to nonlinear problems, nonlinear limiters are often needed for some problems with strong shock. In this work, we use the total variation bounded (TVB) corrected minmod slope limiter [7].

2.4 $L^2$ Stability for Linear Hyperbolic Equation

Although the central DG method on unstructured overlapping meshes can be defined for the nonlinear equation (2), we cannot prove a $L^2$ stability for it when applied to the nonlinear equation (2). Thus in this subsection, we only study the $L^2$ stability for the linear hyperbolic conservation law

$$\begin{aligned} {U}_t+\nabla \cdot \mathbf {F}(U)=0, \end{aligned}$$

(6)

where $\mathbf {F}(U)=(U,U)$.

The central DG method for the linear equation (6) can be defined by: Find $U^{n+1,\star }\in {W}^{\star }$ such that for any $V^{\star } \in W^{\star }|_{K^{\star }}$ with any $K^{\star } \in \mathcal {T}^{\star }$

$$\begin{aligned} \int _{K^C} U^{n+1,C} {V}^C dxdy= & {} \int _{K^C}\left( \theta U^{n,D} + (1-\theta ) U^{n,C}\right) {V}^C dxdy \nonumber \\&+\,\varDelta t \int _{K^C} \left[ (U^{n,D}, U^{n,D}) \cdot \nabla {V}^C \right] dxdy \nonumber \\&-\,\varDelta t \int _{ \partial K^C} \left[ ((U^{n,D}, U^{n,D}) \cdot {\mathbf {n}}_{K^C}) {V}^C \right] ds. \end{aligned}$$

(7)

$$\begin{aligned} \int _{K^D} U^{n+1,D} {V}^D dxdy= & {} \int _{K^D}\left( \theta U^{n,C} + (1-\theta ) U^{n,D}\right) {V}^D dxdy \nonumber \\&+\,\varDelta t \int _{K^D} \left[ (U^{n,C}, U^{n,C}) \cdot \nabla {V}^D \right] dxdy \nonumber \\&-\,\varDelta t \int _{ \partial K^D} \left[ ((U^{n,C}, U^{n,C}) \cdot {\mathbf {n}}_{K^D} ) {V}^D \right] ds. \end{aligned}$$

(8)

where

$$\begin{aligned} {W}^C= & {} \{{{v}}:{{v}}|_{K^C}\in P^k(K^C), \forall \, K^C \in \mathcal {T}^C \},\\ {W}^D= & {} \{{{v}}:{{v}}|_{K^D}\in P^k(K^D), \forall \, K^D \in \mathcal {T}^D \}, \end{aligned}$$

We now take the limit $\varDelta t \rightarrow 0$ to get the semi-discrete version of the central DG method: Find $U^{\star }(\cdot ,t)\in {W}^{\star }$ such that for any $V^{\star } \in {W}^{\star }|_{K^{\star }}$ with any $K^{\star } \in \mathcal {T}^{\star }$

$$\begin{aligned} \int _{K^C} \left( \frac{\partial }{\partial t}U^{C}\right) {V}^C dxdy= & {} \frac{1}{\tau _{max}}\int _{K^C}\left( U^{D} - U^{C}\right) {V}^C dxdy \nonumber \\&+ \int _{K^C} \left[ (U^{D}, U^{D}) \cdot \nabla {V}^C \right] dxdy \nonumber \\&- \int _{ \partial K^C} \left[ ((U^{D}, U^{D}) \cdot {\mathbf {n}}_{K^C}) {V}^C \right] ds. \end{aligned}$$

(9)

$$\begin{aligned} \int _{K^D} \left( \frac{\partial }{\partial t}U^{D}\right) {V}^D dxdy= & {} \frac{1}{\tau _{max}} \int _{K^D}\left( U^{C} - U^{D}\right) {V}^D dxdy \nonumber \\&+\int _{K^D} \left[ (U^{C}, U^{C}) \cdot \nabla {V}^D \right] dxdy \nonumber \\&- \int _{ \partial K^D} \left[ ((U^{C}, U^{C}) \cdot {\mathbf {n}}_{K^D} ) {V}^D \right] ds. \end{aligned}$$

(10)

Theorem 1

The numerical solution $U^{C}$ and $U^{D}$ of the central DG method (9)–(10) satisfies the following $L^2$ stability condition

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\int _{\varOmega } \left( (U^{C})^2 + (U^{D})^2 \right) dxdy =-\frac{1}{\tau _{max}}\int _{\varOmega }\left( U^{D} - U^{C}\right) ^2 dxdy \le 0 \end{aligned}$$

(11)

with compactly supported boundary condition.

Proof

Let $\mathcal {T}=\{K:K=K^C \cap K^D \cap \varOmega , \forall K^C \in \mathcal {T}^C, K^D \in \mathcal {T}^D \}$, which is in fact a refined triangulation of the computational domain. Taking the test functions ${V}^C=U^{C}$ and ${V}^D=U^{D}$ in (9) and (10) respectively, summing up over $K^C \in \mathcal {T}^C$ for (9) and over $K^D \in \mathcal {T}^D$ for (10), and then combing them together, one has

$$\begin{aligned}&\frac{1}{2}\frac{d}{dt}\int _{\varOmega } \left( (U^{C})^2+(U^{D})^2\right) dxdy \nonumber \\&\quad = \frac{1}{\tau _{max}}\int _{\varOmega }\left( U^{D} - U^{C}\right) U^{C} dxdy + \frac{1}{\tau _{max}}\int _{\varOmega }\left( U^{C} - U^{D}\right) U^{D} dxdy \nonumber \\&\qquad + \sum _{K^C \in \mathcal {T}^C}\left( \int _{K^C} \left[ (U^{D}, U^{D}) \cdot \nabla U^{C} \right] dxdy - \int _{ \partial K^C} \left[ ((U^{D}, U^{D}) \cdot {\mathbf {n}}_{K^C}) U^{C} \right] ds \right) \nonumber \\&\qquad + \sum _{K^D \in \mathcal {T}^D} \left( \int _{K^D} \left[ (U^{C}, U^{C}) \cdot \nabla U^{D} \right] dxdy - \int _{ \partial K^D} \left[ ((U^{C}, U^{C}) \cdot {\mathbf {n}}_{K^D} ) U^{D} \right] ds \right) \nonumber \\&\quad = -\frac{1}{\tau _{max}}\int _{\varOmega }\left( U^{D} - U^{C}\right) ^2 dxdy \nonumber \\&\qquad + \sum _{K \in \mathcal {T}}\left( \int _{K} \left[ (U^{D}, U^{D}) \cdot \nabla U^{C} \right] dxdy + \int _{K} \left[ (U^{C}, U^{C}) \cdot \nabla U^{D} \right] dxdy \right) \nonumber \\&\qquad - \sum _{K \in \mathcal {T}}\left( \int _{ \partial K} \left[ ((U^{C}U^{D}, U^{C}U^{D}) \cdot {\mathbf {n}}_{K}) \right] ds \right) \nonumber \\&\quad = -\frac{1}{\tau _{max}}\int _{\varOmega }\left( U^{D} - U^{C}\right) ^2 dxdy + \sum _{K \in \mathcal {T}} \int _{K} \nabla \cdot (U^{C} U^{D}, U^{C} U^{D}) dxdy \nonumber \\&\qquad - \sum _{K \in \mathcal {T}}\left( \int _{ \partial K} \left[ ((U^{C}U^{D}, U^{C}U^{D}) \cdot {\mathbf {n}}_{K}) \right] ds \right) \nonumber \\&\quad = -\frac{1}{\tau _{max}}\int _{\varOmega }\left( U^{D} - U^{C}\right) ^2 dxdy \le 0 \end{aligned}$$

(12)

$\square$

Remark 1

Theorem 1 indicates that the energy dissipation term is $\frac{1}{\tau _{max}}\int _{\varOmega }\left( U^{D} - U^{C}\right) ^2 dxdy$, which is directly related to the difference of the two numerical solutions $U^{C}$ and $U^{D}$.

3 Maximum-Principle-Satisfying Central DG Method

In this section, we will present a high order central DG method satisfying the maximum principle on unstructured overlapping meshes for the scalar conservation law (1).

3.1 Preliminaries and First Order Scheme

As shown in Fig. 2, let $e_i^C, i=1,2,3$ denote the edges of $K^C=A_1A_2A_3$, $K_i^C, i=1,2,3$ be a partition of $K^C$, $K_i^C$ share the edge $e_i^C$ with $K^C$ and make sure the numerical solution $U^{n,D}$ be a smooth polynomial within $K_i^C$, $i=1,2,3$. Similarly, let $e_i^D, i=1,2,3,4$ denote the edges of $K^D=B_1B_2B_3B_4$, $K_i^D, i=1,2,3,4$ be a partition of $K^D$, $K_i^D$ share the edge $e_i^D$ with $K^D$, make sure $U^{n,C}$ be a smooth polynomial within $K_i^D$, $i=1,2,3,4$. Note that the point O in the left picture of Fig. 2 is the geometric center of the triangle $K^C$ and the point Q in the right picture of Fig. 2 is the intersection of the diagonal line of the quadrangle $K^D$. Let ${\mathbf {n}}_i^C$ represent outward unit normal vector of edge $e_i^C$, $l_i^C$ be length of edge $e_i^C, i=1,2,3$ and $|K^C|$ denote the area of cell $K^C$ . Similarly, let ${\mathbf {n}}_i^D$ represent outward unit normal vector of edge $e_i^D$, $l_i^D$ be length of $e_i^D, i=1,2,3,4$ and $|K^D|$ denote the area of cell $K^D$.

Fig. 2

Illustration for notations on a cell $K^C=A_1A_2A_3$ in primal mesh (left) and a cell $K^D=B_1B_2B_3B_4$ in the dual mesh (right)

A first order central DG scheme with $\theta =1$ for (1) can be given by

$$\begin{aligned} U_{K^C}^{n+1,C}= & {} \sum _{i=1}^{3}\frac{|K_i^C|}{|K^C|} U_{K_i^D}^{n,D} - \frac{ \varDelta t}{|K^C|} \sum _{i=1}^{3} l_i^C \mathbf {F}(U_{K_i^D}^{n,D})\cdot {\mathbf {n}}_i^C , \end{aligned}$$

(13)

$$\begin{aligned} U_{K^D}^{n+1,D}= & {} \sum _{i=1}^{4}\frac{|K_i^D|}{|K^D|} U_{K_i^C}^{n,C} - \frac{ \varDelta t}{|K^D|} \sum _{i=1}^{4} l_i^D \mathbf {F}(U_{K_i^C}^{n,C} )\cdot {\mathbf {n}}_i^D . \end{aligned}$$

(14)

Herein, $U_{K^C}^{n,C}$ (resp. $U_{K^D}^{n,D}$) is the numerical solution on element $K^C$ (resp. $K^D$).

Lemma 1

For the first order central DG scheme defined in (13)–(14), if $U_{K^C}^{n,C}, U_{K^D}^{n,D} \in [m,M]$, $\forall K^C, K^D$, then $U_{K^C}^{n+1,C}$ and $U_{K^D}^{n+1,D}$ will belong to [m, M], $\forall K^C, K^D$, under the CFL condition

$$\begin{aligned} a l_{max} \varDelta t \le s_{min}, \end{aligned}$$

(15)

with $a=\max _{U,{\mathbf {n}}}{|\mathbf {F}'(U) \cdot {\mathbf {n}}|}$, $l_{max}=\max \{l_i^C,l_j^D, i=1,2,3,j=1,2,3,4, \forall K^C,K^D\}$, $s_{min}=\min \{|K_i^C|,|K_j^D|, i=1,2,3,j=1,2,3,4, \forall K^C,K^D\}$.

Proof

Since $U_{K^C}^{n+1,C}$ can be viewed as a function of $U_{K_i^D}^{n,D}, i=1,2,3$, we have

$$\begin{aligned} \frac{\partial U_{K^C}^{n+1,C}}{ \partial U_{K_i^D}^{n,D}}= & {} \frac{|K_i^C|}{|K^C|}- \frac{ \varDelta t}{|K^C|} l_i^C \mathbf {F}'(U_{K_i^D}^{n,D})\cdot {\mathbf {n}}_i^C \ge 0 . \end{aligned}$$

(16)

Thus $U_{K^C}^{n+1,C}$ a monotone increasing function of $U_{K_i^D}^{n,D}, i=1,2,3$. Substituting $U_{K_i^D}^{n,D}=d (d=m,M)$ into (27), one gets $U_{K^C}^{n+1,C}=d$, therefore we get $U_{K^C}^{n+1, C} \in [m,M]$. Similarly we obtain $U_{K^D}^{n+1, D} \in [m,M]$. $\square$

3.2 High Order Scheme

A high order scheme satisfied by the cell average of a central DG method for (1), with first order Euler forward time discretization, can be given by

$$\begin{aligned} \bar{U}_{K^C}^{n+1,C}= & {} (1-\theta ) \bar{U}_{K^C}^{n,C} + \frac{\theta }{|K^C|} \int _{K^C} U^{n,D} dxdy \nonumber \\&-\, \frac{ \varDelta t}{|K^C|} \sum _{i=1}^{3}\int _{ e_i^C} \mathbf {F}(U^{n,D})\cdot {\mathbf {n}}_i^C ds, \end{aligned}$$

(17)

$$\begin{aligned} \bar{U}_{K^D}^{n+1,D}= & {} (1-\theta ) \bar{U}_{K^D}^{n,D} + \frac{\theta }{|K^D|} \int _{K^D} U^{n,C} dxdy \nonumber \\&- \, \frac{ \varDelta t}{|K^D|} \sum _{i=1}^{4}\int _{ e_i^D} \mathbf {F}(U^{n,C})\cdot {\mathbf {n}}_i^D ds, \end{aligned}$$

(18)

where $\bar{U}_{K^C}^{n,C}$ (resp. $\bar{U}_{K^D}^{n,D}$) denotes the cell average over $K^C$ (resp. $K^D$) of the numerical solution $U^{n,C}$ (resp. $U^{n,D}$).

Since these integrals on edges in (17)–(18) are always approximated by the $(k+1)$-point Gauss quadrature in the implementation of the central DG method, the scheme satisfied by the cell average (still denoted by $\bar{U}_{K^C}^{n+1,C}, \bar{U}_{K^D}^{n+1,D}$) for (1) becomes

$$\begin{aligned} \bar{U}_{K^C}^{n+1,C}= & {} (1-\theta ) \bar{U}_{K^C}^{n,C} + \frac{\theta }{|K^C|} \int _{K^C} U^{n,D} dxdy \nonumber \\&-\, \frac{ \varDelta t}{|K^C|} \sum _{i=1}^{3} \sum _{\beta =1}^{k+1} l_i^{C} \omega _{\beta } \mathbf {F}(U^{n,D}_{e_i^{C},\beta })\cdot {\mathbf {n}}_i^C , \end{aligned}$$

(19)

$$\begin{aligned} \bar{U}_{K^D}^{n+1,D}= & {} (1-\theta ) \bar{U}_{K^D}^{n,D} + \frac{\theta }{|K^D|} \int _{K^D} U^{n,C} dxdy \nonumber \\&- \, \frac{ \varDelta t}{|K^D|} \sum _{i=1}^{4} \sum _{\beta =1}^{k+1} l_i^{D} \omega _{\beta } \mathbf {F}(U^{n,C}_{e_i^{D},\beta })\cdot {\mathbf {n}}_i^D , \end{aligned}$$

(20)

where $\omega _{\beta },\beta =1,2, \ldots ,k+1$ are the $(k+1)$-point Gauss quadrature weights on the interval $[- \frac{1}{2}, \frac{1}{2}]$ and satisfy $\sum _{\beta =1}^{k+1}\omega _{\beta }=1$, $U^{n,D}_{e_i^{C},\beta }$ is the value of $U^{n,D}$ evaluated at the $\beta$-th Gauss point on edge $e_i^C$, $U^{n,C}_{e_i^{D},\beta }$ is the value of $U^{n,C}$ evaluated at the $\beta$-th Gauss point on edge $e_i^D$.

Note that the numerical solution $U^{n,D}$ (resp. $U^{n,D}$) is a piecewise polynomial over the cell $K^C$ (resp. $K^D$), and thus in the central DG method, (19)–(20) can be rewritten as

$$\begin{aligned} \bar{U}_{K^C}^{n+1,C}= & {} (1-\theta ) \bar{U}_{K^C}^{n,C} + \frac{\theta }{|K^C|}\sum _{i=1}^{3} \int _{K_i^C} U^{n,D} dxdy \nonumber \\&-\, \frac{ \varDelta t}{|K^C|} \sum _{i=1}^{3} \sum _{\beta =1}^{k+1} l_i^{C} \omega _{\beta } \mathbf {F}(U^{n,D}_{e_i^{C},\beta })\cdot {\mathbf {n}}_i^C . \end{aligned}$$

(21)

$$\begin{aligned} \bar{U}_{K^D}^{n+1,D}= & {} (1-\theta ) \bar{U}_{K^D}^{n,D} + \frac{\theta }{|K^D|} \sum _{i=1}^{4} \int _{K_i^D} U^{n,C} dxdy \nonumber \\&- \, \frac{ \varDelta t}{|K^D|} \sum _{i=1}^{4} \sum _{\beta =1}^{k+1} l_i^{D} \omega _{\beta } \mathbf {F}(U^{n,C}_{e_i^{D},\beta })\cdot {\mathbf {n}}_i^D . \end{aligned}$$

(22)

Next, we will reformulate the right hand sides of (21) and (22). To do this, we define seven mappings $g_i(\xi ,\eta )(i=1,2,3)$ and $f_i(\xi ,\eta )(i=1,2,3,4)$ from a square $[-\frac{1}{2},\frac{1}{2}]^2$ to $K_i^C(i=1,2,3)$ and $K_i^D(i=1,2,3,4)$, respectively. It can be observed from Fig. 2 that $K_i^C=OA_iA_{i+1}(i=1,2,3)$ and $K_i^D=QB_iB_{i+1}(i=1,2,3,4)$, herein we used $A_{4}=A_1$ and $B_{5}=B_1$. Thus the seven mappings are defined as follows:

$$\begin{aligned} g_1(\xi ,\eta )= & {} \left( \frac{1}{2}+\eta \right) A_1 + \left( \frac{1}{2}+\xi \right) \left( \frac{1}{2}-\eta \right) A_2 + \left( \frac{1}{2}-\xi \right) \left( \frac{1}{2}-\eta \right) O, \nonumber \\ g_2(\xi ,\eta )= & {} \left( \frac{1}{2}+\eta \right) A_2 + \left( \frac{1}{2}+\xi \right) \left( \frac{1}{2}-\eta \right) A_3 + \left( \frac{1}{2}-\xi \right) \left( \frac{1}{2}-\eta \right) O, \nonumber \\ g_3(\xi ,\eta )= & {} (\frac{1}{2}+\eta )A_3 + \left( \frac{1}{2}+\xi \right) \left( \frac{1}{2}-\eta \right) A_1 + \left( \frac{1}{2}-\xi \right) \left( \frac{1}{2}-\eta \right) O, \nonumber \\ f_1(\xi ,\eta )= & {} \left( \frac{1}{2}+\eta \right) B_1 + \left( \frac{1}{2}+\xi \right) \left( \frac{1}{2}-\eta \right) B_2 + \left( \frac{1}{2}-\xi \right) \left( \frac{1}{2}-\eta \right) Q, \nonumber \\ f_2(\xi ,\eta )= & {} \left( \frac{1}{2}+\eta \right) B_2 + \left( \frac{1}{2}+\xi \right) \left( \frac{1}{2}-\eta \right) B_3 + \left( \frac{1}{2}-\xi \right) \left( \frac{1}{2}-\eta \right) Q, \nonumber \\ f_3(\xi ,\eta )= & {} \left( \frac{1}{2}+\eta \right) B_3 + \left( \frac{1}{2}+\xi \right) \left( \frac{1}{2}-\eta \right) B_4 + \left( \frac{1}{2}-\xi \right) \left( \frac{1}{2}-\eta \right) Q, \nonumber \\ f_4(\xi ,\eta )= & {} \left( \frac{1}{2}+\eta \right) B_4 + \left( \frac{1}{2}+\xi \right) \left( \frac{1}{2}-\eta \right) B_1 + \left( \frac{1}{2}-\xi \right) \left( \frac{1}{2}-\eta \right) Q. \end{aligned}$$

(23)

Then, let $\{ \eta _{\beta }, \beta =1,2, \ldots ,k+1 \}$ be the Gauss qudrature points on $[-\frac{1}{2},\frac{1}{2}]$ with weights $\omega _{\beta }, \beta =1,2, \ldots ,k+1$, and $\{ \hat{\xi }_{\alpha }, \alpha =1,2, \ldots ,N \}$ be the Gauss-Lobatto qudrature points on $[-\frac{1}{2},\frac{1}{2}]$ with weights $\hat{\omega }_{\alpha }, \alpha =1,2, \ldots ,N$, where N is the smallest integer such that $2N-3\ge k$. Therefore, for a two-variable polynomial $p(\xi ,\eta )$, if the degree of $p(\xi ,\eta )$ with respect to its first variable is not more than k and the degree with respect to the second variable is not more than $2k+1$, the following quadrature rule is exact:

$$\begin{aligned} \int _{-\frac{1}{2}}^{\frac{1}{2}}\int _{-\frac{1}{2}}^{\frac{1}{2}}p(\xi ,\eta )d\xi d\eta= & {} \sum _{\alpha =1}^{N}\sum _{\beta =1}^{k+1}\hat{\omega }_{\alpha }\omega _{\beta } p(\hat{\xi }_{\alpha },\eta _{\beta }) \end{aligned}$$

(24)

Utilizing (23) and (24), one has

$$\begin{aligned} \int _{K_i^C} U^{n,D}(x,y) dxdy= & {} \int _{-\frac{1}{2}}^{\frac{1}{2}}\int _{-\frac{1}{2}}^{\frac{1}{2}} U^{n,D}(g_i(\xi ,\eta )) \left| \frac{\partial g_i(\xi ,\eta )}{\partial (\xi ,\eta )}\right| d\xi d\eta \nonumber \\= & {} 2\left| K_i^C\right| \int _{-\frac{1}{2}}^{\frac{1}{2}}\int _{-\frac{1}{2}}^{\frac{1}{2}} U^{n,D}(g_i(\xi ,\eta )) \left( \frac{1}{2}-\eta \right) d\xi d\eta \nonumber \\= & {} 2\left| K_i^C\right| \sum _{\alpha =1}^{N}\sum _{\beta =1}^{k+1} U^{n,D}(g_i(\hat{\xi }_{\alpha },\eta _{\beta })) \left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{\alpha } \omega _{\beta } \nonumber \\= & {} 2\left| K_i^C\right| \sum _{\alpha =1}^{N-1}\sum _{\beta =1}^{k+1} U^{n,D}(g_i(\hat{\xi }_{\alpha },\eta _{\beta })) \left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{\alpha } \omega _{\beta } \nonumber \\&+\, 2\left| K_i^C\right| \sum _{\beta =1}^{k+1} U^{n,D}(g_i(\hat{\xi }_{N},\eta _{\beta })) \left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{N} \omega _{\beta } \nonumber \\= & {} 2\left| K_i^C\right| \sum _{\alpha =1}^{N-1}\sum _{\beta =1}^{k+1}(\frac{1}{2}-\eta _{\beta }) \hat{\omega }_{\alpha } \omega _{\beta } U^{n,D}_{K^C_i,\alpha ,\beta } \nonumber \\&+\, 2\left| K_i^C\right| \sum _{\beta =1}^{k+1} \left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{N} \omega _{\beta }U^{n,D}_{e_i^C,\beta } \end{aligned}$$

(25)

Note that $U^{n,D}(g_i(\xi ,\eta ))$ is a polynomial of degree not more than k with respect to its two variables, and thus $U^{n,D}(g_i(\xi ,\eta )) 2\left| K_i^C\right| (\frac{1}{2}-\eta )$ is a polynomial of degree not more than k and $k+1$ with respect to its two variables, respectively, therefore the third equality in (25) holds exactly. Since $g_i(\hat{\xi }_{N},\eta _{\beta })$ is the $\beta$-th Gauss point on edge $e_i^C$, we have used $U^{n,D}(g_i(\hat{\xi }_{N},\eta _{\beta }))=U^{n,D}_{e^C_i,\beta }$ in the fifth equality, we also set $U^{n,D}(g_i(\hat{\xi }_{\alpha },\eta _{\beta }))=U^{n,D}_{K^C_i,\alpha ,\beta }$.

Similarly, one gets

$$\begin{aligned} \int _{K_i^D} U^{n,C}(x,y) dxdy= & {} \int _{-\frac{1}{2}}^{\frac{1}{2}}\int _{-\frac{1}{2}}^{\frac{1}{2}} U^{n,C}(f_i(\xi ,\eta )) \left| \frac{\partial f_i(\xi ,\eta )}{\partial (\xi ,\eta )}\right| d\xi d\eta \nonumber \\= & {} 2\left| K_i^D\right| \int _{-\frac{1}{2}}^{\frac{1}{2}}\int _{-\frac{1}{2}}^{\frac{1}{2}} U^{n,C}(f_i(\xi ,\eta )) \left( \frac{1}{2}-\eta \right) d\xi d\eta \nonumber \\= & {} 2\left| K_i^D\right| \sum _{\alpha =1}^{N-1}\sum _{\beta =1}^{k+1} U^{n,C}(f_i(\hat{\xi }_{\alpha },\eta _{\beta })) \left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{\alpha } \omega _{\beta } \nonumber \\&+\, 2\left| K_i^D\right| \sum _{\beta =1}^{k+1} U^{n,C}(f_i(\hat{\xi }_{N},\eta _{\beta })) \left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{N} \omega _{\beta } \nonumber \\= & {} 2\left| K_i^D\right| \sum _{\alpha =1}^{N-1}\sum _{\beta =1}^{k+1}\left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{\alpha } \omega _{\beta } U^{n,C}_{K^D_i,\alpha ,\beta } \nonumber \\&+\, 2\left| K_i^D\right| \sum _{\beta =1}^{k+1} \left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{N} \omega _{\beta }U^{n,C}_{e_i^D,\beta } \end{aligned}$$

(26)

where we used $U^{n,C}(f_i(\hat{\xi }_{\alpha },\eta _{\beta }))=U^{n,C}_{K^D_i,\alpha ,\beta }$ and $U^{n,C}(f_i(\hat{\xi }_{N},\eta _{\beta }))=U^{n,C}_{e_i^D,\beta }$ due to the fact that $f_i(\hat{\xi }_{N},\eta _{\beta })$ is the $\beta$-th Gauss point on edge $e_i^D$.

Plugging (25) and (26) into (21) and (22), respectively, one obtains

$$\begin{aligned} \bar{U}_{K^C}^{n+1,C}= & {} (1-\theta ) \bar{U}_{K^C}^{n,C} + \sum _{i=1}^{3} \sum _{\alpha =1}^{N-1}\sum _{\beta =1}^{k+1}\frac{2\theta \left| K_i^C\right| }{|K^C|}\left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{\alpha } \omega _{\beta } U^{n,D}_{K^C_i,\alpha ,\beta } \nonumber \\&+ \sum _{i=1}^{3} \sum _{\beta =1}^{k+1}\left( \frac{2\theta \left| K_i^C\right| }{|K^C|}\left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{N} \omega _{\beta }U^{n,D}_{e_i^C,\beta } - \frac{ \varDelta t}{|K^C|} l_i^{C} \omega _{\beta } \mathbf {F}(U^{n,D}_{e_i^{C},\beta })\cdot {\mathbf {n}}_i^C \right) \nonumber \\= & {} (1-\theta ) \bar{U}_{K^C}^{n,C} + \sum _{i=1}^{3} \sum _{\alpha =1}^{N-1}\sum _{\beta =1}^{k+1}\frac{2\theta \left| K_i^C\right| }{|K^C|}\left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{\alpha } \omega _{\beta } U^{n,D}_{K^C_i,\alpha ,\beta } \nonumber \\&+ \sum _{\beta =1}^{k+1} 2\theta \left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{N} \omega _{\beta } H_{\beta }^C . \nonumber \\ \end{aligned}$$

(27)

$$\begin{aligned} \bar{U}_{K^D}^{n+1,D}= & {} (1-\theta ) \bar{U}_{K^D}^{n,D} + \sum _{i=1}^{4} \sum _{\alpha =1}^{N-1}\sum _{\beta =1}^{k+1}\frac{2\theta \left| K_i^D\right| }{|K^D|}(\frac{1}{2}-\eta _{\beta }) \hat{\omega }_{\alpha } \omega _{\beta } U^{n,C}_{K^D_i,\alpha ,\beta } \nonumber \\&+ \sum _{i=1}^{4} \sum _{\beta =1}^{k+1}\left( \frac{2\theta \left| K_i^D\right| }{|K^D|}\left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{N} \omega _{\beta }U^{n,C}_{e_i^D,\beta } - \frac{ \varDelta t}{|K^D|} l_i^{D} \omega _{\beta } \mathbf {F}(U^{n,C}_{e_i^{D},\beta })\cdot {\mathbf {n}}_i^D \right) \nonumber \\= & {} (1-\theta ) \bar{U}_{K^D}^{n,D} + \sum _{i=1}^{4} \sum _{\alpha =1}^{N-1}\sum _{\beta =1}^{k+1}\frac{2\theta \left| K_i^D\right| }{|K^D|}(\frac{1}{2}-\eta _{\beta }) \hat{\omega }_{\alpha } \omega _{\beta } U^{n,C}_{K^D_i,\alpha ,\beta } \nonumber \\&+ \sum _{\beta =1}^{k+1} 2\theta \left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{N} \omega _{\beta } H_{\beta }^D , \end{aligned}$$

(28)

where

$$\begin{aligned} H_{\beta }^C= & {} \sum _{i=1}^{3} \left( \frac{\left| K_i^C\right| }{|K^C|}U^{n,D}_{e_i^C,\beta } - \frac{ l_i^{C} \varDelta t}{2\theta \left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{N}|K^C|} \mathbf {F}(U^{n,D}_{e_i^{C},\beta })\cdot {\mathbf {n}}_i^C \right) , \end{aligned}$$

(29)

$$\begin{aligned} H_{\beta }^D= & {} \sum _{i=1}^{4} \left( \frac{\left| K_i^D\right| }{|K^D|}U^{n,C}_{e_i^DC,\beta } - \frac{ l_i^{D} \varDelta t}{2\theta \left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{N}|K^D|} \mathbf {F}(U^{n,C}_{e_i^{D},\beta })\cdot {\mathbf {n}}_i^D \right) . \end{aligned}$$

(30)

Let $S_k=\{(\hat{\xi }_{\alpha },\eta _{\beta }): \alpha =1,2, \ldots ,N, \beta =1,2, \ldots ,k+1\}$, $S^C_k=\bigcup _{i=1}^{3} g_i(S_k)$, $S^D_k=\bigcup _{i=1}^{4} f_i(S_k)$, then we have the following theorem from the analysis above.

Theorem 2

For the scheme defined in (17)–(18), assume $\bar{U}_{K^C}^{n, C}, \bar{U}_{K^D}^{n, D} \in [m,M]$, $\forall K^C, K^D$. If $U^{n,C}(x,y) \in [m,M], \forall (x,y)\in S^C_k, \forall K^C$ and $U^{n,D}(x,y) \in [m,M], \forall (x,y)\in S^D_k, \forall K^D$, then $\bar{U}_{K^C}^{n+1, C}$ and $\bar{U}_{K^D}^{n+1, D}$ will belong to [m, M], $\forall K^C, K^D$, under the CFL condition

$$\begin{aligned} a l_{max} \varDelta t \le 2\theta \left( \frac{1}{2}-\eta _{k+1}\right) \hat{\omega }_{N} s_{min} \end{aligned}$$

(31)

Proof

On the one hand, $U^{n,D}_{e_i^C,\beta } \in [m,M], i=1,2,3$ imply that $H_{\beta }^C$ is a monotone increasing function of $U^{n,D}_{e_i^C,\beta }, i=1,2,3$ and belongs to [m, M] under the CFL condition (31) and Lemma 1.

On the other hand, $\sum _{i=1}^{3}\frac{\left| K_i^C\right| }{|K^C|}=1$, $\sum _{\alpha =1}^{N} \hat{\omega }_{\alpha } =1$ and $\sum _{\beta =1}^{k+1} (\frac{1}{2}-\eta _{\beta }) \hat{\omega }_{\alpha } \omega _{\beta } = \frac{1}{2}$ in (27), thus

$$\begin{aligned} (1-\theta ) + \sum _{i=1}^{3} \sum _{\alpha =1}^{N-1}\sum _{\beta =1}^{k+1}\frac{2\theta \left| K_i^C\right| }{|K^C|}\left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{\alpha } \omega _{\beta } + \sum _{\beta =1}^{k+1} 2\theta \left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{N} \omega _{\beta } =1, \end{aligned}$$

therefore, $\bar{U}_{K^C}^{n+1,C}$ can be viewed as a convex combination of $\bar{U}_{K^C}^{n,C}$, $U^{n,D}_{K^C_i,\alpha ,\beta }$, $H_{\beta }^C$, $\alpha =1,2, \ldots ,N-1, \beta =1,2, \ldots ,k+1$.

Substituting $\bar{U}_{K^C}^{n,C}=U^{n,D}_{K^C_i,\alpha ,\beta }=H_{\beta }^C=d, d=m,M, \alpha =1,2, \ldots ,N-1, \beta =1,2, \ldots ,k+1$ into (27), one gets $\bar{U}_{K^C}^{n+1,C}=d$, therefore we have the maximum principle $\bar{U}_{K^C}^{n+1, C} \in [m,M]$. Similarly we obtain $\bar{U}_{K^D}^{n+1, D} \in [m,M]$. $\square$

3.3 Maximum-Principle-Satisfying Limiter

In this subsection, we will give a maximum-principle-satisfying limiter which modifies the central DG solutions $U^{n,C}$ and $U^{n,D}$, with their cell averages in [m, M], into $\tilde{U}^{n,C}$ and $\tilde{U}^{n,D}$ such that the modified solutions will satisfy the sufficient condition in Theorem 2, while maintaining accuracy and local conservation (see [35] for the analysis on accuracy). This limiter is almost the same as the one for DG methods [37], as long as it is applied to $U^{n,C}$ and $U^{n,D}$ separately. This limiter is given as follows. On each mesh element $K^{\star }(\star =C,D)$, we modify the solution $U^{n,\star }$ into

$$\begin{aligned} \tilde{U}^{n,\star }=\sigma (U^{n,\star }-\bar{U}_{K^{\star }}^{n,\star })+ \bar{U}_{K^{\star }}^{n,\star }, \sigma =\min \left\{ 1, |\frac{M-\bar{U}_{K^{\star }}^{n,\star }}{M_K-\bar{U}_{K^{\star }}^{n,\star }} |, |\frac{m-\bar{U}_{K^{\star }}^{n,\star }}{m_K-\bar{U}_{K^{\star }}^{n,\star }} | \right\} \end{aligned}$$

with $M_k=\max _{(x,y)\in S_k^{\star }} U^{n,\star }$ and $m_k=\min _{(x,y)\in S_k^{\star }} U^{n,\star }$.

To achieve better accuracy in time and satisfy the maximum-principle, SSP high order time discretizations will be used [12]. Such discretizations can be written as a convex combination of the forward Euler method, and therefore the proposed schemes with a high order SSP time discretization are still maximum-principle-satisfying. In this paper, we will use three-order TVD Runge–Kutta method for the time discretization. The maximum-principle-satisfying limiter is implemented in each stage of the Runge–Kutta method. When the nonlinear limiter is also used, it is implemented before the maximum-principle-satisfying limiter.

4 Positivity-Preserving Central DG Method

In this section, we will design a positivity-preserving central DG method for solving two-dimensional compressible Euler equations based on the analysis in Sect. 3,

$$\begin{aligned} \mathbf {U}_t+ \nabla \cdot \mathbf {F}(\mathbf {U})=0, \end{aligned}$$

(32)

where

$$\begin{aligned} \mathbf {U}= & {} \left( \rho , \rho u, \rho v, \rho E \right) ^\top ,\\ \mathbf {F}(\mathbf {U})= & {} (F(\mathbf {U}),G(\mathbf {U})),\\ F(\mathbf {U})= & {} \left( \rho u, \rho u^2 + p, \rho uv, \rho Eu + pu \right) ^\top ,\\ G(\mathbf {U})= & {} \left( \rho v, \rho uv, \rho v^2 + p, \rho Ev + pv \right) ^\top . \end{aligned}$$

Here $\rho$ denotes the density, u and v are the velocity components in the x and y direction, respectively, p is the pressure and E is the total energy. For a closure of the system, we use the following equation of state:

$$\begin{aligned} p=(\gamma -1)\rho \left( E-\frac{1}{2}(u^2+v^2)\right) . \end{aligned}$$

(33)

where $\gamma$ are the ratio of specific heats of the fluid.

We define an admissible set

$$\begin{aligned} \mathcal {H}=\left\{ \mathbf {U}=\left( \begin{array}{c} \rho \\ \rho u \\ \rho v \\ \rho E \end{array}\right) : \rho> 0,\; p(\mathbf {U})=(\gamma -1)\left( \rho E- \frac{1}{2}\rho (u^2+v^2)\right) > 0 \right\} , \end{aligned}$$

which is a convex set [35].

4.1 First Order Scheme

A first order cental DG scheme with $\theta =1$ for (32) can be given by

$$\begin{aligned} \mathbf {U}_{K^C}^{n+1,C}= & {} \sum _{i=1}^{3}\frac{|K_i^C|}{|K^C|} \mathbf {U}_{K_i^D}^{n,D} - \frac{ \varDelta t}{|K^C|} \sum _{i=1}^{3} l_i^C \mathbf {F}(\mathbf {U}_{K_i^D}^{n,D})\cdot {\mathbf {n}}_i^C , \end{aligned}$$

(34)

$$\begin{aligned} \mathbf {U}_{K^D}^{n+1,D}= & {} \sum _{i=1}^{4}\frac{|K_i^D|}{|K^D|} \mathbf {U}_{K_i^C}^{n,C} - \frac{ \varDelta t}{|K^D|} \sum _{i=1}^{4} l_i^D \mathbf {F}(\mathbf {U}_{K_i^C}^{n,C} )\cdot {\mathbf {n}}_i^D . \end{aligned}$$

(35)

Herein, $\mathbf {U}_{K^C}^{n,C}$ (resp. $\mathbf {U}_{K^D}^{n,D}$) is the numerical solution on element $K^C$ (resp. $K^D$).

Lemma 2

For the first order cental DG scheme defined in (34)–(35), if $\mathbf {U}_{K^C}^{n,C}$, $\mathbf {U}_{K^D}^{n,D} \in \mathcal {H}$, $\forall K^C, K^D$, then $\mathbf {U}_{K^C}^{n+1,C}$ and $\mathbf {U}_{K^D}^{n+1,D}$ will belong to $\mathcal {H}$, $\forall K^C, K^D$, under the CFL condition

$$\begin{aligned} \tilde{a} l_{max} \varDelta t < s_{min}, \end{aligned}$$

(36)

where $\tilde{a}=||(|{(u,v)} \cdot \mathbf {n}| + c)||_{\infty }$, $c^2=\gamma p/\rho$. $l_{max}$ and $s_{min}$ are same as the ones in Lemma 1.

Proof

The scheme defined in (34) can be rewritten as

$$\begin{aligned} \mathbf {U}_{K^C}^{n+1,C} = \sum _{i=1}^{3} \left( \frac{|K_i^C|}{|K^C|} \mathbf {U}_{K_i^D}^{n,D} - \frac{\varDelta t l_i^C}{|K^C|} \mathbf {F}(\mathbf {U}_{K_i^D}^{n,D})\cdot {\mathbf {n}}_i^C \right) = \sum _{i=1}^{3} \left( \frac{|K_i^C|}{|K^C|} \mathbf {H}_i \right) \end{aligned}$$

(37)

where

$$\begin{aligned} \mathbf {H}_i= & {} \mathbf {U}_{K_i^D}^{n,D} - \frac{\varDelta t l_i^C}{|K_i^C|} \mathbf {F}\left( \mathbf {U}_{K_i^D}^{n,D}\right) \cdot {\mathbf {n}}_i^C , \end{aligned}$$

(38)

Thus $\mathbf {U}_{K^C}^{n+1,C}$ is a convex combination of $\mathbf {H}_i, i=1,2,3$. Then we only need to prove $\mathbf {H}_i \in \mathcal {H}$.

For the sake of convenience, we drop the superscript and the subscript of $\mathbf {U}_{K_i^D}^{n,D}$ and ${\mathbf {n}}_i^C$, and let $\tau = \frac{\varDelta t l_i^C}{|K_i^C|}$. Now we assume $\mathbf {U}=(\rho , \rho u, \rho v, \rho E )^\top \in \mathcal {H}$ and we want to prove $\mathbf {H}_i = \mathbf {U} - \tau \mathbf {F}(\mathbf {U}) \cdot \mathbf {n} \in \mathcal {H}$, $\mathbf {n}=(n_1, n_2)$ is an arbitrary unit vector.

By a direct computation, one has

$$\begin{aligned} \mathbf {H}_i= & {} \mathbf {U} - \tau \mathbf {F}(\mathbf {U}) \cdot \mathbf {n} = \left( \begin{array}{c} \rho q \\ \rho u q - \tau p n_1 \\ \rho v q - \tau p n_2 \\ \rho E q - \tau p s \end{array} \right) \end{aligned}$$

(39)

where $s=(u,v) \cdot \mathbf {n}$, $q=1-\tau s$. Then one gets

$$\begin{aligned} \rho (\mathbf {H}_i)= & {} \rho q , \end{aligned}$$

(40)

$$\begin{aligned} p(\mathbf {H}_i)= & {} (\gamma -1)\left( \rho E q - \tau p s - \frac{(\rho u q - \tau p n_1)^2 +(\rho v q - \tau p n_2)^2}{2 \rho q} \right) \nonumber \\= & {} pq\left( 1-{\frac{\gamma -1}{2\gamma }}c^2\frac{\tau ^2}{q^2} \right) \end{aligned}$$

(41)

Since $\mathbf {U} \in \mathcal {H}$ gives $\rho > 0$ and $p>0$, then

$$\begin{aligned} \mathbf {H}_i \in \mathcal {H}\Leftrightarrow & {} q>0 \text{ and } \sqrt{\frac{\gamma -1}{2\gamma }} \frac{c \tau }{q}< 1 \nonumber \\\Leftrightarrow & {} 0< \tau c < q. \end{aligned}$$

(42)

Herein, we used $\sqrt{\frac{\gamma -1}{2\gamma }}<1$ due to $\gamma >1$. Note that $\tilde{a}=||(|{(u,v)} \cdot \mathbf {n}| + c)||_{\infty }$ and the CFL condition $\tilde{a} l_{max} \varDelta t < s_{min}$, we have $\tilde{a} \tau < 1$ and thus $q> \tilde{a} \tau q = \tau ( \tilde{a}- \tilde{a} \tau s)> \tau ( \tilde{a} - |s|)> \tau c > 0$. Therefore, $\mathbf {H}_i \in \mathcal {H}$ holds and thus $\mathbf {U}_{K^C}^{n+1,C} \in \mathcal {H}$. Similarly, we obtain $\mathbf {U}_{K^D}^{n+1,D} \in \mathcal {H}$. $\square$

Remark 2

The proof of this lemma is along the same lines as in Remark 2.4 of [36], where the authors prove the positivity-preserving property of the first order DG method for the one-dimensional compressible Euler equations. In another work [37], they claim the proof in [36] can be extended to the first order positivity-preserving DG scheme on triangle meshes for two-dimensional compressible Euler equations. The CFL condition (36) is different from the one in the first order positivity-preserving DG scheme for two-dimensional compressible Euler equations [37], and deduces that the time step is about half of the one in the DG method.

4.2 High Order Scheme

A high order scheme satisfied by the cell average of a cental DG method for (32), with first order Euler forward time discretization, can be given by

$$\begin{aligned} \bar{{\mathbf {U}}}_{K^C}^{n+1,C}= & {} (1-\theta ) \bar{{\mathbf {U}}}_{K^C}^{n,C} + \frac{\theta }{|K^C|} \int _{K^C} {\mathbf {U}}^{n,D} dxdy \nonumber \\&- \frac{ \varDelta t}{|K^C|} \sum _{i=1}^{3}\int _{ e_i^C} \mathbf {F}({\mathbf {U}}^{n,D})\cdot {\mathbf {n}}_i^C ds, \end{aligned}$$

(43)

$$\begin{aligned} \bar{{\mathbf {U}}}_{K^D}^{n+1,D}= & {} (1-\theta ) \bar{{\mathbf {U}}}_{K^D}^{n,D} + \frac{\theta }{|K^D|} \int _{K^D} {\mathbf {U}}^{n,C} dxdy \nonumber \\&- \frac{ \varDelta t}{|K^D|} \sum _{i=1}^{4}\int _{ e_i^D} \mathbf {F}({\mathbf {U}}^{n,C})\cdot {\mathbf {n}}_i^D ds, \end{aligned}$$

(44)

where $\bar{{\mathbf {U}}}_{K^C}^{n,C}$ (resp. $\bar{{\mathbf {U}}}_{K^D}^{n,D}$) denotes the cell average over $K^C$ (resp. $K^D$) of the numerical solution ${\mathbf {U}}^{n,C}$ (resp. ${\mathbf {U}}^{n,D}$).

Theorem 3

For the scheme defined in (43)–(44), assume $\bar{{\mathbf {U}}}_{K^C}^{n, C}, \bar{{\mathbf {U}}}_{K^D}^{n, D} \in \mathcal {H}$, $\forall K^C, K^D$. If ${\mathbf {U}}^{n,C}(x,y) \in \mathcal {H}, \forall (x,y)\in S^C_k, \forall K^C$ and ${\mathbf {U}}^{n,D}(x,y) \in \mathcal {H}, \forall (x,y)\in S^D_k, \forall K^D$, then $\bar{{\mathbf {U}}}_{K^C}^{n+1, C}$ and $\bar{{\mathbf {U}}}_{K^D}^{n+1, D}$ will belong to $\mathcal {H}$, $\forall K^C, K^D$, under the CFL condition

$$\begin{aligned} \tilde{a} l_{max} \varDelta t \le 2\theta \left( \frac{1}{2}-\eta _{k+1}\right) \hat{\omega }_{N} s_{min} \end{aligned}$$

(45)

Proof

By using same techniques as in Sect. 3, we can rewrite the scheme (43) as

$$\begin{aligned} \bar{{\mathbf {U}}}_{K^C}^{n+1,C}= & {} (1-\theta ) \bar{{\mathbf {U}}}_{K^C}^{n,C} + \sum _{i=1}^{3} \sum _{\alpha =1}^{N-1}\sum _{\beta =1}^{k+1}\frac{2\theta \left| K_i^C\right| }{|K^C|}\left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{\alpha } \omega _{\beta } {\mathbf {U}}^{n,D}_{K^C_i,\alpha ,\beta } \nonumber \\&+ \sum _{\beta =1}^{k+1} 2\theta \left( \frac{1}{2}-\eta _{\beta }\right) \hat{\omega }_{N} \omega _{\beta } {\mathbf {H}}_{\beta }^C . \nonumber \\ \end{aligned}$$

(46)

where

$$\begin{aligned} \mathbf {H}_{\beta }^C= & {} \sum _{i=1}^{3} \left( \frac{\left| K_i^C\right| }{|K^C|}{\mathbf {U}}^{n,D}_{e_i^C,\beta } - \frac{ l_i^{C} \varDelta t}{2\theta (\frac{1}{2}-\eta _{\beta }) \hat{\omega }_{N}|K^C|} \mathbf {F}({\mathbf {U}}^{n,D}_{e_i^{C},\beta })\cdot {\mathbf {n}}_i^C \right) . \end{aligned}$$

(47)

Under the CFL condition (45), $\mathbf {H}_{\beta }^C$ defined in (47) is a formal first order positivity preserving scheme as in (34), therefore $\mathbf {H}_{\beta }^C \in \mathcal {H}$.

Note that $\bar{{\mathbf {U}}}_{K^C}^{n+1,C}$ is a convex combination of $\bar{{\mathbf {U}}}_{K^C}^{n,C}$, ${\mathbf {U}}^{n,D}_{K^C_i,\alpha ,\beta }$, ${\mathbf {H}}_{\beta }^C$. Since $\mathcal {H}$ is a convex set, one obtains $\bar{{\mathbf {U}}}_{K^C}^{n+1,C} \in \mathcal {H}$. Similarly, $\bar{{\mathbf {U}}}_{K^D}^{n+1,D} \in \mathcal {H}$. $\square$

4.3 Positivity-Preserving Limiter

In this subsection, we will give a positivity-preserving limiter which modifies the cental DG solutions $\mathbf {U}^{n,C}$ and $\mathbf {U}^{n,D}$, with the cell averages in the set $\mathcal {H}$, into $\tilde{{\mathbf {U}}}^{n,C}$ and $\tilde{{\mathbf {U}}}^{n,D}$, such that the modified solutions will satisfy the sufficient condition in Theorem 3, while maintaining accuracy and local conservation (see [36]).

Following [5, 20, 33, 37], the positivity-preserving limiter is given as follows.

• (a) First, we enforce the positivity of density. In each element $K^{\star }, \star =C,D$, we modify the density $\rho ^{n,\star }$ into $\hat{\rho }^{n,\star }$,

  $$\begin{aligned} \hat{\rho }^{n,\star }=\alpha _K(\rho ^{n,\star }-\bar{\rho }^{n,\star })+ \bar{\rho }^{n,\star },~ \alpha _K=\min _{(x,y) \in S_K^{\star }} \left\{ 1, |(\bar{\rho }^{n,\star }-\varepsilon ) /(\bar{\rho }^{n,\star }- \rho ^{n,\star }) | \right\} . \end{aligned}$$

  Here $\varepsilon$ is a small number such that $\bar{\rho }^{n,\star } \ge \varepsilon$ for all $K^{\star }$. In our simulation, $\varepsilon =10^{-13}$ is taken. We now define $\hat{{\mathbf {U}}}^{n,\star }(\hat{\rho }^{n,\star } , (\rho u)^{n,\star }, (\rho v)^{n,\star }, (\rho E)^{n,\star })$.

• (b) Second, we enforce the positivity of pressure. For each $(x,y) \in S_K^{\star }$, we define

  $$\begin{aligned} \delta (x,y)=\left\{ \begin{array}{ll} 1, &{} \text{ if } \hat{p}(\hat{{\mathbf {U}}}^{n,\star })>0 \\ \frac{p(\bar{\mathbf {U}}^{n,\star })}{p(\bar{{\mathbf {U}}}^{n,\star }) -p(\hat{{\mathbf {U}}}^{n,\star })}, &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

  With this, the newly limited numerical solution is given as

  $$\begin{aligned} \tilde{{\mathbf {U}}}^{n,\star }=\beta _K(\hat{{\mathbf {U}}}^{n,\star } -\bar{{\mathbf {U}}}^{n,\star })+ \bar{{\mathbf {U}}}^{n,\star },~\beta _K=\min _{(x,y) \in S_K^{\star }}(\delta (x,y)). \end{aligned}$$

Similar to the discussions in Sect. 3.3, for higher order temporal accuracy, high order SSP time discretizations will be used [12]. With their intrinsic structure of being a convex combination of the Euler forward method, and the admissible set $\mathcal {H}$ being convex, SSP temporal discretizations will keep the positivity-preserving property of the overall methods. When the solutions contains non-smooth structures such as strong shocks, nonlinear limiters are often needed to further improve the numerical stability. In our numerical experiments, a total variation bounded (TVB) corrected minmod slope limiter [7] is applied for some examples and it is implemented before the positivity-preserving limiter.

5 Numerical Examples

In this section, numerical experiments are presented to demonstrate the performance of the proposed methods for solving conservation laws. The time step is set according to the theoretical analysis. Since the numerical results on the primal and dual meshes are similar, we only show the numerical results on the primal mesh.

5.1 Scalar Conservation Laws

5.1.1 Linear Equation

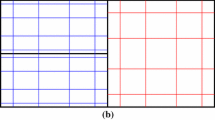
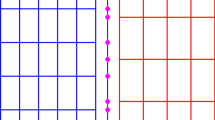
In this test, we solve the linear transport equation $u_t+u_x+u_y=0$ with initial condition $u(x,y,0)=\sin (2\pi (x+y))\in [-1,1]$ and periodic boundary condition. The computational domain is $[0,1]\times [0,1]$. The coarsest primal mesh used in this test consists of 128 similar triangles, which is shown in Fig. 3. Then we refine the mesh by dividing the each triangle into four smaller identical triangles for the purpose of the accuracy test. The $L^2$ and $L^\infty$ errors and orders of accuracy for $\rho$ at $t=0.1$ are listed in Table 1 without the maximum-principle-satisfying limiter and in Table 2 with the maximum-principle-satisfying limiter. The results show that the central DG methods with and without the limiter on the unstructured overlapping meshes are $(k+1)$st order accurate for $P^k$ with $k=1,2$. To demonstrate the effectiveness of the maximum-principle-satisfying limiter, we plot time series of the maximum value and the minimum value of the numerical solution u with or without the maximum-principle-satisfying limiter in Fig. 4. It can be seen from Fig. 4 that most of the time the maximum value and the minimum value of the numerical solution are outside of the domain $[-1,1]$ when the limiter is not used in the simulation, even though the mesh is refined. However these values are always in the domain $[-1,1]$ when using the limiter.

Table 1 The $L^2$ and $L^\infty$ errors and orders of accuracy of u at $t=0.1$ without limiter for linear transport equation

Table 2 The $L^2$ and $L^\infty$ errors and orders of accuracy of u at $t=0.1$ with limiter for linear transport equation

Fig. 3

The coarsest primal mesh (128 elements) for the accuracy test

Fig. 4

Comparison between the numerical solutions with or without the maximum-principle-satisfying limiter. Top: using 128 cells in the primal mesh; bottom: using 8192 cells in the primal mesh; blue line: results without the limiter; red dashed line: results with the limiter (Color figure online)

5.1.2 Diagonal Advection of a Gaussian

In this test, we consider the advection equation $u_t+u_x+u_y=0$ in a square domain $[-1,1]\times [-1,1]$, the initial condition is an axisymmetric Gaussian shape $u(x,y,0)=e^{-75((x-x_0)^2+(y-y_0)^2)} \in [0,1]$, the boundary conditions are Dirichlet. The Gaussian is initially located at $x_0=y_0=-0.5$ and moves diagonally at speed $\sqrt{2}$. This problem is solved until time $t=0.5$ with 8192 similar triangles on the primal mesh which is obtained by refining the mesh shown in Fig. 3 three times. The numerical results at $t=0.5$ are shown in Fig. 5, the exact solution is also plotted in the same picture for a comparison. It can be seen that the numerical solution matches well with the exact solution.

Fig. 5

Diagonal advection of a Gaussian. Left: the contours of the numerical results at $t=0.5$; right: x-profiles ($y=0$), dots: numerical solution, solid line: exact solution

5.1.3 Burgers Equation

We consider the Burgers equation

$$\begin{aligned} u_t + \left( \frac{u^2}{2} \right) _x + \left( \frac{u^2}{2} \right) _y=0 \end{aligned}$$

(48)

with smooth initial condition

$$\begin{aligned} u(x,0)=0.5+\sin (\pi (x+y)) \end{aligned}$$

and periodic boundary condition.

The computational domain is $[-1,1] \times [-1,1]$. The mesh used in this test is same to the test in Sect. 5.1.1. We present $L^2$ and $L^\infty$ errors and orders of accuracy for u at $t=0.05$ in Table 3 without the maximum-principle-satisfying limiter and in Table 4 with the maximum-principle-satisfying limiter. The results also show that the central DG methods on the unstructured overlapping meshes are $(k+1)$st order accurate for $P^k$ with $k=1,2$. Numerical and exact solutions at $t=0.62$ (at the time the solution becomes very sharp) are plotted in Fig. 6, it can be observed the numerical solution is agree with the exact solution.

Table 3 The $L^2$ and $L^\infty$ errors and orders of accuracy of u at $t=0.05$ without limiter for Burgers equation

Table 4 The $L^2$ and $L^\infty$ errors and orders of accuracy of u at $t=0.05$ with limiter for Burgers equation

Fig. 6

Numerical solution at $t=0.62$ for the Burgers equation. Left: numerical result; right: exact solution

5.2 Euler Equations

5.2.1 Accuracy Test

In this test, we solve the Euler equations with initial conditions given by

$$\begin{aligned} \rho (x,y,0)=1+0.99\sin (2\pi (x+y)),\quad u(x,y,0)=v(x,y,0)=1,\quad p(x,y,0)=1. \end{aligned}$$

The computational domain is $[0,1]\times [0,1]$ and the boundary condition is periodic. The mesh used in this test is same to the test in Sect. 5.1.1. The $L^2$ and $L^\infty$ errors and orders of accuracy for $\rho$ at $t=0.1$ are listed in Table 5 without the positivity-preserving limiter and in Table 6 with the positivity-preserving limiter. The results show that the present methods are $(k+1)$st order accurate for $P^k$ approximation with $k=1,2$. We can observe from both tables that the errors are different only on the coarsest mesh with $P^1$ approximation. This is due to the fact that negative value of density appears on the coarsest mesh when using $P^1$ approximation and the limiter is implemented in the computation. While for the refined mesh or when using $P^2$ approximation, no negative value of density appears on these meshes and thus the limiter is actually not implemented.

Table 5 The $L^2$ and $L^\infty$ errors and orders of accuracy of $\rho$ at $t=0.01$ without limiter

Table 6 The $L^2$ and $L^\infty$ errors and orders of accuracy of $\rho$ at $t=0.01$ with limiter

5.2.2 Riemann Problem

In this test, we shall investigate the performance of the central DG methods on unstructured overlapping meshes for the problems with shocks. We consider two Riemann problems with initial conditions given by

$$\begin{aligned} (\rho , u, v, p)=\left\{ \begin{array}{lll} (0.5313, 0.1, 0.1, 0.4), &{}\quad x>0.5,y>0.5, \\ (1.0222, -0.6179, 0.1, 1), &{}\quad x<0.5,y>0.5, \\ (0.8, 0.1, 0.1, 1), &{}\quad x<0.5,y<0.5, \\ (1, 0.1, 0.8276, 1), &{}\quad x>0.5,y<0.5. \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} (\rho , u, v, p)=\left\{ \begin{array}{lll} (1.0, 0, 0.3, 1.0), &{}\quad x>0.5,y>0.5, \\ (2.0, 0, 0.3, 1.0),&{}\quad x<0.5,y>0.5, \\ (1.039, 0, -0.8133, 0.4), &{}\quad x<0.5,y<0.5, \\ (0.5197, 0, -0.4259, 0.4),&{}\quad x>0.5,y<0.5, \end{array}\right. \end{aligned}$$

The computational domain is $[0,1]\times [0,1]$ with 131072 similar triangles on the primal mesh which is obtained by refining the mesh (shown in Fig. 3) five times. The boundary condition is outflow. The numerical results at $t=0.2$ for the first Riemann problem are shown in Fig. 7. The numerical results at $t=0.3$ for the second Riemann problem are shown in Fig. 8. These results match well with the ones in [1].

Fig. 7

The contours of the numerical results at $t=0.2$ for the first Riemann problem. Top left: density; top right: pressure; bottom left: velocity component u; bottom right: velocity component v

Fig. 8

The contours of the numerical results at $t=0.3$ for the second Riemann problem. Top left: density; top right: pressure; bottom left: velocity component u; bottom right: velocity component v

5.2.3 Double Rarefaction Riemann Problem

In this test, we consider a double rarefaction Riemann problem [36], with the initial condition as

$$\begin{aligned} (\rho ,u,v,p)=\left\{ \begin{array}{lcl} (7,-1,0,0.2) , &{} x \le 0 , \\ (7,1,0,0.2), &{} x>0 ~ \end{array}\right. \end{aligned}$$

on the computational domain $[-1,1]\times [0,0.2]$. The primal mesh used in the test includes 3604 elements as shown in Fig. 9. The exact solution contains vacuum, and thus we use positivity-preserving limiter in this example. Since no shock occurs in the problem, we do not use the TVB limiter. The left column of Fig. 10 reports the numerical density and pressure which is in good agreement with the exact solutions shown in right column of Fig. 10. It can be observed that both the low density and low pressure are captured well.

Fig. 9

The primal mesh (3604 elements) for the double rarefaction problem

Fig. 10

The numerical results at $t=0.6$ for the double rarefaction problem. Top left: numerical density; top right: exact density; bottom left: numerical pressure; bottom right: exact pressure

5.2.4 Shock Diffraction Problem

In this test, we consider a shock diffraction problem where shock passing a sharp convex corner, which has been a benchmark problem in computational fluid dynamics and was tested in many works [30, 37]. Standard numerical methods often result in negative density and/or negative pressure, and it is important to utilize positivity-preserving methods to simulate this example. The initial condition is given by

$$\begin{aligned} (\rho ,u,v,p) =\left\{ \begin{array}{lll} (7.04113,4.07795,0,30.05945), &{}\quad x \le 0.5, y>6, \\ (1.4,0,0,1), &{}\quad \text{ otherwise } , \end{array}\right. \end{aligned}$$

on an irregular computational domain$[0,13]\times [0,11]-[0,1]\times [6x,6]$ which is divided into 27086 triangular elements on the primal mesh, the part of mesh is shown in Fig. 11. We use inflow boundary condition at $\{x=0, y\in [6,11]\}$, reflective boundary condition at $\{x\in [0,1], y=6\}$ and $\{x\in [0,1], y=6x\}$, and outflow boundary condition elsewhere. The primal mesh is shown in Fig. 11, with 27086 elements. In Fig. 12, the computed density and pressure at $t=2.3$ are plotted, and no negative pressure or density is encountered during the simulation with the presented positivity-preserving central DG methods.

Fig. 11

Part of the primal mesh (27086 elements) for the shock diffraction problem

Fig. 12

The numerical results at $t=2.3$ for the shock diffraction problem. Left: density; right: pressure

6 Conclusions

In this paper, we have developed a family of high order accurate central DG methods defined on unstructured overlapping meshes for the conservation laws in two-dimensional spaces, including the maximum-principle-satisfying central DG methods and the positivity-preserving central DG methods. The maximum-principle-satisfying limiter and positivity-preserving limiter are implemented locally. Some numerical experiments are carried out in this paper, which demonstrate the validity and accuracy of proposed method. Therefore, we will extend the present method to other problems in the future works, such as MHD equations [28], attraction-repulsion system with nonlinear diffusion [23] and Biot’s equations [2].