1 Introduction

How to treat the free interface and how to solve the flow fields are the two key points of simulating a two-medium flow with a clear free interface. Because of its linear discontinuity characteristic, severe nonphysical oscillations may arise in the vicinity of the free interface, especially in the presence of strong shock and large density ratio, even when a well established numerical method for single-medium flow is applied directly to the multi-medium flow. Therefore, the free interface needs to be treated accurately and stably to avoid/reduce nonphysical oscillations. To treat the free interface, there are basically two types of approaches being developed: diffuse-interface methods (like Volume of Fluid (VOF) method [22], Phase Field method [13], et al.) and sharp-interface methods (like Level Set (LS) + Ghost Fluid Method (GFM) [15, 28, 29, 35], Front Tracking (FT) method [17, 19], Cut Cell (CC) method [2, 7, 26, 33, 41], et al.). Also, some methods have been developed by combining the concepts of diffuse-interface method and sharp-interface method, like the VOF + interface reconstruction method [38] and the coupled LS and VOF method [40].

Different from diffuse-interface methods, sharp-interface methods provide more accurate description of the free interfaces, although the methods like FT and CC need more work on geometry calculation and need special consideration for topological changes. In the CC method in [7], the LS approach is included to help evolve the interface and calculate geometrical parameters, the structured adaptive mesh refinement (AMR) technology [3, 4] is endowed with a corridor of irregular cut cells around the interface. The fluxes at the interface are calculated from two-medium exact Riemann solver, and include the effects of shear force and heat transfer, which are decided by a set of interface jump conditions across the interface.

On the other hand, the flow field solver needs to fit the interface method to give best result. Many numerical methods for single-medium flows have been extended to multi-medium flows, such as finite difference method [18, 42], finite volume method [7, 30], discontinuous Galerkin (DG) method [14, 34, 35, 45], et al.

The DG method, originally introduced in 1973 by Reed and Hill [37] for the time independent linear hyperbolic equation, is in the class of high order finite element methods. It has been developed for solving nonlinear hyperbolic conservation laws [8,9,10,11]. Since the basis functions can be discontinuous, the DG method is very flexible to achieve any order of accuracy and handle complicated geometry and boundary conditions. It is also a very compact numerical scheme due to the extremely local data structure. These advantages make the DG method having potential to work well with the CC method. A DG + CC method has been developed to deal with elliptic interface problems and conjugate heat transfer problems [39].

In this paper, a sharp interface Runge–Kutta DG method is developed with AMR and CC method for two-medium flows, governed by the Euler equations. We follow Chang et al. [7] to treat the free interface using the CC method. The free interface is represented by curved cut faces and evolved by solving the LS equation with high order upstream central schemes [32]. Every mixed cell is divided into two cut cells by a cut face. The two-medium exact Riemann solver [7] is applied on the cut faces with the input states obtained from the solution representation in the two single-medium cut cells adjacent to a cut face. The Runge–Kutta DG method built on structured adaptive meshes with cut cells around the interface is applied to calculate each single-medium flow. Comparing with the FVM (finite volume method) based method, current method avoids to use a big stencil, including cut cells, to reconstruct high order polynomials near the free interface, which may produce numerical oscillations around the free interface. Also, the AMR synchronization method and positivity-preserving limiters applied in current work keep the accuracy order while maintaining conservation, and make current method more robust.

The remainder of the paper is organized as follows. In Sect. 2, we present the mathematical formulation of the governing equations, containing the Euler equations and the LS equation. Section 3 is devoted to the detail of the numerical methods. In Sect. 4, numerical experiments are presented to illustrate the accuracy and robustness of the proposed method. Finally, concluding remarks are given in Sect. 5.

2 Governing Equations

2.1 Euler Equations in 2D

We first consider inviscid and compressible two-medium flows in two-dimensional space governed by the Euler equations in the conservation form:

$$\begin{aligned} \frac{\partial \mathbf{U}}{\partial t}+\nabla \cdot \mathbf{F}(\mathbf{U})=0, \end{aligned}$$
(1)

where

$$\begin{aligned} \mathbf U=\left( \begin{array}{c} \rho \\ \rho u \\ \rho v \\ \rho E \end{array}\right) ;~ \mathbf{F}(\mathbf{U})=\left( \begin{array}{c} \rho u \\ \rho u^2 + p \\ \rho uv \\ \rho Eu + pu \end{array}\right) +\left( \begin{array}{c} \rho v \\ \rho uv \\ \rho v^2 + p \\ \rho Ev + pv \end{array}\right) =\mathbf{F}_1+\mathbf{F}_2. \end{aligned}$$

Here \(\rho \) denotes the density, u and v are the velocity components in x and y directions, respectively, p is the pressure and \(E=e+\frac{1}{2}(u^2+v^2)\) denotes the total specific energy, e is the specific internal energy.

Equation of state is needed for the closure of system (1). Here, the stiffened gas equation of state is applied:

$$\begin{aligned} p=\frac{\gamma -1}{\gamma } C_p \rho T - p_{\infty }, e=\frac{C_p}{\gamma }T+\frac{p_{\infty }}{\rho }. \end{aligned}$$
(2)

where T is the temperature, \(\gamma \) is the heat capacity ratio, \(C_p\) is the specific heat at constant pressure and \(p_{\infty }\) is a constant for each fluid.

2.2 Governing Equations for Axisymmetric Problems in 3D

Axisymmetric problems with respect to x-axis in 3D can be governed by

$$\begin{aligned} \frac{\partial \tilde{\mathbf{U}}}{\partial t}+ \tilde{\nabla }\cdot \tilde{\mathbf{F}}({{\mathbf {U}}})=\tilde{\mathbf{S}}, \end{aligned}$$
(3)

where

$$\begin{aligned} \tilde{\mathbf{U}}= & {} \left( \begin{array}{c} \rho \\ \rho u \\ \rho v_r \\ \rho E \end{array}\right) ;~ \tilde{\mathbf{F}}=\left( \begin{array}{c} \rho u \\ \rho u^2 + p \\ \rho uv_r \\ \rho Eu + pu \end{array}\right) + \left( \begin{array}{c} \rho v_r \\ \rho v_r u \\ \rho v_r^2 + p \\ \rho Ev_r + pv_r \end{array}\right) =\tilde{\mathbf{F}}_1+\tilde{\mathbf{F}}_2;\\ \tilde{\mathbf{S}}= & {} -\frac{1}{r}\left( \begin{array}{c} \rho v_r \\ \rho v_r u \\ \rho v_r^2 \\ \rho Ev_r + pv_r \end{array}\right) . \end{aligned}$$

Equation (3) comes from the 3D Euler equations in cylindrical coordinates \((x,r,\theta )\) by considering the axisymmetry. We still use Eq. (2) as the equation of state for Eq. (3).

2.3 Level-Set Equation

This work follows Chang, Deng and Theofanous [7] to track the free interface of a two-medium flow, with the help of the LS equation:

$$\begin{aligned} \frac{\partial \varphi }{\partial t} +\mathbf{u}_{\varphi } \cdot \nabla \varphi =0. \end{aligned}$$
(4)

where \(\varphi \) denotes a signed distance function, \(\mathbf{u}_{\varphi }\) denotes the nearest interfacial velocity.

3 Numerical Schemes

3.1 Meshes

3.1.1 Structured AMR

In order to resolve the interfacial region effectively and save the calculation time, our numerical methods are based on the structured AMR technology [3, 4]. The structured adaptive mesh is a multi-level, dynamic hierarchy of nested, structured-grid patches and is constructed in a quadtree-like fashion. Refinement of mesh occurs according to criteria on the distance from a material interface (and/or on magnitudes of pressure/density gradient) as in Fig. 1. Any cell that meets these criteria is split into four equal cells, until the specified levels in the hierarchy are exhausted. The process is reversed when a group of cells falls away from meeting such criteria. Deactivated cells are handled in a manner that does not waste memory space.

Fig. 1
figure 1

The AMR structure embeds cut-cells. Left density contours; right the adaptive meshes

Full size image

3.1.2 Cut Cell

In the cut cell method, the free interface of two-medium flows divides every mixed cell into two small subcells, which may be triangle, quadrangle or pentagon with one curved edge. These subcells are called cut cells (Fig. 2). The intersection points of the regular faces and the free interface are called cut points (Fig. 2). Thus, the free interface is represented by piecewise cut faces (Fig. 2). Some resulted cut cells can be very small so that the time step needs to be small due to the limit of the CFL condition. To avoid too small time step, these cut cells (with areas less than a given portion of smallest regular cell) are merged into immediate neighbor cells (the ones with the maximum cell-cell common interface) on the same side of the free interface. More details are referred to [7, 33].

Fig. 2
figure 2

Illustration of cut cells. Left original cut cells, cut points and cut faces; right merging the small cut cells into their immediate neighbor cells

Full size image

3.2 Interface Treatment

As is well known, a free interface needs to be treated accurately and stably to avoid/reduce error propagation.

In this paper, the LS equation (4) is solved on the structured AMR meshes with the high order upstream central scheme [32] to discretize the gradient term and a fourth-order Runge–Kutta method is applied to advance the time step. Both \(\varphi \) and \(\mathbf{u}_{\varphi }\) are defined at the grid points. The grid-point velocity \(\mathbf{u}_{\varphi }\) is set equal to the velocity value at the nearest interfacial point. The velocity on the interface is calculated by the two-medium exact Riemann solver, with initial values given by the DG solution. Then the interface is implicitly defined by the zero-value of the LS function \(\varphi \). Three steps are employed to reconstruct the interface. Step 1, the cut points are determined along the applicable grid lines (the signs of \(\varphi \) are opposite at the endpoints of the grid lines) with fourth-order accuracy least square method. Step 2, a second-order polynomial is reconstructed as an approximation to the local LS function. The zero-level line of the reconstructed local LS function from step 2 may not pass the cut points from step 1 exactly, thus in step 3 the approximation polynomial is finally shifted to make its zero-level line passing through the cut points, which is the cut face connecting the cut points. The so-defined cut face is used to form the cut cells and calculate the curvature, which is given by

$$\begin{aligned} \kappa= & {} \nabla \cdot \left( \frac{\nabla \varphi }{|\nabla \varphi |} \right) =\frac{\varphi _{xx}\varphi _{y}^2-2\varphi _{x}\varphi _{y}\varphi _{xy} +\varphi _{yy}\varphi _{x}^2}{(\varphi _{x}^2+\varphi _{y}^2)^{3/2}}~. \end{aligned}$$

More details are referred to [7].

As pointed by [1, 7, 48], the signed distance character of LS values at the grid points near the interface keeps well when the closest interface velocity is used to evolve the LS equation (4), so that the requirement of re-initialization of LS values is reduced—normally re-initialization is needed after every few thousand steps. But it is still needed after some time steps, especially when big curvature appears near the interface. In our method, a geometrical method is applied by calculating the distance of a grid point to the interface at the nearest. This ensures that the re-initialization does not change the interface location and also that the LS value has correct gradient near the interface.

3.3 DG Methods

For the sake of convenience, we only present the numerical methods for Eq. (1) as the one for Eq. (3) is similar.

Suppose that \({{\mathcal {T}}}\) is a family of partitions of the computational domain \(\varOmega \). For any cell \(K \in {{\mathcal {T}}} \), which may be a rectangle from the structured AMR, or a cut cell from the CC method, define \(h_K := {{\mathrm {diameter}}}(K)\) and \(h := \max _{K \in {{\mathcal {T}}} } (h_K)\). Let \(m_K\) be the number of edges of cell K, for each edge \(e_K^i(i=1,2,\ldots ,m_K)\) of K , the outward unit normal vector is denoted by \({{\mathbf n}}_K^i\).

In a high order DG method, the approximation to the conservative variable \({{\mathbf U}}\) is denoted by \({{\mathbf U}}_h\), which belongs to the finite dimensional space,

$$\begin{aligned} {{\mathcal {V}}}_{h}={{\mathcal {V}}}_{h}^{k} \equiv \{ \mathbf{{v}} \in [L^2(\varOmega )]^4:\mathbf{{v}}|_{K}\in [P^k(K)]^4~, \forall K \in {{\mathcal {T}}} \}, \end{aligned}$$

where \(P^k(K)\) is the space of polynomials of degree no more than k on cell K.

The choice of basis for the finite dimensional space \({{\mathcal {V}}}_{h}\) does not affect the proposed algorithm. However, a suitable basis may simplify the implementation and the calculation due to the complex elements near the interface. For a rectangular element from the structured AMR technology, the orthogonal basis functions as usual [12] is applied. For a cut cell related to the free interface, we seek a set of basis functions which are also orthogonal. For this purpose, we apply the Gram-Schmidt orthogonalization to the reference basis \(\{1, x, y, xy, x^2, y^2, \ldots \}\), this gives the orthogonal basis functions on a cut cell.

Let \({{\mathbf {x}}}\) denote the point (x, y) in the computational domain, then the semi-discretized DG methods for the system (1) is given by: looking for the approximate solution \({{\mathbf U}}_{h}({{\mathbf {x}}},t) \in \mathcal {V}_{h}\), for all test function \(\mathbf V({{\mathbf {x}}})\in \mathcal {V}_{h}\), such that

$$\begin{aligned} {\frac{\partial }{\partial t}{\int }_{K}{{{\mathbf U}}_{h}({{\mathbf {x}}},t)} \cdot {{\mathbf V}}({{\mathbf {x}}})}d{\varOmega }= & {} {\int }_{K}{{{\mathbf F}}}({{\mathbf U}}_{h} ({{\mathbf {x}}},t))\cdot \nabla {{\mathbf V}}({{\mathbf {x}}}) d{\varOmega } \nonumber \\&- \sum _{i=1}^{m_K}{\int }_{e_K^i} {\hat{{{\mathbf F}}}({{\mathbf U}}_{h} ({{\mathbf {x}}},t))|_{e_K^i}\cdot {{\mathbf n}}_{K}^i} {{\mathbf V}} ({{\mathbf {x}}}) d{\varGamma }~, \end{aligned}$$
(5)

where \({\hat{{{\mathbf F}}}({{\mathbf U}}_{h}({{\mathbf {x}}},t))}\) is the numerical flux, which will be discussed in the next section.

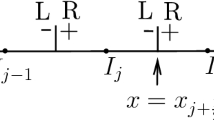
For the sake of convenience, time discretization is given by using the Euler forward scheme in this section. In practice, to achieve better accuracy in time, the four-stage Runge–Kutta method is applied in the numerical tests in this paper. On a cut cell or a regular cell at time \(t_n\) which changes to a cut cell at time \(t_{n+1}\), the fully discretized scheme is given by

$$\begin{aligned} {{\int }_{K_{n+1}} {{\mathbf U}}_{h}^{n+1} \cdot {{\mathbf V}}({\mathbf {x}})}d{\varOmega }= & {} {{\int }_{K_{n}}{{{\mathbf U}}_{h}^{n}} \cdot \mathbf V(\mathbf {x})}d{\varOmega } + \Delta t_n {\int }_{K_{n}}{{\mathbf F}}({{\mathbf U}}_{h}^{n})\cdot \nabla {{\mathbf V}}({\mathbf {x}}) d{\varOmega } \nonumber \\&- \Delta t_n \sum _{i=1}^{m_K}{\int }_{e_{K_{n}}^i} {\hat{{\mathbf F}} ({{\mathbf U}}_{h}^{n})|_{e_{K_{n}}^i}\cdot {{\mathbf n}}_{K_{n}}^i} {{\mathbf V}} ({{\mathbf {x}}}) d{\varGamma } \end{aligned}$$
(6)

Here, \(\Delta t_n\) denotes the time step from time \(t_n\) to \(t_{n+1}\). As shown in Fig. 3 (left), the interface at \(t_n\) is denoted by the blue solid line, and the one at \(t_{n+1}\) by the red dashed line. In Fig. 3 (middle), the cut cells at \(t_n\) are denoted by \(C_1\), \(C_2\), \(C_3\) and \(C_4\). \(C_5\) is a regular cell. Due to the movement of the interface, \(C_4\) becomes smaller and is merged into \(C_5\), so the cut cells at \(t_{n+1}\) become \(C_6\), \(C_7\), \(C_8\) and \(C_9\) as shown in Fig. 3 (right). Then the elements \(K_{n}\) and \(K_{n+1}\) in Eq. (6) can be listed in Table 1.

On a regular cell which does not change from time \(t_n\) to \(t_{n+1}\), \(K_{n}\) and \(K_{n+1}\) denote the same regular cell, and the fully discretized scheme is still given by (6).

Fig. 3
figure 3

Illustration of the cut cells from time \(t_n\) to \(t_{n+1}\). Left original cut cells and interface at time \(t_n\) and \(t_{n+1}\); middle merged cut cells at time \(t_n\); right merged cut cells at time \(t_{n+1}\)

Full size image
Table 1 The partner cell \(K_{n}\) of \(K_{n+1}\) in Eq. (6)
Full size table

3.4 Calculation of the Numerical Fluxes

In the present method, the numerical fluxes on the regular faces are defined by

$$\begin{aligned} \hat{{\mathbf F}}(U_{h}^n)|_{e_K^i} \cdot {{\mathbf n}}_{K}^i= & {} {\mathcal {F}} ({{\mathbf U}}_{h}^{n,int(K)}|_{e_K^i}, {{\mathbf U}}_{h}^{n,ext(K)}|_{e_K^i}, {{\mathbf n}}_{K}^i)~, \end{aligned}$$
(7)

where \({{\mathbf U}}_{h}^{n,int(K)}|_{e_K^i}\) and \({{\mathbf U}}_{h}^{n,ext(K)}|_{e_K^i}\) are the approximations to the values on the edge \(e_K^i\) obtained from the interior and the exterior of K at time \(t_n\). This work uses the local Lax–Friedrichs flux

$$\begin{aligned} {{\mathcal {F}}}(a_1, a_2, {{\mathbf n}})= & {} \frac{1}{2}\left[ {{\mathbf F}}(a_1) \cdot {{\mathbf n}} + {{\mathbf F}}(a_2) \cdot {{\mathbf n}} - \alpha (a_2 - a_1) \right] \, \nonumber \\ \alpha= & {} \max \left( (u+c, v+c) \cdot {{{\mathbf n}}} \right) , \end{aligned}$$
(8)

where the maximum is taken over the cells where \(a_1\) and \(a_2\) are defined, and c denotes the sound speed.

The numerical fluxes on the cut faces can be defined by [7],

$$\begin{aligned} \left( \hat{{\mathbf F}}(U_{h}^n)|_{e_K^i} \cdot {{\mathbf n}}_{K}^i \right) _j= & {} \left( 0, p_j^{\star }n_x, p_j^{\star }n_y, p_j^{\star }{u}_{n} \right) ^\top ~, \end{aligned}$$
(9)

Here, the subscript \(j=1,2\) denotes the fluid, \({{\mathbf n}}_{K}^i=(n_x,n_y)\), \(n_x\) and \(n_y\) are the components of \({{\mathbf n}}_{K}^i\) in x and y directions, respectively. \(u_n\) is the normal velocity component of the interface velocity \(\mathbf{u}_{\varphi }\), \(p_j^{\star }\) is the pressure on the cut faces satisfying the jump condition \(p_2^{\star }-p_1^{\star }=\sigma \kappa \) due to the surface tension coefficient \(\sigma \). The two-medium exact Riemann solver is applied to calculate \(\mathbf{u}_{\varphi }\) and \(p_j^{\star }\). Due to the Lagrangian movement of cut faces, there are not convective terms in the fluxes. We refer to [7] for more details.

3.5 Synchronization of the Solutions and Fluxes

There are solutions and fluxes on different levels of mesh and edge, so synchronization is needed on the solutions and fluxes at each time step, and it should be conservative.

Given \({{\mathbf U}}_{h,up}\) as the solution on the upper level of mesh, we transfer the solution to the lower level by \(L^2\) projection, namely, the solution on the lower level of mesh \({{\mathbf U}}_{h, low}\) satisfies

$$\begin{aligned} \langle {{\mathbf U}}_{h,low}|_{K}\,, {{\mathbf V}} \rangle _{L^2(K)}=\langle {{\mathbf U}}_{h,up}|_{K}\,, {{\mathbf V}} \rangle _{L^2(K)}=\sum _{m,n=0}^{1}\langle {{\mathbf U}}_{h,up}|_{K^{mn}}\,, {{\mathbf V}} \rangle _{L^2(K^{mn})}\,, \end{aligned}$$
(10)

where \(K^{mn}\) (\(m,n=0,1\)) are the four subcells of K on the upper level. And vice versa.

For the fluxes, we also use the \(L^2\) projection to transfer the fluxes from the edges of the upper level of mesh to those of the lower level of mesh, namely,

$$\begin{aligned} \langle \hat{{\mathbf F}} |_{e_K^i}\cdot {{\mathbf n}}_K^i \,, {{\mathbf V}} \rangle _{L^2(e_K^i)}=\sum _{m=0}^{1}\langle \hat{{{\mathbf F}}} |_{e_K^{i,m}}\cdot {{\mathbf n}}_K^{i,m} \,, {{\mathbf V}} \rangle _{L^2(e_K^{i,m})}, \end{aligned}$$
(11)

where \(e_K^{i,m}\) (\(m=0,1\)) are the two uniform sub-faces of \(e_K^i\) on the upper level, and \(\mathbf n_K^{i,m}\) is the outward unit normal vector of \(e_K^{i,m}\).

Fig. 4
figure 4

Illustration of cut cells with curved cut faces. Left for integral; right for limiter

Full size image

3.6 Integral on Cut Cell, Limiters

The accuracy of the integrals in Eq. (6), especially on cut cells, could affect the result of the algorithm. Hence, we must pay more attention to the integrals on cut cells. As shown in Fig. 4 (left), the curved line EFG is a cut face, which divides the cell ABCD into two cut cells AEFG and BCDGFE. In order to calculate the integral on BCDGFE, it is divided into five triangular subcells by connecting the cell center O with the five vertexes, then each subcell is transformed into a reference element \({\mathcal {E}}=\{{\mathbf {\xi }}=(\xi _1,\xi _2)| 0 \le \xi _1 \le 1, 0 \le \xi _2 \le 1, 0 \le \xi _1+\xi _2 \le 1 \}\) by using parameterizations, finally the Gaussian quadrature rule is applied on the reference element. For the integral on the cut cells AEFG, we also transform it into the reference element \({\mathcal {E}}\) and then apply the Gaussian quadrature rule.

When applied to problems containing discontinuous solution, the RKDG methods may produce oscillations. Nonlinear limiters are often applied to control these oscillations. Many limiters have been developed in the literature. In this paper, we use the corrected total variation bounded (TVB) minmod slope limiter [12] for the solution polynomials on regular elements. While for the solution polynomials on cut cells, the following limiter is applied.

As shown in Fig. 4 (right), consider the cut cell K, which has three neighbor cells \(K_1, K_2\) and \(K_3\) to the right side of the interface. Points \(C, C_1, C_2\) and \(C_3\) are the cell centers of \(K, K_1, K_2\) and \(K_3\), respectively. Suppose that the solution polynomial on K is \(u=u_{0,K} + u_{1,K} \phi _1(\mathbf {x}) + u_{2,K} \phi _2(\mathbf {x})\). Due to the orthogonality of the basis functions, \(u_{0,K}\) is the cell average of the solution u. Similarly, assume that the cell averages of the solutions on \(K_1, K_2, K_3\) are \(u_{0,K_1}, u_{0,K_2}\) and \(u_{0,K_3}\), respectively. Using the cell centers and the cell averages of the solutions on \(K_{1}\) and \(K_{2}\), we solve the following linear system with respect to \(u_{1}\) and \(u_{2}\):

$$\begin{aligned} \left\{ \begin{array}{ccc} u_{1} \phi _1({C_1}) + u_{2} \phi _2({C_1}) &{}=&{} u_{0,K_1} - u_{0,K}, \\ u_{1} \phi _1({C_2}) + u_{2} \phi _2({C_2}) &{}=&{} u_{0,K_2} - u_{0,K}. \end{array}\right. \end{aligned}$$
(12)

Denoting the solution of Eq. (12) by \(u_{1, 12}\) and \( u_{2, 12}\), then they are good approximations to the linear terms \(u_{1,K}\) and \(u_{2,K}\), respectively. Analogously, we could get \(u_{1, 23}\) and \( u_{2, 23}\) (\(u_{1, 31}\) and \( u_{2, 31}\)) by using the corresponding information from \(K_{2}\) and \( K_{3}\) (\(K_{3}\) and \( K_{1}\)). Then we respectively modify \(u_{1,K}\) and \(u_{2,K}\) by

$$\begin{aligned} \tilde{u}_{1,K}= & {} \bar{m}(u_{1,K}, u_{1, 12}, u_{1, 23}, u_{1, 31}),\end{aligned}$$
(13)
$$\begin{aligned} \tilde{u}_{2,K}= & {} \bar{m}(u_{2,K}, u_{2, 12}, u_{2, 23}, u_{2, 31}), \end{aligned}$$
(14)

where \(\bar{m}\) is the modified minmod function [9].

When applied to problems containing low density or temperature, the RKDG methods may produce nonphysical negative density or temperature. Therefore the positivity-preserving limiters defined on rectangles [47] and triangles [46] are applied when considering such problems.

3.7 Solution Procedure

The whole procedure of current method in advancing from time \(t_n\) to \(t_{n+1}\) can be summarized as follows:

  1. 1.

    Refine or coarsen AMR mesh if needed, synchronize solutions.

  2. 2.

    Reconstruct variable values on faces, apply TVB limiter and positivity-preserving limiter if needed.

  3. 3.

    Calculate the fluxes on all the faces at time \(t_n\). Synchronize fluxes. Get the interface velocity and the pressure on all cut faces.

  4. 4.

    Solve the LS equation to get the LS values at time \(t_{n+1}\). From the LS values, get cut points, cut faces and cut cells at time \(t_{n+1}\). Re-initialize the LS function if needed.

  5. 5.

    Advance solutions on regular cells and cut cells from \({{\mathbf U}}_{h}^{n}\) to \({{\mathbf U}}_{h}^{n+1}\).

4 Numerical Results

In this section, numerical experiments are presented to demonstrate the performance of the proposed method for various two-medium flows. In the first part, the accuracy and convergence of the proposed method are investigated by using three 1D shock-tube problems. In the second part, the order of accuracy is firstly presented for the advection of a smooth solution on a 2D grid, and then shock–bubble interaction problems and oscillation of a liquid cylinder in 2D space are tested to show the ability of treating complex free interfaces by the proposed method. The shock-rigid body interaction problems in two dimensional space and in three dimensional space (axisymmetric) are also tested, as the first step of applying RKDG with CC method to study the fluid-structure problems in the future work.

The total accumulation errors (TAE) on cut cells of density are also tested to evaluate the error near the interface. The total accumulation error is defined by

$$\begin{aligned} {TAE}=\frac{1}{|\varOmega |T}\sum _{K,i}\varepsilon _{K,i}|K|\Delta t_i, \end{aligned}$$
(15)

where

$$\begin{aligned} \varepsilon _{K,i}=\left\{ \begin{array}{lll} \rho _{h,K,i}-\rho _{K,i}, &{} &{} \text{ if } K \text{ is } \text{ a } \text{ cut } \text{ cell } \text{ at } \text{ time } \text{ level } i \\ 0, &{} &{} \text{ otherwise } \end{array}\right. \end{aligned}$$
(16)

where \(|\varOmega |\) and |K| denote the area of the computational domain \(\varOmega \) and the cell K, respectively, \(\Delta t_i\) is the i-th time step and \(T=\sum _i \Delta t_i\), \(\rho _{h,K,i}\) and \(\rho _{K,i}\) represent the numerical and exact solutions of density on cell K, respectively.

All simulations were performed with both \(P^1\) and \(P^2\) approximations. To save space, we only show \(P^2\) results here.

4.1 One-Dimensional Examples

4.1.1 Air–Helium Shock-Tube Problem

In this example, an air–helium shock-tube problem is considered. The interface is initially located at \(x_0=0\) m. The left is air and the right is helium. The initial conditions are given by [23, 24]

$$\begin{aligned} \left( \rho , u, p, T\right) =\left\{ \begin{array}{ll} (2.282\,\hbox {g}/\hbox {l}, 246.6\,\hbox {m}/\hbox {s}, 2.56\,\hbox {bar}, 390.4\,\hbox {K }) , &{} \texttt { if } x \le x_0, \\ (0.167\,\hbox {g}/\hbox {l}, 0\,\hbox {m}/\hbox {s}, 1.01\,\hbox {bar}, 293.15\,\hbox {K}) , &{}\texttt { if } x > x_0. \end{array} \right. \end{aligned}$$
(17)

The state parameters are \(\gamma =1.4\) and \(C_p=1004.85\) J/(kg K) for air, \(\gamma =1.63\) and \(C_p=5353.65\) J/(kg K) for helium, \(p_{\infty }=0\) for both gases.

The computational domain is taken as \([-5.0\,\hbox {m},5.0\,\hbox {m}]\) with mesh size \(0.01\,\hbox {m}\). This problem is calculated up to \(t=2.29\,\hbox {ms}\). The TVB minmod slope limiter [12] and the positivity-preserving limiter [47] are used in the numerical implementation. The numerical results from the proposed method are illustrated in Fig. 5. The exact solutions are also plotted in the same figure for comparison. It shows that the numerical solutions match well with the exact solutions, the material interface is tracked sharply, and the shock front is captured correctly by the proposed method.

Fig. 5
figure 5

The numerical and exact solutions for the air–helium shock-tube problem. Dots numerical solutions; solid line exact solutions

Full size image

4.1.2 Air–SF6 Shock-Tube Problem

An air–SF6 shock-tube problem is tested in this section. The problem produces a two-shock propagation. The interface is initially located at \(x_0=0\,\hbox {m}\). The left is air and the right is SF6. The initial conditions are given by

$$\begin{aligned} \left( \rho , u, p, T\right) =\left\{ \begin{array}{ll} (1.59\,{\hbox {g}}/{\hbox {l}}, 104.89\,{\hbox {m}}/{\hbox {s}}, 1.51\,\hbox {bar}, 330.67\,\hbox {K} ) , &{} \texttt { if } x \le x_0, \\ (5.99\,{\hbox {g}}/{\hbox {l}}, 0\,{\hbox {m}}/{\hbox {s}}, 1.0\,\hbox {bar}, 293.15\,\hbox {K} ) , &{}\texttt { if } x > x_0. \end{array} \right. \end{aligned}$$
(18)

The state parameters are \(\gamma =1.4\) and \(C_p=1004.85\,\hbox {J}/(\hbox {kg} \cdot \hbox {K})\) for air, \(\gamma =1.093\) and \(C_p=669.48\,\hbox {J}/(\hbox {kg} \cdot \hbox {K})\) for SF6, \(p_{\infty }=0\) for both gases.

The computational domain is taken as \([-5.0\,\hbox {m},5.0\,\hbox {m}]\) with mesh size \(0.01\,\hbox {m}\). We compute this problem up to \(t=8.0\,\hbox {ms}\). The TVB minmod slope limiter [12] is used in the numerical implementation. The numerical results from the proposed method are illustrated in Fig. 6, which are in agreement with the exact solutions. It also shows that the material interface and the shock fronts are captured correctly by the proposed method.

Fig. 6
figure 6

The numerical and exact solutions for the air–SF6 shock-tube problem. Dots numerical solutions; solid line exact solutions

Full size image

4.1.3 Water–Air Shock-Tube Problem

In this section, an water–air shock-tube problem is tested. The interface is initially located at \(x_0=0\,\hbox {m}\). The left is water and the right is air. The initial conditions are given by

$$\begin{aligned} \left( \rho , u, p, T\right) =\left\{ \begin{array}{ll} (1499.77\,{\hbox {g}}/{\hbox {l}}, 181.52\,{\hbox {m}}/{\hbox {s}}, 10^6\,\hbox {Pa}, 195.34\,\hbox {K}) , &{} \texttt { if } x \le x_0, \\ (1.224\,{\hbox {g}}/{\hbox {l}}, 0\,{\hbox {m}}/{\hbox {s}}, 10^5\,\hbox {Pa}, 279.99\,\hbox {K}) , &{}\texttt { if } x > x_0. \end{array} \right. \end{aligned}$$
(19)

The state parameters are \(\gamma =1.4\), \(p_{\infty }=0\) and \(C_p=1004.85\,\hbox {J}/(\hbox {kg} \cdot \hbox {K})\) for air, \(\gamma =2.788103\), \(C_p=4190\,\hbox {J}/(\hbox {kg} \cdot \hbox {K})\) and \(p_{\infty }=7.862511 \times 10^8\) for water.

The computational domain is taken as \([-5.0\,\hbox {m},5.0\,\hbox {m}]\) with mesh size \(0.01\,\hbox {m}\). We compute this problem up to \(t=2.0 ms\). The TVB minmod slope limiter [12] and the positivity-preserving limiter [47] are used in the numerical implementation. Figure 7 shows the numerical results from the proposed method and the exact solutions. It also can be seed from the figure that the material interface is tracked sharply, and the shock front is captured correctly by the proposed method.

Fig. 7
figure 7

The numerical and exact solutions for the air–water shock-tube problem. Dots numerical solutions; solid line exact solutions

Full size image

4.2 Two-Dimensional Examples

4.2.1 Accuracy Test

In order to test the order of accuracy of the proposed method for two dimensional problems, we consider a problem in domain \([-1m,1m]\times [-1m,1m]\) with a smooth solution. The initial condition is

$$\begin{aligned} \left( \rho , u, v, p\right) =\left\{ \begin{array}{cccccccc} ( 1+0.1\sin (\pi (x+y))\,{\hbox {g}}/{\hbox {l}}, 1\,{\hbox {m}}/{\hbox {s}}, 1\,{\hbox {m}}/{\hbox {s}}, 1\,\hbox {bar} ) , &{} \texttt { if } r \le 0.4, \\ ( 1+0.1\sin (\pi (x+y))\,{\hbox {g}}/{\hbox {l}}, 1\,{\hbox {m}}/{\hbox {s}}, 1\,{\hbox {m}}/{\hbox {s}}, 1\,\hbox {bar}) , &{}\texttt { if } r > 0.4, \end{array} \right. \end{aligned}$$
(20)

where \(r=\sqrt{x^2+y^2}\). \(r=0.4\) is an artificial interface. In the computation, \(\gamma =1.6\), \(p_{\infty }=0\,\hbox {Pa}\), the periodic boundary condition is used, this problem is computed up to \(t=0.01s\). This problem has exact solution

$$\begin{aligned} \left( \rho , u, v, p\right) =(1+0.1\sin (\pi (x+y-2t)) \hbox {g/l}, 1\,\hbox {m/s}, 1\,\hbox {m/s}, 1\,\hbox {bar}). \end{aligned}$$
(21)

We show the total accumulation error of density in Table 2. It shows that the average order of accuracy of calculations on cut cells is 1.86, very close to 2.

Table 2 The total accumulation error of the density for accuracy test
Full size table

Removing the free interface, the calculation is in one smooth phase, then the \(L^2\) error of density is shown in Table 3. The average order of accuracy is 2.83, very close to 3, showing the effective 3rd order accuracy of this \(P^2\) DG calculation.

Table 3 The \(L^2\) error of the density for accuracy test
Full size table

4.2.2 Air Shock–Helium Bubble Interaction

In this example, we consider a weak shock (shock Mach number Ms \(=\) 1.22) impacting on a helium bubble in air. The geometry for this problem is shown in Fig. 8. Due to the symmetry of the problem, we choose the upper half of the flow field (ABCD in Fig. 8) as the computational domain. The center of the helium bubble is initially located at (0 mm,0 mm). Initial conditions are same as those in [44], given by

$$\begin{aligned} (\rho , u, v, p) =\left\{ \begin{array}{lcl} ( 1.686\,{\hbox {g}}/{\hbox {l}}, -113.524\,{\hbox {m}}/{\hbox {s}}, 0\,{\hbox {m}}/{\hbox {s}}, 159060\,\hbox {Pa}) , x> 30 \text{ mm }, \\ ( 1.225\,{\hbox {g}}/{\hbox {l}}, 0\,{\hbox {m}}/{\hbox {s}}, 0\,{\hbox {m}}/{\hbox {s}}, 101325\,\hbox {Pa}) , x < 30 \text{ mm }, r > 25 \text{ mm }, \\ ( 0.2228\,{\hbox {g}}/{\hbox {l}}, 0\,{\hbox {m}}/{\hbox {s}}, 0\,{\hbox {m}}/{\hbox {s}}, 101325\,\hbox {Pa}) , r \le 25 \text{ mm }. \end{array} \right. \end{aligned}$$

with \(r=\sqrt{x^2+y^2}\). The state parameters are \(\gamma =1.4\) and \(C_p=1004.85\,\hbox {J}/(\hbox {kg} \cdot \hbox {K})\) for air, and \(\gamma =1.648\) and \(C_p=5193.2\,\hbox {J}/(\hbox {kg} \cdot \hbox {K})\) for helium, \(p_{\infty }=0\) for both gases. The boundary conditions are inviscid on the upper boundary (CD) and symmetric on the lower boundary (AB), outflow on the left boundary (AD) and inflow on the right boundary (BC).

Fig. 8
figure 8

The geometry for a weak shock impacting on a helium bubble in air

Full size image

Numerical and experimental investigations of this problem have been carried out in [21, 25, 35, 36, 44]. In this problem, the incident shock refracts at the bubble surface, and is partly transmitted inside the helium bubble and partly reflected from the bubble surface and back into the air. Due to the higher sound speed in the helium bubble than that in the surrounding air, the refracted shock inside the bubble is well ahead of the incident shock. When the refracted shock inside the bubble interacts with the rear interface of the bubble and transmits into the air, the incident shock just passes over the top of the bubble.

We use four layer meshes with \( 200\times 10\) mesh cells on the base mesh, so that in the top mesh there is 160 mesh cells in the full vertical 89mm domain, same as that in [44]. The TVB minmod slope limiter [12] and the limiter on cut cells are used in the numerical implementation. The numerical density contours at \(t=102, 245, 427, 647\,\upmu \hbox {s}\) are shown in Fig. 9, comparing with the experimental results in [21] and the numerical results from [36] and [44]. The time \(t=0\,\upmu \hbox {s}\) here is defined at the moment when the shock hits the right interface of the helium bubble. Current method and the front tracking method in [44] are both sharp interface methods, give clearer interfaces than the diffuse interface method used in [36]. Our simulated bubble shapes look more consistent with the experimental ones than those in [44], especially at the \(647\,\upmu \hbox {s}\).

Fig. 9
figure 9

Comparison between the numerical density contours (right column) with the experimental shadowgraphs [21] (left column), [36] (second column) , [44] (third column) at \(t=102, 245, 427, 647\,\upmu \hbox {s}\), from top to bottom, for a Ms = 1.22 shock impacting on a helium bubble in air

Full size image

4.2.3 Water Shock–Air Bubble Interaction

This case concerns a strong water shock impacting on an air bubble in water. The geometry and the initial conditions for this problem are shown in Fig. 10. All the parameters are made non-dimensional for this example. The computational domain is taken as \([-3,3]\times [-3,3]\) The boundary conditions are inflow on the left boundary and outflow on other boundaries.

Fig. 10
figure 10

The geometry for a strong shock impacting on an air bubble in water

Full size image

This problem has been investigated in [20, 27, 31, 35, 45]. In order to capture the complex physics occurring in this problem, we use four layer meshes with \( 60\times 60\) cells on the base mesh. The three types of limiters presented in Sect. 3.6 are used in the numerical implementation. The numerical density, pressure and velocity (u) contours \(t=0.05, 0.18, 0.31\) and 0.47 are plotted in Fig. 11. It can be observed from these plots that the incident shock refracts at the bubble surface at early time (\(t=0.05\)), a reflected rarefaction wave is formed in the water. As the incident shock proceeds, the incident shock passes over the top of the bubble (\(t=0.18\)). With the interaction between the incident shock and the gas bubble, the bubble interface continues to deform, more and more of the reflected rarefaction fan spread (\(t =0.31\)), and the incident shock passes over the whole bubble. Finally, the rarefaction wave overtakes the incident shock (\(t =0.47\)). During the whole process, the bubble is compressed to be smaller and smaller, we show the time history of the bubble shape in Fig. 12. In this problem, there is a transmitted shock inside the gas bubble, which can be observed from the density and velocity contour plots shown in Fig. 11. It can be seen from Fig. 11 that there is no oscillation at the interface compared to the results reported in [45].

In addition, we investigate the computational cost of the key algorithms (AMR, LS\(+\)CC, DG and Limiters). The result is listed in Table 4, in which “LS\(+\)CC” means the LS solver and the Cut Cell method, and “Limiters” means the three limiters presented in Sect. 3.6. It can be seen from this table that the DG solver for Euler equations takes half of the whole computing time, while the AMR only takes a little time (\(0.88\%\)).

Fig. 11
figure 11

Density, pressure and velocity (u) contours at \(t=0.05, 0.18, 0.31\) and 0.47 for a strong shock impacting on an air bubble in water. Left column density; middle column pressure; right column velocity (u)

Full size image
Fig. 12
figure 12

Evolution of the bubble shape for a strong shock impacting on an air bubble in water

Full size image

4.2.4 Detached Shock on a Rigid Stationary Cylinder or Sphere

In supersonic flow the reflection from a rigid stationary body stabilizes into a stationary solution. A bow shock whose distance (denoted by \(\delta \)) from the rigid body decreases as the flow Mach number increases.

By regarding the solid body as a special phase, the interface can again be described by curved cut faces. Applying inviscid boundary condition on the cut faces, and ignore the calculation inside the solid body, this proposed method can be applied to deal with the fluid-rigid body interaction problems.

In the computations, we consider a cylindrical rigid body and a spherical rigid body located at the origin. The diameter of the rigid body is taken as \(D=1\,\hbox {m}\). For the cylindrical rigid body, the computational domain is taken as \([-8\,\hbox {m}, 8\,\hbox {m}]\times [-6\,\hbox {m}, 6\,\hbox {m}]\). We use three layer meshes with \(80\times 60\) mesh cells on the base mesh. The boundary conditions are inflow on the left boundary and outflow on other boundaries. We solve Eq. (1) for this case. For the spherical rigid body, the computational domain is taken as \([-8\,\hbox {m}, 8\,\hbox {m}]\times [0\,\hbox {m}, 6\,\hbox {m}]\). We use three layer meshes with \(80\times 30\) mesh cells on the base mesh. The boundary conditions are inflow on the left boundary, symmetric on the lower boundary and outflow on other boundaries. We solve Eq. (3) for this case. The three types of limiters presented in Sect. 3.6 are used in the numerical implementation.

Different incident flows with Mach number between 1.3 and 2.8 are tested. Figure 13 shows a pressure contours of a stationary solution formed by an incident flow with Mach number 2.2 (left) and the relationship between the detached distance \(\delta /D\) and the Mach number of the incident flow (right). Current simulation results match well with the experimental data and the previous numerical results in [7].

4.2.5 Surface Tension Driven Oscillations of an Inviscid Liquid Drop

In this work, the surface tension is applied in the similar way as in [7], in which the effect of surface tension is considered as a supplemental pressure and calculated together with regular pressure by the two-medium exact Riemann solver on the cut faces. In this way, it is treated sharply and does not have the time step limit when using the continuum surface force (CSF) model [5]. Here the oscillations of an inviscid liquid drop due to the surface tension is considered, to show the effect of this surface tension calculation in current method. The initial surface shape of the liquid drop is given by \(r=r_0+\epsilon \cos (n \theta )\), the theoretical frequency of the oscillation is [16]

$$\begin{aligned} \omega _n=\sqrt{\frac{(n^3-n)\sigma }{(\rho _d+\rho _e)r_0^3}}, \end{aligned}$$
(22)

where \(\epsilon \) is the disturbance, n is the mode of the drop, \(\sigma \) is the surface tension coefficient, \(\rho _d\) and \(\rho _e\) are the densities of the drop and external fluid, respectively. Then the period of oscillation is \(t_c=2\pi /\omega _n\). This problem has been studied in [7, 16, 43].

Table 4 The computing times of the key algorithms (unit: seconds)
Full size table
Fig. 13
figure 13

Detached shock on a cylinder or sphere. Left example pressure contours of a stationary solution formed by a shock-cylinder interaction; right detached distance \(\delta /D\) versus Mach number of the incident flow

Full size image

In the test simulations, \(n=2\), \(\epsilon =0.1\), \(\rho _d=100\,{\hbox {g}}/{\hbox {l}}\) and \(\rho _e=1\,{\hbox {g}}/{\hbox {l}}\) are fixed, \(\sigma \) and \(r_0\) are varied to vary the periods of oscillations. The three types of limiters presented in Sect. 3.6 are used in the numerical implementation. The comparison between the simulation results and the theoretical results is shown in Table 5. It shows that the proposed adaptive RKDG method with cut cell, together with the surface tension calculation, is very accurate, even to very low speed problems with very strong surface tensions. Two typical evolution curves of the total kinetic energy are shown in Fig. 14.

Table 5 Summary of the computational runs for the oscillations of an inviscid liquid drop due to surface tension
Full size table
Fig. 14
figure 14

Evolution of the total kinetic energy of freely oscillating drops under the influence of surface tension (Cases 4 and 4a)

Full size image

5 Conclusions

In this paper, a conservative, consistent, sharp-interface adaptive Runge–Kutta discontinuous Galerkin method with cut cell method is developed for the simulation of the compressible inviscid two-medium flows. Two-dimensional and axisymmetric calculations are realized. Curved cut face is applied to get higher accuracy in the calculation around the interface. High order, conservative synchronization method on the AMR is realized in the DG framework. Positivity-preserving limiter is applied to avoid possible nonphysical negative density and temperature in the numerical calculations. Surface tension is considered in a sharp interface way, so that it can deal with very strong surface tension without the limit on time step. Numerical results for gas–gas, gas–liquid and gas–solid (stationary rigid body) flows demonstrate that the combination of the adaptive Runge–Kutta discontinuous Galerkin method and the cut cell method works well. In the future work, we shall extend the method to compressible viscous two-medium flows and fluid-structure interactions. The compactness of DG method helps to reduce the problems from big stencil in high order finite volume calculation, and will also be helpful in the future parallelization. Combining RKDG and cut cell method also makes it possible to develop higher order methods for compressible multi-phase flows.