1 Introduction

In this paper, we apply local discontinuous Galerkin (LDG) method on overlapping meshes [15] for the following linear parabolic equations in one space dimension:

$$\begin{aligned} \begin{aligned} u_t-u_{xx}&=0,\quad x\in [0,2\pi ],\,\,t>0,\\ u(x,0)&=u_0(x),\quad x\in [0,2\pi ], \end{aligned} \end{aligned}$$
(1.1)

subject to periodic boundary conditions.

The discontinuous Galerkin (DG) methods are a class of finite element methods with completely discontinuous piecewise polynomials as the numerical approximations. The DG method was first introduced in the framework of neutron linear transportation by Reed and Hill [25] in 1973. Subsequently, the Runge–Kutta discontinuous Galerkin (RKDG) methods were proposed for hyperbolic conservation laws in a series of papers [7,8,9,10]. Later, in [11], Cockburn and Shu introduced the LDG method to solve the convection–diffusion equations. Their idea was motivated by Bassi and Rebay [1], where the compressible Navier–Stokes equations were successfully solved. In [11], the authors introduced an auxiliary variable q to represent the derivative of the primary variable u and thus rewrite (1.1) into the following system of first order equations

$$\begin{aligned} \begin{aligned} u_t-q_x&=0,\\ q-u_x&=0. \end{aligned} \end{aligned}$$
(1.2)

Then one can solve u and q on the same mesh [11].

The LDG method is one of the most important numerical methods for convection–diffusion equations. However, for some special convection–diffusion systems, such as chemotaxis model [21, 24] and miscible displacements in porous media [12, 13], the LDG methods are not easy to construct and analyze. In each of the two models, the convection term is the product of one of the primary variables and the derivative of the other primary variable. Most of the well established numerical fluxes for the convection terms, such as the upwind fluxes, cannot be applied, since the coefficients of the convection terms turn out to be discontinuous after the spatial discretization. It is well known that hyperbolic equations with discontinuous coefficients are in general not well-posed [16, 20]. Therefore, the DG schemes may not be stable when applied to those model equations. Within the DG framework, there are three main different ways to bridge this gap. Firstly, in [18, 22, 31] the authors combined the convection terms and diffusion terms together and obtain the optimal error estimates. The idea was motivated by Wang et al. [26,27,28], where \(u_x\) and the jump of u across the cell interfaces were proved to be bounded by q. Moreover, to make the numerical solutions to be physically relevant, we have to add a very large penalty which depends on the numerical approximations of the derivatives of the primary variables [5, 19, 22, 29]. The second approach is to apply the flux-free numerical methods such as the Central DG (CDG) methods [23]. However, for CDG methods, we have to solve each equation in (1.2) on both the primary and dual meshes, which may double the computational cost. The last idea is to apply the Staggered DG (SDG) methods [6]. However, the method requires some continuity of the numerical approximations, and hence it is not easy to apply limiters to the numerical solutions. Recently, one of the authors in this paper introduced a new LDG method in [15], where we solve u and q on the primitive and dual meshes, respectively. To construct the dual mesh, we perturb the midpoint in each cell of the primary mesh, and use them as the cell interfaces of the dual mesh. We denote \(\alpha \in [-\,1/2,1/2]\) as the perturbation constance, see [15] for more details. The stability and suboptimal error estimates of the new LDG scheme were also given in [15]. Since q is continuous across the cell interfaces in the primitive mesh, we can apply the upwind fluxes for the convection term for the complicated systems discussed above. Moreover, with the new idea, it is possible to construct third-order maximum-principle-preserving LDG methods on the overlapping meshes [14]. However, if the dual mesh is generated by the midpoint in each cell of the primitive mesh and piecewise odd order polynomials are applied, then the new method may not yield optimal convergence rates when applied to the pure linear parabolic equations [15]. This is the main reason why in the SDG method, the numerical approximations are required to be continuous across some of the cell interfaces. Several alternatives to gain the optimal convergence rates were also introduced in [15].

Unfortunately, it is still unclear why the accuracy given in [15] is not optimal. To solve this problem, we would like to apply Fourier analysis to quantitatively analyze the error between the numerical and exact solutions. In [33], the authors applied Fourier analysis to show the conditions of instability of some DG schemes for linear parabolic equations with periodic boundary conditions on uniform meshes. Later, this idea was extended to investigate the superconvergence of the DG scheme for linear hyperbolic equations in [34] and direct DG methods for parabolic equations in [32]. Motivated by the works given above, we take the initial condition as \(u_0(x)=e^{i\omega x}\) and rewrite the LDG scheme on overlapping meshes into an equivalent finite difference scheme. For simplicity, we only consider \(P^1\) and \(P^2\) polynomials, and the extension to high-order polynomials, though quite complicated, can be obtained following the same lines. We will write out the amplification matrix and explore the eigenvalues and eigenvectors. For \(P^1\) case, we anticipate two eigenvalues and only one of them should be physically relevant. We find that if \(\alpha =0\), the nonphysical eigenvalue does not decay during mesh refinement, and the scheme will generate a spurious wave that degenerate the accuracy of the scheme. However, if \(\alpha \ne 0\), the nonphysical eigenvalue will decay exponentially fast during mesh refinement. Hence the nonphysical wave does not contribute much toward the numerical approximations, and keeps the accuracy. For the \(P^2\) case, no matter which \(\alpha \) we choose, both of the two nonphysical eigenvalues decay exponential fast during mesh refinement. Finally, by using Taylor’s expansion, we can find out the leading term between the exact and numerical approximations, which gives us the order of accuracy of the scheme.

Moreover, with the quantitative error estimate, we can find some superconvergence points. Superconvergence of DG methods have been studied intensively for parabolic equations, see [2,3,4, 30] as an incomplete list. Different from the previous works, we have no idea about the position of the superconvergence points. For simplicity, we take \(k=1\) as an example. We choose two points in each cell to be determined, denoted as a and b, as the superconvergence points. Then we apply the Fourier analysis and write out the error between the numerical and exact solutions at the two points. The leading terms of the errors should be functions of \(\alpha \), a and b. By setting the them to be zero, we can find the relationship among \(\alpha \), a and b. Hence, for fixed \(\alpha \), we can solve for a and b as the superconvergence points.

The rest of the paper is organized as follows. We first discuss the LDG scheme for one dimensional heat equation on overlapping mesh in Sect. 2. In Sect. 3, we demonstrate the quantitative error estimate using Fourier analysis for piecewise \(P^k\) polynomials with \(k=1,2\). The superconvergence of the solution will be given in Sect. 4. In Sect. 5, some numerical experiments will be demonstrated to verify the theoretical results. We will end in Sect. 6 with concluding remarks.

2 LDG Method on Overlapping Meshes

In this section, we present the formulation of the LDG method on overlapping meshes and study the linear parabolic equation (1.2).

2.1 Overlapping Meshes

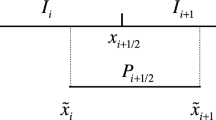
Different from the LDG method introduced in [11] where u and q are solved on the same mesh, our new method solves (1.2) on two meshes, as shown in Fig. 1.

Fig. 1
figure 1

Overlapping meshes

Full size image

Let

$$\begin{aligned} 0=x_{\frac{1}{2}}<x_{\frac{3}{2}}<\cdots <x_{N+\frac{1}{2}}=2\pi \end{aligned}$$

be a uniform partition of the domain \([0,2\pi ]\) with mesh size \(h=\displaystyle \frac{2\pi }{N}\). We denote

$$\begin{aligned} I_j=\left[ x_{j-\frac{1}{2}},x_{j+\frac{1}{2}}\right] \quad \text {and}\quad x_j=\frac{1}{2}\left( x_{j+\frac{1}{2}}+x_{j-\frac{1}{2}}\right) ,\quad j=1,\ldots ,N, \end{aligned}$$

as the cells and cell centers of the primitive mesh, respectively.

Based on the primitive mesh, we move each cell center within the corresponding cell to obtain the dual mesh, which is used to solve the auxiliary variable q. Then the cell interfaces of the dual mesh are given as

$$\begin{aligned} x_j^\alpha =x_j+\alpha h,\,\,\, j=1,\ldots ,N, \end{aligned}$$
(2.1)

where \(-\frac{1}{2}\le \alpha \le \frac{1}{2}\) is the perturbation constant of the midpoint in the primitive mesh. In this paper, we assume \(\alpha \) to be a constant independent of the cells. Actually, the dual mesh contains all the cell \(J_j=[x^\alpha _{j},x^\alpha _{j+1}]\), where we define \(x^\alpha _{N+1}=x^\alpha _{1}+2\pi \) due to the periodic boundary condition. For simplicity, we define \(J_0=J_N=[0,x^\alpha _{1}]\cup [x^\alpha _{N},2\pi ]\).

2.2 LDG Scheme

In this subsection, we proceed to construct the LDG method on the overlapping meshes given above.

The finite element spaces are

$$\begin{aligned} V^k_h&=\left\{ v\,:v|_{I_j}\in P^k(I_j),\,j=1,\ldots ,N\right\} ,\\ W^k_h&=\left\{ v\,:v|_{J_j}\in P^k(J_j),\,j=1,\ldots ,N\right\} , \end{aligned}$$

where \(P^k(I_j)\) and \(P^k(J_j)\) denote the set of polynomials of degree up to k on \(I_j\) and \(J_j\), respectively. It is easy to see that the elements in \(V^k_h\) and \(W^k_h\) are continuous across the cell interfaces on the dual and primitive meshes, respectively. Therefore, it may not be necessary to introduce the numerical fluxes in the LDG scheme. For simplicity, we also use u and q as the numerical approximations. Then the LDG scheme on overlapping meshes is to find \(u\in V^k_h\) and \(q\in W^k_h\) such that for any \(v\in V^k_h\) and \(w\in W^k_h\) we have

$$\begin{aligned} \int _{I_j}u_tvdx&=-\int _{I_j}qv_xdx+q_{j+\frac{1}{2}}v^-_{j+\frac{1}{2}} -q_{j-\frac{1}{2}}v^+_{j-\frac{1}{2}}, \end{aligned}$$
(2.2)
$$\begin{aligned} \int _{J_j}qwdx&=-\int _{J_j}uw_xdx+u^\alpha _{j+1}(w^\alpha _{j+1})^{-} -u^{\alpha }_{j}(w^\alpha _{j})^{+}, \end{aligned}$$
(2.3)

where \(q_{j+\frac{1}{2}}=q(x_{j+\frac{1}{2}})\), \(u^\alpha _{j+1}=u(x^\alpha _{j+1})\), \(v^-_{j-\frac{1}{2}}=v^-(x_{j-\frac{1}{2}})\) and \((w^\alpha _{j})^-=w^-(x^\alpha _{j})\). Likewise for \(v^+_{j-\frac{1}{2}}\) and \((w^\alpha _{j})^+\). If \(\alpha =\pm \frac{1}{2}\), the dual mesh agrees with the primitive mesh and the LDG methods turn out to be the traditional LDG methods with alternating fluxes discussed in [11]. For example, when \(\alpha =\frac{1}{2}\), the numerical fluxes in the traditional LDG methods in [11] should be given as \({\hat{q}}_{j+\frac{1}{2}}=q^+_{j+\frac{1}{2}}\) and \({\hat{u}}_{j+\frac{1}{2}}=u^-_{j+\frac{1}{2}}\). However, to code up the two special cases, we can simply take \(\alpha =\pm \frac{1}{2}\) and this is exactly the code for the traditional LDG methods given in [11].

To implement the schemes (2.2) and (2.3), we define \(\phi ^\ell _j(x)\) and \(\varphi ^\ell _j(x)\), \(\ell =0,1,\ldots ,k\), as the local bases of \(P^k(I_j)\) and \(P^k(J_j)\), respectively. Then we can represent the numerical solution as

$$\begin{aligned} u(x)&=\sum _{\ell =0}^{k}u_j^\ell \phi ^\ell _j(x),\,\,\,\,x\in I_j, \end{aligned}$$
(2.4)
$$\begin{aligned} q(x)&=\sum _{\ell =0}^{k}q_j^\ell \varphi ^\ell _j(x),\,\,\,\,x\in J_j. \end{aligned}$$
(2.5)

Substitute (2.4) and (2.5) into (2.2) and (2.3) to obtain

$$\begin{aligned} \frac{d\mathbf{u }_j}{dt}=\frac{1}{h^{2}} \left( A\mathbf{u }_{j-1}+B\mathbf{u }_{j}+C\mathbf{u }_{j+1}\right) , \end{aligned}$$
(2.6)

where \(\mathbf{u }_j=\left( u_j^0,\ldots ,u_j^{k}\right) ^T\), and A, B, C are \((k+1)\times (k+1)\) constant matrices.

Following [34], we define

$$\begin{aligned} x_{j+\frac{2\ell -k}{2(k+1)}}&=x_j +\left( \frac{2\ell -k}{2(k+1)}\right) h,\,\,\,\,\ell =0,\ldots ,k,\\ x^\alpha _{j+\frac{2\ell +1}{2(k+1)}}&=x^\alpha _j +\left( \frac{2\ell +1}{2(k+1)}\right) h,\,\,\,\,\ell =0,\ldots ,k, \end{aligned}$$

as the grid points in cell \(I_j\) and \(J_j\), respectively. Then we can construct Lagrange interpolation polynomials at the grid points as the local bases of \(P^k(I_j)\), and \(P^k(J_j)\). With the Lagrange bases, \(\mathbf{u }_j=\left( u_j^0,\ldots ,u_j^{k}\right) ^T\) turns out to be the point values of the numerical approximations at the grid points in cell \(I_j\). Hence, we rewrite the LDG scheme into a finite difference scheme.

Remark 2.1

To apply Fourier analysis, it is not necessary to choose globally uniformly distributed grid points as we treat the point values at the grid points in each cell as a vector. Therefore, we only need to construct uniform cells. We will choose other grid points to find out the superconvergence points in Sect. 4.

3 Error Analysis

In this section, we proceed to analyze the error between the numerical and exact solutions at the grid points given in Sect. 2. Numerical experiments in [15] demonstrated that, the accuracy may not be optimal only if odd order polynomials were applied. Therefore, we only analyze the LDG scheme with piecewise \(P^1\) and \(P^2\) polynomials in this section to find out the reason of accuracy degeneration.

3.1 The \(P^1\) Case

In this subsection, we present the details of error analysis for the piecewise linear case i.e. \(k=1\). The local basis functions on cell \(I_j\) are \(\phi _{j-\frac{1}{4}}(x)\), \(\phi _{j+\frac{1}{4}}(x)\), which are Lagrange polynomials based on \(x_{j-\frac{1}{4}}\), \(x_{j+\frac{1}{4}}\). Also, the local basis functions on cell \(J_j\) are \(\varphi _{j+\frac{1}{4}}(x)\), \(\varphi _{j+\frac{3}{4}}(x)\), which are Lagrange polynomials based on \(x^\alpha _{j+\frac{1}{4}}\), \(x^\alpha _{j+\frac{3}{4}}\). Then the solutions can be written as

$$\begin{aligned} u(x)&=u_{j-\frac{1}{4}}\phi _{j-\frac{1}{4}}(x) +u_{j+\frac{1}{4}}\phi _{j+\frac{1}{4}}(x),\,\,\,\, x\in I_j,\\ q(x)&=q^\alpha _{j+\frac{1}{4}}\varphi _{j+\frac{1}{4}}(x) +q^{\alpha }_{j+\frac{3}{4}}\varphi _{j+\frac{3}{4}}(x),\,\,\,\, x\in J_j. \end{aligned}$$

For \(j=1,\cdots ,N\), the finite difference representation of the LDG scheme (2.3) is

$$\begin{aligned} \begin{pmatrix} q^\alpha _{j+\frac{1}{4}}\\ q^\alpha _{j+\frac{3}{4}} \end{pmatrix}= \frac{1}{4h}\left[ Q_1\begin{pmatrix} u_{j-\frac{1}{4}}\\ u_{j+\frac{1}{4}} \end{pmatrix} +Q_2\begin{pmatrix} u_{j+\frac{3}{4}}\\ u_{j+\frac{5}{4}} \end{pmatrix}\right] , \end{aligned}$$

where

$$\begin{aligned}&Q_1=\begin{pmatrix} -\,5+14\alpha +12\alpha ^2&{}\quad 1-26\alpha -12\alpha ^2\\ 1+2\alpha -12\alpha ^2&{}\quad -5+10\alpha +12\alpha ^2 \end{pmatrix},\\&Q_2=\begin{pmatrix} 5+10\alpha -12\alpha ^2&{}\quad -1+2\alpha +12\alpha ^2\\ -\,1-26\alpha +12\alpha ^2&{}\quad 5+14\alpha -12\alpha ^2 \end{pmatrix}. \end{aligned}$$

Moreover, the finite difference representation of the LDG scheme (2.2) can be written as

$$\begin{aligned} \begin{pmatrix} u'_{j-\frac{1}{4}}\\ u'_{j+\frac{1}{4}} \end{pmatrix}= \frac{1}{4h}\left[ U_1\begin{pmatrix} q^\alpha _{j-\frac{3}{4}}\\ q^\alpha _{j-\frac{1}{4}} \end{pmatrix} +U_2\begin{pmatrix} q^\alpha _{j+\frac{1}{4}}\\ q^\alpha _{j+\frac{3}{4}} \end{pmatrix}\right] , \end{aligned}$$

where

$$\begin{aligned}&U_1=\begin{pmatrix} -\,5-14\alpha +12\alpha ^2&{}\quad 1+26\alpha -12\alpha ^2\\ 1-2\alpha -12\alpha ^2&{}\quad -\,5-10\alpha +12\alpha ^2 \end{pmatrix},\\&U_2=\begin{pmatrix} 5-10\alpha -12\alpha ^2&{}\quad -1-2\alpha +12\alpha ^2\\ -1+26\alpha +12\alpha ^2&{}\quad 5-14\alpha -12\alpha ^2 \end{pmatrix}. \end{aligned}$$

Here \(u'\) denotes the time derivative of u. After some simply algebra, we can obtain

$$\begin{aligned} \frac{d\mathbf{u }_j}{dt}=\frac{1}{h^2}\left( A\mathbf{u }_{j-1} +2B\mathbf{u }_{j}+C\mathbf{u }_{j+1}\right) , \end{aligned}$$
(3.1)

with

$$\begin{aligned} \begin{aligned} A&=\frac{1}{8}\begin{pmatrix} 13 + 14 \alpha - 144 \alpha ^2 - 168 \alpha ^3 + 144 \alpha ^4 &{} -5 - 2 \alpha + 384 \alpha ^2 + 24 \alpha ^3 - 144 \alpha ^4\\ -\,5 + 2 \alpha + 48 \alpha ^2 - 24 \alpha ^3 - 144 \alpha ^4 &{} 13 - 14 \alpha - 96 \alpha ^2 + 168 \alpha ^3 + 144 \alpha ^4 \end{pmatrix},\\ B&=\frac{1}{8}\begin{pmatrix} -13 - 14 \alpha - 168 \alpha ^2 + 168 \alpha ^3 - 144 \alpha ^4 &{} 5 + 2 \alpha + 72 \alpha ^2 - 24 \alpha ^3 + 144 \alpha ^4\\ 5 - 2 \alpha + 72 \alpha ^2 + 24 \alpha ^3 + 144 \alpha ^4 &{} -13 + 14 \alpha - 168 \alpha ^2 - 168 \alpha ^3 - 144 \alpha ^4 \end{pmatrix},\\ C&=\frac{1}{8}\begin{pmatrix} 13 + 14 \alpha - 96 \alpha ^2 - 168 \alpha ^3 + 144 \alpha ^4 &{} -5 - 2 \alpha + 48 \alpha ^2 + 24 \alpha ^3 - 144 \alpha ^4\\ -\,5 + 2 \alpha + 384 \alpha ^2 - 24 \alpha ^3 - 144 \alpha ^4 &{} 13 - 14 \alpha - 144 \alpha ^2 + 168 \alpha ^3 + 144 \alpha ^4 \end{pmatrix}. \end{aligned}\nonumber \\ \end{aligned}$$
(3.2)

Next, we will use the standard Fourier analysis to solve (3.1). We consider a general Fourier mode and assume

$$\begin{aligned} \begin{pmatrix} u_{j-\frac{1}{4}}(t)\\ u_{j+\frac{1}{4}}(t) \end{pmatrix}=\begin{pmatrix} {\hat{u}}_{-\frac{1}{4}}(t)\\ {\hat{u}}_{+\frac{1}{4}}(t) \end{pmatrix}e^{i\omega x_j}. \end{aligned}$$

Substitute the above into (3.1), we get the following ODE system

$$\begin{aligned} \begin{pmatrix} {\hat{u}}'_{-\frac{1}{4}}(t)\\ {\hat{u}}'_{+\frac{1}{4}}(t) \end{pmatrix}=G\begin{pmatrix} {\hat{u}}_{-\frac{1}{4}}(t)\\ {\hat{u}}_{+\frac{1}{4}}(t) \end{pmatrix}, \end{aligned}$$

where the amplification matrix G is

$$\begin{aligned} G=\frac{1}{h^2}\left( Ae^{-i\xi }+2B+Ce^{i\xi }\right) ,\,\,\,\,\, \xi =\omega h, \end{aligned}$$
(3.3)

with the matrices A, B, C given in (3.2). For simplicity, we assume \(\omega =1\), then \(\xi =h\). The two eigenvalues of the amplification matrices are

$$\begin{aligned} \lambda _{1,2}\!=\!\frac{1}{8h^2}\left( 13 \!-\! 26 e^{i\xi } \!+\! 13 e^{2i\xi } \!+\! 144 \alpha ^4 (-1 \!+\! e^{i\xi })^2 \!-\! 24 \alpha ^2 (5 \!+\! 14 e^{i\xi } \!+\! 5 e^{2i\xi })\mp \sqrt{\beta }\right) , \end{aligned}$$
(3.4)

where

$$\begin{aligned} \begin{aligned} \beta&=25 (-1 + e^{i\xi })^4 + 20736 \alpha ^8 (-1 +e^{i\xi })^4 - 6912 \alpha ^6 (-1 + e^{i\xi })^2 (5 + 14e^{i\xi } + 5 e^{2i\xi })\\&\quad -\,48 \alpha ^2 (-1 + e^{i\xi })^2 (41 + 38 e^{i\xi } + 41 e^{2i\xi }) + 288 \alpha ^4 (55 + 260 e^{i\xi } + 522 e^{2i\xi } \\&\quad + 260 e^{3i\xi } + 55 e^{4i\xi }). \end{aligned} \end{aligned}$$
(3.5)

Moreover, the corresponding eigenvectors are

$$\begin{aligned} V_{1,2}=\begin{pmatrix} -\,14 \alpha (-1 + e^{i\xi })^2 + 168 \alpha ^3 (-1 + e^{i\xi })^2 - 24 \alpha ^2 (-1 + e^{2i\xi }) \pm \sqrt{\beta }\\ 5 (-1 + e^{i\xi })^2 - 2 \alpha (-1 + e^{i\xi })^2 + 24 \alpha ^3 (-1 + e^{i\xi })^2 + 144 \alpha ^4 (-1 + e^{i\xi })^2 \\ - 48 \alpha ^2 (1 + 3 e^{i\xi } + 8 e^{2i\xi }) \end{pmatrix}, \end{aligned}$$
(3.6)

with \(\beta \) given in (3.5). Then the general solution of the ODE system (3.1) is

$$\begin{aligned} \begin{pmatrix} {\hat{u}}_{-\frac{1}{4}}(t)\\ {\hat{u}}_{+\frac{1}{4}}(t) \end{pmatrix}=C_{11}e^{\lambda _1t}V_1+C_{12}e^{\lambda _2t}V_2, \end{aligned}$$
(3.7)

where the constants \(C_{11}\) and \(C_{12}\) are determined by the initial condition

$$\begin{aligned} \begin{pmatrix} {\hat{u}}_{-\frac{1}{4}}(0)\\ {\hat{u}}_{+\frac{1}{4}}(0) \end{pmatrix}=\begin{pmatrix} e^{-\frac{i\xi }{4}}\\ e^{\frac{i\xi }{4}} \end{pmatrix}. \end{aligned}$$

Therefore, we have the explicit solution of the LDG scheme with \(P^1\) polynomials. The quantitative error will arise when we compare the numerical approximations with the exact solutions U(x, t) at the grid points defined by

$$\begin{aligned} \begin{aligned} \left\| e_{-\frac{1}{4}}\right\| _\infty&=\max _{1\le j\le N}\vert U(x_{j-\frac{1}{4}},t) -{u}_{j-\frac{1}{4}}(t)\vert ,\\ \left\| e_{+\frac{1}{4}}\right\| _\infty&=\max _{1\le j\le N}\vert U(x_{j+\frac{1}{4}},t)-{u}_{j+\frac{1}{4}}(t)\vert . \end{aligned} \end{aligned}$$

However, it is not easy to write the analytical form the of errors. Therefore, we would like to apply Taylor’s expansion with respect to \(\xi \) at \(\xi =0\). Then two eigenvalues of the amplification matrix can be rewritten as

  1. 1.

    For \(\alpha =0\),

    $$\begin{aligned} \lambda _{1}&=-\,\frac{9}{4}+\frac{3}{16}\xi ^2-\frac{1}{160}\xi ^{4} +\frac{1}{8960}\xi ^6+O(\xi ^7)\\ \lambda _{2}&=-\,1+\frac{1}{12}\xi ^2-\frac{1}{360}\xi ^4+\frac{1}{20160}\xi ^6+O(\xi ^7). \end{aligned}$$
  2. 2.

    For \(\alpha \ne 0\),

    $$\begin{aligned} \lambda _{1}&=-\,\frac{9}{4}+30\alpha ^2-36\alpha ^4-\frac{144\alpha ^2}{\xi ^2} +\xi ^2\left( \frac{13}{48}-\frac{5\alpha ^2}{2}+3\alpha ^4\right) \\&\quad -\xi ^4\left( \frac{1}{360}+\frac{5}{6912\alpha ^2}-\frac{\alpha ^2}{16} +\frac{\alpha ^4}{10}\right) \\&\quad +\,\xi ^6\left( \frac{383}{483840}+\frac{25}{3981312\alpha ^4} -\frac{1}{13824\alpha ^2}-\frac{5\alpha ^2}{1008}+\frac{47\alpha ^4}{6720}\right) +O(\xi ^7),\\ \lambda _{2}&=-\,1-\xi ^4\left( \frac{1}{160}-\frac{5}{9612\alpha ^2} -\frac{\alpha ^2}{48}\right) \\&\quad -\,\xi ^6\left( \frac{61}{96768}+\frac{25}{3981312\alpha ^4} -\frac{1}{13824\alpha ^2}-\frac{\alpha ^2}{288}+\frac{\alpha ^4}{192}\right) +O(\xi ^7)). \end{aligned}$$

It is easy to see that \(\lambda _2\) is the physical eigenvalue, while \(\lambda _1\) is the nonphysical one. For \(\alpha \ne 0\), the fourth term in \(\lambda _1\) makes the first term in (3.7) decay exponentially fast. In the analysis, we only need to take \(\lambda _2\) into account and omit the contribution of \(\lambda _1\). However, for \(\alpha =0\), the contribution of \(\lambda _1\) is not negligible, leading to a nonphysical wave. With some basic computation, we have the quantitative error:

For \(\alpha =0\),

$$\begin{aligned} \begin{aligned} \left\| e_{+\frac{1}{4}}\right\| _\infty&=\frac{1}{4}e^{-t}(-1+e^{-\frac{5}{4}t)}\xi \\&\quad +\,\frac{e^{-3t}\left[ (-3 +16t^2-6e^{-\frac{5}{4}t}(-1 + 9 t)+3e^{-\frac{5}{2}t})(-1 + 18 t)\right] }{1152(-1+e^{-\frac{5}{4}t})}\xi ^3+O(\xi ^4). \end{aligned} \end{aligned}$$
(3.8)

For \(\alpha \ne 0\),

$$\begin{aligned} \begin{aligned} \left\| e_{+\frac{1}{4}}\right\| _\infty =&\frac{(-1 + 12 \alpha ^2) e^{-t}}{9\alpha }\xi ^2\\&\quad +\,\Big [75 - 940 \alpha ^2 - 4080 \alpha ^4 + 72000 \alpha ^6 - 103680 \alpha ^8 - 138240 \alpha ^7 (-1 + t) \\&\quad +\, 80 \alpha (-1 + 5 t) \,\,\,+ 2304 \alpha ^5 (-15 + 23 t) - 192 \alpha ^3 (-15 + 43 t)\Big ]\\&\quad \times \frac{(-1 + 12 \alpha ^2) e^{-t}}{552960\alpha (\alpha - 12 \alpha ^3)^2}\xi ^4+O(\xi ^5). \end{aligned} \end{aligned}$$
(3.9)

The error \(\Vert e_{-\frac{1}{4}}\Vert _\infty \) is similar, so we omit it here. From the error, we can see that for \(\alpha =0\) the error is indeed first order accurate, while it is second order accurate for \(\alpha \ne 0\).

Remark 3.1

In this subsection, we only consider the case for \(\omega =1\). The analysis for general \(\omega \) can be performed following the same lines and the results are basically the same, so we omitted the details for simplicity.

3.2 The \(P^2\) Case

In this subsection, we will use the same approach given in Sect. 3.1 to demonstrate the error analysis for the \(P^2\) case. Denote the local basis functions for cell \(I_j\) as \(\phi _{j-\frac{1}{3}}(x), \phi _{j}(x), \phi _{j+\frac{1}{3}}(x)\), which are Lagrangian polynomials based on the points \(x_{j-\frac{1}{3}}, x_{j}, x_{j+\frac{1}{3}}\). The local basis functions for cell \(J_j\) are \(\varphi _{j+\frac{1}{6}}(x)\), \(\varphi _{j+\frac{1}{2}}(x)\), \(\varphi _{j+\frac{5}{6}}(x)\), which are Lagrangian polynomials based on the points \(x^\alpha _{j+\frac{1}{6}}\), \(x^\alpha _{j+\frac{1}{2}}\), \(x^\alpha _{j+\frac{5}{6}}\). Then the solutions can be represented as

$$\begin{aligned} u(x)&=u_{j-\frac{1}{3}}\phi _{j-\frac{1}{3}}(x)+u_{j}\phi _{j}(x) +u_{j+\frac{1}{3}}\phi _{j+\frac{1}{3}}(x),\,\,\,\, x\in I_j,\\ q(x)&=q^\alpha _{j+\frac{1}{6}}\varphi _{j+\frac{1}{6}}(x) +q^{\alpha }_{j+\frac{1}{2}}\varphi _{j+\frac{1}{2}}(x) +q^\alpha _{j+\frac{5}{6}}\varphi _{j+\frac{5}{6}}(x),\,\,\,\, x\in J_j. \end{aligned}$$

It is quite complicated to write out the exact forms the eigenvalues and eigenvectors for the \(P^2\) case. Therefore, we will only consider two special cases, namely \(\alpha =0\) and \(\alpha =\frac{1}{2}\).

Following the same procedure given in Sect. 3.1, the LDG scheme can be written into the matrix form (2.6) with

$$\begin{aligned} \mathbf{u }_j=\left( u_{j-\frac{1}{3}}, u_{j}, u_{j+\frac{1}{3}} \right) ^T, \end{aligned}$$
(3.10)

and for \(\alpha =0\),

$$\begin{aligned} A= & {} \frac{1}{512}\begin{pmatrix} -\,385&{}\quad 1674&{}\quad 1063\\ -\,14&{}\quad -\,318&{}\quad 1755\\ 95&{}\quad -\,310&{}\quad 7 \end{pmatrix}, B=\frac{1}{256}\begin{pmatrix} -\,2211&{}\quad 278&{}\quad 861\\ 585&{}\quad -\,2562&{}\quad 585\\ 861&{}\quad 278&{}\quad -\,2211 \end{pmatrix},\nonumber \\ C= & {} \frac{1}{512}\begin{pmatrix} 7&{}\quad -\,310&{}\quad 95\\ 1755&{}\quad -\,318&{}\quad -\,45\\ 1755&{}\quad -\,318&{}\quad -\,45\\ \end{pmatrix}, \end{aligned}$$
(3.11)

and for \(\alpha =\frac{1}{2}\),

$$\begin{aligned} A= & {} \frac{1}{16}\begin{pmatrix} 153&{}\quad -\,510&{}\quad 765\\ 9&{}\quad -\,20&{}\quad 45\\ -\,15&{}\quad 50&{}\quad -\,75 \end{pmatrix}, B=\frac{1}{4}\begin{pmatrix} -\,151&{}\quad 42&{}\quad 13\\ 63&{}\quad -\,186&{}\quad 171\\ -\,13&{}\quad 226&{}\quad -\,311 \end{pmatrix},\nonumber \\ C= & {} \frac{1}{16}\begin{pmatrix} -\,29&{}\quad 6&{}\quad -\,1\\ -\,261&{}\quad 54&{}\quad -\,9\\ 667&{}\quad -138&{}\quad 23 \end{pmatrix}. \end{aligned}$$
(3.12)

Again, the standard Fourier analysis will be applied and assume

$$\begin{aligned} \begin{pmatrix} u_{j-\frac{1}{3}}(t)\\ u_{j}(t)\\ u_{j+\frac{1}{3}}(t) \end{pmatrix}=\begin{pmatrix} {\hat{u}}_{-\frac{1}{3}}(t)\\ {\hat{u}}_{0}(t)\\ {\hat{u}}_{+\frac{1}{3}}(t) \end{pmatrix}e^{i\omega x_j}. \end{aligned}$$
(3.13)

For simplicity, we also assume \(\omega =1\). Substituting the above into (2.6), we can obtain the ODE system

$$\begin{aligned} \begin{pmatrix} {\hat{u}}'_{j-\frac{1}{3}}(t)\\ {\hat{u}}'_{j}(t)\\ {\hat{u}}'_{j+\frac{1}{3}}(t) \end{pmatrix}=G\begin{pmatrix} {\hat{u}}_{-\frac{1}{3}}(t)\\ {\hat{u}}_{0}(t)\\ {\hat{u}}_{+\frac{1}{3}}(t) \end{pmatrix}, \end{aligned}$$
(3.14)

where the amplification matrix G is given by (3.3) with A, B and C defined in (3.11) or (3.12) for \(\alpha =0\) and \(\alpha =\frac{1}{2}\), respectively. Denote \(\lambda _i\) and \(V_i\), \(i=1,2,3\), to be the eigenvalues and corresponding eigenvectors of G, respectively. Then for \(\alpha =0\),

$$\begin{aligned} \lambda _{1}&=-\,1-\frac{596651 i}{3072}\xi ^3+\frac{4058334841}{3276800}\xi ^4+\frac{3345594197 i}{737280}\xi ^5\\&-\frac{405767495830801}{33030144000}\xi ^6+O(\xi ^7)\\ \lambda _{2,3}&=\frac{151}{128}-\frac{15}{\xi ^2}\pm \frac{7\sqrt{15}}{8\xi } \mp \frac{2419\sqrt{15}}{20480}\xi \mp \frac{29}{512}\xi ^2+\left( \frac{596651 i}{6144}\mp \frac{13228737901}{20971520 \sqrt{15}}\right) \xi ^3\\&\mp \frac{\left( 36524902209 + 16115508640\sqrt{15}i\right) }{58982400}\xi ^4\\&+\,\frac{\left( -5481421532364800 i\pm 2436959051302733\sqrt{15}\right) }{2415919104000}\xi ^5\\&+\,\frac{\left( 405767493603601\pm 180998522537910 \sqrt{15}i\right) }{66060288000}\xi ^6+O(\xi ^7). \end{aligned}$$

and

$$\begin{aligned} V_{1}&=\begin{pmatrix} -\,720 - 1200 i \xi + 1204 \xi ^2 + 897 i \xi ^3+O(\xi ^4)\\ -\,720 - 1440 i \xi + 1644 \xi ^2 + 1368 i \xi ^3+O(\xi ^4)\\ -\,720 - 1680 i \xi + 2164 \xi ^2 + 1999 i \xi ^3+O(\xi ^4) \end{pmatrix},\\ V_{2,3}&=\begin{pmatrix} -\,53760 (12 i \mp \sqrt{15}) \xi +224 (5095 \pm 232 i \sqrt{15}) \xi ^2 + (1198544 i \mp 22769 \sqrt{15}) \xi ^3+O(\xi ^4)\\ \mp 161280 \sqrt{15} \xi \mp 3360 (59 + 96 \sqrt{15}i) \xi ^2 - (396480 i \mp 367571 \sqrt{15}) \xi ^3+O(\xi ^4)\\ 53760 (12 i \pm \sqrt{15}) \xi - 224 (6425i \mp 728 \sqrt{15}i) \xi ^2 - 3(598128 i \pm 81659 \sqrt{15}) \xi ^3+O(\xi ^4) \end{pmatrix}; \end{aligned}$$

and for \(\alpha =\frac{1}{2}\),

$$\begin{aligned} \lambda _{1}&=-\,1-\frac{1144 i}{3}\xi ^3+\frac{14300}{9}\xi ^4+\frac{110783530 i}{29187}\xi ^5-\frac{42485046399193}{6401682000}\xi ^6+O(\xi ^7)\\ \lambda _{2,3}&=-\,1\pm \frac{38}{\sqrt{69}}-\frac{6(13\mp \sqrt{69})}{\xi ^2}+\left( \frac{1}{8}\mp \frac{6821}{1656 \sqrt{69}}\right) \xi ^2-\frac{44 i}{3}\left( 13\mp 3\sqrt{69}\right) \xi ^3\\&\quad -\,\left( \frac{572003}{720}\mp \frac{38588405903}{3427920\sqrt{69} }\right) \xi ^4-11 i\frac{\left( 5035615 \mp 894279 \sqrt{69}\right) }{29187}\xi ^5\\&\quad +\,\frac{\left( 502441935138015571557 \mp 74298976612868552411 \sqrt{69}\right) }{151416730953936000}\xi ^6+O(\xi ^7). \end{aligned}$$

and

$$\begin{aligned} V_{1}&=\begin{pmatrix} 3600 + 6000 i \xi - 5246 \xi ^2 - 3221 i \xi ^3+O(\xi ^4)\\ 3600 + 7200 i \xi - 7446 \xi ^2 - 5313 i \xi ^3+O(\xi ^4)\\ 3600 + 8400 i \xi - 10046\xi ^2 - 8245 i \xi ^3+O(\xi ^4) \end{pmatrix},\\ V_{2,3}&=\begin{pmatrix} 1656 (141 \mp 7 \sqrt{69}) +138 i (1507 \mp 39 \sqrt{69})\xi -10 (7222 \pm 749 \sqrt{69}) \xi ^2 +O(\xi ^3)\\ 24840 (3 \mp \sqrt{69}) +414 i (269\mp 113 \sqrt{69})\xi -6 (6532 \pm 6957 \sqrt{69}) \xi ^2+O(\xi ^3)\\ \frac{1}{3}\left( -4968 (171 \mp 17 \sqrt{69}) -414 i (3293 \mp 361 \sqrt{69})\xi + (937572 \mp 117690 \sqrt{69}) \xi ^2\right) +O(\xi ^3) \end{pmatrix}. \end{aligned}$$

Then the general solution of the ODE system (3.14) is

$$\begin{aligned} \begin{pmatrix} {\hat{u}}_{-\frac{1}{3}}(t)\\ {\hat{u}}_{0}(t)\\ {\hat{u}}_{+\frac{1}{3}}(t) \end{pmatrix}=C_{21}e^{\lambda _1t}V_1+C_{22}e^{\lambda _2t}V_2+C_{23}e^{\lambda _3t}V_3, \end{aligned}$$
(3.15)

where the constants \(C_{21}\), \(C_{22}\) and \(C_{23}\) are determined by the initial condition

$$\begin{aligned} \begin{pmatrix} {\hat{u}}_{-\frac{1}{3}}(0)\\ {\hat{u}}_{0}(0)\\ {\hat{u}}_{+\frac{1}{3}}(0) \end{pmatrix}=\begin{pmatrix} e^{-\frac{i\xi }{3}}\\ 1\\ e^{\frac{i\xi }{3}} \end{pmatrix}. \end{aligned}$$

We can see that, \(\lambda _1\) is the physical eigenvalue while \(\lambda _{2,3}\) are the nonphysical ones. Moreover, it is easy to observe that the second and third terms in (3.15) are decreasing exponentially fast with respect to the mesh size h, hence we can ignore the contribution from them. With some basic computation, we can obtain the quantitative error estimates:

for \(\alpha =0\),

$$\begin{aligned} \begin{aligned} \left\| e_{-\frac{1}{3}}\right\| _\infty :=&\,\max _{1\le j\le N}\vert U(x_{j-\frac{1}{3}},t)-u_{j-\frac{1}{3}}(t)\vert \\ =&\,\frac{(832 + 80547885 t) e^{-t}}{414720}\xi ^3\\&+\,\frac{(10979996079226880 + 1066737149124583495680 t + 48349276106069021512077 t^2) e^{-t}}{1019215872000(832 + 80547885 t) }\xi ^5\\&+\,O(\xi ^6), \end{aligned} \end{aligned}$$
$$\begin{aligned} \begin{aligned} \left\| e_{0}\right\| _\infty :=&\max _{1\le j\le N}\vert U(x_{j},t)-u_{j}(t)\vert \\ =&\frac{596651 t e^{-t}}{3072}\xi ^3\\&+\,\frac{(26214400 + 976011547208325120 t - 14799288676482712431 t^2)t e^{-t}}{25128767324160000 t^2}\xi ^5+O(\xi ^6),\\ \left\| e_{+\frac{1}{3}}\right\| _\infty :=&\max _{1\le j\le N}\vert U(x_{j+\frac{1}{3}},t)-u_{j+\frac{1}{3}}(t)\vert \\ =&\frac{(-832 + 80547885 t) e^{-t}}{414720}\xi ^3\\&+\,\frac{(-10979996079226880 + 1066737149124583495680 t + 48349276106069021512077 t^2) e^{-t}}{1019215872000(832 - 80547885 t) }\xi ^5\\&+\,O(\xi ^6), \end{aligned} \end{aligned}$$

and for \(\alpha =\frac{1}{2}\),

$$\begin{aligned} \begin{aligned} \left\| e_{-\frac{1}{3}}\right\| _\infty&=\frac{(-1 + 494208 t) e^{-t}}{1296}\xi ^3\\&\quad +\,\frac{(-85477574647 + 42232234477694976 t + 806689123688448000 t^2) e^{-t}}{3362342400(1 - 494208 t) }\xi ^5+O(\xi ^6),\\ \left\| e_{0}\right\| _\infty&=\frac{(-1 + 91520 t)e^{-t}}{240}\xi ^3\\&\quad +\,\frac{(512868994643 - 47003527618544640 t + 746934373785600000 t^2) e^{-t}}{16811712000(1 - 91520 t)}\xi ^5+O(\xi ^6),\\ \left\| e_{+\frac{1}{3}}\right\| _\infty&=\frac{(23 + 2471040 t) e^{-t}}{6480}\xi ^3\\&\quad +\,\frac{13(-151230865483 - 16134718463170560 t + 1551325237862400000 t^2) e^{-t}}{16811712000(23 + 2471040 t)}\xi ^5\\&\quad +\,O(\xi ^6). \end{aligned} \end{aligned}$$

We can see that, both cases yield optimal convergence rates.

4 Superconvergence

In this section, we will consider the one-dimensional linear parabolic equation and investigate the superconvergence of the LDG scheme. We take the perturbation constant \(\alpha \ne 0\). For simplicity, the finite element spaces are made up of piecewise linear polynomials. The extension to high-order cases, though quite complicated, can be obtain following the same lines. The Fourier analysis technique discussed in Sect. 3 will be used to investigate a relationship between the perturbation constant \(\alpha \) of the dual cells and the superconvergence points. However, the superconvergence property discussed in this section only works for uniform meshes. For general random meshes, the superconvergence points are not easy to derive.

The basis functions in this section are different from those discussed in Sect. 3. We are using \(\phi _{j-\frac{1}{2}}(x)\), \(\phi _{j+\frac{1}{2}}(x)\), which are Lagrange polynomials based on the grid points \(x_{j-\frac{1}{2}}\), \(x_{j+\frac{1}{2}}\) as the local basis functions for cell \(I_j\). Also, the local basis functions for cell \(J_j\) are \(\varphi _{j}(x)\), \(\varphi _{j+1}(x)\), which are the Lagrange polynomials based on the grid points \(x^\alpha _{j}\), \(x^\alpha _{j+1}\). Then the solutions can be represented as

$$\begin{aligned} u(x)&=u_{j-\frac{1}{2}}\phi _{j-\frac{1}{2}}(x) +u_{j+\frac{1}{2}}\phi _{j+\frac{1}{2}}(x),\,\,\,\, x\in I_j,\\ q(x)&=q^\alpha _{j}\varphi _{j}(x)+q^\alpha _{j+1}\varphi _{j+1}(x),\,\,\,\, x\in J_j. \end{aligned}$$

Following the same analysis in Sect. 3, the LDG scheme can be written into the matrix form (3.1) with

$$\begin{aligned} \begin{aligned} A&=\frac{1}{8}\begin{pmatrix} 13 + 16 \alpha - 24\alpha ^2 - 192 \alpha ^3 + 144 \alpha ^4 &{} -5 +8 \alpha + 408 \alpha ^2 -96 \alpha ^3 - 144 \alpha ^4\\ -5 -8 \alpha + 24 \alpha ^2 +96 \alpha ^3 - 144 \alpha ^4 &{} 13 - 16 \alpha - 216 \alpha ^2 + 192 \alpha ^3 + 144 \alpha ^4 \end{pmatrix},\\ B&=\frac{1}{8}\begin{pmatrix} -13 - 16 \alpha - 216 \alpha ^2 + 192 \alpha ^3 + 144 \alpha ^4 &{} 5 -8 \alpha + 72 \alpha ^2 +96 \alpha ^3 + 144 \alpha ^4\\ 5 +8 \alpha + 72 \alpha ^2 -96 \alpha ^3 + 144 \alpha ^4 &{} -13 + 16 \alpha - 168 \alpha ^2 - 192 \alpha ^3 - 144 \alpha ^4 \end{pmatrix},\\ C&=\frac{1}{8}\begin{pmatrix} 13 + 16\alpha - 216 \alpha ^2 - 192 \alpha ^3 + 144 \alpha ^4 &{} -5 +8 \alpha + 24 \alpha ^2 -96 \alpha ^3 - 144 \alpha ^4\\ -5 -8 \alpha + 408 \alpha ^2 +96 \alpha ^3 - 144 \alpha ^4 &{} 13 - 16 \alpha - 24 \alpha ^2 + 192 \alpha ^3 + 144 \alpha ^4 \end{pmatrix}. \end{aligned}\nonumber \\ \end{aligned}$$
(4.1)

To observe the superconvergence property, we would like the initial error to be superconvergent at the superconvergence points. Therefore, we can take the initial discretization to be the polynomial interpolation at the superconvergence points. To locate those points, we first map each physical cell into the reference interval \([-\frac{1}{2},\frac{1}{2}]\), and denote the superconvergence points in the reference interval to be a and b. Then we map the two points back to the physical cell, and denote them as \(x_j^a\) and \(x_j^b\) in cell \(I_j\). It is easy to check that

$$\begin{aligned} x_j^a=x_j+ah,\quad x_j^b=x_j+bh. \end{aligned}$$

Then, the initial numerical solution in cell \(I_j\) would be

$$\begin{aligned} y=\frac{e^{i\omega x_j^b}-e^{i\omega x_j^a}}{x_j^b-x_j^a}x+\frac{x_j^be^{i\omega x_j^a}-x_j^ae^{i\omega x_j^b}}{x_j^b-x_j^a}. \end{aligned}$$

We evaluate the above interpolation at \(x_{j-\frac{1}{2}}\), \(x_{j+\frac{1}{2}}\) to obtain

$$\begin{aligned} y\left( x_{j-\frac{1}{2}}\right)= & {} \frac{\left( b+\frac{1}{2}\right) e^{i\xi a}-\left( a+\frac{1}{2}\right) e^{i\xi b}}{b-a}e^{i\omega x_j},\\ y\left( x_{j+\frac{1}{2}}\right)= & {} \frac{\left( b-\frac{1}{2}\right) e^{i\xi a}-\left( a-\frac{1}{2}\right) e^{i\xi b}}{b-a}e^{i\omega x_j}. \end{aligned}$$

Then the initial condition of a general Fourier mode

$$\begin{aligned} \begin{pmatrix} u_{j-\frac{1}{2}}(t)\\ u_{j+\frac{1}{2}}(t) \end{pmatrix}=\begin{pmatrix} {\hat{u}}_{-\frac{1}{2}}(t)\\ {\hat{u}}_{+\frac{1}{2}}(t) \end{pmatrix}e^{i\omega x_j}, \end{aligned}$$
(4.2)

can be written as

$$\begin{aligned} \begin{pmatrix} {\hat{u}}_{-\frac{1}{2}}(0)\\ {\hat{u}}_{+\frac{1}{2}}(0) \end{pmatrix}=\begin{pmatrix} \frac{\left( b+\frac{1}{2}\right) e^{i\xi a}-\left( a+\frac{1}{2}\right) e^{i\xi b}}{b-a}\\ \frac{\left( b-\frac{1}{2}\right) e^{i\xi a}-\left( a-\frac{1}{2}\right) e^{i\xi b}}{b-a} \end{pmatrix}. \end{aligned}$$
(4.3)

In this problem, the two eigenvalues and the corresponding eigenvectors of the amplification matrix are the same as (3.4) and (3.6), respectively. Then following the same analysis in Sect. 3.1, we can write

$$\begin{aligned} \begin{pmatrix} {\hat{u}}_{-\frac{1}{2}}(t)\\ {\hat{u}}_{\frac{1}{2}}(t) \end{pmatrix}=C_{11}e^{\lambda _1t}V_1+C_{12}e^{\lambda _2t}V_2, \end{aligned}$$
(4.4)

where the two constants \(C_{11}\) and \(C_{12}\) are determined by the initial condition (4.3). After we obtain the numerical approximations at \(x_{j-\frac{1}{2}}\) and \(x_{j+\frac{1}{2}}\) at the final time T, a direct linear function interpolation would yield the numerical solution at \(x_j^a\) and \(x_j^b\), denoted as \(u^{a}_j(t)\) and \(u^{b}_j(t)\), respectively, which further leads to the quantitative error estimates

$$\begin{aligned} \begin{aligned} \left\| e_{a}\right\| _\infty :=&\,\max _{1\le j\le N}\vert U(x_j^a,t)-u^{a}_j(t)\vert \\ =&\,\frac{a (1 + 12 a \alpha + 12 b \alpha - 12 \alpha ^2) e^{-t}}{24 \alpha }\xi ^2\\&\quad +\,\frac{96 a^3 \alpha ^2 + 384 a^2 b \alpha ^2 + 2 \alpha (1 + 12 b \alpha - 12 \alpha ^2) + a (-5 + 96 (1 + b^2) \alpha ^2 - 144 \alpha ^4)e^{-t}}{576\alpha ^2 }\xi ^3\\&\quad +\,O(\xi ^4),\\ \left\| e_{b}\right\| _\infty :=&\,\max _{1\le j\le N}\vert U(x_j^b,t)-u_j^{b}(t)\vert \\ =&\,\frac{b (1 + 12 a \alpha + 12 b \alpha - 12 \alpha ^2) e^{-t}}{24 \alpha }\xi ^2\\&\quad +\,\frac{96 b^3 \alpha ^2 + 384 a b^2 \alpha ^2 + 2 \alpha (1 + 12 a \alpha - 12 \alpha ^2) + b (-5 + 96 (1 + a^2) \alpha ^2 - 144 \alpha ^4)e^{-t}}{576\alpha ^2 }\xi ^3.\\&\quad +\,O(\xi ^4) \end{aligned} \end{aligned}$$

To set the coefficients of the leading term to be zero, we have

$$\begin{aligned} a+b=\frac{12\alpha ^2-1}{12\alpha } \end{aligned}$$
(4.5)

Then we can state the following theorem.

Theorem 4.1

Consider the LDG scheme (2.2), (2.3) on uniform meshes with mesh size h. Suppose the finite element space is made up of piecewise \(P^1\) polynomials and the condition (4.5) is satisfied. Assume the initial solution is the interpolation of the exact solution at \(x_j^a=x_j+ah\) and \(x_j^b=x_j+bh\) in cell \(I_j\), then we have

$$\begin{aligned} |U(x_j^a)-u_j^a|=O(h^3),\quad |U(x_j^b)-u_j^b|=O(h^3). \end{aligned}$$

where U is the exact solution, and \(u_j^a\) and \(u_j^b\) are the numerical solution evaluated at \(x_j^a\) and \(x_j^b\), respectively.

Remark 4.1

We choose \(\phi _{j-\frac{1}{2}}(x)\), \(\phi _{j+\frac{1}{2}}(x)\) as the local basis only because we would like to demonstrate the general approach to find the superconvergence points. Actually, one may choose any other basis, e.g. those given in Sect. 3.1. However, no matter which basis to choose, one has to construct interpolation polynomial at the superconvergence points as the initial discretization and evaluate the error at the same points. Then the superconvergence points can be determined by taking the leading term of the error to be zero.

5 Numerical Experiments

In this section, we will use numerical experiments to demonstrate the accuracy and superconvergence of the LDG method for one dimensional linear heat equation on overlapping meshes. First, we will demonstrate the accuracy using piecewise polynomials of degree \(k=1\). Next, we will show numerical experiments for superconvergence. Moreover, we use the third-order SSP Runge–Kutta method for time discretization [17] with time step \(\Delta t=0.01h^2\) to reduce the time error and take the final time \(\hbox {T}=1\).

Table 1 Example 5.1: \(\alpha =0\), \(\alpha =0.05\), \(\alpha =0.25\), \(\alpha =0.5\)
Full size table

Example 5.1

We solve the following heat equation in one space dimension

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t=u_{xx},\,\,\,\,x\in [0,2\pi ],\\ u(x,0)=\sin (x). \end{array}\right. } \end{aligned}$$
(5.1)

Clearly, the exact solution is

$$\begin{aligned} u(x,t)=e^{-t}\sin (x). \end{aligned}$$

We consider uniform meshes and take \(\alpha =0\) in (2.1), i.e, the dual mesh is generated by using the midpoint of the primitive mesh. Moreover, we also take \(\alpha =0.05\) which is closed to 0, \(\alpha =0.25\) which is away from 0, and \(\alpha =0.5\) that the dual mesh agrees with the primitive mesh. We compute the error between the numerical and exact solutions and the results under \(L^2\)-norm are given in Table 1. From the table, we can observe suboptimal accuracy when taking \(\alpha =0\) with piecewise linear polynomials. To obtain optimal accuracy, we can choose \(\alpha \ne 0\). In case of quadratic polynomials, we can observe optimal accuracy for any \(\alpha \) we take that confirm the our theoretical results.

Next, we proceed to verify the superconvergence property discussed in Sect. 4 and compute the error

$$\begin{aligned} \max _j\left\{ |U(x_j^a)-u_j^a|, |U(x_j^b)-u_j^b|\right\} . \end{aligned}$$

We first take \(\alpha =0.25\), then \(a+b=-\frac{1}{12}\). One example would be \(a=-\frac{1}{6}\) and \(b=\frac{1}{12}\), and the result is given in Table 2. We can observe third-order convergence, which verifies Theorem 4.1. Next, we take \(\alpha =0.5\), then \(a+b=\frac{1}{3}\). In this case, the dual mesh agrees with the primitive mesh. In [30] we have demonstrated third-order superconvergence at the right-biased Radau points \((a=-\frac{1}{6}, b=\frac{1}{2})\). We will choose some other superconvergence points, for example, \(a=-\frac{1}{8}\) and \(b=\frac{11}{24}\), and the results are given in Table 2. From the table, we can also observe third-order superconvergence which verifies Theorem 4.1. The numerical experiments for superconvergence work for uniform meshes only, not for non-uniform meshes. However, the superconvergence points for non-uniform meshes must be those for uniform meshes. Therefore, our work can provide some candidates for non-uniform meshes.

Table 2 Example 5.1: Superconvergence with \(\alpha =0.25\) and \(\alpha =0.5\)
Full size table

6 Conclusion

In this paper, we applied Fourier analysis to demonstrate the quantitative error estimates of the LDG methods on overlapping meshes with piecewise \(P^k\) polynomials (\(k=1,2\)) for linear parabolic equations in one space dimension. We analyzed the reason for the accuracy degeneration. Some superconvergence points were also investigated.