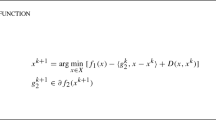A proximal bundle method for a class of nonconvex nonsmooth composite optimization problems

Abstract

In this paper, a proximal bundle method is proposed for a class of nonconvex nonsmooth composite optimization problems. The composite problem considered here is the sum of two functions: one is convex and the other is nonconvex. Local convexification strategy is adopted for the nonconvex function and the corresponding convexification parameter varies along iterations. Then the sum of the convex function and the extended function is dynamically constructed to approximate the primal problem. To choose a suitable cutting plane model for the approximation function, here we consider the sum of two cutting planes, which are designed respectively for the convex function and the extended function. By choosing appropriate descent condition, our method can keep track of the relationship between primal problem and approximate models. Under mild conditions, the convergence is proved and the accumulation point of iterations is a stationary point of the primal problem. Two polynomial problems and twelve DC (difference of convex) problems are referred in numerical experiments. The preliminary numerical results show that the proposed method is effective for solving these testing problems.

1 Introduction

In this article, we focus on a class of composite problem, which has the following form:

$$\begin{aligned} \min _{x\in \textbf{R}^N}\psi (x):=f(x)+h(x), \end{aligned}$$

(1.1)

where $f: \textbf{R}^N\rightarrow \textbf{R}$ is a convex function and $h: \textbf{R}^N\rightarrow \textbf{R}$ is a nonconvex function. Note that the functions f and h are all not necessarily differentiable. In fact, the problem (1.1) may be seen in many practical applications: image reconstruction, engineering, finance, optimal control and statistics.

Example 1

(Regularized minimization mapping) Many signal and image reconstruction problems minimize a function having the following form ($0<q\le 1$):

$$\begin{aligned} \frac{1}{2}\left\| Ax-b\right\| ^2+\tau \Vert x\Vert _q, \end{aligned}$$

for $x\in \textbf{R}^N$, $b\in \textbf{R}^M$, A is a matrix with $M\times N$ dimensions, $\tau$ is a positive parameter and $\Vert x\Vert _q=(\sum _{i=1}^N |x_i|^q)^{\frac{1}{q}}$. The above function can be seen as the sum of a convex function and a lower-$c^2$ function.

Example 2

(Transformation of constraint problems) Consider the following constraint problem:

$$\begin{aligned} \min f(x), \ \ \ \ \text {s.t.} \ \ \ c_i(x)\le 0, \ \ i=1,\cdots ,m, \end{aligned}$$

where f is finite convex and $c_i,\ i=1,\cdots ,m$ is nonconvex function. It is clear that the above constraint problem can be converted into a problem which has only one constraint c(x), where $c(x):=\max \{c_i(x), i=1,\cdots ,m\}$. By the definition of c(x), the function c is not necessary convex and smooth. By the penalty strategy, the new generated problem can be converted into the following unconstrained problem:

$$\begin{aligned} \min _{x\in \textbf{R}^N} f(x)+\lambda c_{+}(x), \end{aligned}$$

where $c_{+}(x)=\max \{c(x),0\}$ and $\lambda \ge 0$. Setting $h(x)=\lambda c_{+}(x)$, the above problem is in the form of (1.1).

Example 3

(DC problem) The minimization of difference of convex functions (DC) is defined as

$$\begin{aligned} \min _{x\in \textbf{R}^N} f_1(x)-f_2(x), \end{aligned}$$

where $f_1,f_2$ are finite convex and all not necessarily differentiable. If we set $h(x)=-f_2(x)$, then the above problem has the form of problem (1.1).

Many researchers [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18] are devoted to developing the implementable algorithms for solving the problems with the form of sum of two functions. These algorithms include the well known operator splitting methods [5, 6, 13], alternating direction methods [7,8,9,10, 14, 15], primal-dual extragradient methods [11] and bundle methods [12, 24] and so on. Concretely, the sum of two smooth and convex functions can be seen in [4, 15]; the sum of a nonsmooth convex function and a smooth convex function can be found in [4, 15]; the sum of two separable convex functions with diffrent variables can be seen in [12, 16, 17]; the sum of a nonsmooth convex function and a nonconvex smooth function can be found in [18]; the sum of two nonconvex functions can be seen in [8] and so on. By viewing these papers, their central ideas are exploiting the separable structure of the primal objective functions. As for nonconvex cases, the prox-regularity and prox-boundedness techniques are considered as the essential theoretical basis to design practical implementable algorithms. In this paper, we consider the convexification strategy and utilize the above theoretical basis to design a class of implementable proximal bundle algorithms. Bundle methods [12, 19, 22, 23] are recognized as highly effective methods for solving nonsmooth optimization problems. Proximal bundle method is one class of bundle methods, which has been successfully used to solve unconstrained convex optimization problems with discontinuous first derivatives [19,20,21,22,23]. In bundle methods, the nonnegative linearization error plays an important role in ensuring the convergence of the algorithms. In convex cases, the linearization error is always nonnegative. However, in nonconvex cases, the linearization error may be negative. In order to circumvent this drawback, some methods [24,25,26,27,28,29,30] about refining the subgradient locality measure are proposed. In this paper, we adopt the convexification technique for handling the nonconvex function h to ensure the corresponding linearization error nonnegative.

Motivated by the redistributed strategy in [24] and the idea of building the cutting plane models in [12], we propose a nonconvex proximal bundle method for solving the composite problem (1.1) and this new method also works well for some DC problems. Although our algorithm is similar to that in [12, 24], they are much different. In [24], the authors focused on a single nonconvex function (lower-$c^2$). The authors in [12] considered the sum of two convex functions. In this article, we present a proximal bundle method for solving the primal optimization problem (1.1). The advantages of the proposed method are as follows: (i) the proximal parameter is dynamically divided into two parameters: one is used to convexificate function h(x) to ensure its linearization errors nonnegative and the other is regarded as the proximal parameter; (ii) The cutting planes for the convex function and convexification function are designed respectively. Since the sum of maxima is bigger than the maximum of the sum, then we sum up the two cutting models in order to obtain a better approximate model for the modified optimization problem; (iii) The proposed method can keep track of the relationship between the original problem (1.1) and the generated piecewise linear model. This maintains a powerful connection between the model functions and the primal function.

The paper is organized as follows. In Sect. 2, we review some definitions in variational analysis and some preliminaries in proximal bundle methods and give some notations. Section 3 introduces our proximal bundle method. In Sect. 4, the global convergence is analyzed under some mild conditions. The numerical results about polynomial functions and some DC problems are presented in Sect. 5. Some conclusions are given in Sect. 6.

2 Preliminaries

In this section, we firstly recall some concepts and results in variational analysis, which will be used in our paper. Then the redistributed strategy is discussed. Meanwhile, some notations for the bundles of functions f and h are considered.

2.1 Concepts and properties

Throughout the paper, we assume the functions f and h are all proper and regular (see [1, Definition 7.25]). Notably, we make use of the limiting subdifferential for the nonconvex function h, denoted by $\partial h(x)$ in [1]. The limiting subdifferential of function h at point $\hat{x}$ is defined by

$$\begin{aligned} \partial h(\hat{x}):=\limsup _{x\rightarrow \hat{x}\ h(x)\rightarrow h(\hat{x})}\left\{ v: \liminf _{x\rightarrow \hat{x}\ x\ne \hat{x}}\frac{h(x)-h(\hat{x})-\langle v, x-\hat{x}\rangle }{\Vert x-\hat{x}\Vert } \ge 0\right\} . \end{aligned}$$

For the convex function f, the common subdifferential in convex analysis is adopted, which is defined as

$$\begin{aligned} \partial f(\hat{x}):=\{ v \ | f(x)\ge f(\hat{x}) + \langle v, x-\hat{x}\rangle \}, \end{aligned}$$

for all $x\in dom(f)$. In convex optimization, $\epsilon -$subdifferential is defined by

$$\begin{aligned} \partial _{\epsilon }f(x):=\{ g\in \textbf{R}^N : f(y)\ge f(x)+\langle g, y-x\rangle -\epsilon \}, \end{aligned}$$

(2.1)

where $\epsilon \ge 0$, $x, y\in dom(f)$. Specially, if $\epsilon = 0$, by the above definition, we have $\partial _{0}f(x)=\partial f(x)$.

In this paper, we consider a class of special nonconvex functions, i.e., lower-$c^2$ function which is presented in the following definition.

Definition 2.1

[1] A function $\psi : \mathcal {O} \rightarrow \textbf{R}$, where $\mathcal {O}$ is an open subset of $\textbf{R}^N$, is said to be lower-$c^2$ on $\mathcal {O}$, if on some neighborhood V of each $\hat{x} \in \mathcal {O}$, there is a representation:

$$\begin{aligned} \psi (x)=\max _{t\in T}\psi _t(x), \end{aligned}$$

in which the function $\psi _t$ are of class $C^2$ on V and the index set T is a compact space such that $\psi _t(x)$ and $\nabla _{x}\psi _t(x)$ depend continuously not just on x but on $(t,x)\in T\times V$.

In the following, we state a theorem which presents a much important property of lower-$c^2$ functions which can also be found in [1, Theorem 10.33]. For completeness, we state it but omit its proof.

Theorem 2.1

[1, Theorem 10.33] Any finite convex function is lower-$c^2$. In fact, a function F is lower-$c^2$ on an open set $\mathcal {O}\in \textbf{R}^N$, if and only if, relative to some neighborhood of each point of $\mathcal {O}$, there is an expression $F(x)=G(x)-H(x)$, in which G is a finite convex function and function H is $C^2$; indeed, H can be taken to be a convex, quadratic function, even of form $\frac{\rho }{2}\Vert \cdot \Vert ^2$.

Another statement of Theorem 2.1 is that the function F is lower-$c^2$ on an open set $\mathcal {O}\in \textbf{R}^N$ if F is finite on $\mathcal {O}$ and for any $x\in \mathcal {O}$, there exists a threshold $\bar{\rho }\ge 0$ such that $F+\frac{\rho }{2}\Vert \cdot \Vert ^2$ is convex on an open neighborhood $\mathcal {O}^{'}$ of x for all $\rho \ge \bar{\rho }$, where $\Vert \cdot \Vert$ stands for standard Euclidean norm, unless specified otherwise. Specifically, if F is finite and convex, then F is a lower-$c^2$ function and the threshold $\bar{\rho }\equiv 0$. In this paper, it is reasonable to deal with the primal problem (1.1) by adding quadric terms to convexificate function h.

2.2 Nonconvex setting and compression technique

In the convex case, at each iteration i, the classical bundle methods keep track of the bundle of information in each iteration, which includes the past function values and subgradient values. For example, for a convex function f, the bundle has the form of $\mathcal {B}_f^n=\{(x^i,f_i=f(x^i),g^i=g(x^i)\in \partial f(x^i)), i\in I_n\},$ where $I_n \subseteq \{0,1,\cdots ,n\}$ is an index set. Along iterations, a sequence of iterative points are generated. These iterative points are divided into two types: one type improves the approximate models’ accuracy; the other type not only improves the models’ accuracy but also decreases significantly the objective function. The corresponding iterations of the algorithmic scheme are respectively called null steps and serious steps. Usually, the serious steps are referred to as proximal center or stability center in the literature, which are denoted by $\hat{x}^{k(n)}$. When it is clear in the context, we drop the explicit dependence of k on the current iteration index n to alleviate notation. It is obvious that a cutting plane model is a lower approximate to the primal problem in convex cases and $\widetilde{f}(y)\approx f(x^i)$ holds for any y sufficiently approximates to $x^i$. In convex case, the linearization error $e_{f,i}^k:=f(\hat{x}^k)-f(x^i)-\langle g_f^i, \hat{x}^k-x^i \rangle$ is always nonnegative which plays an important role to ensure the convergence of bundle algorithms. However, in nonconvex cases, the linearization error may be negative and it becomes much difficult for the proof of convergence and the algorithms for convex optimization can not be directly applied.

For the composite function (1.1), we consider a special nonconvex function h, lower-$c^2$ function. It is clear that the linearization errors $e_{h,i}^k$ may be negative. By Theorem 2.1, we know that there exists a threshold $\bar{\rho }$ such that the augmented function $\varphi _{n}(\cdot )$

$$\begin{aligned} \varphi _{n}(x):= h(x)+\frac{\eta _n}{2}\Vert x-\hat{x}^k\Vert ^2, \end{aligned}$$

(2.2)

is convex in the set $\mathcal {V}$ whenever $\eta _n \ge \bar{\rho }$ holds. But the value $\bar{\rho }$ is not known in prior, then if $\eta _n < \bar{\rho }$, the augmented function $\varphi _{n}$ may not be a convex function in the set $\mathcal {V}$. However by the definition of the linearization error, we have that if we choose the convexification parameter $\eta _n$ suitably, the linearization error of the augmented function $\varphi _{n}(\cdot )$ may be nonnegative. Concretely for any $i \in I_n$, the linearization errors for functions h and $\varphi _n$ are as follows:

$$\begin{aligned} e_{h,i}^k=h(\hat{x}^k)-h(x^i)-\langle g_h^i, \hat{x}^k-x^i \rangle , \ \ \text {for}\ \ g_h^i\in \partial h(x^i). \end{aligned}$$

and

$$\begin{aligned} e_{\varphi ,i}^k=\varphi _n(\hat{x}^k)-\varphi _n(x^i)-\langle g_{\varphi }^i, \hat{x}^k-x^i \rangle , \ \ \text {for}\ \ g_{\varphi }^i\in \partial \varphi _n(x^i). \end{aligned}$$

By the definition of function $\varphi _n$, we have $\varphi _n(\hat{x}^k) = h(\hat{x}^k)$. With the calculation of the subdifferential and the relationship (2.2), we have

$$\begin{aligned} g_{\varphi }^i = g_h^i+ \eta _n(x^i-\hat{x}^k). \end{aligned}$$

and

$$\begin{aligned} e_{\varphi ,i}^k=h(\hat{x}^k)-h(x^i)-\frac{\eta _n}{2}\Vert x^i-\hat{x}^k\Vert ^2-\langle g_h^i+\eta _n(x^i-\hat{x}^k), \hat{x}^k-x^i \rangle = e_{h,i}^k+ \frac{\eta _n}{2}\Vert x^i-\hat{x}^k\Vert ^2. \end{aligned}$$

(2.3)

Then by choosing suitable parameter $\eta _n$, we may make sure that the linearization errors of function $\varphi _n$ in index set $I_n$ to be nonnegative. Next we give the rule for parameter $\eta _n$,

$$\begin{aligned} \eta _n \ge \overline{\eta }_n:=\max \left\{ \max \left\{ -\frac{2e_{h,i}^k}{\Vert x^i-\hat{x}^k\Vert ^2}, \right\} ,0\right\} + \gamma \ \ \ \text {with }i \in I_n\text { and }\Vert x^i-\hat{x}^k\Vert \ne 0 , \end{aligned}$$

(2.4)

where $\gamma$ is a positive constant. By the rule, we have that for all $i \in I_n$, $e_{\varphi ,i}^k \ge \frac{\gamma }{2}\Vert x^i-\hat{x}^k\Vert ^2 \ge 0$ holds. Similar rules for the parameter $\eta _n$ can also be seen in [19, 24] and reference therein. Note also that the parameter $\eta _n$ may vary along iterations.

In the following, our attention will be paid to the approximation function $\phi _{n}(x)$ of $\psi (x)$, which is defined as follows:

$$\begin{aligned} \phi _{n}(x):=f(x)+\varphi _{n}(x). \end{aligned}$$

(2.5)

In fact, function $\phi _{n}$ can also be regarded as a local “convexification" of the problem (1.1). For convex function f, its linearization error is defined by

$$\begin{aligned} e_{f,i}^k=f(\hat{x}^k)-f(x^i)-\langle g_f^i, \hat{x}^k-x^i \rangle \ge 0, \ \ \text {for}\ \ g_f^i\in \partial f(x^i), \ \ \text {and}\ \ \forall i \in I_n. \end{aligned}$$

Note that since function f is finite convex, by (2.1), we have $g_f^i\in \partial _{e_{f,i}^k} f(\hat{x}^k)$. Meanwhile, if $\eta _n \ge \bar{\rho }$, it also holds $g_{\varphi }^i\in \partial _{e_{\varphi ,i}^k} \varphi _{n}(\hat{x}^k)$.

Based on the linearization errors, the bundles of f and h can respectively be

$$\begin{aligned} \mathcal {B}_f^n= & {} \left\{ \left( e_{f,i}^k\in \textbf{R}_{+}, g_f^i\in \partial _{e_{f,i}^k} f(\hat{x}^k)\right) , i\in I_n \right\} , \ \ \ \text {and}\ \ \ \left( \hat{x}^k, f(\hat{x}^k), g_f^k\in \partial f(\hat{x}^k)\right) , \\ \mathcal {B}_h^n= & {} \left\{ \left( x^i,h_i=h(x^i),g_h^i\in \partial h(x^i), e_{h,i}^k\right) , i\in I_n\right\} . \end{aligned}$$

Then the cutting planes for f and $\varphi _{n}$ at the current serious step $\hat{x}^k$ are stated as follows:

$$\begin{aligned} \widetilde{f}_n(x)=\max _{i\in I_n}\left\{ f_i+\langle g_f^i, x-x^i \rangle \right\} =f(\hat{x}^k)+\max _{i\in I_n}\left\{ -e_{f,i}^k+ \langle g_f^i, x-\hat{x}^k \rangle \right\} , \end{aligned}$$

(2.6a)

and

$$\begin{aligned} \begin{aligned} \widetilde{\varphi }_{n}(x)=&\max _{i\in I_n}\left\{ \varphi _{n}(x^i)+ \langle g_h^i+ \eta _n(x^i-\hat{x}^k), x-x^i \rangle \right\} \\ =&h(\hat{x}^k)+\max _{i\in I_n}\left\{ -\left( e_{h,i}^k+ \frac{\eta _n}{2}\Vert x^i-\hat{x}^k\Vert ^2 \right) +\langle g_h^i+\eta _n(x^i-\hat{x}^k),x-\hat{x}^k \rangle \right\} . \end{aligned} \end{aligned}$$

(2.6b)

To ensure the sequence of approximate points is well defined and the corresponding algorithm is convergent, the approximate models must be carefully chosen. In this paper, we regard $\widetilde{f}_n(x)+ \widetilde{\varphi }_{n}(x)$ as the cutting plane model for the approximate function $\phi _n$. For simplify, we note

$$\begin{aligned} \widetilde{\phi }_n(x):= \widetilde{f}_n(x)+ \widetilde{\varphi }_{n}(x). \end{aligned}$$

(2.6c)

Then the next point $x^{n+1}$ may be solved by the following quadratic programming (QP) subproblems:

$$\begin{aligned} x^{n+1}:=\arg \min _{x\in \textbf{R}^N} \left\{ \widetilde{\phi }_n(x)+\frac{\mu _n}{2}\Vert x-\hat{x}^k\Vert ^2 \right\} , \end{aligned}$$

(2.7)

where $\mu _n >0$ is called proximal parameter. By (2.6a) and (2.6b), we have that function $\widetilde{\phi }_n$ is convex. Since $\mu _n >0$, it holds that $x^{n+1}$ is the unique solution of subproblem (2.7) with $x^{n+1}=p_{\mu _n}\widetilde{\phi }_n(\hat{x}^k)$.

The following lemma shows the relationship between the new point $x^{n+1}$ and the current stability center $\hat{x}^k$. Similar conclusion can also be found in [33, Lemma 10.6]. Let $S_n=\{z\in [0,1]^{|I_n|}: \sum _{i\in I_n} z^{i}=1\}$ denote a unit simplex in $\textbf{R}^{|I_n|}$.

Lemma 2.1

Let $x^{n+1}$ be the unique solution to the subproblem (2.7) and the proximal parameter $\mu _n > 0$. Then we have

$$\begin{aligned} x^{n+1}=\hat{x}^{k}-\frac{1}{\mu _{n}}\hat{G}^{k}, \end{aligned}$$

(2.8)

where

$$\begin{aligned} \hat{G}^{k}:= \sum _{i\in I_n}\alpha _1^i g_f^i+\sum _{i\in I_n}\alpha _2^i g_{\varphi }^i, \end{aligned}$$

(2.9)

and $\alpha _{1}=(\alpha _{1}^{1},\cdots ,\alpha _{1}^{|I_n|}) \in S_n$, $\alpha _{2}=(\alpha _{2}^{1},\cdots ,\alpha _{2}^{|I_n|}) \in S_n$ is a solution to

$$\begin{aligned} \min _{\alpha _{1},\ \alpha _{2}\in \textbf{R}_{+}^{|I_n|}} \left\{ \frac{1}{2\mu _n}\left\| \ \sum _{i\in I_n}\alpha _1^i g_f^i+ \sum _{i\in I_n}\alpha _2^i g_{\varphi }^i \right\| ^{2}+\sum _{i\in I_n}\alpha _1^{i}e_f^{i,k}+\sum _{i\in I_n}\alpha _2^{i}e_{\varphi }^{i,k}\right\} . \end{aligned}$$

(2.10)

In addition, the following relations hold:

• (i) $\hat{G}^{k}\in \partial \left( \widetilde{f}_n+\widetilde{\varphi }_{n}\right) (x^{n+1})$;

• (ii) $f(\hat{x}^k)+ h(\hat{x}^k)-\widetilde{f}_n(x^{n+1})- \widetilde{\varphi }_{n}(x^{n+1}) = \mu _n\Vert x^{n+1}-\hat{x}^k\Vert ^2 + \varepsilon _{n+1}$, where $\varepsilon _{n+1}=\sum _{i\in I_n}\alpha _1^ie_f^{i,k}+\sum _{i\in I_n}\alpha _2^{i} e_{\varphi }^{i,k}$.

Proof

Write the objective function of (2.7) as a QP subproblem with two extra scalar variables $r_1$ and $r_2$ as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \min _{(x,\ r_1,r_2)\in \textbf{R}^N\times \textbf{R} \times \textbf{R}} \ \ {} &{} \ r_1+r_2+\frac{\mu _n}{2}\Vert x-\hat{x}^k\Vert ^2 \\ \ \ \ \ \displaystyle \ \ \ \text { s. t.} &{} r_1 \ge f(\hat{x}^k)-e_f^{i,k}+\langle g_f^i, x-\hat{x}^k \rangle , \ \ \ \forall i\in I_n, \\ \ \ \ \ \displaystyle \ \ \ \ \ \ \ \ \ \ &{} r_2 \ge h(\hat{x}^k)-e_{\varphi }^{i,k}+\langle g_{\varphi }^i, x-\hat{x}^k \rangle , \ \ \ \forall i\in I_n. \end{array}\right. } \end{aligned}$$

The corresponding Lagrange function is, for $\alpha _1,\ \alpha _2 \in \textbf{R}_{+}^{|I_n|}$,

$$\begin{aligned} \begin{aligned} L(x,r_1,r_2,\alpha _1,\alpha _2)=&r_1+r_2+\frac{\mu _n}{2}\Vert x-\hat{x}^k\Vert ^2\\&\quad + \sum _{i\in I_n}\alpha _1^i\left( f(\hat{x}^k)-e_f^{i,k}+\langle g_f^i, x-\hat{x}^k \rangle -r_1\right) \\&\quad +\sum _{i\in I_n}\alpha _2^i\left( h(\hat{x}^k)-e_{\varphi }^{i,k}+\langle g_{\varphi }^i, x-\hat{x}^k \rangle -r_2\right) \\ =&\left( 1-\sum _{i\in I_n}\alpha _1^i\right) r_1+ \left( 1-\sum _{i\in I_n}\alpha _2^i\right) r_2\\&\quad +\frac{\mu _n}{2}\Vert x-\hat{x}^k\Vert ^2 + \sum _{i\in I_n}\alpha _1^i\left( f(\hat{x}^k)-e_f^{i,k}+\langle g_f^i, x-\hat{x}^k \rangle \right) \\&\quad \displaystyle +\sum _{i\in I_n}\alpha _2^i\left( h(\hat{x}^k)-e_{\varphi }^{i,k}+\langle g_{\varphi }^i, x-\hat{x}^k \rangle \right) . \end{aligned} \end{aligned}$$

(2.11)

In view of strong convexity, (2.7) has the unique solution $x^{n+1}$. Furthermore, the equivalent problem (2.11) has affine constraints, and there exists optimal multiplier $(\alpha _1, \alpha _2)$ associate with $x^{n+1}$. Since there is no duality gap, the optimal solution $(x^{n+1},\alpha _1, \alpha _2)$ can also be obtained either by solving the primal problem or solving its dual, i.e.,

$$\begin{aligned} (2.11)\equiv \min _{(x,r_1,r_2)} \ \max _{(\alpha _1, \alpha _2)}\ L(x,r_1,r_2,\alpha _1,\alpha _2)\equiv \max _{(\alpha _1, \alpha _2)}\ \min _{(x,r_1,r_2)}\ L(x,r_1,r_2,\alpha _1,\alpha _2). \end{aligned}$$

All the problems above have the same finite optimal value. However, the dual problem involves the unconstrained minimization of the function L with respect to $r_1$ and $r_2$. When the dual value is finite, the terms multiplying $r_1$ and $r_2$ in L have to vanish, i.e., $\alpha _1$ and $\alpha _2$ must lie in the unit simplex $S_n$. As a result, $(x^{n+1},\alpha _1, \alpha _2)$ solves the primal and dual problems

$$\begin{aligned} \min _{x\in \textbf{R}^N}\max _{(\alpha _1,\alpha _2)\in \textbf{R}_+^{|I_n|}\times \textbf{R}_+^{|I_n|}} \ L(x,\alpha _1,\alpha _2) \equiv \max _{(\alpha _1,\alpha _2)\in \textbf{R}_+^{|I_n|}\times \textbf{R}_+^{|I_n|}}\ \ \min _{x\in \textbf{R}^N}\ L(x,\alpha _1,\alpha _2). \end{aligned}$$

where

$$\begin{aligned} L(x,\alpha _1,\alpha _2)= & {} f(\hat{x}^k)+ h(\hat{x}^k)+\frac{\mu _n}{2}\Vert x-\hat{x}^k\Vert ^2 + \sum _{i\in I_n}\alpha _1^i\left( -e_f^{i,k}+\langle g_f^i, x-\hat{x}^k \rangle \right) \\{} & {} +\sum _{i\in I_n}\alpha _2^i\left( -e_{\varphi }^{i,k}+\langle g_{\varphi }^i, x-\hat{x}^k \rangle \right) . \end{aligned}$$

Consider the last dual problem, for each $(\alpha _1, \alpha _2) \in S_n\times S_n$ fixed, defining $x(\alpha _1, \alpha _2)=\arg \min _x$ $\ L(x,\alpha _1,\alpha _2)$, the optimality condition is $0=\nabla _x L(x,\alpha _1,\alpha _2)$, i.e.,

$$\begin{aligned} 0=\mu _n(x-\hat{x}^k)+ \sum _{i\in I_n}\alpha _1^ig_f^i+\sum _{i\in I_n}\alpha _2^ig_{\varphi }^i, \end{aligned}$$

(2.12)

then the relation (2.8) holds.

To prove $(\alpha _1, \alpha _2)$ solves (2.10),we can multiply (2.12) by $x-\hat{x}^k$ and by $\frac{1}{\mu _n}\left( \sum _{i\in I_n}\alpha _1^ig_f^i+\sum _{i\in I_n}\alpha _2^ig_{\varphi }^i\right)$ respectively, then it holds

$$\begin{aligned} \begin{aligned} 0=&\displaystyle \mu _n\left\| x-\hat{x}^k\right\| ^2+ \sum _{i\in I_n}\alpha _1^i\langle g_f^i, x-\hat{x}^k\rangle +\sum _{i\in I_n}\alpha _2^i\langle g_{\varphi }^i, x-\hat{x}^k\rangle \\ =&\sum _{i\in I_n}\alpha _1^i\langle g_f^i, x-\hat{x}^k\rangle +\sum _{i\in I_n}\alpha _2^i\langle g_{\varphi }^i, x-\hat{x}^k\rangle \\&\quad + \frac{1}{\mu _n}\left\| \sum _{i\in I_n}\alpha _1^ig_f^i+\sum _{i\in I_n}\alpha _2^ig_{\varphi }^i\right\| ^2 ,\\ \end{aligned} \end{aligned}$$

which implies that

$$\begin{aligned} \mu _n\left\| x-\hat{x}^k\right\| ^2 = \frac{1}{\mu _n}\left\| \sum _{i\in I_n}\alpha _1^ig_f^i+\sum _{i\in I_n}\alpha _2^ig_{\varphi }^i\right\| ^2, \end{aligned}$$

and

$$\begin{aligned} L(x,\alpha _1,\alpha _2)= & {} f(\hat{x}^k)+ h(\hat{x}^k)-\frac{1}{2\mu _n}\left\| \sum _{i\in I_n}\alpha _1^ig_f^i+\sum _{i\in I_n}\alpha _2^ig_{\varphi }^i\right\| ^2-\sum _{i\in I_n}\alpha _1^ie_f^{i,k}\\{} & {} -\sum _{i\in I_n}\alpha _2^i e_{\varphi }^{i,k}. \end{aligned}$$

Based on above discussions, $(\alpha _1, \alpha _2)$ solves

$$\begin{aligned} \begin{aligned}&\max _{(\alpha _1,\alpha _2)\in S_n\times S_n} \ L(x,\alpha _1,\alpha _2)= f(\hat{x}^k)+ h(\hat{x}^k) \\&\quad - \min _{(\alpha _1,\alpha _2)\in S_n\times S_n} \left\{ \frac{1}{2\mu _n}\left\| \sum _{i\in I_n}\alpha _1^ig_f^i+\sum _{i\in I_n}\alpha _2^ig_{\varphi }^i\right\| ^2+\sum _{i\in I_n}\alpha _1^ie_f^{i,k}+\sum _{i\in I_n}\alpha _2^i e_{\varphi }^{i,k}\right\} , \end{aligned} \end{aligned}$$

(2.13)

so the relation (2.10) holds. The assertion (i) follows from the optimality condition of (2.7) and (2.9). Next we show the assertion (ii). Since there is no duality gap, the primal optimal value in (2.7) is equal to the dual optimal value in (2.13), i.e.,

$$\begin{aligned} \begin{aligned}&\widetilde{f}_n(x^{n+1})+ \widetilde{\varphi }_{n}(x^{n+1})+\frac{\mu _n}{2}\Vert x^{n+1}-\hat{x}^k\Vert ^2\\&\quad = f(\hat{x}^k)+ h(\hat{x}^k) \\&\quad - \frac{1}{2\mu _n}\left\| \sum _{i\in I_n}\alpha _1^ig_f^i+\sum _{i\in I_n}\alpha _2^ig_{\varphi }^i\right\| ^2 -\left( \sum _{i\in I_n}\alpha _1^ie_f^{i,k}+\sum _{i\in I_n}\alpha _2^i e_{\varphi }^{i,k}\right) . \end{aligned} \end{aligned}$$

By (2.8), the above inequality can be rewritten as

$$\begin{aligned} \begin{aligned}&f(\hat{x}^k)+ h(\hat{x}^k)-\widetilde{f}_n(x^{n+1})- \widetilde{\varphi }_{n}(x^{n+1}) \\&\quad = \frac{\mu _n}{2}\Vert x^{n+1}-\hat{x}^k\Vert ^2 +\frac{1}{2\mu _n}\left\| \sum _{i\in I_n}\alpha _1^ig_f^i +\sum _{i\in I_n}\alpha _2^ig_{\varphi }^i\right\| ^2 +\varepsilon _{n+1}\\&\quad = \frac{1}{2\mu _n}\left\| \hat{G}^k\right\| ^2+\frac{1}{2\mu _n}\left\| \hat{G}^k\right\| ^2+ \varepsilon _{n+1} \\&\quad = \frac{1}{\mu _n}\left\| \hat{G}^k\right\| ^2+ \varepsilon _{n+1} = \mu _n\Vert x^{n+1}-\hat{x}^k\Vert ^2 + \varepsilon _{n+1},\\ \end{aligned} \end{aligned}$$

where $\varepsilon _{n+1}=\sum _{i\in I_n}\alpha _1^ie_f^{i,k}+\sum _{i\in I_n}\alpha _2^i e_{\varphi }^{i,k}$. This completes the proof. $\square$

By the convexity of $\widetilde{f}_n$ and $\widetilde{\varphi }_{n}$ and the calculus rule of subdifferentials in convex analysis, it holds

$$\begin{aligned} \partial (\widetilde{f}_n+\widetilde{\varphi }_{n})(x^{n+1})=\partial \widetilde{f}_n(x^{n+1})+ \partial \widetilde{\varphi }_{n}(x^{n+1}). \end{aligned}$$

As the iteration proceeds, the data in the bundle become too much, which will affect the algorithm’s efficiency. For the sake of efficiency, the cardinality for $I_n$ should not grow beyond control as n increases. To overcome this shortcoming, the reformulated bundle opens the ways of mechanism. One is known as the bundle compression, which allows to keep bounded the cardinality of $I_n$ as $n\rightarrow \infty$, without impairing the convergence of the method. Another way is to keep only active data, and this technique is called bundle aggregate. The aggregate information of the bundle includes as least as two: one is the aggregation information and the other is the new generated information. In this paper, we use both techniques, and also append the current serious step information to the bundle. In the following, we regard $J_{1,n}^{act}$ and $J_{2,n}^{act}$ as the active index set, i.e.,

$$\begin{aligned} J_{1,n}^{act}:=\{i\in I_n \ \ |\ \ \alpha _{1}^i >0 \}, \ \ \ \alpha _{1} \in S_n\text { satisfying }(2.10). \end{aligned}$$

and

$$\begin{aligned} J_{2,n}^{act}:=\{i\in I_n \ \ |\ \ \alpha _{2}^i >0 \}, \ \ \ \alpha _{2} \in S_n\text { satisfying }(2.10). \end{aligned}$$

At the same time, we introduce the negative indices which can also be seen in [24, 32] for the aggregate bundle, that is, $I_n \subseteq \{-n, -n+1,\cdots , 0, 1, \cdots , n \}$. Meanwhile, we give the following definitions

$$\begin{aligned} e_{f,-n}^k=\sum _{i\in I_n}\alpha _1^i e_{f,i}^k\, \ \ \ \ \ \ e_{\varphi ,-n}^k=\sum _{i\in I_n}\alpha _2^i e_{\varphi ,i}^k=\sum _{i\in I_n}\left( e_{h,i}^k+ \frac{\eta _n}{2}\Vert x^i-\hat{x}^k\Vert ^2\right) \, \end{aligned}$$

and

$$\begin{aligned} g_f^{-n}=\sum _{i\in I_n}\alpha _1^i g_f^i\, \ \ \ \ \ \ \ g_{\varphi }^{-n}=\sum _{i\in I_n}\alpha _2^ig_{\varphi }^{i}=\sum _{i\in I_n}\alpha _2^i\left( g_h^i+\eta _n(x^i-\hat{x}^k)\right) . \end{aligned}$$

Then, for the aggregative error $\varepsilon ^{n+1}$, by the above definitions, we have

$$\begin{aligned} \varepsilon ^{n+1}= & {} \sum _{i\in I_n}\alpha _1^i e_{f,i}^k +\sum _{i\in I_n}\alpha _2^i e_{\varphi ,i}^k=e_{f,-n}^k+e_{\varphi ,-n}^k\\= & {} \sum _{i\in J_{1,n}^{act}}\alpha _1^i e_{f,i}^k +\sum _{i\in J_{2,n}^{act}}\alpha _2^i \left( e_{h,i}^k+ \frac{\eta _n}{2}\Vert x^i-\hat{x}^k\Vert ^2\right) . \end{aligned}$$

For the aggregate subgradient $\hat{G}^k$, it holds

$$\begin{aligned} \hat{G}^k= & {} \sum _{i\in I_n}\alpha _1^i g_f^i+\sum _{i\in I_n}\alpha _2^i\left( g_h^i+\eta _n(x^i-\hat{x}^k)\right) = g_{f}^{-n}+g_{\varphi }^{-n}\\= & {} \sum _{i\in J_{1, n}^{act}}\alpha _1^i g_f^i+\sum _{i\in J_{2, n}^{act}}\alpha _2^i \left( g_h^i+\eta _n(x^i-\hat{x}^k)\right) . \end{aligned}$$

Note that for all $\iota \in J_{1,n}^{act}\bigcap J_{2,n}^{act}$ and $\iota =-n$, the following two equalities hold

$$\begin{aligned} \widetilde{f}_n(x^{n+1})= & {} f(\hat{x}^k)-e_{f,{\iota }}^k+ \langle g_f^{\iota }, x^{n+1}-\hat{x}^k \rangle , \end{aligned}$$

(2.14a)

$$\begin{aligned} \widetilde{\varphi }_{n}(x^{n+1})= & {} \varphi _{n}(\hat{x}^k)-\left( e_{h,\iota }^k+ \frac{\eta _n}{2}\Vert x^{\iota }-\hat{x}^k\Vert ^2 \right) +\langle g_h^{\iota }+\eta _n(x^{\iota }-\hat{x}^k),x^{n+1}-\hat{x}^k \rangle . \end{aligned}$$

(2.14b)

3 The proximal bundle algorithm

In this section, we will present our algorithm for the problem (1.1). Before that, we firstly give some necessary notations for the algorithm. The predicted decrease at $x^{n+1}$ for functions f and $\varphi _{n}$ are respectively defined by:

$$\begin{aligned} \delta _{n+1}^{f}:= f(\hat{x}^k)-\widetilde{f_n}(x^{n+1}), \end{aligned}$$

and

$$\begin{aligned} \delta _{n+1}^{\varphi }:= \varphi _n(\hat{x}^k) + \frac{\eta _n}{2}\Vert x^{n+1}-\hat{x}^k\Vert ^2 - \widetilde{\varphi }_{n}(x^{n+1})= h(\hat{x}^k) + \frac{\eta _n}{2}\Vert x^{n+1}-\hat{x}^k\Vert ^2 - \widetilde{\varphi }_{n}(x^{n+1}). \end{aligned}$$

By the convexity of function f, we have $\delta _{n+1}^{f} \ge 0$. By (2.2), (2.6b) and the choice of the parameter $\eta _n$, we have $\delta _{n+1}^{\varphi } \ge 0$. For the approximate function $\phi _n$, we definite its predict decrease as follows

$$\begin{aligned} \delta _{n+1} := \delta _{n+1}^{f} + \delta _{n+1}^{\varphi }. \end{aligned}$$

(3.1)

By the above discussions, it holds that $\delta _{n+1} \ge 0$. In fact, according to Lemma 2.1 and (3.1), if we set $R_n=\eta _n+\mu _n$, then it holds that

$$\begin{aligned} \delta _{n+1} = \mu _n \Vert x^{n+1}-\hat{x}^k\Vert ^2 +\frac{\eta _n}{2}\Vert x^{n+1}-\hat{x}^k\Vert ^2 + \varepsilon ^{n+1} = \frac{R_n+\mu _n}{2}\Vert x^{n+1}-\hat{x}^k\Vert ^2 + \varepsilon ^{n+1}. \end{aligned}$$

Now we present our proximal bundle algorithm for problem (1.1).

Algorithm 1

(Nonconvex Nonsmooth Proximal Bundle Method for a class of composite optimization)

Step 0 (Input and Initialization):

Select an initial starting point $x^0$, an unacceptable increase parameter $M_0 >0$, an initial parameter $R_0 >0$, a stopping tolerance $TOL_{stop} \ge 0$, a convexification grow parameter $\Gamma _{\eta } >1$, a proximal grow parameter $\Gamma _{\mu } >1$ and an Armijo-like parameter $m \in (0,1)$. Set the initial iteration counter $n=0$, the serious step counter $k=k(n)=0,$ the bundle index set $I_{0}=\{0\}$ and $\hat{x}^0=x^0.$ Call the black box to compute $f^0,\ g_f^0,\ h^0,\ g_h^0$ and set $e_{f,0}^{0}=0,\ e_{h,0}^{0}=0$. Choose the starting parameter distribution $(\mu _0, \eta _0) = (R_0, 0)$;

Step 1 (Model generation and QP subproblem):

Having the current proximal center $\hat{x}^k$, the current bundle $\mathcal {B}_f^n$ and $\mathcal {B}_{h}^n$ with index set $I_n$, and the current proximal parameter distribution $(\mu _n, \eta _n)$ with $\eta _n \le R_n$. Compute $\widetilde{f}_n(x)$ from (2.6a) and $\widetilde{\varphi }_{n}(x)$ from (2.6b). Solve (2.7) and (3.1) to get $x^{n+1}$ and $\delta _{n+1}$, respectively. Meanwhile, we get the optimal simplicial multipliers $(\alpha _1, \alpha _2) \in S_n \times S_n$ for (2.8). We give two choices for a new index set, which satisfies

$$\begin{aligned} \ \text {Either}\ \ J_n^{act} \subseteq I_{n+1}\ \ \text {and}\ \ \{ n+1, i_k\} \subseteq I_{n+1}\ \ \ \text {Or}\ \ \{ -n\} \subseteq I_{n+1}\ \ \text {and}\ \ \{ n+1, i_k\} \subseteq I_{n+1}\ \end{aligned}$$

where $i_k$ is the iterative index giving the current serious points, i.e., $\hat{x}^k=x^{i_k}$ and $J_n^{act}:=J_{1,n}^{act}\bigcup J_{2,n}^{act}$. Then, go to Step 2;

Step 2 (Stopping criterion):

If $\delta _{n+1} \le TOL_{stop}$, then stop. Otherwise, go to Step 3;

Step 3 (Serious step testing):

If the descent condition

$$\begin{aligned} \psi (x^{n+1}) \le \psi (\hat{x}^k)-m\delta _{n+1}, \end{aligned}$$

(3.2)

holds, then declare a serious step, and set $k(n+1)=k+1$, $i_{k+1}=n+1$, and $\hat{x}^{k+1}=x^{n+1}$. Update the bundles, go to Step 4; otherwise, declare a null step, and set $k(n+1)=k(n)$, go to Step 4;

Step 4 (Update convexification parameter $\eta$ ):

Set

$$\begin{aligned} \left\{ \begin{aligned}&\eta _{n+1}=\eta _n,\ \ \ \ \ \ \ \ \ if\ \ \overline{\eta }_{n+1} \le \eta _n; \\&\eta _{n+1}=\Gamma \overline{\eta }_{n+1} \ \ \ \ \ if\ \ \overline{\eta }_{n+1} > \eta _n; \end{aligned} \right. \end{aligned}$$

(3.3)

where $\overline{\eta }_{n+1}$ is computed by (2.4) with n replaced by $n+1$;

Step 5 (Update model proximal parameter  $\mu$ ):

If the following testing condition

$$\begin{aligned} \psi (x^{n+1})> \psi (\hat{x}^k)+ M_0, \end{aligned}$$

holds, then the objective increase is unacceptable, restart the algorithm by setting:

$$\begin{aligned} \eta _0:=\eta _n,\ \ \mu _0:=\Gamma \mu _n,\ \ R_0:=\eta _0 + \mu _0, \ x^0:=\hat{x}^k,\ k(0):=0,\ i_0:=0,\ I_0:=\{0\},\ n:=0, \end{aligned}$$

then go to Step 1; otherwise, increase k by 1 in the case of the serious step. In all cases, increase n by 1, and loop to Step 1. $\square$

Remark 3.1

Note that the updating strategies for serious steps and null steps are much different in bundle methods. If a serious step occurs, the linearization errors and the stability center are updated, that is, the new generated point is regarded as a new stability center and the corresponding linearization errors update along the new center. If a null step happens, the new generated information should be added into the bundle to improve approximate accuracy and the linearization errors keep unchanged.

When the descent condition (3.2) is satisfied, the new generated iterative point $x^{n+1}$ is regarded as a new serious point, i.e., $\hat{x}^{k+1}=x^{n+1}$, the linearization errors for functions f, h and $\varphi _{n}$ can be respectively updated as follows:

$$\begin{aligned} e_{f,i}^{k+1}= & {} e_{f,i}^{k}+f(\hat{x}^{k+1})-f(\hat{x}^{k})-\langle g_f^i, \hat{x}^{k+1}-\hat{x}^{k}\rangle , \ \ \forall \ i \in I_{n+1}, \end{aligned}$$

(3.4a)

$$\begin{aligned} e_{h,i}^{k+1}= & {} e_{h,i}^{k}+h(\hat{x}^{k+1})-h(\hat{x}^{k})-\langle g_h^i, \hat{x}^{k+1}-\hat{x}^{k}\rangle , \ \ \forall \ i \in I_{n+1}, \end{aligned}$$

(3.4b)

and

$$\begin{aligned} e_{\varphi ,i}^{k+1}= e_{h,i}^{k+1}+ \frac{\eta _n}{2}\Vert x^i-\hat{x}^{k+1}\Vert ^2, \quad \forall \ i \in I_{n+1}. \end{aligned}$$

(3.4c)

In the following, we prove that the stopping test is reasonable and the algorithm is well defined. Before that, we first present our assumption which is always used in bundle methods and can also be seen in [11, 22, 24] and reference therein.

Assumption 3.1

The level set

$$\begin{aligned} \mathcal {T}:=\{ x\in \textbf{R}^N: \ \psi (x) \le \psi (\hat{x}^0) + M_0 \ \} \end{aligned}$$

is compact.

For $\eta _n > 0$, the augmented function $h(x)+\frac{\eta _n}{2}\Vert x-\hat{x}^k\Vert ^2$ is somehow “more convex” than the function h(x). By Assumption 3.1 and Theorem 2.1, there exists a threshold $\bar{\rho }$ such that for any $\eta \ge \bar{\rho }$, it holds that

$$\begin{aligned} \text {The function}\ h(\cdot )+\frac{\eta }{2}\Vert \cdot -\hat{x}^k\Vert ^2 \ \text {is convex on }\mathcal {T}. \end{aligned}$$

where $\hat{x}^k$ is current stability center. At this moment, for functions f and $\varphi _{n}$, the cutting planes model functions satisfy $\widetilde{f}_n(\cdot ) \le f(\cdot )$ and $\widetilde{\varphi }_{n}(\cdot ) \le \varphi _{n}(\cdot )$, thus $\mu _n(\hat{x}^k-x^{n+1}) \in \partial (\widetilde{f}_n+\widetilde{\varphi }_{n})(x^{n+1})$ implies that for all $x \in \mathcal {T}$, we have

$$\begin{aligned}{} & {} \phi _n(x) \ge \widetilde{f}_n(x) + \widetilde{\varphi }_{n}(x) \ge \phi _n(x^{n+1})+ \mu _n\left\langle \hat{x}^k-x^{n+1}, x-x^{n+1} \right\rangle \\{} & {} \quad - \left[ \phi _n(x^{n+1})- \widetilde{f}_n(x^{n+1}) - \widetilde{\varphi }_{n}(x^{n+1})\right] , \end{aligned}$$

where $\phi _n(x)$ is defined in (2.5). In particular, for $x = p_{\mu _n}\phi _n(\hat{x}^k)$, we obtain

$$\begin{aligned} \phi _n\left( p_{\mu _n}\phi _n(\hat{x}^k) \right)\ge & {} \widetilde{f}_n\left( p_{\mu _n}\phi _n(\hat{x}^k)\right) + \widetilde{\varphi }_{n}\left( p_{\mu _n}\phi _n(\hat{x}^k)\right) \\\ge & {} \phi _n(x^{n+1})+ \mu _n\left\langle \hat{x}^k-x^{n+1}, p_{\mu _n}\phi _n(\hat{x}^k)-x^{n+1} \right\rangle \\{} & {} \quad - \left[ \phi _n(x^{n+1})- \widetilde{f}_n(x^{n+1}) - \widetilde{\varphi }_{n}(x^{n+1})\right] . \end{aligned}$$

Similarly, since $p_{\mu _n}\phi _n(\hat{x}^k)$ is characterized by $\mu _n(\hat{x}^k - p_{\mu _n}\phi _n(\hat{x}^k)) \in \partial \phi _n(\hat{x}^k)$, the associate subgradient inequality becomes

$$\begin{aligned} \phi _n(x^{n+1}) \ge \phi _n\left( p_{\mu _n}\phi _n(\hat{x}^k)\right) + \mu _n\left\langle \hat{x}^k-p_{\mu _n}\phi _n(\hat{x}^k), x^{n+1}- p_{\mu _n}\phi _n(\hat{x}^k) \right\rangle . \end{aligned}$$

Combining above two inequalities and it yields that

$$\begin{aligned} \phi _n(x^{n+1})-\widetilde{f}_n(x^{n+1}) - \widetilde{\varphi }_{n}(x^{n+1}) \ge \mu _n \Vert x^{n+1}- p_{\mu _n}\phi _n(\hat{x}^k)\Vert ^2. \end{aligned}$$

By the descent condition (3.2), we get that the stopping criterion in Algorithm 1 is reasonable.

In the following, we will show that the restart steps in Algorithm 1 is finite. Before that, we should note that all lower-$c^2$ functions are locally Lipschitz continuous (see [1, Theorem 10.31]), then f and h are all locally Lipschitz continuous. The compactness of $\mathcal {T}$ allows us to find the Lipschitz constants for functions f and h, denoted by $L_f$ and $L_h$ respectively.

Lemma 3.1

Consider $\{x^n\}$ generated by Algorithm 1 and $i_k \in I_n$, then there can be only a finite number of restarts in Step 5 in Algorithm 1. Moreover, the sequence $\{\mu _n\}$ finally becomes a constant sequence.

Proof

Firstly, the new iterative point $x^{n+1}$ is well defined by the convexity of $\widetilde{\phi }_n(\cdot )$. As functions f and h are Lipschitz continuous, $\psi$ is also Lipschitz continuous in $\mathcal {T}$ and denoting its Lipschitz constant is $L:=L_f + L_h$. By the Lipschitz continuity of $\psi$, there exists $\epsilon >0$ such that, for any $\widetilde{x} \in \{ x: \psi (x) \le \psi (\hat{x}^0)\}$, the open set $B_{\epsilon }(\widetilde{x})$ is contained in $\mathcal {T}$. Note that

$$\begin{aligned} p_{\mu _n}(\widetilde{f}_n+\widetilde{\varphi }_{n})(\hat{x}^k)= & {} \arg \min _{x}\left\{ \widetilde{f}_n(x)+\widetilde{\varphi }_{n}(x) + \mu _n\Vert x-\hat{x}^k \Vert ^2/2\right\} \\\in & {} \left\{ x: \widetilde{f}_n(x)+\widetilde{\varphi }_{n}(x) + \mu _n\Vert x-\hat{x}^k \Vert ^2/2 \le \widetilde{f}_n(\hat{x}^k)+\widetilde{\varphi }_{n}(\hat{x}^k)\right\} \\ {}\in & {} \left\{ x: \widetilde{f}_n(\hat{x}^k)+\widetilde{\varphi }_{n}(\hat{x}^k) + \langle g^{i_k}, x-\hat{x}^k \rangle \right. \\{} & {} \left. + \mu _n\Vert x-\hat{x}^k \Vert ^2/2 \le \widetilde{f}_n(\hat{x}^k)+\widetilde{\varphi }_{n}(\hat{x}^k) \right\} \\\in & {} \left\{ x: -\Vert g^{i_k}\Vert \ \Vert x-\hat{x}^k\Vert + \mu _n\Vert x-\hat{x}^k \Vert ^2/2 \le 0 \right\} \\\in & {} \left\{ x: \Vert x-\hat{x}^k\Vert \le 2L/\mu _n \right\} . \end{aligned}$$

where $i_k \in I_n$, and $g^{i_k} \in \partial (\widetilde{f}_n+\widetilde{\varphi }_{n})(\hat{x}^k)$. It holds $g^{i_k} \in \partial \phi _n(\hat{x}^k)$ and $\Vert g^{i_k}\Vert \le L$. In Step 5, $\mu _n$ increases when the restart steps happen, or keep unchanged when the restart steps do not happen, eventually $\mu _n$ becomes large enough so that the relationship $2L/\mu _n < \epsilon$ holds. Noting that $\psi (\hat{x}^k) \le \psi (\hat{x}^0)$ for any new generated point $\hat{x}^k$ in Algorithm 1 completes the proof. $\square$

4 The convergence theory

In this section, we give the convergence of Algorithm 1. There are different techniques in dealing with $\widetilde{\phi }_{n}(x)$. In [19], the authors use the bundle compression to handle the information in bundles, but they don’t allow to erase the active bundle information. In [24], the authors also utilize the bundle compression technique and they allow to erase active bundle elements in order to use aggregate technique. In our algorithm, we use the latter technique.

Lemma 4.1

Consider the approximate model functions (2.6a) and (2.6b) and $\widetilde{\phi }_n(x)$. then we have:

• (i) Condition

  $$\begin{aligned} \widetilde{\phi }_n(x) \ \text { is} \ \ \text { a } \ \ \text {convex}\ \ \text {function}, \end{aligned}$$

  is always satisfied.

• (ii) If for any index n, $\eta _n \ge \bar{\eta }_n$ with $\bar{\eta }_n$ defined in (2.4), then

  $$\begin{aligned} \widetilde{\phi }_n(\hat{x}^k) \le \psi (\hat{x}^k), \end{aligned}$$

• (iii) If the condition $\eta _{n+1} = \eta _n \ge \bar{\rho }$ holds, $x^{n+1}$ is a null point and either $J_n^{act} \subseteq I_{n+1}$ or $-n \in I_{n+1}$, then

  $$\begin{aligned}{} & {} \widetilde{\phi }_{n+1}(x) \ge \widetilde{\phi }_n(x^{n+1})+\mu _{n}\langle \hat{x}^k-x^{n+1}, x-x^{n+1} \rangle , \ \nonumber \\{} & {} \qquad \quad \ \text { for}\ \ \text {all}\ \ x \in \textbf{R}^N,\ \text { and if }x^{n+1}\text { is a null step,} \end{aligned}$$

  (4.1)

• (iv) If index $n\in I_n$, then for some $g_f^n\in \partial f(x^n)$, $\ g_h^n\in \partial h(x^n)$ and all $x\in \textbf{R}^N$, we have

  $$\begin{aligned} \widetilde{\phi }_n(x) \ge \psi (x^n)+\frac{\eta _n}{2}\Vert x^n-\hat{x}^k\Vert ^2+\langle g_f^n+g_h^n+\eta _n(x^n-\hat{x}^k),x-\hat{x}^k \rangle . \end{aligned}$$

Proof

(i) By (2.6a), (2.6b) and (2.6c), $\widetilde{\phi }_n(x)$ is defined as a sum of the point-wise maximum of a finite collection of affine functions, therefore, $\widetilde{\phi }_n(x)$ is convex, and item (i) is always satisfied.

(ii) By the definition of $\widetilde{\phi }_n(x)$, i.e., (2.6c), it holds that

$$\begin{aligned} \widetilde{\phi }_n(\hat{x}^k)= & {} \widetilde{f}_n(\hat{x}^k)+\widetilde{\varphi }_{n}(\hat{x}^k)=f(\hat{x}^k)+\max _{i\in I_n}\left\{ -e_{f,i}^k\right\} +h(\hat{x}^k)\\{} & {} +\max _{i\in I_n}\left\{ -\left( e_{h,i}^k+ \frac{\eta _n}{2}\Vert x^i-\hat{x}^k\Vert ^2 \right) \right\} . \end{aligned}$$

By the convexity of f and the choice for the parameter $\eta _n$, it holds that for any $i \in I_n$

$$\begin{aligned} e_{f,i}^k \ge 0,\ \ \text {and}\ \ e_{h,i}^k+ \frac{\eta _n}{2}\Vert x^i-\hat{x}^k\Vert ^2 \ge 0. \end{aligned}$$

Combining the above two inequalities, we have

$$\begin{aligned} \widetilde{\phi }_n(\hat{x}^k)= \widetilde{f}_n(\hat{x}^k)+\widetilde{\varphi }_{n}(\hat{x}^k) \le f(\hat{x}^k)+ h(\hat{x}^k)=\psi (\hat{x}^k), \end{aligned}$$

then (ii) holds.

(iii) Suppose that $\eta _{n+1}=\eta _n \ge \bar{\rho }$ and $x^{n+1}$ is a null step, then we have $k(n+1)=k(n)=k$. By (2.6a), (2.6b), (2.6c) and $\eta _{n+1}=\eta _n$, for all $x \in \textbf{R}^N$ and all $l \in I_{n+1}$, we have

$$\begin{aligned} \begin{array}{ll} \phi _{n+1}(x) &{}\ge \displaystyle \widetilde{\phi }_{n+1}(x)=\widetilde{f}_{n+1}(x)+ \widetilde{\varphi }_{{n+1}}(x)\\ &{}\displaystyle \ge f(\hat{x}^k)-e_{f,l}^k + \langle g_f^{l}, x -\hat{x}^k \rangle + h(\hat{x}^k)-e_{h,l}^k\\ &{}\quad -\frac{\eta _n}{2}\Vert x^{l}-\hat{x}^k \Vert ^2 + \langle g_h^{l}+\eta _n(x^{l}-\hat{x}^k), x-\hat{x}^k \rangle , \end{array} \end{aligned}$$

(4.2)

where the inequality holds by (2.6a), (2.6b) and $\eta _{n+1}=\eta _n$. In particular, (4.2) also holds for all $l \in J_n^{act}$ or $l = -n$ in $I_{n+1}$ by the assumption. For such indices and $\eta _{n+1}=\eta _n$, (2.14b) and (2.14a) imply that

$$\begin{aligned} f(\hat{x}^k) -e_{f,l}^k = \widetilde{f}_n(x^{n+1})- \langle g_{f}^l, x^{n+1} - \hat{x}^k \rangle , \end{aligned}$$

and

$$\begin{aligned} \varphi _{n}(\hat{x}^k)-e_{f,l}^k-\frac{\eta _n}{2}\Vert x^{l}-\hat{x}^k \Vert ^2 = \widetilde{\varphi }_{n}(x^{n+1})- \langle g_h^{l}+\eta _n(x^{l}-\hat{x}^k), x^{n+1}-\hat{x}^k \rangle . \end{aligned}$$

With (4.2), for all $l\in J_n^{act}$ or $l=-n$, we have

$$\begin{aligned} \widetilde{\phi }_{n+1}(x)\ge & {} \widetilde{f}_n(x^{n+1})+ \widetilde{\varphi }_{n}(x^{n+1})- \langle g_{f}^l+g_h^{l}+\eta _n(x^{l}-\hat{x}^k), x-x^{n+1} \rangle \\= & {} \widetilde{\phi }_n(x^{n+1}) - \langle g_{f}^l+g_h^{l}+\eta _n(x^{l}-\hat{x}^k), x-x^{n+1} \rangle . \end{aligned}$$

For the case $\{ -n \} \in I_{n+1}$, by Lemma 2.1, we have that item (iii) holds. Next, we show the case of $J_{n}^{act} \subseteq I_{n+1}$. Since QP subproblem (2.7) is strictly convex, then the solution $x^{n+1}$ is unique. Meanwhile, there exists optimal nonnegative multiplier $(\overline{\alpha }_1,\overline{\alpha }_2)\in S_{n}\times S_{n}$ and they satisfy

$$\begin{aligned} \left\{ \begin{aligned}&\ \overline{\alpha }_1^i>0,\ \ \text {for all }i\in J_{1; n}^{act}, \ \ \overline{\alpha }_2^i >0, \ \\&\text {for all }i\in J_{2; n}^{act},\ \sum _{i\in J_{1; n}^{act}} \overline{\alpha }_1^i=1, \ \ \text {and} \sum _{i\in J_{2; n}^{act}} \overline{\alpha }_2^i=1, \\&\ \ \widetilde{\phi }_n(x^{n+1})= \sum _{i\in J_{1,n}^{act}}\overline{\alpha }_i\left( f_i+ \langle g_f^i,x^{n+1}-x^i\rangle \right) \\&+ \sum _{i\in J_{2,n}^{act}}\overline{\alpha }_i\left[ h(x^i)+ \frac{\eta _n}{2}\Vert x^{i}-\hat{x}^k\Vert ^2+ \langle g_{\varphi }^i,x^{n+1}-x^i\rangle \right] , \\&\ \ \hat{G}^k = \mu _n (\hat{x}^k-x^{n+1}) = \sum _{i\in J_{1,n}^{act}}\overline{\alpha }_1^i g_f^i\\&+\sum _{i\in J_{2,n}^{act}}\overline{\alpha }_2^i g_{\varphi }^i \in \partial (f+\varphi _{n})(x^{n+1})=\partial f(x^{n+1})+ \partial \varphi _{n}(x^{n+1}). \end{aligned} \right. \end{aligned}$$

It follows that

$$\begin{aligned} \widetilde{\phi }_n(x^{n+1})= \sum _{i\in J_{1,n}^{act}}\overline{\alpha }_1^i f_i+ \sum _{i\in J_{2,n}^{act}}\overline{\alpha }_2^i \left( h(x^i)+ \frac{\eta _n}{2}\Vert x^{i}-\hat{x}^k\Vert ^2\right) + \left\langle \hat{G}^k, x^{n+1}-x^i\right\rangle . \end{aligned}$$

Note that for each $x \in \textbf{R}^N$ and $i \in I_{n+1}$, it holds that

$$\begin{aligned} \widetilde{f}_{n+1}(x) \ge f_i+\langle g_f^i,x-x^i\rangle , \end{aligned}$$

and

$$\begin{aligned} \widetilde{\varphi }_{n+1}(x) \ge h(x^i)+ \frac{\eta _{n+1}}{2}\Vert x^{i}-\hat{x}^k\Vert ^2+ \langle g_h^i+\eta _{n+1}(x^i-\hat{x}^k),x-x^i\rangle . \end{aligned}$$

As a result, writing the above inequalities for the convex sum of indices $i\in J_{1;n}^{act}$, $i\in J_{2;n}^{act}$ and using that $\eta _{n+1}=\eta _n$, we have

$$\begin{aligned} \widetilde{\phi }_{n+1}(x)= & {} \sum _{i\in J_{1;n}^{act}}\overline{\alpha }_1^i \widetilde{f}_{n+1}(x) + \sum _{i\in J_{2;n}^{act}}\overline{\alpha }_2^i \widetilde{\varphi }_{n+1}(x) \\\ge & {} \sum _{i\in J_{1,n}^{act}}\overline{\alpha }_1^i f_i+ \sum _{i\in J_{2,n}^{act}}\overline{\alpha }_2^i \left( h(x^i)+ \frac{\eta _n}{2}\Vert x^{i}-\hat{x}^k\Vert ^2\right) \\{} & {} \quad + \left\langle \sum _{i\in J_{1;n}^{act}}\overline{\alpha }_1^i g_f^i+ \sum _{i\in J_{2;n}^{act}}\overline{\alpha }_2^i(g_h^i+\eta _n(x^i-\hat{x}^k)), x-x^i \right\rangle \\= & {} \widetilde{\phi }_{n}(x^{n+1})+\mu _{n}\langle \hat{x}^k-x^{n+1}, x-x^{n+1} \rangle . \end{aligned}$$

Then by the definition of $J_{n}^{act}$, we have that item (iii) holds for the case of $J_{n}^{act} \subseteq I_{n+1}$.

By (2.6a), (2.6b), (2.6c) and setting $i=n$, it is straightforward to item (iv). $\square$

Lemma 4.2

Consider the approximate model functions (2.6c) and Algorithm 1. Then there exists index $\tilde{n}$, such that for all $n \ge \tilde{n}$, the parameters $\eta _n, \mu _n \ \text {and} \ R_n$ stabilize:

$$\begin{aligned} \tilde{\eta } \equiv \eta _n,\ \ \tilde{\mu } \equiv \mu _n,\ \ and\ \ \tilde{R} \equiv R_n= \tilde{\eta } + \tilde{\mu }. \end{aligned}$$

Proof

By Lemma 3.1, there is a finite restart steps in Algorithm 1. Once there are no more restart steps, according Algorithm 1, $\mu _n$ will be kept unchanged. Then there exists an index $n_{\mu }$ and from the index $n_{\mu }$ on, $\mu _n=\tilde{\mu }$ holds. In the algorithm, $\eta _n$ is nondecreasing: either $\eta _{n+1}=\eta _n$ or $\eta _{n+1}=\Gamma _{\eta } \overline{\eta }_{n+1}$ where $\Gamma _{\eta } >1$ and $\overline{\eta }_{n+1} > \eta _{n}$. Suppose that $\{\eta _n\}$ is not to stabilize, then there must be an infinite subsequence of iterations at which $\eta _{n+1}$ is increased at least in a factor of $\Gamma _{\eta }$. But this leads to a contradiction. Since function h is lower-$c^2$ in the compact set $\mathcal {T}$, there exists a threshold $\bar{\rho }$ such that for any $\eta \ge \bar{\rho }$, the augment function $\varphi _n(\cdot )=h(\cdot )+ \frac{\eta }{2}\Vert \cdot -\hat{x}^k\Vert$ is convex in the set $\mathcal {T}$, then the approximate function $\phi _n(x)$ is also convex in the set $\mathcal {T}$. Since the sequence $\{ \eta _{n} \}$ is increased, then there exists an index $n_{\eta }$ such that from that index on, $\eta _n$ keeps unchanged,i.e, $\eta _{n_{\eta }+j}\equiv \eta _{n_{\eta }}$ for all $j \ge 0$. Let $\tilde{\eta }$ be $\eta _{\tilde{n}}$ and $\tilde{n} = \max \{ n_{\mu }, n_{\eta } \}$, then the conclusion is followed. $\square$

By Lemma 4.1 and Lemma 4.2, we have that our approximate model (2.6c) is reasonable, which satisfies the criteria in [19]. In addition, if $\tilde{\eta } \ge \bar{\rho }$, the approximate model (2.6c) is a lower approximation to function $\phi _n(x)$.

In order to verify the convergent properties, we set $TOL_{stop}=0$. Note that if Algorithm 1 stops at some index n, this means that $\delta _{n+1}=0$, i.e.,

$$\begin{aligned} \ f(\hat{x}^k)-\widetilde{f}_n(x^{n+1})=0, \ \ \ \text {and}\ \ \ \ h(\hat{x}^k) + \frac{\eta _n}{2}\Vert x^{n+1}-\hat{x}^k\Vert ^2 - \widetilde{\varphi }_{n}(x^{n+1})=0. \end{aligned}$$

(4.3)

By the above equalities, we have

$$\begin{aligned} \psi (\hat{x}^k)+\frac{\eta _n}{2}\Vert x^{n+1}-\hat{x}^k\Vert ^2 =\widetilde{\phi }_{n}(x^{n+1}). \end{aligned}$$

(4.4)

Since $x^{n+1}=p_{\mu _n}\widetilde{\phi }_{n}(\hat{x}^k)$, then it holds that

$$\begin{aligned} \widetilde{\phi }_{n}(x^{n+1})+\frac{\mu _n}{2}\Vert x^{n+1}-\hat{x}^k\Vert ^2 \le \widetilde{\phi }_{n}(\hat{x}^k)+\frac{\mu _n}{2}\Vert \hat{x}^k-\hat{x}^k\Vert ^2=\widetilde{\phi }_{n}(\hat{x}^k). \end{aligned}$$

Based on (4.4) and the above inequality, we have

$$\begin{aligned} \psi (\hat{x}^k)+\frac{\eta _n+\mu _n}{2}\Vert x^{n+1}-\hat{x}^k\Vert ^2 \le \widetilde{\phi }_{n}(\hat{x}^k). \end{aligned}$$

By Lemma 4.1, it holds $\widetilde{\phi }_n(\hat{x}^k) \le \psi (\hat{x}^k)$. By the above discussions, we have

$$\begin{aligned} \psi (\hat{x}^k) +\frac{\eta _n+\mu _n}{2}\Vert x^{n+1}-\hat{x}^k\Vert ^2 \le \psi (\hat{x}^k), \end{aligned}$$

then it holds that $\hat{x}^k=x^{n+1}=p_{\mu _n}\widetilde{\phi }_{n}(\hat{x}^k)$. However, suppose that $\eta _n$ largely enough to guarantee $h(\cdot )+\eta _n\Vert \cdot -\hat{x}^k\Vert ^2/2$ is convex in $\mathcal {T}$. This implies that $\psi (\hat{x}^k)=\widetilde{\phi }_n(\hat{x}^k)=\widetilde{f}_n(\hat{x}^k)+\widetilde{\varphi }_{n}(\hat{x}^k)$ holds. By $\hat{x}^k=x^{n+1}=p_{\mu _n}\widetilde{\phi }_{n}(\hat{x}^k)$ and (2.6c), it always holds that

$$\begin{aligned} \begin{aligned}&\psi (\hat{x}^k)=\widetilde{f}_n(\hat{x}^k)+\widetilde{\varphi }_{n}(\hat{x}^k) \le \widetilde{f}_n(x)+\widetilde{\varphi }_{n}(x)+\frac{\mu _n}{2}\Vert x-\hat{x}^k\Vert ^2, \ \ \text { with }\forall x\in \textbf{R}^N, \\&\quad \le f(x)+h(x)+ \frac{\eta _n}{2}\Vert x-\hat{x}^k\Vert ^2\\&\quad +\frac{\mu _n}{2}\Vert x-\hat{x}^k\Vert ^2, \ \ \text { with }\forall x\in \mathcal {T}, \\&\quad \le \psi (x)+ \frac{\eta _n+\mu _n}{2}\Vert x-\hat{x}^k\Vert ^2, \ \ \ \text { with }\forall x\in \textbf{R}^N. \end{aligned} \end{aligned}$$

(4.5)

Note that in the second inequality, we can also return to $x\in \textbf{R}^N$ by the definition of $\mathcal {T}$, i.e., for any $x \notin \mathcal {T}$

$$\begin{aligned} \psi (\hat{x}^k) \le \psi (\hat{x}^0)< \psi (\hat{x}^0)+ M_0< \psi (x) < \psi (x)+ \frac{\eta _n+\mu _n}{2}\Vert x-\hat{x}^k\Vert ^2. \end{aligned}$$

Therefore, we have

$$\begin{aligned} \hat{x}^k=p_{\mu _n+\eta _n}\psi (\hat{x}^k). \end{aligned}$$

This means that if Algorithm 1 stops in finite iterations, the current stability center $\hat{x}^k$ is a solution to the composite problem (1.1). In the following, we assume Algorithm 1 never stops.

Lemma 4.3

Consider the sequence $\{x^n\}$ generated by Algorithm 1, then $\{\widetilde{\phi }_{n}(x^{n+1})+ \frac{\mu _n}{2}\Vert x^{n+1}-\hat{x}^k\Vert ^2 \}$ is eventually strictly increasing and convergent.

Proof

Taking index n large enough so that $\eta _n$ and $\mu _n$ keep unchanged, i.e, $\tilde{\eta }=\eta _n$ and $\tilde{\mu }=\mu _n$. Consider the following function:

$$\begin{aligned} L_n(y):=\widetilde{\phi }_{n}(x^{n+1})+ \frac{\tilde{\mu }}{2}\Vert x^{n+1}-\hat{x}^k\Vert ^2+\frac{\tilde{\mu }}{2}\Vert y-x^{n+1}\Vert ^2, \end{aligned}$$

(4.6)

and set $s^{n+1}:=\tilde{\mu }(\hat{x}^k-x^{n+1})$. By the optimal condition of QP subproblem (2.7), it holds that $s^{n+1}\in \partial \widetilde{\phi }_{n}(x^{n+1})$. Since $x^{n+1}$ is the unique solution of QP problem (2.7), then we have

$$\begin{aligned} L_n(x^{n+1}) \le \widetilde{\phi }_{n}(\hat{x}^k)+ \frac{\tilde{\mu }}{2}\Vert \hat{x}^k-\hat{x}^k\Vert ^2= \widetilde{\phi }_{n}(\hat{x}^k). \end{aligned}$$

By stem (ii) in Lemma 4.1 and the above inequality, it holds that

$$\begin{aligned} L_n(x^{n+1}) \le \psi (\hat{x}^k), \ \ \ \ \forall \ \ n=0, 1, \cdots . \end{aligned}$$

(4.7)

That means the function $L_n$ is upper bounded. Considering (4.1) with $x=x^{n+2}$, we have

$$\begin{aligned} \widetilde{\phi }_{n+1}(x^{n+2}) \ge \widetilde{\phi }_{n}(x^{n+1}) + \tilde{\mu }\langle \hat{x}^k-x^{n+1},\ x^{n+2}-x^{n+1}\rangle . \end{aligned}$$

By (4.6) with index $n+1$ and taking $y=x^{n+2}$, we have

$$\begin{aligned} L_{n+1}(x^{n+2})= & {} \widetilde{\phi }_{n+1}(x^{n+2})+ \frac{\tilde{\mu }}{2}\Vert x^{n+2}-\hat{x}^k\Vert ^2+ \frac{\tilde{\mu }}{2}\Vert x^{n+2}-x^{n+2}\Vert ^2\\= & {} \widetilde{\phi }_{n+1}(x^{n+2})+ \frac{\tilde{\mu }}{2}\Vert x^{n+2}-\hat{x}^k\Vert ^2. \end{aligned}$$

Hence, by the above discussions, it holds that

$$\begin{aligned} L_{n+1}(x^{n+2}) \ge L_n(x^{n+1}) + \langle s^{n+1},\ x^{n+2}-x^{n+1}\rangle + \frac{\tilde{\mu }}{2}\Vert x^{n+2}-\hat{x}^k\Vert ^2-\frac{\tilde{\mu }}{2}\Vert x^{n+1}-\hat{x}^k\Vert ^2. \end{aligned}$$

Note that the two rightmost terms in the above inequality satisfy the following relationship:

$$\begin{aligned}{} & {} \frac{\tilde{\mu }}{2}\Vert x^{n+2}-\hat{x}^k\Vert ^2-\frac{\tilde{\mu }}{2}\Vert x^{n+1}-\hat{x}^k\Vert ^2 \\{} & {} \quad = \tilde{\mu } \langle \hat{x}^k-x^{n+1},\ x^{n+1}-x^{n+2} \rangle + \frac{\tilde{\mu }}{2}\Vert x^{n+2}-x^{n+1}\Vert ^2 \\{} & {} \quad = \langle -s^{n+1}, x^{n+2}-x^{n+1}\rangle + \frac{\tilde{\mu }}{2}\Vert x^{n+2}-x^{n+1}\Vert ^2. \end{aligned}$$

Therefore, it holds that

$$\begin{aligned} L_{n+1}(x^{n+2}) \ge L_n(x^{n+1}) + \frac{\tilde{\mu }}{2}\Vert x^{n+2}-x^{n+1}\Vert ^2. \end{aligned}$$

By the definition of $L_n$, it holds that

$$\begin{aligned} L_{n+1}(x^{n+2})= & {} \widetilde{\phi }_{n+1}(x^{n+1})+ \frac{\tilde{\mu }}{2}\Vert x^{n+2}-\hat{x}^k\Vert ^2, \ \text {and} \\ L_n(x^{n+1})= & {} \widetilde{\phi }_{n}(x^{n+1})+ \frac{\tilde{\mu }}{2}\Vert x^{n+1}-\hat{x}^k\Vert ^2. \end{aligned}$$

Hence, the sequence $\displaystyle \left\{ \widetilde{\phi }_{n}(x^{n+1})+ \frac{\mu _n}{2}\Vert x^{n+1}-\hat{x}^k\Vert ^2 \right\}$ is strictly increasing for n large enough. By (4.7), it is also bounded above, so it converges. $\square$

The convergent analysis in bundle methods is usually divided into two different cases depending on whether a finite or an infinite number of serious steps is generated. Now we give the convergent analyses of Algorithm 1.

Theorem 4.1

Consider Algorithm 1 with $TOL_{stop}=0$ and suppose there is no termination and $\tilde{\eta } > \bar{\rho }$ holds, then the following conclusions hold:

• (i) If only finite number of serious steps are generated in Algorithm 1 and the last serious step is denoted by $\hat{x}$, followed by an infinite sequence of null steps, then $x^{n+1}\rightarrow \hat{x}$, as $n \rightarrow + \infty$ and $\hat{x}$ is a stationary point of the composite problem (1.1).

• (ii) If there is an infinite number of serious steps generated by Algorithm 1, then any accumulation point of the sequence $\{ \hat{x}^k\}$ is a stationary point of the composite problem (1.1).

Proof

• (i) Consider the iterations n, which is generated after the last serious point $\hat{x}$. There are only null steps. By Lemma 4.3, we have that, as $n\rightarrow \infty$, the algorithm generates an infinite sequence $\{x^n\}$ converging to $\bar{p}:=p_{\tilde{\eta }+\tilde{\mu }}\psi (\hat{x})$ with

  $$\begin{aligned} \lim _{n\rightarrow \infty }\left( \widetilde{\phi }_{n}(x^{n+1})+\frac{\mu _n}{2}\Vert x^{n+1}-\hat{x}\Vert ^2\right) = \psi (\bar{p}) + \frac{\tilde{\eta }+\tilde{\mu }}{2}\Vert \bar{p} - \hat{x}\Vert ^2. \end{aligned}$$

  By the definition of the predict descent and (3.1), it is followed as

  $$\begin{aligned} \delta _{n+1}= & {} \delta _{n+1}^{f} + \delta _{n+1}^{\varphi } = f(\hat{x}^k)-\widetilde{f}_n(x^{n+1}) + h(\hat{x}) \\{} & {} + \frac{\eta _n}{2}\Vert x^{n+1}-\hat{x}\Vert ^2 - \widetilde{\varphi }_{n}(x^{n+1}) \\\rightarrow & {} f(\hat{x}) + h(\hat{x}) + \frac{\tilde{\eta }}{2}\Vert \bar{p}-\hat{x}\Vert ^2 -f(\bar{p})-h(\bar{p}) \\{} & {} - \frac{\tilde{\eta }}{2}\Vert \bar{p}-\hat{x}\Vert ^2,\ \ \ \text {when }I_n\ni n\rightarrow \infty \\= & {} \psi (\hat{x}) - \psi (\bar{p}). \end{aligned}$$

  Since $x^{n+1}$ is a null step, then the serious step test is not satisfied, i.e.

  $$\begin{aligned} \psi (x^{n+1}) > \psi (\hat{x})-m \delta _{n+1}, \end{aligned}$$

  Taking $n\rightarrow \infty$, it holds

  $$\begin{aligned} \psi (\bar{p}) \ge \psi (\hat{x})-m \lim _{n\rightarrow \infty }\delta _{n+1} = \psi (\hat{x})-m(\psi (\hat{x}) - \psi (\bar{p})). \end{aligned}$$

  By the above inequality and $m \in (0,1)$, we have

  $$\begin{aligned} \psi (\bar{p}) \ge \psi (\hat{x}). \end{aligned}$$

  Meanwhile, $\bar{p}=p_{\tilde{R}}\psi (\hat{x})$ means that

  $$\begin{aligned} \psi (\bar{p}) + \frac{\tilde{\eta }+ \tilde{\mu }}{2}\Vert \bar{p}-\hat{x} \Vert ^2 \le \psi (\hat{x} ) + \frac{\tilde{\eta }+ \tilde{\mu }}{2}\Vert \hat{x} -\hat{x} \Vert ^2 = \psi (\hat{x}). \end{aligned}$$

  So we have $\psi (\bar{p}) = \psi (\hat{x})$ and $\bar{p}=\hat{x}$. That is, $\hat{x}:=p_{\tilde{\eta }+ \tilde{\mu }}\psi (\hat{x})$, so $\hat{x}$ is a stationary point of $\psi (x)$.

• (ii) By Lemma 3.1, the sequence $\{ x^k\} \in \mathcal {T}$, where $\mathcal {T}$ is compact, has an accumulation point, that is, for some infinite set $\Lambda$, $\hat{x}^k \rightarrow \widetilde{x} \in \mathcal {T}$ as $\Lambda \ni k \rightarrow \infty$. Since the iteration $k+1$ is a serious step, then we have $\hat{x}^{k+1} = x^{i_{k+1}}$. To simply the notation, we set $j_k=i_{k+1}-1$, then $\hat{x}^{k+1}=p_{\tilde{\mu }}\ \widetilde{\phi }_{j_k}(\hat{x}^k)$. The telescopic sum of descent test for the subsequence of serious steps implies that as $k \rightarrow \infty$, either $\psi (\hat{x}^k)\downarrow -\infty$ or $\delta _{i_{k+1}} \rightarrow 0$. Since $\psi$ is the sum of two finite functions, then we have $\delta _{i_{k+1}} \rightarrow 0$. Consider $k \in \Lambda$, since $\Vert \hat{x}^{k+1}-\hat{x}^k\Vert ^2 \rightarrow 0$, $\hat{x}^{k+1}$ and $\hat{x}^k$ converge to $\widetilde{x}$ as $\Lambda \ni k \rightarrow \infty$, then $\widetilde{\phi }_{j_k}(\hat{x}^{k+1}) \rightarrow \psi (\widetilde{x})$ holds. But the conditions $\hat{x}^{k+1}=p_{\tilde{\mu }}\ \widetilde{\phi }_{n}\hat{x}^k)$ and $\tilde{\eta } > \bar{\rho }$ imply that for all $x\in \mathcal {L}$, we have

  $$\begin{aligned} \widetilde{\phi }_{j_k}(\hat{x}^{k+1}) +\frac{\tilde{\mu }}{2}\Vert \hat{x}^{k+1}-\hat{x}^k\Vert ^2 \le \psi (x)+\frac{\tilde{\eta }+\tilde{\mu }}{2}\Vert x-\hat{x}^k\Vert ^2. \end{aligned}$$

  Therefore, for $k \rightarrow +\infty$, we have

  $$\begin{aligned} \psi (\widetilde{x}) \le \psi (x)+ \frac{\tilde{\eta }+\tilde{\mu }}{2}\Vert x-\widetilde{x}\Vert ^2, \ \ \text {for all }x \in \mathcal {T}. \end{aligned}$$

  As $\widetilde{x} \in \mathcal {T}$, and for any $x \not \in \mathcal {T}$, it holds that

  $$\begin{aligned} \psi (\widetilde{x}) \le \psi (\hat{x}^0)+M_0 \le \psi (x) \le \psi (x)+\frac{\tilde{\eta }+ \tilde{\mu }}{2}\Vert x-\widetilde{x} \Vert ^2. \end{aligned}$$

  Hence, by the above discussions,we have

  $$\begin{aligned} \psi (\widetilde{x}) \le \psi (x)+\frac{\tilde{\eta }+ \tilde{\mu }}{2}\Vert x-\widetilde{x} \Vert ^2, \text {for all }x \in \textbf{R}^N. \end{aligned}$$

  In other words, that means $\widetilde{x}=p_{\tilde{\eta }+\tilde{\mu }}\psi (x)$. Since $\tilde{\eta } > \bar{\rho }$, we have $0\in \partial \psi (\widetilde{x})$. The conclusion holds. $\square$

5 Numerical results

In this section, we focus on the numerical performance of Algorithm 1. The numerical experiments will be divided into two parts. Two polynomial functions which be seen in [24, 34, 35] are provided in the first subsection. In the second subsection, we devote to deal with some DC problems, which are taken from [36,37,38]. Meanwhile, we code Algorithm 1 in MATLAB R2016 and run it on a PC with 2.10 GHz CPU. The Quadratic programming solver for Algorithm 1 is Quadprog.m, which is available in the Optimization Toolbox in MATLAB.

5.1 Polynomial functions optimization

In this subsection, we firstly introduce two nonconvex polynomial problems developed in [24, 34, 35]. Concretely, for each $i=1,\cdots , N$, let the function $g_i: \textbf{R}^N \rightarrow \textbf{R}$ be defined by

$$\begin{aligned} g_i(x)=(ix_i^2-2x_i-K) + \sum _{j=1}^{N}x_j, \ \ \ \text {where }x\in \textbf{R}^N, \text {and }K\text { is a constant}. \end{aligned}$$

The two polynomial functions have the following forms:

$$\begin{aligned} \psi _1(x):= \sum _{i=1}^{N}\left| g_i(x)\right| + \frac{\Vert x\Vert ^2}{2}, \ \ \ \ \text {and} \ \ \ \ \ \psi _2(x):= \sum _{i=1}^{N}\left| g_i(x)\right| + \frac{\Vert x\Vert }{2}. \end{aligned}$$

The above two polynomial functions have some important properties (see in [24]): they are nonconvex and nonsmooth; they are globally lower-$c^2$, bounded below and level coercive; If $K=0$, they have the same optimal value 0 and the same global minimization solution $\textbf{0}$. If we denote $h(x):= \sum _{i=1}^{N}\left| g_i(x)\right|$ and $f(x)=\frac{1}{2}\Vert x\Vert ^2$ or $f(x)=\frac{1}{2}\Vert x\Vert$, then the above functions satisfy the conditions in the problem (1.1). Figures 1, 2, 3 show that functions h,  $\psi _1$ and $\psi _2$ are nonconvex with $K=0$ and $N=2$.

Fig. 1

The 3D image of h(x)

Fig. 2

The 3D image of $\psi _1(x)$

Fig. 3

The 3D image of $\psi _2(x)$

In the following, we first check the numerical behaviour of Algorithm 1 for $\psi _1(x)$ by comparing it with the the RedistProx method in [24]. Similar to that in [24], here we consider the cases of $K=0$ and $N\in \{1,2,3,4,5,6,7,8,9,10\}$. The parameters referred in Algorithm 1 are that

$$\begin{aligned} x_0= & {} [1,1,\cdots ,1]^T, \quad m=0.01,\quad \Gamma _{\eta }=2, \quad \Gamma _{\mu }=2, \quad M_0=10, \\ R_0= & {} 10 \quad I_n=\{0,1,\cdots ,n\}. \end{aligned}$$

The parameters for the RedistProx method in [24] are as default. Meanwhile, we also stop the method when the number of function evaluations is greater than 300, which can also be found in [24]. To compare the numerical performance of Algorithm 1, we adopt the computational results of the RedistProx algorithm in [24]. The numerical results are reported in Table 1 for $\psi _1(x)$. The columns of Tables 1 and 2 have the following meanings:

• Dim: the the tested problem dimension. Nu: the number of null steps.

• Ns: the number of serious steps. Nf: the number of oracle function evaluations used.

• fk: the minimal function value found. $\delta _k$: the value of $\delta$ at the final iteration.

Table 1 The numerical results of Algorithm 1 and RedistProx algorithm for $\psi _1(x)$

From Table 1, we see that Algorithm 1 can not solve successfully $\psi _1(x)$ with $N=6$. However, it can be solved by selecting $m=0.05$ with the results $Nu=202$, $Ns=75$, $Nf=278$, $fk=1.69e-07$ and $\delta _k= 5.7577e-07$. Even under $m=0.1$, the number of iteration decreases: $Nu=77$, $Ns=60$, $Nf=138$, $fk=1.8373e-07$ and $\delta _k= 6.0042e-07$. This denotes there exists different parameter values for variable dimensions. Although the number of iteration in Algorithm 1 is relatively a little bigger than that in the RedistProx method, the minimal function values in Algorithm 1 are more precise than that in RedistProx method. The more precise minimal function values indicate that our model is more accurate. The descent condition (3.2) means the objective function values decrease along all serious steps. In fact, it is a weaker condition than that of its components decreasing along serious steps. Figure 4 illustrates that the objective function value decreases along all serious steps comparing one of its components increasing along some serious steps.

Fig. 4

The values of $\psi _1(x)$ and its components with $N=1$

Fig. 5

The values of components of proximal parameter in function $\psi _1(x)$ with $N=17$ along Nf iterations

Next, we focus on the numerical performance of $\psi _2(x)$ and the results and the comparisons can be found in Table 2. The parameters are the same as above except $R_0$, here we select $R_0=100$. In Table 2, although function $\psi _2(x)$ with $N=1$ does not be solved effectively by Algorithm 1, Algorithm 1 obtains more precise minimal function values except the case of $N=1,2,3$. Hence, Algorithm 1 is more attractive.

Table 2 The numerical results of Algorithm 1 and RedistProx algorithm for $\psi _2(x)$

In the following, we consider higher dimension to Algorithm 1. The parameters for the cases of $N\in \{ 11, 12, 13, 14, 15, 16, 17, 18, 19\}$ are that: $m=0.01$, $\Gamma _{\eta }=2$, $\Gamma _{\mu }=2$, $M_0=10$ and $R_0=1000$. For the stopping rules, $TOL_{stop}$ here is $10^{-5}$ and the maximal function evaluations is 800. For $N\in \{ 20, 50,80\}$, we take $TOL_{stop}=10^{-4}$ and other parameters keep unchanged. For the case of $N=100$, we take $TOL_{stop}=10^{-4}$ and $M_0=100$ and the other parameters keep unchanged. The corresponding results are reported in Table 3. From Table 3, Algorithm 1 may solve all the problems successfully which indicate Algorithm 1 is effective. Figure 5 shows that the convexification parameter $\eta$ and proximal parameter $\mu$ ultimately keep unchanged, which illustrates the conclusions of Lemma 3.1 and Lemma 4.2.

Table 3 The numerical results of Algorithm 1 with higher dimensions for $\psi _1(x)$ and $\psi _2(x)$

5.2 The results for some DC problems

In this subsection, twelve nonsmooth DC problems are firstly tested for the effectiveness of Algorithm 1. These functions can be expressed as $\psi (x)=f(x)-g(x)$ where functions f and g are convex. By taking $h(x)=-g(x)$, it can be converted into the form of the objective function in this paper. The testing problems are presented in Table 4 where Pr denotes the index of problems and $\psi ^{*}$ means the optimal value of the objective function.

Table 4 The testing problems

The parameters in Algorithm 1 for the above DC problems are as follows: $m=0.1$, $\Gamma _{\eta }=2$, $\Gamma _{\mu }=2$, $M_0=10$ and $R_0=10$. We also stop Algorithm 1 when the number of function evaluations is bigger than 1000. For parameter $TOL_{stop}$, we consider it for different choices. For $N\le 10$, we take $TOL_{stop}=10^{-5}$, otherwise, Meanwhile, we take $TOL_{stop}=10^{-4}$. Tables 5 and 6 show the numerical results of Algorithm 1 to these problems. The columns Pr, N, $\delta _k$ and $\psi _k$ denote the index of problems, the dimension of variable x, the value of $\delta _n$ at the finial iteration and the minimum function value found, respectively.

Table 5 The numerical results of Algorithm 1 for Problems 1-11

Table 6 The numerical results of Algorithm 1 for Problem 2

From Tables 5, 6, these problems can be successfully solved by Algorithm 1 that indicates Algorithm 1 is effective and reliable. Meanwhile, Fig. 6 shows that parameters $\eta$ and $\mu$ ultimately keep unchanged, which also illustrates the conclusions of Lemma 3.1 and Lemma 4.2. Next, we compare the numerical results of Algorithm 1 with that of the PALNCO method in [8] for Problems 1,2 and 9. he PALNCO method was designed by the authors for minimizing the sum of two nonsmooth functions and proximal alternating linearization technique was referred. The parameters for Algorithm 1 keep unchanged except $R_0=20$ and the parameters for the PALNCO method are as default. The results are reported in Table 7 which shows that our algorithm is comparable to the PALNCO method.

Table 7 The numerical results of Algorithm 1 and PALNCO method

Fig. 6

The values of $\eta$ and $\mu$ along Nf for Problem 9 with N=50

In the following, we compare the numerical performance of Algorithm 1 with the PBDC method [36], the MPBNGC method [39], the nonsmooth DCA method [40, 41], the TCM method [38], the NCVX method [30] and the penalty NCVX method [31] in small dimension ($N < 10$). Here we take the data in [36]. For the nonsmooth DCA method [40, 41], we take the maximum number of the number of evaluation f and h as the number of function evaluation. The numerical results are presented in Tables 8 and 9. Meanwhile, the column with $^{*}$ denotes that the obtained objective function value is not optimal. From Tables 8 and 9, It is clear that Algorithm 1 can successfully solve all the above DC problems. Although Algorithm 1 is comparable with the PBDC method and the MPBNGC method, it is competitive to the nonsmooth DCA method, the NCVX method and the penalty NCVX method for the testing DC problems.

Table 8 The numerical results of Algorithm 1, PBDC, MPBNGC and DCA methods

Table 9 The numerical results of Algorithm 1, TCM, NCVX and penalty NCVX methods

Based on continuous approximations to the Demyanov-Rubinov quasidifferential, the authors [37] proposed an effective method (called the DCQF method ) for the unconstrained DC problems. In the following, we focus on the numerical performance of Algorithm 1 and compare it with the DCQF method. Similar to that in [37], we take $TOL_{stop}=10^{-4}$ and keep other parameters unchanged. The numerical results can be found in Table 10. It is easy to see that our algorithm is much effective for problems 9,11-12 even in a higher dimension and the number of function values evaluated in our work is smaller that that in [37]. In order to compare the number of iteration intuitively, we adopt the method in [42] and present the performance profiles of iterations in Fig. 7 which indicates Algorithm 1 is more effective and reliable.

Table 10 The numerical results of Algorithm 1 and DCQF method

Fig. 7

Performance profiles of Algorithm 1 and DCQF algorithm in iterations

6 Conclusions

In this paper, we focus on a class of composite problem which is the sum of a finite convex function and a special nonconvex function. For the special nonconvex function (lower-$c^2$), we adopt the convexification technique. The corresponding parameter $\eta _n$ is computed dynamically along iterations. We utilize the sum of the convex function and the augment function to approximate the primal problem. Meanwhile, the sum of the cutting plan models for the convex function and the augment function is regarded as the cutting plan model for the approximate function. A class of proximal bundle methods are designed. Under mild conditions, the convergence is obtained and the accumulation point of iterative points is a stationary point of primal problem. Two polynomial functions and twelve DC problems are referred in the numerical experiment. The numerical results show that our algorithm is interesting and attractive.