A proximal bundle method for constrained nonsmooth nonconvex optimization with inexact information

Abstract

We propose an inexact proximal bundle method for constrained nonsmooth nonconvex optimization problems whose objective and constraint functions are known through oracles which provide inexact information. The errors in function and subgradient evaluations might be unknown, but are merely bounded. To handle the nonconvexity, we first use the redistributed idea, and consider even more difficulties by introducing inexactness in the available information. We further examine the modified improvement function for a series of difficulties caused by the constrained functions. The numerical results show the good performance of our inexact method for a large class of nonconvex optimization problems. The approach is also assessed on semi-infinite programming problems, and some encouraging numerical experiences are provided.

1 Introduction

We consider the constrained nonconvex nonsmooth optimization problem

$$\begin{aligned} \begin{array}{ll} \min \limits _{x\in \mathbf R ^{n}}&{}\quad f(x)\\ s.t. &{}\quad c(x)\le 0, \ \ x\in \mathcal {X}, \end{array} \end{aligned}$$

(1.1)

where $f,\,c$: $\mathbf R ^n\rightarrow \mathbf R$ are locally Lipschitz functions, and $\mathcal {X}$ is a convex compact subset of $\mathbf R ^n$. Further, we assume that for fixed accuracy tolerances, the approximate function values and subgradients of f and c can be obtained by some inexact oracle for each given point. The errors in the function values and subgradients might be unknown, but are bounded by universal constants.

The above framework (1.1) arises in many optimization problems from real-life applications. For some problems, as in $H_\infty$-control problems [2, 42], SIP problems [43] and stochastic programming problems, computing exact information is too expensive, or even out-of-reach, whereas evaluating some inexact information is still possible. Most methods based on exact information can only be used for solving some simplifications of these problems.

Nonsmooth optimization problems are, in general, difficult to solve, even when they are unconstrained. Bundle methods are currently recognized as the most robust and reliable for nonsmooth optimization; see e.g., [1, 21, 24, 31] for more detailed comments. In particular, bundle methods can be thought of as replacing the objective function f by a cutting-plane model to formulate a subproblem whose solution gives the next iteration and obtains the new bundle elements.

Bundle methods for nonconvex problems using exact information were developed in [14, 15, 18, 26, 29, 36, 37, 40, 54, 55] for more detailed comments. Except for [18, 55], all of these methods that desired positive linearization errors did so by redefining them. That is, most of previous methods handle nonconvexity by downshitfing the so-called linearization errors if they are negative. The cutting-planes models in [18, 55] are special in the sense that they no longer model the objective function f but rather certain local convexification. Our proximal bundle method here is along the lines of [18].

Bundle methods capable of handling inexact oracles have received much attention in the last few years. They have been discussed in [25] since 1985. Inexact evaluations of subgradient in subgradient methods date back to [5, 30, 41] in the convex setting, and [47] for nonconvex optimization. Different from earlier works [41, 47], allow nonvanishing errors. Nonvanishing errors of both functions and subgradient values in convex bundle methods were first considered in [48], and further studied in [31]. Besides, several variants have been developed, i.e., [20, 31] for general approaches [9], for energy planning [6, 10], for a stochastic optimization framework [33], for a combinatorial context [43], for SIP problems, and [7] for a detailed summary. As far as we know, the only two other works dealing with inexact information in bundle methods for nonconvex optimization are [19, 42].

For constrained problems, such as problem (1.1) considered here, more sophisticated methods need to come into play. One possibility is to solve an equivalent unconstrained problem with an exact penalty objective function; see [27, 28] for convex constrained problems, and [55] for nonconvex case. These approaches, however, possess some shortcomings, which are typical whenever a penalty function is employed. Specifically, computing a suitable value of the penalty parameter is sometimes too expensive. Besides, if a large value of the penalty parameter is required to guarantee the exactness of a given penalty function, then numerical difficulties arise. Hence, bundle methods in [35, 46] introduce a so-called improvement function

$$\begin{aligned} h_{\tau }(x)=\max \left\{ f(x)-\tau , c(x) \right\} , \end{aligned}$$

(1.2)

where $\tau$ is generated by the former iterative points. It is one of the most effective tools to handle constrained optimization. In this paper, we change $\tau$ into the $f(x^k)$ plus a weighted measure of its feasibility. Thus there is a balance between the search for feasibility and the reduction of the objective function. The details will be discussed in Sect. 2.1

The cutting-plane model in our method no longer approximates penalty function of the objective function as in [55], or the improvement function as in [24, 46]. It is given by a maximum value function of the piecewise linear models of the local convexification of the objective function f and constraint function c. Hence, our approach can not be viewed as an unconstrained proximal bundle method applied to the function $h_{\tau }(x)$. Another feature of our algorithm is infeasibility in this paper. With respect to [24, 39], the advantage is that it is not necessary to compute a feasible point to start the algorithm. Also, since serious steps can be infeasible, monotonicity in f is not enforced. Infeasible bundle methods are very rare and valuable.

In this paper, we propose an infeasible proximal bundle method with inexact information for solving (1.1). Above all, the sequence of iterative points of our inexact bundle method converges to an approximate optimal point at most $\epsilon$ asymptotically under a mild assumption. To be specific, the limit value $f^*$ and $c^*$ of the sequences $\{f^k\}$ and $\{c^k\}$, respectively, satisfy

$$\begin{aligned} \mathrm{if }\ c^*\le 0{:}\,f^*\le f(y)+ \epsilon \end{aligned}$$

for all y in a neighbourhood. If the feasible set of (1.1) is empty, then $c^*\le c(y)+\epsilon$ for all y.

This paper is organized as follows. In Sect. 2, we state basic conceptual comments, inexact oracle and basic properties of the improvement function. The cutting-planes model and the algorithm itself are stated in Sect. 3, where some preliminary properties also are established. Asymptotic analysis is considered in Sect. 4, and convergence analysis is provided in Sect. 5. Numerical experiments are presented in Sect. 6.

2 Background, assumptions and notation

The description of this work starts with conceptual comments and results of variational analysis, then passes to technical details gradually. We assume that the objective function f and constraint function c are proper [44, p. 5], regular [44, Def 7.25], and locally Lipschitz with full domain.

2.1 Background and assumptions

In this subsection, we first recall concepts and results of variational analysis that will be of use in this paper. The closed ball in $\mathbf R ^n$ with the center in $x \in \mathbf R ^n$ and radius $\rho > 0$ is denoted by $B_{\rho }(x)$. We shall use $\partial f(\bar{x})$ to denote the subdifferential of f at the point $\bar{x}$. By noting the regularity of f, the subdifferential mapping is well-defined and is given by

$$\begin{aligned} \partial f(\bar{x}) :=\left\{ v \in \mathbf{R }^n{:}\,f(x)\ge f(\bar{x})+\langle v,x-\bar{x}\rangle +\circ (|x-\bar{x}|), \ \mathrm{for\ all} \ x \in \mathbf R ^n \right\} , \end{aligned}$$

(2.1)

and each element of this subdifferential is called subgradient. Besides, the Clarke directional derivative [3] in x in direction $d \in \mathbf R ^n$ is given as

$$\begin{aligned} f^{0}(x,d):=\lim _{h\rightarrow 0,}\sup _{t\downarrow 0}\frac{f(x+h+td)-f(x+h)}{t}, \end{aligned}$$

and alternative definition is

$$\begin{aligned} f^{0}(x,d):= \max _{g \in \partial f(x)} g^\mathrm{T}d. \end{aligned}$$

Given an open set $\mathcal {O}$ containing $\mathcal {X}$, a locally Lipschitz function $f{:}\,\mathcal {O}\rightarrow \mathbf R$, is called to be lower-$C^1$, if on some neighborhood V of every $\tilde{y} \in \mathcal {O}$, there exists an expression as [49]:

$$\begin{aligned} f(y):=\max \limits _{s\in S} g(y,s), \end{aligned}$$

(2.2)

where the derivative $D_{y}g$ is jointly continuous and the index set S is a compact set. Our nonconvex proximal bundle method is given for lower-$C^1$ functions, and we define the following equivalence given in [8, The 2, Cor 3] and [49, Prop 2.4] as

• The locally Lipschitz function f is lower-$C^1$ on $\mathcal {O}$.

• Its Clarke subdifferential $\partial f$ is submonotone at every $\tilde{y} \in \mathcal {O}$. That means for every $\tilde{y}\in \mathcal {O}$ and for all $\theta >0$ there exists $\rho >0$ such that

  $$\begin{aligned}&\left\langle q^1-q^2, z^1-z^2 \right\rangle \ge -\theta \Vert z^1-z^2\Vert ,\\&\quad \mathrm{for \ all} \ z^1, z^2\in B_{\rho }(\tilde{y}) \ \ \mathrm{and} \ \ q^1\in \partial f(z^1), q^2\in \partial f(z^2). \end{aligned}$$

• For all $\tilde{y}\in \mathcal {O}$ and for all $\theta >0$ there exists $\rho >0$ such that $\forall \ y\in B_{\rho }(\tilde{y})$ and $q\in \partial f(y)$

  $$\begin{aligned} f (y+u)-f (x) \ge \langle q,u \rangle -\theta \Vert u\Vert , \end{aligned}$$

  (2.3)

  whenever $\Vert u\Vert <\rho$ and $y+u \in B_{\rho }(\tilde{y})$.

• For every $\tilde{y}\in \mathcal {O}$ and for all $\theta >0$ there exists $\rho >0$ such that

  $$\begin{aligned} f(ty^1+(1-t)y^2)\le tf(y^1)+(1-t)f(y^2)+\theta t(1-t)\Vert y^1-y^2\Vert , \end{aligned}$$

  for all $t\in (0,1)$ and $y^1, y^2 \in B_{\rho }(\tilde{y})$.

If the optimal value $f_{\mathrm{min}}$ of the problem (1.1) is known in advance, the solution of (1.1) can be obtained by minimizing $h_{\mathrm{min}}(y)=\max \Big \{ f(y)-f_{\mathrm{min}}, c(x)\Big \}.$ Notice that if $x^*$ is a solution of the problem (1.1), then $h_{\mathrm{min}}(x^*)=0$. Hence, Lemaréchal [35] first changed $f_{\mathrm{min}}$ into a lower bound $\underline{f}^k$. The sequence $\{\underline{f}^k\}$, however, is not available, thus it is not possible for proximal bundle methods. Some alternatives were proposed in [1, 23, 32, 35, 43, 46]. For instance [43], replaced $\underline{f}^k$ by the objective function value at the current stability center $x^k$ as

$$\begin{aligned} h_{x^k}(y)= \max \left\{ f(y)-f(x^k), \ c(y) \right\} . \end{aligned}$$

(2.4)

However, all of them may not be suitable for nonconvex optimization with inexact oracle in this paper. Based on [32], we replace $\tau$ by $f(x^k)$ plus a weighted measure of its feasibility

$$\begin{aligned} h_{x^k}(y):= \max \left\{ f(y) -\theta _1^{x^k}, c(y)-\theta _2^{x^k} \right\} , \end{aligned}$$

(2.5)

with

$$\begin{aligned} \theta _1^{x^k}:=f(x^k)+s_k \max \{0,c(x^k)\}, \ \ \theta _2^{x^k}:=t_k \max \{0,c(x^k) \}, \end{aligned}$$

(2.6)

where $s_k>0$ and $t_k>0$ are penalty parameters. The penalty parameters $s_k$ and $t_k$ are bounded, and updated depending on a constant along the iterative process. Moreover, as shown below $h_{x^k}(\cdot )$ is nonnegative at each stability center, and used for the optimality measure.

We introduce the following extended MFCQ (see [22, 51]) for this nonsmooth SIP.

Assumption 1

(The constraint qualification) Suppose that $x^*$ is a local solution of the problem (1.1). There exists some direction d of $\mathcal {F}:=\{ x\in \mathcal {X}{:}\,c(x)\le 0\}$ at $x^*$, satisfies

$$\begin{aligned} c^{0}(x^*,d)<0. \end{aligned}$$

(2.7)

We now give the following necessary condition of optimality measure.

Lemma 2.1

Suppose $x^*$ is a local solution of the problem (1.1), and there exists a constant $\rho ^*$ such that $f(y)\ge f(x^*)$ for all $y\in B_{\rho ^*}(x^*)\bigcap \mathcal {X}$. Then the following statements hold:

• (i) For all $y \in \mathcal {X}$, it holds that

  $$\begin{aligned} \min \left\{ h_{x^*}(y){:}\, y \in \mathcal {X}\right\} = h_{x^*}(x^*)= 0, \ for \ all \ y \in B_{\rho ^*}(x^*)\cap \mathcal {X}. \end{aligned}$$

  (2.8)

• (ii) $0 \in \partial h_{x^*}(x^*)$, and there exist $\mu _0$ and $\mu _{1}$ satisfying

  $$\begin{aligned}&0\in \mu _0\partial f(x^*)+\mu \partial c (x^*)+\partial i_{\mathcal {X}}(x^*),\nonumber \\&\mu \ge 0, \ \mu +\mu _0=1, \ \mu c(x^*)=0, \ c(x^*)\le 0, \end{aligned}$$

  (2.9)

  where $i_{\mathcal {X}}(x^*)$ denotes the indicator function of the set $\mathcal {X}$.

• (iii) If, in addition, Assumption 1 holds, then $x^*$ is a KKT point of the problem (1.1).

Proof

Since $x^*$ is a local solution of the problem (1.1), we conclude that

$$\begin{aligned} c(x^*)\le 0 \ \ \mathrm{and} \ \ f(x^*)\le f(y), \ for \ all \ y \in B_{\rho ^*}(x^*)\cap \mathcal {X}. \end{aligned}$$

Together with the relation (2.6), we can obtain

$$\begin{aligned} \theta _1^{x^*}=f(x^*) \ \ \mathrm{and} \ \ \theta _2^{x^*}=0. \end{aligned}$$

That means, for all $y\in B_{\rho ^*}(x^*)\cap \mathcal {X}$,

$$\begin{aligned} h_{x^*}(y)= \max \limits \Big \{ f(y)-f(x^*), c(y)\Big \}\ge 0= h_{x^*}(x^*), \end{aligned}$$

which implies that the relation (2.8) holds. From here, the first item (i) follows.

It follows from [24, Lemma 2.15] that $0 \in \partial (h_{x^*}(x^*)+i_{\mathcal {X}}(x^*))$. Hence the point $x^*$ is a FJ point of (1.1) and the conditions (2.9) hold. To see item (iii),

$$\begin{aligned} \begin{array}{ll} 0 &{} \in \partial (h_{x^*}(x^*)+i_{\mathcal {X}}(x^*))\\ &{}=conv \Big \{ \partial f(x^*)\cup \partial c(x^*) \Big \}+\partial i_{\mathcal {X}}(x^*). \end{array} \end{aligned}$$

If $\mu _0$ is zero in condition (2.9) we obtain $\mu =1$ and $-g^*\in \partial i_{\mathcal {X}}(x^*)$ for some $g^*\in \partial c(x^*)$. By noting d is a feasible direction of $\mathcal {F}$, we get that $\langle g^*, d\rangle \ge 0$. Thus we obtain

$$\begin{aligned} 0\le \max \left\{ \langle g,d\rangle |g \in \partial c(x^*) \right\} =c^0(x^*,d), \end{aligned}$$

which is an contradiction with (2.7). Hence the constant $\mu _0$ is strictly positive. Together with the conditions (2.9), we obtain that

$$\begin{aligned} \begin{array}{ll} &{} 0\in \partial f(x^*)+\nu \partial c (x^*)+\partial i_{\mathcal {X}}(x^*),\\ &{} \nu \ge 0, \ c(x^*)\le 0, \ \nu c(x^*)=0, \end{array} \end{aligned}$$

since one may take $\nu =\frac{\mu }{\mu _0}$. Hence, $x^*$ is a KKT point of the problem (1.1).$\square$

2.2 Available information

The algorithm herein will hinge around previously generated information. Suppose that $y^j$ is an iterative point at jth step, and $x^k$ denotes the kth stability center. Let $j_k$ denote the jth iteration giving the stability center $x^k$, i.e., $x^k:=y^{j_k}$. The stability center is considered as the “best” known point up to the kth iteration.

We assume that at any $y^j$, the oracle provides

$$\begin{aligned} \begin{array}{l} \left\{ \begin{array}{ll} f^j \ \mathrm{and} \ c^j \ &{}\quad \mathrm{estimate \ for \ the \ function \ values, \ and} \\ g^j_{f} \ \mathrm{and} \ g^j_{c} \ &{}\quad \mathrm{estimate \ for \ the \ respective \ subgradients}. \end{array}\right. \\ \end{array}\end{aligned}$$

(2.10)

For each $y^j \in \mathcal {X}$, the oracle provides us with

$$\begin{aligned} \begin{array}{llll} \left\{ \begin{array}{llll} f\text {-}\mathrm{oracle\ information} \left[ \begin{array}{llll} f^j = f(y^j)-\sigma _{j} \ \mathrm{and} \\ g_{f}^j \in \partial f (y^j)+B_{\varepsilon _{j}} (0); \end{array}\right. \\ c\text {-}\mathrm{oracle\ information} \left[ \begin{array}{llll} c^j = c(y^j)-\sigma _{j} \ \mathrm{and} \\ g_{c}^j \in \partial c (y^j)+B_{\varepsilon _{j}} (0). \end{array}\right. \end{array}\right. \\ \end{array}\end{aligned}$$

(2.11)

At each stability center $x^k$, for simplicity, we denote

$$\begin{aligned} \begin{array}{llll} \left[ \begin{array}{llll} \hat{f}^k = f(x^k)-\hat{\sigma }_{k} \ \mathrm{and} \\ \hat{g}_{f}^k \in \partial f (x^k)+ B_{\hat{\varepsilon }_{k}} (0); \end{array}\right. \ \ \ \left[ \begin{array}{llll} \hat{c}^k = c(x^k)-\hat{\sigma }_{k} \\ \hat{g}_{c}^k \in \partial c(x^k)+ B_{\hat{\varepsilon }_{k}} (0). \end{array}\right. \end{array}\end{aligned}$$

(2.12)

Since the sign of error $\sigma _{j}$ is not specified, the exact function values may be either underestimated or overestimated by $f^j$ and $c^j$. Throughout this section we will make the assumption that the error on each of these estimates is bounded, i.e., there exist corresponding bounds $\bar{\sigma }$ and $\bar{\varepsilon }$, such that

$$\begin{aligned} -\bar{\sigma }\le \sigma _{j}\le \bar{\sigma } \ \ \mathrm{and} \ \ 0\le \varepsilon _{j} \le \bar{\varepsilon } \ \ \mathrm{for \ all} \ j, \end{aligned}$$

where both bounds $\bar{\sigma }$ and $\bar{\varepsilon }$ are generally unknown.

3 Defining the inexact algorithm

3.1 The model

Based on the modified improvement function (2.5) and the inexact oracle (2.11), we define the kth inexact modified improvement function at the stability center $x^k$ as follows:

$$\begin{aligned} h_{k}(y):= \max \left\{ f^{y} -\theta _1^k, c^{y}-\theta _2^k \right\} , \end{aligned}$$

(3.1)

where $f^y:=f(y)-\sigma _{y},\,c^y:=c(y)-\sigma _{y}$, and

$$\begin{aligned} \theta _1^k=\hat{f}^k+s_k \max \{0,\hat{c}^k\}, \ \ \theta _2^k=t_k \max \{0,\hat{c}^k\}. \end{aligned}$$

(3.2)

Both penalty parameters $s_k$ and $t_k$ are updated depending on a constant $\varpi >0$, and satisfy

$$\begin{aligned} s_{k}\ge 0,\ \ t_{k} \in [0,1] \ \mathrm{satisfying} \ s_{k}-t_{k}\ge \varpi . \end{aligned}$$

(3.3)

Since penalty parameters $s_{k}$ and $t_k$ are bounded, they must be well-defined along the iterative process. Considering (3.1) and the oracle assumption, we obtain

$$\begin{aligned} h_{k} (x^k)= & {} \max \Big \{ -s_k \max \{0,\hat{c}^k\}, \hat{c}^k-t_k \max \{0,\hat{c}^k\} \Big \}\nonumber \\= & {} \left\{ \begin{array}{ll} 0, &{}\quad \mathrm{if} \ \hat{c}^k \le 0, \\ (1-t_k)\hat{c}^k, \ \ &{}\quad \mathrm{if} \ \hat{c}^k > 0. \end{array}\right. \end{aligned}$$

(3.4)

The strategy (3.3) for updating $s_{k}$ and $t_{k}$ can ensure the nonnegativity $h_{k}(x^k)\ge 0$.

It is worth noting that the past information gives the cutting plane model. Just as a classic method in [46], if f and c are convex functions with exact oracle, then the cutting plane model was given as

$$\begin{aligned} \varphi _{l}(y)=\max \limits _{i\in \mathcal {B}_l } \Big \{ h_{x^k}(y^i)+\langle g_h^i,y-y^i \rangle \Big \}, \ \ \mathrm{where} \ g_h^i\in \partial h_{x^k}(y^i). \end{aligned}$$

(3.5)

However, considering the negativity of the linearization error and the non-monotonicity for the nonconvex function $h_{x^k}(\cdot )$, as a result many more difficulties are introduced. Besides, the computations for the value $h_{k}(y^i)$ and its subgradient $g_h^i$, at each iteration, are relatively expensive. Thus, the formula (3.5) does not apply to our nonconvex optimization in our setting. Then we have to deal with them adequately along the iterative process.

The oracle output is collected along the iterative process to form the “Bundle” of information

$$\begin{aligned} \begin{array}{lllll} &{} \mathcal {B}_{k}^f:=\Big \{(x^{j}, f^{j}, g^j_{{f}}){:}\, j\in L_k^f \Big \} \ \ \mathrm{for} \ L_k^f\subset \{1,\ldots , k\};\\ &{} \mathcal {B}_k^c :=\Big \{(x^{j},c^{j}, g^j_{{c}}){:}\, j\in L_k^c \Big \} \ \ \ \mathrm{for} \ L_k^c\subset \{1,\ldots , k\}, \end{array}\end{aligned}$$

(3.6)

where $L_k^f$ and $L_k^c$ are respectively index sets for the objective function and the constrained function at the kth iteration. We now define respectively the linearization errors for f and c at $x^k$ as

$$\begin{aligned}&e_{f_{j}}^k:=\hat{f}^k-f^j-\left\langle g^j_{{f}},x^k-y^j\right\rangle , \ \ j\in L_k^f,\nonumber \\&e_{c_{j}}^k:=\hat{c}^k-c^j-\left\langle g^j_{{c}},x^k-y^j\right\rangle , \ \ j\in L_k^c. \end{aligned}$$

(3.7)

Possible negativity of linearization errors is more strictly linked to nonconvexity of f and c compared to inexact oracle information. Some appropriate adjustments should be introduced, such as by adding the second-order relation

$$\begin{aligned} p_j^k:=\frac{\mu _{k}}{2}\Vert y^j-x^k\Vert ^2 \end{aligned}$$

where $\mu _k$ is the so-called convexification parameter.

Having this information, the kth approximate piecewise-linear models for $f,\,c$ are generated by

$$\begin{aligned} \check{f}_k (y)= & {} \max \limits _{j\in L_k^f } \left\{ f_j^k+\left\langle \hat{g}_{f_j}^k, y-y^j \right\rangle \right\} \nonumber \\= & {} \hat{f}^k+\max \limits _{j\in L_k^f } \left\{ -\hat{e}_{f_j}^k+\left\langle \hat{g}_{f_j}^k,y-x^k \right\rangle \right\} , \end{aligned}$$

(3.8a)

$$\begin{aligned} \check{c}_{k} (y)= & {} \max \limits _{j\in L_k^c } \left\{ c^k_j+\left\langle \hat{g}_{c_j}^k,y-y^j \right\rangle \right\} \nonumber \\= & {} \hat{c}^k+\max \limits _{j\in L_k^c } \left\{ -\hat{e}_{c_j}^k+\left\langle \hat{g}_{c_j}^k,y-x^k \right\rangle \right\} , \end{aligned}$$

(3.8b)

where

$$\begin{aligned} f^k_j:=f^j+p_j^k \ \ \mathrm{and} \ \ \hat{e}_{f_{j}}^k:= e_{f_{j}}^k+p_j^k, \ \mathrm{for\ all} \ j\in L_k^f, \end{aligned}$$

(3.9a)

$$\begin{aligned} c^k_j:=c^j+p_j^k \ \ \mathrm{and} \ \ \hat{e}_{c_{j}}^k:= e_{c_{j}}^k+p_j^k, \ \mathrm{for\ all} \ j\in L_k^c, \end{aligned}$$

(3.9b)

$$\begin{aligned} \hat{g}_{f_j}^k:= g_{{f}}^j+\mu _{k}(y^j-x^k), \ \ j\in L_k^f \ \ \mathrm{and} \ \ \hat{g}_{c_j}^k:= g_{{c}}^j+\mu _{k}(y^j-x^k), \ \ j\in L_k^c. \end{aligned}$$

(3.9c)

The challenge is therefore to select $\mu _k$ sufficiently large that $\hat{e}_{f_{j}}^k\ge 0$ and $\hat{e}_{c_{j}}^k\ge 0$ for all j but sufficiently small to remain manageable. Inspired by [17], we define the parameter as follows:

$$\begin{aligned} \mu _{{k}}:=\max \Big \{\max _{j\in L_k^f/ \{j_k\}} \frac{-2 e_{f_j}^k}{\Vert y^j-x^k\Vert ^2}, \ \max _{j\in L_k^c/ \{j_k\}} \frac{-2 e_{c_j}^k}{\Vert y^j-x^k\Vert ^2}, 0 \Big \}+\iota , \ \mathrm{where} \ \iota >0. \end{aligned}$$

(3.10)

Different from (3.5), having piecewise-linear models (3.8), the kth inexact improvement function is modelled by the following model function:

$$\begin{aligned} \Psi _k(y)= \left\{ \check{f}_{k} (y)-\theta _1^k, \check{c}_{k} (y)-\theta _2^k \right\} , \end{aligned}$$

(3.11)

By this mean, the model function will maintain powerful relationships with the original functions f and c.

3.2 Inexact proximal bundle method

Let $\Vert \cdot \Vert$ be the Euclidean norm, $\Vert \cdot \Vert _{k}$ primal metrics and $|\cdot |_{k}$ dual metrics. The iterative point $y^{k+1}$ is nothing but the computation of the proximal point of the model function (3.11), with prox-center (stability center) $x^k$ and a variable prox-metric depending on matrices $M_k$. More specifically, the positive definite matrix $M_k$ of order n has the form

$$\begin{aligned} M_k:= A_k + \eta _{k} I, \end{aligned}$$

where the parameter $\eta _{k}>0,\,A_k$ is a symmetric $n\times n$ matrix, and I the identity matrix of order n. As a result, we introduce the corresponding primal and dual metrics for each $z\in \mathbf R ^n$ as follows:

$$\begin{aligned} \texttt { primal metrics}{:}\,\Vert z\Vert _{k}^2:=z^\mathrm{T} M_{k} z \ \ \ \ \mathrm{and} \ \ \ \ \texttt { dual metrics}{:}\,|z|_{k}^2:=z^\mathrm{T} (M_{k})^{-1} z.\nonumber \\ \end{aligned}$$

(3.12)

Let $\lambda _{\mathrm{max}}$ and $\lambda _{\mathrm{min}}$ denote, respectively, the maximum eigenvalue and the minimum eigenvalue, then

$$\begin{aligned} \lambda _{\mathrm{max}}(M_k)= \lambda _{\mathrm{max}}(A_k)+\eta _{k} \ \ \mathrm{and} \ \ \lambda _{\mathrm{min}}((M_k)^{-1})= \frac{1}{\lambda _{\mathrm{max}}(A_k)+\eta _{k}}. \end{aligned}$$

(3.13)

As a result, by the Euclidean norm, it holds that

$$\begin{aligned} \Vert z\Vert _{k}^2\ge (\lambda _{\mathrm{min}}(A_k)+\eta _{k})\Vert z\Vert ^2 \ \ \ \ \mathrm{and} \ \ \ \ |z|_{k}^2\ge \frac{1}{(\lambda _{\mathrm{max}}(A_k)+\eta _{k})}\Vert z\Vert ^2. \end{aligned}$$

(3.14)

Given a positive definite matrix $M_k$, the next iterative point $y^{k+1}$ is generated by solving the following quadratic programming (QP) problem

$$\begin{aligned} \min \limits _{y\in \mathcal {X}} \Psi _{k}(y)+\frac{1}{2}\Vert y-x^k\Vert _{k}^2. \end{aligned}$$

(3.15)

If $y^{k+1}$ satisfies the descent condition, then $x^{k+1}=y^{k+1}$ declares a serious point (a new stability center). Otherwise, it declares a null step, i.e., $x^{k+1}=x^{k}$ and only updates the next piecewise linear model. With (3.15) as a QP$(\mathcal {B}_k)$ with an extra scalar variable r as follows

$$\begin{aligned} \begin{array}{lll} \min \limits _{(y,r)\in \mathcal {X}\times \mathbf R } &{}\quad r+\frac{1}{2}\Vert y-x^k\Vert _{k}^2,\\ s.t. &{}\quad \hat{f}^k-\theta _1^k-\hat{e}_{f_j}^k+\left\langle \hat{g}_{{f_j}}^k,y-x^k \right\rangle \le r, \ \ j\in L_k^f,\\ &{}\quad \hat{c}^k-\theta _2^k-\hat{e}_{c_j}^k+\left\langle \hat{g}_{{c_j}}^k,y-x^k \right\rangle \le r, \ \ j\in L_k^c. \end{array}\end{aligned}$$

(3.16)

More precisely, let $(\lambda ^k, \gamma ^k) \in \mathbf R _{+}^{|L^f_k|}\times \mathbf R _{+}^{|L^c_k|}$ denote the optimal solution of the dual problem of (3.16), considering the primal and dual optimal variables, then the following relations are easily recognized to hold:

$$\begin{aligned} y^{k+1}= x^k-M_k^{-1} (G^k+\alpha ^k) \end{aligned}$$

(3.17)

where

$$\begin{aligned} \begin{array}{llll} G^{k}:=\sum \limits _{j \in L_k^{f}} \lambda ^k_j\hat{g}_{{f_j}}^k +\sum \limits _{j \in L_k^{c}} \gamma ^k_j \hat{g}_{{c_j}}^{k}\in \partial \Psi _{k}(y^{k+1}),\ \ \alpha ^k \in \partial i_{\mathcal {X}}(y^{k+1}), \end{array} \end{aligned}$$

(3.18a)

$$\begin{aligned} \sum \limits _{j \in L^f_k} \lambda ^k_j +\sum \limits _{i \in L^c_k} \gamma ^k_j =1, \ \mathrm{with} \ \lambda ^k_j \ge 0, \ j \in L^f_k \ \mathrm{and} \ \gamma ^k_j \ge 0, \ j \in L^c_k. \end{aligned}$$

(3.18b)

After solving the problem (3.16), the aggregate linearization

$$\begin{aligned} \psi _{k}(y):=\Psi _{k}(y^{k+1})+\left\langle G^k, y-y^{k+1}\right\rangle \end{aligned}$$

(3.19)

which is an affine function, and implies that $\psi _{k}(y^{k+1})=\Psi _{k}(y^{k+1}),\,G^k =\nabla \psi _{k}(y)$. Clearly, because $G^k\in \partial \Psi _{k}(y^{k+1})$,

$$\begin{aligned} \psi _{k}(y)\le \Psi _{k}(y), \ \ \mathrm{for \ all} \ y \in \mathbf R ^n. \end{aligned}$$

(3.20)

The another ingredient in the bundle method is given by the aggregate error, defined by

$$\begin{aligned} V_k:= & {} h_k (x^k)-\psi _{k}(x^{k})\\= & {} h_k (x^k)-\Psi _{k}(y^{k+1})-\left\langle G^k, x^k-y^{k+1}\right\rangle .\nonumber \end{aligned}$$

(3.21)

For our setting, the noise introduced by the nonconvexity and inordinate noise is judged “too large” when the function value at the stability center is below the minimum model value. To judge the inordinate noise, we check the following noise measurement quantity as

$$\begin{aligned} h_k (x^k)-\left( \Psi _{k}(y^{k+1})+\frac{1}{2} \Vert y^{k+1}-x^k \Vert _k^2\right) <0. \end{aligned}$$

(3.22)

To measure progress towards the solution of (1.1), we define the predicted decrease

$$\begin{aligned} \delta _{k}:=h_k (x^k)-\Psi _{k}(y^{k+1})+\left\langle \alpha ^k, x^k-y^{k+1}\right\rangle . \end{aligned}$$

(3.23)

By using the relations (3.12), (3.17) and (3.21), we can obtain

$$\begin{aligned} \delta _{k}= & {} V_k+\left\langle G^k+\alpha ^k, x^k-y^{k+1}\right\rangle \nonumber \\= & {} V_k+\Vert x^k-y^{k+1}\Vert _k^2\\= & {} V_k+|G^k+\alpha ^k|_k^2.\nonumber \end{aligned}$$

(3.24)

Only when the measurement (3.22) does not hold, i.e., the noise is acceptable, then we examine the new iterative point $y^{k+1}$ by checking the descent condition

$$\begin{aligned} \begin{array}{lll} \left\{ \begin{array}{llll} f^{k+1} \le \hat{f}^k -m\delta _k \ \ \mathrm{and} \ \ c^{k+1}\le 0, \ \ &{}\quad \mathrm{if} \ \ \hat{c}^k\le 0, \\ \ c^{k+1}\le \hat{c}^k -m\delta _k, \ \ &{}\quad \mathrm{if} \ \ \hat{c}^k> 0 \end{array}\right. \\ \end{array} \end{aligned}$$

(3.25)

to ensure whether $y^{k+1}$ is good enough to develop into a new stability center. Otherwise, it declares a null step, and the stability center is fixed. The descent condition (3.25) measures the progress towards the solution of (1.1) from two ways. If $\hat{c}^k\le 0$, it reduces the objective value without losing feasibility by checking the first condition in (3.25). Otherwise, when $\hat{c}^k> 0$, the emphasis is put on reducing infeasibility by checking the second condition in (3.25).

Lemma 3.1

Suppose $(r_{k}, y^{k+1})$ is the optimal solution of $QP(\mathcal {B}_k)$. The aggregate linearization error $V_k$ satisfies the following relation:

$$\begin{aligned} V_k\ge \sum \limits _{j \in L_k^{f}}\lambda ^k_j \hat{e}_{f_j}^{k} +\sum \limits _{j \in L_k^{c}}\gamma ^k_j \hat{e}_{c_j}^k>0 \end{aligned}$$

(3.26)

Proof

The Lagrange function of (3.16) can be rewritten as

$$\begin{aligned} \begin{array}{lll} L(y^{k+1}, \lambda ^k,\gamma ^k)&{}= \sum \limits _{j \in L_k^{f}} \lambda ^k_j (\hat{f}^k-\theta _1^k)+ \sum \limits _{j \in L_k^{c}} \gamma ^k_j (\hat{c}^k-\theta _2^k) +\frac{1}{2}\Vert y^{k+1}-x^k\Vert _{k}^2\\ &{} \quad +\,\sum \limits _{j \in L_k^{ f}} \lambda ^k_j \left( -\hat{e}_{f_j}^k+\left\langle \hat{g}_{f_j}^k, y^{k+1}-x^k \right\rangle \right) +\sum \limits _{j \in L_l^{c}} \gamma ^l_j \left( -\hat{e}_{c_j}^{k}+\left\langle \hat{g}_{c_j}^{k}, y^{k+1}-x^k \right\rangle \right) , \end{array} \end{aligned}$$

which implies that

$$\begin{aligned} L(y^{k+1}, \lambda ^k,\gamma ^k)= & {} \sum \limits _{j \in L_k^{f}} \lambda ^k_j (\hat{f}^k-\theta _1^k)+ \sum \limits _{j \in L_k^{c}} \gamma ^k_j (\hat{c}^k-\theta _2^k) +\frac{1}{2}\Vert y^{k+1}-x^k\Vert _{k}^2\\&\quad -\,\left( \sum \limits _{j \in L_k^{ f}} \lambda ^k_{j} \hat{e}_{f_j}^k +\sum \limits _{j \in L_k^{c}} \gamma ^k_j \hat{e}_{c_j}^{k}\right) + \left\langle G^{k}, y^{k+1}-x^k \right\rangle . \end{aligned}$$

On the other hand,

$$\begin{aligned} L(y^{k+1},\lambda ^k,\gamma ^k) = \Psi _k(y^{k+1})+\frac{1}{2}\Vert y^{k+1}-x^k\Vert _{k}^2, \end{aligned}$$

implies that

$$\begin{aligned}&\sum \limits _{j \in L_k^{ f}} \lambda ^k_{j} \hat{e}_{f_j}^k +\sum \limits _{j \in L_k^{c}} \gamma ^k_j \hat{e}_{c_j}^{k}= \sum \limits _{j \in L_k^{f}} \lambda ^k_j (\hat{f}^k-\theta _1^k)\nonumber \\&\quad +\,\sum \limits _{j \in L_k^{c}} \gamma ^k_j (\hat{c}^k-\theta _2^k) -\Psi _k(y^{k+1})+\left\langle G^{k}, y^{k+1}-x^k \right\rangle . \end{aligned}$$

(3.27)

By noting (3.1), we can obtain that

$$\begin{aligned} h_{k}(x^k)=\max \left\{ \hat{f}^k -\theta _1^k, \hat{c}^k -\theta _2^k \right\} \ge \sum \limits _{j \in L_k^{f}} \lambda ^k_j \left( \hat{f}^k-\theta _1^k\right) + \sum \limits _{j \in L_k^{c}} \gamma ^k_j \left( \hat{c}^k-\theta _2^k\right) . \end{aligned}$$

Together with the functional relations (3.19) and (3.21), we obtain that

$$\begin{aligned} V_k \ge \sum \limits _{j \in L_k^{ f}} \lambda ^k_{j} \hat{e}_{f_j}^k +\sum \limits _{j \in L_k^{c}} \gamma ^k_j \hat{e}_{c_j}^{k}. \end{aligned}$$

It follows from (3.10) for selecting $\mu _{k}$ that the relation (3.26) holds. From here, the required result follows. $\square$

Our method is based on the ideas of [31], and extend them to nonconvex constrained optimization problems. We now give our bundle method for solving problem (1.1)

We now suppose that $\{\mu _{k}\}$ is bounded. Boundedness of the sequence of $\{\mu _{k}\}$ has been proved in [17, 55] for the lower-$C^2$ functions with an exact oracle. In theory, inexactness may result in an unbounded $\mu _k$ in our setting. The numerical experiments in Sect. 6 show that $\{\mu _{k}\}$ is bounded under various kinds of perturbations, and our inexact method is satisfactory.

4 Asymptotic analysis

We now analyze the different cases that can arise when Algorithm 3.1 loops forever. As usual in the convergence analysis of bundle methods, we consider the following two possible cases:

• either there are infinitely many serious steps, or

• there is an finite number of serious steps, followed by infinitely many null steps.

We start with the case of infinitely many serious steps.

4.1 Infinite serious steps

Theorem 4.1

Suppose that Algorithm 3.1 generates an infinite sequence $\{x^k\}$ of serious steps. Let $\mathcal {L}_s$ denote the set gathering indices of serious steps. Then $\delta _k \rightarrow 0$ and $V_k \rightarrow 0$ as $\mathcal {L}_s\ni k\rightarrow \infty$.

• In addition, if the series $\sum \nolimits _{k\in \mathcal {L}_s}\frac{1}{\lambda _{\mathrm{max}}(A_k)+\eta _{k}}$ is divergent, then $\liminf \nolimits _{k\rightarrow \infty } \Vert G^k+\alpha ^k\Vert =0$. Besides, there exists some subsequence $\mathcal {K}_s \subseteq \mathcal {L}_s$ and an accumulation $\hat{x}$ such that $x^k\rightarrow \hat{x}$ and $G^k\rightarrow \hat{G}$ as $\mathcal {K}_s\ni k\rightarrow \infty$.

• If, instead of the above weaker condition, the sequence $\{{\lambda _{\mathrm{max}}(A_k)+\eta _{k}}\}$ is bounded above, then $\lim \nolimits _{k\rightarrow \infty }\Vert G^k+\alpha ^k\Vert =0$, and same assertions hold for all accumulation points of the sequence $\{x^k\}$.

Proof

We examine the following two different possibilities respectively. In the first case, if there exists some $\tilde{k}$ such that $\hat{c}^{\tilde{k}}\le 0$, together with satisfaction of the first condition in (3.25), this means that

$$\begin{aligned} \hat{c}^{k+1}\le 0, \ \ \mathrm{for \ all} \ \mathcal {L}_s \ni k\ge \tilde{k}. \end{aligned}$$

and

$$\begin{aligned} 0<m\delta _k \le \hat{f}^k -\hat{f}^{k+1}, \ \ \mathrm{for \ all} \ \mathcal {L}_s \ni k\ge \tilde{k}. \end{aligned}$$

(4.1)

Together with the basic assumptions on f, we can obtain that the sequence $\{\hat{f}^k\}_{\mathcal {L}_s}$ is decreasing and bounded. Hence there exists some $\hat{f}$ such that the sequence $\{ \hat{f}^k\}_{\mathcal {L}_s }$ converges to $\hat{f}$ satisfying $\hat{f}\le \hat{f}^k$ for all $k\ge \tilde{k}$ in $\mathcal {L}_s$. Summing up the relations (4.1), we obtain that

$$\begin{aligned} \sum _{ \mathcal {L}_s \ni k\ge \tilde{k}}\delta _k \le \frac{1}{m}\sum _{ \mathcal {L}_s \ni k\ge \tilde{k}} (\hat{f}^k -\hat{f}^{k+1}) =\frac{1}{m}(\hat{f}^{\tilde{k}} -\hat{f}), \end{aligned}$$

which implies $\delta _k\rightarrow 0$ as $\mathcal {L}_s \ni k\rightarrow \infty$.

On the other hand, if $\hat{c}^{k}>0$ for all $k\in \mathcal {L}_s$, then (3.25) implies that

$$\begin{aligned} 0<\delta _k\le \frac{1}{m}(\hat{c}^k -\hat{c}^{k+1}). \end{aligned}$$

By the same argument, the sequence $\{\hat{c}^k\}$ is decreasing and bounded below. Then it converges to a value $\hat{c}$ satisfying $\hat{c} \le \hat{c}^k$ for all $k\ge \tilde{k}$ in $\mathcal {L}_s$. As a result, summing up the above relation over all $\mathcal {L}_s$, we see that

$$\begin{aligned} \sum _{k\in \mathcal {L}_s}\delta _k \le \frac{1}{m}\sum _{ k\in \mathcal {L}_s} (\hat{c}^k -\hat{c}^{k+1}) =\frac{1}{m}( \hat{c}^{0} -\hat{c}), \end{aligned}$$

which means $\lim \nolimits _{k\in \mathcal {L}_s} \delta _k=0$. Together with (3.14) and (3.24) we see that

$$\begin{aligned} 0\le V_k\le \delta _k \ \ \mathrm{and} \ \ \frac{1}{\lambda _{\mathrm{max}}(A_k)+\eta _{k}}\Vert G^k+\alpha ^k\Vert ^2\le \mid G^k+\alpha ^k\mid _{k}^2\le \delta _k, \end{aligned}$$

and, hence $V_k\rightarrow 0$ as $\mathcal {L}_s\ni k\rightarrow \infty$.

By noting the relation (3.24), we obtain that

$$\begin{aligned} \sum _{k\in \mathcal {L}_s}\delta _k=\sum _{k\in \mathcal {L}_s}\left( V_k+\mid G^k+\alpha ^k\mid _{k}^2\right) < \infty . \end{aligned}$$

Since all the quantities are nonnegative, and together with (3.14), it holds that

$$\begin{aligned} 0<\sum _{k\in \mathcal {L}_s}\frac{1}{\lambda _{\mathrm{max}}(A_k)+\eta _{k}}\Vert G^k+\alpha ^k\Vert ^2 \le \sum _{k\in \mathcal {L}_s}\mid G^k+\alpha ^k\mid _{k}^2< \infty . \end{aligned}$$

If a weaker condition holds, i.e., $\sum \nolimits _{k\in \mathcal {L}_s}\frac{1}{\lambda _{\mathrm{max}}(A_k)+\eta _{k}}$ is divergent, then we can obtain $\liminf \nolimits _{k\rightarrow \infty } \Vert G^k+\alpha ^k\Vert =0$. Passing onto the subsequence $\mathcal {K}_s$, if necessary, we can suppose $\{x^k\}\rightarrow \hat{x}$ and $G^k\rightarrow \hat{G}$ as $\mathcal {K}_s \ni k\rightarrow \infty$. From here first item is now proven. Furthermore, if the sequence $\{\lambda _{\mathrm{max}}(A_k)+\eta _{k}\}$ is bounded above, we obtain that

$$\begin{aligned} \Vert G^k+\alpha ^k\Vert \rightarrow 0, \ \ \ \mathcal {L}_s\ni k\rightarrow \infty , \end{aligned}$$

(4.2)

which implies that the same assertions can be proven for all accumulations of $\{x^k\}$. From here all results have been proven. $\square$

4.2 Infinitely many consecutive null steps

The another case refers to finitely many serious steps, which implies Algorithm 3.1 makes infinitely many consecutive null steps. Let $\hat{k}$ denote the last serious index, and $\hat{x}:=x^{\hat{k}}$ be the last stability center. By adjusting the strategy of the bundle management, the model is ensured to satisfy the following conditions whenever k and $k+1$ are two consecutive null indexes:

$$\begin{aligned}&\check{f}_{k+1} (y) \ge \hat{f}^{k+1}-\hat{e}_{f_{k+1}}^{k+1}+\left\langle \hat{g}_{f_{k+1}}^{k+1},y-\hat{x} \right\rangle ,\nonumber \\&\check{c}_{k+1} (y) \ge \hat{c}^{k+1}-\hat{e}_{c_{k+1}}^{k+1}+\left\langle \hat{g}_{c_{k+1}}^{k+1},y-\hat{x} \right\rangle , \end{aligned}$$

(4.3)

and

$$\begin{aligned} \Psi _{k+1}(y) \ge \psi _{k}(y). \end{aligned}$$

(4.4)

Moreover, let $r_{k}$ denote the objective function optimal value of the (3.15), i.e.,

$$\begin{aligned} r_{k}:=\Psi _{k}(y^{k+1})+\frac{1}{2}\Vert y^{k+1}-x^k\Vert _k^2. \end{aligned}$$

(4.5)

We first prove the following preliminary result regarding relations between consecutive terms of the sequence $\{r_{k}\}$.

Lemma 4.1

Suppose that Algorithm 3.1 takes a finite number of serious steps. The optimal values $r_{k+1}$ and $r_{k}$ satisfy

$$\begin{aligned} r_{k+1}\ge r_{k}+\frac{1}{2}\Vert y^{k+2}-y^{k+1}\Vert _{k}^2. \end{aligned}$$

(4.6)

Then, the following relations hold:

$$\begin{aligned} \begin{array}{lll} \lim \limits _{k\rightarrow \infty }\Vert y^{k+2}-y^{k+1}\Vert _{k}^2=0\\ \lim \limits _{k\rightarrow \infty } \left( r_{k+1}- r_{k}-\frac{1}{2}\Vert y^{k+2}-y^{k+1}\Vert _{k}^2\right) =0. \end{array}\end{aligned}$$

(4.7)

Proof

By noting the definition of $\psi _{k}$ in (3.19), it is easy to see that

$$\begin{aligned} \psi _{k}(y)= & {} \Psi _{k}(y^{k+1})+\left\langle G^k, y-y^{k+1}\right\rangle \\= & {} \Psi _{k}(y^{k+1})+(\hat{x}-y^{k+1})^\mathrm{T}M_k( y-y^{k+1}) -\left\langle \alpha ^k, y-y^{k+1}\right\rangle \\\ge & {} \Psi _{k}(y^{k+1})+\frac{1}{2}\Vert y^{k+1}-\hat{x}\Vert _k^2 +\frac{1}{2}\Vert y-y^{k+1}\Vert _k^2 -\frac{1}{2}\Vert y-\hat{x}\Vert _{k}^2\\= & {} r_k+\frac{1}{2}\Vert y-y^{k+1}\Vert _{k}^2 -\frac{1}{2}\Vert y-\hat{x}\Vert _k^2, \end{aligned}$$

where the inequality has used $\alpha ^k \in \partial i_{\mathcal {X}}(y^{k+1})$, and the last equality follows from (4.5). Hence we can obtain that

$$\begin{aligned} \psi _{k}(y)+\frac{1}{2}\Vert y-\hat{x}\Vert _{k}^2\ge r_k+\frac{1}{2}\Vert y-y^{k+1}\Vert _{k}^2. \end{aligned}$$

(4.8)

By evaluating at $y=\hat{x}$, it follows that

$$\begin{aligned} r_k+\frac{1}{2}\Vert \hat{x}-y^{k+1}\Vert _{k}^2\le \psi _{k}(\hat{x})\le \Psi _{k}(\hat{x}), \end{aligned}$$

where the last inequality has used (3.20), i.e., $\psi _{k}(y)\le \Psi _{k}(y)$. Hence the sequence $\{r_k\}$ is bounded from above. From (4.4), (4.8), and by noting the fact $M_{k+1}\succeq M_{k}$, we can obtain that

$$\begin{aligned} r_k+\frac{1}{2} \Vert y-y^{k+1}\Vert _{k}^2 \le \Psi _{k+1}(y)+\frac{1}{2}\Vert y-\hat{x}\Vert _{k}^2 \le \Psi _{k+1}(y)+\frac{1}{2}\Vert y-\hat{x}\Vert _{k+1}^2. \end{aligned}$$

By evaluating at $y=y^{k+2}$, we obtain that

$$\begin{aligned} r_k+\frac{1}{2}\Vert y^{k+2}-y^{k+1}\Vert _{k}^2 \le r_{k+1}=\Psi _{k+1}(y^{k+2})+\frac{1}{2}\Vert y^{k+2}-\hat{x}\Vert _{k+1}^2, \end{aligned}$$

which implies that the relation (4.6) holds. Since the sequence $\{r_k\}$ is monotone increasing and bounded from above, we also obtain the result (4.7) holds. $\square$

Theorem 4.2

Suppose that Algorithm 3.1 generates a finite sequence of serious steps, and the sequence $\{\mu _k\}$ be bounded. Let $\mathcal {L}_n$ denote the set gathering indices of iterations larger than $\hat{k}$. Then $\delta _k \rightarrow 0$ and $V_k \rightarrow 0$ as $\mathcal {L}_n \ni k\rightarrow \infty$.

• If, in addition, $\liminf \nolimits _{k\rightarrow \infty } \frac{1}{\eta _{k}} >0$, then there exists a subsequence $\mathcal {K}_n\subseteq \mathcal {L}_n$, such that $\Vert G^k+\alpha ^k\Vert \rightarrow 0,\,y^k \rightarrow \hat{x}$ and $G^k\rightarrow \bar{G}$ as $\mathcal {K}_n\ni k\rightarrow \infty$.

• If, instead of the above weaker condition, there exists $\eta _{\mathrm{max}}>0$ such that $\eta _{k}\le \eta _{\mathrm{max}}$, then $\Vert G^k+\alpha ^k\Vert \rightarrow 0$ and $y^k \rightarrow \hat{x}$ as $\rightarrow \infty$.

Proof

For convenience, let $\hat{x}=x^{k},\,\hat{f}=\hat{f}^{k},\,\hat{c}=\hat{c}^{k},\,\hat{A}=A_{\hat{k}}$ $\hat{\theta }_1=\theta _1^k,\,\hat{\theta }_2=\theta _2^k$, and $\hat{h}=h_{k}(x^k)$ for all $k\ge \hat{k}$. By noting the definition of the inexact improvement function, we can obtain that

$$\begin{aligned} h_{k}(y^{k+1})= & {} \max \Big \{ f^{k+1} -\theta _1^k, c^{k+1}-\theta _2^k \Big \}\\= & {} \left\{ \begin{array}{llll} \max \Big \{ f^{k+1} -\hat{f}-s_k \hat{c}, c^{k+1}-t_k \hat{c} \Big \}, &{}\quad \mathrm{if} \ \hat{c} >0, \\ \max \Big \{ f^{k+1} -\hat{f}, c^{k+1} \Big \}, \ \ &{}\quad \mathrm{if} \ \hat{c} \le 0 \end{array}\right. \\ \end{aligned}$$

If $\hat{c}>0$, yields,

$$\begin{aligned} h_{x^k}(y^{k+1})\ge & {} c^{k+1}-t_k \hat{c}\nonumber \\\ge & {} \hat{c}-t_k \hat{c} -m\delta _k\nonumber \\= & {} \hat{h}-m\delta _k, \end{aligned}$$

(4.9)

where the second inequality follows from (3.25), and the last equality has used the relation (3.4).

On the other hand, if $\hat{c} \le 0$, it follows from (3.4) that $\hat{h}=0$. By combining with (3.25), we get

$$\begin{aligned} \begin{array}{lll} h_{k}(y^{k+1})&{}\ge \left\{ \begin{array}{llll} f^{k+1} -\hat{f}, \ \ \ \ \mathrm{and} \\ c^{k+1} \end{array}\right. \\ &{}>\left\{ \begin{array}{llll} -m\delta _k, &{} \mathrm{if} \ f^{k+1}> \hat{f} -m\delta _k, \\ 0, \ \ &{} \mathrm{if} \ c^{k+1}> 0 \end{array}\right. \\ &{}\ge \hat{h}-m\delta _k. \end{array}\end{aligned}$$

(4.10)

By adding $\delta _k$ to both terms, we can obtain that

$$\begin{aligned} 0 \le (1-m)\delta _k< h_{k}(y^{k+1})-\hat{h}+\delta _k \le h_{k}(y^{k+1})-\Psi _{k}(y^{k+1}), \end{aligned}$$

(4.11)

where the last inequality has used the relation (3.23), that is

$$\begin{aligned} -\hat{h}+\delta _{k} =-\Psi _{k}(y^{k+1})+\langle \alpha ^k, \hat{x}-y^{k+1}\rangle \le -\Psi _{k}(y^{k+1}). \end{aligned}$$

Following (3.9) and (4.3), we can observe that

$$\begin{aligned}&\check{f}_{k+1} (y^{k+2}) \ge \hat{f}-\hat{e}_{f_{k+1}}^{k+1}+\left\langle \hat{g}_{f_{k+1}}^{k+1},y^{k+2}-\hat{x} \right\rangle \nonumber \\&\quad =f^{k+1}+\left\langle g_{{f_{k+1}}},\hat{x}-y^{k+1} \right\rangle -\frac{\mu _{k+1}}{2}\Vert y^{k+1}-\hat{x}\Vert ^2 +\left\langle g_{{f_{k+1}}}+\mu _{k+1}(y^{k+1}-\hat{x}),y^{k+2}-\hat{x} \right\rangle \nonumber \\&\quad \ge f^{k+1}+\left\langle g_{{f_{{k+1}}}},y^{k+2}-y^{k+1} \right\rangle +\mu _{k+1}\left\langle y^{k+1}-\hat{x},y^{k+2}-y^{k+1} \right\rangle \nonumber \\&\quad =f^{k+1}+\left\langle \hat{g}_{{f_{k+1}}}^{k+1},y^{k+2}-y^{k+1} \right\rangle . \end{aligned}$$

(4.12)

By the same argument, we obtain that

$$\begin{aligned} \check{c}_{k+1} (y^{k+2}) \ge c^{k+1}+\left\langle \hat{g}_{c_{k+1}}^{k+1},y^{k+2}-y^{k+1} \right\rangle . \end{aligned}$$

(4.13)

Besides, from (3.11), (4.12) and (4.13), we get

$$\begin{aligned} \Psi _{k+1}(y^{k+2})= & {} \left\{ \check{f}_{{k+1}} (y^{k+2})-\hat{\theta }_1, \check{c}_{{k+1}} (y^{k+2})-\hat{\theta }_2\right\} \\\ge & {} \left\{ f^{k+1}+\left\langle \hat{g}_{f_{k+1}}^{k+1}, y^{k+2}-y^{k+1} \right\rangle -\hat{\theta }_1, c^{k+1}+\left\langle \hat{g}_{c_{k+1}}^{k+1},y^{k+2}-y^{k+1} \right\rangle -\hat{\theta }_2 \right\} . \end{aligned}$$

By noting the sequence $\{y^k\}\subset \mathcal {X}$, there exists a positive constant $N>0$ such that $\Vert y^k-\hat{x}\Vert \le N$ for all k. Therefore,

$$\begin{aligned} \Psi _{k+1}(y^{k+2})\ge & {} \Big \{ f^{k+1}-\theta _1^k, c^{k+1}-\theta _2^k \Big \}-(L+\mu _{{k+1}}N)\Vert y^{k+2}-y^{k+1}\Vert \\= & {} h_{k}(y^{k+1})-(L+\mu _{{k+1}}N)\Vert y^{k+2}-y^{k+1}\Vert , \end{aligned}$$

where the inequality has used the fact that $g_c^{k+1}$ and $g_f^{k+1}$ are bounded (recall that f and c are locally Lipschitzian). By combining with (4.11), we obtain that

$$\begin{aligned}&0 \le (1-m)\delta _k\\&< \Psi _{k+1}(y^{k+2}) -\Psi _{k}(y^{k+1})+ (L+\mu _{{k+1}}N) \Vert y^{k+2}-y^{k+1}\Vert \\&=r_{{k+1}}-\frac{1}{2}\Vert y^{k+2}-\hat{x}\Vert _{k+1}^2-r_{k}+\frac{1}{2}\Vert y^{k+1}-\hat{x}\Vert _{k}^2 +(L+\mu _{{k+1}}N)\Vert y^{k+2}-y^{k+1}\Vert , \end{aligned}$$

where the last equality comes from the relation (4.5). From the relation (3.14) and the condition $M_{k+1}\succ M_k$, we get

$$\begin{aligned} \begin{array}{ll} &{}0 \le (1-m)\delta _k \\ &{}\quad <r_{k+1}-r_{k}-\frac{1}{2}\Vert y^{k+2}-\hat{x}\Vert _{k}^2+\frac{1}{2}\Vert y^{k+1}-\hat{x}\Vert _{k}^2 +(L+\mu _{{k+1}}N)\Vert y^{k+2}-y^{k+1}\Vert \\ &{}\quad =\frac{1}{2}\Vert y^{k+2}-y^{k+1}\Vert _{k}^2 -\frac{1}{2}\Vert y^{k+2}-\hat{x}\Vert _{k}^2+\frac{1}{2}\Vert y^{k+1}-\hat{x}\Vert _{k}^2\\ &{}\qquad +\,(L+\mu _{{k+1}}N)\Vert y^{k+2}-y^{k+1}\Vert + r_{k+1}-r_{k}-\frac{1}{2}\Vert y^{k+2}-y^{k+1}\Vert _{k}^2\\ &{}\quad =\langle y^{k+2}-y^{k+1}, M_{k}^{-1} (G^k+\alpha ^k) \rangle +(L+\mu _{{k+1}}N) \Vert y^{k+2}-y^{k+1}\Vert + r_{k+1}-r_{k}-\frac{1}{2}\Vert y^{k+2}-y^{k+1}\Vert _{k}^2\\ &{}\quad \le \langle y^{k+2}-y^{k+1}, \frac{1}{\lambda _{\mathrm{min}}(\hat{A})+\hat{\eta }} (G^k+\alpha ^k) \rangle +(L+\mu _{{k+1}}N) \Vert y^{k+2}-y^{k+1}\Vert + r_{k+1}-r_{k}-\frac{1}{2}\Vert y^{k+2}-y^{k+1}\Vert _{k}^2\\ &{}\quad \le \left( L+\mu _{{k+1}}N+\frac{1}{\lambda _{\mathrm{min}}(\hat{A})+\hat{\eta }} \Vert G^k\Vert \right) \Vert y^{k+2}-y^{k+1}\Vert + r_{k+1}-r_{k}-\frac{1}{2}\Vert y^{k+2}-y^{k+1}\Vert _{k}^2\\ &{}\quad \le \left( L+\mu _{{k+1}}N+\frac{L}{\lambda _{\mathrm{min}}(\hat{A})+\hat{\eta }}\right) \Vert y^{k+2}-y^{k+1}\Vert + r_{k+1}-r_{k}-\frac{1}{2}\Vert y^{k+2}-y^{k+1}\Vert _{k}^2, \end{array} \end{aligned}$$

where the last inequality follows from $G^k \in conv\{g_f^{j},\ g_c^{j}, \ j\in L_k \}$ and $\hat{\eta }:=\eta _{\hat{k}}\le \eta _{k}$ for all $k\ge \hat{k}$. Passing to the limit as $k\rightarrow \infty$, and using (4.7) in Lemma 4.1, we obtain that $\lim \nolimits _{k\rightarrow \infty } \delta _k=0$. Together with (3.14) and (3.24) we see that

$$\begin{aligned} 0\le V_k\le \delta _{k} \ \ \ \mathrm{and} \ \ \ \frac{1}{\left( \lambda _{\mathrm{max}}(\hat{A})+\eta _{k}\right) }\Vert G^k+\alpha ^k\Vert ^2\le \mid G^k+\alpha ^k\mid _{k}^2\le \delta _k, \end{aligned}$$

Since $\liminf \nolimits _{k\rightarrow \infty } \frac{1}{\eta _{k}} >0$, we obtain that $\lim \nolimits _{\mathcal {K}\ni k\rightarrow \infty } V_k=0$ and $\lim \nolimits _{\mathcal {K} \ni k\rightarrow \infty } \Vert G^k+\alpha ^k\Vert =0$ for some subsequence $\mathcal {K}$. Furthermore, it is follows from (3.17) and $M_{k+1}\succeq M_{k}$ that $\lim \nolimits _{\mathcal {K} \ni k\rightarrow \infty } y^{k}=\hat{x}$. If $\eta _{k}\le \eta _{\mathrm{max}}$, it is obviously that $\Vert G^k+\alpha ^k\Vert \rightarrow 0$ and $y^k \rightarrow \hat{x}$ as $\rightarrow \infty$. From here the results have been proved. $\square$

5 Convergence results

One of purposes of conditions (3.3) is to ensure satisfaction of the relations stated in the following lemma. Let $x^*$ denote an accumulation point of $\{x^k\},\,(f^*,c^*)$ and $(s_*,t_*)$ be the limit points of $\{(f^k,c^k)\}$ and $\{(x_k,t_k)\}$ respectively. We can define the constant $\varpi$ in (3.3) satisfying $\varpi >\frac{1}{c^{*}}(\max \nolimits _{x\in \mathcal {X} } \{f(y)-c(y)\}-f^{*})$, which implies that the penalty parameters $s_{k},\,t_k$ satisfy

$$\begin{aligned} s_{k}-t_{k}>\left( \max _{x\in \mathcal {X} } \{f(y)-c(y)\}-f^{*}\right) \big /c^{*}. \end{aligned}$$

(5.1)

Theorem 5.1

Suppose that Algorithm 3.1 solves (1.1) satisfying (2.11), (2.12) with penalty parameters $s_k$ and $t_k$ satisfying (3.3).

If the algorithm loops forever, then for each $\theta ^*>0$, there exists a positive constant $\rho ^*$ such that

• $$\begin{aligned} (1-t^*)\max \{c^*,0\} \le \max \Big \{ f(y)-f^*-s_*\max \{c^*,0\}, c(y)-t_*\max \{c^*,0\} \Big \}+\epsilon ,\nonumber \\ \end{aligned}$$

  (5.2)

  for all $y \in B_{\rho ^*}(x^*) \bigcap \mathcal {X}$, where $\epsilon :=(\theta ^*+\bar{\varepsilon })\rho ^*+\bar{\sigma }$.

• If $c^*>0$ then

  $$\begin{aligned} c^* \le c(y)+\epsilon \ \ \mathrm{for\ all} \ y. \end{aligned}$$

• If $c^*<0$ and $X_{\epsilon }:=\{y\in X:c(y)< -\epsilon \}$ is not empty set, it holds that

  $$\begin{aligned} f^*\le f(y)+\epsilon \ \ \mathrm{for \ all } \ \ y\in X_{\epsilon }. \end{aligned}$$

Proof

If Algorithm 3.1 loops forever, since the set $\mathcal {X}$ is compact and $x^k \in \mathcal {X}$, there exists an index set $\mathcal {L}'$ such that $\{x^k\}_{k\in \mathcal {L}'}\rightarrow x^*$, and recalling that when $\mathcal {L}'=\mathcal {L}_{s}$ eventually $x^*=\lim \nolimits _{k\rightarrow \infty }y^k$. Let $q_{{f}}^j\in \partial f(x^j)$ and by noting (3.7) and (3.9), we obtain that

$$\begin{aligned}&\hat{f}^k+\left\langle g_{{f}}^j, y-x^k \right\rangle +p_j^k-\hat{e}_{f_j}^k\nonumber \\&\quad =f^j+\left\langle g_{{f}}^j, y-y^j \right\rangle \nonumber \\&\quad = f(y^j)+\left\langle q_{{f}}^j, y-y^j \right\rangle -\sigma _{j} + \left\langle g_{{f}}^j-q_{{f}}^j, y-y^j \right\rangle , \end{aligned}$$

(5.3)

where the last equality follows from (2.11). By noting the definition of lower-$\mathcal {C}^1$, then for all $y^j$ and $\theta ^j>0$, there exists $\rho ^j >0$ such that

$$\begin{aligned} f (y)-f (y^j) \ge \langle q_{{f}}^j,y-y^j \rangle -\theta ^j \Vert y-y^j\Vert ,\ \mathrm{for \ all} \ y\in B_{\rho ^j}(y^j), \end{aligned}$$

which combined with the relation (5.3), implies that

$$\begin{aligned}&\hat{f}^k+\left\langle g_{{f}}^j, y-x^k \right\rangle +p_j^k-\hat{e}_{f_j}^k\nonumber \\&\quad \le f(y)+(\theta ^j+\varepsilon _j) \Vert y-y^j\Vert -\sigma _{j}\nonumber \\&\quad \le f(y)+(\theta ^j+\varepsilon _j)\rho ^{j}-\sigma _{j}. \end{aligned}$$

(5.4)

Together with satisfaction of (3.9c), i.e., $g_{{f}}^j= \hat{g}_{f_j}^k-\mu _k(y^j-x^k)$, it holds that

$$\begin{aligned}&f(y)+(\theta ^j+\varepsilon _j)\rho ^{j}-\sigma _{j}\\&\quad \ge \hat{f}^k+\left\langle g_{{f}}^j, y-x^k \right\rangle +p_j^k-\hat{e}_{f_j}^k\\&\quad =\hat{f}^k-\hat{e}_{f_j}^k+\left\langle \hat{g}_{{f_j}}^k, y-x^k \right\rangle -\mu _{k} \left\langle y^j-x^k, y-x^k \right\rangle +p_j^k\\&\quad \ge \hat{f}^k-\hat{e}_{{f_j}}^k+\left\langle \hat{g}_{{f_j}}^k, y-x^k \right\rangle -\mu _{k} \left\langle y^j-x^k, y-x^k \right\rangle , \end{aligned}$$

where the last inequality follows from $p_j^k\ge 0$. The above relation will eventually mean that

$$\begin{aligned} f(y)\ge \hat{f}^k-\hat{e}_{f_j}^k+\left\langle \hat{g}_{f_j}^k, y-x^k \right\rangle -\mu _{k} \left\langle y^j-x^k, y-x^k \right\rangle -(\theta ^j+\varepsilon _j)\rho ^{j}+\sigma _{j}. \end{aligned}$$

(5.5)

By same argument, it holds that

$$\begin{aligned} c(y) \ge \hat{c}^k-\hat{e}_{c_j}^k+\langle \hat{g}_{c_j}^k, y-x^k \rangle -\mu _{k} \langle y^j-x^k, y-x^k \rangle -(\theta ^j+\varepsilon _j)\rho ^{j}+\sigma _{j}. \end{aligned}$$

(5.6)

It follows from (5.5) and (5.6) that

$$\begin{aligned}&\max \left\{ f(y)-\theta _1^{k}, c(y)-\theta _2^{k}\right\} +(\theta ^j+\bar{\varepsilon })\rho ^j+\bar{\sigma }\\&\qquad \ge -\left( \sum \limits _{j \in L_k^{f}}\lambda ^k_j \hat{e}_{f_j}^k +\sum \limits _{j \in L_k^{c}}\gamma ^k_j \hat{e}_{c_j}^{k}\right) +\langle G^k, y-x^k \rangle +\sum \limits _{j \in L_k^{f}} \lambda ^k_j (\hat{f}^k-\theta _1^k)+ \sum \limits _{j \in L_k^{c}} \gamma ^k_j (\hat{c}^k-\theta _2^k)\\&\qquad -\,\mu _k \langle \sum \limits _{j \in L_k^{f}} \lambda ^k_j(y^j-x^k) +\sum \limits _{j \in L_k^{c}} \gamma ^k_j(y^j-x^k), y-x^k \rangle . \end{aligned}$$

Besides, by noting (3.27) and (3.23) it holds that

$$\begin{aligned}&\sum \limits _{j \in L_k^{f}} \lambda ^k_j (\hat{f}^k-\theta _1^k)+ \sum \limits _{j \in L_k^{c}} \gamma ^k_j (\hat{c}^k-\theta _2^k)\nonumber \\&\quad = \sum \limits _{j \in L_k^{ f}} \lambda ^k_{j} \hat{e}_{f_j}^k +\sum \limits _{j \in L_k^{c}} \gamma ^k_j \hat{e}_{c_j}^{k}+\Psi _k(y^{k+1})-\langle G^{k}, y^{k+1}-x^k \rangle \nonumber \\&\quad =\sum \limits _{j \in L_k^{ f}} \lambda ^k_{j} \hat{e}_{f_j}^k +\sum \limits _{j \in L_k^{c}} \gamma ^k_j \hat{e}_{c_j}^{k} +h_{k}(x^k)-\delta _{k}+ \mid G^k+\alpha ^k\mid _{k}^2\nonumber \\&\quad =\sum \limits _{j \in L_k^{ f}} \lambda ^k_{j} \hat{e}_{f_j}^k +\sum \limits _{j \in L_k^{c}} \gamma ^k_j \hat{e}_{c_j}^{k} +h_{k}(x^k)-V_k, \end{aligned}$$

(5.7)

which implies that

$$\begin{aligned}&\max \left\{ f(y)-\theta _1^k, c(y)-\theta _2^k\right\} +(\theta ^j+\bar{\varepsilon })\rho ^j+\bar{\sigma }\\&\quad \ge h_{k}x^k)-V_k+\left\langle G^k, y-x^k \right\rangle -\mu _k \left\langle \sum \limits _{j \in L_k^{f}} \lambda ^k_j (y^j-x^k) +\sum \limits _{j \in L_k^{c}} \gamma ^k_j (y^j-x^k), y-x^k \right\rangle . \end{aligned}$$

By noting Theorem 4.1, Theorem 4.2 and Lemma 5.1, and passing to the limit in above relation as $k\rightarrow \infty$, we obtain that

$$\begin{aligned}&\max \Big \{f(y)-f^*-s_*\max \{c^*,0\}, c(y)-t_*\max \{c^*,0\}\Big \} +(\theta ^*+\bar{\varepsilon })\rho ^*+\bar{\sigma }\\&\quad \ge (1-t_*)\max \{c^*,0\}+\langle \bar{G}, y-\bar{x} \rangle . \end{aligned}$$

As already seen, $G^k+\alpha ^k\rightarrow G^*+\alpha ^*=0$ and $\alpha ^* \in \partial i_{\mathcal {X}}(x^*)$, implies that $-G^*\in \partial i_{\mathcal {X}}(x^*)$, thus $\langle -G^*, y-x^*\rangle \le 0$. From here the result in first item has been proven.

To show second item, consider the condition of $c^*>0$. Recalling the relation (5.1), yields

$$\begin{aligned} (s_*-t_*)c^*>f(y)-c(y)-f^*, \end{aligned}$$

which implies that

$$\begin{aligned} f(y)-f^*-s_*\max \{c^*,0\}< c(y)-t_*\max \{c^*,0\}. \end{aligned}$$

Together with the relation (5.2), we obtain that

$$\begin{aligned} c^*\le c(y)+\epsilon . \end{aligned}$$

Then the result in second item has been proven.

Finally, to see item (iii), consider condition $c^*<0$. According to (5.2), it holds that

$$\begin{aligned} 0\le \max \Big \{ f(y)-f^*,c(y) \Big \} +\epsilon , \end{aligned}$$

which means $f^*\le f(y)+\epsilon$ for $x\in X_{\epsilon }$. From here all results have been proven. $\square$

From the third statement of lower-$C^1$ in (2.3), the constants $\theta ^*$ and $\rho ^*$ for the point $x^*$ can be set small enough. Thus Theorem 5.1 states that, as long as $\theta ^*$ and $\rho ^*$ are chosen properly, the constant $\epsilon$ should meet the required precision accordingly. Besides, Theorem 5.1 also indicate that, if the parameter $s_k$ is updated quickly (see e.g., $s_{k+1}=2 s_{k}$ if $\hat{c}^k>0$, and $s_{k+1}=s_{k}$ otherwise), Algorithm 3.1 will eventually find a point infeasible up to the accuracy problem (1.1). Meanwhile, by noting the relation $c(y)>c^*-\epsilon$, then the feasible set of (1.1) may be empty set or very small. Otherwise, the set $X_{\epsilon }$ should be nonempty as long as the accuracy $\epsilon$ is small enough and an approximate local solution of (1.1) will be detected.

Our inexact bundle method can also be given for lower-$C^2$ functions. The function f is lower-$C^2$ on a open set $\mathcal {M}$ as long as it is finite value on an open set $\mathcal {M}$ and for any point $\bar{x} \in \mathcal {M}$ there exists a constant $R_\mathrm{th}>0$ such that $f+\frac{r}{2}|-\bar{x}|^2$ is convex on an open neighborhood $\mathcal {M}'$ of $\bar{x}$ for all $r>R_\mathrm{th}$. It has been shown the lower-$C^2$ functions are locally Lipschitz continuous.

The prox-regularity is essential when working with proximal points in a nonconvex setting. Specifically, if f is a prox-regular locally Lipschitz function, then it is lower-$C^2$ function. The finite convex function is lower-$C^2$ [44, Theorem 10.31]. There are also some other lower-$C^2$ functions, i.e., $C^2$ functions, strongly amenable functions, and if f is l.s.c., proper, and prox-bounded, then the opposite of Moreau envelopes $e_\lambda f$ is lower-$C^2$.

By applying [38, Prop. 10.54] and [55, Lemma 4.2], we obtain that there exist two thresholds $\mu _{f},\,\mu _{c}$, such that for all $\mu \ge \rho ^{id} :=\max \{\mu _{f}, \mu _{c}\}$, and any given point $y\in \mathcal {L}_0$ (a nonempty compact set), the functions $f(\cdot )+\frac{\mu }{2}|\cdot -y|^2,\,c(\cdot )+\frac{\mu }{2}|\cdot -y|^2$ are convex on $\mathcal {L}_0$. Besides, the positive threshold $\rho ^{id}$ can be updated along iterations, by using data in the bundle generated by Algorithm 3.1. Besides, from [55, Lemma 4.2] the parameter $\mu _{k}$ remain unchanged eventually, that is there exist $\hat{k}>0$ and $\bar{\mu }>0$, such that $\mu _{k}=\bar{\mu }, \ \mathrm{for \ all \ } k>\hat{k}$. The similar results as Theorem 5.1 can be proved naturally.

6 Numerical experiments

To assess practical performance of our inexact proximal bundle method, we coded Algorithm 3.1 in Matlab and ran it on a PC with 1.80 GHz CPU. Quadratic programming solver is QuadProg.m, which is available in the Optimization Toolbox.

6.1 Parameters for the proximal bundle method

We first set, respectively, the minimum and maximum positive thresholds to be $\eta _{\mathrm{min}}=10^{-5}$ and $\eta _{\mathrm{max}}=10^{9}$. Once the number of active elements in the bundle $\mathcal {G}_l$ is more than $num(\mathcal {G}_{\mathrm{max}})=50$, the bundle should be compressed. The initial value of the prox-parameter is started $\eta _0=1$.

We first compute $\tilde{\eta }_{k}$ by using the reverse quasi-Newton scalar

$$\begin{aligned} \tilde{\eta }_{{k}}:= \left\{ \frac{|\chi ^k-\chi ^{k-1}|^2}{(\chi ^k-\chi ^{k-1})^\mathrm{T}(y^k-y^{k-1})}{:}\,\chi ^k=G^k+\alpha ^k, \ \chi ^{k-1}=G^{k-1}+\alpha ^{k-1} \right\} . \end{aligned}$$

Just as [37], the prox-parameter $\eta _{{k+1}}$ will be updated at each serious steps as below.

$$\begin{aligned} \eta _{{k+1}}=\min \{ \eta , \eta _{\mathrm{max}} \}, \end{aligned}$$

where

$$\begin{aligned} \eta := \left\{ \begin{array}{ll} \max \{ \eta _{\mathrm{min}}, \eta _{k}, -1.01\lambda _{\mathrm{min}}(A_k) \}, \ &{}\quad \mathrm{if} \ \lambda _{\mathrm{min}}(A_k)<0\\ \max \{ \eta _{\mathrm{min}}, \tilde{\eta }_{k}, \}, \ &{}\quad \mathrm{if} \ \lambda _{\mathrm{min}}(A_k)=0\\ \max \{ 0, \lambda _{\mathrm{min}}(A_k)- \tilde{\eta }_{k} \}, \ &{}\quad \mathrm{if} \ \lambda _{\mathrm{min}}(A_k)>0. \end{array}\right. \end{aligned}$$

(6.1)

If the kth iteration declares a null step, then the prox-parameter $\eta _{k}$ remains constant. This strategy satisfies the condition of the parameters in Theorems 4.1 and 4.2. If necessary, $\eta _{{k+1}}$ is projected so that $\eta _{{k+1}}=[\eta _{\mathrm{min}}, \eta _{\mathrm{max}}]$.

Let $\iota =2$, and update the convexification parameter $\mu _{k}$ by using the relation (3.10), i.e.,

$$\begin{aligned} \mu _{{k}}:=\max \left\{ \max _{j\in L_k^f, y^j\ne x^k} \frac{-e_{f_j}^k}{\frac{1}{2}\Vert y^j-x^k\Vert ^2}, \ \max _{j\in L_k^c, y^j\ne x^k} \frac{-e_{c_j}^k}{\frac{1}{2}\Vert y^j-x^k\Vert ^2},0 \right\} +\iota , \end{aligned}$$

which is similar to the strategy in [18]. And in [18, Lem 3] and [55, Lem 4.2], for the exact oracle (i.e., $\bar{\sigma }=0$ and $\bar{\varepsilon }=0$) it has proven that the sequence $\{\mu _{k}\}$ is boundedness. Yet the boundedness of $\{\mu _{k}\}$ would be difficult to prove without additional coercive assumptions on the behavior of the errors in our setting. It is worth noting that the penalty parameters $s_{k}$ and $t_{k}$ is updated, which depends on a constant $\varpi$ defining in (5.1). Considering the basic assumptions on $f,\,c$ and $\mathcal {X}$, we can obtain that the values of both functions on the set $\mathcal {X}$ are bounded. Thus the constant $\varpi$ is bounded, and as a result $s_{k}$ and $t_{k}$ are well-defined in this work.

6.2 Examples for nonconvex optimization problems

In this subsection, we first introduce the nonconvex test problems. We prefer a series of polynomial functions developed in [11]; see also [12, 18]. For each $i=1, 2,\ldots , n$, the function $h_i{:}\,R^n \rightarrow R$ is defined by

$$\begin{aligned} h_i(x)=\sum \limits _{j=1}^{n} x_{j}+(ix_{i}^2-2x_i), \end{aligned}$$

(6.2)

where M is a fixed constant. There are five classes of test functions defined by $h_i$ in [12] as objective functions

$$\begin{aligned} f_1 (x):=\sum \limits _{i=1}^{n}|h_i(x)|, \end{aligned}$$

(6.3a)

$$\begin{aligned} f_2 (x):=\max \limits _{i=1,\ldots , n}|h_i(x)|, \end{aligned}$$

(6.3b)

$$\begin{aligned} f_3(x):=\sum \limits _{i=1}^{n}|h_i(x)|+\frac{1}{2}|x|^2, \end{aligned}$$

(6.3c)

$$\begin{aligned} f_4 (x):=\sum \limits _{i=1}^{n}|h_i(x)|+\frac{1}{2}|x|, \end{aligned}$$

(6.3d)

It has been proved in [12, 18] that they are nonconvex, globally lower-$C^1$, bounded on compact $\mathcal {X}$, and level coercive. We can obtain that $0=\min \nolimits _{x} f_{i}$ and $\{0\} \subseteq \arg \min \nolimits _{x} f_{i}$ for $i = 1, 2, 3, 4$. Thus we can define the compact $\mathcal {X}:=B_{15}(0)$.

For constraint functions, we consider the pointwise maximum of a finite collection of quadratic functions developed in [17], i.e.,

$$\begin{aligned} c(x):=\max _{i=1,2,\ldots , n} \left\{ \langle x, A_i x\rangle +\langle B_i, x \rangle +C_i\right\} , \end{aligned}$$

(6.4)

where $A_i$ are $n \times n$ matrices, $B_i \in \mathbf R ^{ n}$, and $C_i \in \mathbf R$ for $i = 1, 2,\dots , n$. Here all the coefficients $A_i,\,B_i$, and $C_i$ are uniformly distributed in [−5, 5], which are chosen randomly by matlab code. The functions as (6.4) have many important practical advantages. Firstly, they are always lower-$\mathcal {C}^2$ (semiconvex), prox-bounded, and prox-regular, but may be nonconvex since $A_i$ are not necessary to be positive definite. Secondly, the sequence of the convexification parameter $\{\mu _{k}\}$ for $c(\cdot )$ is fixed as

$$\begin{aligned} \mu = \max \left\{ | A_i+A_i^\mathrm{T}|{:}\,i = 1, 2, \ldots n\right\} . \end{aligned}$$

As a result, the large enough convexification parameters $\mu$ for $c(\cdot )$ can be estimated in advance. Thirdly, many different examples are easily obtained just by randomly generating $A_i,\,b_i$ and $c_i$ and choosing values for n and N. Lastly, the oracles (2.11) and (2.12) are easy to obtain the inexact information of the constrained functions.

We considered the following test problems

$$\begin{aligned} \begin{array}{lll} \min \limits _{x\in \mathbf R ^{n}}&{}\quad f_{i}(x)\\ s.t.&{}\quad c(x)\le 0, \ \ x\in \mathcal {X}, \end{array} \end{aligned}$$

for $i=1,\ldots ,4$ and $n=5,\ldots ,15,20$. For each test, it is well known that the optimum point is $x^*=(0,\ldots ,0)\in \mathbf R ^n$. Hence, each $f_i$ is clearly bounded below by 0. To check the precision, we will report the objective function value in last serious point. The remaining parameters of all of these tests are the same and listed below:

• stopping tolerance $tol_{stop}=1.0\mathrm{e}-06$, initial starting point $x_0=(1,\ldots ,1)$;

• prox-parameter $\eta _0 =5$, convexification parameter $\mu _0=5$;

• Armijo-like parameter $m= 0.55$, positive constant $\iota =2$;

• penalty parameters $s_0=15$ and $t_0=0$, stopping tolerance tol$_{stop}=10^{-6}$;

• initial variable prox-metric $A_0=I$ ($n\times n$ identity matrix).

6.3 Comparison with penalty proximal bundle method

In this subsection, we examine the performances of Algorithm 3.1 with inexact oracles. At each evaluation, we use inexact function values and subgradients as $f(y^j)-\sigma _{j},\,g_{f}^j= \tilde{g}_{f}^j+\varepsilon _{j}$ and $c(y^j)-\sigma _{j},\,g_{c}^j= \tilde{g}_{c}^j+\varepsilon _{j}$, where $\tilde{g}_{f}^j \in \partial f (y^j)$ and $\tilde{g}_{c}^j \in \partial c(y^j)$. To provide a brief comparison of Algorithm 3.1 to other research, we compared our results with those obtained by the penalty proximal bundle method (PPBM) in [55].

Table 1 Comparison between Algorithm 3.1 and PPBM for $f_1$ with $n=5,\ldots 10$

Table 2 Comparison between Algorithm 3.1 and PPBM for objective function $f_1$ with $n=11,\ldots ,15,20$

Table 3 Comparison between Algorithm 3.1 and PPBM for $f_2$ with $n=5,\ldots ,10$

Table 4 Comparison between Algorithm 3.1 and PPBM for $f_2$ with $n=11,\ldots ,15,20$

Table 5 Comparison between Algorithm 3.1 and PPBM for objective function $f_3$ with $n=5,\ldots ,10$

Table 6 Comparison between Algorithm 3.1 and PPBM for $f_3$ with $n=11,\ldots ,15,20$

Table 7 Comparison between Algorithm 3.1 and PPBM for objective function $f_4$ with $n=5,\ldots ,10$

Table 8 Comparison between Algorithm 3.1 and PPBM for $f_4$ with $n=11,\ldots ,15,20$

Our results for deterministic tests are summarized in following tables, in which n denotes dimension. The following notations are used as

$$\begin{aligned} \begin{array}{lllllll} \mathtt{Time} -- \mathrm{the \ CPU \ time (sec.)} &{}x^* -- \mathrm{the \ optimal \ point,}\\ f_{final} -- \mathrm{the \ final \ objective\ value,} &{} c_{final}--\mathrm{the \ final \ constrained \ value,}\\ \mathtt{Ni} -- \mathrm{the \ number \ of \ iterations,} &{} \mathtt{Ki} -- \mathrm{the \ number \ of \ serious \ iterations.} \end{array} \end{aligned}$$

Our numerical results for general nonconvex examples are reported in Tables 1, 2, 3, 4, 5, 6, 7 and  8, which show a reasonable performance of Algorithm 3.1.

We analyze the results in more detail as follows:

• For objective function $f_{1}$, we tested 12 nonconcex examples with $n=5,\ldots ,15,20$. We use constant noise $\sigma _{j} = 0.01$ and $\varepsilon _{j}=0.01\,*\,\texttt {ones}(n,1)$ for all j. Tables 1 and 2 show that values of $f_{final}$ obtained by Algorithm 3.1 are two orders of magnitude smaller than PPBM in most cases. Thus, Algorithm 3.1 succeeds in obtaining a reasonably high accuracy, while spend less time in all cases. Besides, the percentage of serious steps (Ki) in total iterations (Ni) is above 90% in many cases, which means that most iterations are reliable and Algorithm 3.1 is effective.

• To introduce errors in the available information, we use random noises $\sigma _j=0.1\,*\,\texttt {random}($ ‘Normal’, 0, 0.1) and $\varepsilon _j=0.1\,*\,\texttt {random}($ ‘Normal’, 0, 0.1, n, 1), which generates random numbers from the normal distribution with mean 0 and standard deviation 0.1, and scalars n and 1 are the row and column dimensions. Tables 3 and 4 show the results of Algorithm 3.1 as compared to PPBM for the objective function $f_{2}$ with $n=5,\ldots ,15,20$. We observe that Algorithm 3.1 only needs one-half of the cpu time of PPBM. In particular, if $n=20$, the value of $\texttt {time}$ of our method is just one-third of PPBM. We also see that Algorithm 3.1 always produces better (lower) objective values than PPMB for all examples.

• For the objective function $f_3$, we also tested 12 nonconvex examples with $n=5,\ldots ,15,20$ from randomly generated initial points. For these nonconvex examples, we introduce random noises $\sigma _j=0.1\,*\,\texttt {unifrnd}(0,1)$ and $\varepsilon _j=0.1\,*\,\texttt {unifrnd}(0,1,n,1)$. The matlab code $\texttt {unifrnd}(0,1,n,1)$ returns an $n-$dimensional column vector, and all elements are generated from the same distribution in the interval [0, 1]. From Tables 5 and 6, it observes that Algorithm 3.1 always produces better (lower) objective values than PPMB, while spend less time in most cases. Thus, Algorithm 3.1 performs better than PPBM for the objective function $f_{3}$.

• For the objective function $f_4$, we also tested 12 nonconvex examples with $n = 5,\ldots ,15,20$ from a fixed initial point $x^0=ones(n,1)$. For these nonconvex examples, we introduce random noises $\sigma _j= 0.1\,*\,\texttt {normrnd}(0,0.2)$ and $\varepsilon _j= 0.1\,*\,\texttt {normrnd}(0,0.2,n,1)$. The matlab code $\texttt {normrnd}(0,0.2,n,1)$ generates random numbers from the normal distribution with mean 0 and standard deviation 0.2, where scalars n and 1 are the row and column dimensions. From Tables 7 and 8, it seems that our method succeeds in obtaining better objective values, at the price of less time than PPBM. In most of cases, the number of serious steps (Ki) is much more than the number of null steps, which implies that our inexact method is high efficiency.

6.4 Impact of noise on solution accuracy

To analyse the errors in the available information, we test five different types of inexact oracle:

• $\texttt {NN}$ (No noise): $\sigma _{j}=\bar{\sigma }= 0$ and $\varepsilon _j=\bar{\varepsilon }= 0$, for all j,

• $\texttt {CN}$ (Constant noise): $\bar{\sigma }= \sigma _j = 0.01$ and $\varepsilon _j=\bar{\varepsilon }=0.01$, for all j,

• $\texttt {VN}$ (Vanishing noise): $\bar{\sigma }= 0.01,\,\sigma _j=\min \{0.01, \frac{\Vert y^j\Vert }{100}\},\,\varepsilon _j=\min \{0.01,\frac{\Vert y^j\Vert }{100}\}$, for all j,

• $\texttt {CGN}$ (Constant Gradient noise): $\bar{\sigma }=\sigma _j=0$ and $\varepsilon _j=\bar{\varepsilon }=0.05$, for all j,

• $\texttt {VGN}$ (Vanishing Gradient noise): $\bar{\sigma }=\sigma _j=0$ and $\varepsilon _j=\min \{0.01,\frac{\Vert y^j\Vert }{100}\}$, for all j.

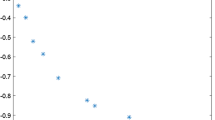
Considering the optimum value of all the test problems is zero, we can use the formula Precision$=|\log _{10}(f_{final})|$ to check the performance of the various methods. Figures 1 and 2 report the average performance of Algorithm 3.1 when noise is introduced (the results are averaged across all 10 runs). To better reveal the influence of noise, we also report the results of NN (no noise). Figure 1 reports the results for constant noise (CN and CGN) with $\texttt {tol}=10^{-6}$. We can observe that Algorithm 3.1 can achieve an acceptable accuracy for the type CN. The results of CGN are better than those of CN, although still notably deviations than when exact calculations are available. Figure 2 reports the precision results of Algorithm 3.1 for vanishing noise (VN and VGN). The vanishing noise results in reducing the accuracy for $\texttt {tol}= 10^{-6}$, generally better than in the constant noise cases.

6.5 Comparison with FSQP-GS and SLQP-GS

In this subsection, we aim to compare the practical effectiveness of Algorithm 3.1 with a sequential quadratic programming algorithm (SLQP-GS) [4] and a feasible SQP-GS algorithm (FSQP-GS) [52]. We test the following two examples, which are taken from [4, 45] respectively. In all numerical experiments, we choose the same initial points as FSQP-GS in [52] for all examples in this subsection.

To analyse the errors in the available information, we consider four different types of inexact oracle:

• Constant noise (CN): $\sigma _{j} = 0.01$ and $\varepsilon _{j}=0.01*\texttt {ones}(n,1)$ for all j;

• $\sigma _j=0.1*\texttt {random}$ (‘Normal’, 0, 0.1) and $\varepsilon _j=0.1*\texttt {random}$ (‘Normal’,0, 0.1, n, 1) for all j;

• $\sigma _j=0.1*\texttt {unifrnd}(0,1)$ and $\varepsilon _j=0.1*\texttt {unifrnd}(0,1,n,1)$ for all j;

• $\sigma _j= 0.1*\texttt {normrnd}(0,0.2)$ and $\varepsilon _j= 0.1*\texttt {normrnd}(0,0.2,n,1)$ for all j.

Example 1

Constrained nonsmooth Rosenbrock problem [4]:

$$\begin{aligned} \begin{array}{ll} \min \limits _{x} &{}\quad 8| x_{1}^2-x_{2}|+(1-x_{1})^2 \\ s.t. &{}\quad \max \{\sqrt{2}x_{1},2x_{2}\}\le 1 \end{array} \end{aligned}$$

The solution of this problem is $x^*=(\frac{\sqrt{2}}{2},\frac{1}{2})$ at which both the objective function and the constraint function are nondifferentiable. In this numerical experiment, we set the initial points $(0.066661, -0.350366)^\mathrm{T}$ and $(0.433746,-1.447530)^\mathrm{T}$ respectively.

Fig. 1

Precision for Algorithm 3.1 for noise forms $\texttt {NN},\,\texttt {CN}$ and $\texttt {CGN}$ with $\texttt {tol}=10^{-6}$

Fig. 2

Precision for Algorithm 3.1 for noise forms $\texttt {NN},\,\texttt {VN}$ and $\texttt {VGN}$ with $\texttt {tol}=10^{-6}$

Example 2

Rosen–Suzuki problem [45]:

$$\begin{aligned} \begin{array}{ll} \min \limits _{x} &{}\quad f(x)=\max \{f_{i}(x){:}\,i=1,\ldots ,4\} \\ s.t. &{}\quad \max \{c_{i}(x){:}\,i=1,2,3\}\le 0, \end{array} \end{aligned}$$

where $f_1(x)=x^2_1+x^2_2+2x^2_3+x^2_4-5x_1-5x_2-21x_3+7x_4,\,f_2(x)=f_1(x)+10c_1(x),\,f_3(x)=f_1(x)+10c_2(x),\,f_4(x)=f_1(x)+10c_3(x),\,c_1(x) = x^2_1+x^2_2+x^2_3+x^2_4+x_1-x_2+x_3-x_4-8,\,c_2(x)=x^2_1+2x^2_2+x^2_3+2x^2_4-x_1-x_4-10,\,c_3(x)=x^2_1+x^2_2+x^2_3+2x_1-x_2-x_4-5$. In our numerical experiment, we set the initial points $(1, 1, 1, 1)^\mathrm{T}$ and $(0, 0, 0, 0)^\mathrm{T}$ respectively.

From Tables 9 and 10, it observes that Algorithm 3.1 (CN) needs a fewer number of iterations than FSQP-GS and SLQP-GS for all examples. Tables 9 and 10 also show that Algorithm 3.1 (CN) always obtains similar objective values with SLQP-GS and FSQP-GS, while spends less time for most cases. In general, Algorithm 3.1(CN) performs slightly better than FSQP-GS and SLQP-GS for all examples. Besides, we also consider random noises, which are generated randomly by using matlab codes $\texttt {random},\,\texttt {unifrnd}$ and $\texttt {normrnd}$. From Tables 9 and 10, it observes that Algorithm 3.1(rand) and Algorithm 3.1(unifrnd) are comparable for FSQP-GS and SLQP-GS for most cases. Algorithm  3.1(normrnd) spends much time for some cases, than FSQP-GS and SLQP-GS.

Table 9 Comparison with FSQP-GS and SLQP-GS for Examples 1

Table 10 Comparison with FSQP-GS and SLQP-GS for Examples 2

6.6 Results for semi-infinite programming problems

For benchmarking purposes we will investigate the computational behaviour and convergence results for SIP problems. We will compare the performance of Algorithm 3.1 by using Constant noise with the central cutting plane algorithm (CCPA) [34] and the SIP solver fseminf in MATLAB toolbox. The SIP problem has the following abstract structure

$$\begin{aligned} \begin{array}{lll} \min \limits _{x} &{} f(x), \\ s.t. &{} g(x,v)\le 0, \ \mathrm{for \ all} \ v \in V, \end{array}\end{aligned}$$

(6.5)

where $f(x){:}\,\mathbf R ^n \rightarrow \mathbf R$ is locally Lipschitz and not necessary differentiable; g: $\mathbf R ^n \times V \rightarrow \mathbf R$ is twice continuously differentiable; and V is a nonempty compact subset of $\mathbf R ^n$.

We first consider the so-called lower level problem

$$\begin{aligned} \min \limits _{v \in V} -g(\bar{x},v), \end{aligned}$$

(6.6)

to obtain the global solution. The difficulty lies in the fact that $-g(\bar{x},v_{glob})$ is the globally optimal value of (6.6) which might be hard to obtain numerically. In fact, most of standard nonlinear problem solvers can only be expected to output a local minimizer $v_{loc}$. Many works aim at structuring a sequence of convexifications of the lower level problem by using the technologies in [13, 50] to solve the auxiliary problems with convex lower levels. In fact, the function c needs only an inexact value with a given fixed accuracy $\omega$. That is we only want to obtain an approximate solution $v(\bar{x})$ such that $c(\bar{x},v(\bar{x}))\ge c(\bar{x})-\omega .$ The iterative rules in [14, 19] can generate more and more accurate solutions to (6.6), until a $\omega$-optimal solution.

The numerical results are listed in Table 11, where the following notations are used as

$$\begin{aligned}\begin{array}{lllllll} x^*{:}\,\mathrm{the \ optimal \ point,} &{}f^*{:}\,\mathrm{the \ final \ objective\ value,}\\ \mathrm{Time} (s){:}\,\mathrm{the \ CPU \ time \ of \ Algorithm \ 3.1}, &{} \mathrm{Time_{max}} (s){:}\,\mathrm{the \ CPU \ time \ for \ (6.6)},\\ \mathrm{Iter}{:}\, \mathrm{the \ number \ of \ iterations \ of \ Algorithm \ 3.1,} \end{array} \end{aligned}$$

Example 3

Finding the Chebyshev approximation of the function, and has been tested by Floudas and Stein [13, Example 5.1]:

$$\begin{aligned} \begin{array}{ll} \min &{}\quad f(x)=x_4,\\ s.t. &{}\quad g_{1}(x,y)= sin(\pi y)-x_{3}y^{2}-x_{2}y-x_{1}-x_{4}\le 0, \\ &{}\quad g_{2}(x,y)= -sin(\pi y)+x_{3}y^{2}+x_{2}y+x_{1}-x_{4}\le 0, \\ &{}\quad \mathrm{for \ all} \ Y=[0,1]. \end{array} \end{aligned}$$

Example 4

The following SIP problem is tested by Kortanek and No [34], and stemmed from Tichatschke and Nebeling [53]:

$$\begin{aligned} \begin{array}{ll} \min &{}\quad f(x)=(x_1-2)^2+(x_2-0.2)^2,\\ s.t. &{}\quad g(x,y)=(5sin(\pi \sqrt{y})/(1+y^2))x^2_1-x_2 \le 0,\\ &{}\quad \mathrm{for\ all } \ Y=[0, 1]. \end{array} \end{aligned}$$

Example 5

The problem is discussed by Goberna and Löpez [16], and Zhang and Wu [56]:

$$\begin{aligned} \begin{array}{ll} \min &{}\quad f(x)=x_1^2+x_2^2,\\ s.t. &{}\quad g(x,y)=\cos (y)x_{1}+\sin (y)x_{2}- \left( 1+\cos (y)+\sin (y)\right) \le 0, \\ &{}\quad \mathrm{for \ all} \ Y=[\pi , \frac{3}{2}\pi ], \end{array} \end{aligned}$$

Although the feasible set is not bounded, the objective function is level bounded on the feasible set.

Example 6

Consider the following problem, which was tested by Kortanek and No [34]:

$$\begin{aligned} \begin{array}{ll} \min &{}\quad f(x)=x_1^2+x_2^2+x_2^3,\\ s.t. &{}\quad g(x,y)= x_1+x_2 \exp (x_3 y)+\exp (2y)-2\sin (4y)\le 0,\\ &{}\quad \mathrm{for \ all} \ Y=[0,1]. \end{array} \end{aligned}$$

Example 7

The following convex SIP problem has been tested by Kortanek and No [34]:

$$\begin{aligned} \begin{array}{ll} \min &{}\quad f(x)=x_1^2+x_2^2,\\ s.t. &{}\quad c(x,y)= (x_1^2+ x_2^2-4)y_{1}+((x_1-2)^2 + (x_2^2-2)^2-4)y_{2}\le 0, \\ &{}\quad x_{1}\in [0,2], \ x_{2}\in [0,2], \ Y=[0,1]\times [0,1]. \end{array} \end{aligned}$$

Observe that the problem satisfies the Slater CQ and the feasible set is bounded.

Table 11 Comparison of results for Examples 3–7

The numerical results of Examples 3–7 are reported in Table 11. One can observe in Table 11 that Algorithm 3.1 performs well and provides an optimal solution to each example. Besides, the inexact solution of subproblem (6.6) can be obtained effectively, which means the inexact oracle is reasonable. To obtain a similar optimal solution, the SIP solver fseminf and the CCPA took much time than our method. In our opinion, the performance of Algorithm 3.1 for solving Examples 3–7 is better than that of the CCPA and the SIP solver fseminf.