A hybrid grey wolf optimizer for engineering design problems

Abstract

Grey wolf optimizer (GWO) is one of the most popular metaheuristics, and it has been presented as highly competitive with other comparison methods. However, the basic GWO needs some improvement, such as premature convergence and imbalance between exploitation and exploration. To address these weaknesses, this paper develops a hybrid grey wolf optimizer (HGWO), which combines the Halton sequence, dimension learning-based, crisscross strategy, and Cauchy mutation strategy. Firstly, the Halton sequence is used to enlarge the search scope and improve the diversity of the solutions. Then, the dimension learning-based is used for position update to balance exploitation and exploration. Furthermore, the crisscross strategy is introduced to enhance convergence precision. Finally, the Cauchy mutation strategy is adapted to avoid falling into the local optimum. The effectiveness of HGWO is demonstrated by comparing it with advanced algorithms on the 15 benchmark functions in different dimensions. The results illustrate that HGWO outperforms other advanced algorithms. Moreover, HGWO is used to solve eight real-world engineering problems, and the results demonstrate that HGWO is superior to different advanced algorithms.

1 Introduction

Recently, many scholars have favored metaheuristics due to their simple structure and high solution efficiency, especially their application in engineering problems, which have attracted more attention from researchers (Rao et al. 2023). Ewees et al. (2018) divided optimization problems into three categories: constrained, unconstrained, and constrained engineering optimization problems. In solving an optimization problem, finding the optimal value of the situation in a reasonable time is necessary, which is urgently needed to design an effective optimization method. With the rapid development of computer technology, many metaheuristics have emerged. Currently, there are many popular metaheuristics, for example, grey wolf optimizer (GWO) (Mirjalili et al. 2014), whale optimization algorithm (WOA) (Mirjalili and Lewis 2016), sparrow search algorithm (SSA) (Xue and Shen 2020), gaining-sharing knowledge-based (GSK) (Mohamed et al. 2020), arithmetic optimization algorithm (AOA) (Abualigah et al. 2021), artificial hummingbird algorithm (AHA) (Zhao et al. 2022), honey badger algorithm (HBA) (Hashim et al. 2022), young’s double-slit experiment (YDSE) (Abdel-Basset et al. 2023). However, the advantages of different metaheuristics can be combined, which results in methods known as the hybrid method. Such approaches are used in many research papers: multi-strategy improved slime mould algorithm (MSMA) (Deng and Liu 2023) and enhanced opposition-based grey wolf optimizer (EOBGWO) (Chandran and Mohapatra 2023).

GWO is a metaheuristic proposed by Mirjalili et al. (2014), inspired by the hunting activities of grey wolves. And it has three leaders who lead the population toward the optimal value. Compared with other metaheuristics, GWO has more competitive performance, few control parameters, and a simple search mechanism. However, similar to other algorithms, there are some drawbacks associated with GWO, such as premature convergence and imbalance between exploitation and exploration. Thus, some strategies are introduced to overcome its deficiencies. Here, we briefly review the major works of GWO to understand its shortcomings.

Aiming at the shortcomings of GWO, scholars have been inspired to conduct in-depth research and propose improved methods. Nadimi-Shahraki et al. (2021) developed an improved grey wolf optimizer to alleviate the lack of population diversity. Rodríguez et al. (2021) proposed a modified version of the GWO called group-based synchronous-asynchronous grey wolf optimizer that integrates a synchronous–asynchronous processing scheme and a set of different nonlinear functions to improve the weakness of basic GWO. Fan et al. (2021) proposed a grey wolf optimizer based on a beetle antenna strategy to enhance the global search ability and reduce unnecessary searches. Yu et al. (2022) introduced a reinforced exploitation and exploration GWO, which combines a random search based on the tournament selection and a well-designed mechanism. Wang et al. (2022) suggested a variant of the GWO called the cross-dimensional coordination grey wolf optimizer, which utilizes a novel learning technique for engineering problems. İnaç et al. (2022) developed a random weighted grey wolf optimizer to improve the search performance. Duan and Yu (2023) proposed an improved GWO based on the combination of GWO and sine cosine algorithm to prevent convergence prematurely. Jain et al. (2023) combined genetic learning and GWO to improve the intelligence of GWO’s leading agents and solve real-world optimization problems. Yao et al. (2023) developed an entropy-based grey wolf optimizer based on an information entropy-based population generation strategy and a nonlinear convergence strategy for global optimization problems. Ma et al. (2024) proposed an ameliorated grey wolf optimizer (AGWO) that integrated the opposition-based learning strategy to balance between exploration and exploitation.

Through a review of GWO improvement literature, although a series of improvement studies of GWO have been carried out and the performance of GWO has been improved, there are still some shortcomings. On the one hand, improvements mainly based on the combination of GWO and other algorithms can easily lead to the loss of evolutionary direction, are challenging to implement, and quickly fall into local optimality (Yu et al. 2023). On the other hand, GWO is improved using only a single strategy, such as adaptive parameters or weights. Mohammed et al. (2024) changed the control parameters by introducing the golden ratio, but the improvement effect was not noticeable. In contrast, combining multiple strategies can significantly improve the performance of GWO. Mafarja et al. (2023) proposed a multi-strategy grey wolf optimizer to improve the shortcomings of the basic GWO, using an embedding strategy of convergence control parameters, multiple exploration strategy, and multiple exploitation strategy. Ahmed et al. (2023) introduced a new variant of GWO, which integrates memory, evolutionary operators, and a stochastic local search technique to address the limitation of basic GWO. Currently, existing research is dedicated to introducing different new strategies into GWO, the effective combination of multiple strategies can improve the performance of GWO (Luo et al. 2023; Zhao et al. 2023). In addition, the “No Free Lunch” theory (Wolpert and Macready 1997) states that existing algorithms cannot wholly solve all possible optimization problems, which means that such algorithms may produce suitable optimization results for some problems but unacceptable results for other problems (Zaman and Gharehchopogh 2022). Therefore, the above reasons prompted this study to propose a new algorithm.

This paper proposes a variant of the GWO called the hybrid grey wolf optimizer (HGWO) that integrates the Halton sequence, dimension learning-based, crisscross strategy, and Cauchy mutation strategy. It aims to address premature convergence and imbalance between exploitation and exploration. Firstly, the Halton sequence is used to enlarge the search scope and improve the diversity of the solutions. Then, the dimension learning-based is used for position update to balance exploitation and exploration. Furthermore, the crisscross strategy is introduced to enhance convergence precision. Finally, the Cauchy mutation strategy is adapted to avoid falling into the local optimum. Integrating those strategies removes the deficiencies of GWO and dramatically enhances the performance of the primary method.

To verify the efficiency of the HGWO, this study differs from other research in the following areas. Firstly, it is compared with ten advanced algorithms, including GWO, WOA, SSA, GSK, AOA, AHA, HBA, MSMA, EOBGWO, and AGWO on 15 benchmark functions. Then, two non-parametric tests (Wilcoxon signed-rank test and Friedman test) are examined. Furthermore, HGWO has been used in eight engineering problems and compared with other algorithms. The results indicate that HGWO performed well regarding solution quality and stability. The main contributions of this study can be summarized as follows:

• 1. The Halton sequence strategy can enlarge the search scope and improve the diversity of the solutions.

• 2. Introducing the dimension learning-based for position update to balance between exploitation and exploration.

• 3. The crisscross strategy is introduced to enhance convergence precision, and the Cauchy mutation strategy is adapted to avoid falling into the local optimum.

• 4. To verify the performance of HGWO, we compared it with other advanced algorithms on 15 benchmark functions of different dimensions and eight real-world engineering problems.

The rest of the study consists of five parts. In Sect. 2, we present the basic GWO. In Sect. 3, HGWO is introduced. In Sect. 4, we evaluate HGWO’s performance based on benchmark functions. In Sect. 5, we apply the HGWO to deal with engineering issues. In the end, Sect. 6 draws conclusions and future works.

2 Grey wolf optimizer

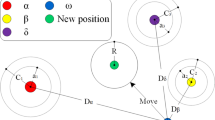
The grey wolf optimizer (GWO) simulates the population hunting behavior of grey wolves in nature. The wolves are divided into four categories: $\alpha$ wolf, $\beta$ wolf, $\delta$ wolf, and $\omega$ wolf. Among them, the $\alpha$ wolf, as the wolf that is best in the population, coordinates and manages all essential decision-making matters. The $\beta$ wolf is mainly responsible for assisting the $\alpha$ wolf in making decisions. The $\delta$ wolf obeys the dispatches of the $\alpha$ and $\beta$ wolf and is responsible for surveillance and sentry monitoring. Moreover, the $\omega$ wolf is mainly responsible for maintaining the internal balance of the grey wolf population. There are three phases in the hunting of wolves, as shown below.

① Surrounding: to surround the prey, the grey wolf needs to calculate the distance to the prey based on the approximate location of the prey and then move towards the prey. The formulas are as shown in Eqs. (1–2).

$$D = \left| {C \cdot X_{p} \left( {\text{t}} \right) - X\left( {\text{t}} \right)} \right|$$

(1)

$$X\left( {t + 1} \right) = X_{p} \left( t \right) - A \cdot D$$

(2)

where t denotes the iteration of current, $X_{p}$ denotes the location of prey, $X$ denotes the wolf’s location, A denotes the convergence factor, and C denotes the oscillation factor, see Eqs. (3–4).

$$A = 2 \cdot a \cdot r_{1} - a$$

(3)

$$C = 2 \cdot r_{2}$$

(4)

$$a = 2 - t \cdot \left( {\frac{2}{{t_{max} }}} \right)$$

(5)

where $a$ is the distance control parameter, $r_{1}$ is random in [0, 1], $r_{2}$ is random in [0, 1], and $t_{max}$ is the maximum number of iterations.

② Hunting: throughout the hunting process, $\alpha$ wolf determine the location of their prey and keep moving toward it. $\beta$ and $\delta$ wolves follow the $\alpha$ wolf to hunt prey and guide other wolves to surround the prey. The other wolves move towards the $\alpha$ wolf, $\beta$ wolf, and $\delta$ wolf to complete the encirclement of the prey. The movement formulas are as follows.

$$\left\{ {\begin{array}{*{20}l} {D_{\alpha } = \left| {C_{1} \cdot X_{\alpha } \left( t \right) - X\left( t \right)} \right|} \hfill \\ {D_{\beta } = \left| {C_{2} \cdot X_{\beta } \left( t \right) - X\left( t \right)} \right|} \hfill \\ {D_{\delta } = \left| {C_{3} \cdot X_{\delta } \left( t \right) - X\left( t \right)} \right|} \hfill \\ \end{array} } \right.$$

(6)

where $X_{\alpha }$ denotes $\alpha$ wolf’s location, $X_{\beta }$ denotes $\beta$ wolf’s location, $X_{\delta }$ denotes $\delta$ wolf’s location.

$$\left\{ {\begin{array}{*{20}l} {X_{1} \left( t \right) = X_{\alpha } \left( t \right) - A_{1} \cdot D_{\alpha } } \hfill \\ {X_{2} \left( t \right) = X_{\beta } \left( t \right) - A_{2} \cdot D_{\beta } } \hfill \\ {X_{3} \left( t \right) = X_{\delta } \left( t \right) - A_{3} \cdot D_{\delta } } \hfill \\ \end{array} } \right.$$

(7)

$$X\left( {t + 1} \right) = \frac{{X_{1} \left( t \right) + X_{2} \left( t \right) + X_{3} \left( t \right)}}{3}$$

(8)

③ Attacking: grey wolves finish hunting when the prey no longer moves. For the sake of imitation of the nearing prey, $a$ is reduced step by step, so the fluctuation of A is reduced step by step. If the value of A is within the range, the wolves will revise places at any location. Specifically, if |A|< 1, the grey wolves attack the prey; if |A|> 1, the grey wolves separate from their prey, hoping to find more suitable prey.

The GWO’s flowchart is illustrated in Fig. 1.

Fig. 1

The flowchart of GWO

3 The proposed hybrid grey wolf optimizer

In the basic GWO, $\alpha$, $\beta$, and $\delta$ lead $\omega$ wolves to obtain an optimum value. In this way, it is easy to result in an imbalance between global exploration and local exploitation. Hence, we present a hybrid grey wolf optimizer (HGWO) to address these deficiencies. Firstly, the Halton sequence is used to enlarge the search scope and increase the diversity of the population. Then, the dimension learning-based is used for position update to balance exploitation and exploration. Furthermore, the crisscross strategy is introduced to enhance convergence precision. Finally, the Cauchy mutation strategy is adapted to avoid falling into the local optimum. In this section, the HGWO is presented and described in detail. The detailed flowchart of the proposed HGWO is shown in Fig. 2.

Fig. 2

The flowchart of HGWO

3.1 Halton sequence strategy

The Halton sequence is used to produce pseudo-random numbers, and the ergodic nature of pseudo-random numbers makes the population more evenly distributed throughout the search domain (Li et al. 2022), which is beneficial to reducing the search blind area of grey wolves, thereby improving the quality and diversity of the initial solution. This study introduces the two-dimensional Halton sequence initialization population implementation process to understand the Halton sequence principle better. Specifically, two prime numbers greater than or equal to two are selected as the basic quantities, and the basic quantities are continuously divided to reconstruct a set of evenly distributed points without repetition. The specific formulas are as shown in Eqs. (9–12).

$$n = \mathop \sum \limits_{i = 0}^{m} b_{i} \cdot p^{i} = b_{m} \cdot p^{m} + \cdots + b_{1} \cdot p^{1} + b_{0}$$

(9)

$$\theta \left( n \right) = b_{0} p^{ - 1} + b_{1} p^{ - 2} + \cdots + b_{m} p^{ - m - 1}$$

(10)

$$H\left( n \right) = \left[ {\theta_{1} \left( n \right),\theta_{2} \left( n \right)} \right]$$

(11)

$$X_{n} = H\left( n \right) \cdot \left( {UB - LB} \right) + LB$$

(12)

where $n$ is any integer in [1, N], $p$ is prime and $p \ge 2$, $b_{i}$ is the constant coefficient, and $b_{i} \in \left\{ {0,1, \ldots ,p - 1} \right\}$, $\theta \left( n \right)$ indicates sequence function, $H\left( n \right)$ indicates two-dimensional uniform Halton sequence, $X_{n}$ indicates the Halton sequence initializing the grey wolf population.

The initial random population generated by GWO is presented in Fig. 3. Figure 4 shows the initial distribution population produced using the Halton sequence, where the basic quantities of the Halton sequence are two and three.

Fig. 3

Random populations

Fig. 4

Halton populations

3.2 Nonlinear parameter

The exploration and exploitation are crucial to their optimization performance in metaheuristics. Since hunting and attacking prey in GWO are related to $a$, coordinating GWO's exploration and exploitation is a scheme worthy of further research. Exploration is the key for the population to use position updates to search a wide area and avoid the algorithm falling into local optimality. The exploitation mainly uses the population’s existing information to search specific neighborhoods in the solution space. If $a$ is more extensive, it means that the algorithm has better exploration, which is helpful to avoid the algorithm falling into the local optimum; if $a$ is smaller, it means that it has more robust exploitation, which can speed up the convergence speed of the algorithm. However, in the basic GWO, with the number of iterations, $a$ decreases linearly from 2 to 0, which only partially reflects the exploration and exploitation. On this basis, this study designed a nonlinear decreasing control parameter $a$ that changes rapidly in the early iteration and relatively slowly in the later iteration to balance the exploration and exploitation of GWO, $a$ is described in Eq. (13) as follows.

$$a = 2 \cdot \left( {1 - \sqrt {\frac{t}{{t_{max} }}} } \right)$$

(13)

where t and $t_{max}$ denote current and maximum iteration, respectively.

3.3 Dimension learning-based population search strategy

In the basic GWO, $\alpha$, $\beta$, and $\delta$ guide $\omega$ wolves toward regions in the search space where optimal solutions are expected to be found. In this way, it is easy to result in an imbalance between exploration and exploitation. Moreover, it is easy to reduce population diversity. Hence, to address these deficiencies, the dimension learning-based population search strategy proposed in the literature (Nadimi-Shahraki et al. 2021) is introduced to update the position. This principle is mainly based on the grey wolves in the population learning from their neighboring grey wolves during the hunting process. Among them, Eq. (14) indicates that the current grey wolf learns from each other by its different neighbors and randomly selected wolves in the population. Equation (15) represents finding the neighbor of the current grey wolf. The specific description is shown in Eqs. (14–15).

$$X_{i} \left( {t + 1} \right) = X_{i} \left( t \right) + r \times \left( {X_{n} \left( t \right) - X_{r} \left( t \right)} \right)$$

(14)

$$X_{n} \left( t \right) = \{ X_{j} \left( t \right)|D\left( {X_{i} \left( t \right),X_{j} \left( t \right)} \right) \le D\left( {X_{i} \left( t \right),X_{i} \left( {t + 1} \right)} \right),X_{j} \left( t \right) \in N\}$$

(15)

where $X_{i}$ represents the current position of the ith grey wolf, $X_{n}$ denotes a randomly selected neighbor grey wolf, $X_{r}$ indicates a random selection of a grey wolf from population N, $r$ is random in [0, 1], $D\left( {X_{i} \left( t \right),X_{j} \left( t \right)} \right)$ indicates the Euclidean distance between the position of the ith grey wolf and the jth grey wolf.

3.4 Crisscross strategy

Since the grey wolf continues to move closer to the first three better individuals during the iteration process, with the iteration increases, the population will likely gather around the local optimal solution, thereby reducing the algorithm's solving ability. To avoid the occurrence of the above situation, this section will introduce the crisscross strategy (Meng et al. 2014), which has been used to improve the performance of many metaheuristics (Hu et al. 2022; Su et al. 2023). After executing the dimension learning-based population search strategy in Sect. 3.3, the grey wolf population performs horizontal and vertical crossover operations, which can improve global exploration to solve complex optimization problems, thereby improving convergence speed and solution precision.

3.4.1 Horizontal crossover

The horizontal crossover is an arithmetic crossover in all dimensions between two different grey wolves, allowing different individuals to learn from each other, increase global exploration, and prevent premature convergence of the population, thereby improving the convergence speed and solution accuracy. Assume the ith parent grey wolf $X_{i}$ and the kth parent grey wolf $X_{k}$ are accustomed to performing horizontal crossover operations on the jth dimension. Equations (16–17) can calculate their offspring.

$$X_{ij}{\prime} = r_{1} \times X_{ij} + \left( {1 - r_{1} } \right) \times X_{kj} + c_{1} \times \left( {X_{ij} - X_{kj} } \right)$$

(16)

$$X_{kj}{\prime} = r_{2} \times X_{kj} + \left( {1 - r_{2} } \right) \times X_{ij} + c_{2} \times \left( {X_{kj} - X_{ij} } \right)$$

(17)

where $X_{ij}{\prime}$ and $X_{kj}{\prime}$ are the offspring of $X_{ij}$ and $X_{kj}$, respectively. $r_{1}$ and $r_{2}$ are random in [0,1], $c_{1}$ and $c_{2}$ are random in [− 1,1]. The new solutions generated by horizontal crossover operation must be compared with the pre-crossover to retain the better grey wolves.

3.4.2 Vertical crossover

The vertical crossover is an arithmetic crossover operation on all individuals between two dimensions. During the entire iteration process, each vertical crossover operation produces only one offspring to provide the stagnant dimension with the opportunity to jump out of the local optimum without destroying other dimensions that may be globally optimal. Assume the $j_{1}$th and the $j_{2}$th dimensions of grey wolf $X_{i}$ are accustomed to performing vertical crossover operations. Equation (18) can calculate their offspring.

$$X_{ij}{\prime} = r \times X_{{ij_{1} }} + \left( {1 - r} \right) \times X_{{ij_{2} }}$$

(18)

where $X_{ij}{\prime}$ is the offspring of $X_{{ij_{1} }}$ and $X_{{ij_{2} }}$, and $r$ is random in [0,1]. The new solutions generated by vertical crossover operation must be compared with the pre-crossover to retain the better grey wolves.

3.5 Cauchy mutation strategy

It can be seen from the grey wolf optimization process that the search process is led by the first three grey wolves with better fitness in the current grey wolf population. At the end of the search process, the grey wolf population will quickly gather near the positions of the first three wolves, resulting in profound population convergence, thereby increasing the probability that the algorithm will fall into a local optimum. However, Cauchy mutation comes from the Cauchy distribution, which is a continuous probability distribution common in probability theory, with a large probability density in the middle and small probability density at both ends. Since the Cauchy distribution has the characteristics of long and flat ends, the perturbation ability of the Cauchy mutation is powerful. The probability density function of the standard Cauchy distribution is shown in Eq. (19). Therefore, this study introduces the Cauchy mutation strategy, which searches the local area of the first three grey wolves, generates random disturbances within the potential optimal solution range, expands the search range, and generates the possibility of new solutions, which enhances the algorithm to jump out of the local optimum, as shown in Eq. (20).

$$f\left( x \right) = \frac{1}{{\pi \left( {1 + x^{2} } \right)}}$$

(19)

$$\left\{ {\begin{array}{*{20}l} {X_{\alpha } \left( t \right){\prime} = X_{\alpha } \left( t \right) \times Cauchy\left( {0,1} \right)} \hfill \\ {X_{\beta } \left( t \right){\prime} = X_{\beta } \left( t \right) \times Cauchy\left( {0,1} \right)} \hfill \\ {X_{\delta } \left( t \right){\prime} = X_{\delta } \left( t \right) \times Cauchy\left( {0,1} \right)} \hfill \\ \end{array} } \right.$$

(20)

where $X_{\alpha }{\prime}$, $X_{\beta }{\prime}$, and $X_{\delta }{\prime}$ are the positions generated by $\alpha$, $\beta$, and $\delta$ grey wolf after Cauchy mutation, respectively. $f\left( x \right)$ represents the standard Cauchy distribution function.

3.6 The computational complexity of HGWO

In this section, we mainly introduce the computational complexity of HGWO. Generally speaking, metaheuristics are complex systems containing stochastic processes, so it is unreasonable to use traditional estimation methods, that is, to study complexity from a deterministic perspective. Therefore, this study draws on the practice of Rodríguez et al. (2021) and uses Big-O notation to evaluate the computational complexity of HGWO.

The computational complexity is affected by the population size N, the dimension D, and the maximum number of iterations $t_{max}$. The computational complexity of basic GWO is $O\left( {N \cdot D \cdot t_{max} } \right)$. To facilitate the determination of the computational complexity of HGWO, it is divided into two parts: I and II (see Algorithm 1). Part I presents the initialization (see lines 1–2), and part II presents the main loop (see lines 3–14). Firstly, the computational complexity of Section ① to initialize the population is $O\left( {N \cdot D + N} \right)$. Then, the computational complexity of Section ② is $O\left( {N \cdot {\text{log}}\left( N \right) \cdot t_{max} } \right)$, the computational complexity of Section ③ is $O\left( {N \cdot D \cdot t_{max} } \right)$, the computational complexity of Section ④ is $O\left( {\left( {\frac{N}{2} \cdot D + N} \right) \cdot t_{max} } \right)$, the computational complexity of Section ⑤ is $O\left( {3 \cdot D \cdot t_{max} } \right)$. Finally, the computational complexity of Section ⑥ is $O\left( {N \cdot t_{max} } \right)$. Thus, the total computational complexity of the HGWO is $O( N \cdot D + N + N \cdot \log \left( N \right) \cdot t_{max} + N \cdot D \cdot t_{max} + ( {\frac{N}{2} \cdot D + N} ) \cdot t_{max} + 3 \cdot D \cdot t_{max}+$ $N \cdot t_{max} ) \approx O( {N \cdot D \cdot t_{max} })$. As a result, the computational complexity of the proposed HGWO is not increased, but the performance is different. See the Table 1 for details.

Algorithm 1

Pseudo-code of HGWO

Table 1 Detailed steps for computational complexity

4 Experimental results

In this section, the performance of the proposed HGWO is evaluated by 15 benchmark functions in different dimensions. The whole experiments are carried out from the following six parts: (1) experimental setup and benchmark functions; (2) comparison with other methods; (3) effectiveness of introduced strategies; (4) convergence analysis of HGWO; (5) diversity analysis of HGWO; and (6) non-parametric statistical analysis.

4.1 Experimental setup and benchmark functions

The HGWO is evaluated in 15 benchmark functions. The GWO and nine other methods between 2016 and 2024, including WOA, SSA, GSK, AOA, AHA, HBA, MSMA, EOBGWO, and AGWO, are used as a competition to investigate HGWO. Table 2 describes the parameters of different methods. The values are the same as those in the corresponding references.

Table 2 Parameter of different methods

$F_{1}$ to $F_{5}$ are unimodal functions, $F_{6}$ to $F_{9}$ are multimodal functions, and $F_{10}$ to $F_{15}$ are fixed dimension functions. The corresponding formula of functions, dimension, range, and theoretical optimal value are presented in Table 3. Several related studies have used these benchmark functions (Abd Elaziz et al. 2017). All the experiments were carried out on PYTHON 3.9 software and the MacOS Catalina system, and the hardware details were Intel Core i7 CPU (2.8 GHz) and 16 GB RAM.

Table 3 Characteristics of benchmark functions

4.2 Comparison with other methods

This section compares HGWO with GWO, WOA, SSA, GSK, AOA, AHA, HBA, MSMA, EOBGWO, and AGWO on the 15 benchmark functions given in Table 3. The parameter settings are detailed in Table 2. In Tables 4, 5 and 6, comparison methods for benchmark functions in dimension = 30, 100, and 500 are described as the best, worst, average (Avg), and standard deviation (Std). The optimal value is marked in bold. Since AGWO has discussed the performance of most functions in Table 3 in 30 dimensions in its own published paper, the results of AGWO directly follow the results of the published paper.

Table 4 Experimental results of different methods in 30-dimensional

Table 5 Experimental results of different methods in 100−dimensional

Table 6 Experimental results of different methods in 500-dimensional

From Tables 4, 5 and 6, HGWO generally obtains the best results. Among them, for the $F_{3}$ function in Table 4, the average is 2.69E−06, 4.82E−10, 4.48E−07, 71.40, 2.39E+04, 1.93E−131, 2.53E−12, 7.69E−53, 7.77E−13, 0, and 0 for GWO, WOA, SSA, GSK, AOA, AHA, HBA, MSMA, EOBGWO, AGWO, and HGWO, respectively. Based on these results, the theoretical optimal values of unimodal ($F_{1}$, $F_{3}$–$F_{5}$), multimodal ($F_{6}$, $F_{9}$), and fixed dimension ($F_{10}$–$F_{14}$) are obtained by HGWO. For the $F_{2}$ function in Table 4, MSMA and AGWO found better Avg values. For the $F_{15}$ function in Table 4, EOBGWO found better best and worst values. It is worth noting that HGWO outperforms other methods by tens of orders of magnitude in all indicators on the $F_{8}$ function, which shows that HGWO can exploit more efficiently. It can be seen from Tables 5 and 6 that as the dimension increases, the performance of EOBGWO decreases significantly, especially the $F_{3}$ function. Furthermore, we also use the standard deviation (Std) metric to validate the stability of HGWO. The smaller the standard deviation, the better the stability of the algorithm. Tables 4, 5 and 6 show that HGWO obtains smaller values on most benchmark functions, indicating that HGWO has good stability.

4.3 Effectiveness of introduced strategies

This section is mainly to verify the effectiveness of different strategies and compare HGWO with GWO containing only a single strategy, including the Halton sequence initialized population grey wolf optimizer (GWO1), the dimension learning-based position update strategy grey wolf optimizer (GWO2), the crisscross strategy grey wolf optimizer (GWO3), and the Cauchy mutation strategy grey wolf optimizer (GWO4). The specific results are shown in Table 7. The optimal value is marked in bold.

Table 7 Experimental results of HGWO and different strategies in 30-dimensional

From Table 7, for most functions, the average and best values obtained by GWO1 are one to two orders of magnitude higher than those of GWO, which means the Halton sequence strategy effectively improves population diversity. Then, GWO2 also performs better than GWO, which indicates using Euclidean distance to obtain neighboring solutions to balance exploration and exploitation. Moreover, GWO3 has other enhancement effects for different functions, which brings better solutions than GWO on unimodal functions, indicating that GWO3 continuously retains higher quality grey wolves and converges quickly. Finally, GWO4 can find better solutions in the late iteration. However, it is worth noting that a single strategy has some limitations for GWO, making it impossible to maintain a high optimality search for different functions. Therefore, by combining the above four improvement strategies, HGWO can obtain better solutions.

4.4 Convergence analysis of HGWO

This section mainly discusses the convergence of HGWO and other advanced algorithms such as GWO, WOA, SSA, GSK, AOA, AHA, HBA, MSMA, EOBGWO, and AGWO on 15 benchmark functions. The convergence curve indicates the relationship between the fitness and the iterations, which is mainly used to analyze the optimization behavior of the proposed HGWO. Figure 5 shows the convergence curves of different algorithms in detail.

Fig. 5

Convergence curves of different methods on 15 benchmark functions

From Fig. 5, HGWO achieves the least number of iterations in the case of similar accuracy, WOA, SSA, GSK, AHA, and HBA are smoother, and they have lower accuracy. Moreover, for the $F_{7}$ function, HGWO shows noticeable fluctuations decrease with the lapse of iteration, which suggests that the dimension learning-based position update strategy can find better solutions. Furthermore, compared to EOBGWO and AGWO, HGWO can find a smaller resolution, which indicates that it can outperform the compared methods in various benchmark functions.

4.5 Diversity analysis of HGWO

This section analyzes the diversity of HGWO and GWO, WOA, SSA, GSK, AOA, AHA, HBA, MSMA, EOBGWO, and AGWO on 15 benchmark functions. In this study, we use the diversity metric proposed by Osuna-Enciso et al. (2022) to measure the diversity of the algorithm. The specific metric is as shown in Eqs. (21–23). Table 8 shows the diverse results of different algorithms in detail. The optimal value is marked in bold.

$$nVOL = \sqrt {\frac{{V_{pop} }}{{V_{lim} }}}$$

(21)

$$V_{lim} = \sqrt {\mathop \prod \limits_{i = 1}^{D} \left| {u_{i} - l_{i} } \right|}$$

(22)

$$V_{pop} = \sqrt {\mathop \prod \limits_{i = 1}^{D} \left( {y_{i} \cdot y_{i} } \right)}$$

(23)

where Eq. (21) is used to assess the diversity of the algorithm, Eq. (22) corresponds to the boundary constraint of the search space, and Eq. (23) represents the spatial distribution of the population during the iterative process. $u_{i}$ and $l_{i}$ represent the upper and lower bounds of the ith dimension, respectively. $y_{i}$ represents the interquartile range of the ith dimension.

Table 8 Diversity results of different algorithms

From Table 8, HGWO has obtained better values on most benchmark functions, which is much smaller than other comparison algorithms, including GWO, WOA, SSA, GSK, AOA, AHA, HBA, MSMA, EOBGWO, and AGWO, indicating that the introduction of Halton sequence strategy improved the limitation of insufficient population diversity of the basic GWO, and further verified the effectiveness of the proposed HGWO.

4.6 Non-parametric statistical analysis

This section mainly verifies the performance of the proposed HGWO further. Non-parametric statistical methods (Cleophas and Zwinderman 2011), including the Wilcoxon signed-rank test and Friedman test, are used to conduct statistical tests on HGWO and ten other advanced algorithms. Among them, the significance level p is set to 5%. The specific results are shown in Tables 9 and 10 for details.

Table 9 Experimental results of the Wilcoxon signed-rank test

Table 10 Experimental results of the Friedman test

From Table 9, HGWO is significantly different from GWO, WOA, SSA, GSK, AOA, AHA, HBA, MSMA, EOBGWO, and AGWO for all benchmark functions, indicating that HGWO performs superior to the different methods. From Table 10, HGWO is the best compared to other methods in the Friedman test, and the Chi-Square is 48.73 and p < 0.05. Therefore, it is also shown that there is a remarkable difference between HGWO and GWO, WOA, SSA, GSK, AOA, AHA, HBA, MSMA, EOBGWO, and AGWO.

5 Experiments on engineering design problems

This section also applies the proposed HGWO to solve eight engineering optimization problems, such as welded beam design, pressure vessel, three-bar truss, tension/compression spring, speed reducer, tubular column, piston lever, and heat exchanger. In this experiment, the maximum number of iterations is 1000, population size is 30, the best results obtained from 30 runs are compared with the results shown in the corresponding references (Meng et al. 2014; Mirjalili and Lewis 2016; Nadimi-Shahraki et al. 2020; Abualigah et al. 2021; Chandran and Mohapatra 2023; Seyyedabbasi and Kiani 2023; Hu et al. 2023). In Tables 11, 12, 13, 14, 15, 16, 17, and 18, the optimal value is marked in bold.

5.1 Welded beam design

There are seven restrictions on the problem: $g_{1} \left( x \right)$ to ${ }g_{7} \left( x \right)$, as well as four decision variables, which are the weld width ($x_{1}$), the bar length ($x_{2}$), the bar height ($x_{3}$), and the bar width ($x_{4}$) (Coello 2000). Mathematically, the details are shown in Eqs. (24–31).

From Table 11, HGWO performs better than others in that it provides a more reliable solution in which the optimal variables are $\left[ {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right]$ = [0.1679, 3.3724, 10.0000, 0.1680] and the optimal objective’ value is $f\left( x \right)$ = 1.5092, it proves the efficiency of HGWO in practical applications.

Table 11 The results of a welded beam

Function:

$$\min f\left( x \right) = 1.10471x_{1}^{2} x_{2} + 0.04811x_{3} x_{4} \left( {14 + x_{2} } \right)$$

(24)

Subject to:

$$g_{1} \left( x \right) = \tau \left( x \right) - \tau_{max} \le 0$$

(25)

$$g_{2} \left( x \right) = \sigma \left( x \right) - \sigma_{max} \le 0$$

(26)

$$g_{3} \left( x \right) = \delta \left( x \right) - \delta_{max} \le 0$$

(27)

$$g_{4} \left( x \right) = x_{1} - x_{4} \le 0$$

(28)

$$g_{5} \left( x \right) = P - P_{c} \left( x \right) \le 0$$

(29)

$$g_{6} \left( x \right) = 0.125 - x_{1} \le 0$$

(30)

$$g_{7} \left( x \right) = 1.10471x_{1}^{2} + 0.04811x_{3} x_{4} \left( {14 + x_{2} } \right) - 5 \le 0$$

(31)

Variable range:

$$\begin{aligned} &\uptau \left( x \right) = \sqrt {\left( {\tau^{\prime}} \right)^{2} + 2\tau^{\prime}\tau^{\prime\prime}\frac{{x_{2} }}{2R} + \left( {\tau^{\prime\prime}} \right)^{2} } \\ & \tau^{\prime} = \frac{P}{{\sqrt 2 x_{1} x_{2} }} \\ & \tau^{\prime\prime} = \frac{MR}{J} \\ & M = P\left( {L + \frac{{x_{2} }}{2}} \right) \\ & R = \sqrt {\frac{{x_{2}^{2} }}{4} + \left( {\frac{{x_{1} + x_{3} }}{2}} \right)^{2} } \\ \end{aligned}$$

$$\begin{aligned} & J = 2\left\{ {\sqrt 2 x_{1} x_{2} \left[ {\frac{{x_{2}^{2} }}{4} + \left( {\frac{{x_{1} + x_{3} }}{2}} \right)^{2} } \right]} \right\} \\ & \sigma \left( x \right) = \frac{6PL}{{x_{4} x_{3}^{2} }} \\ & \delta \left( x \right) = \frac{{6PL^{3} }}{{Ex_{3}^{2} x_{4} }} \\ & P_{c} \left( x \right) = \frac{{4.013E\sqrt {\frac{{x_{3}^{2} x_{4}^{6} }}{36}} }}{{L^{2} }}\left( {1 - \frac{{x_{3} }}{2L}\sqrt{\frac{E}{4G}} } \right) \\ \end{aligned}$$

$\begin{aligned} & P = 6000lb,\; L = 14 in.,\; \delta_{max} = 0.25 in.,\; E = 30{,}000{,}000 psi \\ & G = 12{,}000{,}000 psi,\; \tau_{max} = 13{,}600 psi,\; \sigma_{max} = 30{,}000 psi \\ & 0.1 \le x_{1} ,x_{4} \le 2, 0.1 \le x_{2} ,x_{3} \le 10 \\ \end{aligned}$

5.2 Pressure vessel

There are four kinds of constraints: $g_{1} \left( x \right)$ to ${ }g_{4} \left( x \right)$, as well as four decision variables, such as shell width ($x_{1}$), head width ($x_{2}$), inner radius ($x_{3}$), and cylindrical height ($x_{4}$) (Sandgren 1990). Mathematically, the details are shown in Eqs. (32–36).

From Table 12, HGWO performs better than others in that it provides a more reliable solution in which the optimum variables are $\left[ {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right]$ = [0.7782, 0.3850, 40.3209, 199.9919] and optimal objective’ value is $f\left( x \right)$ = 5887.04.

Table 12 The results of pressure vessel

Function:

$$\min f\left( x \right) = 0.6224x_{1} x_{3} x_{4} + 1.7781x_{2} x_{3}^{2} + 3.1661x_{4} x_{1}^{2} + 19.84x_{3} x_{1}^{2}$$

(32)

Subject to:

$$g_{1} \left( x \right) = - x_{1} + 0.0193x_{3} \le 0$$

(33)

$$g_{2} \left( x \right) = - x_{2} + 0.00954x_{3} \le 0$$

(34)

$$g_{3} \left( x \right) = - \pi x_{4} x_{3}^{2} - \frac{4}{3}\pi x_{3}^{3} + 1{,}296{,}000 \le 0$$

(35)

$$g_{4} \left( x \right) = x_{4} - 240 \le 0$$

(36)

Variable range:

$$0 \le x_{1} ,\;x_{2} \le 99,\; 10 \le x_{3} ,\;x_{4} \le 200$$

5.3 Three-bar truss

There are three kinds of constraints: $g_{1} \left( x \right)$ to $g_{3} \left( x \right)$, and two decision variables, which are the cross-sectional of component 1 ($x_{1}$) and the cross-section of component 2 ($x_{2}$) (Save 1983). Mathematically, the details are shown in Eqs. (37–40).

From Table 13, HGWO is superior to others in that it provides a more reliable solution in which the optimal variables are $\left[ {x_{1} ,x_{2} } \right]$ = [0.78878, 0.40794], and the optimal objective’ value is $f\left( x \right)$ = 263.8958. Moreover, it is proved that HGWO is effective in practice.

Table 13 The result of the three-bar truss

Function:

$$\min f\left( x \right) = \left( {2\sqrt 2 x_{1} + x_{2} } \right) \cdot l$$

(37)

Subject to:

$$g_{1} \left( x \right) = \frac{{\sqrt 2 x_{1} + x_{2} }}{{\left( {\sqrt 2 x_{1}^{2} + 2x_{1} x_{2} } \right)}} \cdot P - \sigma \le 0$$

(38)

$$g_{2} \left( x \right) = \frac{{x_{2} }}{{\left( {\sqrt 2 x_{1}^{2} + 2x_{1} x_{2} } \right)}} \cdot P - \sigma \le 0$$

(39)

$$g_{3} \left( x \right) = \frac{1}{{\left( {x_{1} + \sqrt 2 x_{2} } \right)}} \cdot P - \sigma \le 0$$

(40)

Variable range:

$$\begin{aligned} & l = 100 \,{\text{cm}},\;\; P = 2\, {\text{kN/cm}}^{2} ,\; \;\sigma = 2 \,{\text{kN/cm}}^{2} \\ & 0 \le x_{1} ,x_{2} \le 1 \\ \end{aligned}$$

5.4 Tension/compression spring

There are four constraints: $g_{1} \left( x \right)$ to $g_{4} \left( x \right)$, as well as three decision variables, which are the wire diameter ($x_{1}$), the average coil diameter ($x_{2}$), and the number of active coils ($x_{3}$) (Coello 2000). Mathematically, the details are shown in Eqs. (41–45).

From Table 14, HGWO is superior to others in that it provides a more reliable solution in which the optimum variables are $\left[ {x_{1} ,x_{2} ,x_{3} } \right]$ = [0.0515, 0.3537, 11.4643] and the optimal objective’ value is $f\left( x \right)$ = 1.2667238E−02.

Table 14 The result of tension/compression spring

Function:

$$\min f\left( x \right) = x_{1}^{2} x_{2} \left( {2 + x_{3} } \right)$$

(41)

Subject to:

$$g_{1} \left( x \right) = 1 - \frac{{x_{2}^{3} x_{3} }}{{71785x_{1}^{4} }} \le 0$$

(42)

$$g_{2} \left( x \right) = \frac{{4x_{2}^{2} - x_{1} x_{2} }}{{12566\left( {x_{2} x_{1}^{3} - x_{1}^{4} } \right)}} + \frac{1}{{5108x_{1}^{2} }} - 1 \le 0$$

(43)

$$g_{3} \left( x \right) = 1 - \frac{{140.45x_{1} }}{{x_{2}^{2} x_{3} }} \le 0$$

(44)

$$g_{4} \left( x \right) = \frac{{x_{1} + x_{2} }}{1.5} - 1 \le 0$$

(45)

Variable range:

$$0.05 \le x_{1} \le 2, \;\;0.25 \le x_{2} \le 1.3,\;\; 2 \le x_{3} \le 15$$

5.5 Speed reducer

In this model, the constraints include $g_{1} \left( x \right)$ to ${ }g_{11} \left( x \right)$. It has seven variables: face width ($x_{1}$), the module of teeth ($x_{2}$), number of teeth in the pinion ($x_{3}$), length of the first shaft between bearings ($x_{4}$), size of the other shaft between bearings ($x_{5}$), the diameter of the first shaft ($x_{6}$), and diameter of the other shaft ($x_{7}$) (Hu et al. 2023), $f\left( x \right)$ is the minimum weight of speed reducer. Mathematically, the details are shown in Eqs. (46–57).

Function:

$$\min f\left( x \right) = 0.7854x_{1} x_{2}^{2} \left( {3.3333x_{3}^{2} + 14.9334x_{3} - 43.0934} \right) - 1.508x_{1} \left( {x_{6}^{2} + x_{7}^{2} } \right) + 7.4777\left( {x_{6}^{3} + x_{7}^{3} } \right) + 0.7854\left( {x_{4} x_{6}^{2} + x_{5} x_{7}^{2} } \right){ }$$

(46)

Subject to:

$$g_{1} \left( x \right) = \frac{27}{{x_{1} x_{2}^{2} x_{3} }} - 1 \le 0$$

(47)

$$g_{2} \left( x \right) = \frac{397.5}{{x_{1} x_{2}^{2} x_{3}^{2} }} - 1 \le 0$$

(48)

$$g_{3} \left( x \right) = \frac{{1.93x_{4}^{3} }}{{x_{2} x_{3} x_{6}^{4} }} - 1 \le 0$$

(49)

$$g_{4} \left( x \right) = \frac{{1.93x_{5}^{3} }}{{x_{2} x_{3} x_{7}^{4} }} - 1 \le 0$$

(50)

$$g_{5} \left( x \right) = \frac{{\sqrt {\left( {\frac{{745x_{4} }}{{x_{2} x_{3} }}} \right)^{2} + 16.9 \times 10^{6} } }}{{110.0x_{6}^{3} }} - 1 \le 0$$

(51)

$$g_{6} \left( x \right) = \frac{{\sqrt {\left( {\frac{{745x_{5} }}{{x_{2} x_{3} }}} \right)^{2} + 157.5 \times 10^{6} } }}{{85.0x_{6}^{3} }} - 1 \le 0$$

(52)

$$g_{7} \left( x \right) = \frac{{x_{2} x_{3} }}{40} - 1 \le 0$$

(53)

$$g_{8} \left( x \right) = \frac{{5x_{2} }}{{x_{1} }} - 1 \le 0$$

(54)

$$g_{9} \left( x \right) = \frac{{x_{1} }}{{12x_{2} }} - 1 \le 0$$

(55)

$$g_{10} \left( x \right) = \frac{{1.5x_{6} + 1.9}}{{x_{4} }} - 1 \le 0$$

(56)

$$g_{11} \left( x \right) = \frac{{1.1x_{7} + 1.9}}{{x_{5} }} - 1 \le 0$$

(57)

Variable range:

$$\begin{aligned} & 2.6 \le x_{1} \le 3.6, \;\;0.7 \le x_{2} \le 0.8, \;\;17 \le x_{3} \le 28 \\ & 7.3 \le x_{4} \le 8.3, \;\;7.8 \le x_{5} \le 8.3,\;\; 2.9 \le x_{6} \le 3.9, \;\;5 \le x_{7} \le 5.5 \\ \end{aligned}$$

From Table 15, HGWO is superior to others in that it provides a more reliable solution in which the optimum variables are $\left[ {x_{1} ,x_{2} ,x_{3} ,x_{4} ,x_{5} ,x_{6} ,x_{7} } \right]$ = [3.5001, 0.7000, 17.0000, 7.4532, 7.8000, 3.3533, 5.2868] and the optimal objective’ value is $f\left( x \right)$ = 2998.5623.

Table 15 Results of speed reducer problem compared with other methods

5.6 Tubular column

In this model, the constraints include $g_{1} \left( x \right)$ to ${ }g_{6} \left( x \right)$, and the tubular column problem has two variables, $f\left( x \right)$ is the minimum cost of the tubular column (Bayzidi et al. 2021). Mathematically, the details are shown in Eqs. (58–64).

Function:

$$\min f\left( x \right) = 9.8x_{1} x_{2} + 2x_{1}$$

(58)

Subject to:

$$g_{1} \left( x \right) = \frac{P}{{\pi x_{1} x_{2} \sigma_{y} }} - 1 \le 0$$

(59)

$$g_{2} \left( x \right) = \frac{{8PL^{2} }}{{\pi^{3} Ex_{1} x_{2} \left( {x_{1}^{2} + x_{2}^{2} } \right)}} - 1 \le 0$$

(60)

$$g_{3} \left( x \right) = \frac{2.0}{{x_{1} }} - 1 \le 0$$

(61)

$$g_{4} \left( x \right) = \frac{{x_{1} }}{14} - 1 \le 0$$

(62)

$$g_{5} \left( x \right) = \frac{0.2}{{x_{2} }} - 1 \le 0$$

(63)

$$g_{6} \left( x \right) = \frac{{x_{2} }}{0.8} - 1 \le 0$$

(64)

Variable range:

$$\begin{aligned} & P = 2500\,{\text{kgf}},\;\;L = 250\,{\text{cm}},\;\;E = 0.85 \times 10^{6} \,{\text{kgf/cm}}^{2} ,\;\;\sigma_{y} = 500\,{\text{kgf/cm}}^{2} \\ & 2 \le x_{1} \le 14, \;\;0.2 \le x_{2} \le 0.8 \\ \end{aligned}$$

From Table 16, HGWO is superior to others in that it provides a more reliable solution in which the optimum variables are $\left[ {x_{1} ,x_{2} } \right]$ = [5.45113, 0.29197], and the optimal objective’ value is $f\left( x \right)$ = 26.49986.

Table 16 Results of tubular column problem compared with other methods

5.7 Piston lever

In this model, the constraints include $g_{1} \left( x \right)$ to ${ }g_{4} \left( x \right)$. The piston lever problem has four variables, $f\left( x \right)$ is the minimum oil volume of the piston lever (Bayzidi et al. 2021). Mathematically, the details are shown in Eqs. (65–69).

Function:

$$\min f\left( x \right) = \frac{1}{4}\pi x_{3}^{2} \left( {L_{2} - L_{1} } \right)$$

(65)

Subject to:

$$g_{1} \left( x \right) = QLcos\theta - R \times F \le 0$$

(66)

$$g_{2} \left( x \right) = Q\left( {L - x_{4} } \right) - M_{max} \le 0$$

(67)

$$g_{3} \left( x \right) = 1.2\left( {L_{2} - L_{1} } \right) - L_{1} \le 0$$

(68)

$$g_{4} \left( x \right) = \frac{{x_{3} }}{2} - x_{2} \le 0$$

(69)

Variable range:

$$\begin{aligned} & R = \frac{{\left| { - x_{4} \left( {x_{4} sin\theta + x_{1} } \right) + x_{1} \left( {x_{2} - x_{4} cos\theta } \right)} \right|}}{{\sqrt {\left( {x_{4} - x_{2} } \right)^{2} } + x_{1}^{2} }} \\ & F = \frac{{\pi Px_{3}^{2} }}{4} \\ & L_{1} = \sqrt {\left( {x_{4} - x_{2} } \right)^{2} + x_{1}^{2} } \\ & L_{2} = \sqrt {\left( {x_{4} sin\theta + x_{1} } \right)^{2} + \left( {x_{2} - x_{4} cos\theta } \right)^{2} } \\ \end{aligned}$$

$$\begin{aligned} & \theta = 45^{^\circ } ,\;\;Q = 10{,}000\,{\text{lbs}},\;\;L = 240\,{\text{in}}{.} \\ & M_{max} = 1.8 \times 10^{6} \,{\text{lbs}},\;\;P = 1500psi \\ & 0.05 \le x_{1} ,x_{2} ,x_{4} \le 500, 0.05 \le x_{3} \le 120 \\ \end{aligned}$$

From Table 17, HGWO is superior to others in that it provides a more reliable solution in which the optimum variables are $\left[ {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right]$ = [0.0501, 1.0082, 2.0162, 500.0000] with the best objective’ value $f\left( x \right)$ = 1.0576.

Table 17 Results of piston lever problem compared with other methods

5.8 Heat exchanger

This model’s constraints include $g_{1} \left( x \right)$ to ${ }g_{6} \left( x \right)$, and the heat exchanger problem has eight variables (Jaberipour and Khorram 2010). $f\left( x \right)$ is the minimum heat exchanger. Mathematically, the details are shown in Eqs. (70–76).

Function:

$$\min f\left( x \right) = x_{1} + x_{2} + x_{3}$$

(70)

Subject to:

$$g_{1} \left( x \right) = 0.0025\left( {x_{4} + x_{6} } \right) - 1 \le 0$$

(71)

$$g_{2} \left( x \right) = 0.0025\left( {x_{5} + x_{7} - x_{4} } \right) - 1 \le 0$$

(72)

$$g_{3} \left( x \right) = 1 - 0.01\left( {x_{8} - x_{5} } \right) \ge 0$$

(73)

$$g_{4} \left( x \right) = x_{2} x_{7} - 1250x_{5} - x_{2} x_{4} + 1250x_{4} \ge 0$$

(74)

$$g_{5} \left( x \right) = x_{1} x_{6} - 833.33252x_{4} - 100x_{1} + 83{,}333.333 \ge 0$$

(75)

$$g_{6} \left( x \right) = x_{3} x_{8} - x_{3} x_{5} + 2500x_{5} - 1250{,}000 \ge 0$$

(76)

Variable range:

$$100 \le x_{1} \le 10{,}000, 1000 \le x_{2} ,x_{3} \le 10{,}000, 10 \le x_{i} \le 1000\left( {i = 4,5,6,7,8} \right)$$

From Table 18, HGWO is superior to others in that it provides a more reliable solution in which the optimum variables are $\left[ {x_{1} ,x_{2} ,x_{3} ,x_{4} ,x_{5} ,x_{6} ,x_{7} ,x_{8} } \right]$ = [148.705, 1916.619, 5249.030, 122.595, 290.258, 229.805, 232.103, 390.242] with the best objective’ value $f\left( x \right)$ = 7314.354.

Table 18 Results of heat exchanger problem compared with other methods

6 Conclusion and future works

In view of the shortcomings of GWO, this study proposes a hybrid grey wolf optimizer (HGWO). First, the Halton sequence is used to enlarge the search scope and increase the diversity of the population. Then, the dimension learning-based is used for position update to balance exploitation and exploration. Furthermore, the crisscross strategy is used to enhance convergence precision. Finally, the Cauchy mutation strategy is adapted to avoid falling into the local optimum. To explore the performance, comparing with other methods with three dimensions for 15 benchmark functions, the impact of introduced strategies, convergence analysis, diversity analysis, and the non-parametric analysis of HGWO are tested, the results show that HGWO performs better than GWO, WOA, SSA, GSK, AOA, AHA, HBA, MSMA, EOBGWO, and AGWO. Statistically, the performance of HGWO is better than that of other methods. Furthermore, it has been demonstrated that HGWO can effectively address engineering problems.

Although HGWO effectively solves benchmark functions and practical engineering optimization problems, there is still some field for improvement. In future research, single-objective HGWO can be further extended to multi-objective optimization algorithms, and further improving HGWO by introducing adaptive adjustment parameters or combining it with other effective strategies based on information entropy will be one of the future research directions (Liang et al. 2024). In addition, the proposed HGWO may also have great application potential in solving other complex optimization problems, such as flow shop scheduling problems, traveling salesman problems, feature selection, image segmentation, and path planning.