On the m-clique free interval subgraphs polytope: polyhedral analysis and applications

Abstract

In this paper we study the m-clique free interval subgraphs. We investigate the facial structure of the polytope defined as the convex hull of the incidence vectors associated with these subgraphs. We also present some facet-defining inequalities to strengthen the associated linear relaxation. As an application, the generalized open-shop problem with disjunctive constraints (GOSDC) is considered. Indeed, by a projection on a set of variables, the m-clique free interval subgraphs represent the solution of an integer linear program solving the GOSDC presented in this paper. Moreover, we propose exact and heuristic separation algorithms, which are exploited into a Branch-and-cut algorithm for solving the GOSDC. Finally, we present and discuss some computational results.

1 Introduction

Motivated by some important parallel-machine scheduling applications, this paper considers the problem of finding m-clique free interval subgraphs. Here, the term m-clique free means that the subgraph does not contain any clique of size greater than or equal to $m+1$ where m is a given positive number. Indeed, this property is essential to ensure the feasibility of a schedule on a set of parallel machines of cardinality equal to m. More precisely, the considered scheduling application is related to an extension of the open-shop family Gonzales and Sahni (1976) where jobs are assigned to a set of machines and have to be sequenced under some disjunctive constraints. The term disjunctive constraint means that some couples of jobs cannot run at the same time (i.e., the time intervals when these jobs are performed cannot overlap). Such an extension is called generalized open-shop with disjunctive constraints (GOSDC). Given the structure of this scheduling problem, the study of the m-clique free interval subgraphs polytope seems to be of an important utility.

In a more general way, the considered two families of subgraphs (having the interval property or being m-clique free) have attracted the interest of many researchers. One main reason for this increasing interest is that many real-world applications involve solving problems on graphs, which are either interval graphs themselves or are related to interval subgraphs or to cliques in a natural way. Indeed, numerous applications of interval graphs have appeared in the literature including applications to genetic structures, sequential storage and scheduling [see Golumbic 2004; Gacias et al. 2010]. The algorithmic aspects and the combinatorial structures of these subgraphs have been the subject of an intensive research for several decades [see Golumbic (2004) for instance]. In some applications, interval representations with special properties are required. As an illustration, the application of the m-clique free interval subgraphs arises in the context of scheduling and cloud computing [see Hassan Abdel-Jabbar et al. 2016].

Now, we give a formal description of our problem and we present some notations. All graphs in this paper are simple and have no self-loops. Let $G=(V,E)$ be a graph. An undirected graph G is called an interval graph if its vertices can be put into a one-to-one correspondence with a set of intervals I of a linearly ordered set (like the real line) such that two vertices are connected by an edge of G if their corresponding intervals have nonempty intersection.

In other words, an interval graph is the graph showing intersecting intervals on a line. Thus, we associate a set of intervals $I=\{I_{1} ,\ldots ,I_{n}\}$ on a line with the interval graph $G=(V,E)$, where $V=\{1,\ldots ,n\}$ and two vertices, u and v, are linked by an edge if and only if $I_{u}\cap I_{v}\ne \emptyset$.

Clique is a very common structure in many applications since it is composed of a subset of vertices as well as all the possible relationships among them. Therefore, clique detection is playing an important role in various applications, such as social recommendation Mokotoff and Chretienne (2002) and network routing.

More formally, a clique can be defined as follows. Let $G=(V,E)$ be an undirected graph. A clique in G is a subset $S\subset V$ such that for any two vertices $v_{i},v_{j}\in S$ there exists an edge $(v_{i},v_{j})\in E$.

Using the same notation, an m-clique in G is a clique $S\subset V$ with $|S|=m+1$. Finally, we recall that a graph is m-clique free if it does not contain any m-clique.

In parallel machines scheduling some jobs in different machines can share any time units, the jobs can be represented with nodes and edges indicate there is a shared time units between jobs in different machines. For instance, if we consider 2 machines with the same speed and two jobs of lenght 3, then if the first job starts on the machine 1 at time $t=0$ and the second one starts on the machine 2 at time $t=1$, then there exists an edge between the vertices associated with these two jobs. But, if the second job starts on machine 2 at time $t=4$, then this edge does not exists. Thus, the solution is mathematically formalized as a graph $G=(V,E)$ where V denotes the set of vertices (associated with jobs) and E denotes the set of relationships between vertices (intersections of jobs on the time line). However, when we assign jobs to m parallel machines, the solution is feasible for two types of graphs (i.e., an interval graph or a m-clique free graph).

2 Polyhedral analysis

Let ${\mathcal {I}}:=\{I\subseteq E\ |\ G[I]$ induces an m-clique free interval graph$\}$. The vector $z^{I}$ is called the incidence vector associated with I, i.e., $z^{I}=(z^{I}_{e})_{e \in {E}}$ , where $z^{I}_{e}=1$ if $e \in I$ and $z^{I}_{e}=0$ otherwise. We define the m-Clique Free Interval Subgraph Polytope (MCFISP) as follows:

$$\begin{aligned} \mathrm {P}_{{\mathcal {I}}} (G,m):= conv \{ z^{I} \in \{0,1\}^{\vert E \vert } \ \vert \ I \in {\mathcal {I}}\}, \end{aligned}$$

First, we give the dimension of $\mathrm {P}_{{\mathcal {I}}} (G,m)$.

Proposition 1

Polytope $P_{{\mathcal {I}}}(G,m)$ is full dimensional.

Proof

We will exhibit $|E|+1$ elements of Polytope $P_{{\mathcal {I}}}(G,m)$ whose incidence vectors are affinely independent.

Consider the sets $I_{0}={\emptyset }$, $I_{e}=\{e\}$ for all $e\in E$. Clearly, these sets induce m-clique free interval subgraphs. Moreover, their incidence vectors are affinely independent. Thus, we have $|E|+1$ vectors of $P_{{\mathcal {I}}}(G,m)$ affinely independent and the proof is complete. $\square$

In the following propositions, we prove that the two trivial inequalities define facets.

Proposition 2

Inequalities $z_{e} \ge 0$, $e\in E$, define facets of $P_{{\mathcal {I}}}(G,m)$.

Proof

see the “Appendix”. $\square$

Proposition 3

Inequalities $z_{e} \le 1$, $e\in E$, define facets of $P_{{\mathcal {I}}}(G,m)$.

Proof

see the “Appendix”. $\square$

2.1 Forbidden subgraphs inequalities

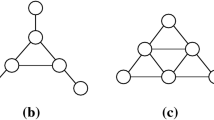
In this section we discuss graph properties in order to identify valid inequalities. Properties on interval graphs have been studied in Lekkeikerker and Boland (1962). The authors give all forbidden subgraphs in interval graphs. Indeed, if a graph does not contain any one of the five subgraphs given in Fig.  1, then it is an interval graph. The two first forbidden subgraphs are called Bipartite Claw and Umbrella. These subgraphs are defined on only seven nodes. The three last forbidden subgraphs are defined on various number of nodes. The n-net subgraphs are composed of $n+4$ nodes $\{1,\ldots ,n,a,b,c,d\}$ , where the edges are $\{a-b, 1-c, n-d\}\cup \{1-b, 2-b, 3-b,\ldots , n-b\}\cup \{1-2, 2-3,\ldots , (n-1)-n\}$. The n-tent subgraphs are defined as follows: the nodes {a, b, c} are connected by a triangle, the nodes $\{1,\ldots ,n\}$ are connected in a line form, nodes 1 and b are connected, node n is linked to c and the nodes in $\{b,c,2,\ldots ,n-1\}$ define a clique. Finally, the fifth forbidden configuration is a hole of more than 3 nodes, which is a cycle without chord. These five forbidden subgraphs ensure that the graph is an interval one. In addition, to be m-clique free, we remind that the graph cannot contain any clique of size greater than or equal to $m+1$.

Fig. 1

Forbidden subgraphs characterization. a Bipartite Claw. b Umbrella. c n-net, $n\ge 2$. d n-tent, $n\ge 3$. e Hole, $n\ge 4$

In the next subsection we describe valid inequalities associated with these forbidden subgraphs and we prove that these inequalities can define facets for $P_{{\mathcal {I}}}(G,m)$ under some specific conditions.

2.1.1 Bipartite claw

In this subsection, we give inequalities to avoid the forbidden bipartite claw subgraph. An example of bipartite claw is given in Fig. 1.

In what follows, we give some notations.

Let us consider the complete graph $K_{7}$ with seven nodes. We partition this graph into BC and ${\overline{BC}}$, where BC is the set of all edges that form the bipartite claw and ${\overline{BC}}$ is the set of edges in the associated complementary graph of BC. Moreover, ${\overline{BC}}$ is partitioned as follows:

• Subset ${\overline{BC}}_{h}^{4}$ contains all the edges such that each of them enables to form a hole of size 4 in a bipartite claw.

• Subset ${\overline{BC}}_{\triangle }$ contains three edges such that when we add one of them to BC, then we obtain a central triangle.

• Subset ${\overline{BC}}_{i}$ contains the edges that are able to form a triangle with the vertex 1.

• Subset ${\overline{BC}}_{h}^{5}$ is composed of all edges such that each of them enables to form a hole of size 5 in the bipartite claw.

Figure 2 shows these subsets.

Fig. 2

Subsets of the complementary Bipartite Claw. a Subset ${\overline{BC}}_i$. b Subset ${\overline{BC}}_h^4$. c Subset ${\overline{BC}}_h^5$. d Subset ${\overline{BC}}_\triangle$

As a consequence, the previous definitions lead explicitly to the following subsets:

• $BC=\{(1,2),(1,3),(1,4),(2,5),(4,7),(3,6)\}$.

• ${\overline{BC}}=\{$ (7, 1), (7, 2), (7, 3), (7, 5), (7, 6), (6, 1), (6, 2), (6, 4), (6, 5), (5, 1), (5, 3), (5, 4), (4, 2), (4, 3), (3, 2) $\}$.

• ${\overline{BC}}_{h}^{4}=\{(3,5)$,(2, 6),(5, 4),(2, 7),(3, 7) ,$(4,6)\}$.

• ${\overline{BC}}_{\triangle }=\{(2,3)$,(2, 4),$(3,4)\}$,

• ${\overline{BC}}_{i}=\{(1,5),(1,6),(1,7)\}$.

• ${\overline{BC}}_{h}^{5}=\{(5,6),(5,7),(6,7)\}$.

We consider two cases, when $m=2$, and when $m\ge 3$.

If $m=2$, then the following inequality is valid:

$$\begin{aligned} \sum _{{e}\in BC}z_{e}\le 5. \end{aligned}$$

(1)

It is worthnoting that keeping all the edges of BC leads to the impossibility of respecting the validity of the constraint for this special case when $m=2$. Indeed, when we add an edge from ${\overline{BC}}_{\triangle }\cup {\overline{BC}}_i$ in Fig. 2d to BC, the resulting subgraph will contain a clique of size 3 and hence would not be an m-clique. Moreover, if we add an edge $e\in {\overline{BC}}^4_{h}\cup {\overline{BC}}^5_{h}$ to BC, then we obtain a hole. If we add another edge to break this hole, then we obtain a clique of size 3.

Proposition 4

Inequality (1) defines a facet of $P_{{\mathcal {I}}}(G,m)$, when $m=2$.

Proof

see the “Appendix”. $\square$

Now, if $m\ge 3$, then the following inequality is valid.

$$\begin{aligned} \sum _{{e}\in BC}z_{e}-\sum _{{e}\in {\overline{BC}}_{\triangle }}z_{e}-\sum _{{e}\in {\overline{BC}}_{i}}z_{e}\le 5 \end{aligned}$$

(2)

Indeed, if we add only one edge (respectively two edges) of ${\overline{BC}}_{\triangle }$ to the bipartite claw, then the resulting subgraph contains $2-net$ (respectively $3-net$), which is already excluded by definition (as we mentioned in 2.1). We can observe that if we add one edge of ${\overline{BC}}_{\triangle }$, for instance (2, 3), and the edge (2, 6) or (3, 5) from ${\overline{BC}}_{h}^{4}$ to BC, then we obtain an m-clique free interval subgraph. Furthermore, if we add also the edge (5, 6), then the result remains an m-clique free interval subgraph. It is clear that when we add one, two or three edges of ${\overline{BC}}_{i}$ to BC, then the result is an m-clique free interval subgraph. The result is the same when we add (2, 4) and (4, 5) to BC.

Proposition 5

Inequality (2) defines a facet of $P_{{\mathcal {I}}}(G,m)$, when $m\ge 3$.

Proof

Let us denote by $az\le \alpha$ the inequality (2). Let $bz\le \beta$ be an equality that defines a facet of $P_{I}(G,m)$, such that $\{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):az=\alpha \}\subseteq \{z\in \mathrm {P} _{{\mathcal {I}}}(G,m):bz=\beta \}$. Since $P_{I}(G,m)$ is full dimensional, we need to prove that there exists $\rho$ such that $b=\rho a$ for some $\rho \in {\mathbb {R}}$.

Let $e_{1},e_{2}\in BC$ be two edges and let us define $I_{1}=BC\setminus \{e_{1}\}$ and $I_{2}=BC\setminus \{{e_{2}}\}$. It is clear that the incidence vectors of $I_{1}$ and $I_{2}$ satisfy inequality (2) with equality. Since $az^{I_{1}}=az^{I_{2}}$, $bz^{I_{1}}=bz^{I_{2}}$, implying that $b(e_{1})=b(e_{2})$. We set $b(e_{1})=\rho$. As $e_{1}$ and $e_{2}$ are arbitrary in BC,  then $b(e)=b(e^{\prime })=\rho$ $\forall e,e^{\prime }\in BC$.

Let $e_{3}\in {\overline{BC}}_{i}$. We can remark that the incidence vectors of $I_{3} =BC\cup \{e_{3}\}$ and $I_{1}$ satisfy inequality (2) with equality. As $az^{I_{3}}=az^{I_{1}}$, then $bz^{I_{3}}=bz^{I_{1}}$, implying that $b(e_{3})=-b(e_{1})$. As $e_{3}$ is arbitrary in ${\overline{BC}}_{i}$ and $e_{1}\in BC$, then $b(e)=-b(e^{\prime \prime })$ for every $e^{\prime \prime } \in {\overline{BC}}_{i}$, which leads to $b(e^{\prime \prime })=-\rho$.

The incidence vectors of the following three sets $I_{4}=BC\cup \{(2,4),(5,4)\}$, $I_{5}=BC\cup \{(2,4),(5,4),(2,7)\}$ and $I_{6}=BC\cup \{(2,4),(5,4),(5,7)\}$ satisfy inequality (2) with equality. Since $az^{I_{4} }=az^{I_{5}}=az^{I_{6}}$, we have $bz^{I_{4}}=bz^{I_{5}}=bz^{I_{6}}$, which implies that $b((2,7))=0$ and $b((5,7))=0$. By symmetry, we have $b((5,4))=b((2,7))=b((6,4))=b((3,7))=b((3,5))=b((2,6))=b((5,7))=b((5,6))=b((6,7))=0$.

Similarly, the incidence vectors of the two sets $I_{7}=BC\setminus \{(1,4)\}$ and $I_{4}$ verify inequality (2) with equality. Since $az^{I_{7}}=az^{I_{4} }$, $bz^{I_{7}}=bz^{I_{4}}$, implying that $b((1,4))=-b((2,4))$. By symmetry, we have $b((2,4))=b((3,4))=b((2,3))=-\rho$.

Let $e_{8}\in E\setminus (BC\cup {\overline{BC}})$. The incidence vectors of sets $I_{8} =(BC\setminus \{(1,2)\})\cup \{e_{8}\}$ and $I_{9}=BC\setminus \{(1,2)\}$ satisfy inequality (2) with equality. Since $az^{I_{8}} =az^{I_{9}}$, $bz^{I_{8}}=bz^{I_{9}}$, which implies that $b(e_{8})=0$. By symmetry, we have $b(e)=0$ $\forall$ $e\in E\setminus (BC\cup {\overline{BC}})$.

To summarize, there exists $\rho$ such that $b=\rho a$ for some $\rho \in {\mathbb {R}}$. $\square$

2.1.2 Umbrella inequalities

For the umbrella subgraph as shown in Fig. 3b, let $G_{u} =(U_{u},E_{u})$ be a graph that constitutes the umbrella and let ${\overline{E}}_{u}$ be a set of the complementary edges for $G_{u}$. In what follows, we will present a family of valid inequalities that avoid the umbrella subgraphs. To analyze this forbidden subgraph we need the following notations:

Let $E_{u}^{i}\subset E_{u}$ be the set of the three edges $\{$(1,3), (1,4), (1,5)$\}$ in the umbrella subgraph. Let $E_{u}^{t}\subset {\overline{E}}_{u}$ be the set of the edges such that when we add one of these edges to the umbrella we create a new triangle. Subset $E_{u}^{c}$ is the dashed edges in Fig. 5a. Finally, $E_{u}^{a}\subset E_{u}$ is the set of the around edges and $E_{u}^{h}\subset {\overline{E}}_{u}$ is the set of edges such that if we add one of them to the umbrella, then they will form a hole of size 4 or of size 5. All these subsets are illustrated in Fig. 4.

Fig. 3

Subsets of umbrella and its complementary. a Set $E_u^i$. b Set $E_u^t \cup E_u^c$. c Set $E_u^a$. d Set $E_u^h$

• $E_{u}^{i}=\{$ (1, 3), (1, 4), (1, 5) $\}$.

• $E_{u}^{t}=\{$ (1, 7), (3, 7), (5, 7) $\}$.

• $E_{u}^{c}=\{(2,4),(3,5),(4,6)\}$.

• $E_{u}^{a}=\{(1,2)$, (2, 3), (3, 4), (4, 5), (5, 6), (1, 6), (4, 7) $\}$.

• $E_{u}^{h}= \{$ (2, 7), (6, 7), (2, 5), (2, 6), (3, 6) $\}$.

It can be observed that the graph induced by $H^{u}=\{E_{u}^{i}\cup E_{u}^{t}\cup E_{u}^{c}\cup E_{u}^{a}\cup E_{u}^{h}\}$ is a complete graph.

When $m=2$, the triangle becomes a forbidden subgraph and the umbrella inequalities are dominated by the inequalities (9) presented in Sect. 2.1.6.

For this forbidden subgraph we focus on the instances for which $m\ge 3$.

When $m=3$, in order to keep all edges of $E_{u}$ it is necessary to add at least one edge of $E_{u}^{t}$. Moreover, when we add an edge from $E_{u}^{c}$ in this case the subgraph contains a clique of size 4. If we add an edge from $E_{u}^{h}$, then the induced subgraph will contain a hole.

Thus, the valid inequalities when $m=3$ will be:

$$\begin{aligned} \sum _{{e}\in E_{u}^{a}\setminus \{(4,7)\}}z_{e}+z_{(2,6)}+z_{(2,5)} +z_{(3,6)}\le 5. \end{aligned}$$

(3)

Proposition 6

Inequality (3) defines a facet of $P_{{\mathcal {I}}}(G,m)$ if $m=3$.

Proof

see the “Appendix”. $\square$

When $m\ge 4$, to find a feasible solution we can add also the edges from $E_{u}^{c}$. Then, the valid inequalities when $m \ge 4$ will be:

$$\begin{aligned}&\sum _{{e}\in E_{u}^{a}} z_{e} - \sum _{{e}\in E_{u}^{t} \cup E_{u}^{c}} z_{e} \le 6. \end{aligned}$$

(4)

Proposition 7

Inequality (4) defines a facet of $P_{{\mathcal {I}}}(G,m)$ if $m\ge 4$.

Proof

see the “Appendix”. $\square$

2.1.3 n-net inequalities

The $n-net$ forbidden subgraph is shown in Fig. 1c. We will give some notations to help in analyzing the $n-net$ forbidden subgraph.

Let $G_{net}=(U_{net},E_{net})$ be the graph that forms a net of size n (i.e., $n-net$) and ${\overline{E}}_{net}$ be the set of complementary edges of $G_{net}$. To avoid to have a subgraph that represents an $n-net$, where $n\ge 2$ we need either to eliminate an edge from the $n-net$ without inducing a hole (this edge does not belong to $E_{net}^{h}$), or to add an edge that does not create a hole (this edge does not belong to $E_{net}^{\bar{h}}$).

To analyze this forbidden subgraph we will use the following notations. From Fig. 1c let us consider:

• $E^{\bar{h}}_{net}=\{(a,c),(a,d)\}\cup \{(c,3),(c,4),\ldots ,(c,n)\}\cup \{(d,1),(d,2),\ldots ,(d,n-2)\}\cup \{(c,d)\}$.

• $E^{h}_{net} =\{(b,2),\ldots ,(b,n-1)\}$.

We propose valid inequalities that delete the $n-net$ forbidden subgraphs.

$$\begin{aligned} \sum _{{e}\in E_{net}\setminus E^{h}_{net}} z_{e} - \sum _{{e}\in {\overline{E}}_{net} \setminus E^{\bar{h}}_{net}} z_{e} \le \vert E_{net}\setminus E^{h}_{net} \vert - 1. \end{aligned}$$

(5)

Proposition 8

Inequality (5) defines a facet of $P_{{\mathcal {I}}}(G,m)$.

Proof

see the “Appendix”. $\square$

2.1.4 n-tent inequalities

Figure 1d shows the $n-tent$ forbidden subgraph. A graph is non-interval if it contains an $n-tent$ forbidden subgraph $G_{tent}$. The subgraph $G_{tent}$ can be transformed into a valid one by adding or removing one or more edges if such modifications do not create a hole.

Let the graph $G_{tent}=(U_{tent},E_{tent})$ be a graph that constitutes an $n-tent$ ($n\ge 3$) and ${\overline{E}}_{tent}$ be the set of complementary edges.

From Fig. 1c

• $E^{h}_{tent}= \{(b,c),(c,4),(b,2)\}$,

• $E^{\bar{h}}_{tent}= \{(1,4),(2,5),\ldots ,(n,n+3)\}$.

We can notice that, all n-tent where $n\ge 5$ contain a clique of size 5 then the clique inequality cuts this n-tent subgraph if $m\le 4$. It is the same idea for all n-tent. Indeed, when $n=4$ (respectively $n=3$), the clique inequality cut these n-tent sub graph if $m=3$ (respectively $m=2$).

The following inequality allows us to avoid the n-tent forbidden subgraphs.

$$\begin{aligned} \sum _{{e}\in E_{tent}\setminus E^{h}_{tent}} z_{e} - \sum _{{e}\in {\overline{E}}_{tent} \setminus E^{\bar{h}}_{tent}} z_{e} \le \vert E_{tent}\setminus E^{h}_{tent} \vert -1. \end{aligned}$$

(6)

Proposition 9

Inequality (6) defines a facet of $P_{{\mathcal {I}}}(G,m)$, when $m\ge 5$ or ($n=4$ and $m=3$) or ($n=3$ and $m=2$).

Proof

see the “Appendix”. $\square$

2.1.5 Hole inequalities

Here, it is convenient to define a hole as an induced subgraph of G isomorphic to $C_{k}$ for some $k\ge 4$, Schrijver (2003). The hole C is a forbidden subgraph as depicted in Fig. 1e. Let C denote the set of edges that form the hole, i.e., $C=\{$ $(u_{1},u_{2})$,$(u_{2},u_{3})$,...,$(u_{|C|-1},u_{|C|})$,$(u_{|C|},u_{1})$ $\}$. If i is multiple of |C|, then $u_{i}=u_{|C|}$. Otherwise, if $i>|C|$, then $u_{i}=u_{i^{\prime }}$, where $i^{\prime }$ is the rest of the euclidean division of i by |C|. Let ${\overline{C}}$ denote the set of all chords of hole C.

Suppose we have a hole of size 4. Obviously, this hole is non-interval graph. Nevertheless, the subgraph induced by a hole can be transformed to a feasible one by adding at least one chord.

Proposition 10

For a hole C, the minimum number of necessary chords that should be added to the hole to be an interval graph is $|C|-3$, when $|C|\ge 4$.

Proof

We prove this proposition by induction. When $|C|=4$, then we need one chord $k_{c}=1$, and then the proposition is true.

Let us assume that the property is true until $|C|=l$ and $k_{c}=l-3$. We need to prove it for a cycle $C^{\prime }$ where $|C^{\prime }|=|C|+1$ and that $k_{c^{\prime } }=|C^{\prime }|-3$. Let ${\tilde{C}}=\{u_{1},u_{2},u_{3},\ldots ,u_{|C|}\}$ be the hole graph given by C where we add $k_{c}$ edges in order to make it hole free and let $(u_{i},u_{i+1})$ be an edge, where $i\in \{1,2,\ldots ,|C|-1\}$. Now, we will construct $\tilde{C^{\prime }}$ from ${\tilde{C}}$ by adding the vertex $u_{|C|+1}$ in ${\tilde{C}}$, by replacing the edge $(u_{i},u_{i+1})$ by $(u_{i},u_{|C|+1})$ and $(u_{|C|+1},u_{i+1})$. Then, we find a unique hole of a size 4 in the new cycle. Therefore, $|\tilde{C^{\prime }}|=l+1$. It is necessary to add one edge to break this hole. Thus, $k_{c^{\prime }}=l^{\prime }-3$ is true. As C and $k_{c}$ are arbitrary, then the property is true for every hole. $\square$

Fig. 4

Hole free subgraphs

Now, we will present valid inequalities for the forbidden hole subgraph.

If $m=2$, then the inequality (7) is valid.

$$\begin{aligned} \sum _{{e}\in C}z_{e}+\sum _{{e}\in {\overline{C}}}z_{e}\le |C|-1. \end{aligned}$$

(7)

Indeed, if we add one chord to hole C, then we will obtain a triangle or another hole and it is not feasible for $m=2$. It is worth to note that this inequality for $m=2$ is equivalent to the clique inequalities described in the next subsection.

If $m\ge 3$, then the following inequality is valid.

$$\begin{aligned} \sum _{{e}\in C} (\vert C \vert -3)z_{e} - \sum _{{e} \in {\overline{C}}} z_{e} \le (\vert C\vert -1)(\vert C \vert -3). \end{aligned}$$

(8)

Proposition 11

Let C be a hole of size greater than 3, then inequality (8) associated with cycle C defines a facet of $P_{{\mathcal {I}}}(G,m)$ if $m\ge 3$.

Proof

Let us denote by $az\le \alpha$ the inequality (8), associated with hole C. Let $bz\le \beta$ be a facet defining inequality of $P_{{\mathcal {I}}}(G,m)$ such that $\{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):az=\alpha \}\subseteq \{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):bz=\beta \}$. We show that $b=\rho a$ for some $\rho$ $\in {\mathbb {R}}$.

Let $e_{1}$ and $e_{2}$ be two distinct edges of hole C. The solutions $I_{1}=C\diagdown \{e_{1}\}$ and $I_{2}=C\diagdown \{e_{2}\}$ are m-clique free interval subgraphs. We deduce that $I_{1},I_{2}$ are solutions. Moreover, we have $az^{I_{1}}=az^{I_{2}}$. Hence, $bz^{I_{1}}=bz^{I_{2}}$. This implies that $b(e_{1})=b(e_{2})$. Set $b(e)=(|C|-3)\rho$. As $e_{1},e_{2}$ are arbitrary then $b(e)=b(e^{\prime })$ $\forall e,e^{\prime }\in C$. We deduce that $b(e)=(|C|-3)\rho$ for all $e\in C$.

Let $u_{i}\in V(C)$. The solution $I_{3}=C\cup (\delta (u)\cap {\overline{C}})$, illustrated in Fig. 4a, and the solution $I_{4}=(I_{3}\setminus \{(u_{i} ,u_{i+2})\})\cup (u_{i+1},u_{i+3})$, illustrated in Fig. 4b, are feasible and verify the inequality (8) with equality. Moreover, we have $az^{I_{3}}=az^{I_{4}}$ and then $bz^{I_{3}}=bz^{I_{4}}$. This implies that $b(u_{i},u_{i+2})=b(u_{i+1},u_{i+3})$. Thus, by symmetry $b((u_{i},u_{i+2}))=b((u_{i+1},u_{i+3}))$ are arbitrary for all $\forall i\in \{1,2,\ldots ,|C|\}$.

The solution $I_{5}=(I_{3}\setminus (u_{i},u_{i+j}))\cup (u_{i+j-1},u_{i+j+1} ))$, illustrated in Fig. 4c, is feasible and verifies the inequality (8) with equality. Therefore, $az^{I_{5}}=az^{I_{3}}$. Hence $bz^{I_{5}}=bz^{I_{3}}$. This implies that $b(u_{i},u_{i+j} )=b(u_{i+j-1},u_{i+j+1})$. As these edges are arbitrary then $b(e)=b(e^{\prime })$ for all $e^{\prime }\in {\overline{C}}$.

Now, we will consider the two solutions $I_{1}$ and $I_{3}$. These solutions are feasible and verify the inequalities (8) with equality. Hence, $az^{I_{1}}=az^{I_{3}}$ and therefore $bz^{I_{1}}=bz^{I_{3}}$. This implies that $b(e_{1})=-\sum _{e^{\prime }\in \delta (u_{i})\setminus C}b(e^{\prime })$. As $e_{1}$ and $u_{i}$ are arbitrary for all $e\in C$ and $u_{i}\in V(C)$, then $b(e_{1})=-(|C|-3)b(e)$. We deduce that $b(e)=-\rho$ $\forall e\in {\overline{C}}$.

Let $e_{3}\in E\setminus (C\cup {\overline{C}})$. The solutions $I_{7}=I_{3} \cup \{e_{3}\}$ and $I_{3}$ are feasible and verify the inequalities (8) with equality. Hence, $az^{I_{7}}=az^{I_{3}}$ and then $bz^{I_{7}}=bz^{I_{3}}$. This implies that $b(e_{3})=0$. As $b(e_{3})$ is arbitrary, then $b(e)=0$ for all $e\in E\setminus (C\cup {\overline{C}})$. $\square$

2.1.6 Clique inequalities

In this section we study the structure of a clique-free subgraph and we propose valid inequalities and facets of $P_{{\mathcal {I}}}(G,m)$.

Proposition 12

Let K be a clique and let V(K) be its set of vertices. If $m=2$, then the following inequality

$$\begin{aligned} \sum _{{e}\in E(K)}z_{e}\le |V(K)|-1 \end{aligned}$$

(9)

is valid and defines a facet of $\mathrm {P}_{{\mathcal {I}}}(G,m)$.

Proof

see the “Appendix”. $\square$

Remark that, the inequalities (9) are equivalent to the hole inequalities and dominate the umbrella inequalities when $m=2$.

Proposition 13

Let K be a clique of size $m+1$. The inequality

$$\begin{aligned} \sum _{{e}\in E(K)} z_{e} \le |E(K)|-1 \end{aligned}$$

(10)

defines a facet of $\mathrm {P}_{{\mathcal {I}}} (G,m)$.

Proof

see the “Appendix”. $\square$

Let f(K, m) be a function giving the minimum number of edges necessary to be removed from E(K) such that the resulting graph $G^{\prime }(K)$ is m-clique free. Let $\alpha =\lceil \frac{|V(K)|}{m}\rceil$, $n_{\alpha -1}=m\alpha -|V(K)|$ and $n_{\alpha }=\frac{|V(K)|-(n_{\alpha -1})(\alpha -1)}{\alpha }$.

Proposition 14

$$\begin{aligned} f(K,m) = n_{\alpha -1} \frac{(\alpha -1)(\alpha -2)}{2}+n_{\alpha } \frac{(\alpha )(\alpha -1)}{2}. \end{aligned}$$

Proof

Let $E^{\prime }$ be a set of f(K, m) edges such that $E(K)\setminus E^{\prime }$ is m-clique free. Note that in the complementary graph ${\overline{G}}(K)$ we have a stable set of size |K|. If we add $E^{\prime }$, then there does not exist a stable of size $m+1$ (m-stable free). Let us consider a minimum set of edges $E^{\prime \prime }\in E(K)$ such that $|E^{\prime \prime }|<|E^{\prime }|$ and $G(K)\setminus E^{\prime \prime }$ is m-clique free and thus ${\overline{G}}(K)\cup E^{\prime \prime }$ is m-stable free. Clearly $E^{\prime \prime }$ is a set of m disjoint cliques ${\mathcal {K}}=\{K_{1},\ldots ,K_{m}\}$, otherwise $E^{\prime \prime }$ is not minimal or contains a stable set of size $m+1$. To have the minimum set of edges, it is important to balance the size of cliques. Indeed, if we have two cliques $K_{i}$ and $K_{j}$ where $|K_{i}|\ge |K_{j}|+2$, then we can easily prove the following result $|E(K_{i})|+|E(K_{j})|>|E(K_{i}\setminus \{u\})|+|E(K_{j}\cup \{u\})|$, where $u\in K_{i}$. Thus, it can be deduced that the maximum difference between the cardinalities of two cliques of ${\mathcal {K}}$ is less or equal to 1. $\square$

Proposition 15

Let K be a clique. The following inequality

$$\begin{aligned} \sum _{{e}\in E(K)} z_{e} \le |E(K)|- f(K,m) \end{aligned}$$

(11)

is valid for $\mathrm {P}_{{\mathcal {I}}}(G,m)$.

Proof

First note that inequality (10) is a special case of inequality (11). However, for the sake of clarity, we prefer to do it step by step. By definition f(K, m) is the minimum number of edges necessary to be removed from E(K) such that the resulting graph $G^{\prime }(K)$ is m-clique free. Thus, the inequality (11) is valid. $\square$

In the next subsection, we will improve this family of inequalities.

2.1.7 Clique–Hole inequalities

In order to get an m-clique free subgraph, we need to remove from G(K) a set of m cliques of similar size $\alpha$ or $\alpha -1$ (as we mentioned in the previous proof). Other holes will remain and they must be avoided. We observe that if we remove m disjoint cliques from G(K), then we obtain a complete bipartite subgraph between all pairs of two cliques. Let $H_{ij}=(K_{i},K_{j},E_{ij})$ be a complete bipartite graph. Note that H contains a hole of a size greater than or equal to 4 if $|K_{i}|\ge 2$ and $|K_{j}|\ge 2$. To remove every hole in $H_{ij}$, the minimum number of edges $E^{\prime }$ necessary to be eliminated is equal to $\max (|K_{i}|,|K_{j}|)-1,$ otherwise we can always take 2 nodes in $K_{i}$ or $K_{j}$ such that these two nodes are not covered by $E^{\prime }$. Note that $E^{\prime }$, with size $\max (|K_{i}|,|K_{j}|)-1$, covers the maximum nodes of $K_{i}$ and $K_{j}$. We can reinforce the inequality (11) by the following inequality. Let $\alpha =\sum _{i\in m}(\max \{|K_{i}|-1,0\})-\max _{i\in m}|K_{i}|-1$.

Proposition 16

Let K be a clique. Then, the inequality

$$\begin{aligned} \sum _{{e}\in E(K)} z_{e} \le |E(K)|- (f(K,m)+\alpha ) \end{aligned}$$

(12)

is valid for $\mathrm {P}_{{\mathcal {I}}}(G,m)$.

Proof

We can notice that if we unbalance two cliques $K_{i}$ and $K_{j}$ to reduce the value $\max (|K_{i}|,|K_{j}|)-1$ by 1, then the number of edges necessary to be removed increases by $\max (|K_{i}|,|K_{j}|)-\min (|K_{i}|,|K_{j}|)$. $\square$

3 Cutting plane algorithms

Cutting plane method allows us to strengthen the linear relaxation by adding inequalities. Cutting plane algorithms mainly consist in generating constraints by means of a separation procedure [see, for example, Jiinger et al. (1995), Aardal and Hoesel (1999), Vallada and Ruiz (2012) and Schrijver (2003)]. Let $z^{*}$ be the incidence vector associated with the value of the variable z in the linear relaxation. The separation problem consists in finding if there exists a valid inequality $az \le b _{0}$ that cuts off the solution $z^{*}$, i.e., $az^{*} > b _{0}$. The separation algorithm associated with a family of inequalities $a^{E^{\prime }}x\le b^{E^{\prime }}$ for all $E^{\prime }\in {\mathcal {E}}^{\prime }$ consists in finding a set $E^{\prime } \in {\mathcal {E}}^{\prime }$ such that $a^{E^{\prime }}z^{*} > b^{E^{\prime }}$.

The results of the previous sections have allowed us to derive some exact separation algorithms and some approximate separation algorithms. Furthermore, at the end of this section we propose a “lazy separation procedure” to ensure that the integer solutions are m-clique free interval subgraphs. In the next paragraphs, we will describe these separation algorithms for all inequalities described in the previous section.

3.1 Bipartite claw separation

In this section we describe the BC separation algorithms. We propose three algorithms to separate the bipartite claw inequalities. One is an exact algorithm and two others are heuristic procedures. We consider only $m\ge 3$ (note that it is easy to adapt the algorithm for $m=2$).

Let the vector $z^{*}\in \mathbb {R^{|E|}}$ be a solution of a linear relaxation. We define a weight for each edge of the complete graph G as follows: $w(e)=z_{e}^{*}$ for all $e\in E$. The separation algorithm consists in finding one bipartite claw BC such that the associated inequality is violated by $z^{*}$. This inequality is then added to the separation linear relaxation. This corresponds to find a bipartite claw $BC\subseteq E$ such that: $\sum _{{e}\in BC}z_{e}^{*}-\sum _{{e} \in {\overline{BC}}_{\triangle }}z_{e}^{*}-\sum _{{e}\in {\overline{BC}}_{i}}z_{e}^{*}>5$.

From Fig. 2d, the subsets are the following:

• $BC=\{(1,2),(1,3),(1,4),(2,5),(4,7),(3,6)\}$.

• ${BC}_{\triangle }=\{(2,3)$,(2, 4),$(3,4)\}$.

• ${\overline{BC}}_{i}=\{(1,5),(1,6),(1,7)\}$.

Proposition 17

If a partial bipartite claw ${\tilde{BC}}$ is not violated by $z^{*}$, then every bipartite claw BC including this partial bipartite claw ${\tilde{BC}}$ is not violated.

It can be observed that, from Fig. 6a if we select the 3 first vertices 1, 2 and 3 such that ($z_{1,2}^{*}+z_{1,3}^{*}-z_{2,3}^{*}$) is less than 1, then there does not exist a violated bipartite claw within these 3 vertices in this position. Indeed, if $z_{e}^{*}=1,\forall e\in BC\setminus \{(1,2),(1,3)\}$ and $z_{e}^{\prime }=0,\forall e^{\prime } \in {\overline{BC}}_{\triangle }$, then we obtain in the best case, a left hand side value less than 5. Indeed, $\sum _{{e}\in BC\setminus \{(1,2),(1,3)\}}z_{e}^{*}=4$. Thus, $4+0+(z_{1,2}^{*}+z_{1,3}^{*}-z_{2,3}^{*})<5$. In the same way, if we add the vertex 4 and the value of ($z_{1,4}^{*}+z_{1,2}^{*}+z_{1,3}^{*} -z_{2,4}^{*}-z_{2,3}^{*}-z_{3,4}^{*}$) is less than 2, then there does not exist a violated bipartite claw within these 4 vertices in this position. In the best case we obtain a left side value that is $3+z_{1,4} ^{*}+z_{1,2}^{*}+z_{1,3}^{*}-z_{2,4}^{*}-z_{2,3}^{*} -z_{3,4}^{*}$. Thus, the left hand side is less than 5 and the value of $\sum _{{e}\in BC\setminus \{(1,2),(1,3),(1,4)\}}z_{e}^{*}=3$. With the same argument we test the weight of all partial subgraphs to drop non interesting bipartite claws. This process is used for the exact and the first heuristic algorithms.

3.1.1 Exact separation (ExBC-sep)

Now, we will explain the exact separation algorithm. The exact algorithm consists in testing all the possible seven vertices in this order (1, 2, 3,...,7). We select the nodes such that the values of the weighted edges in the incidence graph is maximized as follows: the weight of BC, minus the value of edges in ${\overline{BC}} _{\triangle }$, minus the value of edges ${\overline{BC}}_{i}$. The running time of the exact algorithm in the worst case is bounded by $O(n^{7})$. Indeed, we must select the seven vertices such that the weight of the induced graph is maximum and then the number of iterations is bounded by $n^{7}$. Nevertheless, the running time is practically shorter with the improvement we presented before.

3.1.2 Heuristic 1: separation (H1BC-sep)

In this heuristic we start by searching the vertices 1, 2, 3,  and 4 that maximize $w(1,2)+w(1,3)+w(1,4)-w(2,4)-w(2,3)-w(3,4)$ from Fig. 6a based on the results of Bipartite Claw in Sect. 2.1.1. If the value of ($z_{1,2}^{*}+z_{1,3}^{*} +z_{1,4}^{*}-z_{2,4}^{*}-z_{2,3}^{*}-z_{3,4}^{*}$) is greater than 2, then it is still possible to find a violated BC inequality with this set of vertices. After that, using the greedy approach, we search to add the best weighted vertex 5 according to the incident weighted edge, if the partial BC is violated, then we will search for the best vertex 6 and with the same idea we will add vertex 7. If the BC induced by these vertices is violated by $z^{*}$, then we add the inequality to the relaxation. By using this greedy approach, the heuristic running time is $O(n^{4})$.

3.1.3 Heuristic 2: separation (H2BC-sep)

This heuristic follows a greedy approach to find a violated BC inequality. We search at each step the best next vertex to add in BC. The idea is to find the ’best weighted’ edge in the graph. This edge is considered as $z_{1,2}$, if the weight of the edge $z_{1,2}^{*}>0$. The heuristic tries to find with the greedy approach given in Heuristic 1 the next best ordering of vertices 3, 4, ..., 7. This heuristic has $O(n^{2})$ running time.

3.2 Umbrella separation

In this subsection we present three separation algorithms associated with the umbrella inequality. We propose an exact separation algorithm and two heuristics based on a greedy approach. The separation algorithm consists in finding an umbrella, such that the associated inequality is violated by $z^{*}$. If the associated inequality is violated by $z^{*}$, then we add this inequality to the linear relaxation. Thus, we search an umbrella, which is subset of E such that $\sum _{{e}\in E_{u}^{a}}z_{e}^{*}-\sum _{{e}\in E_{u}^{t}\cup E_{u}^{c}}z_{e}^{*}>6$ where $m\ge 4$. Then, it is possible to adapt the algorithm for $m=3$.

3.2.1 Exact separation algorithm

The exact separation algorithm starts by finding first edges $z_{1,2}$ and $z_{2,3}$. If $z_{1,2}^{*}+z_{2,3}^{*}<1$, then the algorithm cannot find an umbrella within these two edges in this position. In the next step, the algorithm searches the best vertex 4, that satisfies $z_{1,2}^{*} +z_{2,3}^{*}+z_{3,4}-z_{2,4}\ge 2$, and then the algorithm adds vertex 5, then vertex 6 and finally vertex 7. Figure 5 illustrates the umbrella and the complementary subgraphs. The running time of the exact algorithm in the worst case is in $O(n^{7} )$.

Fig. 5

Coefficient of umbrella and its complementary edges. a The coefficient of $E_u^t \cup E_u^c$. b The coefficient of $E_u^a$

3.2.2 H1U-sep separation

In this heuristic we start by searching the vertices 1, 2, 3, and 4 that maximize ($z_{1,2}+z_{2,3}+z_{3,4}-z_{2,4}$). In Fig. 5 the coefficient of each edge is illustrated. Figure 6b shows these basic edges. If this value is greater than 4, then we search vertex 6, and then vertex 7. If the umbrella induced by these vertices is violated by $z^{*}$, then we add this inequality. By using the greedy approach the running time is reduced to $O(n^{4})$.

3.2.3 H2U-sep separation

This heuristic follows a greedy approach to find a violated umbrella inequality. We search at each step the best next edge to be added to the umbrella. The heuristic starts by the best weighted edge $z_{1,2}$, then with the greedy approach it searches the best next vertex 3 to be added to the umbrella. By following this order, the best weighted vertexes of the umbrella are determined one after one. If it is violated by $z^{*}$, then the inequality is added. This heuristic has $O(n^{2})$ running time.

Fig. 6

Basic edges for Bipartite Claw and Umbrella. a Basic nodes for BC. b Basic nodes for UH1

3.2.4 n-net separation

In this subsection we describe the n-net separation algorithms. Let the vector $z^{*}\in \mathbb {R^{|E|}}$ be a solution of the linear relaxation. The weighted vector is defined in the previous sections. The separation algorithm consists in finding one n-net where $n\ge 2$, such that the associated inequality is violated by $z^{*}$. This corresponds to find an n-net $\subseteq E$ such that $\sum _{{e}\in E_{net}\setminus E_{net}^{h}} z_{e}^{*}-\sum _{{e}\in {\overline{E}}_{net} \setminus E_{net}^{\bar{h}}} z_{e}^{*}>|E_{net}\setminus E_{net}^{h}|-1$. From Fig. 1c, the subsets are the following:

• $E_{net} =\{(a,b),(c,1),(d,n),(1,2)\ldots ,(n-1,n)\}$,

• $E_{net}^{h} =\{(b,2),\ldots ,(b,n-1)\}$.

Now, we present the n-net separation algorithm. Here, we search an n-net such that $\sum _{{e}\in E_{net}\setminus E_{net}^{h}}z_{e}^{*}-\sum _{{e}\in {\overline{E}}_{net} \setminus E_{net}^{\bar{h}}}z_{e}^{*}>|E_{net}\setminus E_{net}^{h}|-1$.

Fig. 7

Adding one vertex to 2-net to find 3-net. a 2-net. b From 2-net to 3-net. c 3-net

Let us consider Fig. 7a. We search the edge $(a,a_{1})$ with the maximum weight $w((a,a_{1}))$. Then, we search the best vertex $b_{1}$ such that $w((a_{1},b_{1}))$ is maximum. By a greedy search we continue for finding sequentially $c_{1}$ and c. By considering 2-net, if the value of $\sum _{{e}\in E_{net}\setminus E_{net}^{h}}z_{e}^{*}-\sum _{{e}\in {\overline{E}}_{net} \setminus E_{net}^{\bar{h}}}z_{e}^{*}$ is greater than 6, then we try to extend it to a 3-net in the following way: By adding a vertex $(c^{\prime })$ adjacent to c. Figure 7b explains the process, when the dashed edges are added.

It is important to mention that we remove the edge $(a_{1},c_{1})$ (see. Fig. 7c) if $n+1$ net is violated. Then, we add the n-net inequality (if $n\ge 2$) and we stop the algorithm.

The proposed heuristic running time is $O(n^{2}).$

3.2.5 n-tent separation

For the n-tent separation algorithm we propose the following algorithm, which is based on a greedy approach.

Again, the vector $z^{*}\in {\mathbb {R}}^{|E|}$. The n-tent separation algorithm consists in finding an n-tent, such that the associated inequality is violated by $z^{*}$. Thus, we search an n-tent where $n\ge 3$, n-tent$\subseteq E$ such that $\sum _{{e}\in E_{tent}\setminus E_{tent}^{h} }z_{e}-\sum _{{e}\in {\overline{E}}_{tent} \setminus E_{tent}^{\bar{h}}}z_{e} \le |E_{tent}\setminus E_{tent}^{h}|-1$.

Fig. 8

Adding one vertex to 3-tent to find 4-tent. a 3-nent. b 4-tent

We search for the best $z_{a,b}$, and $z_{a,c}$ in the first step (see 8a). In the next step, we search the best nodes 1, 2, 3 one by one using a greedy approach to maximize the sum of n-tent edges, by considering the weight of the edges from n-tent and its complementary. If 2-tent is not found, this means that 3-tent does not exist. If 3-tent is found, then we try to add the best node 4, which is connected with node $c^{\prime }$ and connecting $c^{\prime }$ to $a_{1}$ and to remove $(a_{1},c)$ to have the structure of 4-tent. The heuristic continues for searching for $n+1$-net at each step. If the heuristic failed to find $n+1$-net, then the violated n-net inequality associated with the found n-net will be added. The proposed heuristic running time is $O(n^{3})$.

3.3 Hole separation

Now, we explain the hole separation algorithm, which is based on a greedy approach. As in the previous paragraphs, the relaxed solution is represented by vector $z^{*}\in {\mathbb {R}}^{|E|}$. The separation algorithm consists in finding a forbidden subgraph hole, such that the associated hole inequality is violated by $z^{*}$. Thus, we search a hole of size C where $holeC\subseteq E$ such that $\sum _{{e}\in C}(|C|-3)z_{e}-\sum _{{e}\in {\overline{C}}}z_{e}>(|C|-1)(|C|-3)$.

The algorithm starts by the edge ($u_{1}$,$u_{2}$) with $w((u_{1},u_{2}))$ is maximum (see Fig. 9). By a greedy search, we pick the vertex $u_{3}$ such that $w((u_{2},u_{3}))-w((u_{1},u_{3}))$ is maximum. With the same process, we search a sequence of vertices $u_{4},\ldots ,u_{n}$. In each step, we consider the cycle where we connect $u_{1}$ to $u_{n}$. We find a hole where the associated inequality is violated and then we add it.

Fig. 9

Hole

If $\sum _{{e}\in C}(|C|-3)z_{e}-\sum _{{e}\in {\overline{C}}}z_{e} \le (|C|-1)(|C|-3)$ where C is the incident cycle, then we stop the algorithm since we cannot find a cycle where the associated inequality is violated.

3.4 Clique separation

In this subsection we explain the clique separation algorithm. The vector $z^{*}\in {\mathbb {R}}^{|E|}$ represents the solution. The clique separation algorithm consists in finding a clique, such that the associated inequality is violated by $z^{*}$. More precisely, we search a clique of size K, $E(K)\subseteq E$ such that $\sum _{{e}\in E(K)} z_{e}>|E(K)|-f(K,m)$.

Fig. 10

Clique of size 4

The heuristic starts by the edge (a,b) such that w((a, b)) is maximum. By the greedy search we find the vertex c such that $w((a,c))+w((a,b))+w((c,b))$ is maximum. By the same process we search the vertex d such that $w((a,c))+w((a,b))+w((c,b))+w((b,d))+w((c,d))+w((a,d))$ is maximum (see Fig. 10). In each step we consider the clique where we connect a vertex with all other vertices in the clique. If we find a clique where the associated inequality is violated, then this inequality is added.

If $\sum _{{e}\in E(K)} z_{e} \le |E(K)|- f(K,m)$, then we stop the algorithm, since we cannot find a clique where associated inequality is violated, and we add the inequality of clique of size $n-1$.

3.5 Lazy constraint approach

In this subsection, we propose some algorithms to ensure that a solution given by an integer value vector $\bar{z}\in \{0,1\}^{|V|\times |V|}$ induces an m-clique free interval subgraph. We consider the induced graph $\tilde{G}=(V,{\tilde{E}})$ where ${\tilde{E}}$ contains all edges such that $\bar{z} _{e}=1$. For the interval graph detection, we use the algorithm given in Habib et al. (2000) to check if ${\tilde{G}}$ is an interval graph. If ${\tilde{G}}$ is not an interval graph, then we add an interdiction inequality

$$\begin{aligned} \sum _{{e}\in {\tilde{E}}}z_{e}-\sum _{{e}\in E\setminus {\tilde{E}}}z_{e}\le |{\tilde{E}}|-1. \end{aligned}$$

This algorithm runs in $O(n+mlog(n))$ Habib et al. (2000).

For the clique inequalities, we search the clique of a maximum size. We use the integer linear program given in Pardalos and Xue (1994) to find the maximum clique in ${\tilde{G}}$. Finding the maximum clique in G is an NP-hard problem. We use CPLEX to solve this problem. If ${\tilde{G}}$ contains a clique K of a size greater than m, then we add the following clique inequality associated with K.

$$\begin{aligned} \sum _{{e}\in E(K)}z_{e}\le |E(K)|-1. \end{aligned}$$

We can note that, the lazy constraints are used only to check the validity of an integer solution.

If no clique inequality and no interdiction inequality are generated, then the solution is feasible.

4 Application to the generalized open shop problem with disjunctive constraints

The Generalized Open Shop with Disjunctive Constraints (GOSDC) can be formulated as follows. Let M be the set of machines. For every $i\in M$ we consider the set of jobs $J_{i}$ to be performed on machine i and we denote by ${\mathcal {J}}=\{J_{1},\ldots ,J_{m}\}$ the set of all these sets and by $J=\bigcup _{i\in M}J_{i}$ the union of these sets. We denote by $p_{ij}$ the processing time of job j on its machine i. We consider an incompatibility graph $G_{I}=(V_{I},E_{I})$ such that for each job $j\in J$ we associate a vertex $v_{j}\in V_{I}$ and there exists an edge between $v_{j_{1}}$ and $v_{j_{2}}$ if $j_{1}$ and $j_{2}$ cannot run at the same time. It is worthnoting that it is necessary to consider a linear ordering on each machine. To the best of our knowledge, this special problem has not been studied before.

4.1 Integer linear programming formulation

In this subsection, we present an integer linear programming (ILP) formulation for solving the problem. We need a family of binary variables. In the following, we describe the variables used in the formulation:

$$\begin{aligned} \bar{z}_{j_{1},j_{2}}= & {} \left\{ \begin{array}{l} 1\text { if job }j_{1}\text { runs before job }j_{2} \\ 0\text { otherwise} \end{array} \right. \quad \forall j_{1},j_{2}\in J.\\ z_{j_{1},j_{2}}= & {} \left\{ \begin{array}{l} 1\text { if }j_{1}\text { and }j_{2}\text { run at the same time } \\ 0\text { otherwise} \end{array} \right. \quad \forall j_{1}\in J_{i},\quad j_{2}\in J_{i^{\prime }}|i\ne i^{\prime }\in M. \end{aligned}$$

For every $j\in J$, we consider the variable $y_{j}\in {\mathbb {N}}^{+}$ representing the starting time of job j.

$C_{\text {max}}\in {\mathbb {N}}^{+}$ is the maximum completion time, such that $C_{\text {max}}\le C$, where C is an upper bound obtained heuristically.

The GOSDC can be solved by the following ILP, denoted by $(P_{GOS})$:

$$\begin{aligned}&\min C_{max} \nonumber \\&y_{j} + p_{ij}\le C_{max}, \quad \forall i\in M\qquad \forall j \in J_i, \end{aligned}$$

(13)

$$\begin{aligned}&y_{j_1}+ p_{ij_1} \le y_{j_2}+C {\cdot } \bar{z}_{j_2,{j_1}}, \quad \forall i\in M\qquad \forall j_1\in J_i \text { and } j_2 \in J, \end{aligned}$$

(14)

$$\begin{aligned}&\bar{z}_{j_1,{j_2}}+\bar{z}_{j_2,j_1}=1, \quad \forall i\in M\quad \forall j_1,j_2 \in J_i, \end{aligned}$$

(15)

$$\begin{aligned}&\bar{z}_{j_1,{j_2}}+\bar{z}_{j_2,j_1}=1,\quad \forall (v_{j_1},v_{j_2}) \in E_I, \end{aligned}$$

(16)

$$\begin{aligned}&\bar{z}_{j_1,{j_2}}+\bar{z}_{j_2,j_1}+z_{j_2,j_1}=1, \qquad \forall (v_{j_1},v_{j_2}) \notin E_I, \end{aligned}$$

(17)

$$\begin{aligned}&\sum _{{(j_1,j_2)}\in E(\bar{I})} z_{{j_1},{j_2}}- \sum _{{(j_1,j_2)}\in E\setminus E(\bar{I})} z_{{j_1},{j_2}} \le \vert E(\bar{I})\vert -1, \qquad \forall {\overline{I}} \subseteq \mathcal {{\overline{I}}}, \end{aligned}$$

(18)

$$\begin{aligned}&\sum _{{(j_1,j_2)}\in E(K)} z_{{j_1},{j_2}}\le |E(K)|-1 , \quad \forall K \subseteq {\mathcal {K}}, \end{aligned}$$

(19)

$$\begin{aligned}&C_{max}\in {\mathbb {N}}^{+}, \end{aligned}$$

(20)

$$\begin{aligned}&y_{j}\in {\mathbb {N}}^{+} \quad \forall i\in M\quad \forall j \in J_i, \end{aligned}$$

(21)

$$\begin{aligned}&z_{j_1,j_2}\in \{0,1\} \quad \forall i\in M\quad \forall j_1,j_2 \in J_i, \end{aligned}$$

(22)

$$\begin{aligned}&\bar{z}_{j_2,{j_1}}\in \{0,1\} \quad \forall i\in M\quad \forall j_1,j_2 \in J_i, \end{aligned}$$

(23)

The objective function is to minimize the makespan. Inequalities (13) ensure that the starting time for each job plus its processing time is less than or equal to the total completion time. Inequalities (14) and inequalities (15) guarantee that there is no two jobs running on the same machine at the same time and control the linear ordering. Inequalities (16) ensure that if two jobs are linked by an edge in the compatibility graph, then they do not run at the same time. Indeed, for these two jobs $j_{1}$ and $j_{2}$ either $j_{1}$ before $j_{2}$ or $j_{2}$ before $j_{1}$. Inequalities (17) ensure the three possibilities: $j_{1}$ before $j_{2}$ or $j_{2}$ before $j_{1}$ or they run at the same time. Inequalities (18) and (19) guarantee that the induced subgraphs are m -clique free interval subgraphs. The number of inequalities may be exponential and thus we will use the separation algorithm presented in the previous section.

In the proposed formulation, $\mathcal {{\overline{I}}}$ is the set of all subgraphs such that for all ${\overline{I}}\in \mathcal {{\overline{I}}}$, $G[{\overline{I}}]$ is not an interval subgraph. On the other hand, the set $\mathcal {{K}}$ contains all the cliques of size $m+1$ included in $V_{I}$. It is worth noting that the proposed valid inequalities in the previous part of this paper will ensure that the ILP will restrict the exploration on a reduced feasible space since every feasible schedule of $P_{GOS}$ can be associated with an m-clique free interval subgraph defined on $G_{I}$. In other words, the projection on the variables ${z}_{i,j}$ gives the polytope we previously studied. The constraints (18) and (19) corresponds to m-clique free interval subgraphs.

5 Experimental results

In order to evaluate the efficiency of the inequalities mentioned in Sect. 2.1, we developed the mentioned exact and heuristic separations. All computational results are obtained using Cplex 12.6 and JAVA for implementing exact and heuristic algorithms. The ILP with the valid inequalities is tested on the following proposed benchmark of instances.

The processing times are uniformly distributed between 50 and 150 as it is common in the literature Hall and Posner (2001). The graph density (GD) is equal to 0.5 and calculated as follows: $GD=\frac{|E|}{|V|(|V|-1)}$ where E is the set of edges associated with precedence constraints between jobs and V is the set of vertices associated with jobs. The results are given for 4 families of instances. Each family contains 5 instances with the same parameters.

The numerical tests have been carried out on an Intel Core i5 of 3.4 GHz on linux environment. The required CPU time is measured in seconds. We limit to 3600 s the algorithm running time for each instance, by using 4.0 GB of RAM.

The next tables provide the following information:

• $|J_i|$: Number of jobs per machine.

• m: Number of machines.

• |J|: Number of jobs.

• rootGap : The gap between the lower bounds and the upper bounds ($100\times \frac{UB-LB}{LB}$) at the the root node.

• Method: Inequalities used for the separation:

  • 0: Basic model;

  • 1: Only the bipartite claw inequalities (H1BC-Sep),

  • 2: Only the Umbrella inequalities (H1U-sep),

  • 3: Only the Hole inequalities,

  • 4: Only the Clique–hole inequalities,

  • 5: Only the n-net inequalities,

  • 6: Only the n-tent inequalities,

  • 7: All inequalities of methods 1 to 6,

  • 8: Cplex with only its generic cuts

• Nodes : The number of nodes in the branching tree.

• gap : The gap between the lower bounds and the upper bounds $\left( 100\times \frac{UB-LB}{LB}\right)$.

• CPU: Computational time (limited to 1 h).

• Ct BC: The number of bipartite claw inequalities added in the Branch-and-cut method (B&C).

• Ct UMB: The number of umbrella inequalities added in the B&C.

• Ct H: The number of hole inequalities added in the B&C.

• Ct Q: The number of clique–hole inequalities added in the B&C.

• Ct NN: The number of n-net inequalities added in the B&C.

• Ct NT: The number of n-tent inequalities added in the B&C.

• o/p: The number of solved instances among the 5 tested instances.

For the solving methods numbered 0 to 7 we remove all the proper improvements of CPLEX.

Table 1 Average CPU time

Notice that when $m=2$ we do not test the options 2 and 3 since the hole inequalities, clique inequalities and umbrella inequalities are dominated by or equivalent to the inequalities (9). For the option 4 and $m=2$ we consider an adaptation of the clique separation proposed in Sect. 3.4 where right-hand-side is equal to the number of vertices in the current clique. We present the results where we already selected the best separation algorithm for each family of inequalities i.e., the H1BC-sep for the BC inequalities and the H1U-sep for the umbrella inequalities. Table 1 presents the results for seven different methods. First, we observe that for all instances on 2 machines CPLEX with its proper improvements can solve all of them to optimality. Furthermore, with 5 jobs per machine the number of nodes decreases when we add cuts . In this case, we notice that adding all the inequalities is the best option in order to reduce the number of generated nodes. With 2 machines and 10 jobs per machine, if we do not consider the method 8, we notice that we reduce the CPU time and the option 4 is the most efficient for solving this family of instances. Indeed, the CPU time is only 930 seconds with the method 4. Secondly, if we increase the number of machines, then we cannot solve instances with 5 jobs per machine. However, we can reduce the gap by using our valid inequalities. For 5 jobs per machine and 4 machines, the gap is divided by 2 by using all the inequalities, whereas for 6 machines all methods have the same gap. We can note that the rootGap is not always dependent of the solving method. Two reasons can explain this observation: either it is due to the value of C or it is due to the added inequalities, which focus on only one family of variables.

Table 2 Average number of inequalities

Table 2 presents a complement of informations with the details of the average of the number of generated inequalities during the Branch-and-cut procedure. We remark that, when $m>2$, we generate a small number of clique inequalities.

6 Conclusion and perspectives

In this paper we considered the m-clique free interval subgraphs. We studied the facial structure of their polytope and we proposed some facet-defining inequalities to reinforce the associated linear relaxation. Moreover, the GOSDC was studied as an application in scheduling. Exact and heuristic separation algorithms were presented and used into a Branch-and-cut procedure for solving the GOSDC. Computational experiments were carried out and the results show that the algorithms are capable to solve many instances to optimality within reasonable computation time.

As a perspective, further research in this direction will be helpful to strengthen the integer programming formulations of a large variety of scheduling problems as another application to the m-clique free interval subgraphs.

Appendix

Proof of Proposition 2

Let us denote by $az\le \alpha$ inequality $-z_{e}\le 0$ associated with $e\in E$. Let $bz\le \beta$ be a facet defining inequality of $\mathrm {P} _{{\mathcal {I}}}(G,m)$, such that $\{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):az=\alpha \}\subseteq \{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):bz=\beta \}$. We show that $b=\rho a$ for some $\rho \in {\mathbb {R}}$.

Clearly $I_{0}=\emptyset$ is feasible. Let $I_{0}=\emptyset$ be a solution, and the associated incidence vector $z^{I_{0}}$ verifies $-z_{e}=0$.

Let $e^{\prime }\in E\setminus \{e\}$. The solution $I_{e^{\prime }}=\{e^{\prime }\}$ is feasible and the incidence vector $z^{I_{e^{\prime }}}$ associated with $I_{e^{\prime }}$ verifies $-z_{e} =0$.

Since, $az^{I_{0}}=az^{I_{e^{\prime }}}$, we deduce that $bz^{I_{0}}=bz^{I_{e^{\prime }}}$. This implies that $b(e^{\prime })=0$ for all $e^{\prime }\in E\setminus \{e\}$. Therefore, we set $b(e)=\rho$, and then $b=\rho a$. $\square$

Proof of Proposition 3

Let us denote by $az\le \alpha$ inequality $z_{e}\le 1$ associated with $e\in E$. Let $bz\le \beta$ be a facet defining inequality of $\mathrm {P} _{{\mathcal {I}}}(G,m)$, such that $\{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):az=\alpha \}\subseteq \{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):bz=\beta \}$. We show that $b=\rho a$ for some $\rho \in {\mathbb {R}}$.

Consider the feasible solution $I_{0}=\{e\}$. And the associated incidence vector $z^{I_{0}}$ verifies $z_{e}=1$.

Let $e^{\prime }\in E\setminus \{e\}$. The solution $I_{e^{\prime }}=\{e^{\prime },e\}$ is feasible and the incidence vector $z^{I_{e^{\prime }}}$ associated with $I_{e^{\prime }}$ verifies $z_{e} =1$.

Since, $az^{I_{0}}=az^{I_{e^{\prime }}}$, we deduce that $bz^{I_{0}}=bz^{I_{e^{\prime }}}$. This implies that $b(e^{\prime })=0$ for all $e^{\prime }\in E\setminus \{e\}$. Therefore, we set $b(e)=\rho$, and then $b=\rho a$. $\square$

Proof of Proposition 4

Let us denote by $az\le \alpha$ the inequality (1). Let $bz\le \beta$ be an inequality that defines a facet of $P_{I}(G,m)$, such that $\{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):az=\alpha \}\subseteq \{z\in \mathrm {P} _{{\mathcal {I}}}(G,m):bz=\beta \}$. Since $P_{I}(G,m)$ is full dimensional, we need to prove that there exists $\rho$ such that $b=\rho a$ for some $\rho \in {\mathbb {R}}$.

Let $e_{1},e_{2}\in BC$ be two edges. Clearly, the solutions $I_{1}=BC\setminus \{e_{1}\}$, and $I_{2}=BC\setminus \{{e_{2}}\}$ are feasible. Their incidence vectors satisfy the inequality (1) with equality. Since, $az^{I_{1}}=az^{I_{2}}$, $bz^{I_{1}}=bz^{I_{2}}$, it follows that $b(e_{1})=b(e_{2})$. We set $b(e_{1})=\rho$. As $e_{1}$ and $e_{2}$ are arbitrary in BC, then $b(e)=b(e^{\prime })$ for all $e,e^{\prime }\in BC$.

The solutions $I_{3}=BC\setminus \{(1,4)\}$, and $I_{4}=I_{3}\cup \{(2,4)\}$, $I_{5}=I_{3}\cup \{(5,4)\}$, and $I_{6}=I_{3}\cup \{(5,7)\}$ are feasible. Their incidence vectors satisfy the inequality (1) with equality. Since, $az^{I_{3}}=az^{I_{4}}=az^{I_{4}}=az^{I_{5}}=az^{I_{6}}$, $bz^{I_{3}}=bz^{I_{4}}=bz^{I_{4}}=bz^{I_{5}}=bz^{I_{6}}$, it follows that $b((2,4))=b((5,4))=b((5,7))=0$. By symmetry, $b(e)=0$, for all $e\in {\overline{BC}}_{h}^{4}\cup {\overline{BC}}_{h}^{5}\cup {\overline{BC}} _{\triangle }$.

The solutions $I_{7}=BC\setminus \{(4,7)\}$ and $I_{8}=I_{7}\cup \{(1,7)\}$ are feasible and verify the inequality (1) with equality. Since, $az^{I_{7}} =az^{I_{8}}$, $bz^{I_{7}}=bz^{I_{8}}$, it follows that $b((1,7))=0$. By symmetry, we have $b((1,5))=b((1,6))=0$.

Let $e_{3}\in E\setminus (BC\cup {\overline{BC}})$. The solutions $I_{3}$ and $I_{9}=I_{3}\cup \{e_{3}\}$ are feasible and verify the inequality (1) with equality. Since, $az^{I_{3}}= az^{I_{9}}$, $bz^{I_{3} }=bz^{I_{9}}$, which implies that $b(e_{3})=0$. By symmetry, we have $b(e)=0$ for all $e\in E\setminus (BC\cup {\overline{BC}})$. Thus $b=\rho a$. $\square$

Proof of Proposition 6

Let us denote by $az\le \alpha$ the inequality (3) associated with e. Let $bz\le \beta$ be a facet defining inequality of $P_{I}(G,m)$ such that $\{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):az=\alpha \}\subseteq \{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):bz=\beta \}$. We show that $b=\rho a$ for some $\rho \in {\mathbb {R}}$.

Let $e_{1},e_{2}\in E_{u}^{a}\setminus \{(4,7)\}$. The solutions $I_{1} =E_{u}\setminus \{e_{1}\}$ and $I_{2}=E_{u}\setminus \{e_{2}\}$ are feasible and the incidence vectors $z^{I_{1}}$ and $z^{I_{2}}$ verify the inequality (3) with equality. Moreover, we have $az^{I_{1}}=az^{I_{2}}$. Hence, $bz^{I_{1}}=bz^{I_{2}}$. This implies that $b(e_{1})=b(e_{2})$. We set $b(e_{1})=\rho$. As $e_{1}$ and $e_{2}$ are arbitrary in $E_{u} ^{a}\setminus \{(4,7)\}$, by symmetry, we have $b(e^{\prime })=b(e)=\rho$ for all $e\in E_{u}^{a}\setminus \{(4,7)\}$.

The solution $I_{3}=E_{u}^{a}\setminus \{(4,7),(1,6)\}$ and $I_{4}=(I_{3} \cup \{(2,5)\})\setminus \{(4,5)\}$ are feasible and the incidence vectors $z^{I_{3}}$ and $z^{I_{4}}$ verify the inequality (3) with equality. Moreover, we have $az^{I_{3}}=az^{I_{4}}$. Hence, $bz^{I_{3}}=bz^{I_{4}}$. This implies that $b((4,5))=b((2,5))$. Thus, from the previous results we deduce that $b((2,5))=b(e)$ for all $e\in E_{u}^{a}\setminus \{(4,7)\}$.

The solution $I_{5}=(I_{3}\cup \{(2,6)\})\setminus \{(5,6)\}$ is feasible, such that the incidence vectors $z^{I_{5}}$ and $z^{I_{3}}$ verify the inequality (3) with equality. Moreover, we have $az^{I_{5}} =az^{I_{3}}$. Hence, $bz^{I_{5}}=bz^{I_{6}}$. This implies that $b((2,6))=b((5,6))$. Indeed, from the previous results we have $b((2,6))=b(e)$ for all $e\in E_{u}^{a}\setminus \{(4,7)\}$.

The solution $I_{6}=(I_{3}\cup \{(3,6)\})\setminus \{(5,6)\}$ is feasible and the incidence vector $z^{I_{3}}$ and $z^{I_{6}}$ verify the inequality (3) with equality. Moreover, we have $az^{I_{3}} =az^{I_{6}}$. Hence, $bz^{I_{3}}=bz^{I_{6}}$. This implies that $b((3,6))=b((5,6))$. Indeed, from the previous results we can deduce that $b((3,6))=b(e)$ for all $e\in E_{u}^{a}\setminus \{(4,7)\}$.

The solutions $I_{7}=E_{u}^{a}\setminus \{(4,7)\cup (1,6)\}$ and $I_{8} =(I_{7}\cup \{(4,7)\}\cup E_{u}^{i})$ are feasible and the incidence vectors $z^{I_{7}}$, and $z^{I_{8}}$ verify the inequality (3) with equality. Moreover, we have $az^{I_{7}}=az^{I_{8}}$. Hence $bz^{I_{7}}=bz^{I_{8}}$. This implies that $b(e)=0$ for all $e\in E_{u}^{i}$.

Let $e\in \{(2,7),(3,7),(1,7),(5,7),(6,7)\}$. The solutions $I_{1}$ and $I_{9}=I_{1}\cup \{e\}$ are feasible and the incidence vectors $z^{I_{1}}$, $z^{I_{9}}$ verify the inequality (3) with equality. Moreover, we have $az^{I_{1}}=$ $az^{I_{9}}$. Hence, $bz^{I_{1}}=$ $bz^{I_{9}}$. This implies that $b((2,7))=$ $b((3,7))=$ $b((1,7))=$ $b((5,7))=$ $b((6,7))=0$. Thus $b=\rho a$. $\square$

Proof of Proposition 7

Let us denote by $az\le \alpha$ inequality (4) associated with e. Let $bz \le \beta$ be a facet defining inequality of $P_{I}(G,m)$ such that $\{ z \in \mathrm {P}_{{\mathcal {I}}} (G,m): az = \alpha \} \subseteq \{ z \in \mathrm {P}_{{\mathcal {I}}} (G,m): bz = \beta \}$. We show that $b=\rho a$ for some $\rho \in {\mathbb {R}}$.

Let $e_{1},e_{2}\in E_{u}^{t}\cup E_{u}^{c}$ be two edges, where $e_{1}\ne e_{2}$. We consider the edge sets $I_{1}=E_{u}\cup \{e_{1}\}$ and $I_{2} =E_{u}\cup \{e_{2}\}$ where the incidence vectors $z^{I_{1}}$ and $z^{I_{2}}$ are solutions of $\mathrm {P}_{{\mathcal {I}}}(G,m)$ and satisfy the inequality (4) with equality. Moreover, we have $az^{I_{1}}=az^{I_{2}}$. Thus, $bz^{I_{1}}=bz^{I_{2}}$. This implies that $b(e_{1})=b(e_{2})$. As $e_{1},e_{2}$ are arbitrary, then $b(e)=b(e^{\prime })$ for all $e,e^{\prime }\in E_{u}^{t}\cup E_{u}^{c}$.

Let $e_{3}\in E_{u}^{a}$. The solution $I_{3}=E_{u}\setminus \{e_{3}\}$ is feasible and the incidence vector $z^{I_{3}}$ verifies the inequality (4) with equality. Moreover, we have $az^{I_{1}}=az^{I_{3}}$. Hence, $bz^{I_{1}}=bz^{I_{3}}$. This implies that $b(e_{3})=-b(e_{1})$. Thus, by symmetry we have $b(e^{\prime })=-b(e)$ for all $e\in E_{u}^{t}\cup E_{u}^{c},e^{\prime }\in E_{u}^{a}$.

The solutions $I_{4}=E_{u}\setminus \{(1,6)\}$, $I_{5}=(E_{u}\setminus \{(1,6)\})\cup E_{u}^{i}$, $I_{6}=I_{5}\setminus \{(1,5)\}$, $I_{7} =I_{6}\setminus \{(1,4)\}$ and $I_{8}=I_{7}\setminus \{(1,3)\}$ are feasible. The incidence vectors $z^{I_{4}}$, $z^{I_{5}}$, $z^{I_{6}}$, $z^{I_{7}}$ and $z^{I_{8}}$ verify the inequality (3) with equality. Since $az^{I_{4}}=az^{I_{5}}=az^{I_{6}}=az^{I_{7}}=az^{I_{8}}$, $bz^{I_{4}}=bz^{I_{5}}=bz^{I_{6}}= bz^{I_{7}}=bz^{I_{8}}$, it follows that $b(e)=0$ for all $e\in E_{u}^{i}$.

The solutions $I_{9}=E_{u}\cup \{(2,7),(2,4)\}$, $I_{10}=E_{u}\cup \{(2,5),(2,4)\}$, $I_{11}=E_{u}\cup \{(2,4)\}$, $I_{12}=E_{u}\setminus \{(2,3)\}$, $I_{13}=I_{12}\cup \{(2,6)\}$, $I_{14}=I_{12}\cup \{(2,5)\}$, $I_{15}=E_{u}\setminus \{(5,6)\}$ and $I_{16}=I_{15}\cup \{(3,6)\}$ are feasible and verify the inequality (4) with equality. Since $az^{I_{9}}=az^{I_{10}}= az^{I_{11}}=az^{I_{12}}=az^{I_{13}} =az^{I_{14}}=az^{I_{15}}= az^{I_{16}}$, $bz^{I_{9}} =bz^{I_{10}}= bz^{I_{11}}= bz^{I_{12}}= bz^{I_{13}}=bz^{I_{14}} = bz^{I_{15}} = bz^{I_{16}}$,it follows that $b((2,6))=b((2,5))=b((2,7))=b((6,7))=b((3,6))=0$.

Let $e\in E\setminus (E_{u}\cup \bar{E_{u}})$. The solutions $I_{17} =E_{u}\setminus \{(4,7)\}$ and $I_{18}=I_{17}\cup \{e\}$ are feasible and verify the inequality (4) with equality. Since $az^{I_{17}}= az^{I_{18}}$, $bz^{I_{17}}=bz^{I_{18}}$. By symmetry, we have $b(e)=0$.

We set $b(e)=\rho$ for $e\in E_{u}$ and the proof is ended. $\square$

Proof of Proposition 8

Let us denote by $az\le \alpha$ the inequality (5) associated with e. Let $bz\le \beta$ be a facet defining inequality of $P_{I}(G,m)$ such that $\{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):az=\alpha \}\subseteq \{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):bz=\beta \}$. We show that $b=\rho a$ for some $\rho \in {\mathbb {R}}$.

Let $e_{1},e_{2}\in E_{net}\setminus E_{net}^{h}$ be two edges, where $e_{1}\ne e_{2}$. We consider the edge sets $I_{1}=E_{net}\setminus \{e_{1}\}$ and $I_{2}=E^{net}\setminus \{e_{2}\}$. Their incidence vectors $z^{I_{1}}$ and $z^{I_{2}}$ are solutions of $\mathrm {P}_{{\mathcal {I}}}(G,m)$ and satisfy the inequality (5) with equality. Moreover, we have $az^{I_{1}} =az^{I_{2}}$ and then $bz^{I_{1}}=bz^{I_{2}}$. This implies that $b(e_{1})=b(e_{2})$. As $e_{1},e_{2}$ are arbitrary, then $b(e)=b(e^{\prime })$ for all $e,e^{\prime }\in E_{net}\setminus E_{net}^{h}$.

We consider the edge sets $I_{3}=E_{net}\setminus \{(b,1)\}$ and $I_{4} =E^{net}\setminus (\{(b,1)\}\cup E_{net}^{h}).$Their incidence vectors $z^{I_{3}}$ and $z^{I_{4}}$ are solutions of $\mathrm {P}_{{\mathcal {I}}}(G,m)$ and satisfy the inequality (5) with equality. Moreover, we have $az^{I_{3}}=az^{I_{4}}$. Hence, we have $bz^{I_{3}}=bz^{I_{4}}$. This implies that $b(e)=0$ for all $e\in E_{net}^{h}$.

Let $e_{3}\in {\overline{E}}_{net} \setminus E_{net}^{\bar{h}}$. The solution $I_{5}=E^{net}\cup \{e\}$ is feasible and satisfies the inequality (5) with equality. Moreover, we have $az^{I_{1}}=az^{I_{5}}$ and then $bz^{I_{1}}=bz^{I_{5}}$. This implies that $b(e)=-b(e^{\prime })$ for all $e\in E_{net}\setminus E_{net}^{h}$ and $e^{\prime }\in {\overline{E}}_{net}\setminus E_{net}^{\bar{h}}$.

Considering the edge sets $I_{6}=E^{net}\cup \{(c,2),(c,3),\ldots ,(c,n),(c,d)\}$, $I_{7}=E^{net}\cup \{(c,2)\}$, $I_{8}=E^{net}\cup \{(d,1),(d,2),\ldots ,(d,n-1)\}$, $I_{9}=E^{net}\cup \{(d,n-1)\}$,$I_{10}=E^{net}\cup \{(a,1)\}$, $I_{11} =E^{net}\cup \{(a,1),(a,c)\}$,$I_{12}=E^{net}\cup \{(a,n)\}$, $I_{13} =E^{net}\cup \{(a,n),(a,d)\}$. These edge sets are solutions and satisfy the inequality (5) with equality. Moreover, we have $az^{I_{6}} =az^{I_{7}}=az^{I_{8}} = az^{I_{9}}=az^{I_{10}}=az^{I_{11}} = az^{I_{12}}=az^{I_{13}}$. Hence, we have $bz^{I_{6}}=bz^{I_{7}} =bz^{I_{8}} = bz^{I_{9}}=bz^{I_{10}}=bz^{I_{11}} = bz^{I_{12}} =bz^{I_{13}}$. Thus, $b(e)=0$ for all $e\in E_{net}^{\bar{h}}$.

Let $e\in E\setminus (E_{net}\cup {\overline{E}}_{net} )$. By considering the feasible solutions $I_{14}=E_{net}\setminus \{(a,b)\}$ and $I_{15}=E_{net} \setminus \{(a,b)\}\cup \{e\}$, we have $az^{I_{14}}=az^{I_{15}}$. Hence, $bz^{I_{14}}=bz^{I_{15}}$. This implies that $b(e)=0$.

We set $b(e)=\rho$ for $e\in E_{net}\setminus E_{net}^{h}$ and the proof is complete. $\square$

Proof of Proposition 9

Let us denote by $az\le \alpha$ the inequality (6) associated with e. Let $bz\le \beta$ be a facet defining inequality of $P_{I}(G,m)$ such that $\{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):az=\alpha \}\subseteq \{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):bz=\beta \}$. We show that $b=\rho a$ for some $\rho \in {\mathbb {R}}$.

Let $e_{1},e_{2}\in E_{tent}\setminus E_{tent}^{h}$ be two edges, where $e_{1}\ne e_{2}$. We consider the edge sets $I_{1}=E_{tent}\setminus \{e_{1}\}$ and $I_{2}=E^{tent}\setminus \{e_{2}\}$. Their incidence vectors $z^{I_{1}}$ and $z^{I_{2}}$ are solutions of $\mathrm {P}_{{\mathcal {I}}}(G,m)$ and satisfy the inequality (6) with equality. Moreover, we have $az^{I_{1}}=az^{I_{2}}$ and then $bz^{I_{1}}=bz^{I_{2}}$. This implies that $b(e_{1})=b(e_{2})$. As $e_{1},e_{2}$ are arbitrary, then $b(e)=b(e^{\prime })$ for all $e,e^{\prime }\in E_{tent}\setminus E_{tent}^{h}$.

We consider the edge sets $I_{3}=E_{tent}\setminus \{(a,c)\}$, and $I_{4}=E^{tent}\setminus (\{(a,c)\}\cup \{(b,c)\})$ there incidence vectors $z^{I_{3}}$, and $z^{I_{4}}$ are solutions of $\mathrm {P}_{{\mathcal {I}}}(G,m)$ and satisfy the inequality (6) with equality. Moreover, we have $az^{I_{3}}=az^{I_{4}}$ and then $bz^{I_{3}}=bz^{I_{4}}$. This implies by symmetry that $b((b,c))=b((b,2))=b((c,4))=0$.

Let $e_{3}\in {\overline{E}}_{tent} \setminus E_{tent}^{\bar{h}}$. The solution $I_{5}=E^{tent}\cup \{e\}$ is feasible and satisfies the inequality (6) with equality. Moreover, we have $az^{I_{1}}=az^{I_{5}}$. Hence, $bz^{I_{1}}=bz^{I_{5}}$. This implies that $b(e)=-b(e^{\prime })$ for all $e\in E_{tent}\setminus E_{tent}^{h}$ and $e^{\prime }\in \overline{E_{tent}}\setminus E_{tent}^{\bar{h}}$.

Let $(i,i+3)\in E_{tent}^{\bar{h}}$. The solutions $I_{6}=E^{tent} \cup \{(i,i+3),(i,i+2)\}$ and $I_{7}=E^{tent}\cup \{(i,i+2)\}$ are feasible and satisfy the inequality (6) with equality. Moreover, we have $az^{I_{6}}=az^{I_{7}}$ and then $bz^{I_{6}}=bz^{I_{7}}$. Thus, $b(e)=0$ for all $e\in E_{tent}^{\bar{h}}$.

Let $e\in E\setminus (E_{tent}\cup {\overline{E}}_{tent} )$. By considering the feasible solutions $I_{8}=E_{tent}\setminus \{(a,c)\}$ and $I_{9}=E_{tent} \setminus \{(a,c)\}\cup \{e\}$, we have $az^{I_{8}}=az^{I_{9}}$ and then $bz^{I_{8}}=bz^{I_{9}}$. This implies that $b(e)=0$.

We set $b(e)=\rho$ for $e\in E_{tent}\setminus E_{tent}^{h}$ and the proof is complete. $\square$

Proof of Proposition 12

Remark that if $m=2$, then a solution can be given only by a forest in the subgraph G(K). We deduce that the maximum number of edges in this subgraph is equal to $|V(K)|-1$.

Let us denote by $az\le \alpha$ the inequality (9) associated with e. Let $bz\le \beta$ be a facet defining inequality of $P_{I}(G,m)$ such that $\{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):az=\alpha \}\subseteq \{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):bz=\beta \}$. We show that $b=\rho a$ for some $\rho \in {\mathbb {R}}$.

Let $(u,v),(u,w)\in E(K)$, be two connected edges. Considering a line $T_{uv}$ beginning by (u, v) and finishing by the vertex w and the line $T_{uw}=T_{uv}\setminus \{(u,v)\}\cup \{(u,w)\}$. These two solutions are feasible and satisfy the inequality (9) with equality. Moreover, we have $az^{T_{uv}}=az^{T_{uw}}$. Hence, $bz^{T_{uv}}=bz^{T_{uw}}$. This implies that $b((u,v))=b((u,w))$. By symmetry, we deduce then that $b(e)=b(e^{\prime })$ for all $e,e^{\prime }\in E(K)$.

Let $e\in E\setminus E(K)$. By considering the feasible solution $T_{uv}^{\prime }=T_{uv}\cup \{e\}$, we have $az^{T_{uv}}=az^{T_{uv}^{\prime }}$. Hence, $bz^{T_{uv}}=bz^{T_{uv}^{\prime }}$. This implies that $b(e)=0$. $\square$

Proof of Proposition 13

Let us denote by $az\le \alpha$ the inequality (10) associated with e. Let $bz\le \beta$ be a facet defining inequality of $P_{I}(G,m)$ such that $\{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):az=\alpha \}\subseteq \{z\in \mathrm {P}_{{\mathcal {I}}}(G,m):bz=\beta \}$. We show that $b=\rho a$ for some $\rho \in {\mathbb {R}}$.

Let $e,e^{\prime }$ be two edges in E(K). The solution $I_{1}=E(K)\setminus \{e\}$ and $I_{2}=E(K)\setminus \{e^{\prime }\}$ are feasible and verify the inequality (10) with equality. Hence, $az^{I_{1}}=az^{I_{2}}$. Therefore, $bz^{I_{1}}=bz^{I_{2}}$. This implies that $b(e)=b(e^{\prime })$. We set $b(e)=\rho$. As b(e) and $b(e^{\prime })$ are arbitrary, then $b(e)=b(e^{\prime })$ for all $e,e^{\prime }\in E(K)$.

Let $e_{1}$ be an edge in $E\setminus E(K)$. The solution $I_{3}=I_{1} \cup \{e_{1}\}$ and $I_{1}$ are feasible and verify the inequality (10) with equality. Hence, $az^{I_{1}}=az^{I_{3}}$. Therefore $bz^{I_{1}} =bz^{I_{3}}$. This implies that $b(e_{1})=0$. As $b(e_{1})$ is arbitrary we deduce that $b(e)=0$, for all $e\in E\setminus E(K)$. Thus $b=\rho a$. $\square$