Declawing a graph: polyhedra and Branch-and-Cut algorithms

Abstract

The complete bipartite graph $K_{1,3}$ is called a claw. A graph is said to be claw-free if it contains no induced subgraph isomorphic to a claw. Given a graph G, the NP-hard Graph Declawing Problem (GDP) consists of finding a minimum set $S\subseteq V(G)$ such that $G-S$ is claw-free. This work develops a polyhedral study of the GDP polytope, expliciting its full dimensionality, proposing and testing five families of facets: trivial inequalities, claw inequalities, star inequalities, lantern inequalities, and binary star inequalities. In total, four Branch-and-Cut algorithms with separation heuristics have been developed to test the computational benefits of each proposed family on random graph instances and random interval graph instances. Our results show that the model that uses a separation heuristics proposed for star inequalities achieves better results on both set of instances in almost all cases.

1 Introduction

A graph G is said to be claw-free if it contains no induced subgraph isomorphic to the complete bipartite graph $K_{1,3}$, also called claw. The Graph Declawing Problem (GDP, for short) consists of finding a minimum set $S\subseteq V(G)$ such that $G-S$ is claw-free. Lewis and Yannakakis (1980) prove a general result showing that any vertex deletion problem on undirected/directed graphs for a nontrivial and hereditary property $\Pi$ is NP-Hard. $\Pi$ is considered to be nontrivial if it is true for infinitely many graphs and false for infinitely many graphs, and hereditary if, for any graph H satisfying $\Pi$, every vertex-induced subgraph of H also satisfies $\Pi$. Clearly, being claw-free is a hereditary and nontrivial property; therefore, the GDP is NP-Hard.

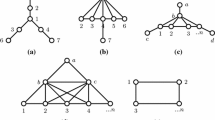
The GDP is related to the resolution of the Unit Interval Vertex Deletion Problem, which consists of converting a given graph into a unit interval graph by removing a minimum subset of vertices such that the resulting graph is free of the following forbidden induced subgraphs: claws, nets, tents, and induced cycles $C_k$ ($k\ge 4$) (see Fig. 1). Studies on the parameterized version of this problem, including kernelization, are developed by van Bevern et al. (2010), van’t Hof and Villanger (2013), Fomin et al. (2013), and Ke et al. (2018).

Fig. 1

Forbidden subgraphs for unit interval graphs: a claw, b net, c tent, d $C_k, k\ge 4$

The GDP is also related with the problem of converting an interval graph into a unit interval graph. An interval graph is the intersection graph of a family of intervals. Formally speaking, G is an interval graph if its vertices can be associated with intervals on the real line such that $uv\in E(G)$ if and only if $I_u \cap I_v \ne \emptyset$, where $I_u$ and $I_v$ are the intervals associated with u and v. A unit interval graph is an interval graph where the intervals can be chosen so that all of them have the same length (or, equivalently, length one). Figure 2 shows a transformation from an interval graph to a unit interval graph.

Fig. 2

Converting an interval graph c associated with a into a unit interval graph d associated with b by removing F from c

Unit interval graphs coincide with proper interval graphs (interval graphs where the intervals can be chosen so that no interval properly contains another) and indifference graphs (defined below). See Bogart and West (1999) for a proof that G is a unit interval graph if and only if G is a proper interval graph, and Roberts (1979) for a proof that G is a unit interval graph if and only if G is an indifference graph.

Indifference graphs are defined in the context of Social Sciences, as discussed in the work by Roberts (1979). A graph G is an indifference graph if there is a function $f: V(G) \rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} (u,v) \in E(G) \Longleftrightarrow |f(u) - f(v)| \le \epsilon , \end{aligned}$$

where $\epsilon$ is a positive number that measures closeness. Informally, this means that u and v are indistinguishable items if and only if, according to f, there is a difference at most $\epsilon$ between their values. But since item values are in general empirically obtained, there is the possibility that some presumably close items are distinguishable. Therefore, one may be interested in removing the fewer items possible to generate a real indifference graph. Since indifference graphs are precisely the claw-free interval graphs (Roberts 1969), this problem is precisely the GDP applied to a given interval graph as input, as the process exemplified in Fig. 2. Fishburn (1985) poses the problem of converting an interval order into an indifference order by the removal of some elements; again, in terms of graphs, this problem is precisely the problem of optimally declawing an interval graph. We remark that the complexity of this problem is still an open question.

Williams et al. (2015) summarize complexity results for the recognition of 4-node induced subgraphs; in particular, claws have an $O(n^{3.257})$ recognition time. Bonomo-Braberman et al. (2020) prove that the GDP is hard to approximate within a constant factor better than 2 assuming the Unique Games Conjecture; moreover, they show that the weighted problem associated with the GDP can be solved in polynomial time for graphs with bounded tree-width and for block graphs. Elimination of claws and diamonds via edge deletion was studied by Cygan et al. (2016). Aravind et al. (2017) present some general results on edge elimination problems, and present the first polynomial kernel for elimination of claws via edge deletion under the assumption of a $K_t$-free input graph.

Properties of claw-free graphs have been deeply investigated by the research community (see the survey by Faudree et al. (1997)). For example, Minty (1980) presents a polynomial-time algorithm for the problem of finding an independent set with maximum weight in a claw-free graph. Hsu and Nemhauser (1982) presents a polynomial-time algorithm for the Minimum Weighted Clique Cover Problem in claw-free perfect graphs. Zhang (1988) proves Bondy’s Conjecture for claw-free graphs. Broersma et al. (2011) present two algorithms that solve the Longest Cycle Problem in polynomial time in claw-free graphs. Hermelin et al. (2014) show that induced subgraph isomorphism for fixed graphs is fixed parameter tractable on claw-free graphs. Hermelin et al. (2019) show that dominating set is fixed parameter tractable on claw-free graphs. Martin et al. (2020) prove that the Disconnected Cut Problem is polynomially solvable for claw-free graphs.

Another application of claw-free graphs appear in resource constrained scheduling. Suppose a set of n jobs $J_1, J_2, \ldots , J_n$ in a distributed computing environment, where each $J_i$ needs exclusive access to a set $R_i$ of resources to execute. Let G be the conflict graph of $J_1, J_2, \ldots , J_n$, where each vertex $v_i$ of G is associated with job $J_i$, and two vertices $v_i$ and $v_j$, $i\ne j$, are linked by an edge if and only if $R_i\cap R_j\ne \emptyset$. In fact, G can be viewed as the intersection graph of a hypergraph, whose hyperedges are $R_1, R_2,\ldots , R_n$. If each job needs access to at most k resources, i.e., $|R_i|\le k$ for every $i=1,\ldots ,n$, then the conflict graph G is $(k+1)$-claw free, where a $(k+1)$-claw in G is an induced subgraph of G isomorphic to a star $K_{1,k+1}$. (In this terminology, a 3-claw is a claw.) See details in (Halldórsson et al. 2003). Note that an independent set in G corresponds to a set of jobs that can execute simultaneously. Finding a maximum independent set in a $(k+1)$-claw free graph is NP-hard for $k\ge 3$ and solvable in polynomial time for $k=2$. Thus, if $k\ge 3$, one can solve the GDP for the conflict graph, obtaining a claw-free conflict graph $G'$, and then find in polynomial time a set of jobs with no conflict.

Up to the author’s knowledge, there is no work in the literature presenting a polyhedral study of the GDP or a method to solve it via integer programming. Therefore, we believe that the studies developed in this work are fully justified.

The remainder of this work is organized as follows. Section 2 defines the GDP polytope and some facet-defining inequalities. Section 3 presents more facet-defining inequalities that require deeper analyses, along with a more precise description of the GDP polytope. Section 4 describes separation heuristics for support graphs needed to generate the inequalities. Section 5 shows computational results for random graphs and interval graph instances. Section 6 contains our conclusions.

2 The graph declawing problem polytope

From now on, G denotes a graph with $|V(G)|=\{1,\ldots ,n\}$. Let $P_{m}$ be the convex hull of m incidence vectors $\chi ^H$ that represent claw-free subgraphs H of a graph G, that is:

$$\begin{aligned} P_{m} = conv\left\{ \chi ^H \in \{0,1\}^{n} \mid H \text { is a claw-free subgraph of } G\right\} . \end{aligned}$$

Say that $P_{m}$ is the GDP polytope of G. Figure 3 shows a claw-free subgraph H induced by $\{1,2,4,6,7\}$ and its incidence vector.

Fig. 3

a A claw-free subgraph $H=G[\{1,2,4,6,7\}]$ and b its incidence vector

The GDP can be described as an optimization problem that aims at finding an incidence vector $x^T=(x_1,x_2,\ldots ,x_n)$ with minimum number of zeros (removed vertices):

$$\begin{aligned}&\min \sum _{i=1}^n (1 - x_{i}) \\&s.t. \ \ \ x \in P_{m} \end{aligned}$$

In order to apply binary integer programming techniques for the GDP, we focus on the characterization of $P_m$, which is n-dimensional and contains the null and all the unit vectors, summing up to $n + 1$ affinely independent vectors. This means that $P_m$ is full dimensional. The full dimensionality of a polytope implies that every facet of it is uniquely defined by an inequality multiplied by some scalar $\alpha$. This fact will be used in the next subsections for proofs of facets. Another useful fact is that a facet of an n-dimensional polytope must have n affinely independent points.

2.1 Trivial inequalities

Theorem 1

The following statements are true:

• 1. Trivial inequalities $0 \le \chi ^{H}$ and $\chi ^{H} \le 1$ are valid for $P_{m}$.

• 2. Inequalities $\chi ^H \ge 0$ induce facets of $P_{m}$.

• 3. Inequalities $\chi ^H \le 1$ induce facets of $P_{m}$.

Proof

• 1. Since all the coordinates of the m incidence vectors of claw-free subgraphs are binary, it is clear that the trivial inequalities are valid for $P_m$.

• 2. Let $x_v$ represent the coordinate $v \in \{1,\ldots ,n\}$ of a vector x. Then $\chi ^H_v = 0$ is satisfied by the null vector and all the unit vectors x with $x_u=1, u \ne v$. These n vectors belong to $P_{m}$ and are affinely independent.

• 3. $\chi ^H_v = 1$ is satisfied by the unit vector x with $x_v=1$ and by the vectors w such that $w_v=1, w_u=1$ for some $u \ne v$, and $w_t=0$ for $t\notin \{u,v\}$. These n vectors belong to $P_{m}$ and are affinely independent.

$\square$

2.2 Claw inequalities

Say that an induced subgraph of G isomorphic to $K_{1,3}$ is a claw subgraph. For simplicity, we denote by abcd a claw subgraph with central vertex a (the vertex with degree three in the claw subgraph). In addition, for a subset S of vertices, sometimes we simply write $\chi ^S$ to mean the incidence vector of the induced subgraph G[S].

Theorem 2

Let

$$\begin{aligned} x_a + x_b + x_c + x_d \le 3 \end{aligned}$$

(1)

be the claw inequality associated with a claw subgraph abcd. Then:

• 1. The claw inequality is valid for $P_m$.

• 2. The claw inequality induces a facet of $P_{m}$.

Proof

• 1. Immediate. A claw inequality forces at least one of $x_a,x_b,x_c,x_d$ to be zero.

• 2. Let w be a vector such that $w_i = 1$ for $i \in \{a,b,c,d\}$ and $w_i = 0$ for $i \notin \{a,b,c,d\}$. Let $u^Tx \le u_0$ be a facet-inducing inequality for the GDP polytope $P_{m}$ such that $F_a = \{ \chi ^H \in P_{m} \mid w^T\chi ^H = 3\} \subseteq F_b = \{ \chi ^H \in P_{m} \mid u^T\chi ^H = u_0\}$. Clearly, $F_a \ne P_{m}$ and $F_a \ne \emptyset$. Thus, a proof that $u=\alpha w$ for some $\alpha \in {\mathbb {R}}$ shows that $F_a$ defines a facet of $P_m$.

For a claw subgraph abcd, the incidence vectors $\chi ^{\{a,b,c\}}$, $\chi ^{\{a,b,d\}}$, $\chi ^{\{b,c,d\}}$, and $\chi ^{\{a,c,d\}}$ are in $F_a \subseteq F_b$. Then, the following equalities hold: $0 = u_0 - u_0 = u^T \chi ^{\{a,b,c\}} - u^T \chi ^{\{a,b,d\}} = u_c - u_d$; $0 = u_0 - u_0 = u^T \chi ^{\{a,b,c\}} - u^T \chi ^{\{a,c,d\}} = u_b - u_d$; $0 = u_0 - u_0 = u^T \chi ^{\{a,b,c\}} - u^T \chi ^{\{b,c,d\}} = u_a - u_d$. This implies $u_a = u_b = u_c = u_d = \alpha$.

For a node $v \notin \{a,b,c,d\}$, if its neighborhood satisfies $|N(v) \cap \{a,b,d\}| \le 2$ then $\chi ^{\{a,b,d,v\}} \in F_a \subseteq F_b$. Then, the following equality holds: $0 = u_0 - u_0 = u^T\chi ^{\{a,b,d,v\}} - u^T\chi ^{\{a,b,d\}} = u_v$; That means $u_v = 0$.

Finally, for a vertex $v \notin \{a,b,c,d\}$ such that $|N(v) \cap \{a,b,d\}| \ge 3$, $\chi ^{\{a,b,c,v\}} \in F_a \subseteq F_b$. Then, the following equality holds: $0 = u_0 - u_0 = u^T\chi ^{\{a,b,c,v\}} - u^T\chi ^{\{a,b,c\}} = u_v$. $\square$

3 Facets derived from star, lantern, and binary star graphs

3.1 Star inequalities

Definition 1

A star graph $S_k$ is a complete bipartite graph $K_{1,k}$, for $k \ge 3$. $S_k$ has a central vertex c whose neighborhood is an independent set $I_k$ of size k. Possible topologies for $S_k$ are illustrated in Fig. 4.

Fig. 4

Star graphs $S_3$, $S_5$, and $S_k$

A star subgraph is an induced subgraph of G isomorphic to a star graph.

Theorem 3

Let $S_k$ be a star subgraph, and consider the corresponding star inequality:

$$\begin{aligned} \sum _{v \in I_k} x_v + (k-2)x_c \le k. \end{aligned}$$

(2)

Then:

• 1. The star inequality is valid for $P_m$.

• 2. The star inequality induces a facet of $P_{m}$.

Proof

• 1. The case $k=3$ corresponds to the claw inequality (see Theorem 2). For $k\ge 4$, the proof is done by induction. Let $S_k^v = S_k-v$ and $S'_3 = S_k[\{i, j, \ell , c\}]$, where $i,j,\ell$ are distinct vertices in $I_k$. Note that $S_k^i$, $S_k^j$, $S_k^{\ell }$, and $S'_3$ are subgraphs of $S_k$. See Fig. 5, where $i = 1, j = 2, \ell = 3$.

Fig. 5

Subgraphs $S_k^i$, $S_k^j$, $S_k^{\ell }$, and $S'_3$ of $S_k$

By induction, the inequalities associated with $S_{k}^i$, $S_{k}^j$, $S_{k}^{\ell }$, and $S'_3$ are valid for $P_m$, and summing them up leads to the valid inequality

$$\begin{aligned} \sum _{v \in I_k}3x_v + (3k - 8)x_c \le 3k. \end{aligned}$$

Adding $2x_c \le 2$ to the above inequality gives

$$\begin{aligned} \sum _{v \in I_k}3x_v + (3k - 6)x_c \le 3k + 2, \end{aligned}$$

and, therefore,

$$\begin{aligned} \sum _{v \in I_k}x_v + (k - 2)x_c \le k + \left\lfloor {\frac{2}{3}}\right\rfloor =k \end{aligned}$$

is valid for $P_m$.

• 2. Let w be a vector such that $w_c = k-2$, $w_i = 1$ for $i \in I_k$, and $w_v=0$ for $v\notin I_k\cup \{c\}$. Let $u^Tx \le u_0$ be a facet-inducing inequality for the GDP polytope $P_{m}$ such that $F_a = \{ \chi ^H \in P_{m} \mid w^T\chi ^H = k\} \subseteq F_b = \{ \chi ^H \in P_{m} \mid u^T\chi ^H = u_0\}$. Clearly, $F_a \ne P_{m}$ and $F_a \ne \emptyset$. Thus, a proof that $u=\alpha w$ for some $\alpha \in {\mathbb {R}}$ shows that $F_a$ defines a facet of $P_m$.

Let $L_{i,j}$ be a claw-free subgraph of $S_k$ such that $L_{i,j} = S_k[\{ i, j, c \}]$, where $\{i,j\} \subset I_k$ and c is the center of $S_k$. Figure 6 shows two examples of such subgraphs.

Fig. 6

Subgraphs $L_{1,2}$ and $L_{1,3}$ of $S_k$

The incidence vectors $\chi ^{I_k}$, $\chi ^{L_{i,j}}$, and $\chi ^{L_{j,k}}$ are in $F_a \subseteq F_b$. Then, the following equalities hold: $0 = u_0 - u_0 = u^T\chi ^{L_{i,j}} - u^T\chi ^{L_{j,k}} = u_{i} - u_{k}$. Therefore, $u_i = u_k = \alpha$. By applying this process to all $v \in I_k$ we get $u_v = \alpha$. Also, $0 = u_0 - u_0 = u^T\chi ^{I_k} - u^T\chi ^{L_{i,j}} = (\sum _{v \in I_k \setminus \{i,j\}} u_v) - u_c$, and this implies $u_c = \alpha (k - 2)$.

For a node $v \notin I_k\cup \{c\}$, if its neighborhood satisfies $|N(v) \cap I_k| < 3$ then $\chi ^{I_k\cup \{v\}} \in F_a \subseteq F_b$. Thus, the following equality holds: $0 = u_0 - u_0 = u^T\chi ^{I_k\cup \{v\}} - u^T\chi ^{I_k} = u_v$.

Finally, for a node $v \notin I_k\cup \{c\}$ such that $|N(v) \cap I_k| \ge 3$, the incidence vector $\chi ^{V(L_{i,j})\cup \{v\}}$, where $\{i,j\} \subset N(v) \cap I_k$, is in $F_a \subseteq F_b$. Then, $0 = u_0 - u_0 = u^T\chi ^{V(L_{i,j})\cup \{v\}} - u^T\chi ^{L_{i,j}} = u_v$. $\square$

3.2 Lantern inequalities

Definition 2

Let $S_k$ and $S_{\ell }$, $k > \ell \ge 3$, be two star graphs such that $S_{\ell }$ has central node $c_1$ and independent set $I_{\ell }$, $S_k$ has central node $c_2$ and independent set $I_k$, and $I_{\ell } \subset I_k$. A lantern graph $L_{\ell k}$ is the union of $S_{\ell }$ and $S_k$. Figure 7 shows some topologies of lantern graphs.

Fig. 7

Lantern graphs $L_{34}$, $L_{3k}$, $L_{\ell (\ell +1)}$, and $L_{\ell k}$

A lantern subgraph is an induced subgraph isomorphic to a lantern graph.

Theorem 4

Let $L_{\ell k}$ be a lantern subgraph, and consider the corresponding lantern inequality:

$$\begin{aligned} \sum _{v \in I_k} x_v + (\ell -2)x_{c_1} + (k-\ell )x_{c_2} \le k. \end{aligned}$$

(3)

Then:

• 1. The lantern inequality is valid for $P_m$.

• 2. The lantern inequality induces a facet of $P_{m}$, except when $k = \ell + 1$ and there is a vertex $v \notin V(L_{\ell k})$ such that $N(v) \cap I_k = I_k$ and $N(v)\cap \{c_1,c_2\}=\emptyset$.

Proof

• 1. The validity of the lantern inequality for $\ell =3$ and $k=4$ can be checked by adding the star inequalities associated with the subgraphs $S'_3 = L_{34}[\{1,2,3,c_1\}]$ and $S'_4 = L_{34}[\{1,2,3,4,c_2\}]$ and the inequality $x_{c_1}+x_{4} \le 2$, obtaining the following valid inequality:

  $$\begin{aligned} \sum _{v \in I_4}x_v + x_{c_1} + x_{c_2} \le 4 + \left\lfloor {\frac{1}{2}}\right\rfloor =4. \end{aligned}$$

Now, consider $L_{\ell k}^v = L_{\ell k}-v$. The case $\ell =3,k=5$ can be checked by adding the inequalities associated with subgraphs $L_{35}^4$, $L_{35}^5$ (where $\{4,5\} \subset I_5$), $S'_3 = L_{35}[\{1,4,5,c_2\}]$, $S'_5 = L_{35}[\{1,2,3,4,5,c_2\}]$ and the valid inequality $x_{c_1} - x_1\le 1$, obtaining the following inequality:

$$\begin{aligned} \sum _{v \in I_5}x_v + x_{c_1} + 2x_{c_2} \le 5 + \left\lfloor {\frac{2}{3}}\right\rfloor =5. \end{aligned}$$

For the case $\ell =3$ and $k > 5$, the proof is done by induction. Note that $L_{3k}^i$, $L_{3k}^j$, $L_{3k}^h$, and $S'_3 = L_{3k}[\{i, j, h, c_2\}]$, for distinct $i,j,h\in I_k \setminus I_3$, are subgraphs of $L_{3k}$. Figure 8 shows subgraphs $L_{3k}^{i}$, $L_{3k}^j$, $L_{3k}^{h}$, and $S'_3$ for $i = 4, j = k-1, h = k$.

By induction, the inequalities associated with $L_{3k}^i$, $L_{3k}^j$, $L_{3k}^h$, and $S'_3$ are valid for $P_m$, and summing them up leads to the valid inequality

$$\begin{aligned} 3 \sum _{v \in I_k} x_v + 3(3 - 2)x_{c_1} + (3k - 11)x_{c_2} \le 3k. \end{aligned}$$

Adding $2x_{c_2} \le 2$, we get that

$$\begin{aligned} \sum _{v \in I_k}x_v + (3 - 2)x_{c_1} + (k - 3)x_{c_2}\le k + \left\lfloor {\frac{2}{3}}\right\rfloor =k \end{aligned}$$

is valid for $P_m$.

Fig. 8

Subgraphs of $L_{3k}$, $k > 5$

For the case $\ell > 3$ and $k \ge \ell + 1$, note that $L_{\ell k}^i$, $L_{\ell k}^j$, $L_{\ell k}^h$, and $S'_3 = L_{\ell k}[\{i, j, h, c_1\}]$, for distinct $i,j,h\in I_{\ell }$, are subgraphs of $L_{\ell k}$. Figure 9 shows subgraphs $L_{\ell k}^i$, $L_{\ell k}^j$, $L_{\ell k}^{h}$, and $S'_3$ for $i = 1, j = 2, h = \ell$.

Fig. 9

Subgraphs of $L_{\ell k}$ for $l > 3$, $k \ge \ell + 1$

By induction, the inequalities associated with $L_{\ell k}^i$, $L_{\ell k}^j$, $L_{\ell k}^h$, and $S'_3$ are valid for $P_m$, and summing them up leads to

$$\begin{aligned} 3 \sum _{v \in I_k}x_v + (3\ell - 8)x_{c_1} + 3(k-\ell )x_{c_2} \le 3k. \end{aligned}$$

Adding $2x_{c_1} \le 2$ we get that

$$\begin{aligned} \sum _{v \in I_k}x_v + (\ell - 2)x_{c_1} + (k - \ell )x_{c_2} \le k \left\lfloor {\frac{2}{3}}\right\rfloor =k \end{aligned}$$

is valid for $P_m$.

• 2. Let w be a vector such that $w_{c_1} = \ell -2$, $w_{c_2} = k - \ell$, $w_i = 1$ for $i \in I_k$, and $w_v=0$ for $v\notin V(L_{\ell k})$. Let $u^Tx \le u_0$ be a facet-inducing inequality for the GDP polytope $P_{m}$ such that $F_a = \{ \chi ^H \in P_{m} \mid w^T\chi ^H = k \} \subseteq F_b = \{ \chi ^H \in P_{m} \mid u^T\chi ^H = u_0\}$. Clearly, $F_a \ne P_{m}$ and $F_a \ne \emptyset$. Thus, a proof that $u=\alpha w$ for some $\alpha \in {\mathbb {R}}$ shows that $w^T\chi ^H = k$ defines a facet of $P_m$.

Let $N_{i,j}$ and $M_{i,j}$ be claw-free subgraphs of $L_{\ell k}$ such that $N_{i,j} = L_{\ell k}[(I_k \setminus I_{\ell })\cup \{i,j,c_1\}]$ and $M_{i,j} = L_{\ell k}[\{i, j, c_1, c_2\}]$, where $i, j\in I_k$, $i\ne j$. Figure 10 shows examples of subgraphs $N_{i,j}$ and $M_{i,j}$.

Fig. 10

Subgraphs of $L_{\ell k}$

Then:

• a) The incidence vectors $\chi ^{M_{i,j}}$ and $\chi ^{M_{j,h}}$ with $\{i,j,h\} \subset I_k$ are in $F_a \subseteq F_b$. Thus, $0 = u_0 - u_0 = u^T\chi ^{M_{i,j}} - u^T\chi ^{M_{j,h}} = u_{i} - u_{h}$. This implies $u_i = u_h = \alpha$ for all choices of $\{i,j,h\} \subset I_k$.

• b) The incidence vectors $\chi ^{I_k}$ and $\chi ^{N_{i,j}}$ with $\{i,j\} \subset I_{\ell }$ are in $F_a \subseteq F_b$. Thus, $0 = u_0 - u_0 = u^T\chi ^{I_k} - u^T\chi ^{N_{i,j}}= (\sum _{v \in I_{\ell } \setminus \{i, j\}} u_v) - u_{c_1}$. This implies $u_{c_1} = \alpha (\ell - 2)$.

• c) The incidence vectors $\chi ^{I_k}$ and $\chi ^{M_{i,j}}$ with $\{i,j\} \subset I_k$ are in $F_a \subseteq F_b$. Thus $0 = u_0 - u_0 = u^T\chi ^{I_k} - u^T\chi ^{M_{i, j}} = (\sum _{v \in I_k \setminus \{i, j\}} u_v) - u_{c_1} - u_{c_2}$. This implies $u_{c_2} = \alpha (k-2) - \alpha (\ell - 2) = \alpha (k - \ell )$.

For a node $v \notin V(L_{\ell k})$ such that $|N(v) \cap I_k| < 3$, $\chi ^{\{v\}\cup I_k}$ is in $F_a \subseteq F_b$. Then, the following equality holds: $0 = u_0 - u_0 = u^T \chi ^{\{v\}\cup I_k} - u^T\chi ^{I_k} = u_v$.

For a node $v \notin V(L_{\ell k})$ such that $|N(v) \cap I_k| > 3$, we have that:

• a) If $k = \ell + 1$ and $k\notin N(v)$, $\chi ^{\{v\}\cup V(N_{i,j})}$ with $i \in I_{\ell } \cap N(v)$ and $j \in I_{\ell }$ is in $F_a \subseteq F_b$. Then, the following equality holds: $0 = u_0 - u_0 = u^T \chi ^{\{v\}\cup V(N_{i,j})} - u^T\chi ^{N_{i,j}} = u_v$.

• b) If $k = \ell + 1$, $k\in N(v)$, and $N(v)\cap I_k \ne I_k$, $\chi ^{\{v\}\cup V(N_{i,j})}$ with $i \in I_{\ell } \cap N(v)$ and $j \notin I_{\ell } \cap N(v)$ is in $F_a \subseteq F_b$. Then, the following equality holds: $0 = u_0 - u_0 = u^T \chi ^{\{v\}\cup V(N_{i,j})} - u^T\chi ^{N_{i,j}} = u_v$.

• c) If $k = \ell + 1$, $N(v) \cap I_k = I_k$, and $c_1 \in N(v)$ or $c_2 \in N(v)$, $\chi ^{\{v\}\cup V(M_{i,j})}$ with $i \in I_{\ell }$ and $j=k$ is in $F_a \subseteq F_b$. Then, the following equality holds: $0 = u_0 - u_0 = u^T \chi ^{\{v\}\cup V(M_{i,j})} - u^T\chi ^{M_{i,j}} = u_v$.

• d) If $k > \ell + 1$ and there is no vertex $i \in (I_k \setminus I_{\ell }) \cap N(v)$, $\chi ^{\{v\}\cup V(N_{i,j})}$ with $i \in I_{\ell } \cap N(v)$ and $j \in I_{\ell }$ is in $F_a \subseteq F_b$. Then, the following equality holds: $0 = u_0 - u_0 = u^T\chi ^{\{v\}\cup V(N_{i,j})} - u^T\chi ^{N_{i,j}} = u_v$.

• e) If $k > \ell + 1$, $c_1 \notin N(v)$, and there is a vertex $i\in (I_k \setminus I_{\ell }) \cap N(v)$, the incidence vector $\chi ^{\{v\}\cup V(M_{i,j})}$ is in $F_a \subseteq F_b$, for $j \in I_k \setminus I_{\ell }$. Then, the following equality holds: $0 = u_0 - u_0 = u^T\chi ^{\{v\}\cup V(M_{i,j})} - u^T\chi ^{M_{i,j}} = u_v$.

• f) If $k > \ell + 1$, $c_1 \in N(v)$, and there is a vertex $i\in (I_k \setminus I_{\ell }) \cap N(v)$, the incidence vector $\chi ^{\{v\}\cup V(M_{i,j})}$ is in $F_a \subseteq F_b$, for $j \in I_{\ell }$. Then, the following equality holds: $0 = u_0 - u_0 = u^T\chi ^{\{v\}\cup V(M_{i,j})} - u^T\chi ^{M_{i,j}} = u_v$.

Note that the only case not covered by the above items (a)-(f) is $k = \ell + 1$, $N(v) \cap I_k = I_k$, and $N(v)\cap \{c_1,c_2\}=\emptyset$. $\square$

3.3 Binary star inequalities

Definition 3

Let $S_{\ell }$ and $S_k$ be two star graphs, $k > \ell \ge 3$, such that $S_{\ell }$ has central node $c_1$ with independent set $I_{\ell }$, $S_k$ has central node $c_2$ with independent set $I_k$, $|I_{\ell }\cap I_k|\ge 2$, and $|I_{\ell } \setminus I_k| = 1$. A binary star graph $B_{\ell k}$ is the union of $S_{\ell }$ and $S_k$. Figure 11 shows some topologies of binary star graphs.

Fig. 11

Examples of binary stars

A binary star subgraph is an induced subgraph isomorphic to a binary star graph.

Theorem 5

Let $B_{\ell k}$ be a binary star subgraph, and consider the corresponding binary star inequality:

$$\begin{aligned} \sum _{v \in I_k \cup I_{\ell }} x_v + (\ell -2)x_{c_1} + (k-\ell )x_{c_2} \le k + 1. \end{aligned}$$

(4)

Then:

• 1. The binary star inequality is valid for $P_m$.

• 2. The binary star inequality induces a facet of $P_{m}$, except when there is a node v such that $N(v) \cap (I_k \cup I_{\ell }) = I_k \cup I_{\ell }$.

Proof

• 1. For $\ell =3$ and $k=4$, the validity can be checked by summing up the claw inequality associated with $S'_3 = B_{34}[\{1, 2, 3, c_1\}]$, the star inequality associated with $S'_4 = B_{34}[\{2, 3, 4, 5, c_2\}]$, and the valid inequality $x_1 + x_4 + x_5 + x_{c_1} \le 4$, yielding the valid inequality:

  $$\begin{aligned} \sum _{v \in I_3 \cup I_4 }x_v + x_{c_1} + x_{c_2} \le 5 + \left\lfloor {\frac{1}{2}}\right\rfloor =5. \end{aligned}$$

For $\ell =3$ and $k\ge 5$, the proof is done by induction. Let $B_{\ell k}^v = B_{\ell k}-v$. Note that $B_{3k}^i$, $B_{3k}^j$, $B_{3k}^h$, and $S'_3 = B_{3k}[\{i, j, h, c_2\}]$, for distinct $i,j,h\in I_k \setminus I_{\ell }$, are subgraphs of $B_{3k}$. Figure 12 shows subgraphs $B_{3k}^{i}$, $B_{3k}^j$, $B_{3k}^{h}$, and $S'_3$ for $i = 4$, $j = k$, and $h = k+1$.

Fig. 12

Subgraphs of $B_{3k}$

By induction, the inequalities associated with $B_{lk}^i$, $B_{lk}^j$, $B_{lk}^h$, and $S'_3$ are valid for $P_m$, and summing them up leads to

$$\begin{aligned} 3 \Big (\sum _{v \in I_k \cup I_\ell }x_v\Big ) + 3(\ell - 2)x_{c_1} + (3k - 3\ell - 2)x_{c_2} \le 3k + 3. \end{aligned}$$

Adding $2x_{c_2} \le 2$ we get that

$$\begin{aligned} \sum _{v \in I_k \cup I_{\ell }}x_v + (\ell - 2)x_{c_1} + (k - \ell )x_{c_2}\le (k + 1) + \left\lfloor {\frac{2}{3}}\right\rfloor =k+1 \end{aligned}$$

is valid for $P_m$.

For $\ell > 3$ and $k \ge \ell + 1$, the proof is also done by induction. Consider the following subgraphs of $B_{\ell k}$: $B_{\ell k}^i$, $B_{\ell k}^j$, $B_{\ell k}^h$, and $S'_3 = B_{\ell k}[\{i, j, h, c_1\}]$, for distinct $i,j,h\in I_{\ell }$. See Fig. 13, where $i = 2$, $j = 3$, and $h = \ell$.

Fig. 13

Subgraphs of $B_{\ell k}$

By induction, the inequalities associated with $B_{\ell k}^i$, $B_{\ell k}^j$, $B_{\ell k}^h$, and $S'_3$ are valid for $P_m$, and summing them up leads to

$$\begin{aligned} 3 \Big (\sum _{v \in I_{\ell } \cup I_{k}}x_v\Big ) + (3\ell - 6 + 1)x_{c_1} + 3(k-\ell )x_{c_2} \le 3k + 3. \end{aligned}$$

Adding $-x_{c_1} \le 0$ we get that

$$\begin{aligned} \sum _{v \in I_{\ell } \cup I_{k}}x_v+ (\ell - 2)x_{c_1} + (k - \ell )x_{c_2} \le k + 1 \end{aligned}$$

is valid for $P_m$.

• 2. Let w be a vector such that: $w_{c_1} = \ell -2$, $w_{c_2} = k - \ell$, $w_i = 1$ for $i \in I_k \cup I_{\ell }$, and $w_v=0$ for $v\notin V(B_{\ell k})$. Let $u^Tx \le u_0$ be a facet-inducing inequality for the GDP polytope $P_{m}$ such that $F_a = \{ \chi ^H \in P_{m} \mid w^T\chi ^H = k + 1 \} \subseteq F_b = \{ \chi ^H \in P_{m} \mid u^T\chi ^H = u_0\}$. Clearly, $F_a \ne P_{m}$ and $F_a \ne \emptyset$. Thus, a proof that $u=\alpha w$ for some $\alpha \in {\mathbb {R}}$ shows that $w^T\chi ^H = k + 1$ defines a facet of $P_m$.

Let $N_{i,j} = B_{\ell k}[(I_k \setminus I_{\ell })\cup \{i, j, c_1\}]$ and $M_{i,j} = B_{\ell k}[(I_{\ell } \setminus I_k)\cup \{i, j, c_1, c_2\}]$ be subgraphs of $B_{\ell k}$ as exemplified in Fig. 14. Observe that $M_{i,j}$ is claw-free when $\{i,j\} \subset I_k \setminus I_{\ell }$ or $i \in I_{\ell } \cap I_k$ and $j \in I_k \setminus I_{\ell }$. Figure 14 shows the graphs $N_{1,2}$, $M_{\ell +1, k}$, and $M_{2,\ell +1}$.

Fig. 14

Subgraphs of $B_{\ell k}$

Then:

• a) The incidence vectors $\chi ^{N_{i,j}}$ and $\chi ^{N_{j,h}}$ with $\{i,j,h\} \subset I_{\ell }$ are in $F_a \subseteq F_b$. Thus $0 = u_0 - u_0 = u^T\chi ^{N_{i,j}} - u^T\chi ^{N_{j,h}} = u_{i} - u_{h}$. This implies $u_i = u_h = \alpha$ for all choices of $\{i,j,h\} \subset I_{\ell }$.

• b) The incidence vectors $\chi ^{M_{i,j}}$ and $\chi ^{M_{j,h}}$ with $\{i,j,h\} \subset I_k \setminus I_{\ell }$ are in $F_a \subseteq F_b$. Thus $0 = u_0 - u_0 = u^T\chi ^{M_{i,j}} - u^T\chi ^{M_{j,h}} = u_{i} - u_{h}$. This implies $u_i = u_h = \alpha$ for all choices of $\{i,j,h\} \subset I_k \setminus I_{\ell }$.

• c) The incidence vectors $\chi ^{I_k \cup I_{\ell }}$ and $\chi ^{N_{i,j}}$ with $\{i,j\} \subset I_{\ell }$ are in $F_a \subseteq F_b$. Thus $0 = u_0 - u_0 = u^T\chi ^{I_k \cup I_{\ell }} - u^T\chi ^{N_{i,j}}= (\sum _{v \in I_{\ell } \setminus \{i, j\}} u_v) - u_{c_1}$. This implies $u_{c_1} = \alpha (\ell - 2)$.

• d) The incidence vectors $\chi ^{I_k \cup I_{\ell }}$ and $\chi ^{M_{i,j}}$ with $\{i,j\} \subset I_k \setminus I_{\ell }$ are in $F_a \subseteq F_b$. Thus, $0 = u_0 - u_0 = u^T\chi ^{I_k \cup I_{\ell }} - u^T\chi ^{M_{i, j}} = (\sum _{v \in (I_k \cup I_{\ell }) \setminus \{i, j\}} u_v) - u_{c_1} - u_{c_2}$. This implies $u_{c_2} = \alpha (k-2) - \alpha (\ell - 2) = \alpha (k - \ell )$.

For a node $v \notin V(B_{\ell k})$ such that $|N(v) \cap (I_k \cup I_{\ell })| < 3$, $\chi ^{\{v\}\cup I_k \cup I_{\ell }}$ is in $F_a \subseteq F_b$. Then, the following equality holds: $0 = u_0 - u_0 = u^T \chi ^{\{v\} \cup I_k \cup I_{\ell }} - u^T\chi ^{I_k \cup I_{\ell }} = u_v$.

For a node $v \notin V(B_{\ell k})$ such that $|N(v) \cap (I_k \cup I_{\ell })| > 3$, we have that:

• a) If there is no vertex $i \in N(v) \cap (I_k \setminus I_{\ell })$, the incidence vector $\chi ^{\{v\}\cup V(N_{i,j})}$, with $i \in N(v) \cap I_{\ell }$ and $j \in I_{\ell }$, is in $F_a \subseteq F_b$. Then, the following equality holds: $0 = u_0 - u_0 = u^T \chi ^{\{v\}\cup V(N_{i,j})} - u^T\chi ^{N_{i,j}} = u_v$.

• b) If there are vertices $i \in N(v) \cap (I_k \setminus I_{\ell })$ and $j \in (I_{\ell } \cap I_k) \setminus N(v)$, the incidence vector $\chi ^{\{v\}\cup V(M_{i,j})}$ is in $F_a \subseteq F_b$. Therefore, the following equality holds: $0 = u_0 - u_0 = u^T \chi ^{\{v\}\cup V(M_{i,j})} - u^T\chi ^{M_{i,j}} = u_v$.

• c) If there is a vertex $i \in N(v) \cap (I_k \setminus I_{\ell })$ and, in addition, $(I_{\ell } \cap I_k) \setminus N(v)=\emptyset$ and $N(v) \cap (I_k \cup I_{\ell }) \ne I_k \cup I_{\ell }$, the incidence vector $\chi ^{\{v\}\cup V(M_{i,j})}$, with $i \in N(v) \cap (I_k \setminus I_{\ell })$ and $j \in (I_k \setminus I_{\ell }) \setminus N(v)$, is in $F_a \subseteq F_b$. Thus, the following equality holds: $0 = u_0 - u_0 = u^T \chi ^{\{v\}\cup V(M_{i,j})} - u^T\chi ^{M_{i,j}} = u_v$.

$\square$

3.4 Formulation for the GDP

A formulation for the GDP is given by combining all the previous facets in the following binary integer programming problem:

$$\begin{aligned} \mathcal{F} :&\ \min \sum _{v\in V(G)} (1 - x_v)\\&\ s.t.\\&\sum _{v \in I_k}x_v + (k-2)x_c \le k,&\text {for all star subgraphs } \ S_k \ \mathrm {of} \ G \\&\sum _{v \in I_k}x_v + (\ell - 2)x_{c_1} + (k-\ell )x_{c_2} \le k,&\text {for all lantern subgraphs } \ L_{\ell k} \ \mathrm {of} \ G\\&\mathop {\sum \limits _{{v \in I_\ell \cup I_k}}} \ x_v + (\ell - 2)x_{c_1} + (k-\ell )x_{c_2} \le k + 1,&\text {for all binary star subgraphs } \ B_{\ell k} \ \mathrm {of} \ G\\&0\le x_v\le 1,&\forall \ v \in V(G)=\{1,\ldots ,n\}\\&x_v \ \text {integer}&\end{aligned}$$

Observe that claw inequalities are star inequalities with $k = 3$.

4 Separation claws, stars, lanterns, and binary stars

${\mathcal {F}}$ can have an exponential number of inequalities, therefore a Branch-and-Cut algorithm is suitable for the solution of the GDP. This section explains how to extract support graphs and separate cuts for a Branch-and-Cut algorithm.

4.1 Extracting claw subgraphs

Claw subgraphs are obtained by verifying all triples of mutually nonadjacent vertices that have a common neighbor v in $O(n^4)$ time. Each claw subgraph is added to a collection ${\mathcal {S}}_1$ of support graphs.

4.2 Extracting maximal star subgraphs

In order to reduce the number of extracted star subgraphs, we consider only stars formed by a central vertex v and a maximal independent set in G[N(v)] (“maximal stars”). For example, Fig. 15 shows star subgraphs $S_3$ and $S_4$ centered at v whose independent sets are maximal in G[N(v)].

Fig. 15

Extraction of maximal stars centered at v c and d from a by using the neighborhood of v b

Since maximal independent sets of a graph are maximal cliques in its complement, an algorithm for maximal clique extraction hybrid(.) proposed by Eppstein and Strash (2011) can be used to extract all maximal stars $S_k$ centered at a vertex v by taking the complement of G[N(v)].

Algorithm 1 summarizes the extraction of the maximal stars $S_k$ of a graph G. Line 1 initializes the collection ${\mathcal {S}}_2$ of support graphs. Line 2 goes through V(G), fixing the center of the star at each iteration. Line 3 computes the complement of G[N(v)]. Line 4 extracts all the maximal cliques in $\overline{G[N(v)]}$ using algorithm hybrid(.). Lines 5–8 add to ${\mathcal {S}}_2$ only maximal stars with independent sets of size at least three.

4.3 Separation for the basic and star models

With the current collection of support graphs at hand, the Branch-and-Cut algorithm solves the relaxed linear programming problem at each Branch-and-Cut node and then searches for all inequalities violated by the current optimal solution $x^*$, measures their violation $\lambda$, and adds the one hundred most violated inequalities to the current node. The equation $\lambda = \sum _{v \in I_k} x^*_v + (k-2)x^*_c - k$ is used to measure the violation. If $\lambda > 0,0001$ the inequality is considered to be violated and is added to a pool of inequalities, in order to choose the one hundred best ones (those with the largest values of $\lambda$).

4.4 Separation for lantern and binary star models

It is not reasonable to extract all lantern and binary star subgraphs previously to the Branch-and-Cut routines. Thus, a separation heuristic is executed during the Branch-and-Cut algorithm at each node of the tree. It begins by finding the one hundred most violated star inequalities using the same strategy described in Sect. 4.3. Let $\mathcal{{S}}_{ violated }$ be the collection of support star graphs associated with such inequalities. Then, for each pair $S_B,S_L$ of distinct support graphs in $\mathcal{{S}}_{{violated}}$, new lantern (binary star) subgraphs are constructed and added to the collection of support lantern (binary star) graphs, and the violation of the associated new inequalities is measured. Finally, the one hundred most violated inequalities are added to the current region See Algorithms 2 and 3 for a brief description of the process used to obtain the new support graphs and associated inequalities. Figures 16 and 17 also illustrate this process. The violation $\lambda$ for both models is measured as follows:

$$\begin{aligned} \lambda = \left\{ \begin{array}{ll} \sum _{v \in I_k} x^*_v + (\ell -2)x^*_{c_1} + (k-\ell )x^*_{c_2} - k, &{} \text {for each support lantern graph} \\ \\ \sum _{v \in I_k \cup I_{\ell }} x^*_v + (\ell -2)x^*_{c_1} + (k-\ell )x^*_{c_2} - (k + 1), &{} \text {for each support binary star graph} \end{array} \right. \end{aligned}$$

If $\lambda > 0,0001$ the inequality is considered to be violated.

Algorithm 2 summarizes how to construct the collection ${\mathcal {L}}$ of support lantern graphs and evaluate the violation of the inequalities associated with such graphs. Line 1 initializes ${\mathcal {L}}$ with ${\mathcal {S}}_{ violated }$. Lines 2 goes through each possible pair $S_B, S_L$ of stars in ${\mathcal {S}}_{ violated }$. Line 6 checks if the independent sets of $S_B$ and $S_L$ have at least three vertices in common, in order to construct valid lantern graphs. Line 7 creates the support lantern graph $L_1$ by taking induced subgraph $G[V(S_B) \cup \{c_L\}]$ formed by $S_B$ and the center of $S_L$, and in line 8 the graph $L_1$ is stored in the collection ${\mathcal {L}}$ of support lantern graphs. Lines 9–11 create and store the support lantern graph $L_2= G[V(S_L) \cup \{c_B\}]$, provided that $I_L$ contains vertices outside $I_B\cap I_L$. Fig. 16 illustrates the construction of $L_1$ and $L_2$.

Algorithm 3 is analogous to Algorithm 2. For each v outside $I_B\cap I_L$, it tries to construct the binary star subgraph $B_v = G[V(S_B) \cup \{v\} \cup \{c_L\}]$ (if $v\in I_L\setminus I_B)$ or $B_v = G[V(S_L) \cup \{v\} \cup \{c_B\}]$ (if $v\in I_B\setminus I_L)$. The collection ${\mathcal {B}}$ stores the support binary star graphs.

Fig. 16

Figure a shows graph G, figures b and c shows two maximal stars $S_L$ and $S_B$ in G, figures d and e shows the two lantern subgraphs $L_1$ and $L_2$ constructed from $S_L$ and $S_B$

Fig. 17

Figure a shows graph G, figures b and c shows two maximal stars $S_L$ and $S_B$ in G, figures d, e, and f shows three binary star subgraphs constructed from $S_L$ and $S_B$

5 Computational results

5.1 Used models

Four binary integer programming models are proposed by combining the inequalities previously presented. The claw model contains only claw inequalities, the star model contains star inequalities associated with maximal stars, the lantern model adds lantern inequalities to the star model, and the binary star model adds binary star inequalities to the star model.

5.2 Random graph instances

Forty random graph instances generated by Bastos et al. (2016) are used to test the four proposed models, with $n\in \{50,100\}$. All of the benchmark instances are available at

https://sites.google.com/view/graphdeclaw/instances.

5.3 Interval graph instances

A random generator is used to create interval graph instances. It receives the number n of intervals, their maximum length, and a time ruler as input parameters. See Algorithm 4 below.

The algorithm maintains a list of intervals ${\mathcal {I}}$ during its execution. It creates the initial and end times for each interval i and checks if i intersects any previously created interval j; if an intersection happens, edge (j, i) is added to E(G).

Twenty seven groups of interval graph instances were created by combining the parameters $n\in \{100, 200, 300\}$, ${time\_ruler} = 100$, and ${interval\_max\_length}\in \{10, 20, 30, 40, 50, 60, 70, 80, 90\}$. For each combination (group), nine instances were created. Interval graph instances are named following the pattern ${x\_y\_z}$-d where $x = n$, $y = {time\_ruler}$, $z = {interval\_max\_length}$, and d is the identification of the test instance.

Table 1 Computational results for random graph instances with $n = 50$

Table 2 Computational results for random graph instances with $n = 50$

5.4 Experimental setup

All algorithms proposed in this work have been developed in C++ with the aid of the mathematical solver CPLEX 11. The computational experiments have been performed on an Intel i7 processor running at 3.4 GHz with 16 GB of RAM, and executing the operating system Linux Ubuntu 14.04.

CPLEX has two internal callbacks to cope with Branch-and-Cut. The first one is the lazy callback, which verifies if any integer solution found by the Branch-and-Cut algorithm is feasible. The second one is the cut callback, which adds valid cuts to the current node being solved at any time during the execution of the Branch-and-Cut algorithm. For the claw and star models, the lazy and cut callbacks were implemented with the same separation routines described in Sect. 4.3. For the lantern and binary star models, the lazy callback uses the separation routine of the star model, and the cut callback uses proper separation routines described in Sects. 4.4 and 13.

Table 3 Computational results for random graph instances with $n = 100$

Table 4 Computational results for random graph instances with $n = 100$

Table 5 Computational results for interval graph instances not solved to optimality

The stop criteria used for the Branch-and-Cut tree are the use of a total memory of 10 Gb and a total time of 6 hours to solve the instances, using only one thread for the processing.

5.5 Comparing the claw, star, lantern, and binary star models for random graph instances

Tables 1 and 2 present results for random graph instances with $n = 50$. All models have been able to solve them optimally. Both tables show the running time, the number of nodes solved, and the number of cuts added by the Branch-and-Cut algorithm for each model. For this set of instances, the star model, when compared with the other models, achieves better running times for all random graph instances.

Comparing only the star and claw models, we observe that the star model has a fewer number of cuts and expanded nodes for all random graph instances. This is an evidence that star inequalities dominate claw inequalities and thus reach optimal solutions faster. For example, for instance 105_6_50, the star model took nearly eight times fewer nodes and four times fewer cuts. This explains the gain in time to find the optimal solution.

The comparison between the star model and the lantern/binary star models is more involved, because for each model there are instances for which it performs well, in terms of number of cuts or number of expanded nodes. But, in general, the star model is still the one with best results. It seems that star inequalities are simpler to manage, and provide a very strong relaxation. For example, instance 106_8_50 generates fewer nodes for the lantern and binary star models, but a worse execution time than the star model. Still for instance 106_8_50, the star model adds fewer cuts – possibly lantern and binary stars inequalities are making the feasible region more difficult to dealt with, forcing the Branch-and-Cut algorithm to take more time to find an optimal solution.

Tables 3 and 4 present results for random graph instances with $n = 100$. Both tables show the separation lower lound, upper bound, running time, number of nodes, and number of cuts for each model. In general, the star model is again the one with best results, although the lantern and binary star models have produced a better lower bound for some instances. Probably, this is due to the time increase these inequalities impose on the Branch-and-Cut tree by reducing the number of nodes.

5.6 Comparing the claw and star models for interval graph instances

Only the claw and star models were used to solve interval graph instances, since chordless cycles with four vertices are forbidden structures for interval graphs, and both lantern and binary star subgraphs contains such cycles.

For instances optimally solved by both models, see Table 6. Instances with density higher than $60\%$ were easier to solve (most of them were solved at the root node).

Table 5 shows the instances not solved to optimality by at least one of the models (Table 6). The star model was able to solve optimally all the instances with $n=200$ and some with $n=300$. But it could not solve instances 300_100_40-9, 300_100_50-1, 300_100_50-3, 300_100_50-7, and 300_100_50-9, because of the large amount of maximal independent sets. In such cases, the claw model achieves better results.

6 Conclusions

In this paper we studied the Graph Declawing Problem (GDP). Some facet-defining inequalities of the GDP polytope were presented. Separation algorithms were proposed and used into a Branch-and-Cut procedure for solving the GDP. Computational experiments were carried out and the results show that the algorithms are able to solve many interval graph instances with $n\in \{100,200,300\}$ using fewer than six hours of processing and 10 Gb of memory for the Branch-and-Cut tree. The computational results also show that random graph instances were harder to solve. Random graph instances with $n=50$ were optimally solved but most random graph instances with $n=100$ were not solved to optimality.

Computational results for interval graph instances optimally solved

See Table 6

Table 6 Computational results for interval graph instances optimally solved