Linear size MIP formulation of Max-Cut: new properties, links with cycle inequalities and computational results

Abstract

We consider the Max-Cut problem on an undirected graph $G=(V,E)$ with $|V|=n$ nodes and $|E|=m$ edges. We investigate a linear size MIP formulation, referred to as (MIP-MaxCut), which can easily be derived via a standard linearization technique. However, the efficiency of the Branch-and-Bound procedure applied to this formulation does not seem to have been investigated so far in the literature. Branch-and-bound based approaches for Max-Cut usually use the semi-metric polytope which has either an exponential size formulation consisting of the cycle inequalities or a compact size formulation consisting of O(mn) triangle inequalities (Barahona and Mahjoub in Math Prog 36:157–173, 1986; Nguyen and Minoux in Networks 69(1):142–150, 2017). However, optimizing over the semi-metric polytope can be computationally demanding due to the slow convergence of cutting-plane algorithms and the high degeneracy of formulations based on the triangle inequalities. In this paper, we exhibit new structural properties of (MIP-MaxCut) that link the binary variables with the cycle inequalities. In particular, we show that fixing a binary variable at 0 or 1 in (MIP-MaxCut) can result in imposing the integrity of several original variables and the satisfaction of a possibly exponential number of cycle inequalities in the semi-metric formulation. Numerical results show that for sparse instances of Max-Cut, our approach exploiting this capability outperforms the branch-and-cut algorithms based on semi-metric polytope when implemented on the same framework; and even without any extra sophistication, the approach is capable of solving hard instances of Max-Cut within acceptable CPU times.

1 Introduction

1.1 The Max-Cut problem

Let $G=(V,E)$ be an undirected graph with $n=|V|$ and $m=|E|$. We suppose that the edges of G are weighted by a vector $c \in \mathbb {R}^E$, the real space of dimension m indexed by the edges in E. In particular, G could be the complete graph $K_n=(V_n,E_n)$ of n nodes. We denote by ij the edge between the two nodes i and j of V. A cut in G associated with a node subset $S \subset V$, denoted $\delta (S)$, is the set of the edges that have exactly one end-node in S. The Max-Cut problem is to find a cut of maximum total weight or equivalently to find a node subset S such that $\sum _{ij \in \delta (S)}c_{ij}$ is maximum.

For each cut $\delta (S)$, the incidence vector associated with $\delta (S)$ is a vector $\chi (\delta (S)) \in \{0,1\}^E$ where

$$\begin{aligned} \chi (\delta (S))_{ij} = \left\{ \begin{array}{l@{\quad }l} 1 \quad &{} \hbox {if} ij \in \delta (S),\\ 0 \quad &{} \hbox {otherwise} \end{array} \right. \end{aligned}$$

Hence, finding a maximum weight cut is equivalent to optimizing over the cut polytope $\mathrm {CUTP}(G)$ which is the convex hull of the incidence vectors associated with the cuts in G.

1.2 Cycle inequalities and the semi-metric polytope

A chordless cycle C in G is a cycle whose induced subgraph is the cycle itself. Let $\mathcal {C}$ be the set of chordless cycles in G. For a vector $x \in \mathbb {R}^E$ and for any subset $F \subseteq E$, let $x(F)=\sum _{e \in F}x_e$.

As a cut always intersects a cycle C in an even number of edges, the incidence vectors associated with the cuts in G satisfy the following cycle inequalities introduced by Barahona and Mahjoub [2]:

$$\begin{aligned}&x(F) -x(C\!{\setminus }\! F) \le |F|-1, \nonumber \\&\quad \forall C \in \mathcal {C} \quad \hbox {and}\quad F \subseteq C\quad \hbox {with} \quad |F| odd, \end{aligned}$$

(1)

The cycle inequalities together with some trivial lower bound and upper bound inequalities define the so-called semi-metric polytope $\mathrm {METP}(G)$ associated with G in $\mathbb {R}^E$:

$$\begin{aligned}&x\quad \hbox {satisfies (1),} \nonumber \\&x_e \ge 0 \quad \forall e \in E \hbox {s.t.}\quad e\quad \hbox {does not belong to any triangle}\nonumber \\&x_e \le 1 \quad \forall e \in E\quad \hbox {s.t.}\quad e\quad \hbox {does not belong to any triangle} \end{aligned}$$

(2)

Hence the semi-metric polytope is a relaxation of $\mathrm {CUTP}(G)$. If we replace the trivial inequalities by the 0/1 constraints $x \in \{0,1\}^E$, we obtain an integer formulation for $\mathrm {CUTP}(G)$. Thus, the semi-metric polytope is a linear programming relaxation for the Max-Cut problem. Moreover, Barahona and Mahjoub [2] showed that the semi-metric polytope coincides with the cut polytope when G is no contractible to $K_5$.

Note that since there is a priori no known polynomial upper bound (in terms of n and m) on the number of chordless cycles and there may be also an exponential number of possible choices for the set F given a chordless cycle C, the above formulation of $\mathrm {METP}(G)$ has a priori an exponential number of inequalities. However, $\mathrm {METP}(G)$ has polynomial size extended formulations [1, 16], called $\mathrm {METP}(K_n)$, which consist of $O(n^2)$ variables where additional variables correspond to the additional edges which complete G to $K_n$. These extended formulations involve the following so-called triangle inequalities:

$$\begin{aligned} x_{ij}+x_{ik}+x_{jk}&\le 2 \hbox { for all }i,j,k \in \mathcal {T}. \end{aligned}$$

(3)

$$\begin{aligned} x_{ij}-x_{ik}-x_{jk}&\le 0, \end{aligned}$$

(4)

$$\begin{aligned} x_{ik}-x_{ij}-x_{jk}&\le 0, \end{aligned}$$

(5)

$$\begin{aligned} x_{jk}-x_{ij}-x_{ik}&\le 0 \hbox { for all }i,j,k \in \mathcal {T}. \end{aligned}$$

(6)

where $\mathcal {T}$ is the set of all (unordered) triples of distinct nodes $i,j,k \in V$ such that at least ij, ik or jk is an edge in E.

The semi-metric polytope forms the core of the linear programming relaxations in many practical solution procedures for the Max-Cut problem. Moreover, when G is sparse, it is well known that the corresponding relaxation given by the semi-metric polytope is quite good. In this case, for the Max-Cut problem on large sparse graphs, branch-and-cut algorithms based on the integer formulation obtained from the cycle inequalities and the 0/1 constraints remain the best approaches so far (SDP approaches do not take advantage of sparsity and are currently limited to medium-size instances, typically less than 300 nodes see e.g. [17]). Hence, optimizing over the semi-metric polytope appears to be of key importance. This is achieved either via a cutting-plane approach (using the polynomial time separation algorithm for the cycle inequalities given in [2]) or by solving the compact extended formulation involving $O(n^2)$ variables and O(nm) constraints. However, solving the latter turns out to be very hard [11] as the linear program to be solved is highly degenerate and its size quickly becomes impractical when n exceeds, say, 150–200.

1.3 A basic unconstrained binary quadratic formulation for Max-Cut

Let $z \in \{0,1\}^V$ (the node set of the hypercube of dimension n indexed by the nodes in V), then z can be viewed as an incidence vector associated with a node subset S in G, such that

$$\begin{aligned} z_i = \left\{ \begin{array}{ll} 1, \quad &{} i \in S,\\ 0, \quad &{}\hbox {otherwise} \end{array} \right. \hbox { for all}\,\ i \in V \end{aligned}$$

We observe that for any edge $ij \in E$, $ij \in \delta (S)$ if and only if the sum $z_i(1-z_j) +z_j(1-z_i) =1$. Hence the Max-Cut problem can be formulated as the following unconstrained 0–1 quadratic program (UBQP):

$$\begin{aligned}&\max \sum _{ij \in E}c_{ij}(z_i(1-z_j) +z_j(1-z_i)) \nonumber \\&\quad \hbox {s.t.}\quad z_{i} \in \{0,1\}\quad \hbox {for all}\quad i \in V. \end{aligned}$$

(7)

A simple direct way of linearizing this problem consists in adding m continuous variables $x_{ij}$ defined by $x_{ij}=z_i(1-z_j)+z_j(1-z_i)$ and applying RLT reformulation [19] on the constraints $0 \le z_i \le 1$, $0 \le z_j \le 1$. This leads to adding the inequalities $z_{i}z_{j}\le z_i$, $z_{i}z_{j}\le z_j$ and $z_{i}z_{j} \ge z_i +z_j-1$ for all $ij \in E$ and replacing $z_iz_j$ by $\frac{z_i+z_j-x_{ij}}{2}$ in the above inequalities. We obtain the following mixed integer formulation (MIP-MaxCut) for Max-Cut.

$$\begin{aligned}&\max \sum _{ij \in E}c_{ij}x_{ij} \nonumber \\&x_{ij}+z_i +z_j \le 2, \end{aligned}$$

(8)

$$\begin{aligned}&x_{ij}-z_i-z_j \le 0,\end{aligned}$$

(9)

$$\begin{aligned}&-x_{ij}+z_i-z_j \le 0, \end{aligned}$$

(10)

$$\begin{aligned}&-x_{ij}-z_i+z_j \le 0 \hbox { for all}\ ij \in E, \end{aligned}$$

(11)

$$\begin{aligned}&z_{i} \in \{0,1\} \hbox { for all}\ i \in V \end{aligned}$$

(12)

The above **formulation has already been known in the literature, in particular, it has been used to explore the links between the boolean quadric polytope (BQP), which is the convex hull of the solutions of (7) in the space $\mathbb {R}^{V+E}$ (with variables $y_{ij}$ for all $ij \in E$ replacing the product $z_iz_j$), and the Max-Cut polytope [10]. More precisely, Hammer [12] showed that the Max-Cut polytope defined on $G+u$ (where $G+u$ is the graph obtained by adding to G an universal vertex u) is equivalent under linear transformations to the BQP defined on G. From this result and the result on the Max-Cut polytope on graphs not contractible to $K_5$ in [2], DeSimone [10] derived a complete description of BQP on graphs not contractible to $K_4$.

However, the possible use of (MIP-MaxCut) in practical solution procedures for Max-Cut does not appear to have attracted much interest in the literature so far. The main reason probably lies in the fact that its linear programming relaxation is very weak. To be convinced of this, just observe that setting $z_{i}=\frac{1}{2}$ for all $i \in V$ makes the variables $x_{ij}$ completely free between 0 and 1 for all $ij \in E$.

1.4 Contributions and organization of the paper

The main contributions of the paper are the following:

• We prove a new property relating the integrity of the variables $z_i$ in (MIP-MaxCut) and the cycle inequalities. More precisely, it is shown that for any edge $ij \in E$, the fact that the variables $z_i$ and $z_j$ are integer could imply simultaneous satisfaction of all (possibly exponentially many) cycle inequalities involving edge ij and the integrity of the variable $x_{ij}$.

• We analyze the impact of this key property when applying a Branch-and-Bound/Cut procedure to the (MIP-MaxCut) formulation. In particular, we show that branching on a variable $z_i$ could have very strong effects such as satisfying a possibly exponential number of cycle inequalities and forcing several variables $x_{ij}$ to be integer valued.

• As an experimental confirmation of our analysis, we present and discuss in Sect. 4 a series of computational results on Max-Cut for a set of large size sparse graph instances obtained by applying a standard Branch-and-Bound solver to (MIP-MaxCut) without using any of the sophisticated techniques previously proposed in the existing literature for the exact solution of such large scale problems. It is observed that the results obtained turn out to significantly outperform a branch-and-cut algorithm based on cycle inequalities implemented on the same platform.

2 Polyhedral link between (MIP-MaxCut) and the cycle inequalities and application for solving Max-Cut

In the present section, we first introduce the concept of pointed triangulation and prove a basic equivalence result (Lemma 1) which turns out to be a basic building block for deriving the link between (MIP-MaxCut) and the cycle inequalities. The computational attractiveness of the new formulation in view of solving the Max-Cut problem via branch-and-bound and branch-and-cut algorithms is also analyzed.

2.1 Pointed triangulation and cycle inequalities

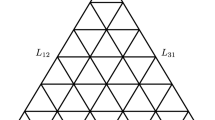
Let us consider any chordless cycle C in G. Let us suppose that the nodes in C are 1, 2, ..., k which are numbered clockwise from 1 (see Fig. 1) and its edges are $i(i+1)$ for $i=1,\ldots ,k-1$ and k1.

Fig. 1

A pointed triangulation of a chordless cycle C

Let us take any subset $F=\{f_1,\ldots ,f_p\} \subseteq C$ with p odd. The cycle inequality associated with C and F reads:

$$\begin{aligned} x(F) - x(C{\setminus } F) \le ~&p-1.&\end{aligned}$$

(13)

Consider the triangulation $\theta$ of C obtained by adding $k-3$ distinct edges (chords) 1j for $j=3,\ldots ,k-1$ (see the thin solid edges in Fig. 1). As the newly added edges all have 1 as an end node, $\theta$ is called pointed triangulation at node 1. Let us call $\bar{E}$ the set of these new added edges and let $E'=E \cup \bar{E}$. The triangle inequalities corresponding to the various triangles thus created read:

Lemma 1

If $x \in [0,1]^{E'}$ satisfies all the triangle inequalities a,i, l,i, r,i and m,i then the restriction of x on $[0,1]^E$, $x_{|E}$, satisfies all the cycle inequalities associated with the cycle C. Conversely, if $x \in [0,1]^E$ satisfies all the cycle inequalities associated with the cycle C then there is an extension of x to $[0,1]^{E'}$ satisfying all the inequalities a,i, l,i, r,i and m,i.

Proof

$\Rightarrow$ The proof of the first part of the lemma given here closely follows the one given in [16] for deriving a different result, namely the fact that the number of triangle inequalities can be reduced to O(nm) instead of $O(n^3)$ in the extension of METP(G) to METP($K_n$). Since the purpose of the present lemma is both to prove Theorem 1 and to provide a constructive way of strengthening the new linear size formulation to be discussed in Sect. 3, we provide the full proof in the appendix for self-containedness.

$\Leftarrow$ Let $x \in [0,1]^E$ be a vector satisfying all the cycle inequalities associated with C. Let us extend x to $x \in [0,1]^{E'}$ by determining the intervals of possible values that the extra variables $x_{1j}$ for $j=3, \ldots ,k-1$ in $E'{\setminus } E$ can take. We will compute the intervals in clockwise order, i.e. for $x_{13}$ first then for $x_{14}$, ...and at the end for $x_{1(k-1)}$. Let us consider $x_{13}$ and the triangle $\{1,2,3\}$, we can see that for the validity of the inequalities a,i, l,i, r,i and m,i associated with this triangle, $x_{13}$ should belong to the interval $I_3= [\max (x_{12}-x_{23},x_{23}-x_{12}),\min (x_{12}+x_{23}, 2-x_{12}-x_{23})]$. Note that if $x_{12}$ and $x_{23}$ belong to [0, 1] then this interval is not empty. To compute the possible values of $x_{14}$, the triangle $\{1,3,4\}$ and the validity of the inequalities a,i, l,i, r,i and m,i associated with this triangle imply that for each possible fixed value of $x_{13}$ (i.e. one of the values in $I_3$), $x_{14}$ should belong to the interval, say $I^{x_{13}}_4$ where $I^{x_{13}}_4=[\max (x_{13}-x_{34},x_{34}-x_{13} ),\min (x_{13}+x_{34}, 2-x_{13}-x_{34})]$. Generally, for $j=4,\ldots , k-1$, for each possible fixed value of $x_{1(j-1)}$ previously computed, $x_{1j}$ should belong to the interval $I^{x_{1(j-1)}}_j= [\max (x_{1(j-1)}-x_{(j-1)j},x_{(j-1)j}-x_{1(j-1)} ),\min (x_{1(j-1)}+x_{(j-1)j}, 2-x_{1(j-1)}-x_{(j-1)j})]$ by the validity of the inequalities a,i, l,i, r,i and m,i associated with the triangle $\{1,(j-1),j\}$. These intervals are always non-empty as a possible fixed value of $x_{1(j-1)}$ is always between 0 and 1. In particular, when $j=k-1$, for a possible fixed value of $x_{1(k-2)}$, we have $x_{1(k-1)} \in I_{k-1}^{x_{1(k-2)}}$. However, by the triangle $\{1,(k-1),k\}$, $x_{1(k-1)}$ should also belong to the following interval $I^2_{k-1}=[\max (x_{1k}-x_{(k-1)k},x_{(k-1)k}-x_{1k} ),\min (x_{1k}+x_{(k-1)k}, 2-x_{1k}-x_{(k-1)k})]$ as the a,i, l,i, r,i and m,i inequalities associated with the triangle $\{1,(k-1),k\}$ should also be satisfied. Hence, for each possible fixed value of $x_{1(k-2)}$, the possible values of $x_{1(k-1)}$ should belong to $I_{k-1}^{x_{1(k-2)}} \cap I^2_{k-1}$. Thus, the extension of x to $[0,1]^{E'}$ requires $I^{x_{1(k-2)}}_{k-1} \cap I^2_{k-1} \ne \emptyset$. We will show that if the opposite happens, i.e. $I^{x_{1(k-2)}}_{k-1} \cap I^2_{k-1} = \emptyset$, then x violates a cycle inequality associated with C, contradicting the initial assumption on x. Thus, let us suppose that $I^{x_{1(k-2)}}_{k-1} \cap I^2_{k-1}=\emptyset$. Then one of following two cases necessarily arises:

• The first case is when the lower bound of $I^2_{k-1}$ is strictly greater than the upper bound of $I^{x_{1(k-2)}}_{k-1}$, i.e. $\max (x_{1k}-x_{(k-1)k},x_{(k-1)k}-x_{1k})>\min (x_{1(k-2)}+x_{(k-2)(k-1)}, 2-x_{1(k-2)}-x_{(k-2)(k-1)})$. Let us suppose that $x_{1k}\ge x_{(k-1)k}$. (The case $x_{1k}\le x_{(k-1)k}$ would be treated in a similar way).

  • (i) $x_{1k}-x_{(k-1)k}>x_{1(k-2)}+x_{(k-2)(k-1)}$. Hence, $x_{1k}-x_{(k-1)k}-x_{1(k-2)}-x_{(k-2)(k-1)}>0$. This can be viewed as the violation of x on the cycle inequality $x(F) -x(C_{k-2}{\setminus } F) \le 0$ where $C_{k-2}=\{1(k-2),(k-2)(k-1),(k-1)k,1k\}$ and $F=\{1k\}$. We can see that replacing $x_{1(k-2)}$ by $\min (x_{1(k-3)}+x_{(k-3)(k-2)},2-x_{1(k-3)}-x_{(k-3)(k-2)})$ -which is a possible fixed value of $x_{1(k-2)}$ with respect to some possible fixed value of $x_{1(k-3)}$ in the above violated cycle inequality -yields another violated cycle inequality associated with the cycle $C_{k-3}=\{1(k-3),(k-3)(k-2),(k-2)(k-1),(k-1)k,1k\}$.

  • (ii) $x_{1k}-x_{(k-1)k}>2-x_{1(k-2)}-x_{(k-2)(k-1)}$. Hence, $x_{1k}+x_{1(k-2)}+x_{(k-2)(k-1)}-x_{(k-1)k}>2$. This can also be viewed as the violation of x on the cycle inequality $x(F) -x(C_{k-2}{\setminus } F) \le 2$ where $C_{k-2}$ as in case (i) and $F=\{1k,1(k-2),(k-2)(k-1)\}$. Similarly as in case (i), replacing $x_{1(k-2)}$ by $\max (x_{1(k-3)}-x_{(k-3)(k-2)},-x_{1(k-3)}+x_{(k-3)(k-2)})$ yields another violated cycle inequality associated with the cycle $C_{k-3}$.

• The second case is when the lower bound of $I^{x_{1(k-2)}}_{k-1}$ is strictly greater than the upper bound of $I^2_{k-1}$, i.e. $\max (x_{1(k-2)}-x_{(k-2)(k-1)},x_{(k-2)(k-1)}-x_{1(k-2)}) > \min (x_{1k}+x_{(k-1)k}, 2-x_{1k}-x_{(k-1)k})$.

  • Suppose that $x_{1(k-2)}>x_{(k-2)(k-1)}$. In this case, $x_{1(k-2)}-x_{(k-2)(k-1)} >x_{1k}+x_{(k-1)k}$ or $x_{1(k-2)}-x_{(k-2)(k-1)} > 2-x_{1k}-x_{(k-1)k}$ and both cases will imply a violated cycle inequality $x(F) -x(C_{k-2}{\setminus } F) \le |F| -1$ where $C_{k-2} =\{1(k-2),(k-2)(k-1),(k-1)k,1k\}$ and F is either $\{1(k-2)\}$ or $\{1(k-2),(k-1)k,1k\}$. In both cases, we can replace $x_{1(k-2)}$ by $\max (x_{1(k-3)}-x_{(k-3)(k-2)},-x_{1(k-3)}+x_{(k-3)(k-2)})$ to obtain another violated cycle inequality associated with the cycle $C_{k-3}$.

  • Suppose that $x_{1(k-2)}<x_{(k-2)(k-1)}$. Similarly as in the previous item, we can replace $x_{1(k-2)}$ by $\min (x_{1(k-3)}+x_{(k-3)(k-2)},2-x_{1(k-3)}-x_{(k-3)(k-2)})$ to obtain another violated cycle inequality associated with the cycle $C_{k-3}$.

In all cases, one can reiterate the above process, which leads to exhibit violated inequalities associated with cycles $C_{k-3}$, $C_{k-4}$,..., $C_2$. By remarking that $C_2=C$, a contradiction is obtained and the proof for the second part of the lemma is completed. $\square$

A major practical and theoretical interest of the pointed triangulation is to provide an alternative compact representation subsuming potentially huge cardinality sets of cycle inequalities as shown in the following corollary.

Corollary 1

Let C be a cycle of size $\Omega (n)$ (i.e. not too small compared to n) in G, the number of cycle inequalities associated with C is in $\Omega (2^{n-1})$ while the number of triangle inequalities resulting from a pointed triangulation of C is $(|C|-2)*4$ which is in O(n).

Another noticeable consequence of Lemma 1 and Corollary 1 is to give linear size extended formulations for the Max-Cut polytope on some special graphs including wheel and cactus graphs.

Corollary 2

Let $G =(V,E)$ be a graph which satisfies the two following conditions: the Max-Cut polytope and the metric polytope coincide for G, (i.e. G is not contractible to $K_5$ [2]) and the number of chordless cycles in G is linear in terms of m or n. Then a linear size extended formulation for the Max-Cut polytope on G , can be obtained by using a pointed triangulation of each chordless cycle, and imposing the various constraints (a,i), (l,i), (r,i) and (m,i) associated with each such chordless cycle.

2.2 Polyhedral link between (MIP-MaxCut) and the cycle inequalities

If we add 0/1 constraints to the linear representation of the semi-metric polytope,

$$\begin{aligned} \hbox {(Metric-IP)} \left\{ \begin{array}{ccc} \max \sum _{ij \in E}c_{ij}x_{ij} &{} \\ x(F) -x(C\!{\setminus }\! F) \quad &{} \le |F|-1 \quad &{} \forall C \in \mathcal {C}\hbox { and } F \subseteq C\hbox { with }|F|\hbox { odd,} \\ x_{ij} \in \{0,1\}\quad &{} \hbox {for all }ij \in E.\quad &{} \end{array} \right. \end{aligned}$$

we obtain (Metric-IP), an IP formulation for Max-Cut. The latter is the standard IP formulation used in LP-based approaches for solving Max-Cut. In the following theorem, we will show that in fact (MIP-MaxCut) is equivalent to (Metric-IP).

Theorem 1

(MIP-MaxCut) is equivalent to (Metric-IP).

Proof

We first show (MIP-MaxCut) $\subseteq$ (Metric-IP). Let $x \in \mathbb {R}^E$ and $z \in \{0,1\}^V$ a feasible solution of (MIP-MaxCut). For any edge $ij \in E$, it is quite easy to verify that when $z_i=z_j=(0 \text { or } 1)$, $x_{ij}=0$ and when $z_i \ne z_j$ then $x_{ij}=1$. Hence $x_{ij} \in \{0,1\}$ for all $ij \in E$. Moreover, one can observe that $x_{ij}=|z_i -z_j|$ or equivalently $x_{ij}=\max (z_i-z_j, z_j-z_i)$. Now, let C be any chordless cycle in G. Let ij be any edge in C and let $F \subseteq C$ such that $p=|F|$ is odd and $ij \in F$. Note that as F is never empty, the case when $ij \notin F$ will be covered by the cases when some other edge $i'j'\ne ij$ belongs to F. Let us build an extended graph $G'=(V',E')$ deduced from G by adding to G a universal node u (i.e. $V'=V \cup \{u\}$ and $E'=E \cup \{ui ~|~ \hbox { for all}\ i \in V\}$) and think of the variable $z_i$ as the variable associated with the edge ui in the extended graph. Let $C_{ij}$ be the cycle obtained by replacing in C the edge ij by the edges ui and uj, i.e. $C_{ij}= (C{\setminus } \{ij\}) \cup \{ui,uj\}$.

We can see that $C_{ij}$ is triangulated by a pointed triangulation at u. As all the triangle inequalities corresponding to this triangulation are expressed in (MIP-MaxCut), by Lemma 1, (x, z) satisfies all the cycle inequalities involving $C_{ij}$. Let $F_{i}=(F{\setminus } \{ij\}) \cup \{ui\}$ and $F_{j}=(F{\setminus } \{ij\}) \cup \{uj\}$. We can observe that $F_{i}$ and $F_{j}$ are two odd subsets of $C_{ij}$ of cardinality p. Hence, the cycle inequalities associated with $C_{ij}$ and respectively $F_i$ and $F_j$ can be expressed as

$$\begin{aligned}&x(F\!{\setminus }\! \{ij\}) +z_i -z_j -x(C\!{\setminus }\! F) \le p-1, \hbox { and}\\&x(F\!{\setminus }\! \{ij\}) +z_j -z_i -x(C\!{\setminus }\! F) \le p-1. \end{aligned}$$

As $x_{ij}=\max (z_i-z_j, z_j-z_i)$, one of the above inequalities gives:

$$\begin{aligned}&x(F\!{\setminus }\! \{ij\}) +x_{ij} -x(C\!{\setminus }\! F) \le p-1, \hbox { i.e.}\\&x(F) -x(C\!{\setminus }\! F) \le p-1. \end{aligned}$$

As C is any cycle in G and ij is any edge in C, we conclude that x satisfies all the cycle inequalities. Moreover, x is integer as shown above, thus x is a feasible solution of (Metric-IP).

Now let us show that (Metric-IP) $\subseteq$ (MIP-MaxCut). Let $x \in \{0,1\}^E$ be any feasible solution of (Metric-IP). Consequently, x is the incidence vector of a cut $\delta (S)$ such that $S\subset V$. Let us build $z \in \{0,1\}^V$ as follows. For all nodes $i \in S$, let us set $z_i=0$ and for all nodes $i \in V\!{\setminus }\! S$, let us set $z_i=1$. It is then easy to see that x and z form a feasible solution for (MIP-MaxCut). $\square$

3 Efficiency of the new MIP formulation for solving Max-Cut

In this section, we discuss the practical use of (MIP-MaxCut) in branch-and-cut algorithms for exactly solving large scale Max-Cut instances, especially in sparse graphs for which linear programming relaxations containing the cycle inequalities are strong enough.

3.1 Properties of (MIP-MaxCut) in a branch-and-bound framework for solving Max-Cut

In particular, we show that using (MIP-MaxCut) could be more efficient than (Metric-IP) in the same branch-and-cut framework. More precisely, a basic branch-and-cut algorithm for solving (Metric-IP) consists of the following tasks:

• Solve linear programs consisting of a system of valid inequalities $Ax \le b$ which contains a subset of the cycle inequalities and other possible valid inequalities for CUTP(G) at each node of the branch-and-bound search tree and possibly generate violated inequalities including violated cycle inequalities to be added to $Ax \le b$.

• Branch on one or several variables x.

A basic branch-and-cut algorithm for solving (MIP-MaxCut) consists of the following tasks:

• Solve linear programs consisting of the same system $Ax \le b$ together with the inequalities (8)–(1112) at each node of the branch-and-bound search tree and possibly generate violated inequalities which may be cycle inequalities to be added to $Ax \le b$.

• Branch on one or several variables z.

The difference between the two algorithms is that instead of generating violated cycle inequalities and branching on the x variables as in the first algorithm, the second algorithm branches on the z variables. The fact that this can be more efficient is a consequence of the following proposition which shows that branching on a variable $\mathbf {z_i}$ is equivalent to branching on several variables $\mathbf {x_{ij}}$ and generating a (possibly exponential) number of cycle inequalities.

Proposition 1

When some variable $z_i$ is fixed at an integer value by branching in a branch-and-bound framework then for all variables $z_j$ fixed at an integer value before $z_i$, the variable $x_{ij}$ is integer valued and the current solution x satisfies all the cycle inequalities such that the set F contains the edge ij.

Proof

As we can see from the proof of Theorem 1, when $z_i$ and $z_j$ are integer, the inequalities (8)–(1112) which involve $z_i$, $z_j$ and $x_{ij}$ force $x_{ij}$ to be integer. Moreover, $x_{ij}=\max (z_i-z_j,z_j-z_i)$. The proof of Theorem 1 uses this fact together with Lemma 1 to prove that all the cycle inequalities such that the set F contains the edge ij are subsequently satisfied. Hence, branching on a variable $z_i$ can have very strong effects:

• on the one hand, this action forces the integrality of all the variables $x_{ij}$ such that $z_j$ is integer valued,

• on the other hand, it forces all the cycle inequalities such that the set F contains the edge ij to be satisfied by the forthcoming solutions. The number of such cycle inequalities may obviously be very big and possibly exponential even if G is sparse.    $\square$

It is then realized that branching in (MIP-MaxCut) can be much more efficient than cut generation and branching in (Metric-IP) where only a small number of cycle inequalities may be added and one variable $x_{ij}$ is fixed at each round of cut generation or branching. This will be confirmed by our numerical results in the next section.

Let us call PCUT(G) the system $Ax\le b$ used as relaxation for CUTP(G) in a branch-and-cut algorithm based on (Metric-IP). Let us call EPCUT(G) the system defined in $\mathbb {R}^{E+V}$ that consists of $Ax\le b$ together with the inequalities (8), (9), (10) and (1112). We have the following theorem.

Theorem 2

The projection of EPCUT(G) on $\mathbb {R}^E$, i.e. on the variables x, is exactly PCUT(G).

Proof

It is clear that the projection of EPCUT(G) on $\mathbb {R}^E$ is contained in PCUT(G) since in every solution (x, z) satisfying EPCUT(G), we have x satisfies $Ax \le b$.

The restriction of EPCUT(G) on the linear variety $z_i=\frac{1}{2}$ for all $i \in V$ is exactly the system $Ax \le b$, i.e. PCUT(G). As the projection of EPCUT(G) on $\mathbb {R}^E$ contains this restriction, $Ax \le b$ is contained in this projection.

Hence, the projection of EPCUT(G) on $\mathbb {R}^E$ is equal to PCUT(G). $\square$

The above theorem states that a system of valid inequalities $Ax \le b$ will give the same upper bound regardless of whether the branch-and-cut algorithm is based on (Metric-IP) or (MIP-MaxCut). Moreover, the bounding procedure in branch-and-cut algorithms based on (MIP-MaxCut) is probably more efficient than those based on (Metric-IP) due to the strong effects of the branching on the variables z. Hence, we have the following important corollary.

Corollary 3

Any existing branch-and-cut algorithms based on (Metric-IP) can be readily adapted to work on (MIP-MaxCut) with more efficiency thanks to the properties of branching on the z variables.

Such an adaption simply consists in switching the branching strategy from variables x to variables z and keeping the same strategy of cut generation. Indeed, in the next sections, we will show by numerical results that with the same initial linear programming relaxation and the same cut generation strategy, a branch-and-cut algorithm based on (MIP-MaxCut) is much more efficient than a branch-and-cut algorithm based on (Metric-IP). This suggests that a potentially interesting idea for future developments might be to adapt recent advanced branch-and-cut algorithms based on (Metric-IP) such as [4, 7], ...to (MIP-MaxCut) to improve their efficiency.

3.2 Building an initial linear programming relaxation

One important factor in LP-based branch-and-bound algorithms is the initial LP to be solved at the root node of the branch-and-bound search tree. This LP should be of reduced size and give a good upper bound for Max-Cut. We will show below that for algorithms using (MIP-MaxCut) as well as (Metric-IP), the question is how to build such an LP by choosing a suitable subset of cycle inequalities. Let us consider the linear programming relaxation (R-MIP-MaxCut) of (MIP-MaxCut). Note that when $z^*_i=\frac{1}{2}$ for all $i \in V$, any vector $x^* \in [0,1]^E$ satisfies the constraints (8), (9), (10) and (1112). Such a $(z^*,x^*)$ then satisfies (R-MIP-MaxCut). Hence, the upper bound given by (R-MIP-MaxCut) is very weak (all $x_{ij}$ equal to 1) when compared with the one provided by (R-Metric), the linear programming relaxation of (Metric-IP). However, the latter is hard to compute since it is highly degenerate [11]. Moreover, the number of cycle inequalities can be huge for big values of n even with an extended formulation of (Metric-IP). Hence, in practical branch-and-bound algorithms for Max-Cut using (Metric-IP), a small subset of the cycle inequalities is usually chosen to be included in the initial LP relaxation, called (iR-Metric), in order to obtain a reasonably good initial upper bound at the root node of the branch-and-bound tree. We can use the same cycle inequalities in the initial LP relaxation, called (iR-MIP-MaxCut), in a branch-and-bound algorithm using (MIP-MaxCut) to obtain the same upper bound as shown in the following theorem.

Proposition 2

(iR-MIP-MaxCut) provides the same upper bound for Max-Cut as (iR-Metric) if both formulations contain the same subset of the cycle inequalities (1).

Proof

The proof directly follows from Theorem 2. $\square$

The above proposition tells us that building the initial LP provides relaxations with the same strength regardless of whether (MIP-MaxCut) or (Metric-IP) is used but it does not tell us how to choose the subset of the cycle inequalities to be included in this LP. We now describe how we have chosen such a subset, denoted by $\mathcal {S}$, of the cycle inequalities in our experiments involving sparse graphs. We consider the two following criteria for selecting $\mathcal {S}$:

• $|\mathcal {S}| \in O(n)$, i.e. the size of the initial LP should be linear in n,

• The upper bound given by $\mathcal {S}$ should be “sufficiently good”.

In order to meet these two criteria, we use an observation borrowed from previous works on Max-Cut on Ising Spin Glass 2D grid instances, namely that the LP that consists of the cycle inequalities expressed for all the 4-cycles gives a very good bound for Max-Cut [13, 15]. Note that the number of 4-cycles in (toroidal) 2D grid graphs is at most n and the number of cycle inequalities expressed on each 4-cycle is 8. Hence the set of the 4-cycles in these graphs satisfies the above two criteria for being selected in $\mathcal {S}$. Notice that for 2D grid graphs, the set of all the 4-cycles forms a cycle basis which generates all the cycles in G by linear combination in the Galois field of two elements GF(2), i.e. based on parity of the intersection of cycles. Hence, for a general sparse graph G, we may take the set of all the cycle inequalities associated with a cycle basis as the set $\mathcal {S}$. Such a set $\mathcal {S}$ may be interesting as cycle inequalities also express the parity of the intersection between cuts and cycles. Moreover, as the number of cycles in a cycle basis is $m-n+1$, and hence O(n) in sparse graphs and thanks to Lemma 1 and Corollary 1, we can represent such a set $\mathcal {S}$ of cycle inequalities by O(n) triangle inequalities. The numerical experiments reported in the next section seem to confirm this analysis.

4 Numerical results

In this section, we present experiments aimed at computing exact solutions based on (MIP-MaxCut) for Max-Cut on sparse graph instances of various types. For comparison, we also run the same experiments with (Metric-IP) instead of (MIP-MaxCut) in the same computer and branch-and-cut algorithmic framework. To be more precise, we present comparative experiments based on the following three variants of branch-and-cut to solve Max-Cut on sparse graph instances.

• (Metric-IP). The branch-and-cut framework applied to the (Metric-IP) formulation in x variables only with branching on the x variables.

• (MIP-MaxCut). The branch-and-cut framework applied to the (MIP-MaxCut) formulation in both z and x variables with branching on the z variables.

• (MIP-MaxCut-SBR). The branch-and-cut framework applied to the (MIP-MaxCut) formulation with a special branching rule (SBR) on the z variables derived from Proposition 1.

4.1 Computer framework

All the experiments have been conducted on an Intel i3-8130 CPU 2.20 GHz computer with 8GB of RAM under Linux Ubuntu 18.4. Single thread have been used for all the runs performed.

4.2 Branch-and-cut framework

4.2.1 LP solver and branch-and-bound search tree handling

CPLEX 12.7.1 has been used as LP solver and for handling the branch-and-bound tree. In particular, for the (Metric-IP) and the (MIP-MaxCut) variants, the default automatic branching rule of CPLEX 12.7.1 has been used for branching on the x variables and on the z variables, respectively. For the (MIP-MaxCut-SBR) variant, we have implemented a special rule for branching (SBR) on the z variables which can be defined as follows:

Special branching rule This rule consists in choosing a variable $z_i$ such that the number of neighbours j with $z_j$ integer in the current solution is greater than the average node degree of the graph. We keep track of $b_i$, which is the number of times a variable $z_i$ has been chosen for branching with this rule (in previous steps of the construction of the branch-and-bound search tree). In case several variables $z_i$ are eligible, we choose any variable with smallest $b_i$.

According to Proposition 1, branching on such a variable $z_i$ would force a number of variables $x_{ij}$ to be integer and would also imply the satisfaction of many of the cycle inequalities. Notice that no other feature of CPLEX has been used, in particular no generic cut generation procedure and no presolve have been activated.

Initial LP The initial LP contains the same subset $\mathcal {S}$ of cycle inequalities in all the three cases. Hence, by Proposition 2, the same initial upper bound for Max-Cut is obtained. To build the set $\mathcal {S}$, we generate a cycle basis B of G and with a fixed parameter k, we perform a pointed triangulation of all the cycles of length at most k in B. The associated triangle inequalities are all added to $\mathcal {S}$.

Violated cycle inequality generation The separation procedure is based on the exact separation algorithm for cycle inequalities which operates on a graph H of 2n nodes (n original nodes and n copies) as described in [2]. The algorithm consists of n calls of the bidirectional Dijkstra algorithm for finding the shortest paths between every original node i for $i=1,\ldots n$ and its copy in H.

In the computational experiments reported in Sects. 4.3.2 and 4.3.3, this procedure is applied to the three variants (Metric-IP), (MIP-MaxCut) and (MIP-MaxCut-SBR). For the toroidal 2D grid instances (Sect. 4.3.1), the separation procedure is only applied to the (Metric-IP) variant since we have observed that adding violated cycle inequalities does not improve the efficiency of the (MIP-MaxCut) and (MIP-MaxCut-SBR) variants.

For the (Metric-IP) variant, the separation procedure is also applied to separate integer solutions if these solutions do not represent cuts.

4.3 Numerical experiments

4.3.1 Toroidal 2D grid instances

Generation of instances We consider instances of toroidal 2D grid graphs which have been generated according to the description in [9]. More precisely, the first and the second half of the edge weights are initialized with $-1$ and $+1$, respectively. Then, a random permutation of the edge weights is computed.

Branch-and-cut tuning To set up the initial LP, we generate the set $\mathcal {S}$ by taking the cycle basis containing all the 4-cycles and by setting $k=4$. We only activate the generation of violated cycle inequalities when the relative gap goes below 0.5% (the relative gap is defined to be the ratio of the difference between the upper bound and the lower bound of the branch-and-bound tree over the lower bound). The separation routine is called every 100 nodes of the branch-and-bound tree.

Numerical results

In Table 1, we compare (Metric-IP) and (MIP-MaxCut). Each entry of the table represents an average taken over ten randomly generated instances. The column CPU is the average CPU time (in seconds) and the column Nodes indicates the average number of nodes of the branch-and-bound search tree. For (Metric-IP), there is an additional column C-Ine which reports the number of violated cycle inequalities generated during the branch-and-cut process. We restrict our experiments to relatively small sizes of toroidal 2D grid instances as (Metric-IP) can not go beyond the size of $50\times 50$ within ten CPU hours. We can see that (MIP-MaxCut) significantly outperforms (Metric-IP) in both CPU time and size of the branch-and-bound search tree. Table 2 reports the average results of (MIP-MaxCut) and (MIP-MaxCut-SBR) on ten random instances of larger sizes $55\times 55$, $60 \times 60$ and $65 \times 65$, respectively. We can see that the special branching rule (SBR) derived from Proposition 1 is more efficient than the default branching rule of CPLEX and helps to improve the results of (MIP-MaxCut).

4.3.2 Rudy instances

Generation of instances We consider 10 instances generated using rudy [18] with $n= 100$ and an edge density of 0.1 (series of instances with prefix pm1s). The edge weights are chosen uniformly from $\{-1, 0, 1\}$.

Branch-and-cut tuning To set up the initial LP, the set $\mathcal {S}$ is built by generating a cycle basis of G and by setting $k=5$. The separation procedure for cycle inequalities is called every ten nodes of the branch-and-bound tree.

Table 1 Comparisons between (Metric-IP) and (MIP-MaxCut) on toroidal 2D grid instances with random $+1/-1$ weights

Table 2 Comparisons between (MIP-MaxCut) and (MIP-MaxCut-SBR) on toroidal 2D grid instances with random $\pm 1$ weights

Numerical results Table 3 reports the performance of (Metric-IP), (MIP-MaxCut) and (MIP-MaxCut-SBR) on 10 rudy instances. In general, (Metric-IP) generates the largest number of cycle inequalities and has the least size of the branch-and-bound search tree but requires more CPU time. (MIP-MaxCut) needs fewer cycle inequalities and features more nodes in the branch-and-bound search tree than (Metric-IP) but spends significantly less CPU time. Finally, (MIP-MaxCut-SBR) achieves the best CPU time on average with a slight increase in the number of generated cycle inequalities and a slight decrease in the size of the branch-and-bound search tree compared to (MIP-MaxCut). Getting into more detail, (MIP-MaxCut-SBR) achieves the best CPU time for seven out of ten instances. (Metric-IP) may give the best CPU time for easy instances but the difference of CPU time as compared to (MIP-MaxCut) and (MIP-MaxCut-SBR) is tiny. Note that we have also run (MIP-MaxCut-SBR) for solving one instance g05_60.0 with $n=60$ of the series with prefix g05 (i.e. unweighted graphs with an edge probability of 0.5) which are known to be difficult to solve for LP-based approaches for Max-Cut. The instance is solved optimally with a CPU time of 18627 seconds. The size of the branch-and-bound search tree is 199457 nodes and only 2356 violated cycle inequalities have been generated. Note that (Metric-IP) and (MIP-MaxCut) are unable to solve this instance within 10 CPU hours.

Table 3 Comparisons of (Metric-IP), (MIP-MaxCut) and (MIP-MaxCut-SBR) on rudy sparse instances with $n=100$

4.3.3 Quadratic 0/1 programming instances

Generation of instances We consider several instances of the quadratic 0/1 programming problem from the BiqMac library [20]. These instances are rather well solved by SDP-based solvers such as BiqMac [17] and BiqCrunch [14] but known to be difficult for LP-based Max-Cut solvers. We particularly experiment on two series of instances: bqp250 ($n=250$) of density 0.1 generated by Beasley [5]; be120 and be250 ($n=120$ and 250) of densities respectively 0.3 and 0.1 generated by Billionnet and Elloumi [6]. Branch-and-Cut tuning To set up the initial LP, the set $\mathcal {S}$ only contains the triangle inequalities involving the binary variables z. Violated cycle inequalities are generated every ten nodes of the branch-and-bound tree. Numerical results The results are reported in Table 4. When the program has not been able to solve the instance to optimality within ten CPU hours, all the column values are represented by a ‘-’. We can see that on average (MIP-MaxCut) significantly outperforms (Metric-IP) in all respects: the CPU time, the number of nodes in the branch-and-bound search tree and the number of cycle inequalities generated. (MIP-MaxCut) reduces the CPU times by a factor between two and four as compared to (Metric-IP). Finally, (MIP-MaxCut-SBR) achieves the best performance. The special branching rule (SBR) really helps to improve (MIP-MaxCut), especially for hard instances such as Bqp250.2 and Bqp250.4 which (MIP-MaxCut) could not solve within 10 CPU hours. The performance of (MIP-MaxCut-SBR) regarding the CPU times is quite satisfactory for a linear programming based algorithm compared to the results reported in [7]. Moreover, the CPU times are in a ratio of 1:6 from the easiest instance to the hardest one (in the same series) which indicates a rather stable behaviour. In any case, this ratio turns out to be much smaller than the one observed for other LP-based or SDP-based algorithms for Max-Cut such as those described for instance in [7,8,9, 14, 17].

Table 4 Numerical results on quadratic 0/1 programming sparse instances. Entries featuring ‘-’ indicate that no exact solution could be obtained within 10 CPU hours

4.4 Concluding remarks on numerical experiments

Our numerical experiments on various sparse instances of Max-Cut confirm the positive impact of using (MIP-MaxCut) instead of (Metric-IP) for sparse instances of Max-Cut. The fact that (MIP-MaxCut-SBR) achieves the best performance on these instances confirms the theoretical relevance of the analysis leading to our Proposition 1 and its potential for suggesting ways of improving practical algorithmic efficiency.

5 Conclusions

In this paper, a linear size MIP formulation for integer metric polyhedra has been proposed and its application to the Max-Cut problem for sparse graphs has been discussed. When the formulation is used for solving Max-Cut via branch-and-bound, a detailed analysis has been carried out which reveals that each step of branching amounts to implicitly imposing simultaneous satisfaction of many cycle inequalities (those inequalities defining the metric polyhedron). Numerical experiments on a series of large size instances involving sparse graphs have confirmed the efficiency of a standard branch-and-bound procedure when applied to the formulation, even without resorting to any of the advanced techniques usually required to cope with large size Max-Cut instances. Among the perspectives thus opened to future investigations, it is clear that further significant improvements in efficiency can be expected from the combined use of the (MIP-MaxCut) formulation with some of the advanced techniques available in the literature, such as: the use of the Volume Algorithm in line with [3, 4] or the contraction-lifting approach from [9]. Implementing such combined procedures can easily be achieved as suggested by Corollary 3.

A Proof of the first part of Lemma 1 [16]

Let $F=\{f_1,\ldots ,f_p\} \subseteq C$ be any odd subset of C. We will show that $x_{|E}$ satisfies

$$\begin{aligned} x(F) - x(C\!{\setminus }\! F) \le p -1. \end{aligned}$$

For brevity, we will refer to the triangle $(1,i,i+1)$ as “triangle i” with $2 \le i \le k-1$. The edges 1i, $i(i+1)$, $1(i+1)$ will be respectively referred to as the left edge, middle edge, right edge of triangle i (in the system stated just before the statement of Lemma 1, the notation ”a“ stands for ”all“, and (a,i) refers to the inequality related to triangle i for which all edges are involved with positive coefficients; l, r, and m stand for ”left“, ”right“, and ”middle“ respectively and the inequalties are labelled (l,i), (r,i) or (m,i) depending on which edge is involved with positive coefficient). Now, for each triangle i with $2 \le i \le k-1$, let us choose one and exactly one of inequalities a,i, l,i, r,i and m,i according to the following rule:

• if the middle edge $i(i+1)$ is an edge $f_q \in F$ with q odd, choose inequality m,i,

• if the middle edge $i(i+1)$ is an edge $f_q \in F$ with q even, choose inequality a,i,

• if the middle edge $i(i+1) \in C\!{\setminus }\! F$, then by scaning clockwise the edges of C from $i(i+1)$ until reaching the node 1, we may or may not meet edges in F. In the former case, let $f_q \in F$ be the first edge in F that we meet.

  • If $f_q$ exists and q is odd, choose inequality r,i,

  • If $f_q$ does not exist or $f_q$ exists and q is even, choose inequality l,i.

We are going to show that the sum over $i=2,\ldots ,k-1$ of the inequalities chosen according to the above rule gives inequality (13). Let us consider first any edge 1j ($3 \le j \le k-1$) which is in $E_n{\setminus } E$ and show that $x_{1j}$ vanishes in the sum. Note that $x_{1j}$ appears only in two chosen inequalities which correspond respectively to the triangles $j-1$ and j. There are four possible cases:

• $(j-1)j$ and $j(j+1) \notin F$, hence the two chosen inequalities for the triangles $j-1$ and j are of the same type: either (l,j-1) and (l,j) or (r,j-1) and (r,j). In both cases, the signs of $x_{1j}$ in these two inequalites are opposite.

• $(j-1)j$ is an edge $f_q \in F$ and $j(j+1) \in C{\setminus } F$. If q is even, then the two chosen inequalities are (a,j-1) and (r,j) in which the signs of $x_{1j}$ are opposite. If q is odd, then the two chosen inequalities are (m,j-1) and (l,j) in which the signs of $x_{1j}$ are also opposite.

• $(j-1)j \in C\!{\setminus }\! F$ and $j(j+1)$ is an edge $f_q \in F$. If q is even, then the two chosen inequalities are (l,j-1) and (a,j) in which the signs of $x_{1j}$ are opposite. If q is odd, then the two chosen inequalities are (r,j-1) and (m,j) in which the sign of $x_{1j}$ are also opposite.

• both $(j-1)j$ and $j(j+1)$ are in F. Let $(j-1)j=f_q \in F$. If q is even, then the two chosen inequalities are (a,j-1) and (m,j) in which the signs of $x_{1j}$ are opposite. Similarly, if q is odd, then the two chosen inequalities are (m,j-1) and (a,j) in which the signs of $x_{1j}$ are opposite.

In all cases, the signs of $x_{1j}$ in the two chosen inequalities containing it are opposite, thus $x_{1j}$ vanishes in the sum.

For any edge $e \in C{\setminus } \{12,(k-1)k\}$, $x_e$ appears only in one of the chosen inequalities which corresponds to the triangle having e as the middle edge. The edges 12 and $(k-1)k$ also appear only once, respectively in the inequalities corresponding to the triangles 2 and $k-1$. It is then clear that for any edge $e \in C$ the coefficient of $x_e$ in the sum is 1 if $e \in F$ and $-1$ if $e \in C\!{\setminus }\! F$.

It remains to show that the sum of the right hand sides is $p-1$. We can see that the only chosen inequalities with non-zero right hand side are of type (a,i), i.e., the ones corresponding to the triangles having $f_q \in F$ with q even as the middle edge. There are clearly $\frac{p-1}{2}$ such inequalities with 2 as the right hand side. The proof of the first part of the lemma is then done.