Introduction

Fractions are fundamental in mathematics education, as they serve as the cornerstone for comprehending more advanced mathematical concepts (Boyce et al., 2021; Byerley, 2019, 2012; Hackengerg & Lee, 2015; Lamon, 2007; Lee, 2017a; Lee & Hackenberg, 2014). Nevertheless, many researchers have reported that elementary preservice teachers (PSTs) face challenges when solving fraction tasks (Lee, 2017b; Lee & Lee, 2021a, b; Lo & Luo, 2012; Lovin et al., 2018; Olanoff et al., 2014; Yeo & Lee, 2022). PSTs often tend to struggle to grasp the meanings underlying computational skills or algorithmic procedural knowledge about fractions (Lee, 2017b; Olanoff et al., 2014; Stoddart et al., 1993). Additionally, PSTs show difficulties when trying to apply pedagogically effective fractional models to support their future teaching of mathematics (Lee & Lee, 2020, 2021a, 2023; Rosli et al., 2013).

To be equipped to teach fractions to pupils, PSTs need to develop sufficient fractional reasoning and the ability to accurately model fractional concepts. However, research on how PSTs use fractional models to demonstrate their fractional reasoning has rarely been conducted (Lee & Lee, 2020; Olanoff et al., 2014). The research on PSTs’ fractional reasoning that has been done has tended to focus on their procedural competencies in relation to the four fundamental fractional operations or only address how PSTs model fractions. These investigations consistently underscore two recurring observations: (1) PSTs often encounter difficulties when performing fraction computations or creating models due to a deficiency in their conceptual grasp of fractions (Lee, 2017b; Lo & Luo, 2012; Olanoff et al., 2014), and (2) instructional approaches that treat fractions as measurable quantities involving the use of iterative fraction language, and/or employ length models, representations, and manipulatives designed to foster the utilization of units and unit iteration, are effective for enhancing PSTs’ fractional reasoning (Amoah & Otchere-Larbi, 2023; Bobos & Sierpinska, 2017; Stevens et al., 2020).

Building upon the existing body of research, in this study, we incorporated the use of the Dynamic Ruler tool (Yeo & Webel, 2024) in tasks designed to investigate PSTs’ fraction-as-measure reasoning. The Dynamic Ruler tool is based on the fraction-as-measure approach, which emphasizes the connection between units of measurements and the magnitude of quantities. This approach helps address challenges with fractions by encouraging PSTs to perceive fractions as single quantities within measurement contexts rather than an arrangement of two distinct parts such as a pre-partitioned whole and a shaded portion that represents the fraction (Davydov & Tsvetkovich, 1991; DeWolf & Vosniadou, 2015; Hackenberg & Lee, 2015; Ni & Zhou, 2005; Soni & Okamoto, 2020; Steffe & Olive, 2010). Also, the Dynamic Ruler tool empowers users to effortlessly generate a multitude of continuous values and constructions by simply dragging a single point. Therefore, the tool facilitates the identification of a co-measurable unit when two or more fractional bars are presented. Because the Dynamic Ruler tool is designed to align with the principles of length models, it can be used to investigate how PSTs demonstrate fraction-as-measure reasoning.

In this study, we investigated how elementary PSTs in the USA and South Korea coordinated units and quantities when solving four fraction-as-measure tasks using the Dynamic Ruler tool. Although we examined the PSTs in two countries, our focus was not on a direct comparison of the fractional reasoning abilities of PSTs in the two countries but an examination of commonalities in how both groups manifested their fractional reasoning using the Dynamic Ruler tool in two different contexts. By analyzing data from two countries with distinct cultural and educational backgrounds, we aimed to explore the extensive variety of fractional reasoning processes exhibited by PSTs, which could yield valuable insights for enhancing the development of PSTs’ fractional reasoning across diverse settings.

In this study, we pursued the following objectives: (1) to scrutinize the reasoning processes of PSTs in the USA and Korea as they engaged with fraction-as-measure tasks using dynamic tools, (2) to categorize the levels of fraction-as-measure reasoning in our sample, (3) to provide a conceptual framework for evaluating PSTs’ fractional reasoning, and (4) to offer research-based insights and recommendations to mathematics educators and teacher preparation programs so as to equip future educators with more effective pedagogical strategies. This study was guided by the following research question: How do PSTs in the USA and South Korea approach fractions-as-measure tasks when utilizing the Dynamic Ruler as a tool?

Literature review

To investigate elementary PSTs’ fraction-as-measure reasoning with a dynamic digital tool and provide them with effective pedagogical strategies, it is essential to understand their fraction knowledge and reasoning. Exploring PSTs’ understanding of fraction-as-measure, which emphasizes the interpretation of fractions as representing quantities or measures, can provide insights into their conceptual development and inform instructional practices. The dynamic digital tool can play a crucial role in examining PSTs’ fraction-as-measure reasoning as it facilitates PSTs’ reasoning through semiotic mediation, which involves the use of signs and symbols. Therefore, in this section, we first review PSTs’ fractional knowledge in general, then focus on the specific topic of PSTs’ fraction-as-measure reasoning, and finish with the use of dynamic digital tool in mathematics education.

PSTs’ fraction knowledge in general

Effectively conveying the intricacies of fractions requires educators to possess a profound comprehension of both the conceptual foundations and the practical procedures related to the concept of fractions and its associated operations. Solely relying on procedural knowledge can hinder understanding the underlying mathematical ideas and the interconnections among various mathematical concepts, as demonstrated by a body of research showing that PSTs who demonstrate strong computational proficiency and a firm grasp of algorithmic procedures often encounter difficulties in grasping the meanings that underlie these procedures (Lee, 2017b; Olanoff et al., 2014; Stoddart et al., 1993). Furthermore, PSTs frequently confront challenges when endeavoring to employ pedagogically sound representations or models to bolster mathematical learning (Rosli et al., 2013).

For instance, Olanoff et al.’s (2014) comprehensive analysis of 43 studies concerning the fractional knowledge of PSTs revealed that grasping the underlying meanings of the procedures and computations they had learned was a recurrent challenge for PSTs. Similarly, Huang et al. (2009) reported that PSTs demonstrated greater procedural knowledge than conceptual understanding of fractions. Furthermore, Rosli et al. (2013) found that PSTs’ superior knowledge of fraction computation significantly exceeded their capacity to work with representations, which is essential for supporting students’ learning and requires a sound conceptual grasp of fractions. When presented with a task involving the addition of 5/6 and 3/4 as measures of pizza consumption, it was observed that 78% of the participating PSTs (N = 150) provided the correct answer. However, a mere 34% visually depicted the overall pizza consumption in a manner that accurately represented the concept of a least common denominator. The predominant approach employed by PSTs resulted in inaccurate representations due to utilization of different unit wholes.

Similarly, Lo and Luo (2012) observed that PSTs encountered challenges when tasked with representing fraction division, whether through verbal explanations or visual diagrams, even when they correctly solved division fraction problems. Tirosh (2000) also observed that PSTs possessed the knowledge required for dividing fractions but encountered difficulties when explaining the procedural steps of fraction division or predicting the primary sources of students’ incorrect responses. Moreover, in an investigation of 111 PSTs’ flexibility when dealing with referent units in the context of solving fraction division problems using a length model, Lee (2017b) found that the majority were capable of performing procedural calculations for fraction division and establishing equivalent fractions. However, they struggled to convey understanding of the quantitative meanings behind fraction division or the concept of generating equivalent fractions.

In an investigation of elementary PSTs’ development of fraction content knowledge, Lovin et al. (2018) focused on five fraction schemes, abstract constructs that offer insight into how students assimilate various situations and operate within them (see Table 1).

Table 1 Five fraction schemes
Full size table

Lovin et al. (2018) substantiated the hierarchy of fraction schemes and operations by demonstrating that mastery of lower-level fraction schemes (i.e., part-whole fraction scheme, partitive unit fraction scheme, partitive fraction scheme) is a prerequisite for advancing to higher levels (i.e., reversible partitive fraction scheme, iterative fraction scheme). Contrary to expectations, however, they also found that even though most PSTs had achieved proficiency in the lower-level schemes, only 27% had progressed to the highest level, iterative fraction scheme. They attributed this outcome to the intricate process of coordinating three levels of units and constructing more advanced fraction schemes, both of which are linked to the fundamental fractional reasoning required for advanced mathematics. Also, they proposed that the prevalence of part-whole reasoning in the K-12 curriculum in the USA (e.g., Watanabe, 2006; Yang et al., 2010) might contribute to the challenges encountered by almost three-fourths of the PSTs in developing a more advanced fraction scheme, which the Common Core State Standards mandate should be mastered by 4th and 5th grade students in order to work with improper fractions as actual numbers.

All of the studies reviewed here revealed PSTs’ struggles with fractions, a common reason for which may be closely related to their whole number bias resulting from treating numerators and denominators of fractions as separate whole numbers rather than as a single quantity (Ni & Zhou, 2005). To address this challenge, in several studies the effectiveness of the “fractions-as-measure” approach has been highlighted.

Fraction-as-measure approach and PSTs’ fraction-as-measure understanding

The fraction-as-measure approach is grounded in the concepts of measurement units and unit hierarchies (Davydov & Tsvetkovich, 1991). This perspective underscores the connection between units of measurement and the magnitude of quantities. For example, in a scenario where a length (L) is measured using a specific unit (u), after four iterations with this unit u, a unit half the size of the original unit may be needed to measure the remaining portion, which introduces the notion of half as a fractional unit. Thus, the given length L is expressed as 4 u and ½ u (or 4 ½ of u).

Some researchers have advocated for measurement as the foundation of number concepts, encompassing all number systems, including whole numbers and fractions (Brousseau et al., 2014; Davydov & Tsvetkovich, 1991). Going back to ancient Egypt, fractions were devised to quantify commodities such as grains and liquids (Ifrah, 2000). Subsequently, the concepts of units of measurement and magnitude of quantities remained fundamental in school mathematics for understanding the relationships between numbers and operations (Kaput, 1985; Schwartz, 1988). However, in modern education, the emphasis on measurement as the source of number concepts has waned due to the development of algebra, which expanded the focus from integers to rational numbers. As a result, educators began to view measurement as less relevant to the formation of rational number concepts, obscuring their practical origins.

Davydov and Tsvetkovich (1991) implemented a teaching experiment based on the measurement of quantities as the historical origin of the fractional number system. Initially, the participating children directly compared lengths, widths, heights, and weights of concrete objects like sticks or pieces of string using mathematical symbols (e.g., + , > , = , <) and represented the relationship between quantity and unit with whole numbers. But as the lessons progressed, the children encountered situations in which whole numbers alone did not suffice for measurement, requiring them to measure a remainder using a new partial unit. If a smaller unit fits a quantity n times and the original unit fits it m times, the ratio between m and n can be represented as n/m. This measurement-based approach introduced fractions as a theoretical concept, helping the children be aware that ideas could be generalized across whole and rational number systems, such as measures and units.

Expanding on this approach, researchers have incorporated measurement-based methods for teaching fractions in both teaching experiments (e.g., Simon et al., 2018) and classroom settings (e.g., Schmittau, 2005; Schmittau & Morris, 2004). For example, Simon et al. (2018) developed a curriculum for teaching fractions with a focus on measurement and conducted one-on-one teaching experiments with fourth-grade students. One task involved measuring a beam using a specific length unit, followed by using a pre-partitioned unit to measure the remainder relative to the given unit. Students developed an initial concept of fractions as a measure and explored the relationship between measurement and iteration. For instance, Kylie showed her understanding of a unit fraction as a partial unit measuring a whole unit by explaining, “It’s one-third… because I’m measuring that—three of these measure one unit.” She also recognized that the unit fraction was a part that iterates a specific number of times to form a unit.

These studies with children demonstrate the advantages of implementing a measurement-based approach to teaching fractions. As PSTs will be teaching such students in the future, it is important for them to understand the fraction-as-measure approach and be familiar with fraction-as-measure reasoning. In this regard, several researchers have explored ways to enhance the fractional knowledge of elementary PSTs through interventions in mathematics pedagogy courses (e.g., Amoah & Otchere-Larbi, 2023; Bobos & Sierpinska, 2017; Stevens et al., 2020). For instance, Stevens et al. (2020) introduced adjustments that emphasized the utilization of iterative fraction language and the deliberate inclusion of improper fractions in a mathematics course for elementary PSTs, resulting in a marked increase in the PSTs’ development of advanced fraction schemes.

Additionally, Bobos and Sierpinska (2017) found that implementing an approach focused on relational reasoning pertaining to quantities while drawing from the measurement-based construct of fractions fostered PSTs’ quantitative reasoning and theoretical thinking, which facilitated the development of their understanding of the concept of fractions as abstract numerical representations signifying the measure of the relationship between two quantities. In a structured six-week intervention, Amoah and Otchere-Larbi (2023) explored the efficacy of employing Cuisenaire rods to enhance PSTs’ understanding of fractions. Their findings yielded three pivotal insights: (1) using Cuisenaire rod significantly elevated the PSTs’ comprehension of fractions; (2) the concept of equivalent fractions should be introduced before teaching the addition and subtraction of fractions; and (3) PSTs’ grasp of fractional concepts was facilitated when instructional materials were presented systematically beginning with the concrete level, progressing through a semi-concrete phase, and culminating at the abstract level.

Results from these studies underscore the potential of measurement-based approaches for enhancing the understanding of fraction concepts. PSTs who have cultivated a perception of fractions-as-measure can approach fractions from a quantitative rather than merely a numerical perspective (Bobos & Sierpinska, 2017; Stevens et al., 2020; Thompson & Saldanha, 2003). However, in these prior studies, only either signs such as iterative fraction language and theoretical thinking or tools such as Cuisenaire rods were considered. In this study, we examined PSTs’ fraction-as-measure reasoning by using the dynamic digital tool, which can be utilized to generate both signs and symbols.

Dynamic digital tool in mathematics education

When digital technologies are employed, the symbols produced through the manipulation of technological instruments are integrated into the user’s cognition and redirected toward other symbolic expressions, such as written words, illustrations, or, within the context of social interaction, non-verbal gestures. In this regard, digital technologies’ generation of signs and symbols has the potential to support the development of semiotic mediation, which refers to the process of deriving meaning through the use of signs.

Vygotsky (1978) distinguished between signs and tools, stating that "The sign acts as an instrument of psychological activity in a manner analogous to the role of a tool in labor (p. 52)." Thus, signs are symbolic tools, such as language and numerical notations, employed in cognitive endeavors, while tools are material implements, like computers and hammers, used for physically executed tasks. Both symbolic and material tools play pivotal roles in facilitating students’ comprehension. For example, a child tackling an addition problem might choose to manipulate a tangible tool, like a snap cube, or employ a symbolic tool, such as a mathematical expression with numerical symbols, which illustrates their complementary nature.

Bartolini Bussi and Mariotti (2008) further articulated the concept of semiotic mediation as the process by which individuals construct meaning through the internalization of symbols originating from external and interpersonal engagements. For instance, utilizing Dynamic Geometry Software (DGS) for drawing involves purpose-driven actions like “drag and drop” afforded by the software, which can become integrated into an individual’s cognitive framework to form personalized interpretations. Furthermore, the employment of “drag and trace” tools facilitates group as well as individual meaning-making, thereby mediating the social process of constructing meaning.

Digital tools have the capacity to generate not only conventional signs but also dynamic mediators, which facilitate students’ comprehension by representing mathematical relationships and properties. For instance, in their examination of the roles of language, gestures, and technology in children’s development of geometric conceptions, Ng and Sinclair (2015) investigated how dynamic digital technology can mediate children’s understanding of the concept of geometric symmetry. One child in their study, while interacting with digitally constructed squares on a screen, described the movement of “specific squares” and subsequently observed that the corresponding points on the opposite side of the symmetry line “will move like opposite." The researchers concluded that using the interactive digital tool enabled the child to experience the dynamic interplay between the line of symmetry and the (pre)image squares as mathematical entities, which facilitated the formalization of the child’s individual mathematical understandings.

Yeo and Webel (2024) also found that the dragging function of Dynamic Rulers played a dynamic mediating role not only in elementary students’ approaches to partitioning a given unit length into smaller components, but also in their conceptions of partial units in tasks involving mental, singular, and multiple partitioning. This dynamic process shed light on their developmental levels as they progressed toward comprehending fractions-as-measure. Through the dragging action, students actively unitized and re-unitized the given unit rod, honing their ability to construct both whole units and partial units. As they developed proficiency in coordinating composite units in a unit-of-units structure, the students showed a wide spectrum of reasoning when measuring specified fractional lengths. For example, students could treat a one-foot length in a 4/4-foot segment as a unit containing four units and divide each of the four units into three parts, resulting in 12 parts in all. This progression shows the potential of using digital tools to strengthen students’ capacity for multiplicative coordination, underlining the importance of recognizing composite units.

Although some research on investigating children’s semiotic mediation in dynamic digital environments has been conducted, there has been limited examination of PSTs’ fractional reasoning using a dynamic digital tool. In this study, we administered a refined version of Dynamic Ruler tasks to examine PSTs’ reasoning in relation to various solution strategies. We posited that the implementation of this dynamic tool would provide valuable insights into the diverse range of PSTs’ fraction-as-measure reasoning processes and in particular shed light on the development of the advanced fractional knowledge and reasoning involved in coordinating three levels of units and conceiving improper fractions as numerical representations that would result from the iteration of a unit fraction.

Methods

Participants and settings

The study involved 142 elementary PSTs, of whom 42 were enrolled in U.S. and 100 in Korean teacher education programs. We selected these two countries due to differences in their approaches to teaching and learning fractions (Yeo & Lee, 2022), which would shed light on commonalities in how elementary PSTs manifested their fractional reasoning when using the Dynamic Ruler tool regardless of their cultural and educational differences.

PSTs in the U.S. cohort were enrolled in a mathematics pedagogy course and had successfully completed two essential mathematics content courses covering topics related to number and operations as well as geometry, algebra, statistics, and probability, which were prerequisites to the mathematics pedagogy course. This course covered comprehensive insights into how various mathematical topics, including but not limited to whole numbers and operations, fractions and operations, patterns, algebraic thinking, geometry, and measurement, which are addressed in the U.S. Common Core State Standards for Mathematics (NGA & CCSSO, 2010) across grades K-8.

The PSTs in the Korean cohort, who were in the second year of their elementary teacher preparation program, were enrolled in a mathematics pedagogy course after completing a course on the theoretical background of Korean mathematics education and mathematics content. In the pedagogical content knowledge, PSTs learned methods for teaching mathematics to elementary students in the areas of number and operations, geometry, patterns, measurement, and statistics, which are aligned with the national curriculum (MOE, 2015). Both nations’ pedagogy courses focused on developing mathematical knowledge for teaching the subject, which involved progressively building on children’s mathematical understanding. Instructors in both settings discussed the objectives of the pedagogy course and shared their instructional materials.

Dynamic ruler

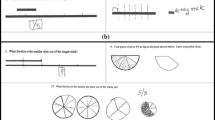
For this study, we developed a new version of a Dynamic Ruler, an interactive tool, to explore measurement tasks. The Dynamic Ruler tool was originally designed to assess elementary students’ fraction concepts based on a fraction-as-measure approach (Yeo & Webel, 2024). However, for this study, the Dynamic Ruler tool was refined and employed within the HTML5 environment. This new version allowed users to measure the linear length of objects with adaptable unit sizes using either touch actions on mobile devices or mouse actions on computers. The Dynamic Ruler offered four interactive functions, as illustrated in Fig. 1: (a) resizing the unit, (b) locating the Dynamic Ruler, (c) trimming the Dynamic Ruler, and (d) selecting alternative Dynamic Rulers (Yeo & Webel, 2024).

Fig. 1
figure 1

Four functions of the Dynamic Ruler tool

Full size image

These interactive features were designed to be utilized within a series of fraction-as-measurement tasks. As the previous version of this dynamic tool was used to explore children’s comprehension of fractions by engaging these features (Yeo & Webel, 2024), we extended the user level from children to elementary PSTs. Following are the rationales for providing these four functions. First, the PSTs could modify the unit size by manipulating the vertical segments horizontally between pieces (Resizing the unit). This action caused a dilation of all units within the ruler. That is, when PSTs extended or contracted an adjustable unit, other parts of variable units were automatically adjusted across the entire tool. Second, PSTs could locate the Dynamic Rulers on any space, facilitating the measurement of specific lengths by placing a Dynamic Ruler adjacent to a targeted object (Locating the Dynamic Ruler). The transparency of the Dynamic Ruler allowed it to be placed in the background of an object, and PSTs could even overlap multiple Dynamic Rulers. Third, PSTs could trim or modify the number of pieces displayed on the ruler by touching a part of it on a tablet PC or clicking on a computer (Trimming the Dynamic Ruler). The last function allowed PSTs to select multiple Dynamic Rulers for comparing units or parts of units (Selecting alternative Dynamic Rulers). This function gave students the autonomy to determine if a single Dynamic Ruler sufficed for their given tasks or add more rulers as needed, choosing from a selection of four Dynamic Rulers (red, green, blue, and purple) at the bottom of the screen.

Instrument and data collection

Following a tutorial session in which they were introduced to the Dynamic Ruler and explored the four functions with the instructors’ guidance, the PSTs completed a questionnaire comprising four distinct fraction-as-measure tasks utilizing the Dynamic Ruler tool. The questionnaire was administered in the format of Google Forms, in which PSTs were asked to take screenshots of their work with the Dynamic Ruler and to explain their reasoning behind their work. When administering the questionnaire, instructors emphasized that PSTs needed to justify the quantitative relationship between two rods by using the Dynamic Ruler rather than providing a simple guess or assumption based on given images.

Referring to Yeo and Webel’s (2024) study, we designed these four tasks for PSTs to explore various ratios between the provided units and quantities, as visually represented in Fig. 2.

Fig. 2
figure 2

Task 1

Full size image

Tasks 1 and 2 specifically focused on the concept of mixed numbers by providing scenarios with unit fractions or improper fractions. Task 3 involved a mixed number featuring a non-unit proper or improper fraction. Task 4 addressed proper fractions. Table 2 summarizes the four tasks used in this study.

Table 2 Summary of four fraction-as-measure tasks
Full size table

For each of these tasks, the following four questions were administered after the student uploaded the required screenshot to probe the problem-solving process involved: (1) What is your answer? (2) How did you get the answer? (3) How did you decide the size of the ruler? (4) Can you find a different answer? We included the third and fourth questions to substantiate the fractional reasoning employed by the PSTs when using the Dynamic Ruler as we believed that the abilities to identify units (Lamon, 2012; Lee & Lee, 2021a; Steffe & Olive, 2010) and to coordinate units in various ways by structuring two bars based on their co-measuring units (Hackengerg & Lee, 2015; Lee & Hackenberg, 2014; Steffe & Olive, 2010) are fundamental criteria for assessing the various levels of fractional reasoning.

The Development of Coding Scheme and Data Analysis

The development of coding scheme

We conceptualized PSTs’ fractional reasoning in terms of fraction operations. Operations refer to mental actions and form the fundamental elements of schemes (von Glasersfeld, 1995). Steffe and Olive (2010) identify three primary fractional operations as follows.

  • Partitioning: dividing a continuous whole into equal segments (e.g., sharing a bar equally among three people)

  • Iterating: creating connected duplicates of a part. (e.g., repeating a 1/3 part three times to make the whole)

  • Disembedding: separating a part from a whole without destroying the whole (e.g., taking a 2/3 out of 3/3 while maintain 2/3 as part of that whole)

These operations are intricately linked to five distinct fraction schemes, ranging from lower to more advanced levels: part-whole, partitive unit, partitive, reversible partitive, and iterative (see Table 1 in the literature review section). By referring to Steffe and Olive’s fraction operations, we created our coding scheme of fraction operations for analyzing PSTs’ actions in dynamic digital environments (see Table 3).

Table 3 Final coding scheme
Full size table

In terms of the Resizing operation, PSTs demonstrated the action of resizing the Dynamic Ruler until it fit into a given bar. The result of this act was similar to traditional partitioning in that both mentally generated equal-sized parts from the whole. However, in this study, PSTs did not need to cut the bar into equal parts as in the traditional act of partitioning because of the dynamism within the Dynamic Ruler tool. The Disembedding operation within the Dynamic Ruler was similar to traditional disembedding operation in that after resizing the Dynamic Ruler, PSTs moved a part to overlap it with other unit length. In terms of the Unitizing operation, PSTs adjusted the Dynamic Ruler to match with the ends of both bars. The result of this act may be interpreted as comparable to the combination of traditional partitioning and iteration operations in that PSTs had to recognize how many pieces one bar was partitioned into and to count how many unit pieces were repeated in the other bar to assign a name to the quantity based on a partition of a unit. Coordinating units refers to identifying at least one common unit that can be used to measure both bars. The traditional iterating operation can be emulated by using the trimming/untrimming feature of the Dynamic Ruler (see Fig. 1c), but the PSTs in this study did not use it within the dynamic learning environment.

Inductive content analysis

We employed a systematic four-phase inductive content analysis approach (Grbich, 2013), which involved the following steps: (1) carefully scrutinizing PSTs’ written responses; (2) engaging in open coding to develop and finalize coding schemes (see Table 3); (3) coding the entire dataset using the established coding schemes; and (4) tabulating the frequencies and interpreting the results. The unit of analysis in this study comprised each PST’s written responses to the set of prompts administered after a screenshot to show how a given task had been solved was uploaded. These written responses and screenshots provided insights into individual PSTs’ processes of fraction-as-measure reasoning, which we explored through the three prompts aimed at elicitation and clarification: What is your answer? How did you get the answer? How did you decide the size of the ruler? While it was observed that PSTs often showed advanced levels of reasoning in response to the last prompt (Can you find a different answer?), we did not code these responses in the current study. When coding the PSTs’ work, to identify characteristics of PSTs’ reasoning in the strategies they used, we separately classified the responses of each PST to the four tasks. To ensure the trustworthiness of our data analysis, we initially conducted separate coding of a sample of 10 responses, which yielded approximately 90% concurrence. We then individually coded the remaining data and resolved any disparities through discussion until we achieved 100% consensus. Finally, we tallied the responses within each category to discern overarching trends.

Although our analysis included whether the PSTs correctly identified the quantitative relationship between the two rods, the primary focus was specifically on how they approached the four fractions-as-measure tasks, that is, the reasoning they used to justify their answers. Therefore, we placed greatest emphasis on the rationale underlying their responses, their methodology for determining unit size, and their ability to adapt their unit coordination perspective in various contexts. For example, even when the PSTs’ answers were correct, if their reasoning was based on estimation of the given images, we assigned the responses to the lower level of “Measuring with estimation.” Building upon this initial data analysis, we categorized the fractional reasoning of PSTs into five distinct groups, which are elaborated upon in the section below.

Results

PSTs’ fraction-as-measure reasoning

Table 4 shows the five levels of PSTs’ fraction-as-measure reasoning we found in our analysis of their strategies for each task in ascending order of sophistication: Limited acknowledgment of length unit, Measuring with estimation, Measuring with length unit additively, Measuring with length unit multiplicatively, and Measuring with length unit with commeasuring. As we analyzed levels of reasoning across a series of tasks, some PSTs showed different levels of reasoning depending on the types of the tasks. It is noteworthy that, even though PSTs exhibited some similarities in their reasoning processes, their approaches to unit coordination and measurement strategies manifested notable variations, predicated upon their comprehension of fractions and length measurement and their utilization of the technological affordances of the Dynamic Ruler. In the following discussion, we provide representative cases of each level from both countries.

Table 4 PSTs’ Reasoning Levels of Fraction-as-Measure Tasks
Full size table

Limited acknowledgment of length unit

At the lowest level, a few PSTs were unsuccessful in their attempts to solve the Dynamic Ruler tasks as they failed to determine the relationships between the leftover parts (i.e., the difference between two rods) and the original unit sizes (i.e., the bottom rod). Having been introduced to the major features of the Dynamic Ruler such as resizing, locating, trimming, and selecting dynamic rulers during the initial tutorial session, they were expected to know how to use the rulers to solve given tasks. In addition, the default length of the Dynamic Ruler was intentionally set to mismatch either with the given unit or the quantity to be measured so as to encourage students to modify the size of the Dynamic Ruler to more accurately represent the given length in relation to the unit. However, some PSTs did not follow this cue and instead employed the Dynamic Ruler in its default state. Two cases, PST A (Korean) and PST B (U.S.), exemplify this particular approach, which involves few fractional operations. PST A used the default size of the Dynamic Ruler without any adjustment, while PST B utilized the default unit size but tried to identify the relationships between the given unit and the unit size of the Dynamic Rulers. Neither PST suggested the possibility of having multiple answers for the tasks.

For example, in her approach to Task 2, PST A used the default sizes of the Dynamic Rulers as given (Fig. 3). She positioned four units of the green Dynamic Ruler to align with the length of the brown rod and concluded that four orange units would be needed to span this length, explaining, “I need four bars. Three orange bars are not enough to make a brown bar, so I need four.” She further articulated her rationale as follows: “To find out the length of the brown bar, I dragged a green bar under the brown bar, and it was exactly the same length as the four green bars.” PST A was the only PST among the cohort of Korean PSTs to demonstrate this level of fraction-as-measure reasoning.

Fig. 3
figure 3

PST A’s solution for Task 2. [Translation] How many orange rods are needed to fit into the brown rod?

Full size image

In her work, PST A did not make any adjustments to the unit size of the Dynamic Ruler in order to measure the brown rod in coordination with the given orange unit size. To solve fraction-as-measure tasks using a Dynamic Ruler, it is necessary to figure out the proportional relationship between the length unit (the orange rod) and the quantity (the brown rod) by adjusting the scalable units of the Dynamic Ruler. However, PST A applied little relational thinking to the two focal rods but rather focused on using the default unit length of the green Dynamic Ruler to measure the quantity of these units in the brown rod.

PST B (U.S.) used the default dimensions of the Dynamic Ruler units in the first two tasks. In both, she showed partial fractional understanding in that she tried to find the difference between two rods by comparing the differences between other rod units and the orange rod unit. For example, in Task 1, she placed the default size units of the purple ruler next to the orange rod (Fig. 4-left). Then, she compared the difference (two purple units) with the orange rod, explaining, “I then compared again the colored boxes with the orange box and saw that the orange box reached two colored boxes at a certain point. I broke down the boxes into 4 different spaces. I then saw that one box and 1/4 of another box was needed.” This statement showed her skill of partitioning but partial understanding of unitization. She explained her reasoning process by partitioning two purple Dynamic Ruler units as the whole into four parts ("I broke down the boxes into 4 different spaces”). However, in the following statement, she elaborated the length unit as one purple unit (“I then saw that one box and 1/4 of another box was needed”). This confusion between units might have come from her partial understanding of unitization for measurement.

Fig. 4
figure 4

PST B’s solution for Tasks 1 and 2

Full size image

Similarly, in Task 2, PST B adhered to the use of the default size of the ruler (Fig. 4-right). Her explanation for placing four green Dynamic Ruler units over the default brown rod was as follows: “I saw that to make up the brown box, we need four boxes.” Notably, PST B showed interest in the relationship between the orange unit rod and the default size of the Dynamic Ruler, noting that, “1 orange box covered one complete colored box and 1/4 of another.” Thus, it appeared that PST B was attempting to employ an alternative unit for the measurement of the brown rod, but she encountered a challenge when she realized the disparity between the sizes of the green Dynamic Ruler and the orange unit.

In sum, the discrepancy may have contributed to her reaching an incorrect response, reflecting limited capacity to engage in unitization. In both tasks, she misinterpreted the whole with different numbers of Dynamic Ruler units. In addition, she did not directly measure the quantity of brown rod units with the orange rod unit. Nevertheless, she showed the emerging potential to understand estimation between the orange rod and Dynamic Ruler units, which transits to the next level of fraction-as-measure reasoning in the following section.

Measuring with estimation

An alternative reasoning method employed by PSTs when solving Dynamic Ruler tasks involved measuring a given unit through dynamic actions such as alignment and resizing, followed by estimating the remaining length as a fraction, which they expressed using fraction terms such as “half” or “quarter.” In this approach, the PSTs were cued by the dynamic digital environment to utilize rational numbers within the context of length measurement.

PST C’s (U.S.) response to Task 1 was “2 and about 1/4 of orange.” She first matched the unit size of the red Dynamic Ruler to the size of the orange rod (Fig. 5) and then moved that Dynamic Ruler up to overlap the brown rod. She then repeated the same process with the green Dynamic Ruler: “I used one orange to measure out; then using observations I concluded it needed 2 at least to get as close as possible.” PST C iterated the red pieces to find how many orange rods would fit into the brown rod, a strategy we labeled as Measuring with estimation as she decided to approximate the leftover (“about ¼”) by finding the relationship between the orange rod and the leftover, commenting, “And then the remaining can be estimated.” She apparently adjusted the Dynamic Ruler to match with the size of the orange rod and estimated the leftover separately by Disembedding. Furthermore, when asked to find a different answer, she seemed to know that she could find fractions by partitioning the given unit into smaller units, as she commented, “Yes. By using smaller pieces, you can cut it into equal parts.” However, she did not perform this operation.

Fig. 5
figure 5

PST C’s solution for Task 2

Full size image

In Task 3, PST D (Korean) employed a strategy similar to PST C’s approach (Fig. 6). He first lined up the red Dynamic Ruler to match the size of the orange rod. However, he moved up the entire ruler and placed it between the orange rod and the brown rod. This was different from PST C’s strategy, which involved multiple rulers to show the length units. Then PST D provided the answer as “Two orange rods and about 1/3.” To figure out the leftover of the brown rod, PST D estimated the length of the leftover in terms of the orange rod, “Using the dynamic ruler, I asked myself, how many orange bars (O) would it take to equalize the length of the brown bar (B) so that it would be the same length as the orange bar (O).” Instead of precisely measuring the fractional value of the remaining part, PST D visually compared the leftover of the brown rod and the given orange unit, resulting in an answer (2 1/3) that was slightly different from the actual answer (2 1/4). PSTs engaging in this level of reasoning separated and guessed the length of the leftover part when measuring with the original unit (Disembedding operation) but could not confirm the fractional values by exploring with the Dynamic Ruler. Therefore, in the following section, we illustrate representative cases in which PSTs were able to precisely measure leftover parts with the Dynamic Ruler (Resizing operation).

Fig. 6
figure 6

PST D’s solution for Task 1. [Translation] How many orange rods are needed to fit into the brown rod?

Full size image

Measuring with length unit additively

At this level of reasoning, the PSTs attended to unit lengths and linked them additively with a numeric structure. They first determined the whole-number component of the measurement by adjusting the size of a Dynamic Ruler unit to align with the given unit. To measure the remaining part, they partitioned another Dynamic Ruler unit into smaller units, iteratively experimenting until they achieved a sub-unit that had the same measurement as the remainder. In such a measuring situation, it is common to gauge the whole units first and then the partial units. Through this process, these PSTs demonstrated their evolving comprehension of a more generalizable relationship between fractional units and the given unit length.

For Task 1, PST E (U.S.) found that “2 and 1/4” orange units were needed to fit into the brown rod (Fig. 7). Initially, she employed the red Dynamic Ruler and matched it with the orange rod (Disembedding operation). After placing three red units, she noticed the leftover needed to be measured with a different size unit. She explained her reasoning process as follows:

I dragged the red ruler until one rod fit the entire orange rod, and then once it was the right size, I dragged it to the brown rod and saw that two full rods fit and then a smaller section. To figure out the smaller section, I used the green ruler and made each of those rods the same size as the end of the red ruler on the brown rod. Once I got the right size, I moved the green ruler to the orange rod and I saw that one orange rod is the size of 4 green rods ….

PST E decided on the size of the red Dynamic Ruler by partitioning the orange rod into 1/4 pieces to find a unit to measure the leftover (Resizing operation).

Fig. 7
figure 7

PST E’s solution for Task 1

Full size image

In Task 2, PST F (Korean) began by determining the number of orange rods that formed a unit to measure the length of the brown rod (Fig. 8), for which she employed the red Dynamic Ruler (Disembedding operation). When she found that three red units as given were not enough to measure the brown rod, she tried using different colored Dynamic Rulers to measure the leftover (Resizing operation). She noted,

If I put as many rods of length that is equal to O into B as possible, I get three [red rods]. If I put as many rods of length that is equal to the length of what’s left into O as possible, we get three [blue rods]. That is, I need one-third more of O, so three and one-third.

Fig. 8
figure 8

PST F’s solution for Task 2. [Translation] How many orange rods are needed to fit into the brown rod?

Full size image

PST F iterated an orange rod sized unit three times to fit into the brown rod and used another sub-unit subsequently to measure the leftover. During this process, measuring the brown rod with whole-number units and the part measured with a new partial unit required representing the relationship between the two parts as rational numbers, which is a fundamental concept of fractions-as-measure.

Measuring with unit length multiplicatively

PSTs employing strategies at this level demonstrated an emerging capacity for generalization in their use of the Dynamic Ruler. They recognized that this digital tool could effectively serve the dual purpose of measuring both a unit length (i.e., the orange rod) and a given quantity (i.e., the brown rod). That is, during the process of measuring a given quantity (i.e., the brown rod) with a unit (i.e., orange rod), to figure out the remaining fractional portion, they resized the Dynamic Ruler to identify a new unit that could evenly subdivide both rods. This level of reasoning can be understood as predicated on multiplicative comparison, wherein a quantity is assessed as a multiple of the unit, a concept well-documented in the work of Thompson and Saldanha (2003).

For Task 1, PST G (U.S.) used the blue Dynamic Ruler to find a single unit that disembedded both rods at the same time (Fig. 9). She noted her reasoning as follows:

I shrunk all the rulers down until I got them to be the same size and reach the length of both boxes and then counted how many boxes filled the orange rod, and then counted how many boxes filled the brown rod.

Fig. 9
figure 9

PST G’s solution for Task 1

Full size image

PST G noticed that 1/4 of the orange rod could measure the orange rod and the brown rod simultaneously (Unitizing operation). She explained her method for finding the coordinating unit: “I decided the ruler size by shrinking it until the boxes were the same size for both shapes, and there was nothing ‘hanging off’ the edge.” This partitioning process was applied to each rod in turn rather than to both simultaneously. However, it is important to note that PST G recognized the need to measure both rods with one partial unit. Although she was not sure she could find different answers, this multiplicative reasoning could bridge her thinking to a more sophisticated level of reasoning.

For Task 2, PST H (Korean) responded that “10/3” of orange rods were needed because he thought “O is 3 pieces and B is 10 pieces” (Fig. 10). He first recognized that the “leftover” could not be accounted for with the undivided orange units. Therefore, he measured the size of the “leftover” as 1/3 of the orange rod and so decided to employ 1/3 of the orange rod as an alternative unit, which he used to find the answer by counting the difference between the number of sub-units in the brown rod and in the orange rod (Unitizing operation). PST H noted, “If I put three rods of the same size as O in B, there would be a leftover part. I reduced it to one-third of the size of O. Therefore, the size of the Dynamic Ruler is one-third of the size of O.” Similar to PST G, PST H also did not recognize different answers while he had a step-by-step process to find a new adjusted unit to measure both rods. Although the PSTs at this level might have had the potential to find different answers, they focused only on a single fractional value. This potential indicates that PSTs could identify multiple answers by grasping a hierarchy between units (Coordinating units operation), which is illustrated in the next section.

Fig. 10
figure 10

PST H’s solution for Task 2. [Translation] How many orange rods are needed to fit into the brown rod?

Full size image

Measuring with length unit using commeasuring

Commeasuring strategies entail measuring the length of A in relation to the unit-length B, where the length of A is m times as extensive as unit-length B. In this case, m is not necessarily confined to whole numbers. This multiplicative reasoning can be extended to recognize the fraction m/n as m times a unit fraction 1/n. PSTs operating at the commeasuring level pursued a deliberate objective, which involved the systematic partitioning of both the unit length (i.e., the orange rod) and the length of the default rod (i.e., the brown rod) into smaller pieces. Therefore, the PSTs at this level recognized that there are multiple units applicable to measuring both quantities.

Using a solution strategy at the level of Measuring with length unit multiplicatively (Fig. 11), PST I (U.S.) sought to identify a unit with which to partition both rods at the same time and elaborated on her process as follows:

I split both bars into equal parts and see how many equal parts of the orange rod fit exactly into the brown rod. Once I find out that the orange rod must be broken into 5 parts, I can count the amount of full and partial parts of the orange rod that fit into the brown rod. Since the brown rod could fit 13 equal parts, we can simplify that to a mixed number since we know 5 parts is equal to a whole. We then get 2 3/5’s of orange rods fit into the brown rod.

Fig. 11
figure 11

PST I’s solution for Task 3

Full size image

As PSTs at this level had a strong understanding of fraction-as-measure, it was natural for them to count the number of unit fractions. PST I identified the unit fraction as 1/5 (“the orange rod must be broken into 5 parts”) and identified the iteration of the unit fraction (“13 equal parts”). This Unitizing is a fundamental operation for the commeasuring level. In addition, PST I showed her understanding of decomposing units into smaller units to find Coordinating units, which show general relationships in length measurement: “If we split the bars into smaller numbers, we may originally get a higher response but once simplified, we will ultimately get the same response.” This relational thinking was the most sophisticated level of fractional reasoning exhibited among the participants in this Dynamic Ruler environment.

PST J (Korean) found the same answer, 13/5, to Task 3. She partitioned the orange rod into smaller units with the blue Dynamic Ruler and then partitioned the brown rod using the same unit size (Fig. 12), which she explained by saying “I made a blue rod that can divide the orange rod into five equal parts. Thirteen blue rods are the same length as the brown rod. Therefore, the two orange rods and 3 blue rods make 13/5.” PST J also understood there were various solutions with equivalent fraction values: “I can divide the orange rod into 25 blue rods. This gives us the fact that the brown rod is two orange rods and 15 blue rods long. Therefore, another answer is 65/25.”

Fig. 12
figure 12

PST J’s solution for Task 3. [Translation] How many orange rods are needed to fit into the brown rod?

Full size image

PSTs’ reasoning patterns across fraction-as-measure tasks

We summarized the fraction-as-measure reasoning levels we found in our sample of PSTs by including the evidence for each level of reasoning. Table 5 shows the distribution of reasoning levels in the U.S. cohort. Across all tasks, a small number of U.S. PSTs exhibited understanding of fraction-as-measure at the level of Limited acknowledgment of length unit. There was little disparity among the U.S. PSTs in their responses to Tasks 1 and 2 (whole number + unit fraction) as they frequently identified fractional quantities by visually estimating the leftover part (Measuring with estimation level) or checking the two rods additively (Measuring with length unit additively level). In their responses to Task 3 (whole number + proper fraction), slightly more U.S. PSTs measured the rods by estimation (Measuring with estimation level). In the responses to Task 4 (only proper fractions), the level of "Measuring with length unit multiplicatively" was the most frequently observed reasoning approach, and almost half of the U.S. PSTs measured the length of the given rods using a single or multiple smaller units (Measuring with length unit multiplicatively and Measuring with length unit with commeasuring levels).

Table 5 Distribution of U.S PSTs’ fraction-as-measure reasoning Levels (N = 42)
Full size table

As shown in Table 6, among the Korean PSTs’ responses across all tasks, only one wrong answer (Limited acknowledgment of length unit level) was given, and a large majority demonstrated knowledge of how to unitize or dissembled the given unit into smaller pieces. In Tasks 1 and 2, Korean PSTs most frequently determined the relationship between the leftover part and the unit rod additively (Measuring with length unit additively level). In addition, they sustained relatively high percentages of other reasoning levels in the other tasks. In Task 3, the highest percentage of Korean PSTs recognized the multiplicative relationships between rods with a single unit (Measuring with length unit multiplicatively level). In Task 4, the previous pattern changed drastically, as about 75% of the Korean PSTs measured quantity with smaller units (Measuring with length unit multiplicatively and Measuring with length unit with commeasuring levels).

Table 6 Distribution of Korean PSTs’ fraction-as-measure reasoning levels (N = 100)
Full size table

Discussion and implications

In this study, we investigated the levels of fractional reasoning among PSTs in two markedly different national settings. We first devised a comprehensive coding scheme, which we subsequently employed to evaluate the fractional reasoning exhibited by PSTs from both countries within a dynamic digital environment, Dynamic Ruler. We identified and labeled five discernible levels of PSTs’ fractional reasoning and illustrated each level. In addressing the primary research question, we determined the validity of two paramount propositions: (1) the role of unit coordination in the development of advanced fractional reasoning is pivotal and (2) the ability to adjust fractional operations to align with the nature of a dynamic digital tool is necessary.

Concerning the first proposition, in a prior investigation, Lovin et al. (2018) attributed a deficiency they identified in the fractional reasoning of PSTs to a lack of unit coordination, which they underscored as a requisite concept for the development of advanced fractional reasoning. Likewise, in our study, the concept of unit coordination played a pivotal role in distinguishing the varied levels of fractional reasoning exhibited by the PSTs in a dynamic digital environment. This observation not only validates findings from previous research but also extends the applicability of such findings to scenarios involving the use of a dynamic digital tool, as distinguished from the use of static tools or a traditional paper-and-pencil environment. For example, PSTs operating at the two most sophisticated levels used dragging to find the point at which they could see the Dynamic Ruler partition both rods, either simultaneously or in turn. That is, dragging worked as a dynamic mediator (Ng & Sinclair, 2015) that served to represent conceptualization of fractions as a measure by identifying appropriate fractional units to measure a given length.

Regarding the second proposition, we shed light on a growing need for newly defined fractional operations within a dynamic digital context. For example, the dynamic affordance of our digital tool, allowing users to drag a bar to produce a ruler that includes the repetition of a unit and to adjust the size of a unit, thereby affecting all remaining units in the ruler, led us to observe that this dragging action results in the simultaneous creation of units through partitioning and iteration. This process bears a resemblance to the conventional use of a ruler in a standard measurement scenario. When measuring the length of an object, one first decides the size of units, then chooses a ruler divided by the unit size. Drawing parallels with Confrey’s (1994) proposed integration of disembedding and iterating for the unification of splitting operations, our research suggests that adjusting the size of a Dynamic Ruler by dragging evokes the potential for the convergence of partitioning and iterating, defined as a unitizing operation, particularly within a dynamic digital setting. While partitioning involves breaking a whole into pieces, iterating involves duplicating a piece a number of times. However, due to the Dynamic Ruler’s dragging feature, PSTs could perceive those two distinctive operations as one continuous operation.

In addition, as a practical implication for developing PSTs’ fractional reasoning, we found that the features of the fraction-as-measure tasks interacted dynamically with the PSTs’ engagement. For example, the PSTs’ fractional reasoning revealed that they exhibited more challenges in Tasks 1–3 than in Task 4 and implemented lower levels of reasoning. This observation underscores the susceptibility of PSTs’ fractional reasoning levels to the inherent features of tasks. Notably, the PSTs demonstrated robust fractional reasoning in Task 4, in which they were asked to identify the fractional amount when the given unit exceeded the default size. This particular task aligns with the common practice of introducing the definition of fractions in area models and length models through determining the partial area or length within the provided whole. The incorporation of such tasks has historically been prominent in traditional mathematical curricula, in which fractions are defined as parts of a whole using area models, as highlighted by Lovin et al. (2018) and Watanabe (2006).

However, in Tasks 1–3, which prompted the PSTs to determine the length of a bar when the given unit is smaller than the default, a shift towards conceptualizing fractions-as-measures becomes imperative because the need to comprehend mixed or improper fractions may not be readily apparent within the conventional frame of fractions as parts of a whole. In light of previous studies that report the historical dominance of the part-whole fraction concept in mathematical curricula, this outcome aligns with expectations. Consequently, it is crucial for mathematics educators to present PSTs with diverse tasks involving unit fractions, proper fractions, improper fractions, and mixed numbers. This approach especially gains significance in light of earlier findings that underscored the importance of the iterative fraction scheme in generating improper fractions (Lovin et al., 2018; Stevens et al., 2020). Additionally, fostering fractional reasoning for identifying larger fractional amounts using a smaller unit proves instrumental in developing reversible reasoning, which is essential for formulating two linear equations such as y = 2/3 x and x = 3/2 y (Hackengerg & Lee, 2015; Lee, 2017a; Lee & Hackenberg, 2014). Hence, tasks similar to those in Tasks 1–3, in which PSTs are asked to identify the fractional amount when the default size surpasses that of the given unit, should be incorporated more frequently into mathematics pedagogy courses.

The PSTs’ engagement in this study manifested their application of reasoning related to fractions-as-measure through the utilization of a dynamic digital technology. Therefore, the results provide valuable insights for improving PSTs’ fractional reasoning in teacher education programs with a digital tool designed based on length models. The dynamic ruler, employed in this study as an evaluative instrument, served as a means to discern PSTs’ fractional reasoning. Notably, recognizing the dynamic ruler’s distinct utility in facilitating the identification of a commeasurable unit when there are two or more fractional bars implies its potential as an intervention tool in mathematics pedagogy courses to enhance PSTs’ advanced fractional reasoning. Furthermore, the ways in which this dynamic tool was implemented yielded invaluable insights into the diverse spectrum of PSTs’ reasoning regarding fractions-as-measure. In light of these implications, the coding scheme developed in this study may serve a dual function, operating not only as a rubric for evaluating PSTs’ fractional reasoning both before and after intervention with the dynamic ruler but also as a guideline for designing learning experiences with broader application to foster the development of PSTs’ fractional reasoning throughout their trajectory of learning fractions-as-measure. Moreover, the successful application of our coding scheme to analyze PSTs’ fractional reasoning in various contexts, spanning Korea (an Eastern country) and the USA (a Western country), implies its potential applicability to a wide international population of elementary PSTs.

We recognize that this study is limited by its sole reliance on a written assessment. Direct engagement with the participants, such as through clinical interviews, may have facilitated a more thorough exploration of their cognitive processes. Consequently, employing additional data sources like interviews and observations could validate and enhance our interpretations. Specifically, we propose conducting follow-up interviews to bolster the credibility of the analysis and the inferences drawn. However, despite these constraints, this study holds significance as it adds value to the development of teacher education initiatives aimed at enhancing prospective teachers’ fractional reasoning. This contribution includes (1) a proposed framework for assessing PSTs’ reasoning regarding fractions-as-measure, and (2) a potential intervention to enhance PSTs’ fractional reasoning.

Furthermore, due to limitations in their ability to use the digital tools, some PSTs might have found it challenging to accurately adjust the Dynamic Rulers while trying to reason properly. This difficulty was particularly noticeable in attempts to align the edges of the bars or determine if a partition accurately matched both the unit and the specified amount. We acknowledge crucial role of the medium in teaching and learning. Thus, PSTs might reason differently in paper and pencil and in digital situations. Therefore, future research might be extended to examine the effects on students’ learning processes of different approaches to fraction-as-measure in teacher education.