Introduction

There has been a general consensus among mathematics educators and their professional organizations that mathematical modeling and/or representations are invaluable to students’ learning by making key mathematical concepts more explicit in a discipline that deals with abstract concepts (Duval, 2006; Greeno & Hall, 1997; McKendree, Small, & Stenning, 2002; Woleck, 2001; Zhang, 1997). Therefore, deep understanding of mathematical connections, representations, and explanations (Ball, Thames, & Phelps, 2008), which is required for the effective use of models and/or representations, is considered to be important specialized knowledge for teaching mathematics. For example, Principles to Actions (National Council of Teachers of Mathematics [NCTM], 2014) includes the teaching practice of using and connecting mathematical representations as a part of a framework designed to strengthen the teaching and learning of mathematics (Hill, Ball, & Schilling, 2008; NCTM, 2014).

Given the importance of conceptual understanding in their use, mathematical models and/or representations do not by themselves guarantee successful learning outcomes. Instead of relying on “magical hope” (Ball, 1992), thoughtful planning and execution based on the affordances and constraints of such models or representations are needed to support student learning (Kamii, Lewis, & Kirkland, 2001).

According to Vig, Murray, and Star (2014), because all models have constraints as well as affordances in supporting learners’ reasoning, as problems get more complex, a breaking point is reached at which models are no longer useful. The breaking point of a model is reached when the procedures needed to use the model become so complex that the focus on conceptually key ideas gets lost. The following anecdotal notes from preservice teachers’ (PSTs’) work with elementary and middle school students illustrate such model breaking points:

Example 1: A PST asked a student to show 1/7 + 2/7 using commercial fraction circle manipulatives. The student explored the fraction circle pieces and responded, “I cannot do it because there are no 1/7th pieces.” The PST then changed the question to 1/5 + 2/5.

Example 2: A PST asked students to multiply a binomial by a binominal, (8x + 11)·(7x−6), using algebra tiles. The students tried to model the algebraic expressions using the tiles, but many students got lost because the coefficient was too large for them to model the multiplication using algebra tiles (see Fig. 1).

Fig. 1
figure 1

An example of students’ work on (8x + 11)·(7x−6) using algebra tiles

Full size image

In their teacher education programs, PSTs are continuously advised of the importance of having students use models and representations to explore concepts and demonstrate their understanding. However, Vig et al. (2014) emphasize that PSTs first need to engage in “the act of identifying model breaking points [that] illustrate the affordances and constraints of the model” (p. 73), as the examples above demonstrate. In light of this need, this study examined a group of elementary PSTs’ explorations and their explanations of their reasoning about affordances and constraints of the area model of fraction addition through a series of tasks. Specifically, this study examined the following questions:

  1. 1.

    What mathematical ideas do PSTs consider critical in modeling fraction addition?

  2. 2.

    What model breaking points do PSTs acknowledge in the use of the area model to add two fractions?

  3. 3.

    What alternative models do PSTs suggest when faced with breaking points?

Literature Review

Pedagogical Content Knowledge and Specialized Knowledge for Teaching

Because what and how one teaches are closely intertwined, highly sophisticated knowledge of both is needed to effectively pair content with the delivery of that content (Hurrell, 2013). To describe this knowledge base, Shulman (1986) proposed three types of knowledge: content knowledge, curricular knowledge, and pedagogical content knowledge (PCK). Previous studies exploring these constructs reported that novice teachers had limited PCK (Lee, Brown, Luft, & Roehrig, 2007), and that teaching experience was necessary but not sufficient for developing strong PCK (Kleickmann et al., 2013), which also required expert guidance and directed practice. Also, prior research found that PCK was more powerful than content knowledge per se in predicting teachers’ instructional quality (Baumert et al., 2010; Hill et al., 2008; Hill, Rowan, & Ball, 2005).

Building on this general conceptualization of teacher knowledge, mathematics education researchers (e.g. Ball et al., 2008; Hill et al., 2008) conceptualized mathematical knowledge for teaching (MKT), which includes four important components: common content knowledge (CCK), specialized content knowledge (SCK), knowledge of content and students (KCS), and knowledge of content and teaching (KCT). For example, in the context of teaching fraction addition with unlike denominators such as 2/3 + 6/5, which is addressed in this study, CCK provides the procedure for adding two such fractions to get the correct answer. SCK may involve any or all of four actions: (1) identifying the sub-concepts needed to understand why finding a common denominator is useful when adding two fractions with unlike denominators, (2) choosing and using effective representations that reveal these key sub-concepts, (3) evaluating whether students’ informal methods are working for adding two given fractions, and (4) justifying why algorithms for adding two fractions with unlike denominators work. KCS is required to anticipate students’ common misconceptions or difficulties, and KCT is related to making pedagogical decisions to help students remediate their misconceptions or difficulties.

In this study, we focus on PSTs’ SCK, which is not directly dependent on the knowledge of students and teaching, but rather refers to the specific content knowledge needed for teaching particular concepts or processes. We decided to focus on PSTs’ SCK as appropriate for their pre-professional status because the majority have had limited access to schools and students and little if any teaching experience, and therefore they have not yet had sufficient opportunities to develop classroom-based knowledge such as KCS and KCT (Morris, Hiebert, & Spitzer, 2009). Thus, this study aimed to investigate how PSTs unpack their mathematical knowledge for teaching fraction addition, which includes making abstract ideas visible for students and selecting effective representations of adding two fractions, and then to identify the sources of PSTs’ difficulties or misconceptions in their uses of models or representations.

Representations and Models

Over the years, various meanings have been tagged to the term representation. It has commonly been used to refer both to a process of the act of constructing mathematical relations as well as to the product of a representational mode used to convey a mathematics idea (Cai, 2006). Also, representations may refer to learners’ mental models of reality (internal representation) as well as to concrete objects or records that show their views of a particular reality (external representation) (Cai, 2006). While in all of its meanings, representation is an important construct in teaching and learning mathematics, choosing and using pedagogically sound external representations is considered as one of the key aspects of SCK. However, prior research has documented that teachers often have limited knowledge of how to use representations, which can negatively affect mathematics teaching and learning (Izsák, 2008; Lee, Brown, & Orrill, 2011; Zazkis & Gadowsky, 2001). For this reason, mathematics educators have acknowledged that PSTs need training in order to be adept at using not only solution representations in their own problem solving but also pedagogical representations in preparation for their future teaching. According to Cai (2005), solution representations are defined as “the visible record generated by a solver to communicate thinking of the solution processes” (p. 137) and pedagogical representations are defined as “representations that teachers and students use as expressions of mathematical knowledge that help explain concepts, relationships, connections or problem-solving processes” (p. 139). In order to choose and use productive pedagogical representations, a teacher should consider the features of the mathematical content to be taught and the familiarity and accessibility of the content to students as well as the students’ capacity to reason with and about the idea (Cai, 2006). That is, what teachers need extends beyond the ability to present their own solution representations as problem solvers. They also need the ability to devise and present pedagogical representations that are meaningful to students. Mastery of this ability often depends on teachers’ beliefs, conceptions, and content knowledge, as well as their knowledge of research and theory about student learning (Cai, 2005; Hill et al., 2008). In sum, choosing and using effective pedagogical representations requires a well-coordinated effort on the teacher’s part, drawing on various kinds of knowledge and appropriate dispositions toward students’ learning.

In the domain of fractions, which is the target topic of this study, PSTs’ solution representations often serve as windows to identify their understandings or misconceptions (Woleck, 2001). Also, selecting effective representations and asking PSTs to make connections between two different representations of the same concept can deepen PSTs’ understanding of fractions and broaden their knowledge of fraction concepts (van de Walle, Karp, & Bam-Williams, 2013). Prior studies have found that mathematical models serve to make fraction concepts transparent to learners and support their reasoning about mathematical concepts and symbols (Hackenberg & Lee, 2015; Lee, 2017; Lee & Hackenberg, 2014; van den Heuvel-Panhuizen, 2003; Vig et al., 2014). Following van den Heuvel-Panhuizen’s (2003) conceptualization, in this study, we defined mathematical models as “materials, visual sketches, paradigmatic situations, schemes, diagrams, and even symbols” (p. 13) that support learners’ managing or interpreting mathematical ideas. Also, we do not distinguish between models and representations but interchangeably use the two terms as ways to illustrate mathematical concepts and procedures (Vig et al., 2014). In the next section, we elaborate on the breaking point of the area model for fraction concepts and fraction addition as theoretically examined by Vig et al. (2014).

Area Model for Fraction Addition

Area models (e.g. circular pie pieces, rectangular regions, geoboard manipulations, drawings on grids or dot paper, pattern blocks) are popularly used to subdivide a whole area into equal parts to support students’ fractional reasoning (Empson, 1999; Kong, 2005; van de Walle et al., 2013). Because they can easily represent the part-whole concept of fractions and the meaning of the relative size of a part to the whole (van de Walle et al., 2013), area models can effectively support fraction concepts taught in the early grades.

Vig et al. (2014) states that to accurately construct and interpret an area model, students “must know that the denominator of the depicted fraction represents the total number of equal size parts that make up the whole, while the numerator represents the [salient] number of shaded parts within that whole” (p. 80). However, to effectively use the area model for fraction concepts, students also need to know the scope of applicability of the model. For example, the circular area model can be easily used to represent certain fractions such as 1/2, 1/4, and 1/8, but it is less useful for representing fractions with odd denominators such as 9 and 11 (as shown in the illustrations of PSTs’ attempts to use models in the introduction section) or very large denominators such as 20 and 30. Thus, for example, Vig et al. (2014) point out that “the utility of circles for illustrating fractions diminishes and even ends at some points; this is the breaking point of the [circular] model” (p. 74).

Area models can be used not only to illustrate fraction meaning but also to assist with fraction operations (Cramer & Henry, 2002; Cramer, Wyberg, & Leavitt, 2008; Kong, 2005; Lee, 2017; Vig et al., 2014). Two key conceptual considerations are important to support understanding of the process of adding two types of fractions (see below) using area models: (1) the preservation of the unit whole, which means the whole of both fractions should be the same size and (2) the preservation of the size of part, which indicates the parts of each of the two fractions should be the same size. As the sizes of the parts differ and the parts are not in a multiplicative relationship with each other, the fraction addition problem becomes more complex, because when two fractions have different sized parts, learners must adjust the models so that both fractions must have the same sized parts. At this point, when dealing with large denominators or denominators that cause difficulty in showing equal partitioning, area models may not be useful.

In order to explain the process in relation with the model breaking point, Vig et al. (2014) distinguished fraction addition problems into two types: those in which both addends are between 0 and 1 (proper fractions), and those in which one or both addends are larger than 1 (improper fractions). First, to successfully add two proper fractions, learners need to (1) create equal-sized wholes, (2) transform both fractions to have the same-sized pieces, and finally (3) add by moving the shaded pieces of one area model to the non-shaded pieces of the other area model. However, to add two fractions that include improper fractions, the use of area models is cumbersome in these ways: (1) because of the improper fractions, the preservation of the whole and the equal-sized parts must be represented with three or four area models instead of two; (2) the shaded pieces must be moved between the two area models depicting proper fractions (less than one) while the complete area model remains intact; and (3) the shaded area models must be correctly interpreted. According to Vig et al. (2014), in the process of solving the latter problem, the area model for fraction addition breaks for two reasons. First, leaners have to do more and more computational work without the model in order to determine the least common denominators of two fractions. Second, learners are highly likely to pay less attention to the important concepts behind the visual depiction such as equal-sized whole and pieces as the complexity of the problem requires more tedious procedural steps. That is, models begin to break “when computation within the model requires an increasing amount of work that is done outside of the model” and “when using the model becomes cumbersome, requiring students to employ extra rules” (p. 86).

A model will almost inevitably break at a certain point because no model is sufficiently robust to be applicable to complex problems such as those including very large numbers. Thus, a teachers’ ability to anticipate breaking points and adjust models while preserving their functions in order to provide alternative models is critical. Accordingly, we asked PSTs to identify breaking points of the area model after solving six types of fraction addition problems using area models and then to suggest alternative models.

Situating the Study

The preceding literature review suggests that there has been a strong emphasis on teachers’ pedagogical content knowledge in developing their ability to select, use, and connect various mathematical models. Also, there are many models available for fractions. However, the models presented in many educational materials are typically limited to simple and clear cases. It may be reasonably assumed, therefore, that while this situation reinforces PSTs’ awareness of the importance of models, it may not adequately prepare them to consider the models’ utility in different cases and how to make sound pedagogical decisions at the point where the models begin to lose their usefulness. To explore this aspect of PSTs’ SCK, the aim of this study was to elicit PSTs’ perspectives on breaking points of area models and their understanding of the scope and characteristics of available fractions models with varied cases.

Methods

Participants

The participants in the study were 83 undergraduate PSTs at two universities in the Midwestern and Southwestern regions of the USA. All participants were pursuing their initial elementary teaching certifications and required to take two or three mathematics content courses and one methods class. At the time of data collection, the PSTs were completing a cursory review of fraction-related Common Core State Standards (National Governors Association Center for Best Practices and Council of Chief State School Officers, 2010) across grades 3–5 and exploring the area, length, and set fraction models.

Tasks and Data Collection

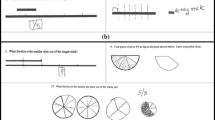
Participants were asked to complete a two-part written survey outside of class time (Fig. 2). Part 1 was a check of PSTs’ basic content knowledge needed for modeling fraction addition and their familiarity with the area model. Part 2 assessed their pedagogical reasoning about model breaking points and their suggestions for alternative models by asking participants to evaluate the effectiveness of the area model for each of a set of six fraction addition problems.

Fig. 2
figure 2

Tasks provided in this study

Full size image

The six fraction addition problems in the above tasks were selected to illustrate various cases of complexity involved in fraction addition (see Table 1).

Table 1 Features of sample problems provided in this study
Full size table

Data Analysis

The data were analyzed both quantitatively and qualitatively. The quantitative analysis provided descriptive information on the overall knowledge and perceptions of participants, including the frequencies of the use of the critical elements of fraction addition models mentioned in part 1, the frequencies of identification of incorrect fraction models in part 1, and the rankings of model effectiveness in part 2.

The qualitative analysis followed an inductive content analysis approach by developing data-driven codes (DeCuir-Gunby, Marshall, & McCulloch, 2011; Grbich, 2007) to analyze participants’ responses to the open-ended questions in narrative form (e.g. justifications for their rankings of model effectiveness for the given fraction addition problems, justifications for their proposed alternative fraction addition models, and justifications for their perceived model breaking points). This process included the following: (a) an initial reading of each PST’s responses by the two researchers, (b) finding common themes and identifying categories and subcategories, (c) coding the data according to the identified categories, and (d) checking inter-rater reliability. For the analysis, a meaning unit, which Graneheim and Lundman (2004) describes as comprised of “words, sentences, or paragraphs containing aspects related to each other through their content and context” (p. 106), was used. The PSTs’ meaning units were coded according to the categories they referenced. After identifying the themes for coding, the two researchers independently coded a random sample of data from 10 PSTs (about 12% of the entire data set). The concordance between the two coders was 89%. For the remaining data, the two coders jointly coded and discrepancies between coders were discussed until an agreement was reached. The inductively developed coding schemes are reported in Tables 2 and 3 as well as in Fig. 3 in the following section. The patterns in the PSTs’ responses are summarized as the frequency of codes.

Table 2 Critical ideas considered by PSTs
Full size table
Table 3 PSTs’ identifications of model breaking points
Full size table
Fig. 3
figure 3

PSTs’ performance of modeling on the given questions

Full size image

Findings and Discussion

This section summarizes PSTs’ identification of critical mathematical ideas in the fraction addition area model, their perceived model breaking points in using the area model, and their suggestions for alternative models when they noticed the model breaking points. In the following sub-sections, frequencies are reported to show the overall tendencies.

PSTs’ Consideration of Critical Ideas in Modeling Fraction Addition

When asked to present key ideas to be considered in using an area model for fraction addition, PSTs shared various ideas as shown in Table 2.

This finding shows that the PSTs considered various aspects of modeling fraction addition, including conceptual, procedural, and representational aspects. The most frequently mentioned was the representational aspect. However, the majority of responses were given in general terms highlighting the clarity and accuracy of the representation, instead of being specific about what it meant to be clear or accurate. Also, much attention was given to the depiction of each fraction addend (e.g. clear depiction of the denominator and the numerator). When asked to evaluate the effectiveness of the given area model for ¼ + ½ (see part 1 in Fig. 2 earlier), most PSTs perceived that the given model was effective. However, it is worth noting that attention was given largely to the representational aspect (e.g. use of colors) and procedural aspects (e.g. showing the common denominator) in their explanations.

The PSTs gave more attention to procedural than to conceptual aspects. In particular, they frequently mentioned the procedure of finding common denominators, demonstrating that they thought this was a necessary step in order to add fractions. van de Walle and Lovin (2006) refer to the myth of common denominators, which is the common belief that in order to add or subtract fractions, one must first obtain their common denominators. They assert that the statement should be replaced with “in order to use the standard algorithm to add or subtract fractions, you must first get common denominators...the algorithm is designed to work only with common denominators” (p. 90). PSTs’ attention to finding the common denominators may allude to their buying into the myth.

The “same whole” concept (i.e. the size of the area model whole must be the same for the two given fractions) should be considered essential to producing an appropriate model for fraction addition. However, as further evidence of their lack of conceptual thinking, this principle was not explicitly addressed by the PSTs, suggesting their unawareness of the same whole requirement in modeling fraction addition.

PSTs’ Performance in Modeling and Consideration of Model Breaking Points

In order to examine PSTs’ considerations of model breaking points, we first asked them to model and solve each of six problems using the area model (see Table 1 earlier) and then to present their considerations of model breaking points.

PSTs’ Performance in Modeling

We coded PSTs’ performance by examining both drawn models and written equations. PSTs’ responses were coded as “correct” (C) when they presented both the correct equation and the correct model, “incorrect” (I) when they produced neither, and “partially correct” (PC) when they presented either the correct equation or the correct model. Figure 3 shows the results.

As questions became more complicated (e.g. featuring use of an improper [sum larger than 1] fraction addend, or denominators with co-primes), the PSTs produced more incorrect or partially correct responses. In PC cases, they mostly provided correct equations but incorrect models. Common reasons for a PC coding included (a) using different sizes for the whole unit 1 when adding fractions (e.g. using two different sizes of rectangles, that is, two different whole units although the two fraction addends were correctly drawn), (b) not showing equal partitioning, or (c) not using the area model (e.g. using the set model).

We also examined the models used by PSTs regardless of the correctness of the models. Overall, the majority of PSTs favored exclusively using one shape for the whole (e.g. 38 PSTs exclusively used a rectangular model and 20 PSTs exclusively used a circular model) (see Fig. 4-1). Nineteen PSTs used a combination of circular and rectangular models, tending to use the circular model for the simple cases such as problems (a) and (b) in part 2 of the questionnaire (see Fig. 2) and the rectangular model for more complicated cases (see Fig. 4-2). Some PSTs exhibited difficulty in using models to solve problems (e) and (f). They tended to show the procedural process for finding the common denominator or just represent the fraction numeral and show the final result involving common denominators without illustrating the process of finding common denominators (see Fig. 4-3). Some PSTs used different models which did not have the same sized wholes. These PSTs used the rectangular area model seemingly without paying attention to the size of whole for each fraction (see Figure 4-4).

Fig. 4
figure 4

Examples of PSTs’ models

Full size image

PSTs’ Consideration of Model Breaking Points.

PSTs ranked the effectiveness of the area model for problems using a scale of 1–6, with 6 representing the case for which the area model was most effective and 1 representing the case for which it was least effective. We added the ranking values associated with each problem to represent the PSTs’ overall assessments. Problem (a) 1/4 + 2/4 was recognized as the case for which the model was most effective (sum of ranking scores 429) whereas problem (f) 2/3 + 6/5 was assessed as the case for which it was most ineffective (ranking score 153). Problems (b) 3/4 + 2/4 and (c) 1/4 + 3/8 were assessed at similar effectiveness levels (ranking scores 343 and 339 respectively) as were problems (d) 3/4 + 9/8 and (e) 1/3 + 1/5 (rank scores 242 and 237 respectively). These results suggest that PSTs perceived the area model as increasingly ineffective as the sum became bigger than one whole or when the two denominators were co-prime. To justify their rankings, PSTs addressed the points at which they perceived the area model lost its effectiveness (see Table 3).

Two major breaking points emerging in the data analysis were related to denominators and the presence of improper fractions or mixed numbers. More specifically, about 67% of PSTs pointed out factors related to denominators of fractions as the basis for their rankings of the effectiveness of models, which had the following order: for fractions with the same denominators, for denominators with a relationship of multiples, and for different denominators. About 41% of PSTs identified the presence of improper fractions or mixed numbers as a condition in which the area model was no longer effective.

Alternative Models Suggested by PSTs

When asked to suggest alternative models for the problems for which the area model was least effective, PSTs proposed a variety of models (see Table 4).

Table 4 Alternative models suggested by PSTs
Full size table

The set model was the most frequently presented alternative model. This is an interesting finding in that the set model is a less frequently used model in school curricula and instruction. Also, although PSTs were asked specifically to present models, the third most frequent response was to present algorithms without models. Notably, some PSTs suggested using commercial manipulatives without further explanation even though it would not be feasible to use them to show such denominators as 1/15 in problems (e) and (f), perhaps alluding to PSTs’ reliance on “magical hope” (Ball, 1992). To justify their alternative models, PSTs provided various explanations (see Table 5).

Table 5 Justifications for alternative models
Full size table

According to the area model breaking points identified, PSTs justified their alternative models by suggesting they could more clearly depict the fractions involved in the addition or could better handle bigger denominators and improper fractions. Also, some suggested that the messiness in using the area model could be overcome by using different models.

Implications for Teacher Education

In this empirical study, most PSTs represented easy fraction addition well but showed difficulties with representing fraction addition that included improper fractions or fractions with unlike and relatively large denominators. These difficulties were associated with the PSTs’ tendency to rely on algorithm-based thinking when they worked on the fraction addition problems featuring complex fractions, following the procedure of first finding common denominators by calculation, getting the answer from their computation, and then attempting to represent the result of the computation using area models. Also, several PSTs revealed many misconceptions in drawing area models, which may confirm findings in prior studies showing that content knowledge impacts the drawing of area models (Ball, 1992; Ball et al., 2008). Moreover, when PSTs were asked to find the point at which the area model was no longer effective for fraction addition, the PSTs identified breaking points as the advent of improper fractions (41%) or large-sized denominators (31%), which is similar to what Vig et al. (2014) suggested. From the findings of this study, we derived the following implications for teacher educators.

First, we recommend that teacher educators encourage PSTs to draw representations as a strategy for engaging in mathematical reasoning, that is, as part of the problem-solving process, rather than merely to show the results of their computations. Drawing representations while reasoning mathematically is related to Cai’s (2005) notion of pedagogical representations because the act of drawing facilitates visually unpacking the important ideas of fraction addition. However, using representations to show the result of a computation is related to Cai’s (2005) notion of solution representations in that it does not guide or reveal the thinking processes involved finding common denominators. In this study, although a majority of the PSTs had difficulty representing fraction additions that involved complex fractions, only half identified the breaking point of the area models. We attributed this result to PSTs’ prevalent use of algorithm-based thinking in representing fraction addition using area models. That is, because PSTs tended to first use their algorithms to add two fractions before drawing the area models, the inclusion of improper or large-sized denominators did not make it difficult to solve the problems, which may have obviated the need to think about model breaking points. Thus, PSTs need to be encouraged to use pedagogical representations more often in their mathematics content courses and be shown how to use them instructionally in their methods courses.

Second, we recommend that teacher educators design tasks that lead PSTs to realize model breaking points by using hands-on graphics to work through problems. In this study, PSTs who drew representations as a means to support their mathematical reasoning about adding two fractions tended to identify breaking points of area models when they faced difficulties in solving the last two problems on the worksheet. That is, the hands-on experience of solving problems using area model representations seemed to help PSTs think about the breaking points. This approach supports the first recommendation in that encouraging PSTs to construct their own representations in order to support and reveal their reasoning processes may be an effective way for them to learn about pedagogical representations and understand the rationale behind using them.

Third, we recommend that teacher educators provide PSTs more opportunities to explore the affordances and constraints of various models, representations, and manipulatives in teacher education programs. In this study, half of PSTs identified breaking points of area models, but as alternatives, many of them proposed set models, which are not effective for addressing the breaking points of the area model because there could be even more limitations in showing how a particular set can be partitioned. This finding may be explained by two reasons: (1) the PSTs preferred to use set models because they made it easy to represent the common denominators that PSTs found in their calculation or (2) the PSTs did not know the breaking point of set models owing to their lack of experience with set models in their teacher education programs. Set models appear to be used infrequently in textbooks and classroom instruction, but learning about them would benefit students by expanding their repertoires and enabling them to discern the capabilities of different models. For effective mathematics teaching, it is unfeasible to use only one type of model because all models have breaking points (Vig et al., 2014) and different models are appropriate for different problems. Thus, mathematics teachers have to know when and in which conditions particular models are effective to use. When considering the nature of teaching, which requires continuous instructional decision-making corresponding to students’ responses and the problem context, teacher educators need to engage PSTs in drawing models as pedagogical as well solution representations, exploring the breaking points of various models, and practicing thinking of possible alternative models by working on tasks similar to those provided in this study.