1 Introduction

Symmetry is a central idea in mathematics (Weyl 1952; Schattschneider 2006); it is an object of study in and of itself, but it is also used as a powerful way of solving problems. While often treated as a static concept, the notion of symmetry as a transformation requires a more dynamic approach in which a particular motion is used to transform one initial figure into another. As Jagoda and Swoboda (2011) argue, while everyday experiences are filled with static symmetric shapes (hearts, stars, etc.), they do not, in general, involve recording consecutive moments of an object’s movement. Thus, the teaching and learning of symmetry requires tools, tasks and communicative opportunities that enable children to focus both on the action of symmetry transformations and the result of such transformations.

While transformations do not appear explicitly in many curricula until later elementary or middle school (Grade 8 in the CCSS; Grade 4 in most Canadian provinces), symmetry can function powerfully as a tool to describe, recognise, classify and create both two- and three-dimensional figures. Indeed, the NCTM Standards for Pre-K through Grade 2 encourage students to “apply transformations and use symmetry to analyse mathematical situations”. In the Western and Northern Canadian Protocol, symmetry is formally introduced in Grade 4 (ages 9–10) where students are asked to identify and create symmetric figures as well as draw one or more lines of symmetry. However, in Grades K-3, students can use symmetry to sort, compare and construct figures. Interestingly, the psychological research suggests that young children attend to symmetry much earlier than formal schooling. Given that young children already have a strong capacity for identifying symmetry (Seo and Ginsburg 2004; Schuler 2001), it makes sense that this concept could be explored much earlier and more robustly through the first years of schooling (Bryant 2008).

Early experience with different forms of reflectional symmetry (not just vertical line symmetry) and dynamic conceptions of symmetry may enable students to develop more flexible spatial abilities so that when they engage in middle school geometry, they are not constrained by prototypical images of symmetry (Hoyles and Healy 1997). Further, dynamic geometry environments (DGEs) can provide transformation-based experiences of symmetry that are difficult to enact with physical manipulatives such as Miras and paper-folding. In the next section we provide an overview of student understanding of symmetry, which has mainly focused on the middle- and high-school grades, with particular attention to studies involving the use of digital technologies. We then outline the theoretical framing for our research and describe the teaching experiment we undertook, providing a detailed description of the functionality of the dynamic sketches we designed, and analyse the children’s emerging conceptions of symmetry.

2 Research on the learning of symmetry

Reviewing the limited literature available in the field, we acknowledge that children have a developmental ability to discriminate between symmetrical and asymmetrical figures. Schuler (2001) suggests that visual discrimination of symmetry has a developmental component and that there is a marked increase in the use of symmetry with each age. Bornstein and Stiles-Davis (1984) link the developmental progression of 4 to 6-year-olds with types of line symmetry. Namely, they found that 4-year-olds discriminated only vertical line symmetry, 5-year-olds, vertical and horizontal line symmetry, and 6-year-olds, vertical, horizontal and oblique symmetry. However, their study focuses exclusively on the visual identification of symmetry, rather than on the relationship between the various elements involved, such as the line of symmetry.

Clements and Sarama (2004) propose that children should work with symmetry in the Pre-K through Grade 2 years and offer a developmental trajectory for transformations and symmetry in which children begin at the Pre-K level to create shapes that have line symmetry, then work in kindergarten and grade one to identify symmetry in 2D objects. In Grade 2, children should identify the mirror lines of shapes with line symmetry. In their approach, children make “flips” with pattern blocks, visualise these flips and predict the outcome of flip motions. Drawing on Duval’s dimensional deconstruction, Perrin-Glorian, Mathé and Leclerc (2013) also support children’s learning of symmetry in the early grades, but insist on the importance of using tools (such as rulers) in order to draw learners’ attention to 1D objects that are involved in reflection (such as the line of symmetry, but also the segments that are reflected). They argue that such an approach plays a crucial role in enabling a continuity between the geometry of primary and secondary school. Their proposal is exemplified by a series of “restoration” tasks in which tool-based construction is used to explore reflectional symmetry beginning in kindergarten and progressing throughout the grades (from ages 6 to 15). The DGE-based trajectory we will describe here also centrally features the use of tools, but takes a different approach in that the reflections have already been performed and the goal is to investigate their behaviour. This will entail different developmental possibilities, which we elaborate below.

Computer-based environments have been shown to help the learning of transformations and symmetry, especially at the middle and high school level. Early research featured the use of Logo environments (Edwards and Zazkis 1993; Hoyles and Healy 1997). At a much earlier grade level, Clements et al. (2001) show that the effects of Logo microworlds on symmetry were particularly strong for kindergarten children. These learners wrote commands to create symmetric figures, tested their symmetries by reflecting their figures and discussed their actions. The researchers argued that the children had to be more explicit and precise in their creation of symmetric figures than they would have to be in a (paper-based) free-hand drawing environment. This possibility for more explicit, precise communication features also in the research carried out at higher grades.

Battista (2008) describes the way in which DGEs offer not only a variety of examples, but, more importantly, a continuous transformation of the draggable objects.Footnote 1 Indeed, there is strong evidence to show that dynamic configurations in DGEs support students’ transition from an exclusively spatio-graphical field to a more theoretical one by helping them attend to the visual invariance of the dynamic diagram, which can be verbally mediated through classroom discussion or teaching intervention (Battista 2008; Laborde et al. 2006; Sinclair and Moss 2012; Kaur 2015). In his study of Grade 5 children using the Shape Maker microworld designed in The Geometer’s Sketchpad (Jackiw 2001), Battista (2007) theorised the effectiveness of dragging in terms of a two-folding assumption. The first relates to the “unconscious visual transformations” by which humans structure space (p. 150). Battista’s second assumption, which he called the transformational-saliency hypothesis, relates more centrally to dragging. This hypothesis essentially states that people notice invariance. Dragging thus changes the way shapes are perceived, moving from a static visual apprehension to a temporal attention to what remains invariant.

Most of the research involving the use of DGEs has focused on the middle and high school grades. With respect to transformations, Hollebrands (2003) found that high school students developed a deeper understanding of them as functions through a seven-week instructional unit using Sketchpad that involved construction tasks as well as blackbox microworlds. However, she did not focus specifically on symmetry. Also at the high school level, Falcade et al. (2007) showed how Cabri-Géomètre (Baulac et al. 1988) could help students grasp the notion of function; they focused on the affordances of the trace tool as a semiotic mediator that could introduce the twofold meaning of trajectory, both global and pointwise. This study is highly relevant to our own in that symmetry involves both global and pointwise (in the form of blocks) meanings with the former described in terms of the property of a given figure and the latter described in terms of the mapping of one part of the figure to the other.

3 Theoretical perspectives

In this section we outline two theoretical perspectives we draw on, both of which have their roots in a Vygotskian tradition. They emphasise the role of tools (including language) in the learning process as well as the role of the teacher as an expert participant in the target discourse. The first is a “communication” perspective that operationalises the notion of thinking, in particular changes in thinking by attending to changes in discourse. The second is a “semiotic mediation” perspective that enables us to understand how tools within the DGE—such as dragging—mediate the children’s understanding of symmetry.

3.1 A communication approach: thinking is talking

Sfard’s (2008) communicational framework is helpful for analysing children’s developmental thinking about symmetry in the classroom. Her non-dualist approach disobjectifies thinking as part and parcel of the process of communicating. Sfard’s approach highlights the way in which talking stops being ‘expressions’ of thinking and becomes the process of thinking in itself. This communicational act can be intrapersonal when thinking within oneself or interpersonal when communicating to someone else. With this view, children’s mathematical thinking can be operationalised by observing their discourse. While mathematical thinking is often considered a cognitive and individual process, we take children’s talk and embodied actions in social settings to be the very unit of our analysis of children’s mathematical thinking. This is, of course, the theoretical assumption that we adopt to situate thinking in practice and in social context (e.g. Sfard 2008; Lave and Wenger 1991). The view that thinking and communicating are inseparable processes—that occur within a community of practice (Wenger 1998) such as the classroom—is a lens that we use to explore our data and not a claim that we seek to verify in this paper.

For Sfard (2008), learning occurs when there is a change in discourse. Her four features of mathematics discourse—word use, visual mediators, endorsed narratives and routines—can be used to analyse one’s mathematical thinking and learning by identifying change in their discourse over time. Sinclair and Moss (2012) showed how a group of kindergarten children shifted their discourse on triangles by changing the way they used the word ‘triangle’; at first, the word was used like a proper noun, in which ‘triangle’ described the three-sided shape in its canonical orientation, and then, after working in a DGE, the word was used as a family name to describe the different kinds of triangle that share the common feature of having three sides. In this paper, we are interested in whether or not there is a change of discourse about symmetry when children, along with their teacher, interact in a DGE.

Word use is a main feature in mathematical discourse; it is “an-all important matter because […] it is what the user is able to say about (and thus to see in) the world” (p. 133). Although Sfard’s four features of mathematics discourse are effective for analysing written, static discourse such as textbooks and written student work, they sometimes fail to account for the full set of resources that young children use to communicate. Spoken discourse is multimodal and communicational acts are not limited to the use of words and visual mediators as in the written discourse. In particular, gestures have been shown to be a central form of communication that complement speech (Kendon 2000) and are co-produced with abstract thinking (McNeill 1992)—and could be seen as functioning either as words or visual mediators in the discourse of the mathematics classroom. Research has shown that gestures can sometimes precede speech (Goldin-Meadow 2003) in mathematical development, or can be co-produced with speech, sometimes redundantly, but sometimes also contributing their own distinct meaning, thereby reducing the amount of speech needed (Goldin-Meadow et al. 2001). Gestures can be especially helpful in communicating visual and temporal mathematical meanings (e.g. Ng and Sinclair 2013; Núñez 2003; Sinclair and Gol Tabaghi 2010), which makes them all the more important in the computer-based classroom environment. Inasmuch as gestures become visible to the gesturer, as well as other members of the classroom, they can also be seen as acting as visual mediators that are created and acted upon to enable mathematical communication. However, unlike most of Sfard’s examples of visual mediators (geometric figures, symbols, number lines, etc.), these are importantly embodied and mobile.

We expand Sfard’s notion of visual mediation because of the temporal nature of DGEs, which enables children to observe and manipulate visual objects that are moving and changing over time. Analogous to the difference between written and spoken discourse that we noted earlier, there is an important distinction between visual mediations from static versus dynamic visual mediators. Mediations from static visual mediators evoke images of static mathematical objects such as triangles or artefacts such as a number line. In contrast, mediations from dynamic mediators may evoke mathematical relationships and properties for their potential to represent mathematical objects of an invariant property continuously. DGEs can produce “a seemingly limitless series of continuously-related examples, and in so doing, to represent visually the entire phase-space or configuration potential of an underlying mathematical construction” (Jackiw and Sinclair 2009, p. 414). For example, a child may realise new mathematical properties by dragging a vertex of a triangle or a point on the number line dynamically. This visual mediation is enabled by the dynamism of the DGE and triggered by the signs that are produced upon dragging in the DGE.

3.2 Semiotic mediation

As discussed in the previous section, dynamic visual mediators evoke mathematical relationships and properties more readily than static visual mediators. For this reason, we draw on the theory of semiotic mediation as a theoretical framework to discuss the complex semiotic process when a sign, such as a visual mediator, is realised. Vygotsky (1978) distinguishes the dialectical relationship between signs and tools as follows: practical tools are those used in the labour, whereas signs are symbolic tools used in the psychological operation. However, as he writes, “The sign acts as an instrument of psychological activity in a manner analogous to the role of a tool in labor” (p. 52).

Externally oriented tools may be transformed into internally oriented ones through the process of internalisation. Internalisation is directed by semiotic processes and rests on a system of signs involved in the social activity, that is, signs such as words, drawings and gestures (Wertsch and Stone 1985). As expounded in the theory of semiotic mediation (TSM) described in Bartolini Bussi and Mariotti (2008), the signs generated by the use of a tool, through the complex process of internalisation accomplished after social interchange, may shape new meanings. Therefore, semiotic mediation is a process of meaning-making through internalising the signs that are produced from an external, intrapersonal activity.

In the lens of semiotic mediation, the functionalities offered by the DGE produce many signs (Mariotti 2009). An external, goal-oriented activity such as “dragging” and “tracing” in a dynamic sketch can be internalised to shape personal meanings. The teacher’s role is to exploit such opportunities by facilitating a meaningful social exchange during the use of the corresponding tools. This perspective is shared by Falcade et al. (2007) in their teaching experiment with high school students on functions. They suggest that the internalisation of the Dragging and Trace tools may contribute to introducing function as covariance and the notions of domain and range. They argued that the role of the teacher is crucial in this process, as she promotes different semiotic activities related to the use of the Dragging and Trace tools, and later facilitates a class discussion in order to guide students to mediate mathematical meaning upon the activities.

Signs evolve throughout a goal-oriented, external activity, while maintaining some of their origins. Bartolini Bussi and Mariotti (2008) identify three main categories of signs. Artefact signs sprout from the use of the artefact and are least distant from the reference to the artefact; their meanings are strictly related to the experience of using the artefact. Mathematical signs have the highest mathematical context and are most distant from the reference to the artefact. Their meanings are mathematical as shared within the community. Pivot signs link the artefact signs to the mathematical signs. They are characterised by their shared meanings in instrumented actions and the mathematical domain (see also Bartolini Bussi and Baccaglini-Frank 2015 for a discussion of pivot signs in their teaching experiments). The diversity of meanings associated with pivot signs can make them problematic to distinguish from artefact signs or from mathematical signs. Bartolini Bussi and Mariotti (2008) add that pivot signs “express a first detachment from the artefact, but still maintaining the link to it in order not to lose the meaning” (p. 757). The polysemy of signs suggests that, in a classroom community, certain words, gestures and uses of visual mediators can mediate meanings at the artefact or mathematical level. Arzarello and Robutti (2008) have called this collection of signs and their mutual relationships a semiotic bundle. In an educational context, the goal of the teacher is to orchestrate a transformation from artefact signs to mathematical signs in a path that students can follow. This can be accomplished through the “semiotic game” (Arzarello 2006; Mariotti and Bartolini Bussi 1998), which happens in teacher–students interaction when the teacher tunes with the students’ semiotic resources and uses them to guide the evolution of mathematical meanings.

To summarise, we use Sfard’s communicational framework to study children’s discourse (thinking) while they engage in a sequence of lessons on symmetry. In addition, we focus on children’s word use, gestures, and use of diagrams during and upon interacting with dynamic visual mediators in the form of DGEs. Within this theoretical perspective, our aim is to study how the dynamic environment changes the way the children think of symmetry and to identify the particular tools that serve as instruments for semiotic mediation in their learning.

4 Methodology of research

In keeping with TSM, we propose a common methodological frame involving classroom-based research, which is the goal and the source of theoretical reflection. As Mariotti (2009) writes, the methodology is consistent with the aims of research design that seeks to develop empirically grounded theories. It involves long-term teaching experiments within the regular classroom that feature collaboration between researchers and teachers. The study we present here is part of a year-long teaching experiment that aimed to better understand the effect of long-term use of DGE-based activities. This involved collaboration between the researchers and both the Grades 1/2 and 2/3 classroom teachers in planning sequences of activities. Although the year-long research project aimed to study longer-term effects, the study of symmetry we report here can be seen as a short-term (three 1-h lessons) classroom intervention (Stylianides and Stylianides 2013) that aims to address particular problems in the teaching and learning of symmetry in a way that may facilitate adoption in other contexts and thus overcome some of the scaling-up obstacles identified in other classroom-based intervention studies.

Also in keeping with the methodology of TSM, we pay particular attention to the role of the teacher in exploiting the signs generated during interactions with Sketchpad. In these lessons, the second author played the role of teacher for most of the activities involving the use of Sketchpad. The regular classroom teachers were present at all times and led many of the follow-up discussions over the course of the year. They did not lead the Sketchpad-based activities because they had little experience in using technology in the classroom and wanted to use the research project as an opportunity to learn how to use dynamic geometry software in their teaching.

4.1 Participants, data collection and methods

The three lessons on symmetry each occurred 2 weeks apart, in a culturally diverse elementary school in Western Canada. The same lessons were taught to two different groups of children (a Grade 1/2 split class and a Grade 2/3 split class—each having about 22 students). Our research team consisted of three people: the second author, who had been taking on the role of a guest-teacher in the classrooms under study, and two research assistants who observed and videotaped the lessons as regular visitors of the school. The classroom teacher was present in each lesson and helped manage various aspects of the lesson. After the first lesson, the Grade 2/3 teacher led an activity in which the children were asked to find symmetric elements in the forest behind the school. The children were surprised that there were so many examples of vertical symmetry. The Grade 1/2 teacher led an activity in which the children were asked to create a symmetric design using coloured pencils—these were drawn in the children’s mathematics journals. Prior to each lesson, the guest-teacher and classroom teacher collaborated on the lesson plan to ensure that the demands of the classes were considered during the delivery of the lessons and that the physical settings and classroom routines reflected those in the children’s regular classrooms.

Each lesson lasted approximately 1 h and included both computer-based activities as well as pencil-and-paper activities, in keeping with the methodology of TSM in which it is crucial to provide opportunities for learners to make their own signs. During the computer-based activities, the children were seated on a carpet in front of a screen where Sketchpad was projected through a desktop computer at the teacher’s desk located in the front of the classroom. During the pencil-and-paper activities, they were seated at two large tables at the back of the classroom where they normally do their seated work. The children had not engaged in formal work on symmetry prior to starting the lessons, and this was their first experience of working with Sketchpad in their regular classrooms. However, they had been accustomed to the lesson structure of sitting on the carpet and having a classroom discussion as initiated by the teacher and then moving to seated work on paper. The research assistants’ video recorded the computer-based part of the lessons from the back of the classroom as well as the paper-and-pencil part of the lessons by walking up to interact with the children at their seats. Approximately 8 h of videotaping data were collected in total from two cameras in two classrooms. In this paper, we report only the results from the Grade 1/2 split classroom, with a particular focus on the first and second lesson.

All data were transcribed and analysed in terms of the teacher’s and children’s word use, gesture and interactions with visual mediators (in the form of DGE and paper-and-pencil diagrams) during the lessons. Our research goals were to investigate: (1) the children’s developing discourse about symmetry through word use, gestures, and use of visual mediators; and (2) the role of technology and teacher mediation in the children’s learning of symmetry in a semiotic lens. Using a semiotic lens led to several methodological choices in the study. First, according to Arzarello (2006), a synchronic analysis can be applied to examine the interrelationships between language, gestures and diagrams at a certain point in time (see also Chen and Herbst 2012). Therefore, all data were transcribed in such a way as to highlight the interplay between words spoken, gestures and use of visual mediators synchronically. For example, the transcripts were accompanied by descriptions of gesturing actions performed simultaneously with speech, and certain gesturing actions that seemed important were included in the analysis. Second, we performed a diachronic analysis to investigate how word use, gestures and use of visual mediators changed over time. We compared, in particular, both the teacher’s and children’s discourse over the course of the lessons, and we looked for evidence of how the children’s evolving discourse was mediated by the tools.

4.2 Design of the sketches

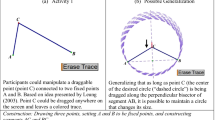
In the present study, pre-made sketches were constructed using Sketchpad. The first sketch, which we will refer to as the “discrete symmetry machine”,Footnote 2 consists of eighteen coloured squares arranged symmetrically around a vertical line of symmetry. These squares move discretely on a square grid background. Dragging any square on one side of the line of symmetry will also move the corresponding square on the other side of the line of symmetry (see Fig. 1a, b). The discrete motion, as well as the use of the grid, was intended to help the children attend to the distance between a square and the line of symmetry. Further, based on Battista’s transformation-saliency hypothesis, it was anticipated that the children would notice the invariance between the distance of the image and pre-image squares to the line of symmetry.

Fig. 1
figure 1

a The discrete symmetry machine; b after dragging one block away from the line; c after dragging the line towards the left; d after rotating the line of symmetry

Full size image

In this sketch, the dragging tool is exploited to visually mediate discrete movement of the pre-image and image, while the grid is used to produce signs relating to distance. In addition, it is possible to translate the line of symmetry by dragging it as a whole (see Fig. 1c) or to rotate it by dragging one of its two defining points to obtain a horizontal or oblique line of symmetry (see Fig. 1d). This draggable point to rotate the line of symmetry was hidden in the first page of the sketch, but made visible in later ones where children were asked to create designs that have horizontal or oblique reflectional symmetry. In this case, the dragging tool is exploited to visually mediate continuous movement of the line of symmetry as well as of the image squares (the pre-image squares remain fixed when the line of symmetry is dragged) (see Fig. 1c).

In this sketch, Sketchpad’s reflection command was used to reflect the blocks to the pre-image. Since dragging the pre-image affects the image, the dynamic and symmetric configurations produced suggest a functional dependency between the block being dragged (independent variable) and its reflected counterpart (dependent variable). This idea of symmetry as a function is extended from Bartolini Bussi and Mariotti (2008) in that “[when] using Dragging tool … the user may experience the combination of the interrelated motion, the free motion of basic points and the dependent motion of the constructed points; in other words, the use of dragging allows one to feel functional dependency as the dependence relation between direct and indirect motion” (p.769, italics in original). The aim of such design is to preserve the content of a sign in its subsequent evolution: from the artefact sign (a block being dragged) to the mathematical sign (independent variable with free motion). Therefore, by this design, we hoped to shift students towards a more dynamic (and functional) one that would highlight the invariances constituting the properties of symmetry. The third lesson introduced a continuous symmetry machine in which the children could drag a point, and observe what happened to the corresponding symmetric point, both of which left traces. Due to lack of space, we do not report on this component of the teaching intervention.

4.3 Teaching sequence

1. First lesson. After an initial survey of the children’s understanding of the word ‘symmetry’, the teacher introduces the “discrete symmetry machine”. Children are asked to observe and describe what they notice about how the symmetry machine works. They are invited to explain what will happen by coming up to the screen and showing their predictions. The teacher uses the children’s descriptions and predictions to emphasise the motion of the squares in relation to the line of symmetry (the square moves along, away from or toward the line) instead of words such as up, down, left and right which are associated with direction of movement. Using large cardboard diagrams of various symmetric and non-symmetric configurations (see Fig. 2a–e), the teacher asks the children to re-create the designs or explain why the symmetry machine could not have created the design. With the latter designs, the children were encouraged to talk about the relations of the coloured blocks that should be present in order for a design to be symmetric, with the intent to direct children’s attention to movement, distance and perpendicularity between the squares and the line of symmetry. The children are then asked to sit at one of the two large tables in the room and to make drawings of configurations that the symmetry machine could produce.

Fig. 2
figure 2

a Vertical symmetry; b vertical symmetry; c not symmetric; d horizontal symmetry; e oblique symmetry

Full size image

2. Second lesson. The second lesson consists of two parts. First, the children are invited to explore the discrete symmetry machine with a horizontal, then oblique, line of symmetry. The teacher encourages the use of the same language developed in the first lesson so that the children describe how the squares move along, away or toward the line of symmetry. Then, a new sketch with only one side of the line of symmetry is shown; the children are told that the symmetry machine is broken and they must thus predict what the other side of the line should look like. The sketch includes different pages, each of which has a broken symmetry machine with a different type of line of symmetry (see Fig. 3a–c). In these sketches, the squares are spread out away from each other on one side of the symmetry. This was made to avoid relational inference of the positions of the squares and therefore to direct more attention on squares in relation to the line of the symmetry. The children are expected to use the relationships they had discussed in the previous lesson to help them decide how to create these symmetric designs. The children then move to the tables to complete two given tasks. The first contains two parts, each asking the children to describe how an asymmetric diagram could be made symmetric—one involving a horizontal line of symmetry and one with an oblique one. In the second task, the children are asked to create their own symmetric designs, one having a horizontal line of symmetry and the other an oblique one.

Fig. 3
figure 3

a Broken horizontal machine; b broken vertical machine; c broken oblique machine

Full size image

5 Results of the teaching experiment

We describe the results in two sections, each pertaining to one of the lessons described above. The three excerpts chosen from the first lesson enable us to compare the children’s initial talk of symmetry with their evolving discourse, where the focus of the lesson was primarily on vertical line symmetry. The two excerpts from the second lesson illustrate how the children learned to talk about properties of symmetry, including horizontal and oblique reflectional symmetry.

5.1 Children’s change of discourse and new ways of talking about symmetry

Excerpt 1 is taken from the discussion during the early part of the first lesson. It is selected to highlight children’s initial thinking about symmetry. The teacher began by asking the children what they knew about symmetry (before she introduced the “discrete symmetry machine”).

Excerpt 1: Children’s discourse before the introduction of the symmetry machine

TFootnote

T = Teacher; S1 = Student 1, S2 = Student 2, etc.… Ss = All students.

:

So your teacher said that you have talked about symmetry yesterday? What did you talk about in terms of symmetry?

S1:

The line of symmetry is like there is a shape, when you make a line across it and you fold it, it’s the same.

T:

What’s the same?

S1:

The shape.

S2:

It has to be two equal sides, like a star.

T:

Do you know anything else in our world that has both vertical and horizontal symmetry?

S3:

A cross.

S4:

A square.

S5:

A rectangle.

T:

How about letters of the alphabet?

S6:

X.

The discussion on what the children knew about symmetry during the first lesson reveals that they thought about symmetry as a property of certain geometric figures: the word ‘symmetry’ thus applied to particular objects. Such objects must have “two equal sides”, which may be seen as a routine for deciding whether a figure is symmetric. S1 also associated symmetry with folding.

The children then moved on to work on computer tasks involving re-creating symmetric designs and explaining why a given design was not produced by the symmetry machine. Initially, they explained that the squares should be “the same” on both sides. They also described the cases that were not symmetry by talking about the colour and positions of the squares in relation to each other. During this discussion, the children frequently used gestures to communicate the positions of the squares. For instance, when asked by the teacher to explain why a given design is not symmetric, a child walked up to the sketch and said, “Well, I just want to say something about the picture, because, this orange one is under the purple, then this one should be under the purple too.” As he talked about the relation of each of the orange and purple squares on both sides of the symmetry, he used his right pinky (little) finger to touch each of the squares on the sketch. During this part of the lesson, all of the children were given the opportunity to come up to the sketch to move the squares. However, the teacher insisted that the children describe the way they were going to move the square in order to help develop a vocabulary of orientation (up, down, towards the line, away from the line). The children successfully completed all items shown in Fig. 2. Items such as those shown in Fig. 2c took the most time as several children were convinced that the design was indeed symmetric. While those who did not think the designs were symmetric initially explained what they should look like in order to be symmetric, the teacher prompted them to explain why the designs were not symmetric. The children eventually described particular relations between the blocks, saying for example that “when this orange is under the purple, then this [orange square on the other side of the symmetry line] should be under the purple too”.

Excerpt 2: S7’s use of gestures after the introduction of the symmetry machine

While the children were working on their drawings during the paper-and-pencil part of the lesson, one of the research assistants asked several children to explain their drawings. The following two excerpts were selected to show the new emerging discourse that had developed over the first lesson, after the introduction of the “discrete symmetry machine”.

(RA = Research Assistant)

RA:

Let me just see what you have, nice! So, you wanna, move this blue…

S7:

If you click on this blue [pointing to blue square with her pencil and her left index finger, see Fig. 4a], the blue will move [bringing two hands together, see Fig. 4b].

Fig. 4
figure 4

a Pointing to “this” blue square; b blue square moving together; c blue square moving toward the left; c blue square moving toward the right (colour figure online)

Full size image
RA:

Oh.

S7:

It will move like opposite, like this one will move to the windows [moving right finger along the paper to her left, see Fig. 4c], and this one will move to the wall [moving her right hand toward her right, along the paper, see Fig. 4d].

Excerpt 3: S8’s use of diagrams after the introduction of the symmetry machine

While Excerpt 2 focuses on the use of gestures in S7’s new discourse, Excerpt 3 is selected to draw attention to the use of diagrams in S8’s discourse:

S8:

If I move the orange upward [draws arrows 1in Fig. 5]; they both would. If I were to move the magenta down [draws arrow 2a], the other magenta will go down [draw arrow 2b]. If I move the blue sideways [draws arrow 3a], it will go opposite [draws arrow 3b].

Fig. 5
figure 5

S8’s drawing during the first lesson

Full size image

The three excerpts show that the children expressed symmetry using very different words compared to the earlier part of the lesson. Using the dragging modality, the children talked about the movement of squares with words such as “move”, “go”, “opposite”, “upward” vs. “downward”, “left” vs. “right”, “sideways”, and “towards the wall” vs. “towards the windows”. These words involve motions and directions to describe the movement of the squares as a product of the symmetric machine. The new word use reflects the children’s new ways of thinking about symmetry: the line of symmetry is no longer an object that “folds” a static shape into two halves, but one that reflects what you do on one side of the line onto the other side.

In addition to word use, other forms of discourse were developed as the children talked about symmetry with their gestures and diagrams. In terms of gestures, they produced hand movements depicting symmetric directions of movement. As seen in S7’s use of gestures, she first put her hands together at the tip of her fingers to talk about where “the blue will move”. Since her gesture (Fig. 4b) was not accompanied by any speech, it could be said that she was relying solely on her gesture to communicate the symmetric movement of the blue squares. She then moved her right hand dramatically from right to left (Fig. 4c) and then left to right (Fig. 4d) depicting the movement of each blue square. This can be taken as her reasoning as to why the blue squares “will move opposite”. Such gestures were not made before the introduction of the symmetry machine. They seemed to emerge in concert from their own diagrams and explanations of them.

Besides gestures, the children also used arrows in their diagrams to communicate the movement of the squares. The inventiveness of this sign is interesting because, traditionally, arrows are not typically used in diagrams illustrating symmetry. From the way S8 talked about his diagram, we see that she was able to use arrows to communicate the movement produced by the symmetry machine. Indeed, she drew three sets of arrows while she was talking about the discrete movement of all three pairs of squares. The dynamic nature of the symmetric machine and the children’s experience with it had helped them to talk and draw in this way. The children were able to talk about symmetry as having dynamic properties (“What you do on one side, you will do to the other side”) as a result of interacting with the symmetry machine.

In the lens of semiotic mediation, the children’s gestures and arrows acted as their own use of signs to communicate the movement of the squares. These gestures and visual mediators operated effectively as signs in the absence of the computer to communicate the symmetric movement. The use of these signs is significant for two reasons. First, they were spontaneously performed and the children were not instructed to use them. Secondly, and more importantly, the creation of their own signs in a multimodal means seems to suggest that the children have internalised the signs offered by the DGE to create personal meanings. Thus, we suggest that the children’s talk of the “squares” through gestures and diagrams were the result of the process of internalisation. Besides visual mediation of the dynamic sketch, the teacher consistently directed children’s attention on the movement of the squares during the lesson, using language (signs) that mediate distance and movement in relation to the line of symmetry. At the end of Lesson 1, we found that the children were able to think about symmetry in terms of movement in relation to the line of symmetry although the way they related distance in relation to the line of symmetry was not yet developed. They did so by communicating in multimodal ways incorporating signs such as gestures and arrows in their drawings.

In summary, there is a change of children’s discourse expressing the notion of symmetry. The children developed new word use and ways of talking about symmetry as movement using gestures and diagrams upon interacting in a dynamic environment. Words such as “move” and “go” had not entered children’s discourse until the introduction of the symmetry machine. In addition, hand gestures and arrows in diagrams depicting movement of squares in relation to the line of symmetry were invented to express the embodied experience of the children. These gestures and drawings were examples of the children’s use of their own signs to communicate movement, through internalising the signs offered by the teacher verbally and the symmetry machine visually.

5.2 Properties and reasoning about symmetry developed

During the second lesson, the teacher worked closely with the children on properties of symmetry using the discrete symmetry machine. The aim of the lesson was two-fold: to introduce symmetry machines with horizontal and oblique lines of symmetry and to construct symmetric figures given one side of the symmetry line. Ultimately, the teacher mediated a discussion on the conditions of line symmetry. She showed examples of asymmetric sketches and asked the children to explain what it is in the sketch that makes it symmetric or not. The children talked about the “amount of space” that should be “the same” between squares on both sides of the line of symmetry. The teacher also used language such as the blocks are “on the same line” and “the same amount of distance between the block and the line of symmetry” to help children attend to properties of symmetry. In addition, she occasionally used her hand and arm to gesture the way the squares are not “on the same line” or do not have the “same distance”. During this part of the lesson, the children actively engaged in the construction of a symmetric figure by talking and reasoning about where the squares should be placed, as seen in the following episode.

Excerpt 4: Class discussion on properties of symmetry

T:

This is somebody who made a very boring design… Only two squares. Even if it’s boring, it can still have symmetry, right?

Ss:

Yes.

T:

Can you help me make it symmetric with this one?

Ss:

[raised their hands].

T:

So ya, you go ahead.

S9:

 <whispered> One, two [pointed at the empty space between the square and the horizontal line, see Fig. 6]. I will move the blue one, right over, up there.

Fig. 6
figure 6

“One, two.” S9 counting the number of “squares in the space”

Full size image
T:

Up there, ok. I saw you were doing something like that [used her left index finger to point towards the empty spaces directly above the blue square]. What were you doing?

S9:

I was counting how many squares in the space.

T:

How many did you figure out?

S9:

Two.

T:

So where do you want me to put the other one?

S9:

Right on the top.

T:

Can you use the fact that this is two squares away to tell me where to put the other one?

S9:

It’s two squares away from the line, so one, two, and three [see Fig. 7].

Fig. 7
figure 7

“It’s two squares away from the line, so one, two, and three”

Full size image
T:

Ok.

In this episode, we see that besides being able to work with horizontal symmetry, S9 also used a toolkit to describe some properties of symmetry as guided by the teacher. This toolkit is made up of a combination of language, gestures and visual mediators and could be used to explain why one figure is symmetric and not the other. Figure 8 illustrates S9’s speech and accompanying gestures while he explained why the blue square should be three units above the line of symmetry in the dynamic sketch. He first whispered “one, two” to “count the number of squares in the space” between the line and the bottom blue square. His gestures acted as pivot signs connecting the instrumental action of the discrete movement of the square and to a mathematical meaning of distance to the line of symmetry. Then, he explained that “it’s two squares away from the line, so one, two, and three”, while he pointed to the empty space three units above the line with his right index finger. S9’s language and bodily actions illustrate two conditions of symmetry, namely distance and perpendicularity, when he explained with both words and hand gestures that the square needed to be placed three units directly above the line of symmetry. This was initiated by the teacher’s acknowledgement of S9’s explanation and her question for S9 to explain his reasoning in terms of distance and direction from the line of symmetry. Here, we note the semiotic game played by the teacher in her use of language and gestures that tune with those of her students, while also moving toward shared, mathematical meanings. This was a deliberate move by the teacher to help students learn beyond Lesson 1 where the children were mainly drawing symmetric figures and discriminating between symmetric and asymmetric figures without using language to support their reasoning. We found further evidence that the children talked about symmetry that involves properties and reasoning in Lesson 2. This reasoning is evident in a subsequent paper task when the children were asked “Why is the square in the wrong place for a symmetry”, as seen in S10’s work:

Fig. 8
figure 8

S10’s reasoning of why the square is in the wrong place for a symmetry

Full size image

Excerpt 5: S10’s drawing and reasoning after Lesson 2

Figure 8 shows S10’s reasoning about symmetry using two different kinds of signs. First, she used the circles on the left figure as signs mediating the distance between the square on the left and the vertical line of symmetry. This helps S10 to reason that the two squares were not equidistant from the line of symmetry. Secondly, S10’s reasoning involved the use of arrows, which were previously used as signs in the children’s work in the first lesson. In both her drawings in Fig. 8, S10 communicated the “wrong place” of the squares by indicating arrows showing her desired movement of the squares. In general, the use of arrows was dominant for the children completing this task whether or not it was indicated correctly. From the nineteen children who responded in this particular task, sixteen of them responded correctly, fourteen of whom drew arrows and two of whom drew the desired placement of square without arrows. Only three children responded to the task incorrectly, either by drawing the arrows in the wrong way or not drawing anything. Also, analysing the classroom activity in which the children had to place the squares in the correct place, seventeen of the twenty-two responses were correct, and all of the children used hand gestures to indicate where the squares should be placed. Our data provides consistent evidence that the children thought about symmetry and properties of symmetry in a dynamic and multimodal way.

6 From tools to signs: the role of dragging

It can be said that the children’s new ways of thinking about symmetry in terms of word use, gestures and diagrams were semiotically mediated both by the use of DGE and the teacher’s word use and gestures. In the discrete symmetry machine, the discrete movement of squares on both sides of the symmetry line produces both artefact and mathematical signs. This polysemy of signs can be found as children communicated their prediction of a square’s movement towards a certain direction as early as in Lesson 1, where they not only spoke of the movement of a particular square (artefact sign) but also related the square as a mathematical object with line symmetry (mathematical sign). For example, S7’s utterances “if you click on this blue, the blue will move” illustrate his interpretation of the squares as artefact signs. Later, the squares transformed as pivot signs when S7 focused his communication on the symmetric movement of the squares, as in “it will move like opposite, like this one will move to the windows, and this one will move to the wall.” These pivot signs seemed to transform into mathematical signs in the children’s drawings where arrows were used to express symmetric movement of the square towards, along and away from the line of symmetry. The transformation from artefact to mathematical signs is important since it facilitated the children to internalise the mathematical signs to create personal meanings. Despite possible criticisms that internalisation in a Vygotskian sense is not a visible and objectifiable process, our data provide strong evidence that the children were able to create personal meaning during their work (both with the DGE and with paper-and-pencil). This claim was supported by the children’s spontaneous use of signs (squares with arrows and gestures indicating movement) in multimodal ways and in the absence of a DGE.

Another important catalyst of the semiotic process was the teacher’s own use of signs as she led the whole-class discussions. Her use of words such as “along the line”, “towards the line” and “away from the line” evoked mathematical meanings of the squares’ movement in relation to the line of symmetry. We observed that the teacher frequently used these words to talk about the movement of squares in both lessons. These words may have been intentionally introduced by the teacher to help children see beyond the squares as pure artefact signs, by focusing on the relative position of the squares to the line of symmetry. Our findings confirm with previous studies that the teacher’s use of language plays a powerful role in shaping how students think about the mathematics at hand (Bartolini Bussi and Mariotti 2008; Falcade et al. 2007).

Besides word use, the teacher also used gestures as semiotic resources to mediate mathematical meaning. For example, she aligned her arm and hand with the squares on opposite sides of the symmetry line when describing that the squares should be “on the same line” perpendicular to the line. She also used her two index fingers (with one finger touching the square and the other touching the line) to act as a referent when describing that the squares should be “the same distance” away from the line of symmetry. Both her arm and hand in these instances have become pivot signs in the process of semiotic mediation. In the case of the arm as a tool, it serves a purpose much like a straight edge would; it signifies straightness. In contrast, the fingers act like a ruler and signify distance between two objects. Together, the teacher was able to mediate the idea that the line of symmetry bisects the line that aligns two symmetric objects. However, the notion of perpendicularity did not emerge very easily. The children could tell visually that there was something wrong if the line of symmetry does not bisect the distance between the squares, but since they had not encountered the notion of perpendicularity before, they had no way of describing the relationship between the line of symmetry and the line connecting the pre-image and image squares. The use of a grid might have provided a useful semiotic mediator for this purpose.

This paper has shown that the dynamic nature of the geometrical tasks initiated a new discourse for the children, which ultimately led to generalising about properties of symmetry. However, this was facilitated not only by the children’s interactions with DGE, but an important component of the process was the teacher’s mediation through her language and gestures. As such, we argue that designing meaningful tasks with DGE along with supporting teachers in developing appropriate technical and descriptive language are necessary to complement an amplified geometry curriculum—one that “moves” children from static conceptions of symmetry to dynamic and embodied ones.

7 Discussion and conclusion

Over the course of the three lessons, which included a large component of whole-class discussion and interaction with the projected images in Sketchpad, as well as opportunities for the children to create drawings based on both the discrete and continuous symmetry machine, the children changed their thinking about symmetry. They began with a static discourse on symmetry that was focused on the intrafigural qualities of shapes and that featured a small example space of shapes with vertical reflectional symmetry. Over the course of the lessons, they began to talk about interfigural qualities, focusing on the functional relationships of a pre-image and its image. This shift was occasioned by the processes of semiotic mediation in which the dragging tool, the language and gestures of the teacher, and the children’s gestures, became shared pivot signs that enabled communication about central features of reflectional symmetry including: the way in which one side of a symmetric design is the same as the other; the way in which one component of a symmetric design is the same distance away from the line of symmetry as its corresponding image; the way in which a pre-image component and its image have to be on the same line relative to the line of symmetry; and, the way in which a pre-image and an image gives rise to parity.

The children produced new words, gestures and diagrams in communicating about symmetry as a result of working with the teacher in the dynamic geometry environment, which includes both the software and also the particular microworlds and tasks that were designed. The discrete symmetric machine seemed to help the children attend to the way in which an image and its pre-image move together according to certain rules (away/toward the line or along the line) and the property of equidistance, as the space between an image and its pre-image. In terms of methodology for future research with young children, this paper underlines the value of an analysis that considers language, gestures and diagrams as a full set or bundle of children’s communication for gaining deep insights into how children learn mathematics.

We see an important interplay between the collective work with the dynamic computer-based environment and the paper-and-pencil individual work at the tables. The former was not intended to evaluate the children’s understanding but, rather, to provide a way for them to explore that understanding through a different medium, in which the temporality of the moving objects would need to be expressed through new signs, which were primarily the arrows that were used by a large number of students. The diagrams they produced occasioned new gestures that enabled the students to further develop their dynamic, functional thinking about symmetry. We call for an amplified curriculum that includes consistent use of DGE in mathematics classrooms to foster children’s embodied and dynamic ways to think about geometry and the development of more geometry tasks that focus on the dynamic nature of geometry with precise learning goals for young children.