1 Introduction

Solid state diffusion is a fundamental materials process that can impact materials properties [1–3]. Germanium (Ge) rivals silicon (Si) for nanoelectronic applications as it has superior carrier mobilities, low dopant activation temperatures and smaller bandgap but is relatively compatible with Si-technology [1–5]. For decades Ge was not considered in microelectronic devices due to its poor quality native oxide [1], however, the introduction of high-k gate dielectric materials has resolved this issue and effectively regenerated the interest on alternative materials [6–9].

In a Ge substrate oxygen (O) contributes in defect processes, but its impact is deemed to be less significant than in Si [1]. This can be traced to the Czochralski-growth process were the concentration of O introduced in Ge is not as high as in Si [1]. Considering, however, that the experimental solubility of O in Ge can be around 1018 cm−3 and that O can also be introduced in Ge through alternative routes (for example via diffusion at the Ge/oxide interface in devices or when oxygen gas is present in the growth atmosphere) it can be present in the Ge substrate at high concentrations [1]. Finally, although Oi are electrically inactive in Ge, they may associate with vacancies to form A-centers or larger oxygen-vacancy complexes that can impact properties [1].

An important issue in solid state physics is the association of the defect Gibbs energy (gi) and the bulk properties in solids [10]. In the model by Varotsos and Alexopoulos [11–13] it was proposed that gi is proportional to the isothermal bulk modulus B and the mean volume per atom Ω (this is also known as cBΩ model). The cBΩ model is important as it leads to the calculation of numerous defect parameters and has been previously used to describe the diffusion and point defect processes in a wide range of systems including semiconductors, oxides and metals [14–19]. In the present study we describe using the cBΩ model the diffusion of O in Ge using the isothermal bulk modulus and the mean volume per atom.

2 Methodology

In a crystal with a single diffusion mechanism the diffusion process can be described by the activation Gibbs energy (gact), which is the sum of the Gibbs formation (gf) and the Gibbs migration (gm) processes. The following relation defines the activation entropy sact and the activation enthalpy hact [14, 15]:

$$ {\text{s}}^{\text{act}} = \left. { - \frac{{{\text{dg}}^{\text{act}} }}{\text{dT}}} \right|_{P} $$
(1)
$$ {\text{h}}^{\text{act}} = {\text{g}}^{\text{act}} + {\text{Ts}}^{\text{act}} $$
(2)

The diffusion coefficient (or diffusivity) D is defined by:

$$ D = fa_{0}^{2} \nu e^{{ - \frac{{g^{\text{act}} }}{{k_{B} T}}}} $$
(3)

where f is the diffusion correlation factor depending on the diffusion mechanism and the structure, a 0 is the lattice constant, ν is the attempt frequency and k B is Boltzmann’s constant.

In the cBΩ model the defect Gibbs energy gi is related to the bulk properties of the material trough the relation [11–13]:

$$ {\text{g}}^{\text{i}} = {\text{c}}^{\text{i}} {\text{B}}\Omega $$
(4)

Combining Eqs. (3) and (4) we obtain:

$$ D = fa_{0}^{2} \nu e^{{ - \frac{{{\text{c}}^{\text{act}} B\Omega }}{{k_{B} T}}}} $$
(5)

Therefore, for an experimentally determined diffusivity D 1 value at T1 the c act can be calculated if the pre-exponential factor \( {\text{fa}}_{0}^{2}\upnu \) can be determined. The calculation of the pre-exponential factor requires the diffusion correlation factor (that is dependent upon the diffusion mechanism and the crystal structure) and the attempt frequency. The attempt frequency is typically approximated by the Debye frequency, an approximation that can lead to errors [15]. Having calculated c act the diffusivity D i at any temperature Ti can be calculated using Eq. 5 provided that the elastic data and expansivity are known for Ti [14, 15]. c act is a constant that can be considered to be to a first approximation to be temperature and pressure independent [15]. An important feature of the cBΩ model is that it can encapsulate anharmonic effects exhibited by the temperature decrease in B and by the thermal expansivity [19].

3 Results and discussion

Controlling oxygen is important in Ge as it may interact with defects forming complexes that will have a deleterious impact upon the performance of devices. These issues are more pronounced in the isostructural Si where O is introduced at high concentrations mainly due to the Czochralski. In Si, O interacts with carbon (C) or vacancies forming numerous defect complexes that impact device properties [20–22].

Concerning Ge, in previous work it was determined that O diffusion in Ge obeys the following Arrhenius relation [23–25]:

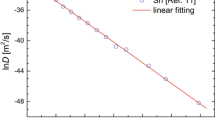
$$ D_{ \exp }^{O} = 3.9e^{{ - \frac{{2.05{\text{eV}}}}{{k_{B} T}}}} \times 10^{ - 5} {\text{m}}^{2} {\text{s}}^{ - 1} $$
(6)

Here we use, the Ge expansivity and isothermal bulk modulus data that was previously reported [26–28]. In Table 1 this data is reported as well as the experimental O interstitial diffusion coefficients derived from Eq. 6. The method of the single experimental measurement (please refer to [14, 15] and references therein) is not unique and other methods have been used to calculate c act including the so-called compensation law [29, 30] and the “mean value” method [31–33]. Commonly in the method of the single experimental measurement the calculated value of c act will be dependent on the errors in the pre-exponential factor, B, Ω and D 1 value, which can be very significant if a single experimental measurement is considered. To avoid the dependence of c act on the experimental uncertainties the mean value method is considered here [29–34]. Here we employ the mean value method where a linear behaviour of lnD O versus \( \frac{{B\Omega }}{{k_{B} T}} \) testifies the validity of the cBΩ model. Additionally, c act can be derived by the slope (refer to Eq. 5). From Fig. 1 it can be concluded that the cBΩ model can be used in O containing Ge. The O diffusion coefficients in Ge are associated to the isothermal bulk modulus and the mean volume per atom via:

$$ D_{{cB\Omega }}^{O} = 1.526e^{{ - \frac{0.1796B\Omega }{{k_{B} T}}}} \times 10^{ - 6} {\text{m}}^{2} {\text{s}}^{ - 1} $$
(7)
Table 1 Calculated and experimental [23–25] O diffusion coefficients in Ge alongside the elastic and expansivity data [26–28] used in the cBΩ model
Full size table
Fig. 1
figure 1

The O diffusion coefficients in Ge with respect to \( \frac{B\Omega }{{k_{B} T}} \)

Full size image

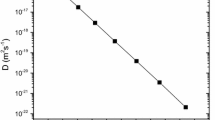
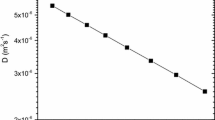
Figure 2 is the Arrhenius plot for O diffusion coefficients in Ge determined by experiment [23–25] and deduced by the cBΩ model using Eq. (7). Figure 2 and Table 1 testify that the results of the cBΩ model are in excellent agreement (within 2 %) with the experimental results [23–25]. Having established the validity of the cBΩ model for O diffusion in Ge other defect properties including migration and formation entropies, which are difficult to determine experimentally can be calculated for a wide temperature range.

Fig. 2
figure 2

The Arrhenius plot for O diffusion in Ge obtained by experiment [23–25] and calculated by the cBΩ model

Full size image

4 Conclusions

In the present study we used cBΩ model to describe O diffusion in Ge. It is shown that there is excellent agreement between the calculated and experimental diffusion coefficients of O in Ge throughout the temperature range considered. Additionally, the cBΩ model can be used to provide information for the formation, migration and defect volumes in Ge over a range of temperatures and pressures and these issues will be considered in future work.