1 Introduction

Germanium (Ge) has superior carrier mobilities, low dopant activation temperatures and smaller band-gap as compared to silicon (Si), which is the mainstream nanoelectronic material [1–5]. Compared to other materials Ge has the technological advantage that it is more compatible with Si-processes and therefore existing equipment may be used for Ge device fabrication [5]. Although Ge was important in the early days of the semiconductor industry the poor quality of germanium dioxide (as compared to silicon dioxide in Si-technology) led to its demise [5]. In recent years the adoption of high-k gate dielectric materials eliminated the requirement of a good quality native oxide and this regenerated the interest on the incorporation of Ge in advanced nanoelectronic devices [6–8].

As the dimensions of devices are a few nanometers the absolute control on the behaviour of dopants in the Ge substrate and in particular dopant diffusion is more important than ever. Indium diffusion in germanium has been investigated experimentally and recent studies have confirmed that it is described by an activation enthalpy of 3.51 eV [9, 10]. In the recent study by Kube et al. [10] the observed concentration independent diffusion profiles were described with the vacancy mechanism with a singly negatively charged mobile indium-vacancy (InV)− defect.

Interconnecting the defect Gibbs energy gi (i = defect formation f, self diffusion activation act, or migration m) and bulk properties in solids is an issue that has led to different models [11–20]. In their model Varotsos and Alexopoulos [13–19] (referred thereafter as the cBΩ model) proposed that gi is proportional to the isothermal bulk modulus B and the mean volume per atom Ω. The cBΩ model describe the diffusion and point defect processes in numerous [21–31], but it has not been systematically employed to investigate the diffusion processes in germanium [32, 33].

The cBΩ model is typically employed in materials with a single diffusion mechanism. Indium in germanium is such a system as its diffusion is dominated by the vacancy mechanism. In the present study we investigate using the cBΩ model the association of the indium diffusion coefficients in germanium with the isothermal bulk modulus and the mean volume per atom.

2 Methodology

For a monoatomic crystal with a single diffusion mechanism such as indium in germanium the dopant diffusion process can be described by the activation Gibbs energy \( ({\text{g}}^{\text{act}} ) \). \( {\text{g}}^{\text{act}} \) is the sum of the Gibbs formation \( ({\text{g}}^{\text{f}} ) \) and the Gibbs migration \( ({\text{g}}^{\text{m}} ) \) processes. The activation entropy \( {\text{s}}^{\text{act}} \) and the activation enthalpy \( {\text{h}}^{\text{act}} \) are given by [21, 24]:

$$ {\text{s}}^{\text{act}} = - \left. {\frac{{{\text{dg}}^{\text{act}} }}{\text{dT}}} \right|_{P} $$
(1)
$$ {\text{h}}^{\text{act}} = {\text{g}}^{\text{act}} + {\text{Ts}}^{\text{act}} $$
(2)

The diffusion coefficient D is defined by:

$$ D = fa_{0}^{2} \nu e^{{ - \frac{{g^{act} }}{{k_{B} T}}}} $$
(3)

where \( f \) is the diffusion correlation factor depending on the diffusion mechanism and the structure, a 0 is the lattice constant, ν is the attempt frequency and k B is Boltzmann’s constant.

In the framework of the cBΩ model the defect Gibbs energy gi is related to the bulk properties of the solid through the relation [13–19]:

$$ {\text{g}}^{\text{i}} = {\text{c}}^{\text{i}} {\text{B}}\Omega $$
(4)

Combining Eqs. (3) and (4):

$$ D = fa_{0}^{2} \nu e^{{ - \frac{{c^{act} B\Omega }}{{k_{B} T}}}} $$
(5)

This implies that for an experimental diffusivity D 1 value at T1 the c act can be calculated as the pre-exponential factor fa 20 ν can be calculated. Then using c act the diffusivity D i at any temperature Ti can be calculated using Eq. 5, with the prerequisite that the elastic data and expansivity are known for Ti. \( c^{act} \) is a constant and can be assumed to a first approximation to be independent of temperature and pressure [21, 24]. Consequently, the diffusion coefficient can be calculated using this model at any temperature and pressure from a single experimental measurement. An important feature of the cBΩ model is that it encapsulates anharmonic effects exhibited by the temperature decrease in B and by the thermal expansivity.

3 Results and discussion

Controlling self- and dopant diffusion during device fabrication is technologically important. Previous experimental and theoretical studies established the prevalence of the vacancy diffusion mechanism in Ge [32–37]. In a recent study Hüger et al. [35] determined that Ge self-diffusion in the temperature range 702–1,177 K can be described with a vacancy mechanism via an Arrhenius relation:

$$ D^{V} = 2.54e^{{ - \frac{3.13}{{k_{B} T}}}} \times 10^{ - 3} {\text{m}}^{2} {\text{s}}^{ - 1} $$
(6)

Kube et al. [10] determined that the indium diffusion in germanium is via a vacancy-mediated mechanism. Singly negatively charged indium-vacancy pairs, (InV)−, are formed through the reaction (InV)− ↔ In − s  + V 0. Here In − s represents the singly negatively charged indium dopant and V 0 the neutral charged state of the V. Indium dopant diffusion germanium in the temperature range 827–1,176 K can be described via the Arrhenius relation [10]:

$$ D^{In} = 0.5123e^{{ - \frac{3.51}{{k_{B} T}}}} {\text{m}}^{ - 2} {\text{s}}^{ - 1} $$
(7)

The expansivity data was taken from Kagaya et al. [38] and the isothermal bulk modulus data from krishman et al. [39]. These values [38–41] are reported in Table 1 alongside the experimental indium diffusion coefficients derived from Eq. 7. The method of the single experimental measurement [17, 21, 24] is not unique and methods have been proposed to calculate \( c^{act} \) such as the compensation law [42, 43] and the “mean value” method [26, 29, 44]. In the method of the single experimental measurement the calculated value of \( c^{act} \) will depend upon the experimental error in the B and Ω parameters and the D 1 value. Additionally, there will be errors in the pre-exponential factor particularly in the case of diffusion mechanisms that are complicated. Here indium diffusion is via a vacancy mechanism and this should involve in the diamond lattice the ring-mechanism of diffusion [45]. In this mechanism the vacancy will need to move away to at least the third nearest neighbor site and return along a different path. This presumes that the indium atom will be bound to the vacancy up to at least the third nearest neighbor site. However, previous experimental and theoretical work supports the view that the interaction of indium to vacancy at the second and third nearest neighbor sites is repulsive [10, 46]. This constitutes the derivation of a reliable pre-exponential factor very difficult.

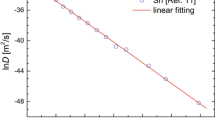
Table 1 Characteristic calculated and experimental [10] indium diffusion coefficients in germanium alongside the elastic and expansivity data [38, 39] used in the cBΩ model
Full size table

In the present study to avoid the dependence of \( c^{act} \) on the experimental uncertainties the mean value method is considered. In this we consider that a linear behavior of lnD In versus \( \frac{{B\Omega }}{{k_{B} T}} \) testifies the validity of the cBΩ model with the slope being \( c^{act} \) (refer to Eq. 5). As it can be seen from Fig. 1 there is such a linear relation, which can be represented by:

$$ D^{In} = 2.03e^{{ - \frac{{0.3078B\Omega }}{{k_{B} T}}}} \times 10^{ - 3} {\text{m}}^{2} {\text{s}}^{ - 1} $$
(8)
Fig. 1
figure 1

The indium dopant diffusion coefficients in germanium with respect to \( \frac{{B\Omega }}{{k_{B} T}} \)

Full size image

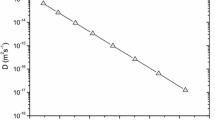
Figure 2 is the Arrhenius plot for indium dopant diffusion coefficients in germanium obtained by experiment [10] and calculated by the cBΩ model. Both this figure and Table 1 shows that the cBΩ model is in excellent agreement with the experimental [10] indium diffusion coefficients in Ge.

Fig. 2
figure 2

The Arrhenius plot for indium dopant diffusion coefficients in germanium obtained by experiment [10] and calculated by the cBΩ model

Full size image

4 Conclusions

In the present study the efficacy of the cBΩ model to describe indium diffusion in germanium is discussed. There is excellent agreement between the calculated and experimental diffusion coefficients of indium in germanium in the temperature range considered. Indium diffusion in Ge is via a vacancy mechanism and in future studies we intend to model using the cBΩ model self-interstitial mediated diffusion and diffusion in binary semiconductor alloys were competing diffusion mechanisms occur.