An approach to robust fault diagnosis in mechanical systems using computational intelligence

Abstract

In this paper a novel approach to design robust fault diagnosis systems in mechanical systems using historical data and computational intelligence techniques is presented. First, the pre-processing of the data to remove the outliers is performed with the aim of reducing the classification errors. To accomplish this objective, the Density Oriented Fuzzy C-Means (DOFCM) algorithm is used. Later on, the Kernel Fuzzy C-Means (KFCM) algorithm is used to achieve greater separability among the classes, and reducing the classification errors. Finally, an optimization process of the parameters used in the training state by the DOFCM and KFCM for improving the classification results is developed using the bioinspired algorithm Ant Colony Optimization. The proposal was validated using the DAMADICS (Development and Application of Methods for Actuator Diagnosis in Industrial Control Systems) benchmark. The satisfactory results obtained indicate the feasibility of the proposal.

Introduction

In modern industries there are higher and increasing requirements associated with the efficiency of processes, the quality of the products and the fulfillment of environmental and industrial safety regulations (Hwang et al. 2010; Venkatasubramanian et al. 2003a).

Mechanical systems exist in almost all manufacturing industries, and a large part of the faults that occur in these industries are associated with this type of systems (Aydin et al. 2014). In general, the faults have an unfavorable impact in the productivity, the environment and the safety of operators. In an industrial context, safety is associated with a set of specifications or standards that manufacturers must meet in order to reduce the accident risks. With this purpose, it is important to incorporate automatic control and supervisory systems into industrial processes, allowing satisfactory operation of these through compensating the effects of perturbations and changes that might occur in them. Therefore, in order to guarantee that the operation of a system satisfies performance specifications, the faults need to be detected and isolated, being these tasks associated to the fault diagnosis systems (Isermann 2011).

In general form, the fault diagnosis methods can be classified into two categories: models-based methods (Camps Echevarría et al. 2014b, a; Ding 2008; Patan 2008; Venkatasubramanian et al. 2003a, b) and process history-based methods (Fan and Wang 2014; Bernal de Lázaro et al. 2016, 2015; Pang et al. 2014; Sina et al. 2014). In the first approach, the diagnosis tools use models which describe the operation of the processes. These tools are based on the residue generation obtained from the difference between the measured variables in the real process, and the values of the same variables obtained from the model. This type of methods entails an elevated knowledge about the characteristics of the processes, their parameters, and operation zones. However, it is usually very difficult to achieve due to the current complexity of the industrial processes. In mechanical systems there are several applications where these techniques have been used (Karami et al. 2010; Kourd et al. 2012).

On the other hand, the approaches based in historical data do not need a mathematical model, and they do not require much prior knowledge of the process parameters (Choudhary et al. 2008; Wang and Hu 2009). These characteristics constitute an advantage for complex systems, where relationships among variables are nonlinear, not totally known, and therefore, it is very difficult to obtain an analytical model that describes efficiently the dynamics of the process. In the case of mechanical systems, some techniques has been used to fault diagnosis. For example, Motor Current Signature Analysis (MCSA) is the most widely used method to detect various motor faults (Sharifi and Ebrahimi 2011). In order to extract fault features of large-scale power equipment from strong background noise, a fault diagnosis method based on the Wavelet de-noising was proposed (Liu et al. 2016), and broken rotor bar faults were detected using a nonlinear time series analysis (Silva et al. 2008).

Among the various techniques used in fault diagnosis of mechanical systems the use of computational intelligence tools as Neural networks (Hou et al. 2003), Support Vector Machines (Hu et al. 2007), and Fuzzy logic (Bocaniala et al. 2005; Rodríguez Ramos et al. 2016) are emphasized. In addition, there has been a significant increase in the use of the fuzzy clustering methods in recent years (Bedoya et al. 2012; Botia et al. 2013; Jahromi et al. 2016; Seera et al. 2015; Xu et al. 2016).

Fuzzy clustering techniques are very important tools of unsupervised data classification (Gosain and Dahika 2016). They can be used to organize data into groups based on similarities among the individual data. Fuzzy clustering deals with the uncertainty and vagueness existing in a wide variety of applications, as for example: image processing, pattern recognition, object recognition, modeling and identification (Jiang et al. 2016; Kesemen et al. 2016; Leski 2016; Saltos and Weber 2016; Thong and Son 2016b; Vonga et al. 2014; Zhang et al. 2016). The main focus of all fuzzy clustering techniques is to improve the clustering by avoiding the influence of the noise and outlier data.

The Fuzzy C-Means (FCM) algorithm (Bezdek 1981), is one of the most widely used algorithm for clustering due to its satisfactory results for overlapped data. Unlike k-means algorithm , it considers the possible membership of the data points to more than one cluster . FCM algorithm obtains very good results with noise free data but are highly sensitive to noisy data and outliers (Gosain and Dahika 2016).

Other similar techniques are Possibilistic C-Means (PCM) (Krishnapuram and Keller 1993) and Possibilistic Fuzzy C-Means (PFCM) (Pal et al. 2005). They analyze each cluster as a possibilistic partition. However, PCM fails to find optimal clusters in the presence of noise (Gosain and Dahika 2016) and PFCM does not yield satisfactory results when data set consists of two clusters which are highly unlike in size and outliers exist (Gosain and Dahika 2016; Kaur et al. 2013). Noise Clustering (NC) (Dave 1991; Dave and Krishnapuram 1997), Credibility Fuzzy C-Means (CFCM) (Chintalapudi and Kam 1998), and Density Oriented Fuzzy C-Means (DOFCM) (Kaur 2011) algorithms were proposed specifically to work efficiently with noisy data.

The clustering output depends upon various parameters such as distribution of data points inside and outside the cluster, shape of the cluster and linear or non-linear separability. The effectiveness of the clustering method strongly relies on the choice of the metric distance adopted. FCM uses Euclidean distance as the distance measure, and therefore, it can only be able to detect hyper spherical clusters. Researchers have proposed other distance measures such as, Mahalanobis distance measure, and Kernel based distance measure in data space and in high dimensional feature space, such that non-hyper spherical/non-linear clusters can be detected (Zhang and Chen 2003, 2004).

Another common problem of fuzzy clustering methods is that their performance depend significantly on the initialization of their parameters. In many occasions, it is necessary to make multiple runs of the algorithm in order to obtain good results which is time consuming, and not always the obtaining of the best solution is guaranteed.

In order to overcome these problems, in this paper a new fault diagnosis methodology in mechanical systems using fuzzy clustering techniques is proposed. The methodology consists of three basic steps. First, the pre-processing of data to remove outliers is performed. To achieve this goal the DOFCM algorithm is used. Second, the classification process is developed. For this, the Kernel Fuzzy C-means (KFCM) algorithm is used to obtain a better separability among classes and therefore, the classification results are improved. Finally, a third step is used to optimize the parameters m (factor that regulates the fuzziness of the resulting partition) and $\sigma$ (bandwidth and indicates the degree of smoothness of the Gaussian kernel function) of the algorithms used in the previous stages using Ant Colony Optimization (ACO) algorithm.

The main contribution of this paper is the obtaining of a robust fault diagnosis scheme in mechanical systems, that adequately combines fuzzy clustering algorithms to solve the drawbacks of this type of technique when the data is affected by noise and outliers, and improving the classification by using kernel tools whose parameters are optimized to obtain the best results.

The organization of the paper is as follows: in “General description of the principal tools used in the proposal” section is presented the general characteristics of the tools used in the proposed methodology. In “Proposal of classification methodology using computational intelligence tools” section, a description of the new classification methodology using fuzzy clustering techniques is presented. The “Benchmark case study: DAMADICS” section presents the case study used to validate the proposed methodology, as well as the experiment design. In “Analysis and discussion of results” section, an analysis of the obtained results is performed. A comparison with recent fuzzy clustering algorithms is performed in “Comparison with other fuzzy clustering algorithms” section. Finally, the conclusions are presented.

General description of the principal tools used in the proposal

Density Oriented Fuzzy C-Means (DOFCM)

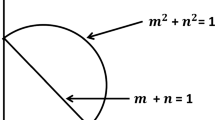
The algorithm attempts to decrease the noise sensitivity in fuzzy clustering by identifying outliers before the clustering process. The DOFCM algorithm creates $c+1$ clusters with c good clusters and one cluster of noise. This algorithm identifies outliers before the construction of the clusters, based on the density of data set, as it is shown in Fig. 1.

Fig. 1

Identification of outliers with the DOFCM algorithm

The neighborhood of a given radius of each point in a data set has to contain at least a minimum number of other points. DOFCM defines a density factor, called the neighborhood membership, which express the measure density of an object in relation to its neighborhood. The neighborhood membership of a point i in X is defined as:

$$\begin{aligned} M^{i}_{neighborhood} = \frac{\eta ^{i}_{neighborhood}}{\eta _{max}} \end{aligned}$$

(1)

where $\eta ^{i}_{neighborhood}$ is the number of points in the point neighborhood i; $\eta _{max}$ is the maximum number of points in the neighborhood of any point in the data set.

If the point q is in the point neighborhood of the point i, q will satisfy:

$$\begin{aligned} q\in X|dist(i,q) \le r_{neighborhood} \end{aligned}$$

(2)

where $r_{neighborhood}$ is the radius of neighborhood, and dist(i, q) is the distance between points i and q. Calculation of neighborhood radius is done in the similar way to (Ester et al. 1996).

Neighborhood membership of each point in the data set X is calculated using Eq. (1). The threshold value $\alpha$ is selected from the complete range of neighborhood membership values, depending on the density of points in the data set. The point will be considered as an outlier if its neighborhood membership is less than $\alpha$. Let i be a point in the data set X, then

$$\begin{aligned} \left\{ \begin{array}{clrr} M^{i}_{neighborhood}< \alpha &{}\text{ then }\, i\, \ { outlier} \\ M^{i}_{neighborhood}\ge \alpha &{}\text{ then }\, i\, \ non-outlier \end{array}\right. \end{aligned}$$

(3)

$\alpha$ can be selected from the range of $M^{i}_{neighborhood}$ values after observing the density of points in the data set and it should be close to zero. Ideally, a point will be classified as outlier only if there is no other point in its neighborhood, i.e., when neighborhood membership is zero or threshold value $\alpha =0$. However, in this scheme, a point is considered as an outlier when its neighborhood membership is less than $\alpha$, where $\alpha$ is a critical parameter to identify the outlier points. Its value depends upon the nature of data set, i.e., taking into account the density of the data set, then, its value will vary for different data sets.

After identifying the outliers, the process of clustering begins. DOFCM reformulates FCM objective function as:

$$\begin{aligned} J_{DOFCM}\left( X;U,v\right) = \sum _{i=1}^{c+1}\sum _{k=1}^{N}\left( \mu _{ik}\right) ^{m}\left( d_{ik}\right) ^{2} \end{aligned}$$

(4)

where, the distances are defined by,

$$\begin{aligned} d^{2}_{ik} = \left( \mathbf {x}_{k} - \mathbf {v}_{i}\right) ^{T}\mathbf {A}_{i}\left( \mathbf {x}_{k} - \mathbf {v}_{i}\right) ,\forall k, i = 1 \,\ldots \,c \end{aligned}$$

(5)

Membership function $\mu _{ik}$ is modified as:

$$\begin{aligned} \mu _{ik} = \left\{ \begin{array}{ll} \frac{1}{\sum _{j=1}^{c}\left( d_{ik}/d_{jk}\right) ^{2/\left( m-1\right) }} &{}\quad \text{ if } \ non-outlier \\ 0 &{}\quad \text{ if } \ { outlier} \end{array}\right. \end{aligned}$$

(6)

To update the centroid, DOFCM algorithm uses Eq. (7) as FCM algorithm. For the constraint on fuzzy membership, DOFCM algorithm uses Eq. (8). The DOFCM algorithm is presented in Algorithm 1.

$$\begin{aligned} \mathbf {v}_{i} = \frac{\sum _{k=1}^{N}\left( \mu _{ik}^{m}\mathbf {x}_{k}\right) }{\sum _{k=1}^{N}\mu _{ik}^{m}} \end{aligned}$$

(7)

$$\begin{aligned} 0 \le \sum _{i=1}^{c}\mu _{ik} \le 1, k = 1,2,\ldots ,N \end{aligned}$$

(8)

Kernel Fuzzy C-Means (KFCM)

KFCM represents the kernel version of FCM. This algorithm uses a kernel function for mapping the data points from the input space to a high dimensional space, as it is shown in Fig. 2.

Fig. 2

KFCM feature space and kernel space

KFCM algorithm modifies the objective function of FCM using the mapping $\varvec{\Phi }$ as:

$$\begin{aligned} J_{KFCM} = \sum _{i=1}^{c}\sum _{k=1}^{N}\left( \mu _{ik}\right) ^{m}\left\| \varvec{\Phi }{\mathbf {(x_{k})}}-{\varvec{\Phi }}{\mathbf {(v_{i})}}\right\| ^{2} \end{aligned}$$

(9)

subject to:

$$\begin{aligned} \sum _{i=1}^{c}\mu _{ik}=1, k = 1,2,\ldots ,N \end{aligned}$$

(10)

where $\left\| {\varvec{\Phi }}{\mathbf {(x_{k})}}-{\varvec{\Phi }}{\mathbf {(v_{i})}}\right\| ^{2}$ is the square of the distance between ${\varvec{\Phi }}{\mathbf {(x_{k})}}$ and ${\varvec{\Phi }}{\mathbf {(v_{i})}}$. The distance in the feature space is calculated through the kernel in the input space as follows:

$$\begin{aligned} \left\| {\varvec{\Phi }}{\mathbf {(x_{k})}}-{\varvec{\Phi }}{\mathbf {(v_{i})}}\right\| ^{2}= & {} \mathbf {K(x_{k},x_{k})}- \mathbf {2K(x_{k},v_{i})} \nonumber \\&+ \mathbf {K(v_{i},v_{i})} \end{aligned}$$

(11)

If the Gaussian kernel is used, then $\mathbf {K(x,x) = 1}$ and $\left\| {\varvec{\Phi }}{\mathbf {(x_{k})}}-{\varvec{\Phi }}{\mathbf {(v_{i})}}\right\| ^{2} = \mathbf {2\left( 1-K(x_{k},v_{i})\right) }$. Thus Eq. (4) can be written as:

$$\begin{aligned} J_{KFCM} = 2\sum _{i=1}^{c}\sum _{k=1}^{N}\left( \mu _{ik}\right) ^{m}\left\| 1-\mathbf {K(x_{k},v_{i})}\right\| ^{2} \end{aligned}$$

(12)

where,

$$\begin{aligned} \mathbf {K(x_{k},v_{i})} = e^{-\left\| \mathbf {x}_{k}-\mathbf {v}_{i}\right\| ^{2}/\sigma ^{2}} \end{aligned}$$

(13)

Minimizing Eq. (12) under the constraint shown in Eq. (10), yields:

$$\begin{aligned} \mu _{ik} = \frac{1}{\sum _{j=1}^{c}\left( \frac{1-\mathbf {K(x_{k},v_{i})}}{1-\mathbf {K(x_{k},v_{j})}}\right) ^{1/\left( m-1\right) }} \end{aligned}$$

(14)

$$\begin{aligned} \mathbf {v}_{i} = \frac{\sum _{k=1}^{N}\left( \mu _{ik}^{m}\mathbf {K(x_{k},v_{i})x_{k}}\right) }{\sum _{k=1}^{N}\mu _{ik}^{m}\mathbf {K(x_{k},v_{i})}} \end{aligned}$$

(15)

The KFCM algorithm is presented in Algorithm 2.

Proposal of classification methodology using computational intelligence tools

The classification scheme proposed in this paper is shown in Fig. 3. It presents an off-line learning or training stage and an online recognition stage. In the training stage the historical data of the process are used to train (modeling the functional stages through the clusters) the fuzzy classifier. After the training, the classifier is used online (recognition) in order to process every new sample taken from the process. The result intends to offer information about the system state to the operator in real-time.

Fig. 3

Classification scheme using fuzzy clustering

The clustering methods create the classes based on a measure of similitude by bringing together the data acquired by a Supervisory Control and Data Acquisition System (SCADA). These classes can be associated to functional states. When fuzzy classifiers are used in the classification process, each sample is compared with the center of each class using a measure of similitude to determine the membership degree of the sample to each class. In general, the highest membership degree determines the class to which the sample is assigned, as it is showed in Eq. (16).

$$\begin{aligned} C_{i} = \left\{ i: max\left\{ \mu _{ik}\right\} , \forall i,k\right\} \end{aligned}$$

(16)

Off-line training

In the first step, the center of each known classes $\mathbf {v={v_{1},v_{2},}}\mathbf {\ldots ,v_{N}}$ is determined by using a historical data set representative of the different operation states of the process. A set of N observations (data points) $\mathbf {X}=[\mathbf {x}_{1},\mathbf {x}_{2},\ldots ,\mathbf {x}_{N}]$ are classified into c+1 groups or classes using the DOFCM algorithm. The c classes represent the normal operation conditions (NOC) of the process, and the faults to be diagnosed. They contain the information to be used in the next step. The other remaining class contains the data points identified as outliers by the DOFCM algorithm, and they are not used in the next step.

In the second step, the KFCM algorithm receives the set of observations classified by the DOFCM algorithm in the c classes. The KFCM algorithm maps these observations into a higher dimensional space in which the classification process obtains better results of satisfactory classifications. The Fig. 4 shows the procedure described in steps 1 and 2.

Fig. 4

Procedure performed by the DOFCM and KFCM algorithms

Finally, a third step to optimize the parameters of the algorithms used in steps 1 and 2 is implemented. In this step, the parameters m and $\sigma$ are estimated to optimize a validity index using an optimization algorithm . This will allow to obtain an improved U partition matrix, and therefore, a better position of the centers of the classes that characterize the different operation states of the system. Later, the estimated values of m in Eqs. (4, 12) and $\sigma$ in Eq. (13) will be used during the online recognition, and it will contribute to improve the classification of the samples obtained by the data acquisition system from the system.

The validity measures are indexes allowing to evaluate quantitatively the result of a clustering method and comparing its behavior when its parameters vary. Some indexes evaluate the resulting U matrix, while others are focused on the geometric resulting structure. The partition coefficient (PC) (Li et al. 2012; Pakhira et al. 2004; Wu and Yang 2005), which measures the fuzziness degree of the partition U, is used as validity measure in this case. Its expression is shown in the Eq. (17).

$$\begin{aligned} PC = \frac{1}{N}\sum _{i=1}^{c}\sum _{k=1}^{N}\left( \mu _{ik}\right) ^{2} \end{aligned}$$

(17)

If the partition U is less fuzzy, the clustering process is better. Being analyzed in a different way, it allows to measure the degree of overlapping among the classes. In this case, the optimum comes up when PC is maximized, i.e., when each pattern belongs to only one group. Likewise, minimum comes up when each pattern belongs to each group.

Therefore, the optimization problem is defined as:

$$\begin{aligned} max\left\{ PC\right\} = \frac{1}{N}\sum _{i=1}^{c}\sum _{k=1}^{N}\left( \mu _{ik}\right) ^{2} \end{aligned}$$

subject to:

$$\begin{aligned} m_{min} < m \le m_{max} \end{aligned}$$

$$\begin{aligned} \sigma _{min} \le \sigma \le \sigma _{max} \end{aligned}$$

In many scientific areas, and in particular in the fault diagnosis field, bio-inspired algorithms have been widely used with excellent results (Camps Echevarría et al. (2010); Liu and Lv 2009; Lobato et al. 2009) to solve optimization problems. They can efficiently locate the neighborhood of the global optimum in most occasions with an acceptable computational time. There is a large number of bio-inspired algorithms, in their original and improved versions. Some examples are Genetic Algorithm (GA), Differential Evolution (DE), Particle Swarm Optimization (PSO) and Ant Colony Optimization (ACO) among others. In this proposal, the typical ACO algorithm was used to obtain the optimum values of the parameters m and $\sigma$ after a comparison with PSO and DE algorithms.

On-line recognition

In this stage the fuzzy clustering algorithms are modified and the updating of the center of each class is not developed. The principal reason for doing this modification is to avoid the incorrect displacement of the center of each class due to an unknown fault of small dimensions with a high latency time.

When an observation k arrives, the DOFCM algorithm classifies it as outlier or as good observation taking into account the results of the training. Then, if the observation k does not belong to the outlier class, the distances between the observation and the class centers determined in the training stage are calculated. Next, the fuzzy membership degree of the observation k to each one of the c classes is obtained. The observation k will be assigned to the class where it has the highest membership degree. The approach used in this stage by using DOFCM-KFCM without the updating of the centers of the classes is described in Algorithm 3.

Benchmark case study: DAMADICS

Process description

In order to apply the proposed methodology to fault diagnosis in the mechanical systems the DAMADICS benchmark was selected. This benchmark represents an actuator (Bartys et al. 2006; Kourd et al. 2012) belonging to the class of intelligent electro-pneumatic devices widespread in industrial environment. The experimental data of the DAMADICS benchmark used in this paper was obtained from http://diag.mchtr.pw.edu.pl/damadics/. This actuator is considered as an assembly of devices consisting of:

• Control valve

• Spring-and-diaphragm pneumatic servomotor

• Positioner

The general structure of this actuator is shown in Fig. 5

Fig. 5

Structure of benchmark actuator system

The control valve acts on the flow of the fluid passing through the pipeline installation. A servomotor carries out a change in the position of the control valve plug, by acting on fluid flow rate. A spring-and-diaphragm pneumatic servomotor is a compressible fluid powered device in which the fluid acts upon the flexible diaphragm, to provide linear motion of the servomotor stem. The positioner is a device applied to eliminate the control-valve-stem miss-positions produced by the external or internal sources such as: friction, clearance in mechanical assemblies, supply pressure variations, hydrodynamic forces, among others. A description of simulated faults is shown in Table 1.

Table 1 Faults simulated in the DAMADICS

The set of measurements of 6 process variables shown in Table 2, were stored with a sample time of 1 second. For each one of the six process states (Normal operation and the five faults) 300 observations were stored for a total of 1800 observations. To this data set were added 300 new observations evenly distributed among the classes in order to represent the possible outliers for each class. Furthermore, white noise was added in the simulation to the measurement and process variables in order to simulate the variability presented in real world processes. The Fig. 6 shows a water level control loop in a tank with gravitational outflow.

Table 2 Measured process variables

Fig. 6

Water level control loop

Experiments

Two sets of three experiments each one were developed.

First, the three experiments presented in Table 3 were performed. In the first one, the step 1 (outliers determination) of the proposed classification scheme was not applied. In this experiment the KFCM algorithm was applied in the step 2. The aim of this experiment was to analyze the effect of the outliers in the final result of the classification process.

In second experiment only the DOFCM algorithm was applied in step 1. The principal aim of this experiment was to analyze the improvement in the performance of the classification process when a kernel function is introduced to obtain a better separation of the classes.

For the third experiment the DOFCM algorithm was selected to be applied in the step 1, and the KFCM algorithm was applied in the second step, respectively. The principal aim of this experiment was to analyze the results obtained in the classification process when both algorithms are adequately combined.

In these experiments the step 3 corresponding to the optimizing of the parameters of the algorithms were not applied. The values of the parameters used for the algorithms were: $Itr\_ {max} = 100$, $\epsilon$ = $10^{-5}$, $m=2$, $\sigma =1$.

Later, similar experiments were performed but including the step of optimizing the parameters of DOFCM and KFCM algorithms with the aim of analyzing the influence of the parameter selection (Param. Opt.) in the results of the classification process. These experiments are presented in Table 4.

Table 3 Experiments performed without step 3

Table 4 Experiments performed with step 3

It is necessary to highlight that to estimate the best parameters to be used in the DOFCM and KFCM algorithm many optimization algorithms can be used. In this paper, the results of three optimization algorithms in their typical structure were compared: DE (Camps Echevarría et al. (2010)), ACO (Camps Echevarría et al. 2014a), and PSO (Díaz et al. 2016). The parameters used by the DE algorithm were: $C_{R} = 0.5$, $F_{S} = 0.1$, $Z = 10$ and they were obtained from (Camps Echevarría et al. (2010)). In the case of ACO, the parameters selected were $k = 63$, $q_{0} = 0.5$, $Z = 50$, $C_{evap} = 0.3$, $C_{inc} = 0.1$ obtained from (Camps Echevarría et al. 2014b). The parameters used by the PSO algorithm were: population $size=20$, $wmax=0.9$, $wmin=0.4$, $c1=2$, $c2=2$ and they were obtained from (Camps Echevarría et al. 2014b).

In all cases a search space of $1 < m \le 2$ and $0.25 \le \sigma \le 20$ were considered, and the following stop criteria were used:

• Criterion 1: Maximum number of evaluations of the objective function ($Eval\_ {max}$ = 100).

• Criterion 2: $(Error = 1- PC )\,< \, \epsilon =0.00001$

DE, PSO and ACO algorithms were ran 10 times and the arithmetic mean of the parameters m, $\sigma$, and number of evaluations of the objective function ($Eval\_Fobj$) were calculated in the experiments 4, 5 and 6. Results are shown in Table 5.

Table 5 Arithmetical mean of the parameters m, $\sigma$ and $Eval\_Fobj$

In order to determine what algorithm (DE, PSO or ACO) was better, Friedman’s non-parametric statistical test was applied to the results obtained in experiments 4, 5 and 6. The result indicates that there are no significant differences in the results obtained by the 3 algorithms.

Finally, the ACO algorithm was selected, considering that it uses less evaluations of the objective function to estimate the parameters (See Table 5).

Analysis and discussion of results

Recognition stage

A very important step in the design of the fault diagnosis system is to analyze the performance of the diagnosis process. The most used criterion for this analysis is the confusion matrix (CM).

Table 6 Confusion matrix for experiment 1: KFCM (NOC: 350, F1: 350, F7: 350, F12: 350, F15: 350, F19: 350)

Table 7 Confusion matrix for experiment 2: DOFCM (NOC: 300, F1: 300, F7: 300, F12: 300, F15: 300, F19: 300, O: 300)

The confusion matrix allows to visualize the performance of the classifier in the classification process. Each $CM_{rs}$ element of a confusion matrix for $r \ne s$, indicates the number of times that the classifier confuses a state r with a state s in a set of $\mathbf {\mathrm {L}}$ experiments. The results obtained from the application of the proposed methodology to fault diagnosis in the modified DAMADICS data set are presented next.

The confusion matrices shown in Tables 6, 7, 8, 9,10 and 11 were obtained using a cross validation process. Cross validation divides the dataset into complementary subsets (d), by performing the analysis on $d-1$ subsets called the training set, and validating the analysis on the other subset called the validation set or testing set. To reduce variability d rounds of cross-validation are performed using a different partition as a validation set in each one. Finally, the validation results are averaged. Figure 7 shows the cross-validation process for four partitions of the data set. In the experiments implemented in the DAMADICS, the cross-validation was performed with 10 partitions of the data set.

Table 8 Confusion matrix for experiment 3: DOFCM-KFCM (NOC: 300, F1: 300, F7: 300, F12: 300, F15: 270, F19: 300)

Table 9 Confusion matrix for experiment 4: KFCM (NOC: 350, F1: 350, F7: 350, F12: 350, F15: 350, F19: 350)

Table 10 Confusion matrix for experiment 5: DOFCM (NOC: 300, F1: 300, F7: 300, F12: 300, F15: 300, F19: 300, O: 300)

Table 11 Confusion matrix for experiment 6: DOFCM-KFCM (NOC: 300, F1: 300, F7: 300, F12: 300, F15: 276, F19: 300)

Experiment 1

Table 6 shows the confusion matrix for experiment 1 where the operation states NOC: Normal Operation Condition, and the faults F1, F7, F12, F15 and F19 were considered. The main diagonal is associated with the number of observations successfully classified. Since the total number of observations per class is known, the accuracy or hit rate (HR), and the overall error (E) can also be computed. The last row shows the general value of the hit rate and the error (GEN).

The results indicate the difficulty of the KFCM algorithm to obtain satisfactory classification results in the presence of outliers. This problem affects the correct classification of the different operating states, principally of F1, F15 and F19.

Fig. 7

Cross validation process

Experiment 2

Table 7 shows that the DOFCM algorithm classifies as outliers 296 observations of the 300 observations added to the dataset (O class) by achieving a 98.67$\%$ of accuracy in this classification part. However, although the DOFCM algorithm identifies the outliers correctly, it is not able to obtain good results in the final classification due to overlaps between classes. This is the case of faults F1 and F15.

Experiment 3

Step 1

The classification results of the step 1 in this experiment are similar to those of the experiment 2 (Table 7). The 300 observations added as outliers were correctly identified in a 98,67$\%$. Because 30 observations of F15 were classified in class O, the class F15 is composed of 270 observations that might be used in the next step.

Fig. 8

Global classification ($\%$) obtained for the experiments 1–3

Step 2

Table 8 shows the confusion matrix where the best classification results are achieved. These results are due to the eliminations of the outliers in a first step, and the application of the kernel function in the second step which allow to achieve a greater separability of the classes.

The satisfactory outcomes obtained in this experiment confirm the validity of the new methodology to fault diagnosis proposed in this paper using computational intelligence techniques.

Fig. 9

Global classification ($\%$) obtained for the experiments 4–6

A summary of the global classification percentages obtained for each experiment are shown in Fig. 8.

Experiment 4

Table 9 shows the confusion matrix for experiment 4. As in experiment 1, the results indicate the difficulty of the KFCM algorithm to obtain satisfactory results in the classification in the presence of outliers. However, with the use of the optimized parameters m and $\sigma$, the results of the operating state classification are improved.

Experiment 5

Table 10 shows a similar behavior of the DOFCM algorithm compared with experiment 2. However, with the use of the optimized parameters m and $\sigma$, the classification results are better.

Experiment 6

Step 1

The classification results of the step 1 in this experiment are similar to those of the experiment 5 (Table 10). The 300 observations added as outliers were correctly identified. Because 24 observations of F15 were classified in class O, the class F15 is composed of 276 observations that might be used in the next step.

Step 2

Table 11 shows the results after applying the KFCM algorithm. The behavior of the DOFCM and KFCM algorithms is similar compared with experiment 3. However, with the use of the optimized parameters m and $\sigma$, the classification results are better.

The excellent results obtained in this experiment confirm the validity of the new methodology to fault diagnosis proposed in this paper using computational intelligence techniques.

A summary of the global classification percentages obtained for the experiments 4, 5, and 6 are shown in Fig. 9.

Comparing the results obtained in the first set of experiments with the results of the second set, it is evident the importance of selecting the best parameters for the DOFCM and KFCM algorithms which support the necessity of the stage 3 in the training process

Analysis of the number of false and missing alarms

In order to evaluate the quality of the fault detection process, the number of false and missing alarms are usually analyzed. According to Yin et al. (2012), these indicators called False Alarm Rate (FAR) and Fault Detection Rate (FDR) can be calculated by:

$$\begin{aligned} FAR = \frac{No.\, of \, samples \left( J>J_{lim}\left| f=0\right. \right) }{total \, samples\left( f=0\right) } \end{aligned}$$

(18)

$$\begin{aligned} FDR = \frac{No.\, of \, samples \left( J>J_{lim}\left| f\ne 0\right. \right) }{total \, samples \left( f\ne 0\right) } \end{aligned}$$

(19)

where J is the output for the used discriminative algorithms by considering the fault detection stage as a binary classification process, and $J_{lim}$ is the threshold that determines whether one sample is classified as a fault or normal operation. The performance of a diagnosis system is satisfactory if low values of the FAR indicator an high values of the FDR indicator are obtained.

Fig. 10

Performance indicator ($\%$) obtained for each experiment

The results obtained for each experiment are summarized in Fig. 10, where it can be seen that in general form all variants have satisfactory performances. The best results are obtained in the experiment 6 which correspond with the application of the fault diagnosis methodology proposed in this paper.

Comparison with other fuzzy clustering algorithms

Recently, some fuzzy clustering algorithms with excellent results have been proposed with the aim of improving the classification in different applications. A comparison with some of these algorithms is developed in this section.

FC-PFS algorithm

Based on theory of picture fuzzy set (PFS), Thong and Son (2016a) proposed a picture fuzzy model for clustering problem called FC-PFS, which was proven to get better clustering quality than other relevant methods. Based on the FCM algorithm, the picture fuzzy clustering algorithm (FC-PFS) modifies the objective function to adapt the fuzzy clustering on PFS (Thong and Son 2016a). The modification includes two points. The first one inherits from FCM’s objective function where the membership degree $\mu$ are replaced by $\mu$($2 - \xi$) which means that one data element belonging to a cluster has both: high value of positive degree and low value of refusal degree (Thong and Son 2016a). The second point is to add the entropy information to the objective function which helps the algorithm to reduce the neutral and refusal degree of an element to become a member of the cluster. The entropy information plays an important role to enhance the clustering quality (Thong and Son 2016a). The values of the parameters used are: $Itr\_ {max} = 100$, $\epsilon = 10^{-5}$, $m = 2$ and $\alpha = 0.6$ (where $\alpha \in (0,1]$ is an exponent coefficient used to control the refusal degree in PFS sets).

PFCA-CD algorithm

In the paper Thong and Son (2016b), is proposed a novel picture fuzzy clustering algorithm for complex data called PFCA-CD that deals with both mix data type and distinct data structures. The idea of this method is the modification of FC-PFS, using a measurement for categorical attributes, multiple centers of one cluster and an evolutionary strategy - Particle Swarm Optimization (PSO). Therein, the multiple centers are used to deal with complex structure of data because data with complex structures have many different shapes that cannot be represented by one center. The values of the parameters used are: $Itr\_ {max} = 100$, $\epsilon = 10^{-5}$, $m = 2$, $\alpha = 0.6$, $C_{1} = C_{2} = 1$ (where $C_{1}, C_{2} \ge 0$ are PSO’s parameters. Generally, $C_{1}, C_{2}$ are often set as 1).

DBWFCM algorithm

A new fuzzy clustering method called density-based weighted FCM (DBWFCM) is proposed in Li et al. (2016). In this algorithm, the weight of an object is decided by the density of the objects around this object. To more objects around this object, the weight of this object is bigger. That means the object that has bigger weight is more likely to be a cluster center. There are two stages of the density-based weighted FCM. The first stage is designed to calculate the weights of every object, the second stage is the clustering stage. The values of the parameters used are: $Itr\_ {max} = 100$, $\epsilon = 10^{-5}$ and $m = 2$.

Table 12 Confusion matrix: FC-PFS (NOC: 350, F1: 350, F7: 350, F12: 350, F15: 350, F19: 350)

Table 13 Confusion matrix: PFCA-CD (NOC: 350, F1: 350, F7: 350, F12: 350, F15: 350, F19: 350)

Table 14 Confusion matrix: DBWFCM (NOC: 350, F1: 350, F7: 350, F12: 350, F15: 350, F19: 350)

Results of the comparison

To establish the comparison, the same data set used in the last experiments was used. Tables 12, 13 and 14 show the results of the confusion matrices related with the algorithms used in the comparison. As it can be observed, the results indicate the difficulty of these algorithms to obtain satisfactory results in the classification in the presence of outliers.

A summary of these results can be seen in Fig. 11, where the global classification percentages obtained for each algorithm are showed. The results obtained with the algorithms used in the comparison (FC-PFS, PFCA-CD, DBWFCM) are smaller than the result obtained with the proposal made in this paper ($96.23\%$).

Fig. 11

Global classification ($\%$) obtained for each algorithm

Figure 12 shows the FAR and FDR values obtained for each one of these algorithms. It is evident that the results obtained with the proposal made in this paper ($\mathrm{FAR} = 0\%$ and $\mathrm{FDR} = 99.05\%$) constitute the best outcomes but the best practice is to support this appreciation by applying statistical tests (García and Herrera 2008; García et al. 2009; Luengo et al. 2009).

Fig. 12

Performance indicator ($\%$) obtained for each algorithm

Statistical tests

First, the non-parametric Friedman test is applied in order to demonstrate that there is at least one algorithm whose results have significant differences with respect to results of the others. Afterwards, if the null-hypothesis of the Friedman test is rejected, it is necessary to make a comparison in pairs to determine the best algorithm(s). For this, the non-parametric Wilcoxon test is applied.

Friedman test

In this case, for four algorithms ($k = 4$) and 10 data sets due to the cross validation ($N = 10$), the value obtained to the Friedman statistic was $F_{F}$ = 241 . With $k = 4$ and $N = 10$, $F_{F}$ is distributed according to the F distribution with $4-1=3$ and $(4-1)\times (10-1)=27$ degrees of freedom. The critical value of F(3,27) for a level of significance $\alpha =0.05$ is 2.9604, then the null-hypothesis is rejected ($F(3,27) \,< \,F_{F}$. This means that at least, there is an algorithm whose results differ significantly from the rest.

Wilcoxon test

Table 15 shows the results of the comparison in pairs of the algorithms (1: FC-PFS, 2: PFCA-CD, 3: DBWFCM, 4: DOFCM-KFCM) using the Wilcoxon test. The first two rows contain the values of the sum of the positive ($R^{+}$) and negative ($R^{-}$) rank for each comparison established. The next two rows show the statistical values T and the critical value of T for a level of significance $\alpha =0.05$. The last row indicates which algorithm was the winner in each comparison. The summary in Table 16 shows how many times each algorithm was the winner. This results validates once again the methodology proposed in this paper.

Table 15 Results of the Wilcoxon test

Table 16 Final result of the comparison between algorithms

Conclusions

The mechanical systems are fundamental elements in the manufacturing industry and a large number of faults in these industries occur in such systems. In the present paper a new robust scheme to fault diagnosis in mechanical systems using computational intelligence techniques is proposed to decrease the unfavorable impact of these faults in the productivity, the environment and the safety of the operators.

In this paper, several experiments were presented with the aim of demonstrating that the best strategy is the one that integrates the DOFCM, KFCM algorithms and an optimization algorithm. In this paper the ACO algorithm was used. The DOFCM algorithm was used in the first step for preprocessing the data to remove the outliers. The KFCM algorithm was used in the second step for the data classification to make use of the advantages introduced by the kernel function in the separability of the classes , in order to obtain better classification outcomes. Finally, the ACO algorithm was used to optimize the parameters of the algorithms used in the previous steps.

Three fuzzy clustering algorithms recently presented in the scientific literature were selected to establish a comparison with the proposed methodology. After comparing the obtained results, it was demonstrated that the proposed methodology obtained the best performance.