Keywords

1 Introduction

In modern industries is a requirement to obtain high level of efficiency, quality of the products, industrial safety, and to accomplish with environmental regulations. Faults in affect the productivity of the industrial plants, in several cases compromises the safety of the operators and they can affect the environment [8].

Mechanical systems represent a fundamental part of the most industrial plants and a significant number of faults in these plants are associated to this type of systems. It is the main reason for which the scientific community dedicate an special attention in the develop of fault diagnosis strategies to mechanical systems [10, 12, 16, 20].

In general, fault diagnosis methods are classified in two large groups: those based on models [3, 5] and those based on historical data [4, 9]. The strategies in the first group are based on residuals obtained from the difference between the measurable signals from the real process and the values obtained from a model of the process. However, obtaining an adequate model for this aim in complex processes is very difficult. In the case of the approaches based on historical data, they do not need a mathematical model, and neither require much prior knowledge of the process parameters [15]. This is an advantage in complex systems, where relationships among variables are nonlinear, and not totally known.

Techniques based on fuzzy tools are increasingly being applied in several scientific areas. Some examples are: image processing [14], control strategies [13], classification [6], and condition monitoring applications [11].

A main aspect in the use of fuzzy sets is the provision of membership grades. In order to enhance the capability of fuzzy sets for capturing and model user provided membership information, researchers have introduced non-standard second order fuzzy sets such as intuitionistic [1] and interval type-2 fuzzy sets [7]. These non-standard fuzzy sets allow the inclusion of imprecision and uncertainty in the specification of membership grades.

In 2013, Prof. Ronald R. Yager introduced another class of non-standard fuzzy subset named Pythagorean fuzzy subset [17]. In [18], it is shown that the space of Pythagorean membership grades is greater than the space of intuitionistic membership grades. This allows the use of the Pythagorean fuzzy sets in a greater set of applications than the intuitionistic fuzzy sets.

The data obtained by the Supervisory Control and Data Acquisition (SCADA) systems from complex industrial processes are frequently corrupted by noise. This introduces uncertainties in the observations which seriously affect the performance of the fault diagnosis systems by increasing the number of false alarms (fault diagnosis system confuses the Normal Operation Condition (NOC) with a fault), and by deteriorating the correct identification and location of faults.

In order to overcome these problems, and to obtain a robust fault diagnosis strategy applied in mechanical systems, an approach based on the use of Pythagorean membership grades is proposed which constitutes the main contribution of this paper. In this sense, a new variant of the Intuitionistic Fuzzy C-Means algorithm, called Pythagorean Fuzzy C-Mean algorithm (PyFCM), and it’s kernel version (KPyFCM), which permits to achieve greater separability among classes and reduce classification errors, are obtained.

The organization of the paper is the following: in Sect. 2, the general characteristics of the tools used in the proposed methodology are presented. In Sect. 3, a description of the classification methodology using fuzzy clustering techniques is presented. In Sect. 4 the proposed methodology is evaluated with the Development and Application of Methods for Actuator Diagnosis in Industrial Control Systems (DAMADICS) benchmark. Next, an analysis of the results obtained and a comparison with other computational tools is developed in Sect. 5. Finally, the conclusions are presented.

2 Materials and Methods

In this section are firstly presented the general characteristics of Intuitionistic FCM (IFCM) algorithm. Next, the general characteristics of the Pythagorean membership grades, the Pythagorean FCM algorithm (PyFCM), and its kernel version (KPyFCM) are also presented.

2.1 Intuitionistic Fuzzy C-Means Algorithm

Intuitionistic fuzzy c-means clustering algorithm is based upon intuitionistic fuzzy set theory given by Atanassov [1] where membership \(\mu (x)\) and nonmembership v(x) functions are considered. An intuitionistic fuzzy set A in X, is written as:

$$\begin{aligned} A = \left\{ x,\mu _{A}(x),v_{A}(x) \left| x \in X \right. \right\} \end{aligned}$$
(1)

where \(\mu _{A}(x) \longrightarrow [0,1]\), \(v_{A}(x) \longrightarrow [0,1]\) are the membership and non-membership degrees of an element in the set A with the condition: \(0\le \mu _{A}(x)+v_{A}(x)\le 1\). For all intuitionistic fuzzy sets, a hesitation degree \(\pi _{A}(x)\) is also indicated [1]. It express the lack of knowledge in defining of whether x belongs to IFS or not and it is given by:

$$\begin{aligned} \pi _{A}(x) = 1 - \mu _{A}(x) - v_{A}(x); 0\le \pi _{A}(x) \le 1 \end{aligned}$$
(2)

Intuitionistic fuzzy c-means objective function contains two terms: (i) modified objective function of conventional FCM using Intuitionistic fuzzy set and (ii) intuitionistic fuzzy entropy (IFE). IFCM minimizes the objective function 3:

$$\begin{aligned} J_{IFCM} = \sum _{i=1}^{c}\sum _{k=1}^{N}\mu _{ik}^{*m}d_{ik}^{2} + \sum _{i=1}^{c}\pi ^{*}_{i}e^{1-\pi ^{*}} \end{aligned}$$
(3)

\(\mu _{ik}^{*} = \mu _{ik}^{m} + \pi _{ik}\), where \(\mu _{ik}^{*}\) denotes the intuitionistic fuzzy membership and \(\mu _{ik}\) denotes the conventional fuzzy membership of the kth data in the ith class. \(\pi _{ik}\) is the hesitation degree, which is defined as:

$$\begin{aligned} \pi _{ik} = 1 - \mu _{ik} - (1 - \mu ^{\alpha }_{ik})^{1/\alpha }, \alpha > 0 \end{aligned}$$
(4)

and it is calculated from Yager’s intuitionistic fuzzy complement as

$$\begin{aligned} N(x) = (1-x^{\alpha })^{1/\alpha }\,\,,\,\,\alpha > 0 \end{aligned}$$
(5)

thus, with the help of Yager’s intuitionistic fuzzy complement, intuitionistic fuzzy set becomes:

$$\begin{aligned} A = \left\{ x,\mu _{A}(x),(1 - \mu _{A}(x)^{\alpha })^{1/\alpha }\left| x \in X \right. \right\} \end{aligned}$$
(6)

and

$$\begin{aligned} \pi ^{*}_{i} = \frac{1}{N}\sum _{k=1}^{N}\pi _{ik}, k \in [1,N] \end{aligned}$$
(7)

The second term in the objective function is called intuitionistic fuzzy entropy (IFE) and it is the measure of fuzziness in a fuzzy set [19]. For intuitionistic fuzzy cases, if \(\mu _{A}(x_{i})\), \(v_{A}(x_{i})\), \(\pi _{A}(x_{i})\) are the membership, non-membership, and hesitation degrees of the elements of the set \(X = {x_{1},x_{2},...,x_{n}}\), then intuitionistic fuzzy entropy, IFE that denotes the degree of intuitionism in fuzzy set, may be given as:

$$\begin{aligned} IFE(A) = \sum _{i=1}^{n}\pi _{A}(x_{i})e^{[1-\pi _{A}(x_{i})]} \end{aligned}$$
(8)

where \(\pi _{A}(x_{i}) = 1 - \mu _{A}(x_{i}) - v_{A}(x_{i})\) IFE is introduced in the objective function to maximize the good points in the class. The goal is to minimize the entropy. Modified cluster centers are:

$$\begin{aligned} v^{*}_{i} = \frac{\sum _{k=1}^{n}\mu ^{*}_{ik}x_{k}}{\sum _{k=1}^{n}\mu ^{*}_{ik}} \end{aligned}$$
(9)

2.2 Pythagorean Fuzzy C-Means Algorithm (PyFCM)

A new class of nonstandard fuzzy sets called Pythagorean fuzzy sets (PFS) is presented in [18]. The membership grades associated with these sets will be named as Pythagorean membership grades.

For expressing the Pythagorean membership grades a pair of values r(x) and d(x) for each \(x \in X\) are assigned. Both values will be called as the strength of commitment at x in the case of \(r(x)\, \in \,[0,1]\) and the direction of commitment in the case of \(d(x)\, \in \, [0,1]\). The values r(x) and d(x) are associated with a pair of membership grades \(A_{Y}(x)\) and \(A_{N}(x)\). These memberships grades indicate the support for membership of x in A and the support against membership of x in A respectively. Next, it is shown that \(A_{Y}(x)\) and \(A_{N}(x)\) are related using the Pythagorean complement with respect to r(x). More specially, the values of \(A_{Y}(x)\) and \(A_{N}(x)\) are defined from r(x) and d(x) as

$$\begin{aligned} A_{Y}(x) = r(x)cos(\theta (x)) \end{aligned}$$
(10)
$$\begin{aligned} A_{N}(x) = r(x)sin(\theta (x)) \end{aligned}$$
(11)

where

$$\begin{aligned} \theta (x) = (1-d(x))\frac{\pi }{2} \end{aligned}$$
(12)

and \(\theta (x)\in [0, \frac{\pi }{2}]\) is expressed in radians.

In [18] is shown that \(A_{Y}\)(x) and \(A_{N}\)(x) are Pythagorean complements with respect to r(x) and that

$$\begin{aligned} A^2_{Y}(x)+A^2_{N}(x)= r^2(x)(cos^{2}(\theta ) + sin^{2}(\theta )) \end{aligned}$$
(13)

In a general form, a Pythagorean membership grade is represented by a pair of values (a, b) such that \(a,b \in [0,1]\) and \(a^{2}\) + \(b^{2}\) \(\le \) 1. In this case, \(a = A_{Y}(x)\), indicates the degree of support for membership of x in A and, b = \(A_{N}(x)\) indicates the degree of support against membership of x in A. Taking into account the pair (a, b), the Eq. (13) can be expressed as \(a^{2}\) + \(b^{2}\) = \(r^{2}\). This indicates that a Pythagorean membership grade is a point of a circle of radius r.

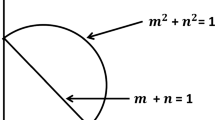
An intuitionistic membership grade presented in [1] is also a pair (a, b) that satisfies \(a,b \in [0,1]\) and \(a + b \le 1\). In [18] was demonstrated that the set of Pythagorean membership grades is greater than the set of intuitionistic membership grades. That result is clearly shown in Fig. 1 taken from [18]. Here, it is possible to observe that intuitionistic membership grades are all points under the line x + y \(\le \) 1 and the Pythagorean membership grades are all points with \(x^{2}\) + \(y^{2}\) \(\le \) 1.

Fig. 1.
figure 1

Comparison of space of Pythagorean and intuitionistic membership grades.

Full size image

Taking into account the theory of Pythagorean fuzzy sets, it can be said that the objective function on the Pythagorean Fuzzy C-Means algorithm (PyFCM) is similar to the one obtained for the IFCM algorithm according Eq. 3. In this case, a hesitation degree, \(\pi _{A}(x)\), is given by:

$$\begin{aligned} \pi _{A}(x) = 1 - \mu ^{2}_{A}(x) - v^{2}_{A}(x); 0\le \pi _{A}(x) \le 1 \end{aligned}$$
(14)

Therefore, in Eq. 3, \(\pi _{ik}\) is defined as:

$$\begin{aligned} \pi _{ik} = 1 - u^{2}_{ik} - (1 - u^{\alpha }_{ik})^{2/\alpha }, \alpha > 0 \end{aligned}$$
(15)

The most important implication of this result is the possibility of using the Pythagorean fuzzy sets in a larger set of situations than intuitionistic fuzzy sets. In the case of fault diagnosis, this result allows to improve the classification process.

Pythagorean membership functions allow the use of a larger set of numeric values and greater in absolute value than those allowed by institutionistic membership functions for assigning the membership degree to an observation. In the classification process, the membership degree to a class is maximized. If there is a larger number of values in the search space and these values are greater in absolute value than the institutionistic case, then, this allows to improve the classification process due to a better separation of classes.

2.3 Pythagorean Fuzzy C-Means Algorithm Based on a Kernel Approach

Kernel version of the PyFCM (KPyFCM) is obtained in order to achieve greater separability among classes, and reduce the classification errors. KPyFCM minimizes the objective function:

$$\begin{aligned} J_{KPyFCM} = \sum _{i=1}^{c}\sum _{k=1}^{N}\mu _{ik}^{*m}\left\| \mathbf {\Phi (x_{k})}-\mathbf {\Phi (v_{i})}\right\| ^{2} + \sum _{i=1}^{c}\pi ^{*}_{i}e^{1-\pi ^{*}} \end{aligned}$$
(16)

where \(\mu _{ik}^{*} = \mu _{ik}^{m} + \pi _{ik}\), \(\pi _{ik}\) hesitation degree, which is defined according to Eq. (15) and \(\pi ^{*}_{i}\) is defined as the Eq. (7).

Also, \(\left\| \mathbf {\Phi (x_{k})}-\mathbf {\Phi (v_{i})}\right\| ^{2}\) is the square of the distance between \(\mathbf {\Phi (x_{k})}\) and \(\mathbf {\Phi (v_{i})}\). The distance in the feature space is calculated through the kernel in the input space as follows:

$$\begin{aligned} \left\| \mathbf {\Phi (x_{k})}-\mathbf {\Phi (v_{i})}\right\| ^{2} = \mathbf {K(x_{k},x_{k})}- \mathbf {2K(x_{k},v_{i})} + \mathbf {K(v_{i},v_{i})} \end{aligned}$$
(17)

One of kernel function more used in the scientific literature is the Gaussian kernel because of it’s easy implementation and satisfactory results. If the Gaussian kernel is used, then \(\mathbf {K(x,x) = 1}\) and \(\left\| \mathbf {\Phi (x_{k})}-\mathbf {\Phi (v_{i})}\right\| ^{2} = \mathbf {2\left( 1-K(x_{k},v_{i})\right) }\). Thus, Eq. (16) can be written as:

$$\begin{aligned} J_{KPyFCM} = 2\sum _{i=1}^{c}\sum _{k=1}^{N}\mu _{ik}^{*m}\left\| 1-\mathbf {K(x_{k},v_{i})}\right\| ^{2} + \sum _{i=1}^{c}\pi ^{*}_{i}e^{1-\pi ^{*}} \end{aligned}$$
(18)

where,

$$\begin{aligned} \mathbf {K(x_{k},v_{i})} = e^{-\left\| \mathbf {x}_{k}-\mathbf {v}_{i}\right\| ^{2}/\sigma ^{2}} \end{aligned}$$
(19)

Minimizing Eq. (18) under the constraint \(\sum _{i=1}^{l}u_{ik}=1, k = 1,2,...,N\), yields:

$$\begin{aligned} \mu _{ik}^{*} = \frac{1}{\sum _{j=1}^{c}\left( \frac{1-\mathbf {K(x_{k},v_{i})}}{1-\mathbf {K(x_{k},v_{j})}}\right) ^{1/\left( m-1\right) }} \end{aligned}$$
(20)
$$\begin{aligned} \mathbf {v}_{i} = \frac{\sum _{k=1}^{N}\left( \mu _{ik}^{*m}\mathbf {K(x_{k},v_{i})x_{k}}\right) }{\sum _{k=1}^{N}\mu _{ik}^{*m}\mathbf {K(x_{k},v_{i})}} \end{aligned}$$
(21)

KPyFCM algorithm is presented in Algorithm 1.

figure a

3 Description of the Proposal

The classification scheme proposed in this paper is shown in Fig. 2. It presents an offline training stage and an online recognition stage. In the training stage, the historical data of the process are used to train (modeling the functional stages through the clusters) a fuzzy classifier. After the training, the classifier is used online (recognition) in order to classify every new sample taken from the process. In this stage, the observations obtained by the SCADA system are classified one by one. In the classification process, the distance between the received observation and each one of the class centers is calculated. Next, the fuzzy membership degree of the observation to each one of the c classes is obtained. The observation will be assigned to the class with highest membership degree. The result intends to offer information about the system state in real-time for the operator.

4 Benchmark Case Study: DAMADICS

In order to apply the proposed methodology to fault diagnosis in the mechanical systems the DAMADICS benchmark was selected. This benchmark represents an actuator [2] belonging to the class of intelligent electro-pneumatic devices widespread in industrial environment. This actuator is considered as an assembly of devices consisting of:

  • Control valve

  • Spring-and-diaphragm pneumatic servomotor

  • Positioner

The general structure of this actuator is shown in Fig. 3

Fig. 2.
figure 2

Classification scheme using fuzzy clustering.

Full size image
Fig. 3.
figure 3

Structure of benchmark actuator system.

Full size image

The control valve acts on the flow of the fluid passing through the pipeline installation. A servomotor carries out a change in the position of the control valve plug, by acting on fluid flow rate. A spring-and-diaphragm pneumatic servomotor is a compressible fluid powered device in which the fluid acts upon the flexible diaphragm, to provide linear motion of the servomotor stem. The positioner is a device applied to eliminate the control-valve-stem miss-positions produced by the external or internal sources such as: friction, clearance in mechanical assemblies, supply pressure variations, hydrodynamic forces, among others. The set of measurements of 6 process variables were stored with a sample time of 1 s. For each one of the six process states (Normal operation and the five faults) 300 observations were stored for a total of 1800 observations. To this data set were added 300 new observations evenly distributed among the classes in order to represent the possible outliers for each class. Furthermore, white noise was added in the simulation to the measurement and process variables in order to simulate the variability present in real world processes. A description of the simulated faults and the measured process variables is shown in Table 1.

Table 1. Faults simulated and measured process variables in DAMADICS
Full size table

5 Analysis of Results

Table 2 shows the confusion matrix for experimental dataset where F1: Fault 1, F7: Fault 7, F12: Fault 12, F15: Fault 15 and F19: Fault 19. The main diagonal is associated with the number of observations successfully classified. Since the total number of observations per class is known, the accuracy (TA) can also be computed. The last row shows the average (AVE) of TA.

Table 2. CM for the DAMADICS process (F1: 300, F7: 300, F12: 300, F15: 300, F19: 300).
Full size table

As several algorithms are presented, it is necessary to analyze if there are significant differences among the results of them. To achieve this, it is necessary to apply statistical tests.

5.1 Statistical Tests

In our case, for six experiments (\(k = 6\)) and 10 datasets (\(N = 10\)), the value of statistical Friedman \(F_{F}\) = 340 was obtained. With \(k = 6\) and \(N = 10\), \(F_{F}\) is distributed according to the F distribution with \(6-1=5\) and \((6-1)\times (10-1)=45\) degrees of freedom. The critical value of F(5,45) for \(\alpha =0.05\) is 2.4221, so the null-hypothesis is rejected (F(5,45) < \(F_{F}\)) which means that at least the average performance of at least one algorithm is significantly different from the average value of the performance of other algorithms and the Wilcoxon test is applied to determine it.

Table 3 shows the results of the comparison in pairs of the algorithms (1: FCM, 2: IFCM, 3: PyFCM, 4: KFCM, 5: KIFCM, 6: KPyFCM) using the Wilcoxon test. The first two rows contain the values of the sum of the positive (\(R^{+}\)) and negative (\(R^{-}\)) rank for each comparison established. The next two rows show the statistical values T and the critical value of T for a level of significance \(\alpha =0.05\). The last row indicates which algorithm was the winner in each comparison.

Table 3. Results of the Wilcoxon test
Full size table

As can be seen, among the FCM, IFCM and PyFCM algorithms, the PyFCM algorithm obtains the better results. In the analysis with the Kernel algorithms, the KPyFCM algorithm obtains the better results. Taking into account all algorithms, it is shown that the KPyFCM algorithm obtains the best results.

6 Conclusions

The main contribution of this work is the development of a robust scheme for condition monitoring in industrial systems by using Pythagorean membership grades. The fundamental motivation for this proposal is based on the fact that the space of Pythagorean membership grades is greater than the space of the standard and intuitionistic membership grades. This allows for a better assignation of the membership grade to the observations obtained from complex industrial processes that are corrupted by noise which introduce high uncertainties, and this seriously affects the performance of the condition monitoring systems.

In the proposal, the FCM algorithm is modified by using Pythagorean fuzzy sets, and a new variant of that algorithm called Pythagorean Fuzzy C-Mean (PyFCM) algorithm is obtained. In addition, a kernel version of the PFCM algorithm (KPyFCM) is obtained in order to achieve greater separability among the classes, for reducing the classification errors. The approach proposed was validated using synthetic datasets and the DAMADICS process benchmark. The promising results obtained indicate the feasibility of the proposal.