1 Introduction

Two synaptically connected neurons communicate via spikes or action potentials (APs). Neglecting the underlying conductance dynamics, one can model the effect of a presynaptic AP as a jump in the voltage of the postsynaptic neuron. The height of this jump then depends on the strength of the synapse. Cortical neurons typically have thousands of presynaptic partners (Braitenberg and Schüz 1998) that often fire asynchronously. Thus, a popular assumption in theoretical work has been that the overall rate of input is high, while each individual presynaptic spike only causes a very small jump in voltage, so that the input can be modeled as a Gaussian process. If one additionally assumes that it is temporally uncorrelated, one obtains the so-called diffusion approximation (DA). Modeling neural input as Gaussian white noise has allowed theoretical insights, ranging from the statistics of single neurons to the dynamics of whole networks (Gerstein and Mandelbrot 1964; Ricciardi and Sacerdote 1979; Lindner and Schimansky-Geier 2001; Brunel 2000). This kind of theory has been extended to correlated Gaussian noise (Brunel and Sergi 1998; Moreno et al. 2002; Fourcaud and Brunel 2002; Moreno-Bote et al. 2008; Schwalger et al. 2015).

The assumption that individual spikes have only a weak effect on postsynaptic voltage, however, is not always justified: In recent experiments, the mean peak height of evoked postsynaptic potentials (EPSPs) has been reported to lie in the range of 1–2mV (Thomson et al. 1993; Markram et al. 1997; Song et al. 2005; Lefort et al. 2009). Further, the distributions of EPSPs can be highly skewed (Song et al. 2005; Lefort et al. 2009), so that individual EPSPs can range up to 8–10mV (Thomson et al. 1993; Lefort et al. 2009; Loebel et al. 2009). For pyramidal neurons, the distance from resting potential to threshold lies between 10 and 20mV (Badel et al. 2008; Lefort et al. 2009). Thus, between 5 and 20 EPSPs – and in some cases even a single strong EPSP – can be sufficient to make the neuron fire. If such large EPSPs dominate the input to the neuron, the DA cannot be expected to yield good results (Nykamp and Tranchina 2000), and one should rather model the input as a shot noise (SN), in which individual events have weights that are drawn from a skewed distribution. In contrast to these expectations, some approximations, such as the moment-closure method for multidimensional integrate-and-fire (IF) models, suggest that there is no difference between neurons driven by Gaussian or shot noise - at least with respect to simple firing statistics (this is critically evaluated by Ly and Tranchina (2007)). Hence, it is important to test the effect of the pulsatile nature of SN input on the firing statistics of IF neurons and to compare it with the case of Gaussian noise.

Integrate-and-fire neurons driven by SN have been analytically studied for a long time (Stein 1965; Holden 1976; Tuckwell 1988), with most studies focusing on the voltage distribution, either in spiking, current-based leaky IF (LIF) neurons (Sirovich et al. 2000; Sirovich 2003; Richardson 2004, Helias et al. 2010a, 2010b, 2011) or in conductance-based neurons far below threshold (Richardson 2004; Richardson and Gerstner 2005, 2006; Wolf and Lindner 2008, 2010). With respect to neural signal transmission, it was found that LIF neurons can faithfully transmit signals even at high frequencies if they are encoded in an SN process, rather than as a current modulation (Helias et al. 2010b; 2011; Richardson and Swarbrick 2010).

Most of the work concerning SN-driven spiking neurons has relied on simulations or approximation; exact analytical results are rare. For perfect IF (PIF) neurons driven by excitatory Poisson shot noise with constant weights, the density of interspike intervals and the power spectrum have been calculated early on by Stein et al. (1972). Some results have been derived without explicit reference to IF neurons but apply directly to their interspike-interval (ISI) density; these comprise the Laplace-transformed first-passage-time density of linear systems driven by excitatory (Tsurui and Osaki 1976; Novikov et al. 2005) or both excitatory and inhibitory (Jacobsen and Jensen 2007) SN with exponentially distributed weights, as well as the mean first-passage time for potentially nonlinear systems driven by excitatory SN with either exponentially distributed or constant weights (Masoliver 1987). Recently, Richardson and Swarbrick (2010) have considered LIF neurons driven by excitatory and inhibitory SN with exponentially distributed weights and given expressions for the firing rate, the susceptibility with respect to a modulation of the input rate, and the power spectrum.

The aim of this paper is methodological: to draw attention to the shot-noise limit of dichotomous noise, which has been used in statistical physics for a long time (van den Broeck 1983), but, as far as we know, never been applied to the description of neural input. We present exact expressions, derived using this limit, in the hope that others may find them useful. Thus, rather than systematically exploring particular effects (or even functional consequences) of SN input, we demonstrate the theory for a few illustrative examples. We provide the complete source code implementing the analytics (in PYTHON and C++) and the simulation (in C++) at http://modeldb.yale.edu/228604.

The paper is organized as follows: We first describe the model in Section 2, before introducing the shot-noise limit of dichotomous noise in Section 3 and discussing the treatment of fixed points in the drift dynamics in Section 4. For general IF neurons, we give expressions for the stationary voltage distribution (Section 5), and the moments of the ISI density (Section 6). For the special case of LIF neurons, we derive the power spectrum in Section 7 and the susceptibility with respect to a current-modulating signal in Section 8. We close with a brief discussion in Section 9.

2 Model

We consider the dynamics

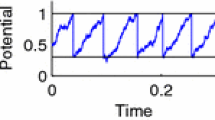
$$ \tau_{\mathrm{m}} \dot{v} = f(v) + \epsilon s(t) + \tau_{\mathrm{m}} X_{\text{in}}(t), $$
(1)

where τ m is the membrane time constant, f(v) is a potentially nonlinear function, 𝜖 ≪ 1, and s(t) is some time-dependent signal. Note that we set 𝜖 = 0, except for the calculation of the susceptibility. Whenever the voltage v crosses a threshold v T , a (postsynaptic) spike is emitted, v is reset to v R and clamped there for an absolute refractory period τ ref (see voltage trace in Fig. 1a). The input X in(t) is a weighted shot noise,

$$ X_{\text{in}}(t) = \sum\limits_{i} a_{i} \delta(t-t_{i}). $$
(2)

Here, a i is the weight and t i the time of the i th presynaptic spike. The a i are drawn from an exponential distribution with mean a; they are all statistically independent of each other and of the spike times t i . The spikes occur according to a homogeneous Poisson process with rate r in,

$$ \left\langle \sum\limits_{i} \delta(t-t_{i}) \right\rangle = r_{\text{in}}. $$
(3)
Fig. 1
figure 1

a Voltage trace of an exponential integrate-and-fire (EIF) neuron driven by excitatory shot noise with exponentially distributed weights. b The shot-noise limit of dichotomous noise: Increasing the noise value in the + state, σ +, while decreasing its mean duration 1/k + such that a, the area under each excursion, remains constant, yields a shot noise with exponentially distributed weights of mean a

Full size image

Common choices for f(v) are f(v) = μ, yielding the perfect integrate-and-fire (PIF) neuron, f(v) = μ − v, the leaky integrate-and-fire (LIF) neuron, f(v) = μ + v 2, the quadratic integrate-and-fire (QIF) neuron, or \(f(v) = \mu - v + {\Delta } \exp [(v-\bar {v}_{T})/{\Delta }]\), the exponential integrate-and-fire (EIF) neuron. Here, μ quantifies a constant input to the neuron; in the EIF, \(\bar {v}_{T}\) sets the position of the (soft) threshold and the slope parameter Δ controls the sharpness of postsynaptic spike onset. In the QIF neuron, one typically chooses reset and threshold at infinity, v R →−∞,v T →∞. For the EIF, the hard threshold can also be set to infinity, v T →∞. In practice, it is sufficient to take large but finite values. For a systematic comparison of the different IF models in the Gaussian noise case, see Fourcaud-Trocmé et al. (2003), Vilela and Lindner (2009b), and Vilela and Lindner (2009a).

A common modeling assumption in theoretical studies is that the a i are sufficiently small and r in sufficiently large that one can approximate X in(t) as a Gaussian white noise. Throughout this paper, we will contrast our results to this so-called diffusion approximation (DA). For the DA, the shot noise input is replaced by a Gaussian white noise with the intensity

$$ D_{\text{eff}} = a^{2} \tau_{\mathrm{m}}^{2} r_{\text{in}}. $$
(4)

Its mean value can be lumped into the function f(v), in which the parameter μ is replaced by a new effective parameter

$$ \mu_{\text{eff}} = \mu + a \tau_{\mathrm{m}} r_{\text{in}}. $$
(5)

Note that D eff differs from the case with fixed synaptic weights, in which it would be \(a^{2} \tau _{\mathrm {m}}^{2} r_{\text {in}} /2\).

As often done, we rescale the voltage axis such that v R = 0 and v T = 1. Thus, for a distance between resting potential and threshold of approximately 10–20mV, the spike weights a = 0.1 and a = 0.2 typically used in the figures shown below correspond to mean EPSP peak heights of 1–2mV and 2–4mV, respectively.

For the DA, we use the known results for the firing rate (Siegert 1951; Ricciardi and Sacerdote 1979; Brunel and Latham 2003; Lindner et al. 2003, for general IF, LIF, or QIF neurons, respectively), the CV (Siegert 1951; Lindner et al. 2003) power spectrum (Lindner et al. 2002), and the susceptibility with respect to current modulation (Brunel et al. 2001; Lindner and Schimansky-Geier 2001).

3 Dichotomous noise and its shot-noise limit

All our results rely on the fact that a dichotomous Markov process (DMP) can be taken to a shot-noise limit (van den Broeck 1983). A dichotomous Markov process (Gardiner 1985; Bena 2006) is a two-state process that jumps between two values, σ + and σ −. Jumps occur at constant rates, k + and k −, where k + is the rate at which transitions from σ + to σ − occur (and vice versa). The residence times within one state are exponentially distributed (with mean 1/k ±).

One obtains the shot-noise limit by taking σ + →∞ and k + →∞ while keeping a = σ +/k + constant. This is illustrated in Fig. 1b: As the limit is taken, the excursions to the plus state get shorter and higher, such that a, the mean area under the excursions, is conserved. The area under individual excursions is an exponentially distributed random number; in the SN limit, this corresponds to exponentially distributed weights of the δ functions.

The recipe for calculating the statistics of shot-noise-driven IF neurons is thus the following: One solves the associated problem for an IF neuron driven by asymmetric dichotomous noise with appropriate boundary conditions and then takes the shot-noise limit on the resulting expression. We have derived expressions for statistical properties of IF neurons driven by dichotomous noise elsewhere (Droste and Lindner 2014, 2017).

In most cases, taking the shot noise limit is rather straighforward: In the expressions for dichotomous noise, one replaces f(v) by f(v) + (σ + + σ −)/2 and σ by (σ + − σ −)/2. Then, one renames k − to r in (the rate of leaving the minus state corresponds to the rate at which input spikes occur), sets σ − = 0, and replaces σ + by a k +, before performing the limit k + →∞. We have previously expressed power spectrum and susceptibility of dichotomous-noise-driven neurons in terms of hypergeometric functions 2 F 1(a,b,c;z) (Abramowitz and Stegun 1972), in which k + appears both in the parameter b as well as, inversely, in the argument z. It can be shown that the limit k + →∞ turns them into confluent hypergeometric functions 1 F 1(a,b;z). For example,

$$\begin{array}{@{}rcl@{}} \lim\limits_{k_{+} \to \infty} {~}_2 F_1&&\left( -i\omega,k_{+} + r_{\text{in}} - i\omega;r_{\text{in}} - i\omega;\frac{v-\mu}{a k_{+}} \right) \\&&= {~}_1 F_1 \left( -i\omega,r_{\text{in}} - i\omega;\frac{v-\mu}{a} \right). \end{array} $$
(6)

Note that if one wants to consider also the limit of vanishing refractory period, it is important to take the shot noise limit first to get consistent results. In the remainder of this paper, we just give the resulting expressions in the shot-noise limit.

4 Importance of fixed points of the drift dynamics

Systems driven by dichotomous noise follow a deterministic dynamics within each of the two noise states, and these deterministic flows can contain fixed points (FPs). It has been pointed out that these FPs call for special attention when such systems are treated analytically (Bena 2006; Droste and Lindner 2014). In particular, when solving differential equations to obtain the probability density, the integration constants need to be chosen separately in N int intervals on the voltage axis, delimited by the threshold v T , the lowest attainable voltage v −, and FPs of the drift dynamics, i.e. points v F for which f(v F ) = 0. An FP is stable if f ′(v F ) < 0 and unstable if f ′(v F ) > 0.

The LIF neuron with μ < v T , for example, has a stable FP at v S = μ. If μ < v R , this is also the lowest attainable voltage (v − = v S = μ), because the excitatory shot noise can kick the neuron only to higher voltages; in this case, N int = 1. Otherwise, the lowest attainable voltage is v − = v R because of the reset rule; here, we have N int = 2 and need to consider the intervals [v R ,μ] and [μ,v T ]. Nonlinear neuron models such as QIF or EIF neurons have in general also an unstable FP, v U , and thus N int = 3 intervals need to be distinguished.

5 Voltage distribution

The stationary probability density for the voltage of IF neurons driven by a dichotomous noise has been derived elsewhere (Droste and Lindner 2014). Taking the shot-noise limit yields, for the i th interval (i = 1…N int),

$$\begin{array}{@{}rcl@{}} P_{0}^{i}(v) &=& \tau_{\mathrm{m}} r_{0} \frac{e^{-{\phi}(v)}}{f(v)} \left( \vphantom{\int\limits_{c_{i}}^{v}}-\left[ \theta(c_{i}\!-v_{R}) - \theta(v-v_{R}) \right]e^{{\phi}(v_{R})}\right.\!\\ &&\left.+\, \frac{1}{a}\! \int\limits_{c_{i}}^{v} dx\; \left[ \theta(x\,-\,v_{R})-\theta(x\,-\,v_{T}) \right] e^{{\phi}(x)} \right), \end{array} $$
(7)

where r 0 is the firing rate, the constant c i depends on the interval,

$$ c_{i} = \left\{\begin{array}{lll} v_{R}^{-} & \parbox[t]{.7\columnwidth}{if \(i=1\) and \(f(v_{T}) >0\),} \\ v_{U} & \parbox[t]{.7\columnwidth}{if one of the interval boundaries is an unstable FP at \(v_{U}\),} \\ v_{T}^{+} & \parbox[t]{.7\columnwidth}{if \(i=N_{\text{int}}\) and \(f(v_{T}) <0\)} \end{array}\right. $$
(8)

(here x + (x −) indicates that the value is to be taken infinitesimally above (below) x), and the function in the exponent is defined as

$$ {\phi}(v) := \frac{v}{a} + \tau_{\mathrm{m}} r_{\text{in}} {\int}^{v} dx\; \frac{1}{f(x)}. $$
(9)

For PIF, LIF, and QIF neuron, closed-form expressions for ϕ(v) are given in Appendix A. For the EIF, the integral has to be obtained numerically.

Note that Eq. (7) gives, strictly speaking, only the continuous part of the probability density; if one considers the voltage during the refractory period to be clamped at v R , then P 0(v) should also contain a δ peak with weight r 0 τ ref, centered at v R . To make comparison between theory and simulation somewhat easier, we discard this trivial contribution also in the simulation by building the histogram of voltage values only when the neuron is not refractory. We emphasize that in higher dimensional models or when using colored noise as an input, it becomes important to take the time evolution of neurons in the refractory state into account.

The firing rate r 0, which appears in Eq. (7), can either be determined from the requirement that the probability density needs to be normalized,

$$ \tau_{\text{ref}} r_{0} + \int\limits_{v_{-}}^{v_{T}} dv\; P_{0}(v) = 1, $$
(10)

or using the recursive relations for the ISI moments given in the following section.

In Fig. 2, we compare Eq. (7) for an EIF neuron to simulation results and the diffusion approximation. The theory matches the histogram obtained in the simulation. For the parameter regime shown, only an average of eight presynaptic spikes occurring in short succession are needed to take the neuron from the resting potential to the unstable fixed point of f(v) (here slightly above 1.4). Because of the relative strength of the single presynaptic spikes, large qualitative differences to the diffusion approximation can be observed. In particular, while the diffusion approximation predicts a rather symmetric and approximately Gaussian distribution for the voltage, the sparse, excitatory shot noise input leads to an asymmetric, clearly non-Gaussian profile.

Fig. 2
figure 2

Voltage distribution in a shot-noise-driven EIF neuron. We compare our theory (Eq. (7), red solid line) to a histogram obtained in a simulation (gray bars) and the diffusion approximation (green dashed line). The discontinuity in the density’s derivative, typical for the DA, is in this example particularly small and hence not visible. Parameters: \(\tau _{\mathrm {m}} = 20 \text { ms}, \mu =-0.1, a=0.2, r_{\text {in}}=0.12\text { kHz}, v_{R} = 0, \bar {v}_{T}=1, {\Delta }=0.2, \tau _{\text {ref}}=2\text { ms}\)

Full size image

It is also interesting to consider the voltage distribution for neuron models with a sharp threshold. In Fig. 3, we plot P 0(v) of a LIF neuron for three different values of μ. Focusing on the value at the threshold, it is apparent that \(P_{0}(v_{T}^{-})\) is finite only for μ > v T . This is reflected in the analytical formula Eq. (7), which yields

$$ P(v_{T}^{-}) = (1-\alpha) \frac{\tau_{\mathrm{m}} r_{0}}{f(v_{T})}, $$
(11)

where

$$ \alpha \!:=\! 1 -\! \left[\! \theta(v_{R}\,-\,c_{N}) e^{{\phi}(v_{R})-{\phi}(v_{T})} +\! \frac{1}{a} \int\limits_{c_{N}}^{v_{T}} dx\; \theta(x\,-\,v_{R}) e^{{\phi}(x)-{\phi}(v_{T})}\!\right]. $$
(12)

It is apparent from Eq. (8) that α = 1 if f(v T ) < 0 and α < 1 for f(v T ) > 0. There is an direct interpretation of α that will become clearer in the next section: it is the fraction of trajectories that cross the threshold because of a kick (rather than by drifting). The probability density can thus only be non-vanishing at the threshold if it is possible to drift across it in the absence of inputs.

Fig. 3
figure 3

Voltage distribution in a shot-noise-driven leaky integrate-and-fire (LIF) neuron for three values of μ . Our theory (Eq. (7), red solid lines) is compared to histograms obtained in simulations (gray bars) and the diffusion approximation (green dashed lines). Remaining parameters: τ m = 20 ms,μ = −0.2,a = 0.2,r in = 0.28 kHz,v R = 0,v T = 1,τ ref = 2 ms

Full size image

If μ < v R (third panel in Fig. 3), the density P 0(v R ) jumps to a higher value when crossing v R from above. This is caused by reset trajectories which, until the next incoming spike occurs, drift to lower voltages.

6 ISI moments of shot-noise-driven IF neurons

We have previously derived recursive relations that allow to obtain the moments of the ISI density of IF neurons driven by dichotomous noise (Droste and Lindner 2014). In the shot-noise limit, they read

$$\begin{array}{@{}rcl@{}} \mathcal{J}_{n}(v) \,=\, \sum\limits_{i=1}^{i(v)} \int\limits_{l_{i}}^{\min(v,r_{i})} dx\; n \frac{\mathcal{M}_{n-1}^{i}(x)}{f(x)} \,+\, \left( \frac{\tau_{\text{ref}}}{\tau_{\mathrm{m}}}\right)^{n} \delta(x\,-\,v_{R}),\\ \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} \mathcal{M}_{n}^{i}(v) \,=\, e^{-{\phi}(v)} \int\limits_{c_{i}}^{v} dx\; e^{{\phi}(x)} &&\left( n \frac{\mathcal{M}_{n-1}^{i}(x)}{f(x)} + \frac{\mathcal{J}_{n}(x)}{a}\right.\\ &&\left.+ \left( \frac{\tau_{\text{ref}}}{\tau_{\mathrm{m}}}\right)^{n} \delta(x - v_{R}) \right), \end{array} $$
(14)

where i(v) denotes the interval that contains v, r i (l i ) is the upper (lower) boundary of the i th interval, c i is defined as in Eq. (8), and where

$$\begin{array}{@{}rcl@{}} \mathcal{J}_{n\!}(v) \!:=\! {\int}_{0}^{\infty} \!dt\;J\!(v,t) t^{n}, \quad \mathcal{\!M}_{n}(v) \!:=\! {\int}_{0}^{\infty} dt\;\!J_{-}(v,t) t^{n}.\\ \end{array} $$
(15)

Here, J(v,t) is the total probability current and J −(v,t) is the probability current due to drift only. The n th ISI moment is then given by

$$ \left\langle T^{n} \right\rangle = \mathcal{J}_{n}(v_{T}). $$
(16)

In Eq. (11), we have introduced α, the fraction of trajectories that cross the threshold directly due to an incoming spike (and not by drifting over the threshold). Expressed via integrated fluxes, it should be given by \(\alpha = \mathcal {J}_{0}(v_{T}) - \mathcal {M}_{0}(v_{T})\). Indeed, evaluating Eqs. (13) and (14) for n = 0 and v = v T recovers the expression given in Eq. (12).

6.1 Firing rate

Using Eqs. (13), (14), the following formula for the firing rate can be obtained:

$$\begin{array}{@{}rcl@{}} r_{0} = &&\left[ \frac{\tau_{\mathrm{m}}}{a} \sum\limits_{i=1}^{N_{\text{int}}} \int\limits_{l_{i}}^{r_{i}} dx\;\int\limits_{x}^{\bar{c}_{i}} dy\; \theta(x-v_{R}) \frac{ e^{{\phi}(x)-{\phi}(y)}}{f(y)}\right.\\&&\left.+ \int\limits_{v_{R}}^{\bar{c}_{1}} dx\; \frac{e^{{\phi}(v_{R})-{\phi}(x)}}{f(x)} + \tau_{\text{ref}} \right]^{-1}, \end{array} $$
(17)

where \(\bar {c}_{i}\) is the interval boundary opposite of c i . For the special case of an LIF neuron with τ ref = 0 and μ → 0, this can be shown to reduce exactly to the formula given by Richardson and Swarbrick (2010) if one sets the inhibitory weights to zero in their expression (Droste 2015, App. B5).

We plot the firing rate of an EIF neuron as a function of the input rate in Fig. 4 for two values of the slope factor Δ. The actual firing rate can be both lower or higher than what the DA predicts, depending on the input rate. For an increased slope factor, the deviations are less pronounced. This can be traced to an effective reduction in the weight of presynaptic spikes: As shown in the inset of Fig. 4, a higher slope factor pushes the effective threshold – the unstable fixed point – to higher voltages. Relative to the distance from resting potential to threshold, the spike weight is thus reduced by increasing Δ, bringing the system closer to the range of validity of the DA.

Fig. 4
figure 4

Firing rate of a EIF neuron as a function of the input rate for two values of the slope factor Δ. Our theory (Eq. (17), solid lines) is compared to simulations (symbols) and the diffusion approximation (dashed lines). Inset: the nonlinearity f(v) for the two values of Δ. The white dot marks the unstable fixed point. Parameters: \(\tau _{\mathrm {m}} = 20 \text { ms}, \mu =-0.1, a=0.1, v_{R} = 0, \bar {v}_{T}= 1, \tau _{\text {ref}}=2\text { ms}\)

Full size image

A particularly pronounced deviation between the SN case and the DA can be observed for very low input rates (shown, in Fig. 5, for an LIF neuron). This is mainly due to the distributed weights in the SN case: no matter how sparsely input arrives, each input spike can potentially cause an output spike if its weight a i > v T − μ, where we have assumed that input is so sparse that the neuron relaxes to μ between input spikes. Thus, for r in ≪ 1, the output firing rate goes linear with the input rate,

$$ r_{0} \approx r_{\text{in}} \exp\left[-\frac{v_{T} - \mu}{a}\right]. $$
(18)

In contrast, the diffusion approximation (and also SN input with weights fixed to a, black squares in Fig. 5) falls off much more rapidly with decreasing input rate.

Fig. 5
figure 5

Firing rate of a LIF neuron as a function of the input rate. Our theory (Eq. (17), red solid lines) is compared to simulations (gray symbols) and the diffusion approximation (green dashed line). Also shown are simulations using spike weights that were either distributed but cut off at \(a_{\max } = 0.4\) (green triangles) or fixed (at a = 0.1) (black squares), the maximally achievable firing rate \(\min (r_{\text {in}}, 1/\tau _{\text {ref}})\), and the asymptotic rate for SN input with exponentially distributed weights (Eq. (18)). Parameters: τ m = 20 ms,μ = 0.5,a = 0.1,v R = 0,v T = 1,τ ref = 2 ms

Full size image

The fact that individual incoming spikes can have a weight larger than the distance from reset to threshold is not necessarily realistic. However, even if we set the weight of all incoming spikes with a i > a max to a max (green triangles in Fig. 5), the decay of the firing rate with decreasing r in is still much slower than predicted by the DA.

6.2 Coefficient of variation

The recursive relations, Eqs. (13), 14), can also be used to calculate the coefficient of variation (CV),

$$ C_{V} = \frac{\sqrt{\left\langle (T-\left\langle{T}\right\rangle)^{2} \right\rangle}}{\left\langle{T}\right\rangle} = \frac{\sqrt{\mathcal{J}_{2}(v_{T}) - {\mathcal{J}_{1}^{2}}(v_{T})}}{\mathcal{J}_{1}(v_{T})}, $$
(19)

which quantifies the regularity of the spiking. For a Poisson process, C V = 1; a lower CV indicates that firing is more regular than for a Poisson process.

In Fig. 6, we plot the CV for of a shot-noise-driven QIF neuron as a function of the mean spike weight a. In order to demonstrate the plausibility of limit cases, we deliberately show an unphysiologically large range for a. For small a, where the assumptions underlying the diffusion approximation are still approximately fulfilled, the CV predicted by the diffusion approximation is still a good match. For very low spike weights, the input is so sparse that spiking becomes a rare event and the output spike train thus becomes Poisson-like with a CV of 1. At (unreasonably) high spike weights, the CV also approaches 1, which is a plausible limit: when a becomes very large, each incoming spike causes an output spike (note that in Fig. 6, τ ref = 0) and the CV approaches that of the Poissonian input. This is in contrast to the DA, which, for a QIF with v R →−∞,v T →∞, predicts a CV of \(1/\sqrt {3}\) (dotted line in Fig. 6) as the noise intensity tends to infinity (Lindner et al. 2003). However, even up to unphysiological mean spike weights of a = 1 (which here corresponds to an average of only two presynaptic spikes needed to reach the threshold), the CV calculated using the DA is not qualitatively different from the exact one.

Fig. 6
figure 6

Coefficient of variation of a quadratic integrate-and-fire (QIF) neuron as a function of the mean spike weight a . Our theory (solid red line) is compared to simulations (gray symbols) and the diffusion approximation (green dashed line). The dashed line marks the value 1, expected for a Poisson process, the dotted line marks \(1/\sqrt {3}\), the asymptotic value expected for the DA with v R →−∞,v T →∞. Parameters: τ m = 20 ms,μ = −1,r in = 0.675 kHz ,v R = −20,v T = 20,τ ref = 0 ms

Full size image

7 Power spectrum of shot-noise-driven LIF neurons

For leaky integrate-and-fire neurons driven by dichotomous noise, we have previously derived expressions for the power spectrum for the parameter regime μ < v T (Droste 2015; Droste and Lindner 2017). Their shot-noise limit reads

$$ {S}_{xx}(f) = {r}_0 \frac{\left| e^{-2\pi i f\tau_{\text{ref}}} {\mathcal{F}}(v_{T},f) \right|^{2}-\left| \frac{r_{\text{in}}}{r_{\text{in}} - 2\pi i f} {\mathcal{G}}(v_{R},f) \right|^{2}}{\left| e^{-2\pi i f\tau_{\text{ref}}} {\mathcal{F}}(v_{T},f) - \frac{r_{\text{in}}}{r_{\text{in}} - 2\pi i f} {\mathcal{G}}(v_{R},f)\right|^{2}}, $$
(20)

where \({\mathcal {F}}(v,f)\) and \({\mathcal {G}}(v,f)\) are given in terms of confluent hypergeometric functions (Abramowitz and Stegun 1972),

$$\begin{array}{@{}rcl@{}} {\mathcal{F}}(v,f) &:=& {~}_1 F_1 \left( -2\pi i f\tau_{\mathrm{m}};(r_{\text{in}} - 2\pi i f)\tau_{\mathrm{m}};\frac{v-\mu}{a} \right) ,\\ \end{array} $$
(21)
$$\begin{array}{@{}rcl@{}} {\mathcal{G}}(v,f)\! &:=& \!{~}_1 F_1 \left( -2\pi i f\tau_{\mathrm{m}};1\,+\,(r_{\text{in}} \,-\, 2\pi i f)\tau_{\mathrm{m}};\frac{v\,-\,\mu}{a} \right) . \\ \end{array} $$
(22)

In Fig. 7, Eq. (20) is compared to simulation results and the diffusion approximation. The SN theory matches simulation results nicely. The DA, in contrast, does not even qualitatively match it. Somewhat surprising is that, in the SN-driven case, the low value of the power spectrum at zero frequency (proportional to the squared CV of the interspike interval) does not translate into a pronounced peak around the firing rate. Hence, although the single interspike interval for this parameter set has a rather low variability (that is close to the value in the DA), the resulting spike sequence does not show a pronounced periodicity.

Fig. 7
figure 7

Power spectrum of an LIF neuron. Theory (Eq. (20), solid red line), compared to simulation results (gray line) and the diffusion approximation (green dashed line). Parameters: τ m = 20 ms,μ = 0.5,α = 0.2,r in = 1 kHz ,v R = 0,v T = 1,τ ref = 2 ms

Full size image

8 Linear response of the firing rate

The susceptibility with respect to a current modulation of LIF neurons driven by dichotomous noise has been derived elsewhere (Droste and Lindner 2017). Its shot-noise limit reads

$$ {\chi}_{\mu}(f)= -\ \frac{{r}_0}{2 \pi i\tau_{\mathrm{m}} f\! -\! 1} \frac{{\mathcal{F}}^{\prime}(v_{T},f) -\frac{r_{\text{in}}}{r_{\text{in}}-2\pi i f}{\mathcal{G}}^{\prime}(v_{R}, f)}{{\mathcal{F}}(v_{T},f)\! -\! e^{2\pi i f\tau_{\text{ref}}}\frac{r_{\text{in}}}{r_{\text{in}}-2\pi i f}{\mathcal{G}}(v_{R}, f)}. $$
(23)

Here, the derivatives of Eqs. (21), (22) with respect to v are given by Abramowitz and Stegun (1972)

$$\begin{array}{@{}rcl@{}} {\mathcal{F}}^{\prime}{\kern-.5pt}({\kern-.5pt}v{\kern-.5pt},{\kern-.5pt}f{\kern-.5pt})\! &:=&\! \frac{-2\pi i f}{a(r_{\text{in}}-2\pi i f)} \\&&\!{\kern-5.5pt} \times {~}_1F_1\! \left( \! \!1\!-2\pi i f\tau_{\mathrm{m}};\!1\,+\,(r_{\text{in}}\,-\,2\pi i f)\tau_{\mathrm{m}};\frac{v\,-\,\mu}{a} \right) ,\!\\ \end{array} $$
(24)
$$\begin{array}{@{}rcl@{}} {\mathcal{G}}^{\prime}{\kern-.5pt}({\kern-.5pt}v{\kern-.5pt},{\kern-.5pt}f{\kern-.5pt})\! &:=&\! \frac{-2\pi i f \tau_{\mathrm{m}}}{a(1 + [r_{\text{in}}-2\pi i f]\tau_{\mathrm{m}})} \\&&\!\!\times{~}_1F_1 \left( \!1\,-\,2\pi i f\tau_{\mathrm{m}};\!2\,+\,(r_{\text{in}}\,-\,2\pi i f)\tau_{\mathrm{m}};\!\frac{v\,-\,\mu}{a} \right) .\\ \end{array} $$
(25)

In Fig. 8, we compare the absolute value and the phase of the susceptibility to simulations and the DA. Especially for high frequencies, a marked deviation from the DA can be observed. This high-frequency behavior of the susceptibility is of particular interest to understand how well neurons can track fast signals; it has thus attracted both experimental and theoretical attention (Fourcaud-Trocmé et al. 2003; Boucsein et al. 2009; Tchumatchenko et al. 2011; Ilin et al. 2013; Ostojic et al. 2015; Doose et al. 2016). With the properties of confluent hypergeometric functions (Abramowitz and Stegun 1972), we find from Eq. (23) for f ≫ 1,

$$\begin{array}{@{}rcl@{}} |{\chi}_{\mu}(f \gg 1)| &=& \frac{{r}_0}{2 \pi a \tau_{\mathrm{m}} f}, \\ \arg[{\chi}_{\mu}(f \gg 1)] &=& \frac{\pi}{2}. \end{array} $$
(26)

This is in contrast to LIF neurons driven by Gaussian white noise (i.e. the DA), for which the absolute value of the susceptibility decays like \(1/\sqrt {f}\) while its phase approaches \(\frac {\pi }{4}\) (see Fourcaud and Brunel 2002, for a comparison of different neuron/noise combinations).

Fig. 8
figure 8

Susceptibility of an LIF neuron with respect to a current modulation. Theory (Eq. (23), solid red line) compared to simulations (gray symbols) and the diffusion approximation (green dashed line). Also shown is the high-frequency behavior of the theory (blue dotted line). Parameters: τ m = 20 ms,μ = 0.5,α = 0.2r in = 0.28 kHz ,v R = 0,v T = 1,τ ref = 2 ms

Full size image

Note that the shot noise limit of a dichotomous-noise-driven LIF neuron can also be used to study the susceptibility with respect to a modulation of the firing rate (Droste 2015), a quantity previously studied by Richardson and Swarbrick (2010).

9 Discussion

We have used the shot-noise limit of dichotomous noise to obtain novel analytical expressions for statistical properties of integrate-and-fire neurons driven by excitatory shot noise with exponentially distributed weights. We have derived exact expressions for the stationary distribution of voltages and the moments of the ISI density for general IF neurons as well as, for LIF neurons, the power spectrum and the susceptibility to a current signal.

Our approach is complementary to others that have previously been employed. We obtain, for instance, the same expression for the Laplace-transform of the first-passage-time density of LIF neurons as Novikov et al. (2005) (not shown), or the same expression for the firing rate as Richardson and Swarbrick (2010) (if one considers only excitatory input). Our expression for the power spectrum provides an alternative formulation to the one given by Richardson and Swarbrick (2010), given in terms of confluent hypergeometric functions that can be evaluated quickly. Exact results for the coefficient of variation (CV), the voltage distribution, or the susceptibility with respect to a current-modulating signal have, to our knowledge, not previously been obtained for SN-driven IF neurons.

For low input rates, the firing rate of the SN-driven neuron was found to be much higher than predicted by the DA. As we have argued, this is mainly due to the exponential distribution of spike weights, which implies that individual presynaptic spikes can be strong enough to make the neuron fire. While arbitrarily high spike weights are not realistic, this effect survives at least partially when we introduce a weight-cutoff, i.e. when we no longer allow single individual spikes to push the neurons across threshold. This may be related to the finding that few strong synapses can stabilize self-sustained spiking activity in recurrent networks (Ikegaya et al. 2013).

An obvious limitation of our approach is that is does not incorporate inhibitory SN input to the neuron. Many of the qualitative results in this paper can be expected to persist also with additional inhibitory input: the probability density at the threshold, for instance, should still only be finite if it can be crossed by drifting, the output firing rate should still be proportional to the (excitatory) input rate when input is sparse, and the CV should still approach 1 in the a →∞ limit. Nevertheless, it would be valuable to have quantitatively exact expressions also for this more realistic case. A possible approach could be to derive statistics for neurons driven by a trichotomous noise (Mankin et al. 1999) and then take a shot noise limit.

Another interesting extension is to consider multiple neurons with shot noise in order to understand the emergence of correlations among neurons in recurrent neural networks. The simplest problem of this kind is the calculation of the count correlations of two uncoupled neurons which are driven by a common noise (de la Rocha et al. 2007). Recent work indicates that a common shot noise has a decisively different effect than a Gaussian noise (Rosenbaum and Josic 2011). Some of the methods developed here may be also useful for tackling this more involved problem.