Integrate-and-fire neurons driven by asymmetric dichotomous noise

Abstract

We consider a general integrate-and-fire (IF) neuron driven by asymmetric dichotomous noise. In contrast to the Gaussian white noise usually used in the so-called diffusion approximation, this noise is colored, i.e., it exhibits temporal correlations. We give an analytical expression for the stationary voltage distribution of a neuron receiving such noise and derive recursive relations for the moments of the first passage time density, which allow us to calculate the firing rate and the coefficient of variation of interspike intervals. We study how correlations in the input affect the rate and regularity of firing under variation of the model’s parameters for leaky and quadratic IF neurons. Further, we consider the limit of small correlation times and find lowest order corrections to the first passage time moments to be proportional to the square root of the correlation time. We show analytically that to this lowest order, correlations always lead to a decrease in firing rate for a leaky IF neuron. All theoretical expressions are compared to simulations of leaky and quadratic IF neurons.

1 Introduction

Models of the integrate-and-fire (IF) type have been widely used in the study of neural systems (reviewed in Burkitt 2006a, b). Usually, they describe neuronal dynamics via a single variable, the membrane voltage $v$, complemented by a fire-and-reset rule that is applied once a voltage threshold is crossed. In numerical as well as analytical studies, this minimal description has allowed insights, for instance, into neuronal information transmission properties (Brunel et al. 2001; Lindner and Schimansky-Geier 2001), the effect of input correlations (De La Rocha et al. 2007; Salinas and Sejnowski 2002; Moreno et al. 2002), or the dynamics of whole networks (Brunel 2000; Softky and Koch 1993; Shadlen and Newsome 1998). Further, it can be readily extended to include more complex behavior, such as spike-frequency adaptation (Liu and Wang 2001; Schwalger et al. 2010), which can then be studied in a well-understood setting. Last but not least, exponential IF models have been shown to be powerful predictors of the dynamics of real pyramidal cells (Badel et al. 2008).

The synaptic input to the neuron is commonly thought of as a sequence of stereotypical spikes with stochastic arrival times; mathematically speaking, it is a point process where each event is a delta function (shot noise). As such discrete input with a potentially rich correlation structure is notoriously difficult to treat analytically, many studies have employed the so-called diffusion approximation, modeling the massive synaptic bombardment as Gaussian white noise. This is usually justified by arguing that the overall input is a superposition of a large number of nearly uncorrelated spike trains and that each individual synaptic event only has a small weight.

However, there are various physiologically observed input characteristics that cannot be accounted for by uncorrelated Gaussian fluctuations. Deviations from Gaussian white noise occur both with respect to the stationary distribution, which is often non-Gaussian, and temporal correlations, which can be pronounced. In other words, a more faithful description of the input is a non-Gaussian colored noise process.

In certain brain states, for example, the input switches between two well distinguishable levels, so-called up and down states of the network (Cowan and Wilson 1994; Shu et al. 2003). Such input is not Gaussian but follows a bimodal distribution; on a coarse level, it can be considered two-valued. Further, in some cells, it has been shown (Markram et al. 1997) that the assumption of many small superposed pulses underlying the Gaussian approximation is violated and that thus, the shot-noise character of synaptic input should be taken into account (Richardson and Gerstner 2005).

Deviations from the assumption of white input (i.e., lack of temporal correlations) are even more severe in many neural systems. The activity of presynaptic cells may be correlated, both among neurons (De La Rocha et al. 2007) and in time (Bair et al. 1994) and superposition of spike trains does not remove temporal correlations (Lindner 2006). This, along with synaptic filtering (Brunel and Sergi 1998; Moreno et al. 2002) and short-term synaptic plasticity (Lindner et al. 2009), leads to an overall input that is colored instead of white.

A simple non-Gaussian colored noise process is dichotomous noise, a Markovian two-valued stochastic process. In physics and biophysics, dichotomous noise has been popular as a modeling tool for a long time (Horsthemke and Lefever 1984; Hänggi and Jung 1995; Bena 2006), both due to its analytical tractability as well as its applicability to “on-off” situations. Dichotomous noise has been used to model a vast number of phenomena, ranging from the movement of molecular motors (Astumian and Bier 1994) to the switching of single spins (Rugar et al. 2004). Some further applications arise because dichotomous noise converges to Gaussian white noise or Poissonian shot noise when taken to appropriate limits (van den Broeck 1983). In contrast to the (likewise exponentially correlated) Gaussian Ornstein–Uhlenbeck process, dichotomous noise is a discrete process, possessing infinitely many cumulant correlation functions.

In neuroscience, dichotomous noise has been used to model the opening and closing of ion channels (Horsthemke and Lefever 1981; Fitzhugh 1983; Goychuk and Hänggi 2000); its use as a model for neural input has been relatively sparse (Salinas and Sejnowski 2002; Lindner 2004a). However, dichotomous noise is interesting in several of the situations mentioned above. Specifically, it can be used to model input (i) from a presynaptic population that undergoes transitions between up and down states, (ii) in the form of finite pulses, and (iii) from a strong single presynaptic bursting cell. More generally, dichotomous noise allows to build a tractable model to explore the effect of temporal correlations and non-Gaussianity of input currents on the firing statistics of neurons.

Here, we apply the well-developed techniques for the study of dichotomous flows (Horsthemke and Lefever 1984; Bena 2006) to neuron models of the IF type. In doing so, the main difference to the problems previously considered in the statistical physics literature lies in the initial and boundary conditions that are imposed by the fire-and-reset rule. In the first part, we derive exact expressions for the stationary distribution of membrane voltages as well as the moments of the first passage time density for a general IF neuron driven by dichotomous noise with asymmetric switching rates. We emphasize that this constitutes one of the rare cases where the firing statistics of a stochastic neural dynamics can be exactly calculated. As a first application, we then use these expressions to study the effect of temporal input correlations on neural firing. In the interest of conciseness, we restrict ourselves to symmetric rates in this case; the general asymmetric case is especially relevant for taking the shot-noise limit and for modeling input from a presynaptic population that switches between up and down states, both of which will be dealt with elsewhere.

The impact of temporal correlations in the input on the firing statistics of a neuron has been studied by a number of authors, mostly using Ornstein–Uhlenbeck (OU) processes (Brunel and Sergi 1998; Fourcaud and Brunel 2002; Salinas and Sejnowski 2002; Brunel and Latham 2003; Middleton et al. 2003; Lindner 2004a; Moreno et al. 2002; Schwalger and Schimansky-Geier 2008). Specifically, one can ask whether the firing rate increases or decreases with increasing correlation time and whether firing becomes more or less regular. Salinas and Sejnowski (2002) have investigated these questions in a setup of perfect and leaky IF neurons receiving symmetric dichotomous noise. They give analytical expressions for firing rate and CV in closed form for the perfect IF and as a series expansion for the leaky IF. For both, they report that firing rate as well as CV increases with increasing correlation time $\tau _c$. When varying $\tau _c$, Salinas and Sejnowski (2002) keep the noise variance fixed. As we argue below, this is the proper choice for input with large $\tau _c$, while for small $\tau _c$, fixing the noise intensity allows for a more meaningful comparison between white and correlated input, and leads to different results (most importantly, we find a decrease instead of an increase in firing rate).

The outline of this paper is as follows: After describing the model and the governing equations (Sect. 2), we calculate exact expressions for the stationary probability density (Sect. 3) of a general IF neuron driven by dichotomous noise. We then give exact recursive relations for the moments of the first passage time density (Sect. 4) and derive a simple approximation for rate and CV that is valid in the limit of long correlation times (Sect. 5). In Sect. 6, we apply these results and study the effect of correlations on firing rate and CV. Specifically, we plot firing rate and CV as a function of the correlation time, the base current, and the noise intensity both for leaky and quadratic IF neurons and compare them with the white-noise-driven case. In all cases, we find the firing rate to be lower for correlated input, while the CV may be either higher or lower. In Sect. 7, we consider the limit of small correlation times and show analytically that to the lowest order in $\tau _c$, the firing rate of leaky IF neurons always decreases with the correlation time. We conclude with a brief discussion of our results in Sect. 8.

2 Model and governing equations

We consider a general IF neuron. Between spikes, its voltage dynamics is described by

$$\begin{aligned} \dot{v} = f(v) + \eta (t), \end{aligned}$$

(1)

where $\eta (t)$ is dichotomous noise and $f(v)$ is a continuous, potentially nonlinear function. Whenever $v$ crosses the threshold $v_T$, it is reset to $v_R$ and a spike is registered. Common choices for $f(v)$ are $f(v) = \mu$, yielding the perfect IF neuron (PIF), $f(v) = \mu - v$, the leaky IF neuron (LIF), and $f(v) = \mu + v^2$, the quadratic IF neuron (QIF), where the parameter $\mu$ quantifies a base current to the neuron. We will use the latter two models for numerical verification of the expressions we derive, but stress that our theory is valid for arbitrary nonlinearities. Note that for ease of notation, we consider non-dimensionalized dynamics where time is measured in units of the membrane time constant.

The dichotomous Markovian process (DMP) $\eta (t)$ is a two-state process; it jumps between the values $\sigma _+$ and $\sigma _-$ (see Fig. 1). Jumps happen at constant rates $k_+$ and $k_-$, where $k_+$ denotes the rate of hopping from $\sigma _+$ to $\sigma _-$ (and vice versa for $k_-$). When $k_+ = k_- = k$ and $\sigma _+ = -\sigma _- = \sigma ,\,\eta (t)$ is called symmetric. Note that asymmetry in the values $\sigma _\pm$ can always be transformed away: a system driven by such noise is equivalent to a system with an additional bias $(\sigma _+ + \sigma _-)/2$, driven by noise with symmetric values $\pm \sigma$, where $\sigma = (\sigma _+ - \sigma _-)/2$. We assume $\sigma _+ > \sigma _-$ and restrict all further analysis to the case $f(v) + \sigma _+ > 0$ for all $v \in [v_R, v_T]$ (thereby excluding scenarios where the neuron would never be able to reach the threshold).

Fig. 1

Dichotomous noise. a Dichotomous noise is a two-state process, jumping between a “+” state with value $\sigma _+$ and a “-” state with value $\sigma _-$ at constant rates $k_+$ and $k_-$. b A sample realization of dichotomous noise. c Voltage time course of an LIF driven by this noise

The time evolution of dichotomous noise is described by the master equation

$$\begin{aligned} \frac{d}{dt} P_+(t)&= - k_+ P_+(t) + k_- P_-(t), \end{aligned}$$

(2)

$$\begin{aligned} \frac{d}{dt} P_-(t)&= k_+ P_+(t) - k_- P_-(t), \end{aligned}$$

(3)

where $P_{\pm }(t)$ is the probability that the DMP takes the value $\sigma _{\pm }$ at time $t$. The solution of this equation is straightforward and well known (Fitzhugh 1983; Horsthemke and Lefever 1984); here, we list important statistics it allows to calculate. The expectation of $\eta (t)$ is

$$\begin{aligned} \left\langle \eta (t) \right\rangle = \frac{k_- \sigma _+}{k_+ + k_-} + \frac{k_+ \sigma _-}{k_+ + k_-}. \end{aligned}$$

(4)

It is apparent that in general, asymmetric dichotomous noise has nonzero mean. The residence times in each state are exponentially distributed with expectation $1/k_\pm$; the variance of the process is

$$\begin{aligned} \mathrm{var}(\eta (t)) = \frac{2 \sigma ^2 k_+ k_-}{(k_+ + k_-)^2}. \end{aligned}$$

(5)

Dichotomous noise is exponentially correlated with the correlation time $\tau _c$ given by

$$\begin{aligned} \tau _c = \frac{1}{k_+ + k_-}. \end{aligned}$$

(6)

Another quantity useful for the comparison to other noise processes is the noise intensity

$$\begin{aligned} D = \frac{2 \sigma ^2 k_+ k_-}{(k_+ + k_-)^3}. \end{aligned}$$

(7)

In accordance with the standard approach for dynamical systems driven by dichotomous noise (Horsthemke and Lefever 1981; Bena 2006), we extend the master equation to the full system (noise process and neuronal dynamics) by considering $P_{\pm }(v,t) dv$, i.e., the probability that the DMP takes the value $\sigma _{\pm }$ and the neuron’s membrane voltage is in the interval $(v, v + dv)$ at time $t$. To this end, we combine the continuity equations that link the change in $P_{\pm }(v,t)$ to the fluxes $J_{\pm }(v,t) = (f(v) + \sigma _{\pm }) P_{\pm }(v,t)$ with Eqs. (2) and (3). Additionally, we need to incorporate the fire-and-reset rule: Trajectories are removed at $v_T$ and reinserted at $v_R$. If $f(v_T) + \sigma _- > 0$, the threshold can be crossed at both noise values. For the moment, we call the respective fluxes over the threshold $r_+(t) {:=} J_+(v_T,t)$ and $r_-(t) {:=} J_-(v_T,t)$; they sum to the instantaneous firing rate, $r(t) = r_+(t) + r_-(t)$. The probability density is thus governed by

$$\begin{aligned} \partial _t P_+(v,t)&= -\partial _v ((f(v) + \sigma _+) P_+(v,t)) \nonumber \\&- k_+ P_+(v,t)+ k_- P_-(v,t)\nonumber \\&+ r_+(t) \left( \delta (v - v_R) - \delta (v - v_T) \right) ,\end{aligned}$$

(8)

$$\begin{aligned} \partial _t P_-(v,t)&= -\partial _v ((f(v) + \sigma _-) P_-(v,t)) \nonumber \\&+ k_+ P_+(v,t)- k_- P_-(v,t)\nonumber \\&+ r_-(t) \left( \delta (v - v_R) - \delta (v - v_T) \right) . \end{aligned}$$

(9)

This describes the stochastic switching between two deterministic flows, the “+” dynamics and the “-” dynamics. The source and sink terms $r_\pm (t) \delta (v - v_R)$ and $r_\pm (t) \delta (v - v_T)$ can be seen as a formal way to prescribe boundary conditions (cf. Richardson and Swarbrick 2010). They implement the fire-and-reset rule and mark the most profound difference to dichotomous noise problems previously treated in the statistical physics literature.

3 Stationary distribution

We first want to calculate the stationary probability distribution of voltages. To this end, we start from the stationarity condition for Eqs. (8) and (9),

$$\begin{aligned} \begin{aligned} 0&= -\left( (\hat{f}(v) + \sigma ) P_+(v)\right) ' \\&\qquad \!\!\! - k_+ P_+(v)+ k_- P_-(v)\\&\qquad \!\!\! + r_0 \alpha \left( \delta (v - v_R) - \delta (v - v_T) \right) , \end{aligned} \end{aligned}$$

(10)

$$\begin{aligned} \begin{aligned} 0&= -\left( (\hat{f}(v) - \sigma ) P_-(v)\right) ' \\&\qquad \!\!\! + k_+ P_+(v)- k_- P_-(v)\\&\qquad \!\!\! + r_0 (1-\alpha ) \left( \delta (v - v_R) - \delta (v - v_T) \right) , \end{aligned} \end{aligned}$$

(11)

where we have symmetrized the DMP values by introducing

$$\begin{aligned} \hat{f}(v) {:=} f(v) + \frac{\sigma _+ + \sigma _-}{2}, \quad \sigma {:=} \frac{\sigma _+ - \sigma _-}{2} \end{aligned}$$

(12)

(to unburden notation, we return to calling this new function $f(v)$ in the following) and where we have expressed the fluxes over the threshold by the stationary firing rate $r_0$ and the ratio

$$\begin{aligned} \alpha {:=} r_+ / r_0, \end{aligned}$$

(13)

which denotes the fraction of trajectories that cross the threshold in the “+” dynamics.

Without solving the equations, we can already assess how the probability density behaves at threshold and reset voltage due to the fire-and-reset rule. To this end, we integrate Eq. (10) from $v_R - \epsilon$ to $v_R + \epsilon$ and let $\epsilon \rightarrow 0$, which yields

$$\begin{aligned} P_+(v_R^+) - P_+(v_R^-) = r_0 \frac{\alpha }{f(v_R) + \sigma }, \end{aligned}$$

(14)

where $P_+(v_R^{\pm }) = \lim _{\epsilon \rightarrow 0}P_+(v_R\pm \epsilon )$. Similarly, integrating from $v_T - \epsilon$ to $v_T + \epsilon$ and taking into account that there is no probability above threshold yields

$$\begin{aligned} P_+(v_T^-) = r_0 \frac{\alpha }{f(v_T) + \sigma }. \end{aligned}$$

(15)

Analogously, we obtain

$$\begin{aligned}&P_-(v_R^+) - P_-(v_R^-) = r_0 \frac{1-\alpha }{f(v_R) - \sigma }, \end{aligned}$$

(16)

$$\begin{aligned}&P_-(v_T^-) = {r_0} \frac{1-\alpha }{f(v_T) - \sigma }. \end{aligned}$$

(17)

Here, we already observe an important difference to the case of IF neurons driven by white noise: The probability density is no longer continuous, but exhibits jumps at $v_R$ and $v_T$ (cf. Fig. 2). This is typical for colored noise and has also been observed for neurons driven by an OU process (Fourcaud and Brunel 2002).

Fig. 2

Stationary probability density compared to the diffusion approximation. Input in both cases is symmetric dichotomous noise with intensity $D = 0.4$ and correlation time $\tau _c = 0.15$. a LIF with $\mu = 0.8, v_R = 0, v_T = 1$. b QIF with $\mu =-0.2, v_R=-\infty , v_T=\infty$. We plot theory (thin lines) and simulation results (circles) and compare them to the analytical results for white noise input with the same $D$ (thick lines, see e.g., Vilela and Lindner 2009). The most prominent qualitative difference lies in the discontinuities that correlated input induces at the (finite) reset and threshold points of the LIF

In the following, we will solve Eqs. (10) and (11) separately below $v_R$ and between $v_R$ and $v_T$, i.e., excluding the source and sink terms. The jump conditions can then be satisfied by choosing the respective integration constants appropriately.

Ultimately, we are interested in the probability that the voltage is in an infinitesimal interval around $v$, independent of the state of the noise. The corresponding probability density is given by

$$\begin{aligned} p(v){:=} P_+(v)+ P_-(v). \end{aligned}$$

(18)

We define also

$$\begin{aligned} q(v){:=} P_+(v)- P_-(v). \end{aligned}$$

(19)

Writing Eqs. (10) and (11) in terms of $p(v)$ and $q(v)$ and adding one equation to the other leads to a stationarity condition for the total flux which can be directly integrated, yielding

$$\begin{aligned} J_0 = f(v)p(v)+ \sigma q(v), \end{aligned}$$

(20)

where $J_0$ is piecewise constant:

$$\begin{aligned} J_0 = {\left\{ \begin{array}{ll} 0 &{} \mathrm{if}\quad v < v_R, \quad v > v_T, \\ r_0 &{} \mathrm{if}\quad v_R < v < v_T. \end{array}\right. } \end{aligned}$$

(21)

Subtracting Eq. (11) from Eq. (10) yields one remaining ordinary differential equation (ODE),

$$\begin{aligned} \left( f(v)q(v)+ \sigma p(v)\right) ' + k_2 p(v)+ k_1 q(v)= 0, \end{aligned}$$

(22)

where

$$\begin{aligned} k_1 {:=} (k_+ + k_-),\quad k_2 {:=} (k_+ - k_-). \end{aligned}$$

(23)

We can eliminate $q(v)$ using Eq. (20) and define $g(v) {:=} f(v)$ $J_0 - (f^2(v)- \sigma ^2) p(v)$; the ODE then reads

$$\begin{aligned} \begin{aligned} g'(v)&= -\frac{f(v)k_1 - \sigma k_2}{f^2(v)- \sigma ^2} g(v) \\&\quad + \frac{J_0}{f^2(v)- \sigma ^2} \left( \sigma ^2 k_1 - \sigma f(v)k_2 \right) . \end{aligned} \end{aligned}$$

(24)

Note that we have divided by $f^2(v)- \sigma ^2$ here, which can lead to singular behavior at points where the “-” dynamics has a fixed point (FP); this is treated in detail below.

Solving the ODE through variation of constants and integrating by parts to simplify the result yields

$$\begin{aligned} \begin{aligned} p(v)&= \frac{e^{-\phi (v)}}{f^2(v)-\sigma ^2} \Bigg [ c + J_0 \left( f(d) e^{\phi (d)} \right. \\&\left. \qquad + \int _{d}^v ds\; e^{\phi (s)} (f'(s) + k_1) \right) \Bigg ], \end{aligned} \end{aligned}$$

(25)

where

$$\begin{aligned} \phi (v) {:=} k_+ \int ^v du\; \frac{1}{f(u) + \sigma } + k_- \int ^v du\; \frac{1}{f(u) - \sigma }. \end{aligned}$$

(26)

In Eq. (25), $d$ can still be chosen freely, as long as $c$ has not been fixed. Equation 25 represents two solutions (one with $J_0 = 0$ for $v < v_R$ and one with $J_0 = r_0$ for $v > v_R$), each with its own integration constant $c$. In order to fully appreciate how these integration constants as well as $r_0$ and $\alpha$ are determined, we first need to discuss how fixed points of the “-” dynamics need to be dealt with.

3.1 Dealing with fixed points in the “-” dynamics

As mentioned above and noted first by Bena et al. (2002), problems may arise at fixed points of the deterministic flows. We only need to consider fixed points in the “-” dynamics, $f(v_F) - \sigma = 0$, as fixed points in the “+” dynamics would be impossible for the system to overcome; such a neuron would never fire. To see how $p(v)$ behaves in the vicinity of a fixed point $v_F$, we approximate $f(v) \approx f(v_F) + f'(v_F) (v - v_F) = \sigma + f'(v_F) (v - v_F)$. This means $f'(v) \approx f'(v_F)$, $f^2(v)-\sigma ^2 \approx 2 \sigma f'(v_F) (v - v_F)$,

$$\begin{aligned} e^{-\phi (v)} \approx \left| v-v_F \right| ^{-\frac{k_-}{f'(v_F)}} \cdot \left| v-v_F+\tfrac{2 \sigma }{f'(v_F)}\right| ^{-\frac{k_+}{f'(v_F)}} \end{aligned}$$

(27)

and thus

$$\begin{aligned} \begin{aligned} p(v)&\approx \frac{\left| v-v_F \right| ^{-\frac{k_-}{f'(v_F)}} \cdot \left| v-v_F+\tfrac{2 \sigma }{f'(v_F)}\right| ^{-\frac{k_+}{f'(v_F)}}}{2 \sigma f'(v_F) (v - v_F)} \\&\quad \cdot \Bigg [ c + J_0 \Big ( f(d) e^{\phi (d)} \\&\quad + \int _{d}^{v} ds\; e^{\phi (s)} (f'(s) + k_1) \Big ) \Bigg ]. \end{aligned} \end{aligned}$$

(28)

Further discussion of this formula depends on whether we are dealing with a stable or an unstable fixed point.

3.1.1 Unstable fixed points

If $v_U$ is an unstable fixed point, $f'(v_U) > 0$ and $p(v)$ diverges,

$$\begin{aligned} p(v)\sim \left| v-v_U\right| ^{-\frac{k_-}{|f'(v_U)|}-1}. \end{aligned}$$

(29)

This is “clearly unphysical and mathematically improper in view of the requirement of normalization” (Bena et al. 2002). Specifically, one would expect the probability to find the system near an unstable fixed point to be low and not high, and more generally, divergences in the probability density are only acceptable if they can be integrated.

As pointed out in Bena et al. 2002, one thus needs to consider separate solutions above and below such fixed points and then choose their integration constants such that divergent terms vanish at $v_U$. In the case considered here, this corresponds to setting $c = 0$ and $d = v_U$, both above and below $v_U$. We can then apply l’Hôpital’s rule to calculate the limit

$$\begin{aligned} \lim \limits _{v \rightarrow v_U} p(v)= \frac{r_0}{2 \sigma } \left( 1 + \frac{k_+}{f'(v_U) + k_-}\right) . \end{aligned}$$

(30)

To see that this does indeed make sense, it is instructive to take one step back and ask: If $p(v)$ must not diverge at $v_U$, which value should it take? At a fixed point of the “-” dynamics, $J_- = (f(v_U) - \sigma ) P_-(v_U) = 0$, so that the whole flux $r_0$ has to be mediated by the “+” dynamics, which fixes

$$\begin{aligned} P_+(v_U) = \frac{r_0}{f(v_U) + \sigma } = \frac{r_0}{2 \sigma }. \end{aligned}$$

(31)

This allows to calculate $P_-(v_U)$ and thus $p(v_U)$ as follows: At $v_U$, Eq. (11) becomes

$$\begin{aligned} \begin{aligned} 0&= -f'(v_U) P_-(v_U) - k_- P_-(v_U) + k_+ \frac{r_0}{2 \sigma }, \end{aligned} \end{aligned}$$

(32)

which can be solved for $P_-(v_U)$, yielding indeed the limit calculated above.

3.1.2 Stable fixed points

For stable fixed points, $f'(v_S) = -|f'(v_S)|$ and one sees from Eq. (28) that the previously problematic term becomes

$$\begin{aligned} \left| v-v_S\right| ^{\frac{k_-}{|f'(v_S)|}-1}. \end{aligned}$$

(33)

For $k_- > |f'(v_S)|$, this does not diverge (trajectories leave toward the “+” state faster than new ones are coming in); for $k_- < |f'(v_S)|$, it diverges but can still be integrated (cf. Fig. 3). Stable fixed points thus pose no fundamental problem; however, we still have to make sure that they lie outside the integration boundaries of the integral in Eq. (25), where they would cause a divergence.

Fig. 3

Behavior of the stationary probability density at fixed points of the “-” dynamics. We plot probability densities (thin lines: theory, circles: simulation results) as well as the nonlinearity $f(v) \pm \sigma$, where stable FPs are marked by black dots and unstable FPs by white dots. a LIF with $\mu = 0.8, v_R = 0, v_T = 1, \sigma = 0.4$ and $k_+ = 1.5$. Depending on the value of $k_-$, $p(v)$ can either be continuous at a stable FP ($k_- = 1.2$) or exhibit an integrable divergence ($k_- = 0.8$). b QIF with $\mu =-0.2, v_R=-\infty , v_T=\infty , \sigma = 3$ and $k_+ = 5$. Again, $p(v)$ is either continuous ($k_- = 4$) or exhibits an integrable divergence ($k_- = 3$) at the stable FP. Note that due to a proper choice of integration constants, it is smooth and continuous at the unstable FP

3.2 Boundary conditions and full solution

In contrast to the case of white-noise-driven IF neurons, the stationary probability density is in general not defined for arbitrarily negative values of $v$. The support of $p(v)$ is the interval $[v_-, v_T]$, where $v_-$ is either the first fixed point smaller than $v_R$, if $f(v_R) - \sigma < 0$, or $v_R$ itself, if $f(v_R) - \sigma > 0$ (in both cases, trajectories cannot cross this point toward smaller values of $v$. It extends to negative infinity only if $f(v_R) - \sigma < 0$, and no fixed point exists below of $v_R$ (such as, e.g., for a PIF with $\mu - \sigma < 0$).

As pointed out above, solutions have to be given separately for intervals that are delimited by $v_R$, $v_T$, and fixed points of the “-” dynamics. The integration constants are either determined by the jump conditions at reset voltage and threshold or, if the interval in question neighbors an unstable fixed point, fixed by the requirement of avoiding divergence (see Fig. 4 for a schematic depiction). If the lower and upper interval boundaries are denoted by $a$ and $b$, the full solution is given by

$$\begin{aligned} p(v) = \frac{r_0 e^{-\phi (v)}}{f^2(v)-\sigma ^2} \cdot {\left\{ \begin{array}{ll} \varGamma _\mathrm{I}(v) &{} \hbox {if}\; b = v_R \hbox {and}\; \hbox {no}\; \hbox {FPs}\; > v_R\\ \varGamma _\mathrm{II}(v) &{}\hbox {if}\; b = v_R\; \hbox {and}\; \hbox {first}\; \hbox {unst.}\; \hbox {FP}\; \hbox {at}\; v_U \\ \varGamma _\mathrm{III}(v) &{}\hbox {if}\; a = v_U\; \hbox {or} \;b=v_U \\ \varGamma _\mathrm{IV}(v) &{} \hbox {if} \;a = v_R\; \hbox {and} \;f(v_R) - \sigma > 0 \\ \varGamma _\mathrm{V}(v) &{} \hbox {if}\;b = v_T\; \hbox {and}\;f(v_T) - \sigma < 0, \end{array}\right. }\nonumber \\ \end{aligned}$$

(34)

where using the abbreviation $h(v) {:=} (\sigma (2\alpha -1)-f(v))e^{\phi (v)}$, the $\varGamma _i(v)$ are given by

$$\begin{aligned}&\varGamma _\mathrm{I}(v) = h(v_R)-h(v_T)\nonumber \\&\qquad \qquad - \int \limits _{v_R}^{v_T} ds\; e^{\phi (s)} (f'(s) + k_1),\end{aligned}$$

(35)

$$\begin{aligned}&\varGamma _\mathrm{II}(v) = h(v_R) - \int \limits _{v_R}^{v_U} ds\; e^{\phi (s)} (f'(s) + k_1),\end{aligned}$$

(36)

$$\begin{aligned}&\varGamma _\mathrm{III}(v) =\int \limits _{v_U}^{v} ds\; e^{\phi (s)} (f'(s) + k_1),\end{aligned}$$

(37)

$$\begin{aligned}&\varGamma _\mathrm{IV}(v) = -h(v_R) + \int \limits _{v_R}^{v} ds\; e^{\phi (s)} (f'(s) + k_1),\end{aligned}$$

(38)

$$\begin{aligned}&\varGamma _\mathrm{V}(v) =-h(v_T) - \int \limits _{v}^{v_T} ds\; e^{\phi (s)} (f'(s) + k_1). \end{aligned}$$

(39)

The above expressions for $p(v)$ still include $r_0$, the stationary firing rate, and $\alpha$, the fraction of trajectories that cross $v_T$ during “+” dynamics. The latter can be calculated as follows: If $f(v_T) - \sigma < 0$, threshold crossings happen only during “+” dynamics, which entails $\alpha = 1$. Otherwise, the integration constant of the rightmost interval is always determined by either an unstable FP or the jump condition at $v_R$, which allows us to use the remaining jump condition at the threshold to calculate $\alpha$ (see Fig. 4). This yields

$$\begin{aligned} \begin{aligned} \alpha&= \frac{1}{2} \left( 1 + \frac{f(v_R) e^{\phi (v_R)} - f(v_T) e^{\phi (v_T)}}{\sigma \left( e^{\phi (v_R)} - e^{\phi (v_T)} \right) } \right. \\&\quad +\left. \frac{\int \limits _{v_R}^{v_T} ds\; e^{\phi (s)} (f'(s) + k_1)}{\sigma \left( e^{\phi (v_R)} - e^{\phi (v_T)} \right) } \right) , \end{aligned} \end{aligned}$$

(40)

if there is no unstable FP, or

$$\begin{aligned} \begin{aligned} \alpha&= \frac{1}{2} \left( 1 + \frac{f(v_T)}{\sigma } \right. \\&\quad \left. -\frac{e^{-\phi (v_T)} \int \limits _{v_U}^{v_T} ds\; e^{\phi (s)} (f'(s) + k_1)}{\sigma } \right) , \end{aligned} \end{aligned}$$

(41)

if the unstable FP next to the threshold is at $v_U$. Finally, the stationary firing rate $r_0$ can be determined by requiring $p(v)$ to be normalized.

Fig. 4

Schematic depiction of how the integration constants for the probability density are determined in different regions (delimited by dashed lines). Integration constants in regions next to unstable fixed points are always chosen to avoid a divergence; the remaining ones are determined by the jump conditions at reset and threshold. If $f(v_T) - \sigma < 0$, threshold crossing happens only via the “+” dynamics, so $\alpha = 1$. If $f(v_T) - \sigma > 0$, the integration constant in the rightmost region is either determined by ensuring non-divergence at the nearest fixed point (necessarily unstable) or the jump condition at the reset, if no such fixed point exists. This allows $\alpha$ to be determined via the jump condition at the threshold. Roman numerals denote which of the solutions $p_\mathrm{I}(v) \cdots p_\mathrm{V}(v)$ applies. Note that commonly used IF models have at most one stable and one unstable fixed point

4 Moments of the inter-spike interval density

The expressions derived in the previous section allow us to calculate the stationary distribution of voltages and the firing rate of an IF neuron driven by dichotomous noise. The firing rate is inversely proportional to the average interspike interval (ISI), i.e., the first moment of the ISI density. Higher moments of the ISI density are also of interest; the second moment, for example, appears in the definition of the coefficient of variation (CV), which is often used to characterize the regularity of neural firing. The ISI density is equivalent to the density of trajectories that, starting at the reset voltage, reach the threshold for the first time after a time $T$, i.e., the first passage time (FPT) density.

In this section, we derive expressions for the moments of the FPT density. To this end, we adopt and adapt the approach outlined (for Gaussian white noise) in Lindner 2004b. The central argument of our derivation is the following: The FPT density $\rho (T)$ corresponds exactly to the (time dependent) flux of probability across the threshold, $j(v_T, T) = J_+(v_T, T) + J_-(v_T, T)$, provided that all trajectories start at $v_R$ at $t = 0$ and that no probability can flow back from above the threshold (otherwise, we would count re-entering trajectories multiple times). Note that we do not need to directly consider the fire-and-reset rule in this case; it only enters through its impact on the initial conditions.

For colored noise that can take continuous values, the “no-backflow” condition is notoriously difficult to implement and often only fulfilled approximately. Here, it amounts to the simple condition $J_-(v_T, t) \ge 0$. For $f(v_T) - \sigma > 0$, this is automatically fulfilled, while for $f(v_T) - \sigma < 0$, it will have to be enforced through the boundary condition $J_-(v_T, t) = 0$. The $n$-th moment of the FPT density is then given by

$$\begin{aligned} \left\langle T^n \right\rangle = \int \limits _0^{\infty } dt\; t^n \left( J_+(v,t) + J_-(v,t) \right) . \end{aligned}$$

(42)

We start by rewriting the master equation Eqs. (8) and (9) in terms of fluxes. We introduce

$$\begin{aligned} j(v,t) {:=} J_+(v,t) + J_-(v,t) \end{aligned}$$

(43)

and

$$\begin{aligned} w(v,t) = J_+(v,t) - J_-(v,t), \end{aligned}$$

(44)

which allows us to write

$$\begin{aligned}&\partial _t \left( \frac{f(v)j(v,t) - \sigma w(v,t)}{f^2(v)- \sigma ^2} \right) = -\partial _v j(v,t), \end{aligned}$$

(45)

$$\begin{aligned}&\partial _t \left( \frac{f(v)w(v,t) - \sigma j(v,t)}{f^2(v)- \sigma ^2} \right) = -\partial _v w(v,t) \nonumber \\&\quad - \gamma _1(v) w(v,t) - \gamma _2(v) j(v,t), \end{aligned}$$

(46)

where

$$\begin{aligned} \gamma _{1/2}(v) {:=} \frac{k_+}{f(v)+ \sigma } \pm \frac{k_-}{f(v)- \sigma }. \end{aligned}$$

(47)

We then multiply both sides by $t^n$ and integrate over $t$ from 0 to $\infty$ (the l.h.s by parts); introducing the abbreviations

$$\begin{aligned}&J_n(v) := \int _0^{\infty } dt\;j(v,t) t^n, \end{aligned}$$

(48)

$$\begin{aligned}&Q_n(v) := \int _0^{\infty } dt\;w(v,t) t^n, \end{aligned}$$

(49)

we obtain

• for $n = 0$

  $$\begin{aligned} \partial _v J_0(v)&= \frac{f(v)j(v,0) - \sigma w(v,0)}{f^2(v)- \sigma ^2}, \end{aligned}$$

  (50)
  $$\begin{aligned} \partial _v Q_0(v)&= \frac{f(v)w(v,0) - \sigma j(v,0)}{f^2(v)- \sigma ^2} \nonumber \\&-\gamma _1(v) Q_0(v) - \gamma _2(v) J_0(v), \end{aligned}$$

  (51)

• for $n > 0$

  $$\begin{aligned} \partial _v J_n(v)&= n \frac{f(v)J_{n-1}(v) - \sigma Q_{n-1}(v)}{f^2(v)- \sigma ^2}, \end{aligned}$$

  (52)
  $$\begin{aligned} \begin{aligned} \partial _v Q_n(v)&= n \frac{f(v)Q_{n-1}(v) - \sigma J_{n-1}(v)}{f^2(v)- \sigma ^2}\\&\quad \!\!\! -\gamma _1(v) Q_n(v) - \gamma _2(v) J_n(v), \end{aligned} \end{aligned}$$

  (53)

where we have used that

$$\begin{aligned} \lim \limits _{t \rightarrow \infty } j(v,t) = \lim \limits _{t \rightarrow \infty } w(v,t) = 0 \quad \forall \quad v < v_T \end{aligned}$$

(54)

(eventually, every trajectory will have crossed the threshold). Given suitable boundary and initial conditions (IC), we can recursively solve these ODEs for $J_n(v)$. Evaluated at the threshold, this is exactly the $n$-th FTP moment,

$$\begin{aligned} \left\langle T^n \right\rangle = J_n(v_T). \end{aligned}$$

(55)

All trajectories start at the reset voltage $v_R$ at $t = 0$, so for $\eta (0) = \sigma$, we have the ICs

$$\begin{aligned} P_+(v, 0) = \delta (v - v_R), \quad P_-(v, 0) = 0 \end{aligned}$$

(56)

(and vice versa for $\eta (0) = -\sigma$). Thus, we actually need to consider two conditional FPT densities

$$\begin{aligned} \rho (T | \eta (0) = \sigma ) \end{aligned}$$

(57)

and

$$\begin{aligned} \rho (T | \eta (0) = -\sigma ). \end{aligned}$$

(58)

The stationary FPT density is then

$$\begin{aligned} \begin{aligned} \rho (T)&= p(\eta (0) = \sigma ) \rho (T | \eta (0) = \sigma ) \\&\quad + p(\eta (0) = -\sigma ) \rho (T | \eta (0) = -\sigma ), \end{aligned} \end{aligned}$$

(59)

where $p(\eta (0) = \sigma ) = \alpha$ is the probability that the last threshold crossing happened in “+” dynamics. Due to the linearity of the problem, we can replace this averaging over the noise upon firing by preparing a “mixed” initial state, $P_+(v, 0) = \alpha \delta (v - v_R)$, $P_-(v, 0) = (1 - \alpha ) \delta (v - v_R)$. We thus have the ICs

$$\begin{aligned}&j(v,0) = \left( \sigma (2 \alpha - 1) + f(v)\right) \delta (v - v_R),\end{aligned}$$

(60)

$$\begin{aligned}&w(v,0) = \left( f(v)(2 \alpha - 1) + \sigma \right) \delta (v - v_R). \end{aligned}$$

(61)

Equations (50, 52) can directly be integrated,

$$\begin{aligned}&J_0(v) = \theta (v - v_R), \end{aligned}$$

(62)

$$\begin{aligned}&J_{n>0}(v) = n \int \limits _{C_n}^v ds\; \frac{f(s) J_{n-1}(s) - \sigma Q_{n-1}(s)}{f^2(s)-\sigma ^2}, \end{aligned}$$

(63)

where $\theta (v)$ is the Heaviside step function and the integration constant in Eq. (62) is fixed by requiring the FPT density to be normalized ($J_0(v_T) = 1$). The other ODEs can be solved by variation of constants, yielding the general solution

$$\begin{aligned} \begin{aligned}&Q_0(v) = e^{-\phi (v)} \left[ D_0 + \int \limits _{E_0}^v ds\; e^{\phi (s)} \right. \\&\quad \cdot \left. \Bigg ( (2 \alpha -1 )\delta (s-v_R) - \gamma _2(s) \theta (s-v_R) \Bigg ) \right] , \end{aligned} \end{aligned}$$

(64)

$$\begin{aligned} \begin{aligned}&Q_{{n>0}}(v) = e^{-\phi (v)} \left[ D_n - \int \limits _{E_n}^v ds\; e^{\phi (s)} \right. \\&\quad \cdot \left. \left( \gamma _2(s) J_n(s) - n \frac{f(s) Q_{n-1}(s) - \sigma J_{n - 1}(s)}{f^2(s)-\sigma ^2} \right) \right] , \end{aligned} \end{aligned}$$

(65)

where we have used $\phi (v) = \int ^v dx\; \gamma _1(x)$ and where $E_n$ can be freely chosen as long as $D_n$ is not fixed.

Unfortunately, it is evident from Eqs. (64) and (65) that the presence of fixed points of the “-” dynamics remains the nuisance that it was in the calculation of the stationary probability density (see Sect. 3.1). Again, we thus need to split the range of possible voltages $[v_-, v_T]$ at fixed points of the “-” dynamics [note that, in contrast to the previous section, we do not need to split at $v_R$, as the jump condition at $v_R$ is already incorporated through the initial conditions Eqs. (60 and 61)].

If an interval borders on an unstable FP, we can avoid a divergence by setting the integration constants $D_n= 0$ and $E_n = v_U$. To see that this makes sense, one can apply l’Hôpital’s rule to calculate the limits of $Q_0(v)$ and $Q_{n>0}(v)$ for $v \rightarrow v_U$ and this choice of values,

$$\begin{aligned}&\lim \limits _{v \rightarrow v_U} Q_0(v) = 1, \end{aligned}$$

(66)

$$\begin{aligned}&\lim \limits _{v \rightarrow v_U} Q_{n>0}(v) = J_n(v_U) \nonumber \\&\quad + \frac{n}{2 k_-} \left( Q_{n - 1}(v_U) - J_{n - 1}(v_U) \right) . \end{aligned}$$

(67)

At an FP of the “-” dynamics, all flux occurs through the “+” state, so there is no difference between $J_{n}(v_U)$ and $Q_{n}(v_U)$. This is reflected in the two limits: According to Eq. (62), $J_0(v_U) = 1$ (unstable FPs occur only above the reset voltage), so we have indeed $J_0(v_U) = Q_0(v_U)$. Eq. (67) extends this to all $n$ by induction, as from $Q_{n - 1}(v_U) = J_{n - 1}(v_U),\,Q_n(v_U) = J_n(v_U)$ follows. This also means that no special treatment of Eq. (63) is necessary at unstable FPs, as the divergence of the integrand cancels exactly for $Q_n(v_U) = J_n(v_U)$.

Boundary conditions for $Q_n(v)$ are well defined in all intervals:

• Leftmost interval. If $f(v_R)-\sigma > 0$, the lower boundary is the reset voltage $v_R$, which all trajectories leave toward the right. For $t > 0$, $P(v_R, t)=0$ and consequently $J_-(v_R, t) = 0$, fixing $Q_0(v_R) = 2 \alpha - 1$ and $Q_{n>0}(v_R) = 0$. Otherwise, if $f(v_R)-\sigma < 0$, the upper boundary of the interval is either an unstable fixed point (see inner intervals) or $v_T$ (with $f(v_T)-\sigma < 0$, see rightmost interval).

• Inner intervals. Inner intervals necessarily have an unstable FP as upper or lower boundary, at which $Q_n(v_U) = J_n(v_U)$.

• Rightmost interval. If $f(v_T)-\sigma < 0$, we need to make sure that there is no flux of probability back across the threshold. This amounts to imposing $J_-(v_T, t) = 0$, implying $Q_n(v_T) = J_n(v_T)$. If $f(v_T)-\sigma > 0$, the “no-backflow” condition is always fulfilled. In this case, we have a condition at the lower boundary of the interval, which is either an unstable FP (demanding $Q_n(v_U) = J_n(v_U)$) or the reset voltage $v_R$ (with $f(v_R)-\sigma > 0$, see leftmost interval).

The integration constant of $J_{n>0}(v)$ is determined as follows: If $f(v_-) - \sigma > 0$, all trajectories leave $v_- = v_R$ instantaneously toward higher values of $v$. Thus, $p(v_-,t) = 0$ for $t > 0$ and consequently $J_{n>0}(v_-) = 0$. If $f(v_-) - \sigma < 0$, $v_-$ is at a stable FP, so that $J_n(v_-) = Q_n(v_-)$. Because $Q_n(v)$ goes to zero as $v$ approaches a stable FP, we again have the condition $J_{n>0}(v_-) = 0$.

The fraction of trajectories that cross the threshold in “+” state, $\alpha$, can be calculated using the expression given in the previous section. An alternative derivation goes as follows: $\alpha$ corresponds to the time-integrated flux in “+” state, $\int _{0}^{\infty } dt\;J_+(v_T,t)$. Thus, it can be determined from the relation

$$\begin{aligned} \alpha = \frac{J_0(v_T)+Q_0(v_T)}{2}, \end{aligned}$$

(68)

in which $Q_0(v_T)$ on the r.h.s. in general also depends on $\alpha$.

If there are no FPs other than a stable FP at $v_-$, we obtain the following recursive relations

$$\begin{aligned}&J_0(v) = \theta (v-v_R), \end{aligned}$$

(69)

$$\begin{aligned}&Q_0(v) = e^{-\phi (v)} \Bigg [ e^{\phi (v_T)} - \theta (v_R - v) e^{\phi (v_R)} + \nonumber \\&\quad \int \limits _{v}^{v_T} ds\; e^{\phi (s)} \gamma _2(s) \theta (s-v_R) \Bigg ],\end{aligned}$$

(70)

$$\begin{aligned}&J_{n > 0}(v) = n \int \limits _{v_-}^v ds\; \frac{f(s) J_{n-1}(s) - \sigma Q_{n - 1}(s)}{f^2(s)-\sigma ^2}, \end{aligned}$$

(71)

$$\begin{aligned}&Q_{n> 0}(v) = e^{-\phi (v)} \left[ J_n(v_T) e^{\phi (v_T)} +\int \limits _{v}^{v_T} ds\; e^{\phi (s)}\right. \nonumber \\&\quad \left. \times \bigg ( \gamma _2(s) J_n(s) - n \frac{f(s) Q_{n-1}(s) - \sigma J_{n - 1}(s)}{f^2(s)-\sigma ^2} \bigg ) \right] . \end{aligned}$$

(72)

This case is relevant if $\sigma$ is sufficiently large, e.g., when considering a limit close to white noise. A general solution that is further transformed to ease numerical integration is given in Appendix 9.

Evaluating Eqs. (69) - (72) recursively, we can now obtain an exact expression for the $n$-th moment of the FPT density,

$$\begin{aligned} \left\langle T^n \right\rangle = J_n(v_T). \end{aligned}$$

(73)

This allows us to calculate, for instance, the stationary firing rate (given here for the case that there is no FP above $v_R$),

$$\begin{aligned} \begin{aligned} r_0&= \left[ \int \limits _{v_-}^{v_T} dx\; \left( \frac{\theta (x-v_R)}{f(x)+\sigma } + \frac{\sigma e^{-\phi (x)}}{f^2(x)-\sigma ^2} \right. \right. \cdot \\&\quad \left. \left. \int \limits _{v_T}^{x} dy\; \frac{2 k_+ \theta (y-v_R) e^{\phi (y)}}{f(y)+\sigma } \right) \right] ^{-1}. \end{aligned} \end{aligned}$$

(74)

Similarly, one may use $J_1(v_T)$ and $J_2(v_T)$ to obtain a lengthy expression for the coefficient of variation $CV = \sqrt{\left\langle T^2 \right\rangle -\left\langle T \right\rangle ^2}/\left\langle T \right\rangle$ (which we do not reproduce here). These exact expressions for firing rate and CV of a general IF neuron driven by asymmetric dichotomous noise are a central result of this work.

5 Approximation for firing rate and CV at large correlation times

When the correlation time of the DMP is large, one can derive a simple quasi-static approximation for the firing rate and CV. While we have already derived exact expressions, valid over the whole range of correlation times, in the previous section, this approximation has its merits in allowing immediate insights into neuronal firing at high $\tau _c$, $\mu$ or $\sigma$, without the need for numerical integration. The approach outlined below shares similarities with those used to study PIF (Middleton et al. 2003) and LIF neurons (Schwalger and Schimansky-Geier 2008) driven by an OU process; however, the two-state nature of the DMP renders the derivation considerably less complicated.

Let us first make the notion of a “large” correlation time more precise. If we fix the DMP $\eta (t)$ in “+” state, we are dealing with a deterministic system $\dot{v} = f(v) + \sigma$. We denote the time that this system takes to go from $v_R$ to $v_T$ by $T_d^+$. If $f(v) - \sigma > 0$ for all $v$ (the neuron also fires if the noise is fixed in “-” state), we can equivalently define a $T_d^-$. We call the correlation time large if $\tau _c \gg T_d^+$, and, in case $T_d^-$ is defined, if also $\tau _c \gg T_d^-$. Note that this implies the same for the residence times in both states, i.e., $1/k_\pm \gg T_d^+$ and $1/k_\pm \gg T_d^-$.

We start with the case where the neuron only fires in “+” state ($f(v) - \sigma < 0$ for some $v$). On average, it emits $1/(k_+ T_d^+) \gg 1$ spikes while in “+” state, followed by one long ISI in the quiescent “-” state. Neglecting “boundary effects” at switching events of the noise, the probability that a randomly picked ISI is a short interval of length $T_d^+$ is thus

$$\begin{aligned} P_s = \frac{\frac{1}{k_+} \frac{1}{T_d^+}}{\frac{1}{k_+} \frac{1}{T_d^+} + 1}, \end{aligned}$$

(75)

while the probability that it is a long interval in “-” state is

$$\begin{aligned} P_l = \frac{1}{\frac{1}{k_+} \frac{1}{T_d^+} + 1}. \end{aligned}$$

(76)

The mean ISI in this limit is given by

$$\begin{aligned} \left\langle T \right\rangle&= T_d^+ P_s + \frac{1}{k_-} P_l \end{aligned}$$

(77)

$$\begin{aligned}&\approx \frac{k_+ + k_-}{k_-}T_d^+, \end{aligned}$$

(78)

where we have used that $1/(k_+ T_d^+) \gg 1$. Similarly, the second moment is given by

$$\begin{aligned} \left\langle T^2 \right\rangle&= \left( T_d^+\right) ^2 P_s + \int \limits _{0}^{\infty } dt'\;t'^2 k_- e^{-k_- t'} P_l \end{aligned}$$

(79)

$$\begin{aligned}&\approx \frac{\frac{T_d^+}{k_+} + \frac{2}{k_-^2}}{\frac{1}{k_+} \frac{1}{T_d^+}}. \end{aligned}$$

(80)

Firing rate and CV thus read

$$\begin{aligned}&r_0 \approx \frac{k_- \frac{1}{T_d^+}}{k_+ + k_-}, \end{aligned}$$

(81)

$$\begin{aligned}&CV \approx \sqrt{\frac{2 k_+}{\left( k_+ + k_-\right) ^2} \frac{1}{T_d^+} }. \end{aligned}$$

(82)

For the case where threshold crossings happen also in “-” state ($f(v) - \sigma > 0$), expressions can be derived using similar reasoning; here, we obtain

$$\begin{aligned}&r_0 \approx \frac{k_- \frac{1}{T_d^+} + k_+ \frac{1}{T_d^-}}{k_+ + k_-}, \end{aligned}$$

(83)

$$\begin{aligned}&CV \approx \sqrt{\frac{k_+ k_-}{\left( k_+ + k_-\right) ^2} \frac{(T_d^+ - T_d^-)^2}{T_d^+ T_d^-} }. \end{aligned}$$

(84)

For symmetric dichotomous noise, the expressions simplify to

$$\begin{aligned}&r_0 \approx \frac{1}{2}\frac{1}{T_d^+}, \end{aligned}$$

(85)

$$\begin{aligned}&CV \approx \sqrt{\frac{\tau _c}{T_d^+} }, \end{aligned}$$

(86)

if $f(v) - \sigma < 0$ for some $v \in [v_R, v_T]$, and

$$\begin{aligned}&r_0 \approx \frac{1}{2} \left( \frac{1}{T_d^+} + \frac{1}{T_d^-} \right) , \end{aligned}$$

(87)

$$\begin{aligned}&CV \approx \sqrt{\frac{1}{4} \frac{(T_d^+ - T_d^-)^2}{T_d^+ T_d^-}}, \end{aligned}$$

(88)

if $f(v) - \sigma > 0$ for all $v \in [v_R, v_T]$.

It remains to calculate

$$\begin{aligned} T_d^\pm = \int \limits _{v_R}^{v_T} \frac{dv}{f(v) \pm \sigma }. \end{aligned}$$

(89)

For the LIF, it reads

$$\begin{aligned} T_d^\pm = \ln \left( \frac{\mu \pm \sigma -v_R}{\mu \pm \sigma -v_T} \right) , \end{aligned}$$

(90)

and for the QIF

$$\begin{aligned} T_d^\pm = \frac{\pi }{\sqrt{\mu \pm \sigma }}. \end{aligned}$$

(91)

We will discuss the implications of these formulas in different limits and scalings in the next section.

6 Application: impact of correlations on firing rate and CV

Can we make general statements about the influence that temporal correlations in the input exert on the firing statistics of a neuron? Does the firing rate increase or decrease when we replace white input by correlated input? Does firing become more or less regular? In order to address such questions, we first need to clarify how to choose parameters to allow for a meaningful comparison between white noise and dichotomous noise. Here and in the following, we consider symmetric dichotomous noise ($k_+ = k_- = k$), but the discussion also applies to the asymmetric case.

When varying the correlation time $\tau _c$, one faces the question of how to parameterize the noise process. One choice is to keep its variance $\sigma ^2$ constant, which in turn means that the noise intensity $D$ varies proportionally to $\tau _c$, as

$$\begin{aligned} D = \frac{\sigma ^2}{2 k} = \sigma ^2 \tau _c. \end{aligned}$$

(92)

Alternatively, one may choose $\tau _c$ and $D$ to parameterize the noise, with the consequence that $\sigma ^2$ varies inversely proportional to $\tau _c$. Choosing one or the other can have a decisive impact on the response of the system and raises questions about how to interpret the observed behavior: Is a change in the response really a manifestation of changed correlations in the input? Or is it rather a consequence of the simultaneous change in $\sigma$ or $D$, i.e., one that would also occur if $\tau _c$ were fixed and only $\sigma$ or $D$ were varied?

The fact that white noise has infinite variance, but a finite intensity suggests that in the limit of small correlation times, the appropriate choice is fixing the noise intensity $D$. This is indeed a common parameterization in the literature when considering the white noise limit of colored noise (van den Broeck 1983; Broeck and Hänggi 1984; Bena 2006; Fourcaud and Brunel 2002; Brunel and Latham 2003). On the other hand, when $\tau _c$ is large, a more sensible choice is fixing $\sigma ^2$ (Schwalger and Schimansky-Geier 2008). This is also the parametrization chosen by Salinas and Sejnowski (2002). We note that an alternative parameterization that interpolates between these two extremes has been used in Alijani and Richardson (2011).

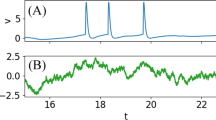
In Fig. 5 A and B, we reproduce Fig. 12a of Salinas and Sejnowski 2002, which shows firing rate and CV of an LIF as a function of $\tau _c$ for different values of $\sigma$ (which are kept fixed for each curve). Additionally, we plot the same curves as a function of $D$ and include results for a white-noise-driven LIF (Fig. 5C,D). Exact expressions for the white noise case have been known for a long time (Siegert 1951, for a summary of results for LIF and QIF see e.g., (Vilela and Lindner 2009). First, we note that for the parameter values for which it converges, the series expansion for the LIF given in Salinas and Sejnowski 2002 is in excellent agreement with our quadrature expressions (the resulting curves are indistinguishable). It can be seen, however, that for small correlation times, much of the observed effect can already be explained by the increase in noise intensity; it is already present if the noise does not contain any correlations at all but is purely white (thick line in Fig. 5C,D). Put differently, the increase in firing rate and CV with $\tau _c$ can be attributed to the increase of the noise intensity $D=\sigma ^2 \tau _c$ at fixed variance. If we instead fix $D$, the firing rate drops with increasing correlation time (illustrated by the symbols in Fig. 5A,C).

Fig. 5

Firing rate (a, c) and CV (b, d) of an LIF at different correlation times/noise intensities. All parameters were chosen as in Fig. 12a of (Salinas and Sejnowski 2002) ($v_R = 1/3, v_T=1, \mu = 0.5$). For each of the thin lines, only $\tau _c$ was varied, while $\sigma$ was kept constant. Both columns show curves for the same parameters; plotted as a function of $\tau _c = 1/(2k)$ in a, b (reproducing Fig. 12a of Salinas and Sejnowski 2002) and as a function of the noise intensity $D = \sigma ^2/(2k)$ in c, d. Four points in parameter space are marked by symbols to ease comparison of the two columns. The thick lines are analytical results for an LIF driven by Gaussian white noise with the same $D$. The insets in the right column show the same plots over a wider range of noise intensities. It can be seen that for small correlation times, much of the change in both mean firing rate and CV can already be explained by the increase in noise intensity. As illustrated by the symbols, the firing rate drops with correlation time if the noise intensity is kept fixed. Note that to compare our non-dimensionalized model quantitatively to the plots in Salinas and Sejnowski 2002, time needs to be multiplied and rate divided by the membrane time constant $\tau _m =$ 10 ms

The analysis in Salinas and Sejnowski 2002 thus applies to input with large correlation times; in order to make statements about input with small $\tau _c$, one should instead keep the noise intensity $D$ fixed. This is the parameterization we use in the rest of this section. In order to fully describe the range of neuronal responses one may observe in this parameterization, we also show and interpret results for large correlation times.

The bounded support of the DMP has consequences that one needs to keep in mind when doing parameter scans: It must be possible for the neuron to fire in the “+” dynamics, which corresponds to demanding $f(v) + \sigma > 0$ for all accessible $v$. If the neuron is in a sub-threshold regime ($f(v) < 0$ for at least some $v$), this imposes a constraint on the possible parameter values. For an LIF, they must fulfill the inequality

$$\begin{aligned} \mu - v_T + \sqrt{\frac{D}{\tau _c}} > 0, \end{aligned}$$

(93)

and for a QIF the inequality

$$\begin{aligned} \mu + \sqrt{\frac{D}{\tau _c}} > 0. \end{aligned}$$

(94)

If $f(v)$ alone is already positive for all $v$, the neuron is in a supra-threshold regime and there is no such constraint; however, for

$$\begin{aligned} f(v) - \sigma > 0 \end{aligned}$$

(95)

the stable fixed point in the “-” dynamics disappears (see Fig. 6). This means that the neuron may fire even if the noise never leaves the “-” state, which has a strong qualitative effect on the rate and, especially, the regularity of firing.

In Figs. 7 and 8, we plot the firing rate (A) and the CV (B) of an LIF and a QIF, respectively, when $\tau _c$ is varied while $D$ is kept constant. First of all, it is apparent that fixing $D$ results in a vastly different picture compared to (Salinas and Sejnowski 2002). In particular, for small $\tau _c$ (where this is the appropriate parameterization), we find that the firing rate actually decreases with increased $\tau _c$; for both LIF and QIF, it is always lower than for white noise input with the same intensity (thick bars). The CV at short correlation times is always larger than for white noise input in the QIF, while it can also be smaller for the LIF in a moderately sub-threshold regime. For larger $\tau _c$, effects of our parameterization become clearly visible: In the supra-threshold case, the decrease in $\sigma ^2$ eventually leads to the disappearance of the stable FP in the “-” dynamics (cf. Fig. 6), leading to a kink in the curves. More dramatically, in the sub-threshold case, firing is no longer possible when the variance becomes to small ($f(v)+\sigma < 0$ for at least some $v$); consequently, curves end at such points.

Fig. 6

Two regimes of firing (here in an LIF). Shown are nonlinearities and FPs (a) and an example time course of input and voltage (b). A correlation time that is much larger than the deterministic time from reset to threshold leads to burst-like behavior if there is a stable FP in the “-” dynamics (left column). However, if the base current is high enough or $\sigma$ is small enough, the neuron may fire even if the DMP $\eta (t)$ is in the “-” state, leading to a much more regular spike train (right column)

Fig. 7

Dependence of the firing rate (a) and the CV (b) of an LIF on the correlation time $\tau _c$. We vary the correlation time while adjusting $\sigma$ to keep $D = 1$ constant. Different curves correspond to different base currents: far sub-threshold ($\mu = -0.8$), slightly sub-threshold ($\mu = 0.8$), and supra-threshold ($\mu = 1.6)$. Thin lines: theory (quadrature results), circles: simulation results, dotted lines: quasi-static approximation (for $\mu = 0.8$ and $\mu =1.6$). Thick bars: theory for white-noise-driven LIF. The firing rate can be seen to be always lower for correlated input compared to the white noise case, while the CV can either be lower or higher

Fig. 8

Dependence of the firing rate (a) and the CV (b) of a QIF on the correlation time $\tau _c (D = 1)$. Different curves correspond to different base currents $\mu$ as indicated. Thin lines: theory (quadrature results), circles: simulation results, dotted lines: quasi-static approximation (for $\mu = -0.1$ and $\mu =1$). Thick bars: theory for white-noise-driven QIF. Again, the firing rate can be seen to be always lower for correlated input compared to the white noise case, while the CV can either be lower or higher

The behavior for $\tau _c \rightarrow \infty$ in the different parameterizations can also be directly read off the expressions from the quasi-static approximation, Eqs. (85)–(88): For fixed $D$ and a supra-threshold $\mu$, both $T_d^+$ and $T_d^-$ converge to $T_d {:=} \int _{v_R}^{v_T} dv/f(v)$ for $\sigma \rightarrow 0$, so for $\tau _c \rightarrow \infty$, the firing rate saturates ($r_0 \rightarrow T_d/2$) and the CV tends to zero. In contrast, when $\sigma ^2$ is fixed, $T_d^+$ and $T_d^-$ are independent of $\tau _c$, and one directly sees that the firing rate saturates, while the CV either diverges $\sim \sqrt{\tau _c}$ (sub-threshold) or saturates (supra-threshold). This is indeed the behavior described in Salinas and Sejnowski 2002. The divergence of the CV $\sim \sqrt{\tau _c}$ was also reported for OU noise with fixed variance (Schwalger and Schimansky-Geier 2008).

In Figs. 9 and 10, we plot the firing rate (A) and the CV (B) of an LIF and a QIF, respectively, as the mean input $\mu$ is varied for three different values of $\tau _c$. The firing rate shows qualitatively the same behavior for LIF and QIF. It can be seen to be lower for correlated than for white noise input, and unsurprisingly, it increases monotonically with $\mu$. The kinks in the curves for $\tau _c= 1$ and $\tau _c= 10$ occur where the stable FP in the “-” dynamics disappears (cf. Fig. 6). For the LIF, the CV may be slightly smaller than for the white noise case even where this FP still exists, whereas for the QIF, it is always larger than for the white noise case for small $\mu$. In the limit $\mu \rightarrow \infty$, both $T_d^+$ and $T_d^-$ decay $\sim (v_T-v_R)/\mu$. Consequently, $r_0$ diverges while the CV tends to zero (this is true for both parameterizations).

Fig. 9

Firing rate (a) and CV (b) of an LIF as a function of the base current $\mu$. Different curves correspond to different correlation times as indicated; $D = 1$. Thin lines: theory (quadrature results), circles: simulation results, dotted lines: quasi-static approximation. Thick lines: theory for white noise case. No simulation results were plotted in the top panel to avoid an overly cluttered presentation. Again, the firing rate can be seen to be always lower for correlated input compared to the white noise case, while the CV may be either higher or lower. The kinks in the curves for both rate and CV occur where $\mu$ becomes large enough that the neuron starts to fire tonically both in the “+” and the “-” state and are qualitatively well captured by the quasi-static approximation

Fig. 10

Firing rate (a) and CV (b) of a QIF as a function of the base current $\mu$. Different curves correspond to different correlation times as indicated; $D = 1$. Thin lines: theory (quadrature results), circles: simulation results, dotted lines: quasi-static approximation. Thick lines: theory for white noise. No simulation results were plotted in the top panel to avoid an overly cluttered presentation. We see qualitatively the same behavior as for the LIF (Fig. 9)

Finally, in Figs. 11 and 12, we plot the firing rate (A) and the CV (B) of an LIF and a QIF, respectively, as a function of the noise intensity. The firing rate can again be seen to decrease with increasing $\tau _c$. For the LIF, the CV shows a minimum at a finite noise intensity, both for white noise input as well as correlated input, if the correlation time is not too large. This is a signature of coherence resonance (Pikovsky and Kurths 1997). In contrast, the QIF is known not to exhibit coherence resonance (in the sense that the CV is minimal at a finite $D$) for white noise input; here, the CV monotonically decreases and, independent of parameters, approaches the value $1/\sqrt{3}$ for large $D$ (Lindner et al. 2003). It can be seen that this changes with correlated input, for which the CV diverges with increasing $D$, leading again to a (potentially very broad) minimum. This is true for arbitrarily small correlation times: For any value of $\tau _c$, there is a value of $D$ at which $T_d^+$ becomes small enough that the quasi-static approximation may be applied. From looking at Eq. (86), it is then apparent that any non-vanishing value of $\tau _c$ eventually leads to a divergence of the CV.

Fig. 11

Firing rate (a) and CV (b) of an LIF as a function of the noise intensity $D$. Different curves correspond to different correlation times (as indicated) and share the same base current $\mu = 0.8$. Thin lines: theory (quadrature results), circles: simulation results, dotted lines: quasi-static approximation. Thick lines: theory for white noise. The firing rate can be seen to be always lower than for the white noise case, while for this particular choice of $\mu$, the CV is always higher

Fig. 12

Firing rate (a) and CV (b) of a QIF as a function of the noise intensity $D$. Different curves correspond to different correlation times (as indicated); $\mu = -0.2$. Thin lines: theory (quadrature results), circles: simulation results, dotted lines: quasi-static approximation. Thick lines: theory for white noise. For a white noise driven QIF, the CV does not diverge in the high-noise limit but monotonically approaches a value of $1/\sqrt{3}$, independent of parameters. Correlations in the input make this universal behavior disappear, leading to a (potentially very broad) minimum in the CV

7 Application: the limit of small correlation times

While our analytical expressions for firing rate and CV show excellent agreement with simulations, it is hard to derive general statements from them. For instance, evaluating our expressions for specific parameters has shown the firing rate to be lower for correlated than for white input for every parameter set we tried (see Figs. 7, 8, 9, 10, 11, 12), raising the question whether this is always the case. However, it seems impossible to answer this question just by looking at the recursive relations Eqs. (69)–(72).

In order to make the difference to white-noise input explicit, we thus expand the recursive relations for the moments of the FPT density for small values of $\tau _c$, similar to what has been done for the case of Gaussian colored noise (Brunel and Sergi 1998; Fourcaud and Brunel 2002; Moreno et al. 2002; Brunel and Latham 2003). In this limit, $\sigma = \sqrt{D/\tau _c}$ is large, so it is sufficient to consider the case with no unstable FP and a stable FP left of $v_R$ (for the QIF, we will discuss the limit $v_R \rightarrow -\infty , v_T \rightarrow \infty$ after doing the expansion in $\tau _c$). We thus start from Eqs. (69)–(72). The function appearing in the exponents, $\phi (v)$, is readily expanded,

$$\begin{aligned} \phi (v)&= \frac{U(v)}{D} - \tau _c\int \limits ^v dx\; \frac{f^3(x)}{D^2} + \mathcal {O}\left( \tau _c^2\right) , \end{aligned}$$

(96)

where we have used the potential

$$\begin{aligned} U(v) {:=} - \int \limits ^v dx\; f(x). \end{aligned}$$

(97)

Consequently, we have

$$\begin{aligned} e^{\phi (v)} = e^{\frac{U(v)}{D}} \left( 1 - \tau _c\int \limits ^v dx\; \frac{f^3(x)}{D^2} \right) + \mathcal {O}\left( \tau _c^2\right) \end{aligned}$$

(98)

As $\gamma _2(v)$ diverges for $\tau _c\rightarrow 0$, it is advantageous to rewrite the recursive relations in terms of $\hat{Q}_n(v) {:=} Q_n(v)/\sigma$; after replacing $\sigma$ by $\sqrt{D/\tau _c}$, they read

$$\begin{aligned}&J_0(v) = \theta (v - v_R), \end{aligned}$$

(99)

$$\begin{aligned}&\hat{Q}_0(v) = e^{-\phi (v)} \Bigg [ \sqrt{\frac{\tau _c}{D}} \bigg ( e^{\phi (v_T)} - \theta (v_R - v) e^{\phi (v_R)}\bigg ) \nonumber \\&\quad - \int \limits _{v}^{v_T} ds\, \frac{e^{\phi (s)} \theta (s-v_R)}{f^2(s) \tau _c - D} \Bigg ],\end{aligned}$$

(100)

$$\begin{aligned}&J_n(v) = n \int \limits _{v_-}^v ds\; \frac{f(s) J_{n-1}(s) \tau _c - D \hat{Q}_{n - 1}(s)}{f^2(s) \tau _c - D}, \end{aligned}$$

(101)

$$\begin{aligned}&\hat{Q}_n(v) = e^{-\phi (v)} \Bigg [ J_n(v_T) e^{\phi (v_T)} \sqrt{\frac{\tau _c}{D}} \nonumber \\&\quad -\int \limits _{v}^{v_T} ds\, e^{\phi (s)} \frac{J_n(s) + n \tau _c \Big ( f(s) \hat{Q}_{n\mathrm - 1}(s) - J_{n\mathrm - 1}(s) \Big )}{f^2(s) \tau _c - D} \Bigg ].\nonumber \\ \end{aligned}$$

(102)

Looking at the above equations, it is apparent that the lowest order contribution due to correlations will in general be of order $\sqrt{\tau _c}$. Expanding in powers of $\sqrt{\tau _c}$ and letting $v_- \rightarrow -\infty$, we obtain

$$\begin{aligned} J_n(v)&= J_n^0(v) + \sqrt{\tau _c} \cdot J_n^c(v) + \mathcal {O}\Big ( \big ( \sqrt{\tau _c} \big )^2 \Big ), \end{aligned}$$

(103)

where

$$\begin{aligned}&J_0^0(v) = \Theta (y-v_R), \end{aligned}$$

(104)

$$\begin{aligned}&J_{n>0}^0(v) = \frac{n}{D} \int \limits _{-\infty }^{v} dx\; e^{\frac{-U(x)}{D}} \int \limits _{x}^{v_T} dy\; e^{\frac{U(y)}{D}} J_{n-1}^0(y), \end{aligned}$$

(105)

$$\begin{aligned}&J_1^c(v) = \int \limits _{-\infty }^{v} dx\, e^{\frac{-U(x)}{D}} \frac{e^{\frac{U(v_T)}{D}} -\Theta (v_R-x) e^{\frac{U(v_R)}{D}}}{\sqrt{D}}, \end{aligned}$$

(106)

$$\begin{aligned} \begin{aligned}&J_{n>1}^c(v) = n \int \limits _{-\infty }^{v} dx\; e^{\frac{-U(x)}{D}} \Bigg [ \frac{e^{\frac{U(v_T)}{D}} J_{n-1}^0(v_T)}{\sqrt{D}} \\&\qquad \qquad + \frac{1}{D} \int \limits _{x}^{v_T} dy\; e^{\frac{U(y)}{D}} J_{n-1}^c(y) \Bigg ]. \end{aligned} \end{aligned}$$

(107)

Equations (104) and (105) give the recursive relations for the FPT moments under Gaussian white noise input (Siegert 1951; Lindner 2004b). When the neuron is driven by dichotomous noise, these FPT moments undergo a correction [Eqs. (106) and (107)] that is in general to the lowest order proportional to $\sqrt{\tau _c}$. Interestingly, this $\sqrt{\tau _c}$ behavior was also found for LIFs driven by an Ornstein–Uhlenbeck process (OU), a Gaussian colored noise (Brunel and Sergi 1998; Moreno et al. 2002).

In Fig. 13, we compare the first-order approximation to firing rate (A) and CV (B) of an LIF to numerical simulations. It is apparent that for small $\tau _c$, the correction decays indeed with the square root of the correlation time. For this particular choice of parameters, the first-order correction can be seen to provide a decent description over the whole range of admissible $\tau _c$ values (for small $\tau _c$, we always find it in excellent agreement with simulations).

For a QIF driven by an OU, the correction to the firing rate has been reported to be linear in $\tau _c$, due to the choice of threshold and reset $v_R$ and $v_T$ at $\pm \infty$ (Brunel and Latham 2003). Indeed, for $v_R \rightarrow -\infty$ and $v_T \rightarrow \infty$, the $\sqrt{\tau _c}$ corrections vanish also for dichotomous noise, as we show in Appendix 10.

Fig. 13

Firing rate (a) and CV (b) of an LIF in the limit of small correlation times ($\mu = 0.5, D = 0.15$). Circles: Simulation results, thick lines: theory for white noise, thin lines: first-order ($\sqrt{\tau _c}$) approximation for dichotomous noise. The insets show the absolute difference between a white-noise-driven LIF and simulation results (circles) as well as the first-order correction (lines) in a log–log plot, demonstrating that, to the lowest order, the correction is indeed $\propto \sqrt{\tau _c}$

Finally, we can now address the question under which conditions the correction to the firing rate is negative. Consider the correction to the mean FPT:

$$\begin{aligned} \begin{aligned} J_1^c(v_T)&= \frac{e^{\frac{U(v_T)}{D}}}{\sqrt{D}} \int \limits _{-\infty }^{v_T} dx\; e^{\frac{-U(x)}{D}} \\&\quad - \frac{e^{\frac{U(v_R)}{D}}}{\sqrt{D}} \int \limits _{-\infty }^{v_R} dx\; e^{\frac{-U(x)}{D}} \end{aligned} \end{aligned}$$

(108)

This correction is positive if

$$\begin{aligned} \vartheta (v_T) > \vartheta (v_R), \end{aligned}$$

(109)

where

$$\begin{aligned} \vartheta (v) {:=} e^{\frac{U(v)}{D}} \int \limits _{-\infty }^{v} dx\; e^{\frac{-U(x)}{D}} \end{aligned}$$

(110)

This is certainly the case if $\vartheta (v)$ is monotonically increasing, i.e., $\vartheta '(v) > 0$ or

$$\begin{aligned} \frac{U'(v)}{D} e^{\frac{U(v)}{D}} \int \limits _{-\infty }^{v} dx\, e^{\frac{-U(x)}{D}} \ge -1. \end{aligned}$$

(111)

If $U'(v) > 0$ this is always true, so let us focus on $U'(v) < 0$. In this case, if $U'(x)$ is monotonically increasing up to $v$, then $-U'(x) \ge -U'(v) \quad \forall \quad x < v$ and

$$\begin{aligned} 1&= e^{\frac{U(v)}{D}} \int \limits _{-\infty }^{v} dx\, \bigg ( -\frac{U'(x)}{D} \bigg ) e^{\frac{-U(x)}{D}} \end{aligned}$$

(112)

$$\begin{aligned}&\ge e^{\frac{U(v)}{D}} \int \limits _{-\infty }^{v} dx\, \bigg ( -\frac{U'(v)}{D} \bigg ) e^{\frac{-U(x)}{D}}. \end{aligned}$$

(113)

Thus, for potential shapes with positive curvature—such as the quadratic potential of the LIF—the correction to the mean FPT is indeed always positive, meaning that to lowest order in $\tau _c$, the firing rate of an LIF always decreases with increasing correlations.

8 Summary and discussion

In this paper, we have theoretically studied IF neurons driven by asymmetric dichotomous noise. We have derived exact analytical expressions for the stationary probability distribution of voltages as well as for the moments of the ISI density. In doing this, we have taken care to ensure the proper treatment of fixed points in the “-” dynamics, which has allowed us to obtain valid expressions in all parameter regimes.

As a first application, we have used our theory to study the impact of temporally correlated input on neural firing, using symmetric dichotomous noise. We have argued that it is advantageous to keep the noise intensity fixed when exploring the effect of input with short correlation times, as opposed to keeping the variance fixed (Salinas and Sejnowski 2002), which is the more appropriate choice for long correlation times. We have then studied the firing rate and CV of LIF and QIF neurons when varying either the correlation time $\tau _c$, the base current $\mu$, or the noise intensity $D$. We have found that, compared to neurons driven by Gaussian white noise with the same $D$, the firing rate always decreases when the input is correlated, while the CV can be either higher or lower.

When varying the base current $\mu$, we find that CVs change abruptly at a certain value of $\mu$ when $\tau _c$ is large, but not for small or vanishing $\tau _c$. This could in principle be used to infer properties of presynaptic activity from single cell recordings in vivo. By measuring the spiking activity of a cell at different values of an injected current, an experimenter could replicate Figs. 9B and 10B. According to our theory, input that can be described by a two-state process with a long correlation time would manifest itself in a sudden drop of the CV as $\mu$ is increased. Such input could for example arise due to up and down states of a presynaptic population. Conversely, input with short or vanishing correlation times would lead to a smoother and weaker dependence of the CV on $\mu$.

Finally, varying $D$, we found that under correlated input, the CV of a QIF no longer converges to the universal value of $1/\sqrt{3}$ for large $D$, as found for white noise (Lindner et al. 2003), but instead diverges. This means that with correlated input, also QIF neurons may exhibit a weak form of coherence resonance (in the sense that the CV is minimal at a finite value of $D$).

We have studied the recursive relations for the ISI moments in the limit of small correlation times and found that, in general, the first-order correction with respect to the diffusion approximation is proportional to $\sqrt{\tau _c}$. The same had previously been observed for LIF neurons driven by an OU process, a different colored noise (Brunel and Sergi 1998; Moreno et al. 2002). For QIF neurons driven by OU processes, the firing rate correction has been shown to be of order $\tau _c$ (Brunel and Latham 2003), which is also recovered in our case, as for $v_R \rightarrow -\infty , v_T \rightarrow \infty$, the corrections proportional to $\sqrt{\tau _c}$ can be shown to vanish. We have also used the expansion in small $\tau _c$ to prove that for potentials with positive curvature (as is the case for LIF neurons), corrections to the firing rate are always negative (to the lowest order in $\tau _c$).

In addition to the qualitative similarities between neurons driven by dichotomous and OU processes at small correlation times, we have found that they agree well even quantitatively (results not shown). We thus expect our conclusions for small correlation times to be relevant also for other noise processes and think that they may help to clarify the effect of input correlations on neural firing, as well as its dependence on the specific choice of neuron model. Beyond the study of input correlations, our theory allows for the exploration of excitatory shot-noise input, as well as the effect of network up and down states. These applications will be pursued elsewhere.

9 Appendix: FPT recursive relations in the general case, transformed to ease numerical integration

Here, we transform the recursive relations for the moments of the FPT density in order to facilitate stable numerical integration near fixed points. We start by considering how Eqs. (62)–(65) behave at unstable FPs. As pointed out, setting $D_n=0$ and $E_n = v_U$ ensures that $Q_0(v)$ and $Q_n(v)$ do not diverge at an unstable FP $v_U$. Also, this choice entails $Q_n(v_U) = J_n(v_U)$, which means that the no divergence occurs in the integrand of Eq. (63),

$$\begin{aligned}&\lim \limits _{s\rightarrow v_U} \frac{f(s) J_{n-1}(s) - \sigma Q_{n-1}(s)}{f^2(s)-\sigma ^2} \end{aligned}$$

(114)

$$\begin{aligned}&\quad = \lim \limits _{s\rightarrow v_U} \frac{\left( f(s) - \sigma \right) J_{n-1}(s)}{(f(s)-\sigma )(f(s)+\sigma )} = \frac{J_{n-1}(v_U)}{2 \sigma }. \end{aligned}$$

(115)

Numerically, however, relying on this cancellation turns out to be problematic. It is thus advisable to rewrite the recursive relations, as shown in the following.

We define

$$\begin{aligned} H_n(v) {:=} \frac{\sigma }{f^2(v)-\sigma ^2} \left( Q_n(v) - J_n(v) \right) . \end{aligned}$$

(116)

With this, $J_{n>0}(v)$ becomes

$$\begin{aligned} J_{n>0}(v) = n \int \limits _{v_-}^v dx\; \frac{J_{n-1}(x)}{f(x)+\sigma } - H_{n-1}(x), \end{aligned}$$

(117)

where we have already satisfied the boundary condition for $J_{n>0}(v)$ by setting the lower integration limit to $v_-$. This means that, going from $\{J_n(v), Q_n(v)\}$ to $\{J_n(v), H_n(v)\}$, we now only need to pay attention to unstable FPs in the calculation of $H_n(v)$, instead of in both calculations. For the calculation of $H_n(v)$, we again need to split the voltage range $v_-$ to $v_T$ into intervals at fixed points of the “-” dynamics.

Expressions for the solution in the $i$th interval, $H_n^i(v)$ can be obtained by plugging Eqs. (62)–(65) into Eq. (116). Exploiting that,

$$\begin{aligned}&J_0(v) = \theta (v-v_R), \end{aligned}$$

(118)

$$\begin{aligned}&\frac{2k_+}{f(v)+\sigma } = \phi '(v) + \gamma _2(v), \end{aligned}$$

(119)

$$\begin{aligned}&J_n'(v) = n \left( \frac{J_{n-1}(v)}{f(v)+\sigma }-H_{n-1}(v)\right) , \end{aligned}$$

(120)

one may rewrite the integrand to obtain

$$\begin{aligned} H^i_0(v)&= \frac{\sigma e^{-\phi (v)}}{f^2(v)-\sigma ^2} \int \limits _{c_i}^v dx\; \Big ( 2(\alpha -1) \delta (x-v_R) - \nonumber \\&\quad \frac{2k_+}{f(x)+\sigma } \theta (x-v_R) \Big ) e^{\phi (x)},\end{aligned}$$

(121)

$$\begin{aligned} H^i_{n>0}(v)&= \frac{e^{-\phi (v)}}{f^2(v)-\sigma ^2} \int \limits _{c_i}^v dx\; \Big ( n(f(x)+\sigma )H_{n-1}(x)\nonumber \\&\quad \frac{2k_+}{f(x)+\sigma } \sigma J_n(x) \Big ) e^{\phi (x)}. \end{aligned}$$

(122)

As for $Q_n(v)$, the solutions in different intervals differ only in their integration constant $c_i$.

It is easily verified that the boundary conditions for $Q_n(v)$ (see Sect. 4) are satisfied by the following choice for $c_i$:

$$\begin{aligned} c_i = {\left\{ \begin{array}{ll} v_R &{} \hbox {if}\;f(v_T)-\sigma >0\; \hbox {and}\; \hbox {the}\; \hbox {left}\; \hbox {interval}\;\hbox {boundary}\;\hbox {is} v_R \\ v_U &{}\hbox {if}\;\hbox {one}\; \hbox {of}\;\hbox {the}\;\hbox {interval}\;\hbox {boundaries}\;\hbox {is}\; \hbox {an}\;\hbox {unstable}\\ &{}\quad \hbox {FP}\;\hbox {at}\;v_U \\ v_T &{} f(v_T)-\sigma <0\; \hbox {and}\; \hbox {the}\;\hbox {right}\; \hbox {interval}\; \hbox {boundary}\; \hbox {is}\;v_T \end{array}\right. } \end{aligned}$$

(123)

Denoting the index of the rightmost interval by $N$ and the left and right boundaries of the $i$th interval by $l_i$ and $r_i$, we have

$$\begin{aligned}&\alpha =1-\frac{k_+ \int \limits _{c_{N}}^{v_T} dx\; \frac{e^{\phi (x)}}{f(x)+\sigma } \theta (v-vr)}{e^{\phi (v_T)} - \theta (v_R-c_{N_i})e^{\phi (v_R)}} \end{aligned}$$

(124)

$$\begin{aligned}&J_0(v) = \theta (v-v_R), \end{aligned}$$

(125)

$$\begin{aligned}&J_{n>0}(v) = n \sum \limits _{i=1}^{N} \int \limits _{l_i}^{\min (r_i,v)} dx\; \frac{J_{n-1}(x)}{f(x)+\sigma } - H_{n-1}^i(x). \end{aligned}$$

(126)

These equations, together with Eqs. (121) and (122), allow for a recursive calculation of the $n$-th ISI moment in the general case.

10 Proof that the $\sqrt{\tau _c}$ correction vanishes for a QIF

Consider first the correction to the mean FPT:

$$\begin{aligned} \begin{aligned} J_1^c(v_T)&= \frac{e^{\frac{U(v_T)}{D}}}{\sqrt{D}} \int \limits _{-\infty }^{v_T} dx\; e^{\frac{-U(x)}{D}} \\&\quad - \frac{e^{\frac{U(v_R)}{D}}}{\sqrt{D}} \int \limits _{-\infty }^{v_R} dx\; e^{\frac{-U(x)}{D}} \end{aligned} \end{aligned}$$

(127)

If $U(v) \rightarrow \infty$ as $v \rightarrow -\infty$ (as is the case for a QIF), l’Hôpital’s rule can be used to show that the second term goes to zero as $v_R$ goes to $-\infty$. It then remains to show that

$$\begin{aligned} \lim \limits _{v_T \rightarrow \infty } \frac{\vartheta (v_T)}{\sqrt{D}} {:=} \lim \limits _{v_T \rightarrow \infty } \frac{e^{\frac{U(v_T)}{D}}}{\sqrt{D}} \int \limits _{-\infty }^{v_T} dx\; e^{\frac{-U(x)}{D}} = 0. \end{aligned}$$

(128)

If the potential additionally has the properties

• 1. $U(v) \rightarrow -\infty$ for $v \rightarrow \infty$,

• 2. there is an $a$ such that $U'(v) < -D v \quad \forall \quad v > a$,

as is the case for the cubic potential of a QIF, then

$$\begin{aligned}&\lim \limits _{v_T \rightarrow \infty } \vartheta (v_T) \end{aligned}$$

(129)

$$\begin{aligned}&\quad = \lim \limits _{v_T \rightarrow \infty } e^{\frac{U(v_T)}{D}} \int \limits _{-\infty }^{v_T} dx\, e^{\frac{-U(x)}{D}} \end{aligned}$$

(130)

$$\begin{aligned}&\quad = \lim \limits _{v_T \rightarrow \infty } \Bigg [\int \limits _{-\infty }^{a} dx\, e^{\frac{U(v_T)-U(x)}{D}} + \int \limits _{a}^{v_T} dx\, e^{\frac{U(v_T)-U(x)}{D}} \Bigg ] \end{aligned}$$

(131)

$$\begin{aligned}&\quad \le \quad 0 + \lim \limits _{v_T \rightarrow \infty } \int \limits _{a}^{v_T} dx\, -\frac{U'(x)}{D x} e^{\frac{U(v_T)-U(x)}{D}} \end{aligned}$$

(132)

$$\begin{aligned}&\quad = \lim \limits _{v_T \rightarrow \infty } \Bigg [ \frac{1}{v_T} - \frac{e^{\frac{U(v_T)-U(a)}{D}}}{a} + \int \limits _{a}^{v_T} dx\, \frac{e^{\frac{U(v_T)-U(x)}{D}}}{x^2} \Bigg ] \end{aligned}$$

(133)

$$\begin{aligned}&\quad \le \lim \limits _{v_T \rightarrow \infty } \Bigg [ \frac{1}{v_T} - \frac{e^{\frac{U(v_T)-U(a)}{D}}}{a} + \int \limits _{a}^{v_T} dx\, \frac{1}{x^2} \Bigg ] \end{aligned}$$

(134)

$$\begin{aligned}&\quad = \frac{1}{a}. \end{aligned}$$

(135)

Thus, $\lim _{v_T \rightarrow \infty } \vartheta (v_T)$ is smaller than any finite value $c$, because we can always choose an $a > 1/c$. The same reasoning can be used to show that the $\sqrt{\tau _c}$ contribution to the $n$-th FPT moment vanishes.