Keywords

1 Introduction

A Junctionless Transistor (JLT) does not have the very high doping concentration gradients or junctions at the source and drain junctions, thereby making fabrication processes easier than MOSFETs with junctions. JLTs has many other advantages like low OFF-state currents, near ideal subthreshold slope (SS ~ 60 mV/dec), high ON-state to OFF-state current ratio, DIBL effects, etc. [1]. Thus, JLTs are potential candidate for sub 20 nm technology nodes and beyond. There are several models for JLT available for the Symmetric Double-Gate (SDG) structures. Colinge et al. [2] proposed the first JL transistor. Duarte et al. [3] studied the electrostatic behavior of JL DG transistor using analytical modeling scheme. Subsequently, Lin et al. [4] developed an analytical model of an electric potential of a double-gated fully depleted junctionless transistor. A universal model for symmetric double-gate JL transistor has been reported [5]. However, all these models have been derived by assuming both gates to be perfectly symmetric but in reality, this may not be possible due to process variations and uncertainties which can affect surface potential and other parameters of SDG junctionless transistor. The JLT can be seen as an Asymmetric Double-Gate (ADG) device structure. Thus, a suitable analytical model is very much essential in incorporating these effects. Lu and Taur [6] proposed analytical models for an asymmetric DG MOSFET to reflect these variations. However, these analytical models work with a 1D Poisson equation, which is valid for the potential distribution of long-channel devices; such models are not suitable for the characteristics of asymmetric short-channel devices. A very few analytical models are available in the literature like the model by Jin et al. [7] for asymmetric model based on symmetric structure for junctionless transistors which cannot be considered as a full analytical model ADG JLT. Since the working principle for junctionless transistor is different, same models are not valid for ADG JLT and such models are rare in available literature. Moreover, to develop a JLT without source and drain junction regions is to make the transistor as small as possible which will increase the chip functionality. Because of all these reasons, models which can predict the behavior of ADG JLTs should be developed.

2 Model Derivation

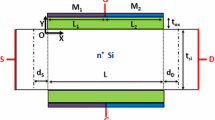
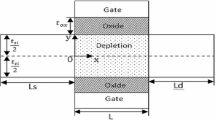
The coordinates, x and y, are as shown in Fig. 1. The Poisson’s equation in the silicon region considering both mobile and bulk fixed charges can be written as

Fig. 1
figure 1

A 3-D asymmetric junctionless DG MOSFET structure

Full size image
$$ \frac{{\partial^{2} \psi (x,y)}}{{\partial x^{2} }} + \frac{{\partial^{2} \psi (x,y)}}{{\partial y^{2} }} = \frac{q}{{\varepsilon_{si} }}\left( - N_{b} + N_{b} e^{{\frac{{q(\psi - \psi_{f} )}}{kT}}}\right) $$
(1)

Equation (1) has no direct analytical solution. Since n-type JL MOSFET is assumed, the body is doped with n-type impurity and the source and the drain are also heavily doped with n-type impurity, where Nb is the bulk doping concentration, \( \psi (x,y) \) is the channel potential, εsi is the silicon permittivity, ψf is the electron quasi-Fermi potential, and q is the electron charge. As Eq. (1) is not directly solvable, we will divide the 2D potential as

$$ \psi (x,y) = \psi_{I} (y) + \psi_{II} (x,y) $$
(2)

where \( \psi_{I} (y) \) is a 1-D function of y and \( \psi_{II} (x,y) \) is a 2-D function of both x and y. Here, \( \psi_{II} (x,y) \) is the potential where asymmetric nature has been included. The boundary conditions at the interface between the gate oxide and the silicon body for asymmetric JLT can be written as

$$ \begin{aligned} & V_{gs} - V_{fb} + \Delta_{fb} - \psi \left( {\frac{{t_{b} }}{2},y} \right) + (t_{ox} - \Delta t_{ox} )\frac{{\varepsilon_{si} }}{{\varepsilon_{ox} }}\frac{{\partial \psi (t_{b} /2,y)}}{\partial x} = 0 \\ & V_{gs} - V_{fb} - \psi \left( { - \frac{{t_{b} }}{2},y} \right) - t_{ox} \frac{{\varepsilon_{si} }}{{\varepsilon_{ox} }}\frac{{\partial \psi (t_{b} /2,y)}}{\partial x} = 0 \\ \end{aligned} $$
(3)

where Vgs, Vfb are gate to source and flat band voltage, respectively, \( \varepsilon_{ox} \) is the oxide permittivity, tox, tb are oxide, and body thickness, respectively, \( \Delta t_{ox} \), \( \Delta_{fb} \), are the asymmetries in the oxide thickness and flatband voltage, respectively. The boundary condition near the drain/source contact can be written as

$$ \begin{aligned} & \psi (x,L) = V_{ds} + V_{bi} \\ & \psi (x,0) = V_{bi} \\ \end{aligned} $$
(4)

where L is the gate length, Vbi is the built-in voltage between the silicon body and source/drain contact. These two functions should satisfy the following equations and the corresponding boundary conditions, respectively. Now the Poisson’s equation for \( \psi_{I} (y) \) can be written as

$$ \frac{{\partial^{2} \psi_{I} (y)}}{{\partial y^{2} }} = \frac{q}{{\varepsilon_{si} }}\left( { - N_{b} + N_{b} e^{{\frac{{q(\psi - \psi_{f} )}}{kT}}} } \right) $$
(5)

The solution of this equation for JLTs which normally operates in the depletion region can be given as [8]

$$ \psi_{I} (y) = V_{gs} - V_{th} - \frac{{qN_{b} T_{b} }}{{8C_{si} }} - V_{th} \,{\text{Lambert}}\,{\text{W}}\left[ {\frac{{q^{2} N_{b} T_{b} }}{{4C_{ox} KT}}e^{{\left( {\frac{{q(V_{gs} - V_{th} - \varPsi_{f} }}{KT}} \right)}} } \right] $$
(6)

where Lambert W is the Lambert W-function, Vth is the threshold voltage, and Csi, Cox are Silicon and oxide capacitors, respectively.

The 2D Poisson’s equation for \( \psi_{II} (x,y) \) is where asymmetric conditions are used can be given as

$$ \frac{{\partial^{2} \psi_{II} (x,y)}}{{\partial x^{2} }} + \frac{{\partial^{2} \psi_{II} (x,y)}}{{\partial y^{2} }} = 0 $$
(7)

The solution of the above equation can be obtained as

$$ \psi_{II} (x,y) = \sum\limits_{n = 1}^{\infty } {\left[ {K_{n} \cos \left( {\frac{n\pi x}{L}} \right) + R_{n} \cos \left( {\frac{n\pi x}{L}} \right)} \right]} \sin \left( {\frac{n\pi y}{L}} \right) $$
(8)

where Kn and Rn are the coefficients. They can be expressed as

$$ K_{n} = \frac{Num1 - Num2}{Den1 - Den2} $$
(9)
$$ \begin{aligned} & Num1 = \left(1 + \frac{{n\varepsilon_{si} \pi t_{ox2} }}{{\varepsilon_{ox} L}}\right)\cos \left(\frac{{n\pi t_{b} }}{2L}\right)A_{n} \\ & Num2 = \left(1 - \frac{{n\varepsilon_{si} \pi t_{ox1} }}{{\varepsilon_{ox} L}}\right)\cos \left(\frac{{n\pi t_{b} }}{2L}\right)B_{n} \\ & Den1 = \left(1 + \frac{{n\pi \varepsilon_{si} t_{ox1} }}{{\varepsilon_{ox} L}}\right)\left(1 + \frac{{n\pi \varepsilon_{si} t_{ox2} }}{{\varepsilon_{ox} L}}\right)\cos \left(\frac{{n\pi t_{b} }}{L}\right) \\ & Den2 = \left(1 + \frac{{n\pi \varepsilon_{si} t_{ox1} }}{{\varepsilon_{ox} L}}\right)\left(1 + \frac{{n\pi \varepsilon_{si} t_{ox2} }}{{\varepsilon_{ox} L}}\right)\cos \left(\frac{{n\pi t_{b} }}{L}\right) \\ & R_{n} = \frac{Num11 - Num22}{Den11 - Den22} \\ \end{aligned} $$
(10)
$$ \begin{aligned} & Num11 = \left(1 - \frac{{n\varepsilon_{si} \pi t_{ox2} }}{{\varepsilon_{ox} L}}\right)\cos \left(\frac{{n\pi t_{b} }}{2L}\right)A_{n} \\ & Num22 = \left(1 + \frac{{n\varepsilon_{si} \pi t_{ox1} }}{{\varepsilon_{ox} L}}\right)\cos \left(\frac{{n\pi t_{b} }}{2L}\right)B_{n} \\ & Den11 = \left(1 - \frac{{n\pi \varepsilon_{si} t_{ox1} }}{{\varepsilon_{ox} L}}\right)\left(1 - \frac{{n\pi \varepsilon_{si} t_{ox2} }}{{\varepsilon_{ox} L}}\right)\cos \left(\frac{{n\pi t_{b} }}{L}\right) \\ & Den22 = \left(1 + \frac{{n\pi \varepsilon_{si} t_{ox1} }}{{\varepsilon_{ox} L}}\right)\left(1 + \frac{{n\pi \varepsilon_{si} t_{ox2} }}{{\varepsilon_{ox} L}}\right)\cos \left(\frac{{n\pi t_{b} }}{L}\right) \\ \end{aligned} $$
(11)

where

$$ \begin{aligned} & A_{n} = \frac{{2qN_{b} L^{2} [\cos (n\pi ) - 1]}}{{\varepsilon_{si} n^{3} \pi^{3} }} + 2V_{ds} \frac{\cos (n\pi )}{n\pi } - 2(V_{gs1} - V_{fb1} - V_{bi} )\frac{\cos (n\pi ) - 1}{n\pi } \\ & B_{n} = \frac{{2qN_{b} L^{2} [\cos (n\pi ) - 1]}}{{\varepsilon_{si} n^{3} \pi^{3} }} + 2V_{ds} \frac{\cos (n\pi )}{n\pi } - 2(V_{gs2} - V_{fb2} - V_{bi} )\frac{\cos (n\pi ) - 1}{n\pi } \\ \end{aligned} $$
(12)

Kn and Rn are decided by the material parameters such as \( \varepsilon_{si} \) and \( \varepsilon_{ox} \) and design parameters such as L, Nb, tox1, tox2, tb and also influence of biases such as Vds and Vgs1 – Vfb1, Vgs2 – Vfb2. For the solution of \( \psi_{II} (x,y) \) till third-order terms taken to get higher accuracies; once \( \psi_{I} (y),\psi_{II} (x,y) \) are calculated, the final expression for potential in channel for ADG JT becomes

$$ \psi (x,y) = \psi_{I} (y) + \psi_{II} (x,y) $$
(13)

3 Model Verification and Discussions

To validate the analytic model for surface potential, we had considered the 3D device as shown in Fig. 1. To include the dependence on the impurity concentrations as well as the transverse and longitudinal electric field values, Lombardi mobility model is employed. For leakage currents issue, the Shockley–Read–Hall (SRH) recombination model is included in the simulation. Fermi–Dirac carrier statistics without impact ionization is utilized in the simulations, but Quantum effect is not considered. Doping concentration in channel ND of 5 × 1019 and 1 × 1020 cm−3, silicon body thickness (Tb)= 10 nm are considered for TCAD simulation. Channel width (W) is 10 nm. In addition, p-type polysilicon is used having doping concentration 1022 cm−3.

A comparative surface potential variation along the channel direction for SDG and ADG JLTs is shown in Fig. 2. Here, for SDG, the oxide thicknesses (tox) are kept same at 1 nm for both top and bottom gates, while for ADG JLT, oxide thicknesses for top gate were kept at similar to SDG JLT, i.e., 1 nm while that of bottom gate kept at 2 nm, the channel lengths for both the transistors were kept at 20 nm. From Fig. 2, we can observe that the characteristic curve for the potential variation is same for both top and bottom surfaces for SDG JLT and also the top surface where we had kept tox same (1 nm). The bottom surface for ADG JLT shows a lower potential curve which is evident from higher tox (2 nm) which leads to lower capacitive action from bottom gate and thus low surface potential compared to the top gate. Moreover, the variations in surface potential curves occur mainly due to two reasons. First, when the device is not in use, nonzero oxide field is present in the silicon dioxide layer. Second, the potential difference between the gate and the source and the potential difference between gate and the drain are different. These two factors contribute to the bending of the potential curve between the source and the drain. With the decrease in the length of the device, the band bending increases which is shown in Fig. 3. Potential variations from source to drain for different channel lengths (20, 10 nm) and similar oxide thicknesses (top 1 nm, back 2 nm) of the ADG JLT are plotted in Fig. 3. From Fig. 3, we can observe that the band bending for channel length (Lg = 20 nm) shown is lesser than that in case for channel length (Lg = 10 nm). In case of the device (Lg = 10 nm) compared to that of device with (Lg = 20 nm), the source and the device are in greater proximity [2]. To observe the severity on surface potential with change in oxide thickness, we have considered different thicknesses of the oxide layers. For first case, we had taken tox top as 1 nm and that of bottom as 2 nm, while for the second case we had correspondingly taken 1 nm and 5 nm, respectively. From Fig. 4, it was evident that for top surface potential, both the cases were almost similar but that of bottom surface potential changes drastically as we go for 2–5 nm. Figure 5 shows the variations of surface potential of ADG JLT for different bias voltages (VGS) with channel length 20 nm and tox front 1 nm and bottom 2 nm. This curve shows that with increase in gate potential, the differences in top and bottom surface potential bending are reduced. This can be explained by the fact that with increase in gate potential more number of charge carriers will be available in the channel; moreover, in the bottom surface, the tox is more, so lesser will be surface potential. This difference gets reduced correspondingly as we increase the gate voltages.

Fig. 2
figure 2

Potential variation along Y-direction of the SDG/ADG device

Full size image
Fig. 3
figure 3

Potential variation along Y-direction for different L for ADG JLT

Full size image
Fig. 4
figure 4

Surface potential for different tox for a 20 nm ADG JLT device

Full size image
Fig. 5
figure 5

Potential variation along Y-direction for different Vgs for ADG JLT

Full size image

4 Conclusion

Here, we have proposed an analytical model of surface potential for Double-Gate Asymmetric Junctionless Transistor (DG AJLT). The model can accurately predict the surface potential including the flatband asymmetry and gate-oxide-thickness asymmetry. The variations of electrical characteristics because of structural asymmetry like the differences of gate oxide thicknesses and gate biases between the top gate and bottom gate oxide can be explained. Further, the models predict the variation of design parameters like body thickness and channel length variations with high accuracy. The models proposed show a very good agreement with the results obtained from 3D TCAD device simulation.