1 Introduction

With recent measurements of gravitational waves and images of black holes , these astrophysical objects are gaining relevance [1, 2]. Black holes arise as predictions of general relativity through Einstein equations [3] and they stand out due to their causal structure [4]. The boundary around a black hole from which nothing can escape is called the event horizon. The mass of an astrophysical black hole can vary from a few solar masses to over a billion solar masses [1, 2]. The black hole mass influences the size of its event horizon; the more massive the black hole, the larger the event horizon . The gravitational field of these objects makes them ideal for testing the nonlinearities of gravitational theory and exploring alternative theories of gravity [6].

An alternative to classical black holes is known as regular black holes [7]. Unlike typical black holes, regular black holes lack a singularity at their core [8], which is the point where geodesics are interrupted [9]. Instead, regular black holes possess a finite curvature of spacetime within their cores, avoiding divergences [10].

Regular black holes offer a potential solution to some of the problems associated with classical black holes, such as the information paradox. The first regular black hole metric was proposed by Bardeen in 1968 [11]. This metric can be interpreted as a solution to Einstein equations when gravity theory is coupled with nonlinear electrodynamics. The source of this electrodynamics can be either an electric or a magnetic charge [12, 13]. Bardeen’s solution initiated the study of regular solutions, which has expanded over time, encompassing several static solutions [14,15,16,17,18,19,20], rotating solutions [21,22,23,24,25,26,27,28], and solutions in alternative theories of gravity [29,30,31,32,33,34]. Additionally, researchers have explored several properties of these black holes [35,36,37,38,39,40,41,42]. While most regular solutions involve an electric or magnetic charge as the source, there are also nonsingular solutions that rely on a scalar field [43, 44], or a combination of these sources [45,46,47,48,49,50]. In the context of modified theories of gravity, in some cases it becomes complicated to obtain the proper sources, and thus it becomes simpler to consider an anisotropic fluid as the source [51,52,53].

In addition to generating regular solutions in the context of black holes, nonlinear electrodynamics brings changes in the study of the properties of these solutions. An example of this is in the study of the thermodynamics of black holes [54,55,56,57,58,59,60]. To maintain entropy’s relation to the black hole area, nonlinear electrodynamics alters the first law of thermodynamics. It is possible to use nonlinear electrodynamics to create solutions with several horizons [61, 62]. In the context of nonlinear electromagnetic theory, photons deviate from geodesic paths [8, 63], modifying the black holes shadows [64,65,66]. Although regular spacetimes are the main focus of the application of nonlinear electrodynamics in the context of black holes, not all spacetimes that arise from nonlinear electrodynamics will be regular [61, 67, 68].

The origin of nonlinear electrodynamics is linked to phenomena of quantum electrodynamics, such as photon-photon scattering [69, 70]. One of the most famous models of this type of theory is the Euler-Heisenberg electrodynamics [71]. Through the effective Lagrangian, this electrodynamics treats the photon-photon scattering through the interaction with virtual electron-positrons. Another model that predicts this interaction between photons is the Born-Infield electrodynamics [72], which arises in a context of regularizing some divergences that appear in Maxwell electromagnetism. The photon-photon scattering has been tested in high-energy Pb-Pb collisions at the Large Hadron Collider (LHC) [73]. In a Pb-Pb collision, the lead ions are highly charged and produce a strong electromagnetic field, which can generate virtual photons. When two virtual photons collide, they can create a real photon, which can be detected by the detectors at the LHC.

Nonlinear electrodynamics is associated with intriguing phenomena such as vacuum birefringence [74, 75]. Birefringence refers to the phenomenon where a material has different refractive indices for other polarization states of light [76]. In a vacuum where there are no material properties to affect the propagation of light, there is no birefringence. However, in the presence of a strong electromagnetic field, the vacuum itself can exhibit birefringence due to quantum effects [74]. This phenomenon is known as vacuum birefringence or vacuum polarization. The Euler-Heisenberg model presents birefringence in vacuum, while the Born-Infield electrodynamics has no birefringence. There are several models of electrodynamics that allow the existence of birefringence in vacuum. One of these models is the inverse electrodynamics [77]. This model is attractive since the birefringence appears even though the electromagnetic Lagrangian depends only on the electromagnetic scalar. Since this electrodynamics is already prominent in the context of electromagnetic theory, we want to explore what contributions it might generate in the context of black holes.

The structure of this article is organized as follows: In Sec. 2, we use the suggested electrodynamics model to check if it is possible to obtain black hole solutions with it. We also analyze the regularity of these solutions and which energy conditions can be violated. In Sec. 3, we calculate some thermodynamic quantities, such as the temperature and the heat capacity, to verify the thermodynamic stability of this solution. Section 4 is dedicated to studying massive and massless geodesics in this spacetime. Section 5 presents our conclusions and future perspectives. We adopt the metric signature \((+,-,-,-)\). We shall work in geometrodynamics units where \(G=\hbar =c=1\).

2 Spacetime, Energy Conditions, and Curvature Singularities

Let’s consider the theory described by the action

$$\begin{aligned} S=\int d^4x \sqrt{-g}\left[ R+2\kappa ^2 L(F)\right] , \end{aligned}$$
(1)

where \(\kappa =8\pi \), R is the curvature scalar, g is the determinant of the metric tensor, \(g_{\mu \nu }\), and L(F) is a general function of the electromagnetic scalar \(F=F^{\mu \nu }F_{\mu \nu }/4\), with \(F_{\mu \nu }\) being the electromagnetic tensor.

The field equations are given by [4]

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R=\kappa ^2T_{\mu \nu }, \end{aligned}$$
(2)

where

$$\begin{aligned} T_{\mu \nu }=\frac{1}{4\pi }\left[ g_{\mu \nu }L(F)-L_F(F){F_\mu }^\alpha F_{\nu \alpha }\right] , \end{aligned}$$
(3)

with \(L_F=dL(F)/dL\).

If we consider a spherically symmetric spacetime, describes by the line element

$$\begin{aligned} ds^2=f(r)dt^2-f^{-1}(r)dr^2-r^2\left( d\theta ^2+\sin ^2\theta d\phi ^2\right) , \end{aligned}$$
(4)

and considering that the source is only magnetically charged, the only nonzero component of the electromagnetic tensor is \(F_{23}=q \sin \theta \).

The components of the field equations are

$$\begin{aligned} -\frac{r \left( f'(r)+2 r L(F)\right) +f(r)-1}{r^2}=0,\end{aligned}$$
(5)
$$\begin{aligned} -\frac{f'(r)}{r}-\frac{f''(r)}{2}-2 L(F)+\frac{2 q^2 L_F(r)}{r^4}=0. \end{aligned}$$
(6)

Once you have the equations of motion, there are two possible paths; impose the metric and obtain the matter content that generates it, or define the matter content and thus solve the equations of motion to obtain the line element.

The Lagrangian that describes the inverse electrodynamics is given by [77]

$$\begin{aligned} L(F)=F\left[ 1+\lambda \left( \frac{\Lambda ^4}{2F}\right) ^{2\delta }\right] . \end{aligned}$$
(7)

The Maxwell theory is recovered to \(\lambda =0\) or \(\Lambda =0\). The parameter \(\lambda \) is dimensionless, \(\Lambda \) has the unit of \(m^{-1/2}\), where m is the black hole mass, and \(\delta \) is just a positive number. Using (7), we find

$$\begin{aligned} L_F(F)=1-4^{-\delta } (2 \delta -1) \lambda \left( \frac{\Lambda ^4}{F}\right) ^{2 \delta }. \end{aligned}$$
(8)

Once we have a magnetic source, the scalar F is given by

$$\begin{aligned} F(r)=\frac{q^2}{2r^4}. \end{aligned}$$
(9)

Using (7), (8), and (9), we solve the field equation and we find

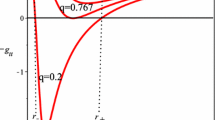
$$\begin{aligned} f(r)=1-\frac{2m}{r}+\frac{q^2}{r^2}+\frac{\lambda q^2 }{(1-8 \delta ) r^2}\left( \frac{\Lambda ^4 r^4}{q^2}\right) ^{2 \delta }. \end{aligned}$$
(10)

This solution is not asymptotically flat to \(\lambda \ne 0\), \(\Lambda \ne 0\), and \(\delta \ne 0\). If \(\lambda =0\) or \(\Lambda =0\), the Reissner-Nordstrom solution is recover. In Fig. 1 we see how the function f(r) behaves in terms of the radial coordinate. There are three horizons; a Cauchy horizon, an event horizon and a type of cosmological horizon.

Fig. 1
figure 1

Behavior of the function f(r) with \(q=0.4m\). In (a) we fixed \(\lambda =0.2\), and \(m^2\Lambda ^4=0.002\). In (b) we fixed \(\delta =1\), and \(m^2\Lambda ^4=0.002\). In (c) we fixed \(\delta =1\), and \(\lambda =0.2\)

Full size image

2.1 Curvature Singularities

In order to verify the existence of curvature singularities, we need to analyze the curvature invariants, that are given by

$$\begin{aligned} R= & \frac{2 \left( 2 r f'(r)+f(r)-1\right) }{r^2}+f''(r),\end{aligned}$$
(11)
$$\begin{aligned} K= & R^{\mu \nu \alpha \beta }R_{\mu \nu \alpha \beta }= \frac{4 \left( r^2 f'(r)^2+(f(r)-1)^2\right) }{r^4}+f''(r)^2, \end{aligned}$$
(12)

where K is the Kretschmann scalar.

If we calculate the curvature scalar we get

$$\begin{aligned} R=-8 \delta \lambda \Lambda ^4 \left( \frac{\Lambda ^4 r^4}{q^2}\right) ^{2 \delta -1}. \end{aligned}$$
(13)

If we choose \(\delta =1/2\), the curvature scalar will be constant and we have a de Sitter type spacetime. In this specific case, the inverse electrodynamics acts like a cosmological constant that permeates the entire spacetime. To \(\delta >1/2\), there is a curvature singularity at \(r\rightarrow \infty \). Although spatial infinity is singular, this point is located beyond the cosmological-type horizon. From the curvature scalar we do not find singularities at \(r=0\). However, to verify the existence of curvature singularities, the Kretschmann scalar can provide more information about the singularities than the curvature scalar [78]. In general, the Kretschmann scalar is not so clear. So that, if we consider the simplest cases, we find

$$\begin{aligned} K= & -\frac{272 \lambda \Lambda ^8}{7}+\frac{48 m^2}{r^6}-\frac{96 m q^2}{r^7}+\frac{160 \lambda \Lambda ^8 m r}{7 q^2}+\frac{1048 \lambda ^2 \Lambda ^{16} r^8}{49 q^4}+\frac{56 q^4}{r^8},\quad \text{ if }\quad \delta =1,\nonumber \\ \end{aligned}$$
(14)
$$\begin{aligned} K= & \frac{48 m^2}{r^6}+\frac{416 \lambda \Lambda ^{16} m r^9}{5 q^6}-\frac{96 m q^2}{r^7}+\frac{3768 \lambda ^2 \Lambda ^{32} r^{24}}{25 q^{12}}-\frac{656 \lambda \Lambda ^{16} r^8}{5 q^4}+\frac{56 q^4}{r^8},\quad \text{ if }\quad \delta =2,\nonumber \\\end{aligned}$$
(15)
$$\begin{aligned} K= & \frac{48 m^2}{r^6}+\frac{3360 \lambda \Lambda ^{24} m r^{17}}{23 q^{10}}-\frac{96 m q^2}{r^7}+\frac{215384 \lambda ^2 \Lambda ^{48} r^{40}}{529 q^{20}}-\frac{5200 \lambda \Lambda ^{24} r^{16}}{23 q^8}+\frac{56 q^4}{r^8},\quad \text{ if }\quad \delta =3,\nonumber \\ \end{aligned}$$
(16)
$$\begin{aligned} K= & \frac{48 m^2}{r^6}+\frac{6496 \lambda \Lambda ^{32} m r^{25}}{31 q^{14}}-\frac{96 m q^2}{r^7}+\frac{760504 \lambda ^2 \Lambda ^{64} r^{56}}{961 q^{28}}-\frac{9968 \lambda \Lambda ^{32} r^{24}}{31 q^{12}}+\frac{56 q^4}{r^8},\quad \text{ if }\quad \delta =4.\nonumber \\ \end{aligned}$$
(17)

This result implies in a curvature singularity at \(r=0\). This means that nonlinear electrodynamics will not always generate a regular solution.

2.2 Energy Conditions

Black hole solutions involving nonlinear electrodynamics usually violate the energy conditions associated with the stress-energy tensor. In order to analyze the energy conditions, we consider the matter sector, which is electromagnetic, written as an anisotropic fluid

$$\begin{aligned} T^{\mu } _{\nu }=\textrm{diag}\left[ \rho ,-p_r,-p_t,-p_t\right] \,, \end{aligned}$$
(18)

where \(\rho \), \(p_r\), and \(p_t\) are the energy density, radial pressure, and tangential pressure, respectively. The fluid quantities are given by

$$\begin{aligned} \rho =-\frac{r f' +f -1}{\kappa ^2 r^2}\,,\qquad p_r=\frac{r f'+f -1}{\kappa ^2 r^2}\,,\qquad p_t=\frac{r f''+2 f' }{2 \kappa ^2 r}\,. \end{aligned}$$
(19)

The classical energy conditions are the null (NEC), weak (WEC), dominant (DEC), and strong (SEC) energy conditions, and are given by the inequalities [79]

$$\begin{aligned} & NEC_{1,2}=WEC_{1,2}=SEC_{1,2} \Longleftrightarrow \rho +p_{r,t}\ge 0, \end{aligned}$$
(20)
$$\begin{aligned} & SEC_3 \Longleftrightarrow \rho +p_r+2p_t\ge 0,\end{aligned}$$
(21)
$$\begin{aligned} & DEC_{1,2} \Longleftrightarrow \rho -|p_{r,t}|\ge 0 \Longleftrightarrow (\rho +p_{r,t}\ge 0) \hbox { and } (\rho -p_{r,t}\ge 0),\end{aligned}$$
(22)
$$\begin{aligned} & DEC_3=WEC_3 \Longleftrightarrow \rho \ge 0, \end{aligned}$$
(23)

As \(DEC_{1,2} \Longleftrightarrow ( (NEC_{1,2}) \hbox { and } (\rho -p_{r,t}\ge 0))\) we assume part of the DEC into the NEC and simply replace \(DEC_{1,2}\Longrightarrow \rho -p_{r,t}\ge 0\).

Using (19), we have

$$\begin{aligned} & NEC_{1} \Longleftrightarrow 0, \qquad NEC_2 \Longleftrightarrow \frac{r^2 f''-2 f +2}{2 \kappa ^2 r^2}\ge 0, \qquad SEC_3 \Longleftrightarrow \frac{r f''+2 f' }{\kappa ^2 r}\ge 0,\end{aligned}$$
(24)
$$\begin{aligned} & DEC_{1} \Longrightarrow \frac{2\left( 1 - f' r - f \right) }{ \kappa ^2r^2}\ge 0,\quad DEC_2 \Longrightarrow -\frac{r^2 f'' +r \left( 4 f' \right) +2 f-2}{2 \kappa ^2 r^2}\ge 0, \quad WEC_3 \Longleftrightarrow -\frac{r f' +f -1}{\kappa ^2 r^2}\ge 0.\nonumber \\ \end{aligned}$$
(25)

We see that \(NEC_1\) is identically satisfied and \(DEC_1=2DEC_3=2WEC_3\). It means that we only need to analyze \(NEC_2\), \(SEC_3\), \(DEC_2\), and \(WEC_3\). Substituting (10) in the energy conditions, we find

$$\begin{aligned} & NEC_2 \Longleftrightarrow -\frac{2 q^2}{\kappa ^2 r^4} \left( (2 \delta -1) \lambda \left( \frac{\Lambda ^4 r^4}{q^2}\right) ^{2 \delta }-1\right) \ge 0,\end{aligned}$$
(26)
$$\begin{aligned} & SEC_3 \Longleftrightarrow -\frac{2 q^2}{\kappa ^2 r^4} \left( (4 \delta -1) \lambda \left( \frac{\Lambda ^4 r^4}{q^2}\right) ^{2 \delta }-1\right) \ge 0,\end{aligned}$$
(27)
$$\begin{aligned} & DEC_2 \Longrightarrow -\frac{4 \delta \lambda \Lambda ^4}{\kappa ^2} \left( \frac{\Lambda ^4 r^4}{q^2}\right) ^{2 \delta -1}\ge 0,\end{aligned}$$
(28)
$$\begin{aligned} & WEC_3 \Longleftrightarrow \frac{q^2}{\kappa ^2 r^4} \left( \lambda \left( \frac{\Lambda ^4 r^4}{q^2}\right) ^{2 \delta }+1\right) \ge 0. \end{aligned}$$
(29)

The only value \(\delta \) at which all energy conditions will be satisfied is for \(\delta =0\). The energy density, \(\rho =WEC_3\), is always positive while the condition \(DEC_2\) is always violated. If \(r>\frac{\sqrt{\left| q\right| } }{\Lambda ((4 \delta -1) \lambda )^{\frac{1}{8\delta } }}\), the strong energy condition is violated. If \(r>\frac{\sqrt{\left| q\right| } }{\Lambda ((2 \delta -1) \lambda )^{\frac{1}{8\delta } }}\), the null energy condition is violated.

3 Thermodynamics

Studying the thermodynamics of a black hole, we can find information about its stability. The first step in this process is to calculate the temperature of the black hole, which is given by [80]

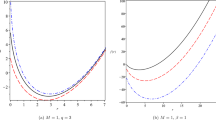
$$\begin{aligned} T=\frac{k}{2\pi }=\left. \frac{f'(r)}{4\pi }\right| _{r_+}=\frac{r_+^2-q^2 \left( \lambda \left( \frac{\Lambda ^4 r_+^4}{q^2}\right) ^{2 \delta }+1\right) }{4 \pi r_+^3}, \end{aligned}$$
(30)

where k is the surface gravity and \(r_+\) is the radius of the event horizon. For \(\lambda =0\), we recover the temperature of the Reissner-Nordstrom case, and if \(q=0\), we recover the Schwarzschild case. In Fig. 2, we analyze the behavior of the temperature as a function of the event horizon radius. To ensure the temperature remains positive, there must be a maximum and a minimum value for the event horizon radius. This type of behavior is already known from solutions such as the Reissner-Nordstrom-de Sitter solution.

Fig. 2
figure 2

Behavior of the temperature with \(q=0.4m\). In (a) we fixed \(\lambda =0.2\) and \(m^2\Lambda ^4=0.002\). In (b) we fixed \(\delta =1\) and \(m^2\Lambda ^4=0.002\). In (c) we fixed \(\delta =1\) and \(\lambda =0.2\)

Full size image

We can extract information about the thermodynamic instability of this solution through the heat capacity, given by [57]

$$\begin{aligned} C=T_k \frac{\partial S}{\partial T_k}=-\frac{2 \pi r_+^2 \left( r_+^2-q^2 \left( \lambda \left( \frac{\Lambda ^4 r_+^4}{q^2}\right) ^{2 \delta }+1\right) \right) }{q^2 \left( (8 \delta -3) \lambda \left( \frac{\Lambda ^4 r_+^4}{q^2}\right) ^{2 \delta }-3\right) +r_+^2}, \end{aligned}$$
(31)

where S is the black hole entropy, that is given by the area law as [80]

$$\begin{aligned} S=\frac{A}{4}=\pi r_+^2, \end{aligned}$$
(32)

with A being the black hole area. A thermodynamically stable solution is indicated by \(C>0\), while \(C<0\) signifies instability [81]. In Fig. 3, a discontinuity in the heat capacity is observed, signifying a phase transition. The black holes is unstable and will continue to evaporate until they reach a stable phase. Although there some values of \(r_+\) in which black holes can exhibit positive heat capacity, such configurations are deemed nonphysical due to their association with negative temperatures. Similarly, some cases of black holes with negative heat capacities; however, like their counterparts, the negative temperature renders these situations nonphysical. Alterations to the solution parameters do not significantly impact the thermodynamic stability of the solution. This behavior, with only one phase transition, is similar to what occurs with the Reissner-Nordstrom-de Sitter solution.

Fig. 3
figure 3

Behavior of the temperature with \(q=0.4m\). In (a) we fixed \(\lambda =0.2\) and \(m^2\Lambda ^4=0.002\). In (b) we fixed \(\delta =1\) and \(m^2\Lambda ^4=0.002\). In (c) we fixed \(\delta =1\) and \(\lambda =0.2\)

Full size image

Usually, the first law of thermodynamics needs corrections in the mass term, internal energy, for black holes involving nonlinear electrodynamics. This generally occurs because the electromagnetic Lagrangian explicitly depends on the mass of the black hole. In the case we are considering in this work, the Lagrangian does not explicitly depend on the mass, so our temperature is the same if we consider the relation \(T=\partial m/\partial S\), but we can still examine the Smarr formula, the first law of thermodynamics in integral form, for our case.

To derive the Smarr formula for our problem, we will express the mass function in terms of entropy and the parameters of our solution as follows:

$$\begin{aligned} m\left( S,q,\lambda ,\Lambda ,\delta \right) = \frac{\sqrt{\pi } \left( \frac{(8 \delta -1) \left( \pi q^2+S\right) }{\pi }-\pi ^{-4 \delta } \lambda q^2 \left( \frac{\Lambda ^4 S^2}{q^2}\right) ^{2 \delta }\right) }{2 (8 \delta -1) \sqrt{S}}. \end{aligned}$$
(33)

If we consider that the function \(m\left( S,q,\lambda ,\Lambda ,\delta \right) \) is a homogeneous function, we can determine the degree of homogeneity by rewriting the function as:

$$\begin{aligned} m\left( l^a S,l^b q,l^c \lambda ,l^d \Lambda ,l^e \delta \right) = \frac{\sqrt{\pi } \left( q^2 l^{2 b} \left( \lambda l^c \left( -\pi ^{-4 \delta l^e}\right) \left( \frac{\Lambda ^4 S^2 l^{2 (a-b+2 d)}}{q^2}\right) ^{2 \delta l^e}+8 \delta l^e-1\right) +\frac{S l^a \left( 8 \delta l^e-1\right) }{\pi }\right) }{2 \sqrt{S l^a} \left( 8 \delta l^e - 1\right) }. \end{aligned}$$
(34)

To isolate l, we choose the values; \(a=1\), \(b=1/2\), \(c=0\), \(d=-1/4\), and \(e=0\), thus obtaining:

$$\begin{aligned} m\left( l S,l^1/2 q,l^0 \lambda ,l^{-1/4} \Lambda ,l^0 \delta \right) = \frac{\sqrt{\pi }\sqrt{l} \left( \frac{(8 \delta -1) \left( \pi q^2+S\right) }{\pi }-\pi ^{-4 \delta } \lambda q^2 \left( \frac{\Lambda ^4 S^2}{q^2}\right) ^{2 \delta }\right) }{2 (8 \delta -1) \sqrt{S}}. \end{aligned}$$
(35)

Thus, we have a degree of homogeneity \(n=1/2\). With this, we can use the properties of a homogeneous function [82] and write the Smarr formula as:

$$\begin{aligned} \frac{1}{2}m\left( S,q,\lambda ,\Lambda ,\delta \right) = T S+\frac{1}{2} A_q q-\frac{1}{4} A_\Lambda \Lambda , \end{aligned}$$
(36)

where

$$\begin{aligned} A_q=\frac{\partial m}{\partial q}, \qquad \text{ and } \qquad A_\Lambda =\frac{\partial m}{\partial \Lambda }. \end{aligned}$$
(37)

Once we have the Smarr formula, the first law is given by

$$\begin{aligned} dm=TdS+A_q dq+A_\Lambda d\Lambda . \end{aligned}$$
(38)

It is interesting to note that, usually, when dealing with solutions involving nonlinear electrodynamics, the first law of thermodynamics requires corrections to the mass term so that the temperature obtained from the first law matches the temperature derived from the surface gravity. However, our first law does not require this correction factor because both methods yield the same expression for the temperature. This is because such corrections are necessary when the electromagnetic Lagrangian, and consequently the energy-momentum tensor, explicitly depend on the black hole’s mass [57], which is not the case in our problem.

4 Geodesics

In this section, we will investigate the motion of particles in the previously obtained spacetime. To do this, we will use the Lagrangian formalism to obtain the equations of motion that describe the movement of particles in the spacetime in question.

Associated with the line element (4), we have the Lagrangian

$$\begin{aligned} 2L_{geo}=\dot{s}^2=g_{\mu \nu }\dot{x}^\mu \dot{x}^\nu =f\dot{t}^2-f^{-1}\dot{r}^2-r^2\left( \dot{\theta }^2+\sin ^2\theta \dot{\phi }^2\right) . \end{aligned}$$
(39)

where the dot represents the derivative with respect to the affine parameter \(\tau \). Using the Euler–Lagrange equations

$$\begin{aligned} \frac{d}{d\tau }\left( \frac{\partial L_{geo}}{\partial \dot{x^\mu }}\right) -\frac{\partial L_{geo}}{\partial x^\mu }=0, \end{aligned}$$
(40)

and considering that the particles are moving in the equatorial plane,Footnote 1\(\theta =\pi /2\), we find that the equations of motion are

$$\begin{aligned} f\dot{t}=E,\end{aligned}$$
(41)
$$\begin{aligned} f\dot{t}^2-f^{-1}\dot{r}^2-r^2 \dot{\phi }^2=\epsilon ,\end{aligned}$$
(42)
$$\begin{aligned} r^2 \dot{\phi }=\ell , \end{aligned}$$
(43)

where E and \(\ell \) are the energy and the angular moment of the particle. For massive particles we have \(\epsilon =1\) and for massless particles we have \(\epsilon =0\).

4.1 Massless Particles

One thing we need to make clear is that photons, which are also massless particles, do not follow null geodesics when we are dealing with nonlinear electrodynamics. Therefore, the analysis we will conduct in this section does not encompass the trajectory of photons.

For massless particles we have

$$\begin{aligned} f\dot{t}^2-f^{-1}\dot{r}^2-r^2 \dot{\phi }^2=0. \end{aligned}$$
(44)

Using the equations (41) and (43), we find the conservation energy equation type

$$\begin{aligned} \dot{r}^2+\frac{\ell ^2}{r^2}\left( 1-\frac{2m}{r}+\frac{q^2}{r^2}+\frac{\lambda q^2}{(1-8\delta )^2}\left( \frac{\Lambda ^4r^4}{q^2}\right) ^{2\delta }\right) =E^2. \end{aligned}$$
(45)

In the right side of the equation above we have the total energy and in the left side we have the kinetic energy, and the effective potential, that is written as

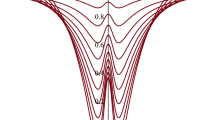
$$\begin{aligned} V_{eff}(r)=\frac{\ell ^2}{r^2}\left( 1-\frac{2m}{r}+\frac{q^2}{r^2}+\frac{\lambda q^2}{(1-8\delta )^2}\left( \frac{\Lambda ^4r^4}{q^2}\right) ^{2\delta }\right) . \end{aligned}$$
(46)

In the Fig. 4 we see that the effective potential for massless particles has a maximum value. This maximum tells us that there is a value of energy such that the particles remain in an unstable orbit. Particles with energy exceeding the effective potential’s maximum will be absorbed by the black hole, and if it has an energy value less than the effective potential maximum, the particles will be scattered. The position where the effective potential has its maximum value is obtained by solving \(V_{eff}'(r_0)=0\). In general, it is not possible to obtain \(r_0\) analytically. If \(q=0\) and \(\lambda =0\), we find that \(r_0=3m\), that is the radius of the photon orbit in the Schwarzschild case. If \(\lambda =0\), we find \(r_0=(3m+\sqrt{9m^2-8q^2})/2\), that is the radius of the photon orbit in the Reissner-Nordstrom case. If we compare the nonlinear cases with Schwarzschild and Reissner-Nordstrom, we notice that for small values of the radial coordinate, the nonlinear values tend to the Reissner-Nordstrom case, as both have the same charge, and differ from the Schwarzschild case. For distant points, Schwarzschild and Reissner-Nordstrom tend to the same value and differ significantly from the nonlinear cases.

Fig. 4
figure 4

Behavior of the effective potential to massless particles to \(\ell =m\). In (a) we fixed \(\lambda =0.2\), \(q=0.4m\), and \(m^2\Lambda ^4=0.002\). In (b) we fixed \(\delta =1\), \(q=0.4m\), and \(m^2\Lambda ^4=0.002\). In (c) we fixed \(\delta =1\), \(q=0.4m\) and \(\lambda =0.2\). In (d) we fixed \(\delta =1\), \(\lambda =0.2\), and \(m^2\Lambda ^4=0.002\)

Full size image
Fig. 5
figure 5

Behavior of the function G for massless particles in terms of the radial coordinate for different values of the impact parameter

Full size image

From equation (45), we get

$$\begin{aligned} G(r)= \left( \frac{dr}{d\phi }\right) ^2=r \left( \frac{r^3}{b^2}+2 m-r\right) +q^2 \left( \frac{\lambda \left( \frac{\Lambda ^4 r^4}{q^2}\right) ^{2 \delta }}{8 \delta -1}-1\right) . \end{aligned}$$
(47)

where \(b=\ell /E\) is the impact parameter. This is the differential equation that describes the motion of massless particles in the spacetime (10). In ideal situations, we could numerically integrate this equation and obtain the trajectories that massless particles follow in this spacetime. However, since the solution is neither asymptotically flat nor asymptotically de Sitter, certain infinities arise that make numerical resolution difficult. Nevertheless, we can still analyze the particle’s motion by examining the sign of the function G, since it is essentially the square of the particle’s radial velocity and therefore should not exhibit negative values.

In Fig. 5, we analyze the function G in terms of the particle’s impact parameter. The parameters related to the nonlinear electrodynamics have a greater influence at points far from the black hole. Since the change in sign occurs near the black hole, the only parameter that will significantly influence this behavior is the impact parameter, which is why we plot the graph considering only the variation of b. For large values of the radial coordinate, G is positive regardless of the chosen value of b, meaning all particles should be able to come from infinity. For small impact parameter values, the particles do not have a turning point (where \(G=0\)) and are absorbed by the black hole. In cases where there are turning points, the particles can return to infinity.

4.2 Massive Particles

To massive particles we have \(\epsilon =1\). Using the equations (41) and (43), we find the conservation energy equation type

$$\begin{aligned} \dot{r}^2+\left( 1+\frac{\ell ^2}{r^2}\right) \left( 1-\frac{2m}{r}+\frac{q^2}{r^2}+\frac{\lambda q^2}{(1-8\delta )^2}\left( \frac{\Lambda ^4r^4}{q^2}\right) ^{2\delta }\right) =E^2. \end{aligned}$$
(48)

The effective potential is given by

$$\begin{aligned} V_{eff}=\left( 1+\frac{\ell ^2}{r^2}\right) \left( 1-\frac{2m}{r}+\frac{q^2}{r^2}+\frac{\lambda q^2}{(1-8\delta )^2}\left( \frac{\Lambda ^4r^4}{q^2}\right) ^{2\delta }\right) . \end{aligned}$$
(49)

In Fig. 6, we analyze the effective potential for the case of massive particles. As with the case of massless particles, we notice that for small values of the radial coordinate, the nonlinear cases approach the Reissner-Nordstrom case, once they have the same charge, and are different from the Schwarzschild case. For large values of the radial coordinate, the nonlinear cases differ significantly from Schwarzschild and Reissner-Nordstrom. It is important to note that in the case of Reissner-Nordstrom and Schwarzschild, for certain values of the particles’ angular momentum, it is possible to have minimum points in the effective potential, thus indicating the presence of stable orbits. This is not true for nonlinear cases. Thus, nonlinearity eliminates the possibility of stable orbits for massive particles. The point where the potential is maximum is obtained by solving \(V'_{eff}(r_0)=0\). Similar to the massless case, it is not possible to solve this problem analytically.

Fig. 6
figure 6

Behavior of the effective potential to massless particles. In (a) we fixed \(\ell =6\), \(\lambda =0.2\), \(q=0.4m\), and \(m^2\Lambda ^4=0.002\). In (b) we fixed \(\ell =6\), \(\delta =1\), \(q=0.4m\), and \(m^2\Lambda ^4=0.002\). In (c) we fixed \(\ell =6\), \(\delta =1\), \(q=0.4m\) and \(\lambda =0.2\). In (d) we fixed \(\ell =6\), \(\delta =1\), \(\lambda =0.2\), and \(m^2\Lambda ^4=0.002\). In (e) we fixed \(\delta =1\), \(q=0.4m\), \(\lambda =0.2\), and \(m^2\Lambda ^4=0.002\)

Full size image
Fig. 7
figure 7

Behavior of the function G for massive particles as a function of the radial coordinate for different values of the total energy, panel (a), and the angular momentum, panel (b), of the particle. In the panel (a) the angular momentum is fixed \(l=12m\) while in the panel (b) the total energy if fixed \(E=4\)

Full size image

From (48), we find

$$\begin{aligned} G(r)=\left( \frac{dr}{d\phi }\right) ^2=\frac{\left( E^2-1\right) r^4}{l^2}+\frac{2 m r^3}{l^2}-\frac{q^2 r^2}{l^2}-\frac{\lambda q^2 r^2 \left( \frac{\Lambda ^4 r^4}{q^2}\right) ^{2 \delta }}{(1-8 \delta ) l^2}+2 m r-\frac{\lambda q^2 \left( \frac{\Lambda ^4 r^4}{q^2}\right) ^{2 \delta }}{1-8 \delta }-q^2-r^2. \end{aligned}$$
(50)

This is the differential equation that describes the motion of massive particles in the spacetime (10). As in the massless case, the equation of motion is problematic to solve, but we can analyze the motion by examining the change in sign of the function G.

From Fig. 7, we can observe that low energy particles can approach the black hole but encounter a returning point and are scattered, while high-energy particles can overcome the scattering potential and do not encounter any turning point, thus being absorbed by the black hole. In the case of angular momentum, the result is the opposite of that with total energy. The greater the particle’s angular momentum, the higher the scattering potential, causing massive particles to reach the turning point earlier. Particles with low angular momentum experience a weaker scattering potential, so they do not have turning points and are consequently absorbed by the black hole.

5 Conclusion

In this work, we obtain black hole solutions that arise when considering inverse electrodynamics, which is a model of nonlinear electrodynamics coupled with general relativity. This solution is magnetically charged and can fall into the Reissner-Nordstrom solution through a given choice of parameters. Through the curvature invariants, we verify that the metric is not asymptotically flat and has curvature singularities in the limits \(r\rightarrow 0\) and \(r\rightarrow \infty \). All energy conditions will be violated, however, the energy density of this solution is always positive.

We analyze the thermodynamic properties of this type of black hole. Through the surface gravity, we verify that, for specific values of the radius of the horizon of events, there are negative temperature values. To avoid these negative temperature values, we must have upper and lower limits on the event horizon size. The thermodynamic stability of this solution is verified through the heat capacity. We confirmed a phase transition between an unstable black hole and a stable black hole. Not all stable and unstable cases are physically viable since some have negative temperatures. These thermodynamic properties, such as limitations on the size of the horizon radius or the fact that the heat capacity exhibits only one phase transition, are also present in other charged solutions like Reissner-Nordstrom-de Sitter.

We study the behavior of massive and massless geodesics in this spacetime. We verified that, in the massless case, the effective potential of the black hole increases significantly with the charge value. At the same time, the other parameters do not change the maximum value of the effective potential. Particles with energy less than the maximum effective potential are scattered, and particles with higher energy are absorbed. As the potential has a maximum value, unstable circular orbits exist for particles with energy equal to the maximum effective potential. In this case, it is not possible to analytically obtain the value of the radius of the unstable orbit. Through the orbit equation, we determine the types of possible orbits. Some particles with a small impact parameter can come from infinity and be absorbed by the black hole, while others, with larger impact parameter values, encounter a turning point before reaching the black hole and are scattered back to infinity. For the massive case, similarly to the massless case, the effective potential has only one maximum without minimums, which is interesting since, in solutions such as Schwarzchild or Reissner-Nordstrom, a minimum is expected, thus creating stable orbits for massive particles. Although the angular momentum, l, changes the maximum value of the effective potential, the shape of the potential itself is not changed. In this way, regardless of the value of angular momentum, we will always have only one unstable orbit. When analyzing the orbit equation for massive particles, we see that particles with small angular momentum have a low scattering potential and end up being absorbed by the black hole, while those with large angular momentum encounter a turning point before the black hole and return to infinity. The energy of the particles also plays an important role: particles with sufficiently high energy can overcome the scattering potential and are absorbed by the black hole, while particles with low energy encounter the turning point before the event horizon and are scattered back to infinity.

Several other properties of solutions can be analyzed in future work. Some cases are quasinormal modes, tidal forces, black hole shadow, and matter accretion.