1 Introduction

Standard GR is very successful in explaining the available data but suffers from the presence of curvature singularities. Singularities are places where general relativity or another classical theory of gravity break down. It has been argued that singularities do not exist in nature. The singularity problem is connected to the existence of black holes. Recently, detection of gravitational waves have put the reality of black holes beyond doubt [1, 2]. However, a full understanding of BH physics requires avoidance of singularities or modification of the corresponding classical theory and addressing quantum effects. Singularities can be avoided if the energy conditions (some reasonable physical conditions that the matter content of the space time satisfies) assumed by the singularity theorems are violated at least in some regions of spacetime. Singularities can be replaced by regular regions filled by some kind of matter that violates the strong energy condition. The first idea, due to Sakharov and Gliner [3, 4] suggest that singularities could be avoided by a non-singular de Sitter core, with equation of state \( p=-\rho \) (\( T_{t}^{t} = T_{r}^{r}\)). Following this idea, a wide class of regular black hole solutions appeared in the literature. A way to classify the solutions is through the type of junctions. If there is no junction, the solution is a continuous solution throughout space time. The first smooth regular black holes solution, based on this idea, was proposed by the Bardeen, in which there are horizons but no singularity and near the centre, the solution tended to a de Sitter core solution. Ayon- Beato and Garca successfully interpreted the Bardeen black hole in the framework of non linear electrodynamics (NED) with gauge-invariant Lagrangian L(F), \(F = F_{\mu \nu } F^{\mu \nu }\), as a magnetic monopole. In NED coupled to General Relativity there exists several regular solutions using the \( F-P \) dual formalism, describing electrically charged black holes and magnetic black holes and monopoles [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. There are also solutions which have boundary surfaces joining the two regions. These solutions are constructed by filling the inner space with matter up to a certain surface and then make a smooth junction, through a space like boundary surface of the Planckian thickness, to the Schwarzschild and Reissner–Nordström solution as was done in [27,28,29]. The third solution is the solution with thin shell layer. The thin shell layer can be time-like, space-like or null [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46].

The construction of a black hole spacetime satisfying the equations of motion is not enough to appreciate the physical significance of the solution. In a realistic scenario, we have to know whether or not the spacetime is robust for small perturbations of the geometry and matter fields. If not, a probe, say a particle moving on the black hole background, may cause a disruptive back reaction; and the possibility of dynamically forming such a black hole through a physical process, such as gravitational collapse, is put in doubt. The complete description of stability of black holes must take into account both the classical and the thermodynamic stability because the Schwarzschild black hole is classically stable at the linear mode level and yet it has a negative specific heat, which signals a (local) thermodynamic instability. In this work, in order to study thermodinamical stability of regular black hole, we will use geometrothermodynamics method. Geometrothermodynamics is a formalism that relates a contact structure of the phase space \(\tau \) with the metric structure on a special subspace of \( \tau \) called the space of equilibrium states \( \varepsilon \) [47]. This geometric study has been considered in several papers by means of different approaches like Weinhold [48, 49], Ruppeiner and Quevedo [50, 51]. In 1975 Weinhold introduced differential geometric concepts into ordinary thermodynamics by considering a kind of metric defined as the second derivatives of internal energy with respect to entropy and other extensive quantities for a thermodynamical system. After that, Ruppeiner introduced another metric and defined the minus second derivatives of entropy with respect to the internal energy and other extensive quantities. It is notable that, the Ruppeiner metric is conformal to the Weinhold metric with the inverse temperature as the conformal factor. In particular, it was found that the Ruppeiner geometry carries information regarding phase structure of thermodynamical systems. Because of their success for their applications in ordinary thermodynamical systems, they have also been employed to study black hole phase structures which led to interesting results. Since these two approaches fail in order to describe phase transition of several black holes Quevedo proposed new types of thermodynamical metrics for studying geometrical structure of the black hole thermodynamics. This method was employed to study the geometrical structure of the phase transition of black holes and proved to be a strong machinery for describing phase transition and stability of black holes [52]. Thermodynamic quantities of regular black hole were studied by Man and Cheng [53]. Ma and Zhao [54, 55] discussed the thermodynamic stability of regular black holes by evaluating the heat capacity at constant magnetic charge \( C_{p} \). A form of the first law of black hole mechanics in the context of nonlinear electrodynamics has been derived by Rasheed [56], but this form of the first law does not satisfy requirements of a regular black hole. By considering some extra terms, Zhang and Gao [57] derive a more general form of the first law.

Another (conventional) way to study the classical stability of a black hole is to perturb of black hole spacetimes and look at the quasi normal modes (QNMs) [58, 59]. These modes are the resonant, nonradial perturbations of black holes that can be excited by external perturbations. They are characterized by a spectrum of discrete, complex frequencies, whose real parts determine the oscillation frequency, and whose imaginary parts determine the rate at which each mode is damped as a result of the emission of radiation. The corresponding frequencies are complex, since the perturbation can fall into the black hole or be radiated to infinity. For black holes, apart from numerical approaches, only the linear problem has been studied. Therefore, the fundamental equations describing the perturbations of black holes reduce to a single second-order ordinary differential equation that is similar to the one dimensional Schrödinger equation for a particle encountering a potential barrier on the infinite line. The nature of the potential precludes an exact, closed-form solution in terms of known functions [58,59,60,61,62,63,64]. Thus there are several approaches to the study of black-hole normal modes: Ferrari and Mashoon [65], replaced the potential barrier in the effective one-dimensional Schrödinger equation by a parametrized analytic potential barrier function for which simple exact solutions are known. The overall shape approximates that of the true black-hole barrier, and the parameters of the barrier function are adjusted to fit the height and curvature of the true barrier at the peak. The barrier is located in photon sphere where waves are formed. In other words, QNM complex frequencies are generated by a family of surface waves lying on its photon sphere [66]. Similarly, QNMs of regular black holes have been studied by several authors [67,68,69].

Apart from the above mentioned issues, the idea of a universe inside a black hole with false vacuum was proposed by Farhi and Guth [70]. They studied an expanding spherical de Sitter space time with initial space like singularity separated by a thin wall from the outside region of the Schwarzschild geometry. In 1989 ideas were considered by Frolov [71] in which the curvature is limited by the Planckian scale. Both Farhi and Frolov models are based on matching the Schwarzschild and de Sitter metrics using thin shell approach which implies that the whole dynamical evolution from the equation of state \(\rho = p = 0\) to \(p = -\rho \). Recently, in [72], cosmological inflation inside a black hole with null junction surface is investigated.

In the present work, we follow the historical trend described above, in order to investigate charged black holes which are free from strong curvature singularities, by employing the idea of nonlinear electrodynamics. It will be shown that a suitable nonlinear Lagrangian for the electromagnetic field leads to an exact, regular black hole solution with a central region having an effective equation of state in the form \( p=-\rho \). An interpretation of this results, together with the stability analysis of the solution are other issues considered in the present work.

This paper is arranged as follows: in the next section the basic equations describing a charged black hole are presented. In Sect. 3 we introduce a regular solution and its properties. In Sect. 4, we discuss stability by using geometrothermodynamic and classical stability criteria by using quasi-normal modes. In Sect. 5 we study the idea of universe inside a black hole. In the final section we will make some concluding remarks.

2 Basic equations

A static spherically symmetric line element can be written in the form

$$\begin{aligned} ds^{2}=-e^{\mu (r)}dt^{2}+e^{\nu (r)}dr^{2}+r^{2}d\Omega ^{2} \end{aligned}$$
(1)

where \( d\Omega ^{2} \) is the metric of a unit 2-sphere. The metric coefficients satisfy the Einstein equations

$$\begin{aligned} G_{\mu \nu }=T_{\mu \nu } \end{aligned}$$
(2)

which reduce to

$$\begin{aligned} T^{t}_{t}= & {} -\rho (r)=-e^{-\nu (r)}\left( \dfrac{\nu ^{'}}{r}-\dfrac{1}{r^{2}} \right) -\dfrac{1}{r^{2}}, \end{aligned}$$
(3)
$$\begin{aligned} T^{r}_{r}= & {} p_{r}(r)=e^{-\nu (r)}\left( \dfrac{\mu ^{'}}{r}+\dfrac{1}{r^{2}} \right) -\dfrac{1}{r^{2}}, \end{aligned}$$
(4)
$$\begin{aligned} T^{\theta }_{\theta }= & {} T^{\phi }_{\phi }=p_{\bot }(r) = e^{-\nu (r)}\left( \dfrac{\mu ^{''}}{r}+\dfrac{\mu ^{'2}}{4} +\dfrac{\mu ^{'}-\nu ^{'}}{2r}-\dfrac{\mu ^{'}\nu ^{'}}{4} \right) . \end{aligned}$$
(5)

Here the prime denotes differentiation with respect to r, \( \rho (r)=-T^{t}_{t} \) is the energy density, \( p_{r}(r)=T^{r}_{r} \) is the radial pressure and \( p_{\perp }=T^{\theta }_{\theta }=T^{\phi }_{\phi } \) is the tangential pressure for anisotropic perfect fluid. By integrating Eq. (3), one gets

$$\begin{aligned} e^{-\nu (r)}=1-\dfrac{2GM(r)}{r}, \qquad M(r)=4\pi \int _{0}^{r}\rho (x)x^{2}dx. \end{aligned}$$
(6)

From \( T^{\mu }_{\nu };\mu =0 \) one can get the TOV equation

$$\begin{aligned} p_{\bot }=p_{r}+\dfrac{r}{2}p_{r}^{'}+(\rho +p_{r})\dfrac{GM(r)+4\pi G r^{3}p_{r}}{2(r-2GM(r))}. \end{aligned}$$
(7)

The boundary conditions are the Schwarzschild behavior at \( r\rightarrow \infty \),

$$\begin{aligned} e^{-\nu (r)}=1-\dfrac{2Gm}{r}, \qquad m=4\pi \int _{0}^{\infty }\rho (r)r^{2}dr, \qquad T_{\mu \nu }=0, \end{aligned}$$
(8)

and the de Sitter behavior at \( r\rightarrow 0 \)

$$\begin{aligned} e^{-\nu (r)}=1-\dfrac{\Lambda }{3}r^{2}, \qquad T_{\mu \nu }=\rho _{0}g_{\mu \nu } \end{aligned}$$
(9)

where \( \Lambda =8\pi G \rho (r=0)=8\pi G \rho _{0} \). The important feature of the de Sitter geometry is the divergence of the geodesic congruences. To investigate the system we impose the following requirements:

(a) Regularity of metric and density at the center. (b) Finiteness of the ADM mass. (c) The weak energy condition for \( T_{\mu \nu } \).

The weak energy condition requires

$$\begin{aligned} T_{\mu \nu }u^{\mu }u^{\nu }\ge 0 \end{aligned}$$
(10)

for every time-like \( u^{\mu } \) which leads to

$$\begin{aligned} \rho \ge 0 \qquad \rho +p_{r}\ge 0 \qquad \rho +p_{t}\ge 0. \end{aligned}$$
(11)

This guarantees that the energy density as measured by any local observer is non-negative.

The requirements imposed on the Eqs. (3–5), enforce the following behavior. Finiteness of the mass Eq. (8) leads to \( \nu (r)=0 \) as \( r\rightarrow \infty \), and requires the density profile \( \rho (r) \) vanish at infinity quicker than \( r^{-3}\). Regularity of density \( \rho (r=0)<\infty \), requires the mass function M(r) to vanish as \( r^{3} \) when \( r\rightarrow 0 \), as a result \( \nu (r)\rightarrow 0 \) as \( r\rightarrow 0 \). The weak energy condition and by the Oppenheimer equation \( \mu =0 \) as \( r\rightarrow 0 \) and \(r \rightarrow \infty \). So the function \(\nu (r)+\mu (r)=0 \) at \(r = 0\) and at \( r\rightarrow \infty \) and its derivative is non-negative. It follows that \( \mu (r)=-\nu (r) \) everywhere.

This class of metrics have the algebraic structure

$$\begin{aligned} T^{t}_{t}=T^{r}_{r}, \qquad T^{\theta }_{\theta }=T^{\phi }_{\phi }. \end{aligned}$$
(12)

For the class of spherically symmetric geometries with the symmetry of a source term given by Eq. (12), the weak energy condition leads inevitably to de Sitter asymptotic i.e. a regular center. The scalar curvature is

$$\begin{aligned} R=2(\rho -p_{\bot }) \end{aligned}$$
(13)

The Ricci scalar changes sign somewhere and space-time experiences smooth changes in topology of space-like hyper surfaces. The existence of zero gravity surface at which the strong energy condition is violated is defined by

$$\begin{aligned} p_{\bot }=-\rho -\dfrac{r}{2}\rho ^{'}=0. \end{aligned}$$
(14)

By using TOV equation we have

$$\begin{aligned} p_{r}=-\rho \qquad p_{\perp }=-\rho -\dfrac{r}{2}\rho ^{'}. \end{aligned}$$
(15)

The weak energy condition gives \( \rho \ge 0 \) and \(\rho ^{'}\le 0\), and thus demands monotonic decreasing of the density profile. This defines the form of the metric that in the region \(0< r < \infty \) it has only minimum and the geometry can have not more than two horizons [5,6,7,8,9,10,11,12].

We now require a spherically symmetric electromagnetic field with an arbitrary gauge invariant Lagrangian L(F), which has stress energy tensor with the algebraic structure (12). But F must vanishes at both zero and infinity to guarantee regularity and so F must have at least one minimum in between, This leads to branching of L(F) as a function of F. This creates problems in an effective geometry whose geodesics are world lines of NED photons. In fact, in nonlinear electromagnetism photons do not propagate along null geodesics of the background geometry, instead they propagate along null geodesics of an effective geometry, which depends on the non linearities of the theory. According to the effective scalar curvature and the effective potential that is felt by the photons the effective geometry itself singular. This singularity is only felt by photons (the photons with energy greater than the height of the barrier of effective potential), the rest of the matter follows geodesics of the background space time [13, 14].

In the following we use the nonlinear electrodynamics as the source of the regular black holes. In nonlinear electrodynamics minimally coupled to gravity, the action is given by

$$\begin{aligned} S=\int d V\left( \dfrac{1}{4}R-L(F)\right) \end{aligned}$$
(16)

where R is the scalar curvature, and \( F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu } \) is the electromagnetic field. L(F) is an arbitrary function of \( F=F_{\mu \nu }F^{\mu \nu } \), which in the weak field regime should have the Maxwell limit. Energy–momentum tensor takes the form

$$\begin{aligned} T_{\mu \nu }=2\dfrac{dL(F)}{dF}F_{\nu \alpha }F_{\mu }^{\alpha }-\dfrac{1}{2}g_{\mu \nu }L(F). \end{aligned}$$
(17)

From Eq. (15), the density and tangential pressures are given by

$$\begin{aligned} \rho =\dfrac{1}{2}L-F\dfrac{dL}{F}, \qquad p_{\bot }=-\dfrac{1}{2}L, \end{aligned}$$
(18)

and scalar curvature is

$$\begin{aligned} R=2\left( L-F\dfrac{dL}{dF}\right) . \end{aligned}$$
(19)

The zero gravity surface follows from Eq. (18)

$$\begin{aligned} p_{\bot }=-\dfrac{1}{2}L=0. \end{aligned}$$
(20)

Electrically charged solutions are found in the alternative form of NED obtained by the Legendre transformation

$$\begin{aligned} H=2FL_{F}-L. \end{aligned}$$
(21)

Defining \( P_{\mu \nu } \equiv L_{F} F_{\mu \nu }\), it can be shown that H is a function of \( P=\frac{1}{4}P_{\mu \nu }P^{\mu \nu }=(L_{F})^{2}F \), \( E(r)=F_{tr}=H_{p}\dfrac{q}{r^{2}} \) i.e, \( dH=(L_{F})^{-1} d((L_{F})^{2}F)=H_{P} dP\). With the help of H one expresses the nonlinear electromagnetic Lagrangian in the action (16) as \( L=2PH_{P}-H \), depending on the antisymmetric tensor \( P_{\mu \nu } \). The weak energy condition requires \( H<0 \) and \( H_{p}>0 \). Interpretation of the results obtained in P framework depends essentially on transformation to F framework where Lagrangian dynamics is specified. The two frames are equivalent only when the function F(P) is monotonic [16,17,18].

3 Regular electric solution

Our solution is described by the metric

$$\begin{aligned} g= & {} -f(r)dt^{2}+f(r)^{-1}dr^{2}+r^{2}d\Omega ^{2}, \quad f(r)=1+\dfrac{q^{2}r^{2}}{r^{4}+q^{2}}-\dfrac{4m\arctan \left( \frac{r^{3}}{q^{2}}\right) }{\pi r}\nonumber \\ \end{aligned}$$
(22)

This metric is obtained by using of the Eq. (6) and the energy density of the form

$$\begin{aligned} T^{t}_{t}= & {} T^{r}_{r}={\frac{{q}^{2} \left( \pi {r}^{10}+12m{q}^{4}+\pi {r}^{4}{q}^{4 }-3\pi {q}^{6}-3\pi {q}^{2}{r}^{6}+12\,m{r}^{8}+24m{q}^{2}{r}^{4} \right) }{ \left( {q}^{4}+{r}^{6} \right) \left( {r}^{4}+{q}^{2 } \right) ^{2}\pi }}\nonumber \\ \end{aligned}$$
(23)

In the limit \( r\rightarrow \infty \)

$$\begin{aligned} \rho \approx \dfrac{q^{2}}{r^{4}}+O \left( \dfrac{1}{r^{6}}\right) . \end{aligned}$$
(24)

So, the density profile at infinity vanishes quicker than \( r^{-3} \), and conforms with the electric field energy density of a point charge.

Moreover, the solution (22) asymptotically behaves as the Reissner–Nordström solution, i.e.,

$$\begin{aligned} -g_{tt}=1-\dfrac{2m}{r}+\dfrac{q^{2}}{r^{2}}. \end{aligned}$$
(25)

from the \( \frac{1}{r} \) term it follows that the parameter m is associated with the mass of the configuration and from the \( \frac{1}{r^{2}} \) term the parameter q is interpreted as the electric charge. For a certain range of the mass and charge, our metric (22) is a black hole. For any non vanishing value of q and m, \( -g_{tt} \) has a single minimum. There exists a single real critical value of \( q=0.7678\) \(\hbox {m}\) (Fig. 1).

Fig. 1
figure 1

The behavior of \( -g_{tt} \) in terms of r for different values of q and \( m=1 \)

Full size image

When \( r\rightarrow 0 \), the metric function (22) behaves as the de Sitter black hole with cosmological constant \( \Lambda =3(\dfrac{4m}{\pi q^{2}}-1)\) if \({\frac{4m}{\pi {q}^{2} }} >1\):

$$\begin{aligned} 1-\left( {\frac{4m}{\pi {q}^{2} }} -1\right) {r }^{2}. \end{aligned}$$
(26)
Fig. 2
figure 2

The behavior of m in terms of q

Full size image

In Fig. 2, we plot the conditions for the existence of black hole and dS core by using conditions of extremal (cold BH) and Eq. (26). As can be seen, for specific range of q and m we have BH with dS center.

Two horizons, a black hole event horizon \( r_{+} \) and an internal Cauchy horizon \( r_{-} \) are shown in Fig. 3, together with zero gravity surface beyond which the strong energy condition is violated. Horizons come together at the value of a mass parameter \( m_{cri} \), which puts a lower limit on the black hole mass. For \(m < m_{cri}\) geometry describes a self-gravitating particle-like structure without horizons. For \(m>m_{cri} \), geometry describes the vacuum non singular black hole, and global structure of the metric is similar to the Reissner–Nordström black hole except that the singularity has been smoothed out.

Fig. 3
figure 3

The behavior of r in terms of m for \(q=1\)

Full size image

Contrary to the usual electromagnetic, the trace of the energy–momentum tensor does not vanish except in the surface that the Ricci scalar is zero, i.e, the surface that the topology changes. Changes in the signature of the Ricci scalar is shown in Fig.4a with dashed circles. As can be seen Ricci scalar is positive in the core and negative outside. From the analytical expressions of the curvature invariant one concludes that the Ricci scalar and other curvature invariants, are regular everywhere (as can be seen from Fig. 4).

Fig. 4
figure 4

The behaviure of R and \(R_{\mu \nu }R^{\mu \nu }\) in terms of r for different values of q and \(m=1\)

Full size image

From Fig. 5, one can conclude that the weak energy condition is satisfied everywhere except in the core. Also, energy density is maximal as \( r \rightarrow 0 \), which corresponds to energy density of vacuum, in this case the electromagnetic vacuum.

Fig. 5
figure 5

The behavior of \( \rho \), \( \rho + p_{r} \) and \( \rho +p_{\perp } \) in terms of r for \( q=0.5 , m=1\)

Full size image
Fig. 6
figure 6

The behavior of F in terms of \( -p \) (left). The behavior of L in terms of F (right)

Full size image

The \(^{t}_{t}\) component of Einstein equations (2) with the Lagrangian (16) yields the basic equation

$$\begin{aligned} G^{t}_{t}=2H(p), \end{aligned}$$
(27)

then by using of Eq. (21) one can get L(F). the function L(F) has only two branches related to one minimum of F. The Lagrangian L(F) which is monotonic function of F, first decreases smoothly along the first branch from its maximal value to \(L_{cusp}\) as F decreases from \(F = 0\) at \(r = 0\) to \(F_{min} = F_{cusp}\), then the Lagrangian increases along the second branch from its minimal value \(L_{cusp} < 0\) to its Maxwell limit \(L\rightarrow F \rightarrow 0\) as F increases from \(F_{cusp}\) to \(F\rightarrow 0\) as \(r \rightarrow 1\) (see Fig. 6). In order to determine the nature of \( r_{cusp} \), one can obtain the effective geometry that associated to a spherically symmetric solution of Einstein\(^{,}\)s equations

$$\begin{aligned} ds^{2}=-\dfrac{f(r)}{\phi (r)}dt^{2}+\dfrac{dr^{2}}{f(r)\phi (r)} +\dfrac{r^{2}}{L_{F}}d\Omega ^{2}, \end{aligned}$$
(28)

where

$$\begin{aligned} \phi (r)=-\dfrac{2q}{r^{3}}\dfrac{1}{\dfrac{dE}{dr}} \end{aligned}$$
(29)

it is useful to study the effective potential that is felt by the photons. According to the symmetries of the metric, two conserved quantities is given by

$$\begin{aligned} E=g_{tt} {\dot{t}} \qquad \hbox {and} \qquad J=\dfrac{r^{2}}{L_{F}}{\dot{\phi }} \end{aligned}$$
(30)

by using of (28) the effective potential for photons is given by

$$\begin{aligned} V_{eff}=\dfrac{f(r)\phi (r)L_{F}J^{2}}{2r^{2}}-\dfrac{\phi (r)^{2}E^{2}}{2}, \end{aligned}$$
(31)

We give in Fig. 7a plots of \(V_{eff}\) for different values of the relevant parameters. As can be seen from Fig. 7a, there is a potential barrier in the right of the outermost singularity. If incident photon with energy greater that the height of the barrier will encounter the first singularity. For a distant observer photons disappear beyond the surface \(r = r_{cusp}\) in the same way as they disappear beyond the event horizon of a black hole. The redshift z of a source as measured by a static observer and using the expression of the effective metric,

$$\begin{aligned} 1+z=\dfrac{\phi (r)}{\sqrt{f(r)}} \end{aligned}$$
(32)

It diverges at the BH horizon where f(r) vanishes, and at the cusp surface \(r = r_{cusp}\) where \( \phi (r) \) diverges. At the cusp the electric field achieves its maximum and in the asymptotic is \( E=\dfrac{q}{r^{2}}+O(\dfrac{1}{r^{4}}) \) (see Fig. 7b). So, by non linear of electrodynamic we create electromagnetic black hole that only felt by photons [13, 14].

Fig. 7
figure 7

The behavior of \( V_{eff} \) in terms of r for \( J=10, E=1 \) (left). The behavior of \( E, \phi \) and \( g_{tt} \) in terms of r for \( m=1, q=0.5 \) (right)

Full size image

4 Stability

We investigate the stability of black holes within classical general relativity via quasi normal modes and using standard methods [65]. External perturbations excite the QNMs which in turn appear as damped vibrations of the black hole. Quasi normal frequencies (QNFs) are complex numbers that encode information on the system’s relevant parameters and on its relaxation after it has been perturbed.

In order to study classical stability, we compute the quasi normal frequency corresponding to the massless scalar perturbations. The equation for these perturbations takes the usual form,

$$\begin{aligned} \dfrac{1}{\sqrt{g}}\partial _{\mu }\left( \sqrt{g}\partial ^{\mu }\phi \right) =0, \end{aligned}$$
(33)

where g is the determinant of the metric. Equation (33) can be separated by decomposing the scalar perturbation into appropriate harmonics,

$$\begin{aligned} \phi =\dfrac{1}{r}\sum e^{i \omega t} \varphi _{lm}(r) Y^{m}_{l}(\Omega ) \end{aligned}$$
(34)

and by introducing the tortoise coordinate

$$\begin{aligned} dx=\dfrac{dr}{f} \end{aligned}$$
(35)

One then can rewrite the radial part of (33) in a Schrödinger form

$$\begin{aligned} \left[ -\dfrac{d^{2}}{dx^{2}}+V(x)-\omega ^{2}\right] \varphi (x)=0, \end{aligned}$$
(36)

with V given by

$$\begin{aligned} V=f\left( \dfrac{l(l+1)}{r^{2}}+\dfrac{f^{'}}{r}\right) \end{aligned}$$
(37)

In a spherical black hole, the effective potential V is independent of frequency and \( V\rightarrow 0 \) as \( x\rightarrow \pm \infty \). The quasi normal modes are defined to be the solutions of (36) with the boundary conditions

$$\begin{aligned} \varphi (x) \varpropto e^{\mp i\omega x} \quad as \quad x \rightarrow \pm \infty \end{aligned}$$
(38)

which correspond to outgoing waves at infinity and ingoing waves at the horizon. It follows from the boundary conditions \( \omega \) must be complex, \( \omega =\omega ^{r}+i\omega ^{i} \). Stability implies that only modes with \( Im(\omega )>0 \) are allowed. Figure 8 illustrates the behavior of the quasi normal frequency with respect to the charge/mass ratio. The real part of the frequency grows with the charge. In Table. 1 the values of quasi normal frequencies are shown which are obtained using the method described in [65]. As one can see, the imaginary part of frequency is positive and it can be concluded that metric is stable.

Fig. 8
figure 8

The real part of the quasi normal frequency corresponding to the scalar perturbations for several values of \( l \ge 2 \) (left), and the imaginary part of the quasi normal frequency for \( l=4 \) (right)

Full size image

We now turn to the geometrothermodynamic description of the black hole. In the space of equilibrium states, we consider a Legendre invariant of Weinhold metric which is given by [48, 49]

$$\begin{aligned} ds_{w}^{2}=Mg_{ab}dE^{a}dE^{b}, \quad g_{ab}=\dfrac{\partial ^{2}M }{\partial E^{a}\partial E^{b}} \end{aligned}$$
(39)

where \(E^{a}= \left\{ s, q\right\} \), s, q being entropy and electric charge. For a static charged black hole, the denominator of Weinhold Ricci scalar

$$\begin{aligned} den(R_{w})= \left( M_{ss}M_{qq}-M_{sq}^{2}\right) ^{2}M^{2} \end{aligned}$$
(40)

where \( M_{ss}= \dfrac{\partial ^{2}M}{\partial s^{2}}\) and \( M_{sq}=\dfrac{\partial ^{2} M}{\partial s \partial q} \).

Table 1 Quasinormal frequencies of the scalar perturbations for \(m=1 \) and \( n=0 \)
Full size table

The roots of the Eq. (40) should coincide with the type two of the phase transitions in the heat capacity. In order to investigate the local stability of a black hole with fixed charge (canonical ensemble), one can investigate the behavior of the heat capacity. The positivity of the heat capacity ensures thermal stability. In addition, the behavior of heat capacity represents two types of phase transition. The changes in the signature of the heat capacity determines type one phase transition and divergency of the heat capacity is denoted by type two phase transition. As can be seen from Fig. 9, at fixed charge as entropy increases, the black hole becomes unstable and at fixed entropy, as charge is increased the black hole remains stable. The changes in signature of the heat capacity and its singularity which is plotted in Figs. 9 and 11, show type one and two phase transitions. Therefore, this black hole is stable only when entropy is between the two phase transitions.

Fig. 9
figure 9

The behavior of heat capacity in terms of s for different values of q and \( m=1 \)

Full size image

In Fig. 10a, the denominator of Weinhold Ricci scalar is plotted. As it can be seen, only one type of phase transition exists which does not coincide other types of phase transitions. On the other hand, as can be seen from Table 1, black hole is classically stable.

Fig. 10
figure 10

The denominator of Weinhold Ricci scalar verses s for different values of q (left), \( M_{ss} \) verses s for different values of q (right)

Full size image
Fig. 11
figure 11

\(C_{q} \) and \( M_{s} \) in terms of s for different values of q

Full size image

5 Universe inside black hole?

To investigate a \(\Lambda BH\) and remove singularity of \( r_{+} \) and \( r_{-} \) and maximal analytic extension we introduce the Finkelstein coordinates, related to radial geodesics of non relativistic test particles, are given by

$$\begin{aligned} \tau= & {} t+\int \sqrt{\dfrac{2M(r)}{r}} \dfrac{dr}{1-\dfrac{2M(r)}{r}}, \end{aligned}$$
(41)
$$\begin{aligned} R= & {} t+\int \sqrt{\dfrac{r}{2 M(r)}} \dfrac{dr}{1-\dfrac{2M(r)}{r}}. \end{aligned}$$
(42)

The metric (22) transforms into the Lemaitre metric

$$\begin{aligned} ds^{2}=-d\tau ^{2}+e^{\lambda (R,\tau )}dR^{2}+r^{2}d\Omega ^{2}, \qquad e^{\lambda }=\dfrac{2M(r)}{r} \end{aligned}$$
(43)

For the metric (43) the Einstein equations reduce to [73, 74]

$$\begin{aligned} r^{'2}+2rr^{''}+p_{r}r^{2}=0 \end{aligned}$$
(44)

Where prime is differentiation with respect to \( \tau \). The further evolution of the function r, velocity \( r^{'} \) are shown in Figs. 12 and 13, obtained by ODE plot of the equation of motion (44) with different initial conditions. For \( r_{0}=1, r^{'}_{0}=1.583 \), numerical calculation of the Eq. (44) shows an exponential growth of \( r(\tau ) \) at the beginning (Fig. 12). Figure 14 shows the pressure components \(p_r\) and \(p_t\) versus r.

$$\begin{aligned} r \propto e^{\alpha \tau } \end{aligned}$$
(45)
Fig. 12
figure 12

r and \( r^{'} \) in terms of \( \tau \) for values of q and m and for initial conditions \( r_{0}=1, r^{'}_{0}=1.583 \)

Full size image

For \( r_{0}=1, r^{'}_{0}=0 \), in the limit \( \tau \rightarrow 0 \) the law of the expansion is (Fig. 13)

$$\begin{aligned} r \propto \tau ^{2} \end{aligned}$$
(46)
Fig. 13
figure 13

r and \( r^{'} \) in terms of \( \tau \) for different values of q and m and for initial conditions \( r_{0}=1, r^{'}_{0}=0 \)

Full size image

For both case, according to the Fig. 15, near the center we have \( p_{\perp }\simeq p_{r}\simeq -\rho \), followed by an anisotropic Kasner-type stage when the anisotropic pressure leads to an anisotropic expansion (with contraction in the radial direction and expansion in the tangential direction).

Fig. 14
figure 14

The behavior of \( p_{r} \) and \( p_{\perp } \) in terms of r

Full size image
Fig. 15
figure 15

The behavior of M in terms of r for \( q=0.5\)

Full size image

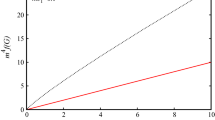
As, can be seen in Fig. 15, the mass is zero at the center and as the universe expands \( m_{ADM} \) increases as \( r^{3}\). Because in the center \( \rho =\rho _{0} \) is constant, this is consistent with the \( M=\rho V=\rho \dfrac{4 \pi }{3}r^{3}\). The general behvior of mass is given by

$$\begin{aligned} M(r)=\dfrac{2m\arctan \left( {\frac{{r}^{3}}{{q}^{2}}} \right) }{\pi } -{\dfrac{{q}^{2}{r}^{3}}{2({r}^{4}+{q}^{2})}}. \end{aligned}$$
(47)

In the limit \( r\rightarrow \infty \)

$$\begin{aligned} M(r)\approx m+O\left( \dfrac{1}{r}\right) , \end{aligned}$$
(48)

while for \( r\rightarrow 0 \)

$$\begin{aligned} M(r)\approx \left( \dfrac{4m}{\pi q^{2}}-1\right) r^{3}+O(r^{7}). \end{aligned}$$
(49)

finally, we study the region near \(r = 0\) as a small false vacuum bubble which can be a seed for the quantum birth of a universe. The standard procedure of quantization results in the Wheeler–DeWitt equation in the minisuperspace for the wave function of universe which reduces to the Schrödinger-like equation

$$\begin{aligned} \dfrac{d^{2}\Psi }{da^{2}}+U(a)\Psi =0. \end{aligned}$$
(50)

If we begin with the FRW metric, the effective potential is

$$\begin{aligned} U(a)=(144 k a^{2}-48 \Lambda a^{4}). \end{aligned}$$
(51)

The superpotential may have a maximum necessary for quantum tunnelling. The superpotential consists of two terms, a curvature term \( 144 k a^{2} \) and the \( \Lambda \) term \( 48 \Lambda a^{4} \). If \( k>0 \) and \( \Lambda >0 \) we have quantum tunnelling. By plotting the effective potential one can investigate the quantum tunnelling [73, 74].

6 Conclusion

In this paper, we introduced regular spherically symmetric electrically charged solutions in the framework of nonlinear electrodynamics coupled to general relativity. Corresponding diagrams for different values of mass and charge were considered. Weak energy condition for the electromagnetic source was shown to be satisfied, while strong energy condition is violated somewhere inside the black hole. We showed that this solution undergoes change in topology in the sense that the Ricci scalar changes its sign. Then, by using common methods in the study of stability of singular black holes, we studied the global stability of the solution by employing the heat capacity, a geometrothermodynamic method, and classical stability analysis through QNMs. We conclude that the black hole is stable under small perturbations of space time. By increasing the mass of the black hole, after phase transition of type two evaporate and vacuum non singular black hole evolves towards a self-gravitating particle-like vacuum structure without horizons. Finally, we speculate that the early universe was inside a primordial black hole. The interior of the black hole was shown to be dS. By numerical calculation, we concluded that for positive cosmological constant and curvature constant the inner universe can enter an accelerated phase.