1 Introduction

Nonclassical quantum states (NQSs) play a central role in quantum information and quantum optics, theoretically and experimentally [1,2,3]. Recent research has shown that NQSs display nonclassical properties such as squeezing, antibunching, sub-Poissonian, and negative values of the Wigner function [4, 5]. Thus, the study of NQSs has been a fundamental topic in modern quantum physics due to their applications in improving the fidelity of quantum teleportation [6], the performance of the quantum key distribution, and quantum metrology [7, 8]. NQSs are generally generated by non-Gaussian operations such as photon addition, subtraction, and various combinations [9,10,11]. These non-Gaussian quantum manipulations can be achieved with optical instruments, such as Mach–Zehnder interferometer [12], optical Kerr medium [13], and BS [14]. The measurement-based protocols are the most famous among all these generation schemes [15, 16]. Photon-adding operations are realized via conditional measurement on a beam splitter [17, 18]. Quantum scissors devices are proposed to generate the superposition of single-photon and vacuum states by truncating a coherent state [19, 20]. BS is a significant linear device used to prepare NQSs and simulate the dissipative environment of quantum states [21]. A class of NQSs is realized using two asymmetric BSs and conditional measurement of a single photon [22].

In this paper, we study the problem of the resulting state in conditional measurement on a tunable beam splitter. As far as we know, most of the previous literature on this aspect is analyzed under approximate conditions or zero or single photon measurement [20, 23]. The highlight of our paper is the study of the nonclassical properties of the output quantum states in the case of arbitrary transmission coefficients and arbitrary photons. Although it may seem simple, this state's explicit analysis and numerical simulation are still highly challenging. Several experimental proposals have been made to generate a mode in an arbitrary photon-number state [24, 25]. Thus, the research results of this paper have some theoretical significance for preparing new NQSs in experiments.

The rest of the paper is organized as follows: in Sect. 2, we present the form of the quantum operator for the BS and obtain the explicit expression of the output quantum state when the input quantum state is the coherent and the Fock state. Section 3 is devoted to studying the probability of detecting the output quantum state and the fidelity of the input and output states. Section 4 studies the statistical properties of the output quantum state such as the Q-function, PND, Mandel parameter, second-order correlation function, and Wigner function. The quadrature squeezing property of BS for the input quantum state is obtained in Sect. 5. The last section discusses our main results of the numerical solution and analytic calculations.

2 Quantum Operator Theory for the BS

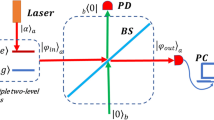
A BS with arbitrary transmittance parameters consists of two input and two output ports (Fig. 1). Here, we denote photon annihilation operators \(a\) and \(b\) for the input modes and \(a^{\prime}\) and \(b^{\prime}\) for the output quantum state. The relationship between the output quantum state and the input quantum state is expressed as

$$\left(\begin{array}{c}{a}^{\prime}\\ {b}{\prime}\end{array}\right)=\left(\begin{array}{cc}\sqrt{T}& \sqrt{R}\\ -\sqrt{R}& \sqrt{T}\end{array}\right)\left(\begin{array}{c}a\\ b\end{array}\right),$$
(1)

where \(R,T\) are the reflectance and transmission of the BS, satisfying the relationship \(R+T=1\) due to the conservation of photon number.

Fig. 1
figure 1

Scheme of the experimental setup for a tunable beam splitter with conditional measurement

Full size image

The effect of BS on the input quantum state is given by the quantum operator \(B\) as

$${\left|\psi \right.\rangle }_{out}=B{\left|\psi \right.\rangle }_{in}.$$
(2)

Noticing the eigenstate of \(a,b\) is the coherent state \(\left|{z}_{a}\right.\rangle ,\left|{z}_{b}\right.\rangle\) and applying \(B^\dagger\left|z_a\right.\rangle\otimes\left|z_b\right.\rangle\) on Eq. (1), one can obtain

$$B^\dagger\left|\begin{pmatrix}z_a\\z_b\end{pmatrix}\right.\rangle=\left|\begin{pmatrix}\sqrt T&-\sqrt R\\\sqrt R&\sqrt T\end{pmatrix}\begin{pmatrix}z_a\\z_b\end{pmatrix}\right.\rangle.$$
(3)

Using the super-completeness relationship of the coherent state, \(B^\dagger\) is given as

$$B^\dagger=\int\frac{d^2z_ad^2z_b}{\pi^2}\left|\begin{pmatrix}\sqrt T&-\sqrt R\\\sqrt R&\sqrt T\end{pmatrix}\begin{pmatrix}z_a\\z_b\end{pmatrix}\right.\rangle\left.\langle\begin{pmatrix}z_a\\z_b\end{pmatrix}\right|.$$
(4)

The direct product of a two-mode coherent state is

$$\left|z_a\right.\rangle\otimes\left|z_b\right.\rangle\equiv\left|\begin{pmatrix}z_a\\z_b\end{pmatrix}\right.\rangle=\text{exp}\left[-\frac12\left(\left|z_a\right|^2+\left|z_b\right|^2\right)+z_aa^\dagger+z_bb^\dagger\right]\left|00\right.\rangle.$$
(5)

According to the techniques of integration within an ordered product of operators (IWOP) [26, 27], the normally ordered form of the two-mode vacuum projection operator is

$$\left|00\right.\rangle\left.\langle00\right|=:\text{exp}\left(-a^\dagger a-b^\dagger b\right):.$$
(6)

Substituting the concrete form of the coherent state in Eq. (5) into Eq. (4) and using Eq. (6), after some direct mathematical integrations, the normal ordering form of \(B^\dagger\) is obtained as

$$B^\dagger=:\text{exp}\left[\left(\sqrt T-1\right)\left(a^\dagger a+b^\dagger b\right)+\sqrt R\left(ab^\dagger-a^\dagger b\right)\right]:.$$
(7)

Taking the Hermitian conjugate of Eq. (7), one has

$$B=:\text{exp}\left[\left(\sqrt T-1\right)\left(a^\dagger a+b^\dagger b\right)+\sqrt R\left(a^\dagger b-ab^\dagger\right)\right]:.$$
(8)

Under the condition measurement for \(b\)-mode input state, Eq. (2) can be reduced to

$${\left|{\psi }_{a}\right.\rangle }_{out}={P}_{d}^{-1/2}\left.\langle m\right|B\left|n\right.\rangle {\left|{\psi }_{a}\right.\rangle }_{in},$$
(9)

where \({P}_{d}\) denotes the success probability of detecting \(m\) registered photons in the outport \(\left|n\right.\rangle\) and \(\left|m\right.\rangle\) represent the input and output Fock states, respectively.

In terms of the coherent representation, the Fock state can be equivalently expressed as [28]

$$\left|n\right.\rangle =\frac{1}{\sqrt{n!}}{\left.\frac{{\partial }^{n}}{\partial {\xi }^{n}}\left|\xi \right.\rangle \right|}_{\xi =0},$$
(10)

where \(\left|\xi\right.\rangle\equiv\text{exp}\left(\xi b^\dagger\right)\left|0\right.\rangle\) is an unnormalized coherent state and satisfies the eigenequation

$$b\left|\xi \right.\rangle =\xi \left|\xi \right.\rangle .$$
(11)

Substituting the normal ordering form of the BS operator in Eq. (8) into Eq. (9) and using Eqs. (10) and (11), we have

$$\begin{array}{c}{\left|\psi_a\right.\rangle}_{out}\\=P_d^{-1/2}\frac1{\sqrt{m!n!}}:exp\left[\left(\sqrt T-1\right)a^\dagger a\right]{\left.\frac{\partial^{m+n}}{\partial\xi^n\partial\xi^{\ast m}}\text{exp}\left(\sqrt T\xi\xi^\ast+\sqrt Ra^\dagger\xi-\sqrt Ra\xi^\ast\right)\right|}_{\xi=\xi^\ast=0}:{\left|\psi_a\right.\rangle}_{in}\\=P_d^{-1/2}\frac1{\sqrt{m!n!}}\left(i\sqrt T\right)^{\left(m+n\right)/2}:exp\left[\left(\sqrt T-1\right)a^\dagger a\right]H_{m,n}\left(-\sqrt{\frac RT}ia^\dagger,\sqrt{\frac RTi}a\right):{\left|\psi_a\right.\rangle}_{in},\end{array}$$
(12)

where we have used the generating function formula of two-variable Hermite polynomials [29]

$${\left.\frac{{\partial }^{m+n}}{\partial {\tau }^{m}\partial {v}^{n}}{\text{exp}}\left(-A\tau v+B\tau +Cv\right)\right|}_{\tau =v=0}={\left(\sqrt{A}\right)}^{m+n}{H}_{m,n}\left(\frac{B}{\sqrt{A}},\frac{C}{\sqrt{A}}\right).$$
(13)

When the input state is prepared in a coherent state \(\left|\alpha \right.\rangle\), the output state in Eq. (12) is easily obtained with the result

$${\left|\psi_\alpha\right.\rangle}_{out}=P_d^{-1/2}\frac1{\sqrt{m!n!}}\left(i\sqrt T\right)^{\left(m+n\right)/2}\text{exp}\left[\left(\sqrt T-1\right)a^\dagger\alpha\right]H_{m,n}\left(-\sqrt{\frac RT}ia^\dagger,\sqrt{\frac RT}i\alpha\right)\left|\alpha\right.\rangle.$$
(14)

In particular, when \(m=n,\) using the relationship between two-variable Hermite polynomial and Laguerre polynomial

$${H}_{n,n}\left(x,y\right)={\left(-1\right)}^{n}n!{L}_{n}\left(xy\right),$$
(15)

Equation (14) is reduce to

$${\left|\psi_{\alpha,n}\right.\rangle}_{out}=P_d^{-1/2}T^n\text{exp}\left(-\frac12\left|\alpha\right|^2+\sqrt Ta^\dagger\alpha\right)L_n\left(RT^{-1}\alpha a^\dagger\right)\left|0\right.\rangle,$$
(16)

which is just the Laguerre-like polynomial photon excited state.

If no photons are recorded in the second output port of the BS, i.e., \(n=0\) and the input state \(\left|\alpha \right.\rangle \otimes \left|0\right.\rangle\), the output channel is prepared in a state

$${\left|{\psi }_{\alpha ,0}\right.\rangle }_{out}={P}_{d}^{-1/2}{\text{exp}}\left(\frac{T-1}{2}{\left|\alpha \right|}^{2}\right)\left|\sqrt{T}\alpha \right.\rangle ,$$
(17)

which is identified as amplitude attenuation of the coherent state due to \(T<1\). Obviously, when \(T=1\), the output quantum state is still the input coherent state as expected. For convenience, we restrict attention to the output state in Eq. (16) with an arbitrary number of probing photons \(n\) and the transmittance of BS.

3 Influence of BS and Condition Measurement

BS redirects the photons in the input quantum state in an indistinguishable manner to the output port and measures one mode via the photon detector. From the view of quantum mechanics, this kind of detection has a certain probability of success. Furthermore, the signal-to-noise ratio (SNR) and fidelity between the output and input state are also related to the parameters of the BS and the number of detected photons. Thus, we mainly discuss the detection probability of the output state and the fidelity between the output state and the input coherent state.

3.1 Detection Probability of the Output State

The detection probability of the output state is necessary for further discussing its statistical and squeezing properties [3, 30]. According to the completeness of the output quantum state in Eq. (16), the specific expression of the detection probability of the output state can be directly calculated as (see Appendix A)

$${P}_{d}={T}^{n}{\left(n!\right)}^{-2}{\text{exp}}\left(-{\left|\alpha \right|}^{2}\right){\left.\frac{{\partial }^{2n}}{\partial {t}^{n}\partial {t}^{{\prime}n}}{\left(1-t\right)}^{-1}{\left(1-{t}^{\prime}\right)}^{-1}{\text{exp}}\left({P}_{1}{P}_{2}{\left|\alpha \right|}^{2}\right)\right|}_{t={t}{\prime}=0},$$
(18)

where

$$\begin{array}{cc}{P}_{1}=\frac{-Rt}{\left(1-t\right)T}+\sqrt{T},& {P}_{2}=\frac{-R{t}^{\prime}}{\left(1-{t}{\prime}\right)T}+\sqrt{T}\end{array}.$$
(19)

Especially for a given total transmission coefficient \(T=1\), the detection probability of the output states has unity success probability, i.e., \({P}_{d}=1\). Figure 2 shows the results for \({P}_{d}\) using Eq. (18) as the function of transmission coefficient \(T\) for the different number of detected photons with \(\alpha =1+2i\). From Fig. 1, we find that \({P}_{d}\) shows a monotonic increasing behavior with the increasing of \(T\) when \(n=0\). For the same high transmittance \(0.9<T<1\), \({P}_{d}\) decreases with the increase in the number of detected photons \(n\). Except \({P}_{d}=1\), the value \(T\) corresponding to the peak of detection success probability decreases with the increase \(n\) in \(0<T<0.8\). When the transmittance of BS is small \(0<T<0.3\), the probability of successful detection \({P}_{d}\) is high when the number of photons in the photon detector is large. Therefore, for low transmittance BS, increasing the number of input photons can increase the probability of successful detection, but for high transmittance BS, the opposite is true.

Fig. 2
figure 2

Plot of the success probability \({P}_{d}\) of getting the output state \({\left|{\psi }_{\alpha ,n}\right.\rangle }_{out}\) as a function of \(T\) with different values of \(n=\mathrm{0,1},\mathrm{2,3}\) for \(\alpha =1+2i\)

Full size image

3.2 Fidelity Between the Output State and the Input Coherent State

In this subsection, under the BS with condition measurement, we introduce the fidelity between the input state \(\left|\alpha \right.\rangle\) and the output state \({\left|{\psi }_{\alpha }\right.\rangle }_{out}\) to assess the influence of the BS, which is defined as [31]

$$F={\left|\langle \alpha {\left|{\psi }_{\alpha }\right.\rangle }_{out}\right|}^{2}.$$
(20)

Substituting Eq. (16) into Eq. (20), the fidelity can be obtained as

$$F={P}_{d}^{-1}{T}^{2n}{\left|{\text{exp}}\left[\left(\sqrt{T}-1\right){\left|\alpha \right|}^{2}\right]{L}_{n}\left(R{T}^{-1}{\left|\alpha \right|}^{2}\right)\right|}^{2}.$$
(21)

In the case of BS complete transmission\(T=1\), the fidelity is\(F=1\). In addition, if the BS transmittance is zero, then the quantum fidelity is also zero, as expected. Figure 3 shows the nature of the variation as a function of with for. It is clear that the fidelity of quantum states is the highest under zero photon detection, and the fidelity value increases with the increase of transmittance\(T\). It can be seen from Fig. 3 that there are two methods to improve the fidelity of the output state: one is to reduce the number of detected photons, and the other is to increase the transmittance of BS. In addition, except for perfect fidelity\(F=1\),\(n=0\), the transmittance corresponding to the peak fidelity increases with the increase of\(n\). Finally, in case\(n=\mathrm{1,2},3\), the fidelity may also be zero when\(0.8<T<0.95\), which requires special attention in experimental observations of quantum optics.

Fig. 3
figure 3

Plot of the fidelity between the output state \({\left|{\psi }_{\alpha ,n}\right.\rangle }_{out}\) and input state \(\left|\alpha \right.\rangle\) as a function of \(T\) with different values of \(n=\mathrm{0,1},\mathrm{2,3}\) for \(\alpha =1+2i\)

Full size image

Preparing output quantum states with high fidelity and high detectability in quantum transmission has attracted much attention. To achieve this goal, we introduce a function

$${F}_{d}={P}_{d}\times F.$$
(22)

Substituting Eqs. (18) and (21) into Eq. (22), we have

$${F}_{d}={T}^{2n}{\left|{\text{exp}}\left[\left(\sqrt{T}-1\right){\left|\alpha \right|}^{2}\right]{L}_{n}\left(R{T}^{-1}{\left|\alpha \right|}^{2}\right)\right|}^{2}.$$
(23)

From Fig. 4, the output quantum state's overall fidelity and detection efficiency will gradually increase as the number of photons under condition measurement decreases for the BSs with high transmittance \(0.95<T<1\). For low transmittance BSs \(0<T<0.1\), the transmittance corresponding to the optimized detection decreases with the increase of photon number \(n\).

Fig. 4
figure 4

\({F}_{d}\) as a function of \(T\) with different values of \(n=\mathrm{0,1},\mathrm{2,3}\) for \(\alpha =1+2i\)

Full size image

4 Statistical Properties

To study the nonclassical statistical properties of the output states in Eq. (16) in more detail, we shall calculate the Husimi-Kano Q function, photon number distribution (PND), Mandel Q-parameter, intensity correlation function, and Wigner function for the output state in Eq. (16).

4.1 Husimi-Kano Q Function

The Husimi-Kano Q function provides a convenient tool for visualizing the properties of quantum states via calculating the expectation values of observables [32, 33]. For a single mode of the quantum state, the Q function corresponds to the diagonal matrix elements of the density operator \(\rho\) in a basis of the coherent state, which is defined as

$$Q\left(\gamma \right)=\frac{1}{\pi }\left.\langle \gamma \right|\rho \left|\gamma \right.\rangle .$$
(24)

For pure states, such as the output state in Eq. (16), Eq. (24) becomes

$$Q\left(\gamma \right)=\frac{1}{\pi }{P}_{d}^{-1}{T}^{2n}{\text{exp}}\left(-{\left|\alpha \right|}^{2}-{\left|\gamma \right|}^{2}\right){\left|{\text{exp}}\left(\sqrt{T}{\gamma }^{*}\alpha \right){L}_{n}\left(R{T}^{-1}\alpha {\gamma }^{*}\right)\right|}^{2}.$$
(25)

In the small values of \(T\) for \(n=2,3\), we see a single peak with a deep crater from Figs. 5(a) and 4(b). With the increase \(n\) the width of the crater increases. In short, from the distribution of the Q function in the q-p phase space, we find that the outstate in Eq. (16) is a non-Gaussian state.

Fig. 5
figure 5

The Q function in p-q phase space with \(\alpha =1+2i\) and \(T=0.1\) for (a) \(n=2\); (b) \(n=3\)

Full size image

4.2 Fluctuations in PND

An important nonclassical property of NQSs is the fluctuation of the PND. This oscillatory behavior has been studied on the PND of different quantum states. In single-mode field states, \({P}_{N}\) is defined as the probability of detecting \(N\) photons in the output state and can be obtained for pure state as

$${P}_{N}={\left|\langle N{\left|{\psi }_{\alpha ,n}\right.\rangle }_{out}\right|}^{2}.$$
(26)

Using Eq. (10) and substituting Eq. (16) into Eq. (26), the PND is obtained as

$${P}_{N}=\frac{1}{N!}{P}_{d}^{-1}{T}^{2n}{\text{exp}}\left(-{\left|\alpha \right|}^{2}\right){\left|{\left.\frac{{\partial }^{N}}{\partial {\xi }^{*N}}{\text{exp}}\left(\sqrt{T}{\xi }^{*}\alpha \right){L}_{n}\left(R{T}^{-1}\alpha {\xi }^{*}\right)\right|}_{{\xi }^{*}=0}\right|}^{2}.$$
(27)

Using Eq. (27), we calculate the PND of the states introduced in Eq. (16). Then, we study the oscillatory behavior of this distribution as a function of \(n\) with \(T=0.9\) and \(\alpha =1+2i\). Our results show that the states' PND exhibits oscillatory behavior known as a nonclassical signature, as can be seen in Figs. 6(a) and 5(d). As shown in Fig. 5(a) \(n=0\), the PND oscillates in small values of \(N\). Moreover, with the increase in the number of detected photons \(n\), the vibration range of the PND gradually increases.

Fig. 6
figure 6

The PND for the state in Eq. (16) with \(\alpha =1+2i\) and \(T=0.6\) for (a) \(n=0\); (b) \(n=1\); (c) \(n=2\); (d) \(n=3\)

Full size image

4.3 Sub-Poissonian Photon Statistics and Antibunching Effect

The PND can also be studied from the uncertainty of photon number in the quantum state. The fluctuation of the photon number operator \(N\) can be defined as

$${\left(\Delta N\right)}^{2}=\langle {N}^{2}\rangle -{\langle N\rangle }^{2},$$
(28)

where \(N\equiv a^\dagger a\) and \(\langle N\rangle\) is the average photon number in a quantum state. For the standard coherent state, \({\left(\Delta N\right)}^{2}=\langle N\rangle\) which implies Poissonian statistics. A state is squeezed if \({\left(\Delta N\right)}^{2}<\langle N\rangle\), i.e., the PND is narrower than that of the coherent states. In addition, the PND of a classical state is broader than that of a coherent state, which implies super-Poisson distribution in the PND.

One of the commonly used criteria for determining the PND is the Mandel parameter [34], which is defined as

$$Q_M=\frac{\langle a^{\dagger2}a^2\rangle}{\langle a^\dagger a\rangle}-\langle a^\dagger a\rangle.$$
(29)

It should be noted that the PND of the state obeys sub-Poissonian photon statistics when \({Q}_{M}<0\).

For the convenience of later analysis, the notation \({U}_{k,l}\) is introduced to represent the average values of the operator \(a^{\dagger k}a^l\) for the state in Eq. (16). According to the generating function of Laguerre polynomials and some quantum operator transformation formulas (see Appendix B), we finally have

$$\begin{array}{c}U_{k,l}\equiv_{out}\left.\langle\psi_{\alpha,n}\right|a^{\dagger k}a^l{\left|\psi_{\alpha,n}\right.\rangle}_{out}\\=\frac1{\left(n!\right)^2}P_d^{-1}T^{2n}\text{exp}\left(-\left|\alpha\right|^2\right){\left.\frac{\partial^{2n}}{\partial t^n\partial t^{'n}}\left(1-t\right)^{-1}\left(1-t'\right)^{-1}\left(K_1\alpha^\ast\right)^k\left(K_2\alpha\right)^l\text{exp}\left(K_1K_2\left|\alpha\right|^2\right)\right|}_{t=t'=0},\end{array}$$
(30)

where \({K}_{1},{K}_{2}\) are defined in Eq. (19). Using Eq. (30), for different values of \(k\) and \(l\), moments of any order \({a}^{k}{a}^{l}\) can be obtained,

Substituting the corresponding form of Eq. (30) into Eq. (29), the Mandel parameter can be given by

$${Q}_{M}=\frac{{U}_{\mathrm{2,2}}}{{U}_{\mathrm{1,1}}}-{U}_{\mathrm{1,1}}.$$
(31)

Particularly when \(n=0\), thus, \({Q}_{M}=0\), therefore, the PND of the output state corresponds to Poissonian statistics, which is independent of the transmission coefficient of the BS. In addition, when \(T=0\), we have \(QM=-1\), which is independent of the number of input photons \(n\). Comparing the three curves in Fig. 7, one can see that the transmittance of the BS corresponding to the first positive value \({Q}_{M}\) increases with the increasing detected photon number. Furthermore, when \(T\to 1,QM\to 0\), which implies the PND of the output state obeys Poissonian photon statistics like a normal coherent state.

Fig. 7
figure 7

The Mandel parameter as a function of \(T\) with \(n=\mathrm{1,2},3\) for \(\alpha =0.5\)

Full size image

The negative value of \({Q}_{M}\) is a sufficient criterion to determine that the PND of the quantum state has a sub-Poissonian distribution. The correlation function is measured by detecting single modes separately using two-photon detectors. Antibunching is used for the nonclassical characterization of the single quantum state. The criterion of antibunching is given in terms of moments of number operator as [35]

$${g}_{0}^{\left(2\right)}=\frac{\langle {N}^{2}\rangle -\langle N\rangle }{{\langle N\rangle }^{2}}-1<0.$$
(32)

Noticing \(N\equiv a^\dagger a\) and using Eq. (30), we have

$$g_0^{\left(2\right)}=\frac{\langle a^{\dagger2}a^2\rangle}{{\langle a^\dagger a\rangle}^2}-1=\frac{U_{2,2}}{\left(U_{1,1}\right)^2}-1.$$
(33)

It is easy to see that \({g}_{0}^{\left(2\right)}=1\) when \(n=0\). Based on the existing parameters in Fig. 8, the output state indicates a photon blockade effect when \(T<0.5\). As the transmittance of BS increases, the antibunching effect decreases in some transmission intervals. As the number of detected photons increases, the range of BS transmission corresponding to the antibunching effect decreases. It is worth noting that there is a final value \({g}_{0}^{\left(2\right)}\to 1\) when \(T\to 1\). According to the analysis in Figs. 6 and Fig. 7, there are two methods for the BSr to produce the NQSs: one is to reduce the transmittance, and the other is to select an appropriate number of input photons.

Fig. 8
figure 8

The second-order correlation function as a function of \(T\) with \(n=\mathrm{1,2},3\) for \(\alpha =1+2i\)

Full size image

4.4 Negativities of Wigner Function

For a single-mode state, the Wigner function is studied as quasi-probability statistical distributions in the two-dimensional phase space, i.e., the real and imaginary parts of the dimensionless complex amplitude \(\gamma \equiv q+ip\) [36]. The Wigner function has theoretical value and can be measured experimentally, and even its negative values can be observed [37, 38]. Thus, negative values of the Wigner function have become effective evidence for judging nonclassical quantum states. For a state with a density matrix \(\rho\), the Wigner function may be written in the coherent state representation as

$$W\left(\gamma ,{\gamma }^{*}\right)=\frac{2{e}^{2{\left|\gamma \right|}^{2}}}{{\pi }^{2}}\int {d}^{2}z\left.\langle -z\right|\rho \left|z\right.\rangle {\text{exp}}\left[2\left({z}^{*}\gamma -z{\gamma }^{*}\right)\right].$$
(34)

Substituting Eq. (16) into Eq. (34) and after some mathematical integration, we get (see Appendix C)

$$W\left(\gamma ,{\gamma }^{*}\right)=\frac{2}{\pi }{e}^{2{\left|\gamma \right|}^{2}}{P}_{d}^{-1}{T}^{2n}{\text{exp}}\left(-{\left|\alpha \right|}^{2}\right)\frac{1}{{\left(n!\right)}^{2}}\frac{{\partial }^{2n}}{\partial {t}^{n}\partial {t}^{{\prime}n}}{\left(1-t\right)}^{-1}{\left(1-{t}{\prime}\right)}^{-1}{\text{exp}}\left({W}_{1}{W}_{2}\right),$$
(35)

where

$${W}_{1}=\left(\sqrt{T}-\frac{t}{1-t}R{T}^{-1}\right){\alpha }^{*}-2{\gamma }^{*},{W}_{2}=-\left(\sqrt{T}-\frac{t}{1-t}R{T}^{-1}\right)\alpha +2\gamma .$$
(36)

In Fig. 9, we have plotted the Wigner function in Eq. (35) for \(n=\mathrm{0,1},\mathrm{2,3}\) with \(\alpha =0.5\) and \(T=0.3\). It is easy to see that the Wigner function takes negative values in some regions expect \(n=0\). This confirms the nonclassical properties of the output state in the BS.

Fig. 9
figure 9

Representations of Wigner distributions in phase space with \(\alpha =0.5\) and \(T=0.3\) for (a) \(n=0\); (b) \(n=1\); (c) \(n=2\); (d) \(n=3\)

Full size image

5 Squeezing Characteristics

The general NQSs have four prominent characteristics: sub-Poisson distribution, the antibunching effect, the negative value of the Wigner function, and the quantum squeezing effect. The squeezed states have been known to exhibit intriguing properties in several experiments. Squeezed states are essential because the quantum fluctuations in one quadrature can fall below the zero-point fluctuations. This section aims to study quadrature squeezing and the degree of squeezing of the introduced states in Eq. (16).

5.1 Quadrature Squeezing

Quadrature squeezing is described by the fluctuations in the two dimensionless Hermitian operators [39]

$$Q=\frac{a+a^\dagger}{\sqrt2},P=\frac{a-a^\dagger}{\sqrt2i},$$
(37)

which satisfy the commutation relation \(\left[Q,P\right]=i\).

Using the common definitions of the variances of the quantum operator \(\Delta O=O-\langle O\rangle\), the quadrature squeezing is defined as

$$S_Q=2\langle\left(\Delta Q\right)^2\rangle-1=2Re\left[\langle a^{\dagger2}\rangle-{\langle a^\dagger\rangle}^2\right]+2\langle a^\dagger a\rangle-2\left|\langle a^\dagger\rangle\right|^2$$
(38)

and

$$S_P=2\langle\left(\Delta P\right)^2\rangle-1=-2Re\left[\langle a^{\dagger2}\rangle-{\langle a^\dagger\rangle}^2\right]+2\langle a^\dagger a\rangle-2\left|\langle a^\dagger\rangle\right|^2.$$
(39)

Once \({S}_{Q}\) or \({S}_{P}\) takes a negative value in the range of \(\left[-\mathrm{1,0}\right)\) for a quantum state, this state is said to be squeezed in \(Q\) or \(P\) in phase space.

Substituting the general expressions in Eq. (30) into Eqs. (38) and (39), \({S}_{Q}\) and \({S}_{P}\) are obtained as

$${S}_{Q}=2Re\left[{U}_{\mathrm{2,0}}-{U}_{\mathrm{1,0}}^{2}\right]+2{U}_{\mathrm{1,1}}-2{\left|{U}_{\mathrm{1,0}}\right|}^{2}$$
(40)

and

$${S}_{P}=-2Re\left[{U}_{\mathrm{2,0}}-{U}_{\mathrm{1,0}}^{2}\right]+2{U}_{\mathrm{1,1}}-2{\left|{U}_{\mathrm{1,0}}\right|}^{2}.$$
(41)

From Fig. 10(a), It is clear to see that when the transmission coefficient of the BS exceeds a specific value, the region \({S}_{Q}<0\) indicates evidence of the squeezing effect for the state in Eq. (16), and the threshold values increase as \(n\) increases. When \(T\to 1\), \({S}_{Q}\to 1\), the squeezing effect of the BS on the input quantum state tends to disappear, however, it can be seen from Fig. 10(b) that \({S}_{p}\) is always greater than zero. That is, no quantum squeezing effect appears in the P direction.

Fig. 10
figure 10

Quadrature squeezing as a function of \(T\) with \(\alpha =0.2\) and \(n=\mathrm{1,2},3\) (a) for \({S}_{Q}\); (b) for \({S}_{P}\)

Full size image

5.2 Degree of Squeezing

To further investigate the squeezing depth of the output quantum state, we take a generalized quadrature operator

$$X_\theta=ae^{-i\theta}+a^\dagger e^{i\theta},$$
(42)

where \(\theta\) is the phase of the homodyne detector [40]. In particular, \(\theta =0,{X}_{0}=Q\) and \(\theta =-\pi /2\), \({X}_{-\pi /2}=P\) are the operators in Eq. (37).

A squeezing depth is defined as

$$S=\frac{\langle:\left(\Delta X_\theta\right)^2:\rangle}{\langle aa^\dagger\rangle-\langle a^\dagger a\rangle},$$
(43)

where \(S\ge -1\). If the value of \(S\) corresponding to a quantum state is between \(-1\) and \(0\), the quantum state is a squeezed state. Furthermore, the smaller the negative value of \(S\), the higher the degree of quantum state squeezing.

Note that the denominator in Eq. (43) is equal to 1 due to the operator commutation relation \(\left[a,{a}\right]=1\). Using Eq. (42), one can expand the numerator in Eq. (43) as

$$\langle:\left(\Delta X_\theta\right)^2:\rangle=\left(\langle a^{\dagger2}\rangle-{\langle a^\dagger\rangle}^2\right)e^{-2i\theta}+\left(\langle a^2\rangle-{\langle a\rangle}^2\right)e^{2i\theta}+2\langle a^\dagger a\rangle-2\langle a^\dagger\rangle\langle a\rangle.$$
(44)

According to mathematical inequalities, one obtains

$$\left(\langle a^{\dagger2}\rangle-{\langle a^\dagger\rangle}^2\right)e^{-2i\theta}+\left(\langle a^2\rangle-{\langle a\rangle}^2\right)e^{2i\theta}\geq-2\left|\langle a^{\dagger2}\rangle-{\langle a^\dagger\rangle}^2\right|.$$
(45)

Thus, the optimized squeezing depth over the phase \(\theta\) is

$$S_{opt}=-2\left|\langle a^{\dagger2}\rangle-{\langle a^\dagger\rangle}^2\right|+2\langle a^\dagger a\rangle-2\left|\langle a^\dagger\rangle\right|^2.$$
(46)

It can be seen from Fig. 11 that the squeezing effect of the BS on the input quantum state has a complex relationship with the transmission coefficient \(T\) and the number of detected photons \(n\). The higher the number of input photons in the Fock state, the higher the maximum squeezing, but simultaneously, the transmittance of the BS needs to be increased. Our numeric results indicate that the region \({S}_{opt}<0\) can be found via changing the transmittance of the BS and the photon number in Fock space, thus realizing the existence of the squeezing phenomenon of the output state in Eq. (16).

Fig. 11
figure 11

The optimized squeezing depth \({S}_{opt}\) as a function of \(T\) with \(\alpha =0.2\) and \(n=\mathrm{1,2},3\)

Full size image

6 Conclusions

We study the output quantum state of the BS for arbitrary photon number detection and transmission when the input states are the coherent state \(\left|\alpha \right.\rangle\) and the Fock state \(\left|n\right.\rangle\). The result quantum state can be considered as a photon-added coherent state in the form of a two-variable Hermite polynomial for detecting \(m\) photons in the photon detector. Under the condition measurement \(m=n\), the output state is the Laguerre polynomial excited coherent state.

Due to the entanglement of the BS, the photon number in the input Fock and the transmittance of BS have a complex influence on the detection efficiency and fidelity of the output quantum states. In general, the fidelity and detection efficiency increase with the increase of BS transmittance \(T\) under zero photon detection. For the BS with high transmittance \(T>0.95\), the output quantum state detection efficiency and fidelity decrease as the photons number in the Fock state increases. By analyzing the Husimi-Kano Q function of the output quantum state, it can be determined that it has a non-Gaussian distribution in phase space. In addition, the numerical results of the PND and Mandel parameter (\({Q}_{M}<0\)) reveal the sub-Poissonian distribution of the output quantum states. The negative value of the Wigner function further confirms that the output quantum state is a non-Gaussian state. At the same time, the results of the second-order correlation function show that the output field has a pronounced antibunching effect. However, these nonclassical quantum phenomena gradually disappear as the transmittance of the beam splitter increases. Therefore, low transmittance BSs and fewer photon inputs are more conducive to preparing NQSs. Furthermore, the output quantum state squeezes in the Q direction but not in the P direction. The squeezing of the result quantum state can be enhanced by appropriately increasing the photons number and the transmittance of BS.

In summary, the effects of the BS and the Fock state on the input coherent state \(\left|\alpha \right.\rangle\) are studied via theoretical models and numerical analysis in detail. These conclusions may have critical applications for further study of NQSs based on BSs.