1 Introduction

In recent years, the generation of various nonclassical states and the study of their nonclassical characteristic have become the most fascinating aspects of quantum optics and quantum information [1,2,3,4,5]. The concepts of entangled states are related to interference of two different quantum states [6,7,8]. Entangled states have many applications for quantum information processing, such as quantum teleportation, quantum-key distribution, and dense coding [9,10,11,12]. Quantum technologies based on two photons entangled states can exhibit some interesting non-classical properties, such as nonlocality, entanglement, squeezing, the standard quantum limit of phase estimation [13,14,15,16].

Using several non-Gaussian operations, various types of entangled states have been produced, such as photon-added coherent states, photon-subtraction state [17, 18]. In addition, nonclassical states can also be generated by linear superposition of two standard coherent states with opposite phase, i.e., Schrödinger cat states [19, 20]. It has been reported that the even cat state exhibits the squeezing effect but has no antibunching effect, while the odd cat state owns an antibunching effect but has no squeezing effect [21, 22]. It is worth noting that these non-classical quantum states are related to coherent states and belong to continuous-variable (CV) quantum states [23,24,25].

CV and discrete-variable (DV) quantum state are two major issues of quantum science. A typical DV entangled state is the NOON state \(\left| \psi \right\rangle_{NooN} = \left( {\left| {N_{1} } \right\rangle \left| {0_{2} } \right\rangle + \left| {0_{1} } \right\rangle \left| {N_{2} } \right\rangle } \right)\), where \(N\) is the photon number and the subscript denotes the corresponding mode. Such states can be considered as macroscopic quantum superposition like cat states [26,27,28,29,30]. In quantum optics, the NOON states are considered as the heart of many quantum-enhanced measurement schemes, such as quantum lithography, quantum metrology [31, 32]. To date, five-photon NOON states have been prepared experimentally [33].

Recently, a type of hybrid entangled states (HES) in the combination of DV (a single photon number state) and CV (a coherent state) resources has been prepared in a free-travelling field [34,35,36]. Moreover, Kreis and van Loock have studied various kinds of HES between CV and DV. Many schemes for the generation of HES have been proposed by using hybrid quantum devices in atomic and molecular physics and quantum optics [37].

The aim of this paper is to construct a new hybrid quantum and to explore its several novel nonclassical properties. We begin by introducing the new state and deriving its normalization constant in Section 2. It will then go on to investigate its entanglement witnesses via degree of entanglement and Einstein–Podolsky–Rosen(EPR)criterion in Section 3. Section 4 will consider both the quantum statistical distribution and nonlocality by Mandel parameter, Wigner function and CHSH inequality. The purpose of the Section 5 is to analyze the phase sensitivity using parity detection and classical Fisher information. Section 6 seeks to find the squeezing properties with sum squeezing and difference squeezing. The final section gives a summary and main conclusion of the findings.

2 NAAN and its Normalization Constant

Let us start with a definition of bipartite NAAN as

$$\left| \psi \right\rangle = N_{c}^{ - 1/2} \left( {\left| {N_{1} } \right\rangle \left| {\alpha_{2} } \right\rangle + e^{i\varphi } \left| {\alpha_{1} } \right\rangle \left| {N_{2} } \right\rangle } \right),$$
(1)

where \(\varphi\) is a relative phase between \(\left| {N_{1} } \right\rangle \left| {\alpha_{2} } \right\rangle\) and \(\left| {\alpha_{1} } \right\rangle \left| {N_{2} } \right\rangle ,\)\(Nc\) is the normalization constant. The subscripts \(1\) and \(2\) will be used in this paper to refer to distinguish variables from different quantum light field modes. For the convenience of analysis, in the following discussion, we take

$$n \equiv n_{1} = n_{2} ,\quad \quad \alpha \equiv \alpha_{1} = \alpha_{2} ,$$
(2)

where \(n_{1} ,n_{2}\) denote the average photon number in the mode1 and 2.

According to the properties of quantum states \(Tr\rho = 1\) and

$$\left\langle {N_{1} } \right|\left. {\alpha_{1} } \right\rangle = \left\langle {N_{2} } \right|\left. {\alpha_{2} } \right\rangle = \frac{{\alpha^{n} }}{{\sqrt {n!} }}e^{{ - \frac{1}{2}\left| \alpha \right|^{2} }} ,$$
(3)

the normalization constant is obtained as

$$N_{c} = 2\left( {\frac{1}{n!}\left| \alpha \right|^{2n} e^{{ - \left| \alpha \right|^{2} }} \cos \varphi + 1} \right).$$
(4)

In particular, when \(\varphi = \alpha = 0\), Eq. (1) reduces to the NOON state \(\left| \psi \right\rangle_{NooN}\). However, when \(N = 0,\alpha = 1\),

$$\left| \psi \right\rangle_{0110} = \frac{1}{{\sqrt {2\left( {1 + e} \right)} }}\sum\limits_{m = 0}^{\infty } \frac{1}{m!}\left( {a_{2}^{{\dag^{m} }} + e^{i\varphi } a_{1}^{\dag m} } \right)\left| {0_{1} } \right\rangle \left| {0_{2} } \right\rangle ,$$
(5)

where we have used

$$\left. {\left| \alpha \right\rangle } \right|_{\alpha = 1} = e^{{ - \frac{1}{2} + a^{\dag } }} \left| 0 \right\rangle = e^{{ - \frac{1}{2}}} \sum\limits_{m = 0}^{\infty } \frac{{a^{{\dag^{m} }} }}{m!}\left| 0 \right\rangle .$$
(6)

Thus, it is easy to see that when \(\varphi = 0,\pi\), the quantum states in Eq. (5) are different from the Bell states in Fock state[38, 39]

$$\left| {\psi^{ \pm } } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {01} \right\rangle \pm \left| {10} \right\rangle } \right).$$
(7)

To our knowledge, the NAAN state in Eq. (1) has not been previously studied and represents a novel symmetric HES which may be considered as a superposition of the NOON states..

3 Entanglement Witnesses

This section will examine the entanglement of the NAAN state via the von Neumann entropy of entanglement and EPR criterion.

3.1 Degree of Entanglement

Different methods have been used to measure the degree of entanglement via different kinds of entropies, such as entropy of entanglement and logarithmic negativity. For the two-mode entangled state, the von Neumann entropy of entanglement is defined as [40, 41]

$$E_{v} \left( \rho \right) = S\left[ {Tr_{2} \left( \rho \right)} \right],$$
(8)

where \(S\left[ \rho \right] = - Tr\left( {\rho \mathop {\log }\nolimits_{2} \rho } \right)\) is von Neumann entropy, \(c_{l}\) and \(Tr_{2} \left( \rho \right)\) denotes the partial transpose of density operator \(\rho\) with respect to \(2\)-mode. For a two-mode pure state, its Schmidt decomposition is

$$\left| {\psi_{12} } \right\rangle = \sum\limits_{k = 0}^{\infty } c_{k} \left| {\alpha_{k1} } \right\rangle \left| {\beta_{k2} } \right\rangle ,$$
(9)

where \(\left| {\alpha_{k1} } \right\rangle\) and \(\left| {\beta_{k2} } \right\rangle\) are orthogonal and normalized basis states and \(c_{k}\) are the superposition coefficients of the basis states [42, 43].

Substituting Eq. (9) into Eq. (8), the von Neumann entropy is obtained as

$$E_{v} \left( \rho \right) = - \sum\limits_{k = 0}^{\infty } \left| {c_{k} } \right|^{2} \mathop {\log }\nolimits_{2} \left| {c_{k} } \right|^{2} .$$
(10)

Thus for the NAAN state shown in Eq. (1), in the number state basis one find that

$$\left| \psi \right\rangle = N_{c}^{ - 1/2} \sum\limits_{{m_{1} ,m_{2} = 0}}^{\infty } \left| {m_{1} } \right\rangle \left| {m_{2} } \right\rangle \left\langle {m_{2} } \right|\left\langle {m_{1} } \right|\left( {\left| {N_{1} } \right\rangle \left| {\alpha_{2} } \right\rangle + e^{i\varphi } \left| {\alpha_{1} } \right\rangle \left| {N_{2} } \right\rangle } \right).$$
(11)

The von Neumann entropy for the NAAN can be obtained

$$E_{v} \left( \rho \right) = - \left| \omega \right|^{2} \mathop {\log }\nolimits_{2} \left| \omega \right|^{2} ,$$
(12)

where

$$\omega = N_{c}^{ - 1/2} \frac{1}{{\sqrt {n!} }}\alpha^{n} e^{{ - \frac{1}{2}\left| \alpha \right|^{2} }} \left( {1 + e^{i\varphi } } \right).$$
(13)

Here we should point out that when \(n = 0,\alpha = 1,\varphi = 0,\)\(E_{v} \left( \rho \right) \to 0.5,\) which is just the maximally entangled coherent states in Ref. [44]. When \(\varphi = \pi\) and \(n \ne 0\), \(E_{v} \left( \rho \right) = 0\), which implies that the odd NAAN state has the lowest degree of entanglement.

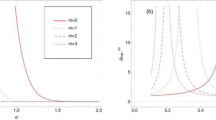
For evaluating the degree of entanglement of the NAAN state, we plot the von Neumann entropy of entanglement for the NAAN states as a function of both \(n\) and \(\varphi\) via Eq. (12). One obvious conclusion is that the degree of entanglement decreases rapidly as the value of \(n\) increases. In addition, when \(n\) is fixed, the entanglement degree of NAAN states is distributed symmetrically about \(\varphi = \pi\). The even NAAN states (\(\varphi = 0,2\pi\)) have a high degree of entanglement (Fig. 1).

Fig. 1
figure 1

The von Neumann entropy of entanglement for the NAAN states as a function of both \(n\) and \(\varphi\) in the case of \(\alpha = 1.\) The value of \(n\) ranges from \(1\) to \(6\) and that of \(\varphi\) ranges from \(0\) to \(2\pi .\)

Full size image

3.2 EPR Criterion

EPR criterion is used to investigate an inseparability of the two-mode state via a pair of EPR-type operators [45, 46]

$$EPR = \Delta^{2} \left( {X_{1} - X_{2} } \right) + \Delta^{2} \left( {P_{1} + P_{2} } \right),$$
(14)

wher \(X_{k} = \left( {a_{k} + a_{k}^{\dag } } \right)/\sqrt 2\) and \(P_{k} = \left( {a_{k} - a_{k}^{\dag } } \right)/\sqrt 2 i\left( {k = 1,2} \right).\)

Using \(\Delta^{2} O = \left\langle {O^{2} } \right\rangle - \left\langle O \right\rangle^{2}\), we get

$$\begin{gathered} EPR = 2\left[ {\left\langle {a_{1}^{\dag } a_{1} + a_{2}^{\dag } a_{2} } \right\rangle - 2\left\langle {a_{1} a_{2} + a_{1}^{\dag } a_{2}^{\dag } } \right\rangle } \right. \hfill \\ \left. { - \left[ {\left( {Re\left\langle {a_{1} - a_{2} } \right\rangle } \right)} \right]^{2} - \left[ {Im\left\langle {a_{1} + a_{2} } \right\rangle } \right]^{2} + 1} \right]. \hfill \\ \end{gathered}$$
(15)

In principle, the EPR criterion of arbitrary inseparable two-mode states satisfies the condition of \(EPR < 2\).To obtain \(EPR\) for the NAAN state, we need to calculate the average values of \(a_{1}^{\dag } a_{1} ,a_{1} a_{2}\) and \(a_{1}\) as (see Appendix 1)

$$\begin{gathered} E_{1} \equiv \left\langle {a_{1}^{\dag } a_{1} } \right\rangle = \left\langle {a_{2}^{\dag } a_{2} } \right\rangle \hfill \\ = N_{c}^{ - 1} \left( {\frac{2}{{\left( {n - 1} \right)!}}\left| \alpha \right|^{2} e^{{ - \left| \alpha \right|^{2} }} \cos \varphi + \left| \alpha \right|^{2} + n} \right), \hfill \\ E_{2} \equiv \left\langle {a_{1} a_{2} } \right\rangle = \frac{2}{{\left( {n - 1} \right)!}}N_{c}^{ - 1} e^{{ - \left| \alpha \right|^{2} }} \alpha^{n + 1} \alpha^{ * n - 1} \cos \varphi , \hfill \\ E_{3} \equiv \left\langle {a_{1} } \right\rangle = \left\langle {a_{2} } \right\rangle \hfill \\ = N_{c}^{ - 1} \left[ {\left( {\frac{1}{{\left( {n - 1} \right)!}}e^{ - i\varphi } \alpha^{ * - 1} + \frac{1}{n!}e^{i\varphi } \alpha } \right)e^{{ - \left| \alpha \right|^{2} }} \left| \alpha \right|^{2n} + \alpha } \right]. \hfill \\ \end{gathered}$$
(16)

Thus, we have

$$\begin{gathered} EPR = 4E_{1} - 8{\text{Re}} E_{2} - 4{\text{Re}} \left( {E_{3}^{2} - 2E_{2} } \right) \hfill \\ - 4{\text{Im}} \left( {E_{3}^{2} + 2E_{2} } \right) + 1. \hfill \\ \end{gathered}$$
(17)

It is shown that when \(n = 0,EPR\) is always less than \(2.\) Using Eqs. (16) and (17), we plot the \(EPR\) as the function of \(\varphi\) with \(n = 1,2,3\) in Fig. 2. It is obvious that when the relative phase \(\varphi\) is fixed, the value of EPR increases with the increase of photon number \(n\), and finally exceeds \(EPR > 2\).

Fig. 2
figure 2

The EPR for the NAAN state as a function \(\varphi\) with \(\alpha = 1\) and \(n = 1,2,3.\)

Full size image

4 Quantum Statistical Distribution for the NAAN State

This section is subdivided into three subsections, i.e., Mandel Q-parameter, Wigner function and violation of the Clauser-Horne-Shimony-Holt (CHSH) inequality.

4.1 Mandel Q-Parameter

Mandel parameter ordinarily is defined as follows [47]

$$Q_{M}^{k} = \frac{{\left\langle {N_{k}^{2} } \right\rangle - \left\langle {N_{k} } \right\rangle^{2} }}{{\left\langle {N_{k} } \right\rangle }} - 1,$$
(18)

where \(N_{k} = a_{k}^{\dag } a_{k}\) and \(k = 1,2\) indicates the \(1\) and \(2\) mode, respectively. Using \(\left( {a_{k}^{\dag } a_{k} } \right)^{2} = a_{k}^{\dag 2} a_{k}^{2} + a_{k}^{\dag } a_{k}\), we have

$$Q_{M}^{k} = \frac{{\left\langle {a_{k}^{\dag 2} a_{k}^{2} } \right\rangle - \left\langle {a_{k}^{\dag } a_{k} } \right\rangle^{2} }}{{\left\langle {a_{k}^{\dag } a_{k} } \right\rangle }}.$$
(19)

The average value of \(a_{k}^{\dag 2} a_{k}^{2}\) is

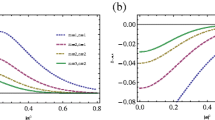
$$\begin{gathered} Q \equiv \left\langle {a_{1}^{\dag 2} a_{1}^{2} } \right\rangle = \left\langle {a_{2}^{\dag 2} a_{2}^{2} } \right\rangle \hfill \\ = N_{c}^{ - 1} \left[ {\frac{2}{{\left( {n - 2} \right)!}}\left| \alpha \right|^{2n} e^{{ - \left| \alpha \right|^{2} }} \cos \varphi + \left| \alpha \right|^{4} + n\left( {n - 1} \right)} \right]. \hfill \\ \end{gathered}$$
(20)

The negativity of Mandel parameter in Eq. (20) indicates that the quantum statistics is sub-Poissonian and shows the non-classicality of the state. Figure 3 shows that \(Q_{M}^{k}\) takes the minimum negative value at \(\varphi = \pi\). Thus, the odd NAAN state has sub-Poissonian photon number distribution for \(n = 2,3,4.\) As \(\alpha\) and \(n\) increase, we have \(Q_{M} > 0\) which imply the non-classical quantum statistical effects of the NAAN state gradually disappear.

Fig. 3
figure 3

The \(Q_{M}\) for the NAAN state as a function of \(\varphi\) with \(\alpha = 1\) and \(n = 2,3,4.\)

Full size image

4.2 Wigner Function

The negativity values in the Wigner function are major criteria on non-classicality of the quantum state [48, 49]. For analyzing the non-classicality of the NAAN state, one can use the definition of two-mode Wigner function as

$$\begin{gathered} W\left( {\gamma_{1} ,\gamma_{2} } \right) = \frac{2}{{\pi^{2} }}e^{{2\left( {\left| {\gamma_{1} } \right|^{2} + \left| {\gamma_{2} } \right|^{2} } \right)}} \hfill \\ \int \frac{{d^{2} z_{1} d^{2} z_{2} }}{{\pi^{2} }}\left\langle { - z_{1} , - z_{2} } \right|\rho \left| {z_{1} ,z_{2} } \right\rangle e^{{ - 2\left( {z_{1} \gamma_{1}^{ * } - z_{1}^{ * } \gamma_{1} } \right) - 2\left( {z_{2} \gamma_{2}^{ * } - z_{2}^{ * } \gamma_{2} } \right)}} , \hfill \\ \end{gathered}$$
(21)

where in the phase space

$$\begin{gathered} \gamma_{1} = \frac{{q_{1} + ip_{1} }}{\sqrt 2 },\quad \quad \gamma_{2} = \frac{{q_{2} + ip_{2} }}{\sqrt 2 }, \hfill \\ q_{ \pm } = \frac{{q_{1} \pm q_{2} }}{\sqrt 2 },\quad \quad \;p_{ \pm } = \frac{{p_{1} \pm p_{2} }}{\sqrt 2 }. \hfill \\ \end{gathered}$$

Substituting Eq. (1) into Eq. (21), one can finally obtain (see Appendix 2)

$$W\left( {\gamma_{1} ,\gamma_{2} } \right) = \frac{2}{{\pi^{2} }}\left( { - 1} \right)^{n} e^{{ - 2\left( {\left| {\gamma_{1} } \right|^{2} + \left| {\gamma_{2} } \right|^{2} } \right)}} N_{c}^{ - 1} \left( {F_{1} + 2ReF_{2} + F_{3} } \right),$$
(22)

where

$$\begin{gathered} F_{1} = L_{m} \left( { - 4\left| {\gamma_{1} } \right|^{2} } \right)\exp \left( {2\alpha \gamma_{2}^{ * } + 2\gamma_{2} \alpha^{ * } - \left| \alpha \right|^{2} } \right), \hfill \\ F_{2} = \frac{1}{n!}e^{i\varphi } \left( {2\gamma_{2} - \alpha } \right)^{n} \left( {\alpha^{ * } - 2\gamma_{1}^{ * } } \right)^{n} \exp \left[ {2\left( {\gamma_{1} \alpha + \alpha \gamma_{2}^{ * } } \right)} \right], \hfill \\ F_{3} = L_{n} \left( { - 4\left| {\gamma_{2} } \right|} \right)^{2} \exp \left( {2\alpha \gamma_{1}^{ * } + 2\gamma_{1} \alpha^{ * } - \left| \alpha \right|^{2} } \right). \hfill \\ \end{gathered}$$
(23)

Comparing with Figs.4(a)-(c), it is not difficult to see that the negative values of Wigner function show that the NAAN states are the non-Gaussian quantum states. In addition, the maximum positive values of even NAAN states are greater than the absolute value of the maximum negative values, while the opposite is true of odd NAAN states. Therefore, from the perspective of quantum statistical distribution, the non-classical properties of odd NAAN states are more obvious than those of even NAAN states. Comparing Fig. 4. (b) and (d), the Wigner function does not change significantly. Thus, it can be seen that when the amplitude of coherent states \(\alpha\) is fixed, the statistical distribution of quantum states mainly depends on the size of particle number \(n\), and has little relationship with the relative phase \(\varphi\).

Fig. 4
figure 4

The Wigner function in \(q_{ + } - p_{ + }\) phase space with \(\alpha = 1\) where the values of \((n,\varphi )\) are respectively (a) \(\left( {2,0} \right),\) (b)\(\left( {3,0} \right),\) (c) \(\left( {4,0} \right),\) (d) \((3,\pi )\)

Full size image

4.3 Violation of the CHSH Inequality

In this subsection, we study the quantum nonlocality test for the NAAN state. Bell has proposed a remarkable inequality imposed by a local hidden variable theory, which enables a quantitative test on nonlocality of quantum states. For the two-mode case, the CHSH inequality based on the Wigner function is expressed as [50]

$$\left| B \right| = \frac{{\pi^{2} }}{4}\left| {W\left( {\gamma_{1} ,\gamma_{2} } \right) + W\left( {\gamma_{1} ,\gamma_{2}^{^{\prime}} } \right) + W\left( {\gamma_{1}^{^{\prime}} ,\gamma_{2} } \right) - W\left( {\gamma_{1}^{^{\prime}} ,\gamma_{2}^{^{\prime}} } \right)} \right| \le 2.$$
(24)

Here by letting

$$\gamma_{1} = 0,\gamma_{2} = 0,\gamma_{1}^{^{\prime}} = \sqrt J ,\gamma_{2}^{^{\prime}} = - \sqrt J ,$$
(25)

one has

$$\left| {B_{J} } \right| = \frac{{\pi^{2} }}{4}\left| {W\left( {0,0} \right) + W\left( {\sqrt J ,0} \right) + W\left( {0, - \sqrt J } \right) - W\left( {\sqrt J , - \sqrt J } \right)} \right|,$$
(26)

where \(J > 0\) is the magnitude of the displacement for the Bell test.

Using Eqs. (22) and (26), the numerical CHSH is obtained with the NAAN state, which are shown in Fig. 5. For \(\varphi = \pi\), we find much stronger violations of the CHSH in the regime \(1 \le n \le 3.\) For \(\varphi = 0,2\pi\), we find violations of the inequality only at \(n = 2.\) In other cases \(0 < \varphi < \pi\) and \(\pi < \varphi < 2\pi ,\) the violations of the inequality obtained with the NAAN state occur over a range of photon numbers \(1 \le n \le 3\). In addition, the violation of the CHSH inequality diminishes for increasing \(n\). The most interesting result is with respect to the CHSH inequality which for the NOON states is violated only for case \(n = 1\), whereas for the NAAN state increasing violations at a wider range of photon numbers \(n > 1.\)

Fig. 5
figure 5

The CHSH quantity \(\left| {B_{J} } \right|\) as a function of \(n\) and \(\varphi\) with \(J = 0.1\) and \(\alpha = 1.5.\)

Full size image

5 Phase Measurement via Parity Detection

Quantum phase measurement plays a very important role in quantum metrology, because it can help us determine how small the accuracy of the phase we can detect. It has been reported that quantum vacuum state can be estimated with an error \(\Delta \varphi \sim 1/\sqrt{N},\) which is just the so-called standard quantum limit. Some nonclassical states and the entangled states, such as NOON states and two-mode squeezed vacuum state, can reach the Heisenberg limit \(\Delta \varphi \sim 1/N\) in a in a photon lossless environmental measurement. There are three types of detection schemes to measure the phase information of the quantum state, i.e., homodyne detection, intensity detection and parity detection. In section, we focus on the parity detection and the classical Fisher information.

5.1 Parity Detection with the NAAN State

The purpose of parity detection is to obtain the average value of parity operators in the quantum state, which has many applications in Wigner function and phase measurement [51,52,53]. Here, we take the parity operator of mode \(1\) as

$$\Pi_{1} = \left( { - 1} \right)^{{a_{1}^{\dag } a_{1} }} = \int \frac{{d^{2} \gamma_{1} }}{\pi }\left| {\gamma_{1} } \right\rangle \left\langle { - \gamma_{1} } \right|,$$
(27)

where \(\left| {\gamma_{1} } \right\rangle\) is the normal coherent state.

Using the eigen-equation of parity operator \(\Pi_{1} \left| {N_{1} } \right\rangle = \left( { - 1} \right)^{n} \left| {N_{1} } \right\rangle\) and \(\Pi_{1} \left| {\alpha_{1} } \right\rangle = \left| { - \alpha_{1} } \right\rangle\), the expectation value of the parity operator for the NAAN state is

$$\left\langle {\Pi_{1} } \right\rangle = N_{c}^{ - 1} \left[ {\frac{2}{n!}\left( { - 1} \right)^{n} \left| \alpha \right|^{2n} e^{{ - \left| \alpha \right|^{2} }} \cos \varphi + e^{{ - 2\left| \alpha \right|^{2} }} + \left( { - 1} \right)^{n} } \right].$$
(28)

It can be seen from the Fig. 6(a) that the average value of parity operator decreases continuously with the increase of \(\alpha .\) The average values parity operator is \(\left\langle {\Pi_{1} } \right\rangle \le 0\) when \(n\) is odd, but greater than zero when \(n\) is even in the case \(\varphi = 0.\) Comparing Figs.6(b)-(c), it is clear to see that the trough or peak of the curve occurs in \(\varphi = \pi\). In addition, the central trough of \(n = 0\) is narrower than that of \(n = 1,2\) under the same parameters. In the case of \(n = 0,1,\) the phase sensitivity of parity measurement increases with the increase of \(\alpha\), but in the case of \(n = 2\), it is opposite. Therefore, to obtain the best phase measurement sensitivity for the NAAN state, the measurement objects are the quantum states with the relative phase \(\varphi = \pi\) and small \(n\) and \(\alpha\) values, especially \(n = 0,\alpha \to 0\).

Fig. 6
figure 6

a The average value of parity operator as a function of \(n\) with \(\alpha = 0,1,1.5\) and \(\varphi = 0.\) \(\left\langle {\Pi_{1} } \right\rangle\) as function of \(\varphi\) with \(\alpha = 0.9,1.0,1.5\) and b \(n = 0\), c \(n = 1,\) d \(n = 2.\)

Full size image

5.2 Classical Fisher Information

After investigating the expectation values of the parity operator, in this subsection, we further consider the classical Fisher information (CFI) based on parity detection in Eq. (28). In general, the CFI can be estimated as [54, 55]

$$F_{c} = \frac{{\left| {\frac{\partial }{\partial \varphi }\left\langle {\Pi_{1} } \right\rangle } \right|^{2} }}{{\Delta^{2} \Pi_{1} }} = \frac{{\left| {\frac{\partial }{\partial \varphi }\left\langle {\Pi_{1} } \right\rangle } \right|^{2} }}{{1 - \left\langle {\Pi_{1} } \right\rangle^{2} }},$$
(29)

where we have used

$$\Delta^{2} \Pi_{1} \equiv \left\langle {\Pi_{1}^{2} } \right\rangle - \left\langle {\Pi_{1} } \right\rangle^{2} = 1 - \left\langle {\Pi_{1} } \right\rangle^{2} .$$
(30)

Using Eq. (28), one obtain

$$\frac{\partial }{\partial \varphi }\left\langle {\Pi_{1} } \right\rangle = - \frac{{\left( {e^{{\left| \alpha \right|^{2} }} - 1} \right)\left| \alpha \right|^{4} \sin \varphi }}{{\left( {2e^{{\left| \alpha \right|^{2} }} + \left| \alpha \right|^{4} \cos \varphi } \right)^{2} }}.$$
(31)

Substituting Eqs. (28) and (31) into (29), the CFI for the NAAN states is obtained

$$F_{c} = \frac{{\left| {K\left[ {\left( { - 1} \right)^{n} e^{{\left| \alpha \right|^{2} }} - 1} \right]\left| \alpha \right|^{2n} n!\sin \varphi } \right|^{2} }}{{\left| {K\left( {2\left( { - 1} \right)^{n} \left| \alpha \right|^{2n} \cos \varphi + n! + n!\left( { - 1} \right)^{n} e^{{\left| \alpha \right|^{2} }} } \right)^{2} } \right| - 4}}$$
(32)

where

$$K = \frac{1}{{\left( {\left| \alpha \right|^{2n} \cos \varphi + e^{{\left| \alpha \right|^{2} }} n!} \right)^{2} }}.$$
(33)

The phase sensitivity of the NAAN state can be estimated by the error propagation formula as

$$\Delta \varphi = \frac{1}{{\sqrt {F_{c} } }}.$$
(34)

From Fig. 7, it is easy to see that the phase fluctuation \(\Delta \varphi\) is the largest at \(\varphi = 0,\pi ,2\pi\). The minimum phase fluctuation is in the range of \(5\pi /6 < \varphi < \pi\) or \(\pi < \varphi < 7\pi /6\). In addition, at the same phase \(\varphi\), the phase uncertainty \(\Delta \varphi\) increases with the increase of photon number \(n\). Furthermore, when the amplitude of the coherent state \(\alpha\) tends to zero, the quantum phase fluctuation also tends to zero, even reaching the Heisenberg limit \(\Delta \varphi = 1/N\).

Fig. 7
figure 7

The phase uncertainty \(\Delta \varphi\) as a function of \(\varphi\) with \(\alpha = 1\) and \(n = 1,2,3.\)

Full size image

6 Squeezing Properties

The investigation of the squeezing effects of the quantum states is of considerable interest since it plays an important role in the quantum theory [56, 57]. There are several different methods used to analyze the squeezing properties of two-mode quantum states, such as sum squeezing, difference squeezing, quadrature squeezing, amplitude-squared squeezing. In principle, it has been studied that sum squeezing can be converted into normal single-mode squeezing using the sum-frequency generation. Therefore, in this section we focus on the sum squeezing and different squeezing properties of the NAAN states.

6.1 Sum Squeezing

For two-mode quantum state, the sum squeezing is associated with a more general operator [58]

$$V_{\theta } = \frac{1}{2}\left( {e^{i\theta } a_{1}^{\dag } a_{2}^{\dag } + e^{ - i\theta } a_{1} a_{2} } \right).$$
(35)

A state is said to be sum squeezed if

$$S_{\theta } \equiv \left\langle {\left( {\Delta V_{\theta } } \right)^{2} } \right\rangle - \frac{1}{4}\left\langle {N_{1} + N_{2} + 1} \right\rangle < 0,$$
(36)

where \(\left\langle {\left( {\Delta V_{\theta } } \right)^{2} } \right\rangle = \left\langle {V_{\theta }^{2} } \right\rangle - \left\langle {V_{\theta } } \right\rangle^{2}\),\(N_{1} = a_{1}^{\dag } a_{1}\) and \(N_{2} = a_{2}^{\dag } a_{2}\)

We define the squeezing factor to quantify the squeezing degree of sum squeezing as

$$S = \frac{{4S_{\theta } }}{{\left\langle {N_{1} + N_{2} + 1} \right\rangle }},$$
(37)

which is bounded by \(- 1 \le S < 0\) for the case of sun squeezing occurs. It is clear to see that the closer \(S\) trends to \(- 1,\) the higher the degree of sum squeezing.

Substituting Eq. (35) into Eq. (37), we can rewrite Eq. (37) as

$$S = \frac{{2\left[ {Re\left( {e^{ - 2i\theta } \left\langle {a_{1}^{2} a_{2}^{2} } \right\rangle } \right) - 2Re^{2} \left( {e^{ - i\theta } \left\langle {a_{1} a_{2} } \right\rangle } \right) + \left\langle {a_{1}^{\dag } a_{1} a_{2}^{\dag } a_{2} } \right\rangle } \right]}}{{\left\langle {a_{1}^{\dag } a_{1} } \right\rangle + \left\langle {a_{2}^{\dag } a_{2} } \right\rangle + 1}},$$
(38)

where \(Re\left( z \right)\) is the real part of a complex number \(z.\)

Expectation values of \(\left\langle {a_{1}^{2} a_{2}^{2} } \right\rangle\) and \(\left\langle {a_{1}^{\dag } a_{1} a_{2}^{\dag } a_{2} } \right\rangle\) are

$$\left\langle {a_{1}^{2} a_{2}^{2} } \right\rangle = N_{c}^{ - 1} \frac{1}{{\left( {n - 2} \right)!}}2\alpha^{n + 2} \alpha^{ * n - 2} e^{{ - \left| \alpha \right|^{2} }} \cos \varphi ,$$
(39)

and

$$\left\langle {a_{1}^{\dag } a_{1} a_{2}^{\dag } a_{2} } \right\rangle = 2N_{c}^{ - 1} \left( {\frac{{\left| \alpha \right|^{2n} }}{n!}n^{2} e^{{ - \left| \alpha \right|^{2} }} \cos \varphi + n\left| \alpha \right|^{2} } \right)$$
(40)

Substituting Eqs. (16), (39) and (40) into (38), We plot in Fig. 8 the sum squeezing degree \(S\) as a function of the relative phase \(\varphi\) with \(n = 1,2,3\) and \(\theta = 0,\alpha = 1.5.\) What stands out in Fig. 8 is that the NAAN state exhibits a maximum degree of sum squeezing under \(n = 1\) and \(\varphi = \pi\) conditions. Visually, \(S\) becomes positive when \(n > 2\) for any \(\varphi\), which means no sum squeezing arises at all. For \(n = 1\), when \(S\) is negative, \(\varphi\) is in the range \(5\pi /6 < \varphi < 7\pi /6\).

Fig. 8
figure 8

The sum squeezing degree \(S\) as a function of \(\varphi\) with \(n = 1,2,3\) and \(\theta = 0,\alpha = 1.5.\)

Full size image

6.2 Difference Squeezing

For the two-mode state, difference squeezing is associated with the operator \(W_{\theta }\) [58]

$$W_{\theta } = \frac{1}{2}\left( {e^{i\theta } a_{1} a_{2}^{\dag } + e^{ - i\theta } a_{1}^{\dag } a_{2} } \right).$$
(41)

A state is said to be difference squeezed along a direction \(\theta\) if

$$\left\langle {\left( {\Delta W_{\theta } } \right)^{2} } \right\rangle < \frac{1}{4}\left| {\left\langle {N_{1} - N_{2} } \right\rangle } \right|.$$
(42)

Noting \(\left\langle {\left( {\Delta W_{\theta } } \right)^{2} } \right\rangle = \left\langle {W_{\theta }^{2} } \right\rangle - \left\langle {W_{\theta } } \right\rangle^{2}\) and \(\left\langle {N_{1} } \right\rangle = \left\langle {N_{2} } \right\rangle\) for the NAAN state??we can rewrite Eq. (42) as

$$\begin{gathered} \left\langle {\left( {\Delta W_{\theta } } \right)^{2} } \right\rangle = 2Re\left( {e^{2i\theta } \left\langle {a_{1}^{2} a_{2}^{\dag 2} } \right\rangle } \right) - 4\left[ {Re\left( {e^{i\phi } \left\langle {a_{1} a_{2}^{\dag } } \right\rangle } \right)} \right]^{2} \hfill \\ + 2\left\langle {a_{1}^{\dag } a_{1} a_{2}^{\dag } a_{2} } \right\rangle + \left\langle {a_{1} a_{1}^{\dag } } \right\rangle + \left\langle {a_{2} a_{2}^{\dag } } \right\rangle < 0. \hfill \\ \end{gathered}$$
(43)

The expected values of operators \(a_{1} a_{2}^{\dag }\) and \(a_{1}^{2} a_{2}^{\dag 2}\) are

$$\left\langle {a_{1} a_{2}^{\dag } } \right\rangle = N_{c}^{ - 1} \frac{1}{n!}\left| \alpha \right|^{2n} e^{{ - \left| \alpha \right|^{2} }} \left( {n^{2} \left| \alpha \right|^{ - 2} e^{ - i\varphi } + \alpha^{ * } e^{i\varphi } } \right),$$
(44)

and

$$\begin{gathered} \left\langle {a_{1}^{2} a_{2}^{\dag 2} } \right\rangle = N_{c}^{ - 1} \left| \alpha \right|^{2n} e^{{ - \left| \alpha \right|^{2} }} \hfill \\ \left( {e^{ - i\varphi } \left| \alpha \right|^{ - 4} \frac{n}{{\left( {n - 3} \right)!}} + e^{i\varphi } \left| \alpha \right|^{4} \sqrt {\frac{{\left( {n + 1} \right)}}{{n!\left( {n + 3} \right)!}}} } \right). \hfill \\ \end{gathered}$$
(45)

We can see from Fig. 9 that \(\left\langle {\left( {\Delta W_{\theta } } \right)^{2} } \right\rangle\) have the smallest value at \(\varphi = \pi\). In addition, \(\left\langle {\left( {\Delta W_{\theta } } \right)^{2} } \right\rangle\) as a function of \(\varphi\) kept positive when \(n = 1,2.\) Thus, we find that the difference squeezing exists only with \(n = 0\).

Fig. 9
figure 9

The \(\left\langle {\left( {\Delta W_{\theta } } \right)^{2} } \right\rangle\) as a function of \(\varphi\) with \(n = 0,1,2\) and \(\theta = \pi ,\alpha = 0.5.\)

Full size image

7 Conclusion

We have proposed a new symmetric hybrid state which is composed by two discrete Fock number states \(\left| N \right\rangle\) and two continuous coherent states \(\left| \alpha \right\rangle\) in two-mode state with an arbitrary phase angle \(\varphi\). We found that this state can be considered as the superpositions of NOON states. Therefore, in the case of \(\varphi = 0,\pi\) and \(\alpha = 1,\) it is different from the normal Bell state.

Evaluating the degree of entanglement of the NAAN states, our results suggest that the even NAAN state (\(\varphi = 0,2\pi\)) has a high degree of entanglement. To rigorously discuss entanglement, EPR criterion was used to analyze entanglement of the NAAN states. It is shown that when \(n = 0\), the NAAN states are always entangled which no dependence on the parameters \(\varphi\) and \(\alpha\). Specifically, when \(n > 3,\) the NAAN states no longer exhibit entangled properties.

Entanglement, non-Gaussian distribution and non-locality are typical properties of non-classical quantum states. Interestingly, through the analysis of Mandel parameter, we find that the odd NAAN states have sub-Poissonian photon number distribution for \(n = 2,3,4.\) Further, the conclusion is confirmed by the analysis of Wigner function. Some strong violations of the CHSH inequality at a wider range of photon numbers \(n = 1,2,3\) were also found.

The relative phase \(\varphi\) of the NAAN states can be considered as a phase-shift parameter between two-arm in a linear Mach–Zehnder interferometer. Thus, through the numerical analysis of parity detection, we find that the best phase measurement sensitivity is obtained when \(\varphi = \pi\) and small values of \(n\) and \(\alpha\), especially \(n = 0,\alpha \to 0\). Furthermore, when the amplitude of the coherent state \(\alpha\) tends to zero, the quantum phase fluctuation also tends to zero, even reaching the Heisenberg limit \(\Delta \varphi = 1/N.\)

The theoretical discussions on sum squeezing show that only when \(n = 1\) and \(\alpha = 0.56\), sum squeezing of the NAAN state arise in the range \(5\pi /6 < \varphi < 7\pi /6\). However, the difference squeezing exists only with \(n = 0\) and \(\alpha = 0.5\) in the range \(5\pi /6 < \varphi < 7\pi /6.\) In summary, the NAAN do not have the properties of sum squeezing and difference squeezing, when \(n > 1\).

Hofmann and Ono have used the quantum interference between down-converted photon pairs and photons from coherent laser light to produce a path entangled multiphoton output state NOON [59]. Thus, the NAAN states may be realized in the same experimental settings. This is an important issue for future work.