1 Introduction

Quantum state engineering has also been extensively studied with the general aim of the preparation of a variety of in traveling fields [1, 2]. These states exhibit strong non-classical features, and could be of great interest for many applications such as quantum metrology [3, 4], quantum teleportation [5] and quantum key distribution [6]. It is necessary to prepare different quantum states to require the need of quantum technology. Therefore an important topic in the fields of quantum optics and quantum information is to generate various states of light and to study their nonclassicality.

Conditional preparation is a well-established technique for the preparation of highly nonclassical states [7, 8]. Throught measuring one of the modes of a bipartite correlated state, the desired state can be projected in other mode for certain results of the measurement. It turned out that a bipartite correlated state can be obtained by using the basic instruments such as beam splitter (BS) and parametric amplifier (PA) [9, 10]. Dakna’s group used conditional measurement on the BS to generate cat-like state [11] and photon-added state [12]. A typical scheme of conditional measurement is the quantum-optical catalysis. The quantum-optical catalysis is simply mixing one photon at the beam splitter and post-select the beam-splitter (BS) output based on detection of one photon, first proposed by Lvovsky and Mlynek [13]. For exampe, by using quantum-optical catalysis, the coherent state is transformed to a non-Gaussian quantum state with abundance nonclassical character [14]. Another typical scheme of conditional measurement is the quantum-scissor [15]. By using quantum-scissor scheme, quantum state with infinite components can be transformed to another quantum state with only finite components [16]. More recently, Quesada et al.[17] considered conditional photonic non-Gaussian state preparation using multimode Gaussian states and photon-number-resolving detectors. Gagatsos and Guha proposed a method to prepare a two-mode coherent-cat-basis Bell state with fidelity close to unity and higher success probability [18]. Su et al. [19] presented a detailed analytic framework for studying multimode non-Gaussian states that are conditionally generated when few modes of a multimode Gaussian state are subject to photon number-resolving detectors. Magana-Loaiza et al.[20] engineered the excitation mode of the field through the simultaneous subtraction of photons from two-mode squeezed vacuum states. All these works are regarding quantum state engineering through conditional measurement.

In recent several years, Xu’s group has several works on the preparation of quantum states by using conditional measurement. A two-mode squeezed vacuum state (TMSVS) is injected in the input channels of a beam splitter and the photon number of the mode in one of the output channels is measured, then a Hermite polynomial excited squeezed state is conditionaly generated in the other output channel [21]. Injecting two separate single-mode squeezed vacuum states into a beam splitter and counting the photons in one of the output channels (conditional measurement or post-detection), another Hermite polynomial excited squeezed state is conditionaly generated in the other channel [22]. Injecting a coherent state in signal mode and two single-photon sources in other two auxiliary modes of SU(3) interferometry, a broad class of useful nonclassical states are obtained in the output signal port after making two single-photon-counting measurements in the two output auxiliary modes [23]. By operating quantum-optical catalysis on each mode of the TMSVS, an entangled non-Gaussian state is obtained with enhanced entanglement properties [24]. By applying the quantum-scissors operations to both modes of the TMSVS, a resulting state with only the twin vacuum and the twin one-photon components has been obtained [25].

However, the conditional measurements in Xu’s above schemes adopte photon-number detection, which is a discrete-variable measurement. Fortuately, there has been an increased interest in condition preparation quantum states based on continuous-variable measurement. Etesse et.al reported the experimental generation of a squeezed cat state from two single photon Fock states. In this protocal, two single Fock states are sent on a symmetrical beam splitter, and a homodyne measurement was performed on one of the two output arms. If the measurement is equal to zero, the other arm is projected on a generated state [26]. In another work, they also demonstrated that different kinds of mesoscopic quantum states of light can be efficiently generated from a simple iterative scheme [27]. Molnar et al. propose two experimental schemes with homodyne measurements for producing coherent-state superpositions which approximate different nonclassical states conditionally in traveling optical fields [28]. Based on the measurement of x quadratures around x = 0, two ideal Schrodinger cat states mixed by a balanced beam splitter were amplified into a larger even cat state [29]. Lance and Jeong et al. presented several schemes to conditionally engineer interesting continuous-variable non-Gaussian quantum states based on a beam-splitter interaction, using an ancilla squeezed vacuum state and conditioning homodyne detection [30, 31].

In this work, inspired by these ideas, we give a theoretical scheme of conditionally generating quantum states by a continuous-variable conditioning scheme, based on a beam-splitter interaction, homodyne detection, and an ancilla squeezed vacuum state. Some quantum properties for the generated quantum state, including density operator, success probability, photon-number representation, Mandel Q parameter and Wigner function, have derived analytically in detail. The paper is organized as follows: In Section 2, we introduce the theoretical scheme of generating quantum state. In Section 3, photon number representaion of the output postselected state are analyzed. Here the fidelity between the input and the output state is also discussed. In Section 4, the sub-Poissonian distribution of the generated state is characterized by the Mandel-Q parameter. In Section 5, we study the Wigner function of the generated state. Conclusions are summarized in the last section.

2 Generating Quantum State

In this section, we introduce our considered theroretical scheme and give the density operator for the generated quantum state.

2.1 Theoretic Scheme

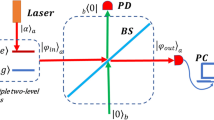
Our setup scheme is depicted in Fig. 1. An input Fock state \(\left \vert m\right \rangle _{a}\) (in input port with mode a) and an ancilla state \( S\left (r\right ) \left \vert 0\right \rangle _{b}\) (in input port with mode b ) are sent on a variable beam splitter, the output state will be a bipartite correlated state

$$ \left\vert \psi_{cor}\right\rangle =B\left( \left\vert m\right\rangle_{a}\otimes S\left( r\right) \left\vert 0\right\rangle_{b}\right) . $$
(1)

Here the beam splitter is also called a breeding beam splitter, whose operator B acting on modes a and b is represented as

$$ B=\exp \left( \theta \left( a^{\dag }b-ab^{\dag }\right) \right) , $$
(2)

where the transmissivity is defined as \(T=\cos \limits ^{2}\theta \) and the reflectivity R = 1 − T. The ancilla state \(S\left (r\right ) \left \vert 0\right \rangle _{b}\) is the squeezed vacuum state with the squeezing operator

$$ S\left( r\right) =\exp \left( \frac{r}{2}(b^{\dag 2}-b^{2})\right) , $$
(3)

(r is the real squeezing parameter). Then, performed a measurement along the quadrature x on one output port with mode b, which is described by the operator

$$ \hat{\Pi}_{b}={\int}_{-x_{0}}^{x_{0}}\left\vert x\right\rangle \left\langle x\right\vert dx, $$
(4)

the other output port with mode a is projected on the postselected state

$$ \rho \left( x_{0}\right) =\frac{1}{P\left( x_{0}\right) }\text{tr}_{b}\left( \hat{\Pi}_{b}\left\vert \psi_{cor}\right\rangle \left\langle \psi_{cor}\right\vert \right) , $$
(5)

The required output state is postselected for the threshold x0. It should be noted that: (1) the state vector

$$ \left\vert x\right\rangle =\pi^{-1/4}\exp \left( -\frac{x^{2}}{2}+\sqrt{2} xb^{\dag }-\frac{b^{\dag 2}}{2}\right) \left\vert 0\right\rangle_{b}, $$
(6)

is the eigenvalue of the quadrature operator \(X_{b}=\left (b+b^{\dag }\right ) /\sqrt {2}\) (satisfying \(X_{b}\left \vert x_{b}\right \rangle =x_{b}\left \vert x_{b}\right \rangle \)); (2) the output measurement falls in the heralding range with \(\left [ -x_{0},x_{0}\right ] \) with the postselection threshold x0; (3) the normalization factor

$$ P\left( x_{0}\right) =\text{tr}_{ab}\left( \hat{\Pi}_{b}\left\vert \psi_{cor}\right\rangle \left\langle \psi_{cor}\right\vert \right) $$
(7)

is just the corresponding success probability of detection.

Fig. 1
figure 1

(Color online) Schematic of the post-selection protocol: an input Fock state \(\left \vert m\right \rangle _{a}\) and an ancilla state \(S\left (r\right ) \left \vert 0\right \rangle _{b}\) are mixed on a variable beamsplitter, and the desired output state \(\protect \rho \left (x_{0}\right ) \) is generated owing to a heralding event based on a quadrature measurement

Full size image

2.2 Density Operator

In order to derive the analytical expressions for the density operator \(\rho \left (x_{0}\right ) \) in (5) and the success probability \(P\left (x_{0}\right ) \) in (7), we list some relations beforehand.

  1. (I)

    Relations for Fock state are

    $$ \begin{array}{@{}rcl@{}} \left\vert m\right\rangle &=&\frac{1}{\sqrt{m!}}\frac{d^{m}}{d{s_{1}^{m}}} e^{s_{1}a^{\dag }}\left\vert 0\right\rangle |_{s_{1}=0}, \end{array} $$
    (8)
    $$ \begin{array}{@{}rcl@{}} \left\langle m\right\vert &=&\frac{1}{\sqrt{m!}}\frac{d^{m}}{d{s_{2}^{m}}} \left\langle 0\right\vert e^{s_{2}a}|_{s_{2}=0}. \end{array} $$
    (9)
  2. (II)

    Relations for \(S\left (r\right ) \left \vert 0\right \rangle \) are

    $$ \begin{array}{@{}rcl@{}} S\left( r\right) \left\vert 0\right\rangle &=&\left( 1-\lambda^{2}\right)^{1/4}e^{\frac{\lambda }{2}b^{\dagger 2}}\left\vert 0\right\rangle_{b}, \end{array} $$
    (10)
    $$ \begin{array}{@{}rcl@{}} \left\langle 0\right\vert S^{\dag }\left( r\right) &=&\left( 1-\lambda^{2}\right)^{1/4}\left\langle 0\right\vert_{b}e^{\frac{\lambda }{2}b^{2}}, \end{array} $$
    (11)

    with \(\lambda =\tanh r\).

  3. (III)

    transformation relations for the beam splitter are

    $$ \begin{array}{@{}rcl@{}} BaB^{\dag } &=&\sqrt{T}a-\sqrt{1-T}b, \end{array} $$
    (12)
    $$ \begin{array}{@{}rcl@{}} BbB^{\dag } &=&\sqrt{1-T}a+\sqrt{T}b. \end{array} $$
    (13)

Using above relations and some other techniques, we finally obtain

$$ \begin{array}{@{}rcl@{}} &&\text{tr}_{b}\left( \hat{\Pi}_{b}\left\vert \psi_{cor}\right\rangle \left\langle \psi_{cor}\right\vert \right) \\ &=&\frac{\pi^{-1/2}\left( 1-\lambda^{2}\right)^{1/2}}{\left( 1+\lambda T\right) m!}\frac{d^{2m}}{d{s_{1}^{m}}d{s_{2}^{m}}}e^{-\frac{1}{2}\frac{R}{ 1+\lambda T}\left( {s_{1}^{2}}+{s_{2}^{2}}\right) } \\ &&{\int}_{-x_{0}}^{x_{0}}e^{-\frac{1-\lambda T}{1+\lambda T}x^{2}-\frac{\sqrt{2 }\sqrt{R}}{1+\lambda T}x\left( s_{1}+s_{2}\right) } \\ &&e^{\frac{1}{2}\frac{\lambda R}{1+\lambda T}a^{\dag 2}+\frac{s_{1}\sqrt{T} \left( \lambda +1\right) + \sqrt{2}\lambda \sqrt{R}\sqrt{T}x}{ 1+\lambda T}a^{\dag }}\left\vert 0\right\rangle_{a} \\ &&\left\langle 0\right\vert_{a}e^{\frac{1}{2}\frac{\lambda R}{1+\lambda T} a^{2}+\frac{s_{2}\sqrt{T}\left( \lambda +1\right) +\sqrt{2} \lambda \sqrt{R}\sqrt{T} x}{1+\lambda T}a} \\ &&dx|_{s_{1}=s_{2}=0}, \end{array} $$
(14)

and

$$ \begin{array}{@{}rcl@{}} P\left( x_{0}\right) &=&\pi^{-1/2}\sqrt{\frac{1-\lambda }{2T\lambda -\lambda +1}}\frac{1}{m!} \\ &&\frac{d^{2m}}{d{s_{1}^{m}}d{s_{2}^{m}}}e^{-\frac{1}{2}\frac{\left( 1-\lambda \right) R}{2T\lambda -\lambda +1}\left( {s_{1}^{2}}+{s_{2}^{2}}\right) +\frac{ \lambda +1}{2T\lambda -\lambda +1}Ts_{1}s_{2}} \\ &&{\int}_{-x_{0}}^{x_{0}}e^{-\frac{1-\lambda }{2T\lambda -\lambda +1}x^{2}- \frac{\sqrt{2}\left( 1-\lambda \right) \sqrt{R}}{2T\lambda -\lambda +1} x\left( s_{1}+s_{2}\right) }dx|_{s_{1}=s_{2}=0}. \end{array} $$
(15)

In our above expressions, we still retain derivatives and integrals due to the complexity of our interaction model.

Knowing (14) and (15), the density operator of the output postselected state is obtained analytically. Obviously, the postselected state is dependent on the interaction parameters, including the number m of the input Fock state, the squeezing parameter r of the anicilla state, the transmissivity T of the beam splitter and the postselection threshold parameter x0. Therefore, one can obtain desirable quantum states by choosing these appropriate parameters.

By using the scientific software Mathematica, we plot the success probability \(P\left (x_{0}\right ) \) as a function of the threshold parameter x0 with different parameters in Fig. 2. Figure 2a is plotted with the same m, r but different T. Figure 2b is plotted with the same m, T but different r. Figure 2c is plotted with the same r, T but different m. From Fig. 2, one can see clearly that the exact meaurement x0 = 0 will lead to a zero success probability. So the output postselected state can be obtained only for x0 > 0. Moreover, the greater the x0 value, the greater the success probability.

Fig. 2
figure 2

(Color online) Success probability \(P\left (x_{0}\right ) \) as a function of the threshold parameter x0 for some different interaction parameters \(\left (m,r,T\right )\). a\(\left (1,0.15,T\right ) \) with T = 0.2, 0.5, 0.6, 0.8; b\(\left (1,r,0.25\right ) \) with r = 0, 0.35, 0.69, 1.03; c\(\left (m,0.35,0.25\right ) \) with m = 1, 2, 5, 8. Each variables in above graphs are corresponding to the solid, dotted, dashed, and dotdashed line, respectively

Full size image

3 Photon-number Representation and Fidelity

In this section, we describe the photon-number representation of the density operator for the output postselected state. Any quantum state with density operator ρ can be expanded as the density matrix [32]

$$ \rho =\sum\limits_{n_{1},n_{2}}^{\infty }p_{n_{1}n_{2}}\left\vert n_{2}\right\rangle \left\langle n_{1}\right\vert , $$
(16)

where \(p_{n_{1}n_{2}}=\left \langle n_{1}\right \vert \rho \left \vert n_{2}\right \rangle \). For the generated state \(\rho \left (x_{0}\right ) \), we can obtain the following expression

$$ \begin{array}{@{}rcl@{}} p_{n_{1}n_{2}} &=&\frac{\pi^{-1/2}\left( 1-\lambda^{2}\right)^{1/2}}{ m!\left( 1+\lambda T\right) \sqrt{n_{1}!n_{2}!}P\left( x_{0}\right) } \\ &&\frac{d^{2m+n_{1}+n_{2}}}{d{s_{1}^{m}}d{s_{2}^{m}}d\mu^{n_{1}}d\nu^{n_{2}}} e^{\frac{\sqrt{T}\left( \lambda +1\right) }{1+\lambda T}\left( s_{1}\mu +s_{2}\nu \right) } \\ &&e^{-\frac{1}{2}\frac{R}{1+\lambda T}\left( {s_{1}^{2}}+{s_{2}^{2}}\right) + \frac{1}{2}\frac{\lambda R}{1+\lambda T}\left( \mu^{2}+\nu^{2}\right) } \\ &&{\int}_{-x_{0}}^{x_{0}}e^{-\frac{1-\lambda T}{1+\lambda T}x^{2}-\frac{\sqrt{2 }\sqrt{R}}{1+\lambda T}x\left( s_{1}+s_{2}\right) + \frac{\sqrt{2} \lambda \sqrt{R}\sqrt{T}}{1+\lambda T}x\left( \mu +\nu \right) }dx \\ &&|_{s_{1}=s_{2}=\mu =\nu =0}, \end{array} $$
(17)

where the following relations

$$ \begin{array}{@{}rcl@{}} \left\langle n_{1}\right\vert &=&\frac{1}{\sqrt{n_{1}!}}\frac{d^{n_{1}}}{ d\mu^{n_{1}}}\left\langle 0\right\vert e^{\mu a}|_{\mu =0}, \end{array} $$
(18)
$$ \begin{array}{@{}rcl@{}} \left\vert n_{2}\right\rangle &=&\frac{1}{\sqrt{n_{2}!}}\frac{d^{n_{2}}}{ d\nu^{n_{2}}}e^{\nu a^{\dag }}\left\vert 0\right\rangle |_{\nu =0} \end{array} $$
(19)

have been used.

Obviously, the density operator matrix of the input state \(\left \vert m\right \rangle \) only include the sole element \(\left \vert m\right \rangle \left \langle m\right \vert \). However, the output postselected state \(\rho \left (x_{0}\right ) \) include other kinds of diagonal and off-diagonal elements \(\left \vert n_{2}\right \rangle \left \langle n_{1}\right \vert \). For the diagonal elements (i.e. n1 = n2 = n,), their probabilities is just the photon number distribution \(p_{nn}=P\left (n\right ) \). In Fig. 3, we plot the density operator matrices and the photon number distributions in two different cases with x0 = 0.025, T = 0.02, r = 0.7, and different m . It is interesting to see that the output postselected state has only odd (even) components if m is odd (even).

Fig. 3
figure 3

(Color online) Photon-number matrix/ Photon number distribution for \(\protect \rho \left (x_{0}\right ) \) with parameters \(\left (x_{0},T,r,m\right ) \). (a/c) \(\left (0.025,0.02,0.7,1\right ) \); (b/d) \(\left (0.025,0.02,0.7,2\right ) \)

Full size image

On the other hand, the fidelity between the output postselected state \(\rho \left (x_{0}\right ) \) and the input state \(\left \vert m\right \rangle \), can be expressed as

$$ F=\text{Tr}\left( \left\vert m\right\rangle \left\langle m\right\vert \rho \left( x_{0}\right) \right) =\left\langle m\right\vert \rho \left( x_{0}\right) \left\vert m\right\rangle =p_{mm}. $$
(20)

Thus if we take n1 = n2 = m in (17), the fidelity can be obtained. Figure 4 shows the fidelity as a function of the threshold parameter x0 with different parameters. From these figures, we find that the fidelity decreases with the value x0 increases.

Fig. 4
figure 4

(Color online) The fidelity F between the input and the generated state, or the probability of component \(\left \vert m\right \rangle \left \langle m\right \vert \) in the generated state, as a function of the threshold parameter x0 for some different interaction parameters \( \left (m,r,T\right ) \). a\(\left (1,0.15,T\right ) \) with T = 0.2, 0.5, 0.6, 0.8; b\(\left (1,r,0.25\right ) \) with r = 0, 0.35, 0.69, 1.03 ; c\(\left (2,0.15,T\right ) \) with T = 0.2, 0.5, 0.6, 0.8. are corresponding to the solid, dotted, dashed, and dotdashed line, respectively

Full size image

4 Mandel Q Parameter

As a typical property of quantum state, the Mandel Q parameter [33]

$$ Q_{M}=\frac{\left\langle a^{\dagger 2}a^{2}\right\rangle }{\left\langle a^{\dagger }a\right\rangle }-\left\langle a^{\dagger }a\right\rangle , $$
(21)

is a good indication to exhibit the sub-Poissionian character. The distribution is Poissonian when Q = 0, and super- (sub-) Poissonian if Q > 0 (Q < 0). For example, a coherent state corresponds to Q = 0 (Poissonian statistics). In order to obtain Mandel Q parameter for the generated state, we firstly the general expression of the expectation value \(\left \langle a^{\dag k}a^{l}\right \rangle \) with arbitrary k and l. Noting

$$ \left\langle a^{\dag k}a^{l}\right\rangle =\text{Tr}\left( a^{\dag k}a^{l}\rho \left( x_{0}\right) \right) , $$
(22)

and making length calculation, we finally obtain

$$ \begin{array}{@{}rcl@{}} &&\left\langle a^{\dag k}a^{l}\right\rangle \\ &=&\frac{\pi^{-1/2}}{P\left( x_{0}\right) }\sqrt{\frac{1-\lambda }{ 2T\lambda -\lambda +1}}\frac{1}{m!} \\ &&\frac{d^{2m+k+l}}{d{s_{1}^{m}}d{s_{2}^{m}}d\mu^{k}d\nu^{l}}e^{-\frac{1}{2} \frac{\left( 1-\lambda \right) R}{2T\lambda -\lambda +1}\left( {s_{1}^{2}}+{s_{2}^{2}}\right) +\frac{\left( \lambda +1\right) T}{2T\lambda -\lambda +1}s_{2}s_{1}} \\ &&e^{\frac{1}{2}\frac{\lambda R}{\lambda +1}\frac{T\lambda +1}{2T\lambda -\lambda +1}\left( \mu^{2}+\nu^{2}\right) +\frac{1}{\lambda +1}\frac{ \lambda^{2}R^{2}}{2T\lambda -\lambda +1}\mu \nu } \\ &&e^{\frac{T\lambda +1}{2T\lambda -\lambda +1}\sqrt{T}\left( \nu s_{1}+\mu s_{2}\right) +\frac{\lambda R\sqrt{T}}{2T\lambda -\lambda +1}\left( \nu s_{2}+\mu s_{1}\right) } \\ &&{\int}_{-x_{0}}^{x_{0}}e^{-\frac{1-\lambda }{2T\lambda -\lambda +1} x^{2}-\frac{\sqrt{2}\left( 1-\lambda \right) \sqrt{R}}{2T\lambda -\lambda +1}x\left( s_{1}+s_{2}\right) + \frac{\sqrt{2}\lambda \sqrt{R}\sqrt{T}}{2T\lambda -\lambda +1}x\left( \nu +\mu \right) }dx \\ &&|_{s_{1}=s_{2}=\mu =\nu =0}, \end{array} $$
(23)

where the following relations

$$ \begin{array}{@{}rcl@{}} a^{\dag k} &=&\frac{d^{k}}{d\mu^{k}}e^{\mu a^{\dag }}|_{\mu =0}, \end{array} $$
(24)
$$ \begin{array}{@{}rcl@{}} a^{l} &=&\frac{d^{l}}{d\nu^{l}}e^{\nu a}|_{\nu =0}, \end{array} $$
(25)

have been used.

The numerical results show that the output postselected state may exhibit sub-Poissonian distribution as long as the interaction parameters is chosen properly. In Fig. 5, we plot the Mandel Q parameter QM as a function x0 with different interaction parameters. In Fig. 6, the feasibility regions of super-Poisson and sub-Poisson distribution are shown in \(\left (x_{0},\lambda \right ) \) space with m = 1 and different T. There is a strong possibility that the sub-Poisson region is located for small parameters λ and x0.

Fig. 5
figure 5

(Color online) Mandel Q parameter QM as a function of the threshold parameter x0 for some different interaction parameters \( \left (m,r,T\right ) \). a\(\left (1,0.15,T\right ) \) with T = 0.2, 0.5, 0.6, 0.8; b\(\left (1,r,0.25\right ) \) with r = 0, 0.35, 0.69, 1.03 ; c\(\left (m,0.35,0.25\right ) \) with m = 1, 2, 5, 8. are corresponding to the solid, dotted, dashed, and dotdashed line, respectively

Full size image
Fig. 6
figure 6

(Color online) Mandel Q parameter QM in space \(\left (x_{0}, \protect \lambda \right ) \) showing feasible region for sub-Poissonian (blue) or super-Poissonian (yellow) with am = 1, T = 0.5; bm = 1, T = 0.02

Full size image

5 Wigner Function

The Wigner function [34] is defined by

$$ W\left( \beta \right) =\frac{2}{\pi }\left\langle D\left( \beta \right) \left( -1\right)^{a^{\dag }a}D^{\dag }\left( \beta \right) \right\rangle , $$
(26)

where \(\left (-1\right )^{a^{\dag }a}\) is the photon number parity operator, \(D\left (\beta \right ) =e^{\beta a^{\dag }-\beta ^{\ast }a}\) is the displacement operator with \(\beta =\left (x+ip\right ) /\sqrt {2}\). The analytical expressions of the Wigner function of our generated quantum state can be given

$$ \begin{array}{@{}rcl@{}} W\left( \beta \right) &=&\frac{2}{\pi }\frac{\pi^{-1/2}}{P\left( x_{0}\right) }\sqrt{\frac{1-\lambda }{2T\lambda -\lambda +1}}\frac{1}{m!} \\ &&e^{-2\left\vert \beta \right\vert^{2}\left( 1+\frac{2}{\lambda +1}\frac{ R^{2}\lambda^{2}}{2T\lambda -\lambda +1}\right) + 2\frac{\lambda R}{\lambda +1}\frac{T\lambda +1}{2T\lambda -\lambda +1}\left( \beta^{2}+\beta^{\ast }{}^{2}\right) } \\ &&\frac{d^{m}}{d{s_{1}^{m}}}\frac{d^{m}}{d{s_{2}^{m}}}e^{-\frac{1}{2}\frac{ R\left( 1-\lambda \right) }{2T\lambda -\lambda +1}\left( {s_{1}^{2}}+{s_{2}^{2}}\right) - \frac{\left( 1+\lambda \right) T}{2T\lambda -\lambda +1}s_{1}s_{2}} \\ &&\times e^{ 2\frac{1+T\lambda }{2T\lambda -\lambda +1 }\sqrt{T}\left( s_{1}\beta^{\ast }+s_{2}\beta \right) -\frac{2\lambda R \sqrt{T}}{2T\lambda -\lambda +1}\left( s_{1}\beta +s_{2}\beta^{\ast }\right) } \\ &&{\int}_{-x_{0}}^{x_{0}}e^{\frac{2T\lambda -\lambda -1}{\lambda +1}x^{2}- \sqrt{2}\sqrt{R}x\left( s_{1}+s_{2}\right) +\frac{2\sqrt{2}\lambda \sqrt{R} \sqrt{T}}{\lambda +1}x\left( \beta + \beta^{\ast }\right) } \\ &&dx|_{s_{1}=s_{2}=0}. \end{array} $$
(27)

In Fig. 7, we plot the Wigner functions of the postselected output state for different cases with x0 = 0.025, r = 0.7 and diferent T, m. One can notice that (1) the figure (a) is similar to the Wigner function of a squeezed single-photon state; (2) the figure (b) is similar to that of a squeezed vacuum state; (3) the figure (c) is similar to the Wigner function of single-photon state; (4) the figure (d) is similar to the Wigner function of two-photon Fock state. It is interesting to note that (1) the output state is more like the character of the input squeezed state for low transmissivity and (2) the output state is more like the character of the input Fock state for high transmissivity.

Fig. 7
figure 7

(Color online) Wigner function of the generated states with some different interaction parameters \(\left (x_{0},T,r,m\right )\)a\(\left (0.025,0.02,0.7,1\right )\); b\(\left (0.025,0.02,0.7,2\right )\); c\( \left (0.025,0.9,0.7,1\right ) \); d\(\left (0.025,0.9,0.7,2\right ) \)

Full size image

6 Conclusion

To summarize, based on the input Fock state, an ancillary squeezed vacuum state, a beam-splitter interaction, and homodyne detection, we generate a postselected quantum state by using a continuous-variable conditional measurement scheme. We derive the analytical expression of the density operator for the output postselected state and discuss the success probability.Some quantum properties, including the photon-number representation, Mandel Q parameter and Wigner function, are investigated in detail. For every property, we give it analytical expression, where the differential and integration forms are remained because of the complexity of the model. By changing the interaction parameters, including the number of the input Fock state, the ancilla squeezing parameter, the beam-splitter transmissivity, and the postselection threshold, we make numerical analysis for all.

Numerical results show that: (1) the success probability is a monotonic increasing function of the threshold x0; (2) The generated have only odd (even) components if the input is odd (even)-Fock state; (3) The sub-Poissionian character of the generated state may exhibit for the small squeezing and small threshold, the sub-Poisson characteristic is more easily displayed; (4) When the transmissivity is high, the output state is more like the input Fock state; While the transmissivity is low, the output state is more like the ancillary squeezed vacuum state.