1 Introduction

In recent years, quantum teleportation (QT) [1,2,3] has received extensive attention and developed rapidly. It is used to transmit unknown states by use of shared entanglement and classical channels between the sender A (conventionally named Alice) and the receiver B (conventionally named Bob). In 1993, Bennett et al. [4] first presented a quantum teleportation scheme in which an arbitrary unknown single qubit state could be teleported from a sender to a distant receiver with the aid of an Einstein-Podolsky-Rosen (EPR) pair [5,6,7]. This protocol was experimentally verified soon in 1997 [8]. Since the original work, due to its important applications in quantum communication, quantum teleportation has attracted widespread attention, and has been widely studied in past years both theoretically and experimentally. In 1998, Karlsson and Bourennane [9] presented a protocol for teleporting a two-qubit state with GHZ states instead of an EPR pair. In 2002, B.S. Shi et al. [10] proposed a teleportation protocol via W state, which could teleport an unknown state probabilistically. In 2005, Deng et al. [11] introduced a symmetric multiparty controlled teleportation scheme for an arbitrary two-particle entangled state [12,13,14,15,16]. In 2013, Zha et al. [17] firstly presented the original bidirectional quantum controlled teleportation protocol via a five-qubit cluster state.

In the past few years, we have witnessed rapid development of quantum teleportation where various quantum states such as Bell states [18], GHZ states [19] and W states have served as different quantum channels [20] to satisfy a variety of different quantum communication scenarios. Besides quantum teleportation, there are some other important quantum communication protocols, such as quantum key distribution (QKD) [21,22,23], quantum secret sharing (QSS) [24,25,26], quantum secure direct communication (QSDC) [27,28,29], joint remote state preparation (JRSP) [30,31,32] and so on. Recently, Min Li et al. [33] proposed an improved quantum teleportation scheme for one five-qubit unknown state with a seven-qubit quantum channel.

In this paper, we put forward an improved scheme with single-qubit measurements only. In this way, our improved scheme possesses higher intrinsic efficiency and requires fewer classical resources and lower technical complexity. The organization of the rest of this paper is as follows. In the next section, we review the scheme proposed by Min Li et al. [33]. In Section 3, the improvement of protocol is studied in details. The comparison is given in Section 4. Finally, a summary is given in Section 5.

2 The Protocol of Min Li et al.

In this section, first of all, we review the idea of Min Li et al. [33]. In their scheme, Alice aims to transmit an unknown five-qubit entangled state to a distant receiver Bob. The five-qubit unknown state they take into account is described by

$$ \vert \chi \rangle_{abcde} =(\alpha \vert 00000\rangle +\beta \vert 00011\rangle +\gamma \vert 11100\rangle +\delta \vert 11111\rangle )_{abcde} $$
(1)

where α, β, γ and δ are unknown coefficients satisfying the relation |α|2 + |β|2 + |γ|2 + |δ|2 = 1. In the beginning, Alice and Bob share a seven-qubit cluster state

$$ \vert \phi \rangle_{1234567} =\frac{1}{2}(\vert 0000000\rangle +\vert 0001101\rangle +\vert 1110010\rangle +\vert 1111111\rangle )_{1234567} $$
(2)

The qubits a, b, c, d, e, 6 and 7 belong to Alice and qubits 1, 2, 3, 4 and 5 belong to Bob respectively. Now the state of the whole system composed of the unknown five-qubit state and the quantum channels is

$$ \vert \tau \rangle_{abcde1234567} =\vert \chi \rangle_{abcde} \otimes \vert \phi \rangle_{1234567} $$
(3)

To achieve teleportation, Alice performs a seven-qubit joint measurement on her qubits a, b, c, d, e, 6 and 7. However, in their scheme, the calculation procedure seems a little complicated. In particular, a seven-qubit joint measurement is a huge technical challenge in terms of current experimental technology. Considering the operational difficulty of their scheme, we propose an improved scheme with single-qubit measurements only instead of a seven-qubit joint measurement.

3 The Improvement

We first recall two important gates, Hadamard gate and CNOT gate.

Hadamard gate is performed onto a single qubit mapping the basis state |0〉 to \(\frac {1}{\sqrt 2} (\vert 0\rangle +\vert 1\rangle )\), and |1〉 to \(\frac {1}{\sqrt 2} (\vert 0\rangle +\vert 1\rangle )\). It’s operation corresponds to the following transformation matrix:

$$ H=\frac{1}{\sqrt 2} \left[ {{\begin{array}{*{20}c} 1 & 1 \\ 1 & {-1} \end{array}} } \right]. $$
(4)

CNOT gate can be represented by the following matrix

$$ CNOT=\left[ {{\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array}} } \right] $$
(5)

It operates on a quantum register consisting of 2 qubits. One is the controlling qubit and the other is the target qubit. If the state of the controlling qubit is 1, the state of the target bit is flipped. Otherwise, the state of the target bit remains the same.

Now, let’s present our improved scheme.

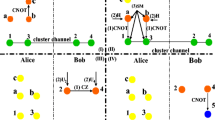
In the first step as shown in Fig. 1(I). Alice performs CNOT gates on her qubits a, b, c, d, e. Firstly, qubit a serves as a controlling qubit and both qubits b and c act as two target qubits. Meanwhile, qubit d works as the controlling qubit and qubit e acts as the target qubit. After that, the following state can be obtained as

$$ \vert \chi \rangle_{abcde} =(\alpha \vert 00\rangle +\beta \vert 01\rangle +\gamma \vert 10\rangle +\delta \vert 11\rangle )_{ad} \vert 000\rangle_{bce} $$
(6)

Now the quantum state of the system composed of qubits a, d, 1, 2, 3, 4, 5, 6, 7 is written as

$$\begin{array}{@{}rcl@{}} \vert \tau \rangle_{ab1234567} &=&\frac{1}{2}(\alpha \vert 00\rangle +\beta \vert 01\rangle +\gamma \vert 10\rangle +\delta \vert 11\rangle_{ad} \otimes \vert 0000000\rangle +\vert 0001101\rangle\\ &&+\vert 1110010\rangle +\vert 1111111\rangle )_{1234567} \end{array} $$
(7)
Fig. 1
figure 1

Sketch of our improved teleportation scheme of five-qubit state with seven-qubit quantum channels. Here H, SM and U denote the Hadamard gate operation, the single-qubit measurement and single-qubit unitary operation, respectively

Full size image

In the second step, as illustrated in Fig. 1(II), Alice performs a CNOT operation on qubits (a,6) and qubits (d,7) where qubits a and d act as controlling qubits and qubits 6 and 7 serve as target qubits, respectively. Now the above state |τ〉ad1234567 evolve to

$$\begin{array}{@{}rcl@{}} \vert {\tau}^{\prime}\rangle_{ad1234567} =\frac{1}{2}[\alpha \vert 00\rangle_{ad} \otimes (\vert 0000000\rangle +\vert 0100011\rangle +\vert 1011100\rangle +\vert 1111111\rangle )_{6712345}\\ +\beta \vert 01\rangle_{ad} \otimes (\vert 0100000\rangle +\vert 0000011\rangle +\vert 1111100\rangle +\vert 1011111\rangle)_{6712345}\\ +\gamma \vert 10\rangle_{ad} \otimes (\vert 1000000\rangle +\vert 1100011\rangle +\vert 0011100\rangle +\vert 0111111\rangle )_{6712345}\\ +\delta \vert 11\rangle_{ad} \otimes (\vert 1100000\rangle +\vert 1000011\rangle +\vert 0111100\rangle +\vert 0011111\rangle )_{6712345} ]\\ \end{array} $$
(8)

Alice performs a Hadamard operation on her qubits a and d, which transforms the state |τ′〉ad1234567 into the following form

$$\begin{array}{@{}rcl@{}} \vert {\tau}^{\prime\prime}\rangle_{ad1234567} &=&\frac{1}{4}[\alpha (\vert 0\rangle +\vert 1\rangle )_{a} (\vert 0\rangle +\vert 1\rangle )_{d} \otimes (\vert 0000000\rangle +\vert 0100011\rangle\\ &&+\vert 1011100\rangle +\vert 1111111\rangle )_{6712345}\\ &&+\beta (\vert 0\rangle +\vert 1\rangle )_{a} (\vert 0\rangle -\vert 1\rangle )_{d} \otimes (\vert 0100000\rangle +\vert 0000011\rangle\\ &&+\vert 1111100\rangle +\vert 1011111\rangle )_{6712345}\\ &&+\gamma (\vert 0\rangle -\vert 1\rangle )_{a} (\vert 0\rangle +\vert 1\rangle )_{d} \otimes (\vert 1000000\rangle +\vert 1100011\rangle\\ &&+\vert 0011100\rangle +\vert 0111111\rangle )_{6712345}\\ &&+\delta (\vert 0\rangle -\vert 1\rangle )_{a} (\vert 0\rangle -\vert 1\rangle )_{d} \otimes (\vert 1100000\rangle +\vert 1000011\rangle\\ &&+\vert 0111100\rangle +\vert 0011111\rangle )_{6712345} ]\\ &=&\frac{1}{4}[\vert 0000\rangle_{ad67} (\alpha \vert 00000\rangle +\beta \vert 00011\rangle +\gamma \vert 11100\rangle +\delta \vert 11111\rangle )_{12345}\\ &&+\vert 0001\rangle_{ad67} (\alpha \vert 00011\rangle +\beta \vert 00000\rangle +\gamma \vert 11111\rangle +\delta \vert 11100\rangle )_{12345}\\ &&+\vert 0010\rangle_{ad67} (\alpha \vert 11100\rangle +\beta \vert 11111\rangle +\gamma \vert 00000\rangle +\delta \vert 00011\rangle )_{12345}\\ &&+\vert 0011\rangle_{ad67} (\alpha \vert 11111\rangle +\beta \vert 11100\rangle +\gamma \vert 00011\rangle +\delta \vert 00000\rangle )_{12345}\\ &&+\vert 0100\rangle_{ad67} (\alpha \vert 00000\rangle - \beta \vert 00011\rangle +\gamma \vert 11100\rangle - \delta \vert 11111\rangle )_{12345}\\ &&+\vert 0101\rangle_{ad67} (\alpha \vert 00011\rangle - \beta \vert 00000\rangle +\gamma \vert 11111\rangle - \delta \vert 11100\rangle )_{12345}\\ &&+\vert 0110\rangle_{ad67} (\alpha \vert 11100\rangle -\beta \vert 11111\rangle +\gamma \vert 00000\rangle - \delta \vert 00011\rangle )_{12345}\\ &&+\vert 0111\rangle_{ad67} (\alpha \vert 11111\rangle - \beta \vert 11100\rangle +\gamma \vert 00011\rangle - \delta \vert 00000\rangle )_{12345}\\ &&+\vert 1000\rangle_{ad67} (\alpha \vert 00000\rangle +\beta \vert 00011\rangle -\gamma \vert 11100\rangle - \delta \vert 11111\rangle )_{12345}\\ &&+\vert 1001\rangle_{ad67} (\alpha \vert 00011\rangle +\beta \vert 00000\rangle -\gamma \vert 11111\rangle - \delta \vert 11100\rangle )_{12345}\\ &&+\vert 1010\rangle_{ad67} (\alpha \vert 11100\rangle +\beta \vert 11111\rangle - \gamma \vert 00000\rangle - \delta \vert 00011\rangle )_{12345}\\ &&+\vert 1011\rangle_{ad67} (\alpha \vert 11111\rangle +\beta \vert 11100\rangle - \gamma \vert 00011\rangle - \delta \vert 00000\rangle )_{12345}\\ &&+\vert 1110\rangle_{ad67} (\alpha \vert 00000\rangle - \beta \vert 00011\rangle - \gamma \vert 11100\rangle +\delta \vert 11111\rangle )_{12345}\\ &&+\vert 1101\rangle_{ad67} (\alpha \vert 00011\rangle - \beta \vert 00000\rangle - \gamma \vert 11111\rangle +\delta \vert 11100\rangle )_{12345}\\ &&+\vert 1110\rangle_{ad67} (\alpha \vert 11100\rangle - \beta \vert 11111\rangle - \gamma \vert 00000\rangle + \delta \vert 00011\rangle )_{12345}\\ &&+\vert 1111\rangle_{ad67} (\alpha \vert 11111\rangle - \beta \vert 11100\rangle - \gamma \vert 00011\rangle +\delta \vert 00000\rangle )_{12345} \end{array} $$
(9)

In the third step as shown in Fig. 1(III), Alice performs a single-qubit measurement with measurement basis {|0〉,|1〉} which is performed on her system of qubits a, d, 6 and 7 and sends her measurement results to Bob via classical channels.

In the final step as depicted in Fig. 1(IV), according to Alice’s measurement outcomes, Bob implements an appropriate unitary operation on his five-qubits 1, 2, 3, 4, 5 to restore the state (α|0000〉 + β|00011〉 + γ|11100〉 + δ|11111〉)abcde. The detail relationship between Alice’s measurement result and Bob’s unitary operation with Pauli matrices \(\sigma _{x} =\left [ {{\begin {array}{*{20}c} 0 & 1 \\ 1 & 0 \end {array}} } \right ]\), \(\sigma _{y} =\left [ {{\begin {array}{*{20}c} 0 & i \\ i & 0 \end {array}} } \right ]\), \(\sigma _{z} =\left [ {{\begin {array}{*{20}c} 1 & 0 \\ 0 & {-1} \end {array}} } \right ]\) and the identity matrix \(I=\left [ {{\begin {array}{*{20}c} 1 & 0 \\ 0 & 1 \end {array}} } \right ]\) are respectively given in Table 1.

Table 1 The corresponding relation between Alices’s measurement results (ARMs) and Bob’s operation U12345
Full size table

For example, if Bob receives the measurement outcome |1111〉, he needs to apply five single-qubit unitary operations (σy)1 ⊗ (σx)2 ⊗ (σx)3 ⊗ (σy)4 ⊗ (σx)5 on his qubits 1, 2, 3, 4, 5 to recover the initial input state (α|00000〉 + β|00011〉 + γ|11100〉 + δ|11111〉)12345.

In this way, finally Bob could obtain the original state |χ〉abcde in (1) with success possibility 100%.

4 Comparison

A comparison is made between our scheme and Ref. [33] from the following four aspects: the cost of quantum resource (QR), the cost of classical resource (CR), intrinsic efficiency of the scheme and the difficulty of necessary operation (NO).

First, both our scheme and Ref. [33] can be implemented with a seven-qubit cluster state acting as the quantum channel. Thus the cost of QR for both schemes is the same, i.e., a seven-qubit cluster state.

Second, in Ref. [33], since Alice performs a seven-qubit joint measurement on qubits a, b, c, d, e, 6 and 7 and her measurement results correspond to seven bits. Therefore, the cost of CR in their scheme is 7. However, in our scheme Alice utilizes a single-qubit measurement on qubits a, d, 6 and 7 and her measurement results is denoted by four bits. This means that in our scheme the cost of CR is 4. By comparing the two schemes, we show that our scheme has lower cost of CR than the scheme in Ref. [33].

Third, efficiency is a main factor that can be utilized for comparing the performance of schemes. In quantum communication schemes, the efficiency can be defined as [34]

$$ \eta =\frac{q_{t}} {q_{s} +b_{t}} $$
(10)

where qt is the number of qubits that consist of the quantum information to be exchanged, qs is the number of the qubits that are used as the quantum channel and bt is the classical bits exchanged between participants. Therefore, in our scheme, for purpose of transmitting an unknown five-qubit entangled state to a distant receiver Bob (qt = 5), Alice should prepare a seven-qubit cluster state (qs = 7) and then informs her measurement results to Bob via a classical channel (bt = 4). Without considering the quantum resources and the classical resources which are used for identity authentication and security checks, qubit efficiency is calculated as η = 5/11. Similarly, according to the definition of qubit efficiency, the qubit efficiency of Ref. [33] is calculated as η1 = 5/14. Consequently, our scheme has higher intrinsic efficiency.

Finally, let us show the necessary operations of our scheme. Here some simple operations such as CNOT, and single-qubit operations in our scheme are utilized. All these operations involved in our scheme could be achieved by present technologies which makes it more feasible.

Therefore, compared with previous study for one five-qubit unknown state with a seven-qubit quantum channel schemes, our scheme has the advantages of consuming fewer classical resources, possessing higher intrinsic efficiency and lessening the difficulty of necessary operations.

5 Summary

In summary, we have revisited and improved the scheme proposed by Min Li et al. for teleporting a five-qubit state using seven-qubit quantum channels with a seven-qubit joint measurement. Considering the feasibility of this scheme, we only employ some simple operations such as single-qubit quantum logic gates, single-qubit measurements and CNOT [35] gates. All these operations are feasible in experiments and our scheme demonstrates a higher efficiency than before. Hence, we improve the previous scheme in a relatively simple way. With the development of quantum communication technology, we hope that it will be actually implemented in labs in the future.