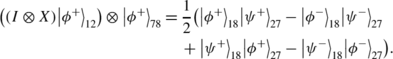1 Introduction

Secret sharing is one of the useful tools in the cryptographic application field, which was firstly introduced by Blakely [1] and Shamir [2], respectively. It is a method to transmit the information but not being lost, destroyed, modified or into wrong hand. The main idea of secret sharing is to divide a secret into many shares such that only enough shares collaborate together can recover the secret.

With the development of quantum information processing, people began to consider the quantum secrete sharing (QSS). In 1999, Hillery et al. [3] proposed an original QSS for sharing a private key with three-particle and four-particle entangled Greenberger-Horne-Zeilinger (GHZ)states. Since then, a lot of QSS protocols [4–9] have been proposed, and the cryptanalysis of QSS has also attracted much attention [10, 11].

Recently, Shi et al. [13] proposed a multiparty quantum secret sharing protocol with Bell states and Bell measurement. In their scheme, only the dealer need to prepare EPR pairs and the agents just need to perform Bell measurement respectively, without performing any unitary operation to obtain the secret. This is more convenient than sharing an arbitrary two-qubit state in practical application [12], since EPR pairs are easily generated than GHZ states.

Unfortunately, Wang et al. [14, 15] pointed out that this QSS scheme was not secure if there are two dishonest agents. Since the EPR pairs are entangled, and there must exist two agents who possess the particles which are entangled with the particles in the dealer’s hand, and can collude to steal the dealer’s secret without the help of the other agents. For example, suppose the four parties are Alice, Bob1, Bob2, Bob3, where Alice is the sender and Bob i (i=1,2,3) are the three agents. Alice shares 4 EPR pairs |ϕ +〉12⊗|ϕ +〉34⊗|ϕ +〉56⊗|ϕ +〉78 with three agents. Assume that Alice holds two particles 1 and 8, and sends the two particles 2 and 3, 4 and 5, 6 and 7 to Bob i (i=1,2,3), respectively. Since

and

so, we can get that Bob1 can infer Bob2’s measurement outcome according to the correlation between the qubits 3, 6 and 4, 5, and Bob3 can easily infer Alice’s measurement outcome according to the correlation between the qubits 1, 8, and 2, 7. Accordingly, Bob1 and Bob3 can infer Alice’s key if they cooperate. if Bob1 and Bob3 are dishonest, It is evident that this attack doesn’t introduces any error since it happens after Alice’s eavesdropping check. Therefore, Bob1 and Bob3 can collaborate to infer Alice’s key without being detected in this four-party protocol and the scheme is not secure. At the same time, L. Joson [16] presented an enhancement of that scheme, which based on the idea that all agents possess two photons to share two classical bits, and an inside attack is prevented.

In this paper, we propose an another scheme to avoid that attack, and even there is only one dishonest agent, the probability of not being detected is less than Shi et al.’s protocol. Besides, after the communication, the particles owned by all parties are still entangled, thus they can be reused.

2 Theoretical Foundation of Multiparty Quantum Secret Sharing with Bell States

Before describing our scheme, we give a brief review about four Bell states and Pauli matrices.

Four Bell states are defined as follows:

then {|ϕ +〉,|ϕ −〉,|ψ +〉,|ψ −〉} forms an orthonormal basis for ℂ4.

Four Pauli matrices are defined as follows:

which are the Hermitian unitary matrix, and {I,X,Y,Z} is an orthonormal basis for M 2.

In this part, we introduce the relationship of all participants’ measure results. We consider four-party QSS Scheme. Suppose they are Alice, Bob1, Bob2, Bob3, where Alice is the sender and Bob i (i=1,2,3) are the agents. Alice shares 4 EPR pairs |ϕ +〉12⊗|ϕ +〉34⊗|ϕ +〉56⊗|ϕ +〉78 with three agents. Assume that Alice holds two particles 1 and 8, and sends the two particles 2 and 3, 4 and 5, 6 and 7 to Bob i (i=1,2,3), respectively.

Firstly, we described the relationship of primary scheme [13] in mathematics as follows:

Theorem 2.1

Define A:ℂ6→ℂ6 and B:ℂ4→ℂ4 by

Then A and B are unitary operators such that

$$(B\otimes B\otimes B) A\bigl(\bigl |\phi^{+}\bigr \rangle _{12}\otimes \bigl |\phi^{+}\bigr \rangle _{34}\otimes \bigl |\phi^{+}\bigr \rangle _{56}\bigr) =\sum_{k=1}^{16}\varepsilon_i \bigl(|a_{k}\rangle|b_{k}\rangle |c_{k}\rangle\bigr), $$

and |a k 〉=|b k 〉⊕|c k 〉 (mod 2), where ε i ∈{−1,1},|a k 〉,|b k 〉,|c k 〉∈{|00〉,|01〉,|10〉,|11〉} (k=1,2,…,16).

Therefore, the sender’s information can be uniquely deduced by all agents without any announcement. In this paper, we add an operator perform in the scheme, and the possible relationships of their measurement results can be show in the following:

Theorem 2.2

Define A:ℂ8→ℂ8 and B:ℂ4→ℂ4 by

Then A and B are unitary operators. Moreover, put

$$|\varPsi \rangle := \bigl |\phi^{+}\bigr \rangle _{12}\otimes \bigl |\phi^{+}\bigr \rangle _{34}\otimes \bigl |\phi^{+}\bigr \rangle _{56}\otimes \bigl |\phi^{+}\bigr \rangle _{78}. $$

Then for every T∈{I,X,iY,Z} (I,X,Y,Z are Pauli matrices), we have

$$ B^{\otimes^4}\bigl(I^{\otimes^2}T^{\otimes^2}I^{\otimes^4}\bigr)A|\varPsi \rangle =\sum _{i=1}^{64}\varepsilon_i|e_i\rangle _{18}|f_i\rangle _{23}|g_i\rangle _{45}|h_i\rangle _{67}, $$
(1)

where ε i ∈{−1,1},|e i 〉18,|f i 〉23,|g i 〉45,|h i 〉67∈{|00〉,|01〉,|10〉,|11〉}, which satisfies

$$|e_i\rangle _{18}=|f_i\rangle _{23}\oplus|g_i\rangle _{45}\oplus|h_i\rangle _{67}\quad (1\leq i\leq 64). $$

(The proof is presented in the Appendix.)

3 Review of Shi et al.’s Multiparty QSS Protocol

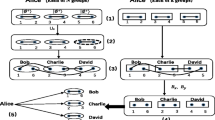
In this section, we give a brief review of Shi et al.’s protocol [13]. A four-party QSS scheme in detail is described as follows (see also Figs. 1, 2, 3, 4):

Fig. 1
figure 1

Alice prepares 4N EPR pairs |ϕ +〉, and performs entanglement swapping

Full size image
Fig. 2
figure 2

Alice prepares six checking sets of sample particles randomly, and inserts them into \(S_{B_{1}}\), \(S_{B_{2}}\), \(S_{C_{1}}\), \(S_{C_{2}}\), \(S_{D_{1}}\), \(S_{D_{2}}\) in random position, respectively

Full size image
Fig. 3
figure 3

Alice holds \(S_{A_{1}}\), \(S_{A_{2}}\), and sends \(S_{B_{1}^{\prime}}\), \(S_{B_{2}^{\prime}}\) , \(S_{C_{1}^{\prime}}\) \(S_{C_{2}^{\prime}}\) , \(S_{D_{1}^{\prime}}\), \(S_{D_{2}^{\prime}}\) to Bob i (i=1,2,3), respectively

Full size image
Fig. 4
figure 4

Each measurement result defines the classical information, and they have the relationship

Full size image

(1) Alice prepares 4N EPR pairs, which are divided into N groups, and each group has three EPR pairs in the same Bell states |ϕ +〉 (i.e. |ϕ −〉, |ψ +〉, |ψ −〉). Moreover, Alice further divides these EPR particles into eight sequences:

which are denoted as \(S_{A_{1}}\), \(S_{A_{2}}\), \(S_{B_{1}}\), \(S_{B_{2}}\), \(S_{C_{1}}\), \(S_{C_{2}}\), \(S_{D_{1}}\) and \(S_{D_{2}}\), respectively.

(2) Alice prepares six checking sets \(R_{B_{1}}\), \(R_{B_{2}}\), \(R_{C_{1}}\), \(R_{C_{2}}\), \(R_{D_{1}}\) and \(R_{D_{2}}\)of sample particles randomly from \(\{|0\rangle,|1\rangle,|+\rangle=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle) ,|-\rangle=\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)\}\). Then Alice inserts these samples randomly into \(S_{B_{1}}\), \(S_{B_{2}}\), \(S_{C_{1}}\), \(S_{C_{2}}\), \(S_{D_{1}}\), \(S_{D_{1}}\) in random position, respectively. The new sequences are denoted as \(S_{B_{1}^{\prime}}\), \(S_{B_{2}^{\prime}}\), \(S_{C_{1}^{\prime}}\), \(S_{C_{2}^{\prime}}\), \(S_{D_{1}^{\prime}}\), \(S_{D_{2}^{\prime}}\), respectively.

(3) Alice sends \(S_{B_{1}^{\prime}}\), \(S_{B_{2}^{\prime}}\), \(S_{C_{1}^{\prime}}\), \(S_{C_{2}^{\prime}}\), \(S_{D_{1}^{\prime}}\), \(S_{D_{2}^{\prime}}\) to Bob i (i=1,2,3), and retains the remaining sequences \(S_{A_{1}}\), \(S_{A_{2}}\).

(4) After confirming that Bob i (i=1,2,3) have received the two sequences. Alice announces the positions and the measurement bases of sample particles \(S_{B_{1}^{\prime}}\), \(S_{B_{2}^{\prime}}\) to Bob1, \(S_{C_{1}^{\prime}}\), \(S_{C_{2}^{\prime}}\) to Bob2, and \(S_{D_{1}^{\prime}}\), \(S_{D_{2}^{\prime}}\) to Bob3. Bob i (i=1,2,3) measure the corresponding checking sets and tell Alice their measurement results, respectively. Alice analyzes the security of the transmissions. If the error rate is hight than the threshold determined by the channel noise, Alice terminates this scheme and restarts, or else they continue to the next step.

(5) Alice, Bob1, Bob2 and Bob3 measure the jth (j=1,2,…,N) two-particle pair (P j (A 1),P j (A 2)), (P j (B 1),P j (B 2)), (P j (C 1),P j (C 2)), and (P j (D 1),P j (D 2)) respectively. There are four kinds of measurement result in Bell states. Each measurement result defines the two bits of classical information: “00” if the result is |ϕ +〉, “01” if it is |ϕ −〉, “10” if it is |ψ +〉, “11” if it is |ψ −〉. Then Alice, Bob1 Bob2 and Bob3 can transform their measured result sequences to classical bits strings K A ,K 1,K 2 and K 3, where K A is the key of Alice, and K i is the shared key of Bob i (i=1,2,3,), respectively. Then Bob i (i=1,2,3) can collaborate to infer Alice’s key, since K A ,K 1, K 2 and K 3 satisfy the relationship: K A =K 1⊕K 2⊕K 3 (mod 2).

4 An Improved Multiparty Quantum Secret Sharing with Bell States and Bell Measurement

Now, we give the detail steps of our QSS scheme with Four-party in the following (see also Fig. 5):

Fig. 5
figure 5

Before the second step, we add a unitary transformation T

Full size image

(1) Alice prepares 4N EPR pairs \(|\phi^{+}\rangle=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)\), which are divided into N groups, and each group has four EPR pairs: |ϕ +〉12, |ϕ +〉34, |ϕ +〉56, |ϕ +〉78. Then she divides these particles into eight sequences:

where P j (1)=P j (2)=(a 1,a 2,…,a 16),a 1=a 2=a 3=a 4=a 5=a 6=a 7=a 8=|0〉, others are |1〉, P j (3)=P j (4)=(b 1,b 2,…,b 16),b 1=b 2=b 3=b 4=b 9=b 10=b 11=b 12=|0〉, others are |1〉, P j (5)=P j (6)=(c 1,c 2,…,c 16),c 1=c 2=c 5=c 6=c 9=c 10=c 13=c 14=|0〉, others are |1〉, P j (7)=P j (8)=(d 1,d 2,…,d 16),d 1=d 3=d 5=d 7=d 9=d 11=d 13=d 15=|0〉, others are |1〉, (j=1,2,…,N).

(2) Alice chooses an operator T from {I,X,Z,iY,} randomly, and transforms P j (2)⊗P j (3) to P j (2∗)⊗P j (3∗) (j=1,2,…,N), where, P j (2∗)⊗P j (3∗)=(T⊗T)(P j (2)⊗P j (3)) (j=1,2,…,N). Then S 2 and S 3 are transformed into \(S_{2}^{*}\) and \(S_{3}^{*}\), while the others are unchanged.

(3) Alice prepares six sets of particles as well which are sufficient for statistical analysis of eavesdropping as the sample sets and stems randomly from {|0〉,|1〉,|+〉,|−〉}. Then Alice inserts these samples randomly into \(S_{2}^{*},S_{3}^{*},S_{4},S_{5},S_{6},S_{7}\), respectively, each sample particle is distributed in a random position. The new sequences are denoted as \(S_{2}^{\clubsuit}, S_{3}^{\clubsuit},S_{4}^{\clubsuit},S_{5}^{\clubsuit},S_{6}^{\clubsuit },S_{7}^{\clubsuit}\), and Alice makes a record of the insertion positions.

(4) Alice sends \(S_{2}^{\clubsuit},S_{3}^{\clubsuit}\) to Bob1, \(S_{4}^{\clubsuit},S_{5}^{\clubsuit}\) to Bob2,\(S_{6}^{\clubsuit},S_{7}^{\clubsuit}\) to Bob3, and retains the remaining sequences S 1,S 8, Alice has to confirm that each agent has actually received two sequences via classical communication.

(5) After being notified when Bob i (i=1,2,3) has received the two sequences, respectively. Alice announces the positions of the sample particles. Bob i (i=1,2,3) choosing measurement basis {|0〉,|1〉} or {|+〉,|−〉} randomly, measure the sample particles according to Alice’s announcement and tell Alice measurement basis and measurement results, respectively. Alice compares the measurement results of the agents with the initial states of the particles in the samples sets and analyzes the security of the transmissions. If the error rate is hight than the threshold determined by the channel noise, Alice terminates this scheme and restarts, or else they continue to the next step.

(6) Alice, Bob1, Bob2 and Bob3 measure the jth (j=1,2,…,N) two-particle pair (P j (1)⊗P j (8)),(P j (2)⊗P j (3)),(P j (4)⊗P j (5)), and (P j (6)⊗P j (7)), respectively. Each measurement result defines the two bits of classical information: “00” if the result is |ϕ +〉, “01” if it is |ϕ −〉, “10” if it is |ψ +〉, “11” if it is |ψ −〉. Then Alice, Bob1, Bob2, Bob3 can transform their measured result sequences to classical bits strings K A ,K 1,K 2, K 3 where K A is the key of Alice, and K i is the shared key of Bob i (i=1,2,3), respectively. Then Bob i (i=1,2,3) can collaborate to infer Alice’s key, since K A ,K 1,K 2 and K 3 satisfy the relationship: K A =K 1⊕K 2⊕K 3 (mod 2).

Remark

In step (2), if Alice chooses the operator T to perform P j (6)⊗P j (7) (j=1,2,…,N), this is considered the same. That is, as long as Alice perform a agent’s two-particles which have one entangled with the sender’s, the scheme is believed the same.

In the following, we generalize this four-party QSS scheme into n-party case. Suppose they are Alice, Bob1, Bob2, Bob3,…,Bob n−1, Alice is the sender and Bob i , (i=1,2,…,n−1) are agents. The multiparty QSS can be described as following:

(1) Alice prepares nN EPR pairs \(|\phi^{+}\rangle=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)\), which are divided into N groups, and each group has n EPR parties: |ϕ +〉12, |ϕ +〉34,…,|ϕ +〉2n−1,2n . Then she divided these particles into 2n sequences:

(2) Alice chooses operator from {I⊗I,X⊗X,Z⊗Z,iY⊗iY,} randomly,and transform P j (2)⊗P j (3) to P j (2∗)⊗P j (3∗) (j=1,2,…,N) , then S 2 and S 3 are transmitted into \(S_{2}^{*}\) and \(S_{3}^{*}\), while the rest unchanged.

(3) Alice prepares 2n−2 sets of particles which are sufficient for statistical analysis of eavesdropping as the sample sets and selected randomly from {|0〉,|1〉,|+〉,|−〉}. Then Alice inserts these samples randomly into \(S_{2}^{*},S_{3}^{*},S_{4},\ldots,S_{2n-2},S_{2n-1}\), respectively, each sample particle is distributed in a random position. The new sequences are denoted as \(S_{2}^{\clubsuit}\), \(S_{3}^{\clubsuit}, \ldots, S_{2n-2}^{\clubsuit}\), \(S_{2n-1}^{\clubsuit}\), and Alice makes a record of the insertion positions and the measurement basis of the sample particles.

(4) Alice sends \(S_{2}^{\clubsuit},S_{3}^{\clubsuit}\) to Bob1, \(S_{4}^{\clubsuit},S_{5}^{\clubsuit}\) to \(\mathrm{Bob}_{2}, \ldots, S_{2n-2}^{\clubsuit}\), \(S_{2n-1}^{\clubsuit}\) to Bob n−1, and retains the remaining sequences S 1,S 2n , Alice has to confirm that each agent has actually received two sequences via classical communication.

(5) Alice being notified that Bob i (i=1,2,…,n−1) has received the two sequences respectively announces the positions of the sample particles. Bob i (i=1,2,3) choosing measurement basis {|0〉,|1〉} or {|+〉,|−〉} randomly, measure the sample particles according to Alice’s announcement and tell Alice measurement basis and measurement results, respectively. Alice compares the measurement results of the agents with the initial states of the particles in the samples sets and analyzes the security of the transmissions. If the error rate is hight than the threshold determined by the channel noise, Alice terminates this scheme and restarts, or else they continue to the next step.

(6) Alice, Bob1, Bob2,…,Bob n−1 measure the jth (j=1,2…,N) two-particle pair (P j (1)⊗P j (2n)),(P j (2)⊗P j (3)),…,(P j (2n−2)⊗P j (2n−1)) with Bell basis, respectively. Each measurement result with Bell basis defines the two bits of classical information: “00” if the result is |ϕ +〉, “01” if it is |ϕ −〉, “10” if it is |ψ +〉, “11” if it is |ψ −〉. Then Alice, Bob1, Bob2,…,Bob n−1 can transform their measurement result sequences to classical bits strings K A ,K 1, K 2,…,K n−1 where K A is the key of Alice, and K i is the shared key of Bob i (i=1,2,…,n−1), respectively. Then Bob i (i=1,2,…,n−1) can collaborate to infer Alice’s key, since K A ,K 1,K 2,…,K n−1 satisfy the relationship: K A =K 1⊕K 2⊕⋯⊕K n−1 (mod 2).

5 Security Analysis

Now we begin to analyze the security of the present scheme. We take the four-party QSS scheme for the case. As mentioned in [12, 13], a dishonest agent has more power to attack than an outside eavesdropper, since he knows partial information legally and tells a lie in the detected proceeding to avoid introducing errors, so our main goal is to prevent the dishonest agents in QSS protocol from finding the secret without other agents. In other word, if all dishonest agents fail to cheat in a QSS scheme, then the scheme is said to be secure.

Suppose there are dishonest agents and they can intercept the particle sequences transmitted from Alice to other agents and resend the fake sequences prepared by themselves to the other agents. Thus they can get the initial particles S i (i=2,3,…,7), after Alice announcing the positions of sample particles, then they can get the information of Alice. But in step (3), Alice inserts randomly some samples in the transmitted sequences, requires the agents to measure them later and checks their measurement results. In fact, the dishonest agents don’t know the sample particles and their positions in the transmitted sequences. therefore whatever fake sequences prepared by dishonest agents, they all bring the error, since each sample particle is randomly selected in four states {|0〉,|1〉,|+〉,|−〉}. Besides in step (5), each agent selects measurement basis randomly to measure the sample sets, so the successful probability is less than \((\frac{1}{4}\times\frac{1}{2})^{m}\), where m is the number of the sample particles in each sequences transmitted to other agent. That is less than the Shi et al.’s QSS protocol.

Furthermore, we analyze the two dishonest agents:

If Bob1 and Bob2 are dishonest or Bob3 and Bob2 are dishonest. Since Bob2 received the particles 4 and 5, they have no relation with Alice’s particles 1 and 8. So the two agents collusion attack get no information about Alice’s ,thus the scheme is secure.

If Bob1 and Bob3 are dishonest. As the particle 2 owned by Bob1 and the particle 7 owned by Bob3 are entangled with the particles 1 and 8 of Alice’s.

In the step (2), Alice performed the particle 2 in P i (2) (i=1,2,…,N) by operator from {I,X,iY,Z}, randomly.

  1. (i)

    When I was selected, for 1≤j≤ N:

  2. (ii)

    When X was selected, for 1≤j≤ N:

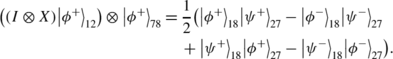
  3. (iii)

    When iY was selected, for 1≤j≤ N:

  4. (iv)

    When Z was selected, for 1≤j≤ N:

Since the operator is randomly in one of four operators {I,X,iY,Z}, the probability of right information deduced by Bob1 and Bob3 is \((\frac{1}{4})^{N}\). where N is the number of groups in the first step, therefore, the present scheme is secure for two dishonest agents.

6 Conclusion

To summarize, we present a multiparty QSS scheme suing entanglement swapping theory and we analyze its security. In this scheme, all agents are not required to prepared entangled states or perform any unitary operation, and the sender check the security only need the agents’ measure results. After the communication, all participants’ particles are entangled and they can be reused.