1 Introduction

Quantum dense coding, originally proposed by Bennett et al. [1] and experimentally realized by Mattle et al. [2], allows each quantum state to carry more than one-bit classical information by using of local operations and entanglement states. Due to its potential applications in the realm of quantum information, dense coding has acquired lots of attention recently, and some theoretical and experimental progresses [3,4,5,6,7,8,9,10,11] have been made in this domain. In 2001, Hao et al. [12] put forward a controlled dense coding scheme using the Greenberger-Horne-Zeilinger (GHZ) state, where the sender can transmit classical information to the receiver, and the supervisor can control the average amount of information by a local measurement. Since that, various schemes for controlled dense coding have been proposed by using of different states. For instance, Huang et al. [13] and Ye et al. [14] explore how to perform controlled dense coding scheme with GHZ state and W state, which are two important types of entangled state for controlled quantum dense coding, and some methods to construct these kinds of entanglement channel are presented in different physical system [15,16,17,18,19,20,21,22]. A scheme for controlled dense coding via a non-symmetric quantum entangled channel is proposed by Liu et al. [23]. Moreover, Nie et al. [24] present an efficient scheme for implementing controlled dense coding by using of the cluster state. Nevertheless, there are also many important and open subjects to be taken into account for controlled dense coding.

In this paper, we propose a four-parties controlled dense coding scheme using the four-qubits maximal slice state, which belongs to partially entangled states. The concrete implementation processes for our proposal with one sender, one receiver and two supervisors are given in detail. One of the two supervisors can make use of the four-qubits partially entangled states to obtain the three-qubits maximally entangled GHZ state via a special measurement, relative to the coefficients of quantum channel. The other supervisor can control the average amount of classical information transmitted from the sender to the receiver by a local measurement. Thus, the two controllers play distinct roles in our scheme for controlled dense coding. Moreover, the total average amount of information does not depend on the superposition factors of quantum channel. Additionally, the physical realization of this proposal is discussed using optical elements, and our results show that this proposal could be applicable in the future.

The rest of this paper are organized as follows: In Section 2, we propose a new scheme to realize controlled dense coding with multi-parties via the four-qubits maximal slice state. The concrete implementation processes of this scheme are elaborated, and the average transmitted classical information is calculated. The physical realization of our scheme is discussed in the optical experiments. in Section 3. The paper concludes with Section 4.

2 Dense Coding via Maximal Slice States

Let us begin with a brief statement of dense coding using two-qubit maximally entangled states. Suppose that the sender Alice and the receiver Bob initially share the following Bell state

$$ |{\Psi}^{+}\rangle= 1/\sqrt{2} (|00\rangle+|11\rangle) $$
(1)

Without loss of generality, the first particle belongs to Alice, while the second particle belongs to Bob. Locally operating on her qubit by one of gates {I, σ z , σ x , iσ y } where I is the identity operator and σx, y, z are three Pauli operators, Alice can obtain one of the four orthogonal Bell states

$$\begin{array}{@{}rcl@{}} \mathbf{I}\otimes \mathbf{I}\cdot|{\Psi}^{+}\rangle= 1/\sqrt{2} (|00\rangle+|11\rangle)=|{\Psi}^{+}\rangle \rightarrow 00&&\\ \sigma_{z}\otimes \mathbf{I}\cdot|{\Psi}^{+}\rangle= 1/\sqrt{2} (|00\rangle-|11\rangle)=|{\Psi}^{-}\rangle \rightarrow 01&&\\ \sigma_{x}\otimes \mathbf{I}\cdot|{\Psi}^{+}\rangle= 1/\sqrt{2} (|01\rangle+|10\rangle)=|{\Phi}^{+}\rangle \rightarrow 10&&\\ i\sigma_{y}\otimes \mathbf{I}\cdot|{\Psi}^{+}\rangle= 1/\sqrt{2} (|01\rangle-|10\rangle)=|{\Phi}^{-}\rangle \rightarrow 11&&\end{array} $$
(2)

In order to realize dense coding, Alice sends her particle to Bob. By making the Bell measurement, Bob is able to obtain two bits of classical information. For instance, if Alice want to send ‘01’, then she applies σ z on her particle, and Bob can determine |Ψ−〉12 via the Bell measurement. Hence, Alice, interacting with only single qubit, can transmit two bits of classical information to Bob.

The purpose of this section is to give a novel scheme to send classical information to Bob controlled by the two supervisors Charlie and Cliff via one partially four-qubits entangled state, which in this paper can be presented as

$$ |MS\rangle_{1234}= 1/\sqrt{2} (|0000\rangle+a|1110\rangle+b|1111\rangle)_{1234} $$
(3)

here |a|2 + |b|2 = 1 is satisfied by the real numbers a and b. The subscript 1, 2, 3 and 4 denote the particles belong to Alice, Bob, Charlie and Cliff, respectively. This kind of states was also known as the maximal slice state in Ref. [25, 26]. If b = 0, particles 4 would be unentangled with other particles, and the resulting state is the maximally four-qubits entangled GHZ state when |b| = 1. For all other values of b, the four qubits are partially entangled. As a matter of fact, it is noting that this kind of partially four-particles entangled quantum channel can be used to realize controlled dense coding. Moreover, the detailed processes of our proposal are elaborated as follows

Step One

The partially four-particles entangled state given by (3) can be rewritten as

$$\begin{array}{@{}rcl@{}} |MS\rangle_{1234}=&&\frac{\sqrt{(1+a)^{2}+b^{2}}}{2}\cdot|x^{+}\rangle_{4}\cdot|GHZ\rangle_{123}\\ &&+\frac{\sqrt{(1-a)^{2}+b^{2}}}{2}\cdot|x^{-}\rangle_{4}\cdot(\sigma_{z}\otimes I\otimes I)\cdot|GHZ\rangle_{123} \end{array} $$
(4)

where

$$\begin{array}{@{}rcl@{}} &&|GHZ\rangle= 1/\sqrt{2}(|000\rangle+|111\rangle) \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} &&|x^{\pm}\rangle=\frac{1\pm a}{\sqrt{(1\pm a)^{2}+b^{2}}}|0\rangle+\frac{\pm b}{\sqrt{(1\pm a)^{2}+b^{2}}}|1\rangle \end{array} $$
(6)

This structure of |MS〉1234 as a superposition of GHZ state makes it can be used for perfect controlled teleportation [26] and controlled remote state preparation [27].

From (4–6), one can find that if Cliff measures particle 4 in the orthogonal basis {|x+〉,|x−〉}, particles 1, 2 and 3 will be left with one of the two maximally entangled states {|GHZ〉,(σ z ⊗ I ⊗ I) ⋅|GHZ〉} depending on Cliff’s measurement outcome. Subsequently, Cliff informs Alice of the measurement results. If the measurement outcome is |x−〉, Alice performs σ z on her particle. Then the maximally three-particles entangled GHZ state can be obtained from the partially four-particles entangled state |MS〉.

Step Two

The second controller Charlie measures his particle 3 under the following basis

$$\begin{array}{@{}rcl@{}} |+\rangle=\cos\theta|0\rangle+\sin\theta|1\rangle, \quad |-\rangle=\sin\theta|0\rangle-\cos\theta|1\rangle \end{array} $$
(7)

here 𝜃 is the measured angle with the region 0 ≤ 𝜃 ≤ π/4. Thus the GHZ state given by (5) can be rewritten as

$$\begin{array}{@{}rcl@{}}\ |GHZ\rangle_{123}=\frac{1}{\sqrt{2}} [ |+\rangle_{3}\cdot|\psi^{+}\rangle_{12}+|-\rangle_{3}\cdot|\phi^{-}\rangle_{12} ] \end{array} $$
(8)

where

$$\begin{array}{@{}rcl@{}} &&|\psi^{+}\rangle=\cos\theta|00\rangle+\sin\theta|11\rangle \end{array} $$
(9)
$$\begin{array}{@{}rcl@{}} &&|\psi^{-}\rangle=\sin\theta|00\rangle-\cos\theta|11\rangle \end{array} $$
(10)

The measurement outcome of particle 3 would be |+〉3 or |−〉3 with the equal probability 1/2.

Step Three

Let us analyze here the case in which particle 3 is under the state |+〉3; the case of |−〉3 can be treated in a similar way. From the measurement outcome |+〉3, Alice has the information that she shares the general entangled state |ψ+〉12 with Bob, whereas Bob does not know this. Then Alice introduces an auxiliary particle m with the initial state |0〉 m , and performs the following unitary operation on particles 1 and m

$$ U(1,m)=\left( \begin{array}{cccc} \frac{\sin\theta}{\cos\theta} & -\sqrt{1-\frac{\sin^{2}\theta}{\cos^{2}\theta}} & 0 & 0 \\ \sqrt{1-\frac{\sin^{2}\theta}{\cos^{2}\theta}} & \frac{\sin\theta}{\cos\theta} & 0 & 0 \\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{array} \right) $$
(11)

Subsequently, |ψ+〉12 ⊗|0〉 m would be shown as

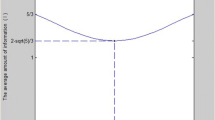
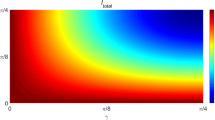
$$\begin{array}{@{}rcl@{}} &&U(1,m)|\psi^{+}\rangle_{12}\otimes|0\rangle_{m} \\ &&=\sqrt{2}\sin\theta\cdot\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)_{12}\otimes|0\rangle_{m}-\sqrt{1-2\sin^{2}\theta}|00\rangle_{12}\otimes|1\rangle_{m} \end{array} $$
(12)

When particle m is |0〉 m , it is noting that we can use the maximally Bell state to realize the dense coding in the standard way [1], and 2 bits of classical information would be transmitted. If Alice obtains |1〉 m , Bob can extract only 1 bit of information [12]. Thus the average classical information are transmitted from Alice to Bob is

$$\begin{array}{@{}rcl@{}} I_{total}&&=I\left[ |\psi^{+}\rangle_{12}\right]+I\left[ |\psi^{-}\rangle_{12}\right]= 2 I\left[ |\psi^{+}\rangle_{12}\right] \\ &&= 2\cdot\left( \frac{1}{\sqrt{2}}\right)^{2}\cdot\left[ 2\cdot2\sin^{2}\theta+ 1\cdot(1-2\sin^{2}\theta) \right]= 2\sin^{2}\theta+ 1 \end{array} $$
(13)

Hence one can get that the equation I t o t a l = 2 bits is satisfied on condition that 𝜃 = π/4, namely, when Charlie measures particle 3 under the basis \(\{|\pm \rangle = 1/\sqrt {2}(|0\rangle \pm |1\rangle )\}\), the classical information becomes 2 bits. This result is in agreement with the classical information in Refs. [1, 2, 12].

3 The Physical Realization Using the Linear Optics

As a matter of fact, many theoretical protocols for quantum information processing [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48] have been presented, especially some ones have been experimentally realized with the use of linear optics [49,50,51,52]. In the following, we will discuss the physical realization of this new proposal based on linear optical elements.

To obtain the four-qubits maximal slice state given by (3), we design a quantum circuit with the initial input |0000〉1234, shown in Fig. 1. With the dot ‘•’ denoting the control qubit, the control-NOT (CNOT) gate U C takes the form of the following 4 × 4 matrix

$$ U_{C}=\left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array} \right), H=\frac{1}{\sqrt{2}}\left( \begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array} \right), U_{1}^{+}=\left( U_{1}^{-}\right)^{\dag}=\left( \begin{array}{cc} \frac{\sqrt{2 + 2b}}{2} & \frac{ a}{\sqrt{2 + 2b}} \\ \frac{-a}{\sqrt{2 + 2b}} & \frac{\sqrt{2 + 2b}}{2} \end{array} \right) $$
(14)

H is the Hadamard operation, and \(U_{1}^{\pm }\) can determined by the parameters a and b, shown as (3). Due to the unitary operations H, U C and \(U_{1}^{\pm }\), we can obtain the desired maximal slice state.

Fig. 1
figure 1

A sketch for obtaining the four-qubits maximal slice state |MS〉1234 from the initial state |0000〉1234. The Hadamard operation H, CNOT gate U C and single-qubit unitary gates \(U_{1}^{\pm }\) are gived by (14). The time evolution goes from left to right

Full size image

It is noting that the two-qubit unitary transformation U(1, m), given by (11), needs to be introduced for our proposal. Moreover, it can be verified that U(1, m) could be performed via the CNOT gate U C and some single-qubit unitary operations together, and could be rewritten as

$$\begin{array}{@{}rcl@{}} U(1,m)=(\sigma_{x}\otimes U^{+}_{2})\cdot U_{C}\cdot(\textbf{I}\otimes U^{-}_{2})\cdot U_{C}\cdot(\sigma_{x}\otimes\textbf{I}) \end{array} $$
(15)

where the single-qubit unitary operation \(U^{\pm }_{2}\) are given by

$$\begin{array}{@{}rcl@{}} U_{2}^{+}=\left( U_{2}^{-}\right)^{\dag}= \left( \begin{array}{rr} \sqrt{\frac{\cos\theta+\sin\theta}{2\cos\theta}} & -\sqrt{\frac{\cos\theta-\sin\theta}{2\cos\theta}} \\ \sqrt{\frac{\cos\theta-\sin\theta}{2\cos\theta}} & \sqrt{\frac{\cos\theta+\sin\theta}{2\cos\theta}} \end{array} \right) \end{array} $$
(16)

here the measured angle 𝜃 is given by (7). In fact, the correspondence quantum circuit for U(1, m) could be expressed in Fig. 2.

Fig. 2
figure 2

A sketch of two-qubit unitary operation U(1, m). Particle 1 is on the top line, and particle m is on the bottom one

Full size image

According to the above analyzes, one can find that the single-qubit unitary transformations, including I, σx, y, z, \(U_{1,2}^{\pm }\), and the two-qubit gate U C are necessary for realizing our proposal of controlled dense coding. Fortunately, arbitrary single-qubit operations can be performed via phase shifters and beam splitters together, namely, I, σx, y, z and \(U_{1,2}^{\pm }\) could be implemented with the linear elements [53]. It has been demonstrated experimentally that U C can be achieved probabilistically only via the linear optics [53,54,55]. Furthermore, one may draw support from nonlinearity or QED systems to implement a deterministic photon U C gate [56,57,58,59,60]. A nearly deterministic linear optical U C gate [56] is presented using cross-Kerr nonlinearity. Wang et al. [57,58,59,60] explored how to realize a deterministic photonic U C gate by means of quantum-dot spin in a double-sided optical microcavity. Hence, all of the unitary operations for the novel protocol could be performed in the optical experiments. Consequently, our proposal can be realizable in near future.

4 Conclusions

In summary, we put forward a novel scheme for the four-parties controlled dense coding via partially quantum channel, which is expressed as the four-qubit maximal slice state. The concrete implementation processes for our proposal with one sender, one receiver and two supervisors are given in detail. The two supervisors play distinct roles in our scheme for controlled dense coding, one of them can utilize the partially quantum channel to obtain the three-qubit maximally entangled GHZ state, and the other supervisor can control the average amount of classical information transmitted from the sender to the receiver. Moreover, the physical realization of this proposal is discussed, and our results show that the novel proposal would be performed by using of the optical elements in near future. From the point of the potential applications of dense coding, we believe that our scheme will play an important role in the field of quantum information processing.