1 Introduction

Dense coding [1] is one of the most important applications of quantum entanglement [2], the key resource of quantum information processing [3]. In the standard scheme of dense coding [1], there are two communicating parties that we refer to as Alice and Bob. They initially share an entangled pair of qubits. Alice first performs a quantum operation on her qubit to encode 2 bits of information into the entangled pair. Then she sends her qubit to Bob through a quantum channel. After receiving Alice’s qubit, Bob manipulates on both qubits of the entangled pair to decode 2 bits of information. Thus, Alice has transmitted 2 bits of information to Bob by sending only 1 qubit.

Many aspects of dense coding have been studied. Among these are generalizations to non-maximally entangled pairs [4–6], to high dimensional quantum systems [6–9], to multi-qubit entangled pairs [7–18], to deterministic dense coding [19–24], to controlled dense coding [25–28], and to simultaneous dense coding [29].

Recently, Di Franco and Ballester investigated teleportation [30] in the case that the receiver’s conditional operations that he needs to perform on his/her qubit, in order to reconstruct the original state to be teleported, is imperfect. They found that an optimization of the teleportation fidelity can be performed by properly replacing the Bell basis in the measurement with an orthogonal non-maximally entangled basis [31].

Teleportation and dense coding are closely related [5, 32]. These two protocols both use entanglement resource between a sender Alice and a receiver Bob. In the teleportation protocol, Alice performs a Bell basis measurement while Bob performs a recovery operation. In the dense coding protocol, Alice performs an encoding operation while Bob performs a Bell basis measurement.

In this paper, we investigate dense coding in the case that Alice’s encoding operations are imperfect. In our model, the result of an imperfect operation is described as the action of a quantum noise process on the output state of the perfect operation. We consider four kinds of quantum noise processes: the depolarizing channel, the bit flip channel, the phase flip channel, and the bit-phase flip channel. We show the relation among the average probability of decoding the correct information, the non-maximally entangled state, the imperfect encoding operations, and the receiver’s measurement basis. We also give Bob’s orthogonal non-maximally entangled measurement basis which maximizes the probability of decoding the correct information.

The remainder of the paper is organized as follows. In Sect. 2, we first describe our model for the non-maximally entangled pairs, imperfect encoding operations and measurement bases. In Sect. 3, Sect. 4, Sect. 5, Sect. 6, we use four kinds of quantum noise processes to describe the imperfect encoding operations. Section 7 is a brief conclusion.

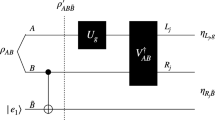
2 Model

In this section, we give the formal description of the entanglement resource, Alice’s imperfect encoding operations, and Bob’s measurement for our model.

According to the Schmidt decomposition [3], a pure non-maximally entangled pair of 2 qubits can be written as

(1)

where θ∈(0,π/4] is a parameter measuring the amount of entanglement. |ϕ (E)〉 reduces to a Bell state when θ=π/4. In our model, the entangled state initially shared between Alice and Bob is a pseudo-pure state, which is particularly interesting in the context of quantum information processing with nuclear magnetic resonance (NMR) [33–39]. The pseudo-pure state shared between Alice and Bob can be written as

(2)

where δ∈[0,1]. ρ (E) can be interpreted as a statistical mixture in which a fraction δ of the qubits is in the pure state |ϕ (E)〉. ρ (E) reduces to the pure state |ϕ (E)〉 when δ=1.

The four encoding operations that Alice uses to encode 2 bits of information are the Pauli matrices:

(3)

The result of an imperfect encoding operation is described as the action of a quantum noise process on the output state of the perfect operation. A quantum noise process can be characterized in an operator-sum representation

(4)

where σ is a density matrix, {K μ } is the set of Kraus operators, \(\sum K_{\mu}K_{\mu}^{\dag}= I\) [3]. We suppose that each encoding operation V∈{I,Z,X,Y} has different reliability, so their corresponding quantum noise process with Kraus operators \(\{K_{\mu}^{V}\}\) has different parameters. This can be justified by the fact that different operations require different times to be performed [31]. The output state of the encoding operation V is (V⊗I)ρ (E)(V †⊗I), and the state after the quantum noise process is

(5)

After receiving Alice’s qubit, Bob measures both qubits in the following non-maximally entangled orthonormal basis:

(6)

where ϕ,ϕ′∈[0,π/2]. Each measurement result |ϕ V 〉 corresponds to Alice’s encoding operation V. {|ϕ V 〉} V=I,Z,X,Y reduces to the Bell basis when ϕ=ϕ′=π/4. If Alice chooses the encoding operation V according to her information to be encoded, the probability for Bob to decode the correct information is

(7)

and the average probability for Bob to decode the correct information is

(8)

We have given the formal description of the entanglement resource, Alice’s imperfect encoding operations, and Bob’s measurement for our further discussion. For θ=π/4, δ=1, , ϕ=ϕ=π/4, this model is the standard dense coding in the perfect setting.

3 Depolarizing Channel

The depolarizing channel is an important type of quantum noise [3]. Imagine we take a single qubit, and with probability p that qubit is depolarized. That is, it is replaced by the completely mixed state, I/2. With probability 1−p the qubit is left untouched. The state of the quantum system after the noise is

(9)

where p∈[0,1]. In the operator-sum representation, the depolarizing channel has Kraus operators

(10)

Suppose that the parameter p of the depolarizing channel depends on the encoding operation V and is denoted as p V . The state after the imperfect encoding operation V is

(11)

If Alice chooses the encoding operation V according to her information to be encoded, the probability for Bob to decode the correct information is

(12)

For V=I,Z,X,Y, we have

(13)

The average probability for Bob to decode the correct information is

(14)

The optimal values of ϕ and ϕ′ to maximize the value of P (av) is summarized in Table 1.

Table 1 The optimal values of ϕ and ϕ′ to maximize the value of P (av) (Depolarizing channel)
Full size table

In the case where θ=π/4, namely Alice and Bob share a maximally entangled pair, the maximal value of P (av) is reached when ϕ=ϕ′=π/4. That is to say, the Bell measurement is optimal.

In the case where θ≠π/4,p I =p Z and p X =p Y , the maximal value of P (av) is reached when ϕ=ϕ′=π/4. The Bell measurement is optimal.

In the case where θ≠π/4,p I =p Z and p X ≠p Y , the maximal value of P (av) is reached when ϕ=π/4 and tan2ϕ′=[4−2(p X +p Y )]tan2θ/(p X −p Y ).

In the case where θ≠π/4,p I ≠p Z and p X =p Y , the maximal value of P (av) is reached when tan2ϕ=[4−2(p I +p Z )]tan2θ/(p Z −p I ) and ϕ′=π/4.

In the case where θ≠π/4,p I ≠p Z and p X ≠p Y , the maximal value of P (av) is reached when tan2ϕ=[4−2(p I +p Z )]tan2θ/(p Z −p I ) and tan2ϕ′=[4−2(p X +p Y )]tan2θ/(p X −p Y ).

The behavior of P (av) for δ=1,p I =0,p Z =p X =p Y , and for the optimal values of ϕ and ϕ′, against p Z and θ, is presented in Fig. 1.

Fig. 1
figure 1

The behavior of P (av) for δ=1, p I =0, p Z =p X =p Y , and for the optimal values of ϕ and ϕ′, against p Z and θ, in the case where the quantum noise process describing the imperfect encoding operation is a depolarizing channel

Full size image

4 Bit Flip Channel

The bit flip channel flips the state of a qubit from |0〉 to |1〉 (and vice versa) with probability p [3]. The state of the quantum system after the noise is

(15)

where p∈[0,1]. In the operator-sum representation, the bit flip channel has Kraus operators

(16)

Suppose that the parameter p of the bit flip channel depends on the encoding operation V and is denoted as p V . The state after the imperfect encoding operation V is

(17)

If Alice chooses the encoding operation V according to her information to be encoded, the probability for Bob to decode the correct information is

(18)

For V=I,Z,X,Y, we have

(19)

The average probability for Bob to decode the correct information is

(20)

The optimal values of ϕ and ϕ′ to maximize the value of P (av) is summarized in Table 2.

Table 2 The optimal values of ϕ and ϕ′ to maximize the value of P (av) (Bit flip channel)
Full size table

In the case where θ=π/4, namely Alice and Bob share a maximally entangled pair, the maximal value of P (av) is reached when ϕ=ϕ′=π/4. That is to say, the Bell measurement is optimal.

In the case where θ≠π/4,p I =p Z and p X =p Y , the maximal value of P (av) is reached when ϕ=ϕ′=π/4. The Bell measurement is optimal.

In the case where θ≠π/4,p I =p Z and p X ≠p Y , the maximal value of P (av) is reached when ϕ=π/4 and tan2ϕ′=(2−p X −p Y )tan2θ/(p X −p Y ).

In the case where θ≠π/4,p I ≠p Z and p X =p Y , the maximal value of P (av) is reached when tan2ϕ=(2−p I −p Z )tan2θ/(p Z −p I ) and ϕ′=π/4.

In the case where θ≠π/4,p I ≠p Z and p X ≠p Y , the maximal value of P (av) is reached when tan2ϕ=(2−p I −p Z )tan2θ/(p Z −p I ) and tan2ϕ′=(2−p X −p Y )tan2θ/(p X −p Y ).

The behavior of P (av) for δ=1,p I =0,p Z =p X =p Y , and for the optimal values of ϕ and ϕ′, against p Z and θ, is presented in Fig. 2.

Fig. 2
figure 2

The behavior of P (av) for δ=1, p I =0, p Z =p X =p Y , and for the optimal values of ϕ and ϕ′, against p Z and θ, in the case where the quantum noise process describing the imperfect encoding operation is a bit flip channel

Full size image

5 Phase Flip Channel

The phase flip channel flips the sign of |1〉 to give −|1〉 with probability p, and leaves |0〉 unchanged [3]. The state of the quantum system after the noise is

(21)

where p∈[0,1]. In the operator-sum representation, the phase flip channel has Kraus operators

$$ K_1 = \sqrt{1-p} I, \qquad K_2 = \sqrt{p} Z. $$
(22)

Suppose that the parameter p of the phase flip channel depends on the encoding operation V and is denoted as p V . The state after the imperfect encoding operation V is

(23)

If Alice chooses the encoding operation V according to her information to be encoded, the probability for Bob to decode the correct information is

(24)

For V=I,Z,X,Y, we have

(25)

The average probability for Bob to decode the correct information is

(26)

The optimal values of ϕ and ϕ′ to maximize the value of P (av) is summarized in Table 3.

Table 3 The optimal values of ϕ and ϕ′ to maximize the value of P (av) (Phase flip channel or Bit-phase flip channel)
Full size table

In the case where p I +p Z ⩽1 and p X +p Y ⩽1, the maximal value of P (av) is reached when ϕ=ϕ′=π/4. That is to say, the Bell measurement is optimal.

In the case where p I +p Z ⩽1 and p X +p Y >1, the maximal value of P (av) is reached when ϕ=π/4 and ϕ′=0.

In the case where p I +p Z >1 and p X +p Y ⩽1, the maximal value of P (av) is reached when ϕ=0 and ϕ′=π/4.

In the case where p I +p Z >1 and p X +p Y >1, the maximal value of P (av) is reached when ϕ=ϕ′=0.

The behavior of P (av) for δ=1,p I =0,p Z =p X =p Y , and for the optimal values of ϕ and ϕ′, against p Z and θ, is presented in Fig. 3.

Fig. 3
figure 3

The behavior of P (av) for δ=1,p I =0,p Z =p X =p Y , and for the optimal values of ϕ and ϕ′, against p Z and θ, in the case where the quantum noise process describing the imperfect encoding operation is a phase flip channel or a bit-phase flip channel

Full size image

6 Bit-Phase Flip Channel

The bit-phase flip channel is a combination of a bit flip and a phase flip [3]. The state of the quantum system after the noise is

(27)

where p∈[0,1]. In the operator-sum representation, the bit-phase flip channel has Kraus operators

(28)

Suppose that the parameter p of the bit-phase flip channel depends on the encoding operation V and is denoted as p V . The state after the imperfect encoding operation is

(29)

If Alice chooses the encoding operation V according to her information to be encoded, the probability for Bob to decode the correct information is

(30)

The average probability for Bob to decode the correct information is

(31)

Equation (31) is the same as Eq. (26), so the behavior of P (av) is the same as the phase flip channel.

7 Conclusion

In this paper, we have investigated the dense coding process with imperfect encoding operations. We characterize the imperfect encoding operation as the perfect encoding operation followed by the quantum noise process. Four kinds of quantum noise processes have been considered. We have shown the relation among the average probability of decoding the correct information, the non-maximally entangled state, the imperfect encoding operations, and the receiver’s measurement basis. We have gave the receiver’s orthogonal non-maximally entangled measurement basis which maximizes the probability of decoding the correct information.