Controlled Dense Coding Using the Maximal Slice States

Abstract

In this paper we investigate the controlled dense coding with the maximal slice states. Three schemes are presented. Our schemes employ the maximal slice states as quantum channel, which consists of the tripartite entangled state from the first party(Alice), the second party(Bob), the third party(Cliff). The supervisor(Cliff) can supervises and controls the channel between Alice and Bob via measurement. Through carrying out local von Neumann measurement, controlled-NOT operation and positive operator-valued measure(POVM), and introducing an auxiliary particle, we can obtain the success probability of dense coding. It is shown that the success probability of information transmitted from Alice to Bob is usually less than one. The average amount of information for each scheme is calculated in detail. These results offer deeper insight into quantum dense coding via quantum channels of partially entangled states.

1 Introduction

Quantum dense coding [1] is a simple yet surprising application of elementary quantum mechanics, which has attracted much attention of many researchers. A variety of theoretical suggestions and experimental efforts have been made in this realm. It is firstly proposed by Charles H. Bennett and Stephen J. Wiesner [2]. In the original scheme, one party(Alice), prepares an EPR pair and sends one of the particles to another party(Bob) who applies one of four unitary operators to the particle, and then returns it to Alice. By measuring the two particles jointly, Alice can reliably learn which operator Bob used. The protocol describes a way to transmit two bits of classical information through manipulation of only one of the entangled pair of spin-1/2 particles, while each of the pair individually could carry only one bit of classical information. Afterward Mattle et al. [3] report the first experimental realization of quantum communication, verifying the increased capacity of a quantum information channel by quantum dense coding. Fang et al. [4] have experimentally implemented quantum dense coding by using NMR quantum logic gates and circuits in quantum computation.

Quantum dense coding deals with efficient information transfer from a sender to a receiver utilizing an entangled channel between the two. It has been widely studied theoretically [5–11] and experimentally [12–15] in the past twenty years. Bose, Lee et al. [5, 6, 11] and Bose et al. [7, 8, 10] have generalized quantum dense coding between two parties to multiparties and mixed state dense coding, respectively. Wang et al. [9] propose a protocol for quantum secure direct communication with quantum superdense coding. Wang et al. [12, 13] show that an optimal dense coding protocol can be constructed with pentaqubit entangled state in cavity QED. Some generalizations of dense coding for continuous variables [16–18] are studied. Chen et al. [19] present a simple scheme for implementing perfect controlled teleportation and dense coding with the genuine pentaqubit entangled state.

Hao et al. [20] have firstly studied controlled dense coding using the GHZ state. It is shown that when using the GHZ state, the success probability of dense coding is controlled by the measurement basis of the third particle just like the fidelity, depending on the measurement of the third particle in teleportation, and the entanglement and communication are also controlled in a quantum way. It was experimentally demonstrated by Jing [18] and Zhang [21] for continuous variables. Subsequently, many researchers generalized the controlled dense coding protocol of the three-particle GHZ quantum channel to the case of a multi-particle quantum channel, such as a (N+2)-particle GHZ quantum channel via a series of local measurements [22], a four-particle non-maximally entangled state [23], GHZ-class state [24, 25], a three-qubit symmetric state [26], a one-dimensional four-particle cluster state [27], a five-atom cluster state [28], a peculiar tripartite entangled state [33], generalized GHZ-Type state [34], extended GHZ-W states [36], a cluster state [37], a four-particle non-maximally entangled state [38], four-particle entangled state [39]. In cavity QED systems, controlled dense coding [29–32, 35] are investigated via generalized measurement and with entanglement concentration.

In quantum dense coding the shared quantum channel between two or more than two parties is generally considered to be a maximally entangled resource. However, perfect entanglement is difficult to preserve. Maximally entangled states usually degrade to partially entangled ones [40].

In real experimental setups, it is always a challenge to obtain a multiqubit maximally entangled resource [41]. Therefore, it is important to identify multiqubit entangled systems which are partially entangled but can be efficiently used as a resource in quantum information processing with optimal success.

In 2008 Gao et al. [42] found that certain partially entangled states called maximal slice (MS) states [43] can also be used for controlled teleportation. The controlled teleportation scheme employing the MS states has 100 % success probability and fidelity of teleportation, which is the same as the GHZ scheme [44]. Later, Kumar et al. [45] propose a three-qubit partially entangled set of states as a shared resource for optimal and faithful quantum information processing. Cai, Li et al. [46, 47] have studied some application of partially entangled states.

Mo et al. [48] have proposed a controlled teleportation scheme which communicates an arbitrary ququart state via two sets of partially entangled GHZ state. The necessary measurements and operations are given detailedly. Although a lot of work has been devoted to studying controlled teleportation and dense coding, very little has been discussed the controlled dense coding with a maximal slice state as communication channel. We show in this paper that the success probability of information transmitted from Alice to Bob is usually less than one. The average amount of information for each scheme is computed in detail. These results offer deeper insight into quantum dense coding via quantum channels of partially entangled states.

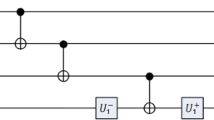
2 Controlled Dense Coding with the Maximal Slice States

We review the quantum dense coding scheme. Let us assume that Alice and Bob initially share the Bell state |Φ〉⁺. Locally operating on her qubit, Alice obtains one of the four orthogonal Bell states I|Φ〉⁺=|Φ〉⁺,σ _X |Φ〉⁺=|Ψ〉⁺,−i σ _Y |Φ〉⁺=|Ψ〉⁻,σ _Z |Φ〉⁺=|Φ〉⁻.Alice then sends her qubit to Bob. By making a Bell measurement, Bob is able to obtain two bits of classical information. The four Bell states are defined by

$$ |{\Phi}\rangle^{\pm}=1/\sqrt{2}(|00\rangle\pm |11\rangle), |{\Psi}\rangle^{\pm}=1/\sqrt{2}(|01\rangle\pm |10\rangle). $$

(1)

The three-qubit partially entangled set of maximal slice (MS) states that we characterize in this paper can be represented as

$$ |{\Phi}\rangle_{123}=1/\sqrt{2}[|000\rangle+\cos\alpha|110\rangle+\sin\alpha|111\rangle], $$

(2)

where qubit 1 is hold by Alice, qubit 2 by Bob and qubit 3 by Cliff respectively. It is the so called maximal slice state. In order to control the quantum channel between Alice and Bob and the amount of information transmitted from Alice to Bob, Cliff performs a von Neumann measurement on his qubit 3 under the basis

$$\begin{array}{llll} |+\rangle_{3}=\cos\beta|0\rangle+\sin\beta|1\rangle, |-\rangle_{3}=\sin\beta|0\rangle-\cos\beta|1\rangle. \end{array} $$

(3)

(β is a measured angle with the region 0 ≤ β ≤ π/4). The MS states can be rewritten as

$$ |{\Phi}\rangle_{123}=|\phi_{12}\rangle|+\rangle_{3}+|\psi_{12}\rangle|-\rangle_{3}, $$

(4)

where

$$ |\phi_{12}\rangle=1/\sqrt{2}[\cos\beta|00\rangle+\cos\beta \cos\alpha|11\rangle+\sin\beta \sin\alpha|11\rangle], $$

(5)

$$ |\psi_{12}\rangle=1/\sqrt{2}[\sin\beta|00\rangle+\sin\beta \cos\alpha|11\rangle-\cos\beta \sin\alpha|11\rangle], $$

(6)

Obviously, the von Neumann measurement of qubit 3 gives the readout |+〉₃ or |−〉₃; each occurs with equal probability 1/2. Now let us analyze here the case in which Cliff’s measurement gives |+〉₃ and the state of qubits 1 and 2 collapses to |ϕ ₁₂〉; the case of |−〉₃ can be treated in a similar fashion. Generally, |ϕ ₁₂〉 is not maximally entangled and the success probability of dense coding with |ϕ ₁₂〉 is less than 1.

Two schemes of dense coding with the MS state are shown below.

• (1) Cliff sends the information of measurement basis and result |+〉₃ to Alice. Alice has the information that she shares the general entangled state |ϕ ₁₂〉 with Bob, whereas Bob does not know this. To obtain the maximal probability Alice introduces an auxiliary qubit |0〉 _{a u x} and performs a unitary operation on her qubit 1 and the auxiliary qubit(which is a collective operation under the basis |0〉₁|0〉 _{a u x} ,|0〉₁|1〉 _{a u x} ,|1〉₁|0〉 _{a u x} ,|1〉₁|1〉 _{a u x} ),

  $$ U_{1}=\left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & \frac{\cos\beta}{\cos(\beta-\alpha)} & \sqrt{1-(\frac{\cos\beta}{\cos(\beta-\alpha)})^{2}} \\ 0 & 0 & \sqrt{1-(\frac{\cos\beta}{\cos(\beta-\alpha)})^{2}} & -\frac{\cos\beta}{\cos(\beta-\alpha)} \end{array} \right) $$

  (7)

  The collective unitary operation U ₁⊗I ₂ transforms the state (|ϕ ₁₂〉⊗|0〉 _{a u x} ) to

  $$\begin{array}{@{}rcl@{}} |\xi\rangle&=&\cos\beta[1/\sqrt{2}(|00\rangle+|11\rangle)]\otimes|0\rangle_{aux}\\&&+1/\sqrt{2}\cos(\beta-\alpha)\sqrt{1-(\frac{\cos\beta}{\cos(\beta-\alpha)})^{2}}|11\rangle\otimes|1\rangle_{aux} \end{array} $$

  (8)

  Then Alice performs a von Neumann measurement on the auxiliary qubit under the basis |0〉 _{a u x} ,|1〉 _{a u x} and informs Bob of the result. If she obtains {|0〉 _{a u x} }, qubits 1 and 2 are maximally entangled. Alice can perform one of the four unitary transformations I,σ _X ,i σ _Y ,σ _Z on qubit 1 and send it to Bob. Then Bob knows he has two qubits in one of the four Bell states resulted from Alice’s transformation. By performing a Bell-basis measurement, Bob can discriminate Alice’s unitary transformation on qubit 1, so 2 bits of information are transmitted. If Alice obtains |1〉 _{a u x} , qubits 1 and 2 are unentangled. Bob can extract only 1 bit of information. So, on average

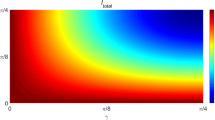
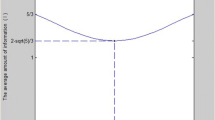
  $$ I_{trans}=3/2\cos^{2}\beta+1/2\cos^{2}(\beta-\alpha) $$

  (9)

  bits of information are transmitted from Alice to Bob.

• (2) Cliff sends his measurement result |+〉₃ to Bob. Bob has the information of the shared state, but Alice does not. Under this condition Bob performs the unitary operation. Alice performs one operation of I,σ _X ,i σ _Y ,σ _Z on qubit 1 and transmits it to Bob. Then Bob’s two-qubit state is one of {cosβ|00〉₁₂± cos(β−α)|11〉₁₂,cosβ|10〉₁₂± cos(β−α)|01〉₁₂} corresponding to Alice’s operation {I,σ _Z ;σ _X ,i σ _Y }, respectively. Bob performs a CNOT operation (Bob’s original qubit 2 is target and the qubit sent by Alice is the controller). The states evolve into unentangled states after the CNOT operation

  $$ \cos\beta|00\rangle_{12}\pm \cos(\beta-\alpha)|11\rangle_{12}\rightarrow (\cos\beta|0\rangle_{1}\pm \cos(\beta-\alpha)|1\rangle_{1})\otimes |0\rangle_{2}, $$

  (10)
  $$ \cos\beta|10\rangle_{12}\pm \cos(\beta-\alpha)|01\rangle_{12}\rightarrow (\cos\beta|1\rangle_{1}\pm \cos(\beta-\alpha)|0\rangle_{1})\otimes |1\rangle_{2} $$

  (11)

  Bob uses a von Neumann measurement on the qubit 2 to get the parity bit. If the result is |0〉₂, Bob knows that Alice performs I, or σ _Z ; if the result is |1〉₂, he knows Alice performs σ _X ,or σ _Y . He can discriminate the two subsets of Alice operations: {I,σ _Z }; or {σ _X ,σ _Y }. Through this measurement Bob gets the parity bit. What Bob needs to do next is to discriminate the two nonorthogonal states {cosβ|0〉₁± cos(β−α)|1〉〉₁} or {cosβ|1〉₁± cos(β−α)|0〉₁}. Bob introduces an auxiliary qubit |0〉 _{a u x} and performs the unitary operation on the qubit 1 and the auxiliary qubit which transforms $1/\sqrt {2}\{(\cos \beta |0\rangle _{1}\pm \cos (\beta -\alpha )|1\rangle _{1})\otimes |0\rangle _{aux}\}$ to

  $$ \cos\beta[1/\sqrt{2}(|0\rangle_{1}\pm|1\rangle_{1})]\otimes|0\rangle_{aux}+1/\sqrt{2}\cos(\beta-\alpha)\sqrt{1-(\frac{\cos\beta}{\cos(\beta-\alpha)})^{2}}|1\rangle_{1}\otimes|1\rangle_{aux}. $$

  (12)

  After that Bob measures the auxiliary qubit. If the outcome is |0〉 _{a u x} , the two states of qubit 1 are orthogonal and he can discriminate the states {cosβ|0〉₁± cos(β−α)|1〉₁} with certainty and the phase bit is obtained. If the outcome is |1〉 _{a u x} , the state of qubit 1 is |1〉₁ and he cannot discriminate {cosβ|0〉₁± cos(β−α)|1〉₁} and he gets nothing. We sum all the information transmitted in this procedure

  $$ I_{trans}=3/2\cos^{2}\beta+1/2\cos^{2}(\beta-\alpha). $$

  (13)

3 Controlled Dense Coding via POVM

In this section, we first consider the case of Cliff’s measurement is |+〉₃, and the other case can be deduced similarly. After receiving the measurement result, Alice directly performs one of the four unitary operators I,σ _X ,i σ _Y ,σ _Z , and maps the joint shared state between her and Bob to the four nonorthogonal states respectively:

$$\begin{array}{@{}rcl@{}} |\zeta_{1}\rangle_{12}&=&1/\sqrt{2}[\cos\beta|00\rangle+\cos(\beta-\alpha)|11\rangle], \end{array} $$

(14)

$$\begin{array}{@{}rcl@{}} |\zeta_{2}\rangle_{12}&=&1/\sqrt{2}[\cos\beta|10\rangle+\cos(\beta-\alpha)|01\rangle], \end{array} $$

(15)

$$\begin{array}{@{}rcl@{}} |\zeta_{3}\rangle_{12}&=&1/\sqrt{2}[-\cos\beta|10\rangle+\cos(\beta-\alpha)|01\rangle], \end{array} $$

(16)

$$\begin{array}{@{}rcl@{}} |\zeta_{4}\rangle_{12}&=&1/\sqrt{2}[\cos\beta|00\rangle-\cos(\beta-\alpha)|11\rangle]. \end{array} $$

(17)

Then Alice sends qubit 1 to Bob, and now Bob has at his disposal two qubits which could be in any one of the four possible states {|ζ ₁〉₁₂,|ζ ₂〉₁₂,|ζ ₃〉₁₂,|ζ ₄〉₁₂}. By performing local unitary transformations, Alice can send only 1-bit information to Bob. However, the above four states are not mutually orthogonal. According to quantum theory, it is obvious that these four non-orthogonal states cannot be distinguished with certainty. But it is known that a set of nonorthogonal states which are linearly independent can be distinguished with some probability of success. In fact, it is easy to find that the above set is actually linearly independent. Therefore Bob can conclusively distinguish these states with some probability of success.

To distinguish the above set, first Bob performs a projection onto the subspaces spanned by the basis states {|00〉,|11〉} and {|01〉,|10〉} with corresponding projective operators are P ₁=|00〉〈00|+|11〉〈11| and P ₂=|01〉〈01|+|10〉〈10| respectively. Obviously, P ₁ and P ₂ are mutually orthogonal, and Bob can discriminate the two subsets of Alice’s operators: {I,σ _Z }; and {σ _X ,i σ _Y }. If Bob obtains P ₁, then he knows that the state will be either |ζ ₁〉₁₂, or |ζ ₄〉₁₂. Similarly, if he obtains P ₂, the state will be either |ζ ₂〉₁₂ or |ζ ₃〉₁₂. After this projective measurement he gets 1 bit of information. Now we suppose Bob obtains P ₁, then he performs a generalized measurement on his two qubit states. In the case, the corresponding positive operator valued measure (POVM) elements in the subspace {|00〉,|11〉} are

$$ M_{1}=\frac{1}{2}\left( \begin{array}{cc} \frac{\cos^{2}\beta}{\cos^{2}(\beta-\alpha)} & \frac{\cos\beta}{\cos(\beta-\alpha)} \\ \frac{\cos\beta}{\cos(\beta-\alpha)} & 1 \end{array} \right) $$

(18)

$$ M_{2}=\frac{1}{2}\left( \begin{array}{cc} \frac{\cos^{2}\beta}{\cos^{2}(\beta-\alpha)} & -\frac{\cos\beta}{\cos(\beta-\alpha)} \\ -\frac{\cos\beta}{\cos(\beta-\alpha)} & 1 \end{array} \right) $$

(19)

$$ M_{3}=\left( \begin{array}{cc} 1-\frac{\cos^{2}\beta}{\cos^{2}(\beta-\alpha)} & 0 \\ 0 & 0 \end{array} \right) $$

(20)

Obviously the condition M ₁ + M ₂ + M ₃ = I ₂ is satisfied.

The generalized measurement has three outcomes. If Bob gets M ₁ then the state is |ζ ₁〉₁₂, if he gets M ₂ then the state is |ζ ₄〉₁₂. However if he gets M ₃ the state is completely indecisive and Bob cannot obtain any information. The success probability of distinguishing |ζ ₁〉₁₂ and |ζ ₄〉₁₂ is $\frac {2\cos ^{2}\beta }{\cos ^{2}\beta +\cos ^{2}(\beta -\alpha )}$ , which is also the probability that Bob obtains another 1 bit of information. Similar procedure can be applied for the case of P ₂, one can easily check that the relevant POVM elements and the success probability are the same. So, in this case, the average amount of information transmitted from Alice to Bob should be expressed as

$$ I_{trans}=3/2\cos^{2}\beta+1/2\cos^{2}(\beta-\alpha) $$

(21)