1 Introduction

Quantum entanglement, the unique resource in quantum information processing, plays an important role in quantum communication, such as quantum teleportation [1–4], quantum key distribution [5–7], quantum dense coding [8–11], quantum entanglement swapping [12–15], conventional parallel quantum computation [16, 17], hyper-parallel photonic quantum computation [18–20], quantum searching [21–25], quantum repeater [26–46], quantum remote state preparation [47–49], controlled remote state preparation [50–56], and so on. Quantum teleportation and quantum remote state preparation(RSP) are two ways for preparing quantum state remotely [47–49]. Quantum teleportation provides a way to teleport an unknown quantum state via quantum entanglement shared in advance [1], while RSP is used to prepare a known state on the remote receiver’s quantum system. The classical communication and entanglement cost in remote state preparation can be reduced due to the sender’s knowledge of prepared state. Moreover, RSP exhibits a trade-off between classical communication and quantum entanglement cost. In RSP, the sender can prepare an arbitrary single-qubit state on the remote receiver’s quantum system by performing corresponding single-qubit measurement on his entangled particle according to his knowledge of prepared state and he need not own the prepared state. RSP has been attached much interest since it is first proposed by Bennett, Lo and Pati [47–49]. Various theoretical schemes for remote preparation of quantum states with different quantum channel has been investigated [57–62] and experimental remote preparation of a single-qubit state with luqid-state NMR and entangled photons has been demonstrated by some groups [63–67].

Recently, another type of multipartite entangled state, cluster state has been studied by some groups [68–71]. In 2001, Briegel and Raussendorf first introduced a class of multipartite entangled state, cluster state, which has high persistency of entanglement [68]. They also shown that cluster state can be used to construct one-way quantum computation which can be realized with only single-qubit measurement [69]. The nonlocality of cluster state has been studied by Scarani and Walther [70, 71]. Researchers have devoted much interest to the study of cluster state since its important application in quantum information and quantum computation. On the one hand, different schemes for creating cluster states with optical elements, cross-Kerr nonlinearities and quantum-dot are proposed [72–74]. On the other hand, theoretical schemes for quantum information processing with cluster states or cluster-type states have been proposed [75–90]. Bai and Mo presented a scheme for quantum information splitting with an unknown eight-qubit cluster state [79]. Zha et al. introduced a way for bidirectional controlled teleporting an unknown single-qubit state via a five-qubit cluster state [80]. In 2013, Zhang et al. proposed a scheme for splitting an unknown two-qubit state by using a six-qubit cluster state as the quantum channel [81]. Wang et al. present a protocol for sharing an arbitrary single-qubit operation with five-qubit cluster states [82]. Nie et al. showed a way for controlled dense coding using a five-atom cluster state [83]. In 2014, Liao et al. presented a scheme to joint remote preparation of an arbitrary two-qubit state via cluster state and cluster-type state [85].

In the past few years, quantum information processing based linear-optical element has attached much interest [91–99]. In 2001, Knill et al. presented a protocol for efficient quantum computation with only linear-optics elements [91]. Trump et al. introduce a way for probabilistic teleportation of an arbitrary single-qubit state with partially entangled state and linear elements [92]. Pan et al. proposed a probabilistic scheme for entanglement purification with ideal entanglement sources and linear optics [93]. In 2010, Sheng and Deng [30] presented a deterministic entanglement purification protocol (EPP) for two-photon systems with parametric down-conversion sources and linear optical elements only.In 2011, Deng [31] proposed a deterministic entanglement purification protocol for multi-photon systems with linear optical elements only. These deterministic EPPs [30, 31] are far different from the conventional EPP [93] as they work in a completely deterministic way, not in a probabilistic way, and they can reduce the quantum resource sacrificed largely. They are very useful in quantum repeaters. In 2013, Ren, Du, and Deng [38] proposed the parameter-splitting method to extract the maximally entangled photons in both the polarization and spatial degrees of freedom (DOFs) when the coefficients of the initial partially hyperentangled states are known. This fascinating method is very efficient and simple in terms of concentrating partially entangled states. It can be achieved with the maximum success probability by performing the protocol only once, resorting to linear-optical elements only, not nonlinearity. In 2014, Li et al. [97] presented an efficient scheme for entanglement concentration of partially entangled x-type state with linear-optical elements.In 2007, Liu et al. [94] report an experiment for remote preparation of arbitrary single-photon pure states and mixed states with linear-optical elements. Xia et al. [95] proposed two schemes for teleportation and controlled teleportation of N-photon GHZ-class states via linear optical elements. Wu et al. proposed a scheme for deterministic remote preparation of arbitrary pure and mixed states via maximally entangled states and linear-optical elements [96]. Recently, Ewert and Loock presented a protocol for 3/4 efficient Bell State Measurement with linear optics and auxiliary photons [98].

Although there are some schemes for remote preparation an arbitrary single-photon state with linear-optical elements, all of them are based on the maximally entangled channel [94, 96, 100]. The parameter of linear-optical element is determined by the information of prepared state [96, 100]. However, in the real application, maximally entangled quantum channel often degrade to a less-entangled quantum channel because of environment noise. In remote state preparation via partially entangled quantum channel with only linear-optical elements, the parameter of linear-optical element can be defined not only by the information of prepared state but also by the state of quantum channel. In this paper, we will presented a scheme for bidirectional controlled remote preparation of an arbitrary single-photon state by using a five-photon cluster-type state as the quantum channel via parameter-splitting method and linear-optical elements. The senders can remote prepare an arbitrary single-qubit state on the remote receivers’ quantum system if they cooperate with the controller. The scheme is more convenient in application since it only requires linear-optical elements and single detectors. Moreover, our scheme for bidirectional controlled remote state preparation of an arbitrary single-qubit state is optimal since the probability that the receiver prepare the original state equals the entanglement of quantum channel.

2 Bidirectional Controlled Remote Preparation of an Arbitrary Single-Photon State with a Five-Photon Cluster State Based Linear-Optical Elements

Similar to Refs. [38, 96],the wave plate R(𝜃) can rotate photon polarization state with an angle 𝜃:

$$\begin{array}{@{}rcl@{}} &&\vert0\rangle\rightarrow \cos\theta\vert0\rangle+\sin\theta\vert1\rangle\\ &&\vert1\rangle\rightarrow -\sin\theta\vert0\rangle+\cos\theta\vert1\rangle \end{array} $$
(1)

where |0〉 and |1〉 denote the horizontal and vertical polarization of a photon. The linear optics element polarizing beam splitter (PBS) transmits the photon in the horizontal polarization |0〉 and reflects photon in the vertical polarization |1〉 [97].

Another polarization measurement basis is X-basis [4]:

$$\begin{array}{@{}rcl@{}} &&\vert0_{x}\rangle=\frac{1}{\sqrt{2}}(\vert0\rangle+\vert1\rangle)\\ &&\vert1_{x}\rangle=\frac{1}{\sqrt{2}}(\vert0\rangle+\vert1\rangle). \end{array} $$
(2)

Similar to Ref. [84], unitary operations X, Z can transform the polarization state of photons

$$\begin{array}{@{}rcl@{}} X=\left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right), Z=\left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right). \end{array} $$
(3)

Now, let us describe the principle our bidirectional controlled remote preparation of an arbitrary single-photon state via a five-photon cluster-type state. For presenting the principle of our scheme clearly, we first discuss bidirectional controlled remote preparation of an arbitrary single-qubit state with a five-qubit cluster state, then generalized it to the case with a five-qubit cluster-type state.

Suppose the quantum state that Alice want Bob to prepare is an arbitrary single-photon state:

$$\begin{array}{@{}rcl@{}} &&\vert\varphi_{1}\rangle=\alpha_{0}\vert0\rangle+\alpha_{1}\vert1\rangle, \end{array} $$
(4)
$$\begin{array}{@{}rcl@{}} &&|\alpha_{0}|^{2}+|\alpha_{1}|^{2}=1 \end{array} $$
(5)

where two complex numbers α 0,α 1 are completely known by Alice but unknown by Bob. And the state that Bob want Alice to prepare is an arbitrary single-qubit state

$$\begin{array}{@{}rcl@{}} &&\vert\varphi_{2}\rangle=\beta_{0}\vert0\rangle+\beta_{1}\vert1\rangle, \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} &&|\beta_{0}|^{2}+|\beta_{1}|^{2}=1. \end{array} $$
(7)

Here two complex numbers β 0 and β 1 are completely known by Bob but unknown by Alice.

Similar to Ref. [84], the five-photon cluster state used for quantum channel can be written as:

$$\begin{array}{@{}rcl@{}} \vert{\Psi}_{1}\rangle=\frac{1}{2}{\sum}_{i_{1},i_{2}=0}^{1}\vert i_{1},i_{1},i_{2},i_{1}\oplus i_{2}, i_{2}\rangle_{A_{1}A_{2}B_{1}CB_{2}}. \end{array} $$
(8)

Here i 1,i 2=0,1, |0〉 and |1〉 denote the horizontal and vertical polarization of a photon, i 1⊕i 2 means i 1+i 2 mod 2.

For bidirectional controlled remote preparation of an arbitrary single-qubit state, all the agents should first share a five-photon cluster state. The agents can exploit entanglement concentration to distill cluster state from the partially entangled state since distribute a five-photon cluster state is difficult in current experiment. The way for concentrating a partially entangled state into a maximally entangled cluster state has been discussed in [89, 90]. After setting up the quantum channel, Alice and Bob perform single-photon measurements on their photons according to their knowledge of prepared states. The controller Charlie performs single-photon measurement on his entangled photons and the receivers can prepare original states on their entangled photons according to the measurement results if they cooperate with the controller.

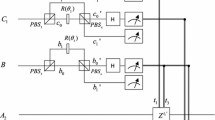
The basic idea for this bidirectional controlled remote preparation of an arbitrary single-photon state is shown in Fig. 1. Alice shares a five-photon cluster state with Bob and Charlie. In detail, Alice sends photons A 2,B 2 to Bob, sends photon C to Charlie, and keeps photons A 1,B 1 in his hand. The state of composite system composed of photons A 1,B 2,B 1,A 2,C is transformed from |Ψ1〉 to |Ψ2〉 after the photons A 1,B 2 pass through P B S 1,P B S 2, respectively.

$$\begin{array}{@{}rcl@{}} \vert{\Psi}_{2}\rangle=\frac{1}{2}{\sum}_{i_{1},i_{2}=0}^{1}\vert i_{1a_{i_{1}}}\rangle_{A_{1}}\vert i_{2b_{i_{2}}}\rangle_{B_{2}}\vert i_{1}\rangle_{A_{2}}\vert i_{2}\rangle_{B_{1}}\vert i_{1}\oplus i_{2}\rangle_{C} \end{array} $$
(9)

where \(a_{i_{1}}(i_{1}=0,1)\) represents two spatial modes of photon \(\phantom {\dot {i}\!}A_{1},b_{i_{2}}(i_{2}=0,1)\) represents two spatial modes of photon B 2.

Fig. 1
figure 1

The quantum circuit for bidirectional controlled remote preparation of an arbitrary single-photon state via a five-qubit cluster state. Qubits A 1,B 1(A 2,B 2;C) are with Alice (Charlie; Bob). Classical information communication from the senders to the receivers are represented by double lines. In the solid line box, X,Z,H denoted the single-qubit operations performed by Alice, Bob and Charlie. Similar to Ref. [38], a 0,a 1 and b 0,b 1 represent two spatial modes of photons A 1 and B 2. \(a_{0}^{\prime },a_{1}^{\prime }\) and \(b_{0}^{\prime },b_{1}^{\prime }\) are another two spatial modes of photons A 1 and B 2

Full size image

For bidirectional controlled remote preparation of an arbitrary single-qubit state, Alice (Bob) first performs some polarization operations on his entangled photon A 1(B 2) according to the information of prepared state, then performs X-basis measurement on his entangled photon. Charlie performs X-basis measurement on his entangled photon C, Bob (Alice) can reconstruct the original state on his entangled photon B 1(A 2) by performing corresponding unitary operations.

Similar to Refs. [38, 96], the polarization operations can be implemented via wave plate. As shown in Fig. 1, the wave plates R(𝜃 1),R(𝜃 2),R(𝜃 3) and R(𝜃 4) in the spatial modes a 0,a 1,b 0 and b 1 can transform the polarization states to the corresponding states:

$$\begin{array}{@{}rcl@{}} \vert0\rangle_{a_{0}}\xrightarrow[]{R(\theta_{1})}\alpha_{0}\vert0\rangle+\alpha_{1}\vert1\rangle\\ \vert1\rangle_{a_{1}}\xrightarrow[]{R(\theta_{2})}\alpha_{0}\vert0\rangle+\alpha_{1}\vert1\rangle\\ \vert0\rangle_{b_{0}}\xrightarrow[]{R(\theta_{3})}\beta_{0}\vert0\rangle+\beta_{1}\vert1\rangle\\ \vert1\rangle_{b_{1}}\xrightarrow[]{R(\theta_{4})}\beta_{0}\vert0\rangle+\beta_{1}\vert1\rangle \end{array} $$
(10)

where \(\theta _{1}=\arccos \alpha _{0}\), \(\theta _{2}=\theta _{1}-\frac {\pi }{2}\), \(\theta _{2}=\arccos \beta _{0}\), \(\theta _{3}=\theta _{2}-\frac {\pi }{2}\).

The state of composite system is transformed from |Ψ2〉 to |Ψ3〉 after photons A 1 and B 2 passes through the wave plates R(𝜃 1), R(𝜃 2), R(𝜃 3) and R(𝜃 4):

$$\begin{array}{@{}rcl@{}} \vert{\Psi}_{3}\rangle=\frac{1}{2}{\sum}_{i_{1},i_{2},j_{1},j_{2}=0}^{1}\alpha_{j_{1}}\beta_{j_{2}}\vert j_{1a_{i_{1}}}\rangle_{A_{1}}\vert j_{2b_{i_{2}}}\rangle_{B_{2}}\\ \vert i_{1}\rangle_{A_{2}}\vert i_{2}\rangle_{B_{1}}\vert i_{1}\oplus i_{2}\rangle_{C} \end{array} $$
(11)

Similar to Refs. [38, 97], the state of composite system composed of five photons is transformed from |Ψ3〉 to |Ψ4〉 after photons A 1, B 2 pass through P B S 3 and P B S 4:

$$\begin{array}{@{}rcl@{}} \vert{\Psi}_{4}\rangle=&&\frac{1}{2}{\sum}_{i_{1},i_{2},\atop j_{1},j_{2}=0}^{1}\alpha_{i_{1}}\beta_{i_{2}}\vert i_{1a_{j_{1}^{\prime}}}\rangle_{A_{1}}\vert i_{2b_{j_{2}}^{\prime}}\rangle_{B_{2}}\\ &&\vert i_{1}\oplus j_{1}\rangle_{A_{2}}\vert i_{2}\oplus j_{2}\rangle_{B_{1}}\vert i_{1}\oplus i_{2}\oplus j_{1}\oplus j_{2}\rangle_{C} \end{array} $$
(12)

As shown in Fig. 1, the subscript \(a_{j_{1}}^{\prime }(j_{1}=0,1)\) represent two output ports of P B S 3 and \(b_{j_{2}}^{\prime }(j_{2}=0,1)\) represent two output ports of P B S 4.

After photons A 1 and B 2 pass through P B S 3 and P B S 4, the state of composite system composed five photons becomes |ψ〉 if photon A 1 and B 2 emitted from spatial modes \(a_{j_{1}}^{\prime }\) and \(b_{j_{2}}^{\prime }(j_{1},j_{2}=0,1)\).

$$\begin{array}{@{}rcl@{}} \vert\psi\rangle=&&{\sum}_{i_{1},i_{2}=0}^{1}\alpha_{i_{1}}\beta_{i_{2}}\vert i_{1}\rangle_{A_{1}}\vert i_{2}\rangle_{B_{2}}\vert i_{1}\oplus j_{1}\rangle_{A_{2}}\vert i_{2}\oplus j_{2}\rangle_{B_{1}}\\&&\vert i_{1}\oplus i_{2}\oplus j_{1}\oplus j_{2}\rangle_{C}. \end{array} $$
(13)

For bidirectional controlled remote preparation of single-qubit state, Alice, Bob and Charlie perform X-basis measurements on their entangled photons A 1, B 2 and C. The receivers can reconstruct the original state |φ 1〉 and |φ 2〉 on their entangled particles A 2 and B 1 by performing corresponding unitary operations. In detail, one can rewrite the state of composite system composed of particles A 1,B 2,A 2,B 1,C as fellows(without normalization):

$$\begin{array}{@{}rcl@{}} \vert\psi\rangle=&&{\sum}_{t_{1},t_{2},t_{3}\atop i_{1},i_{2}=0}^{1}(-1)^{i_{1}t_{1}^{\prime}}(-1)^{i_{2}t_{2}^{\prime}}\alpha_{i_{1}}\beta_{i_{2}}\vert t_{1x}\rangle_{A_{1}}\vert t_{2x}\rangle_{B_{2}}\\&&\vert t_{3x}\rangle_{C}\vert i_{1}\oplus j_{1}\rangle_{A_{2}}\vert i_{2}\oplus j_{2}\rangle_{B_{1}} \end{array} $$
(14)

where \(t_{1}^{\prime }=t_{1}+t_{3}\), \(t_{2}^{\prime }=t_{2}+t_{3}\). The state of photons A 2,B 1 collapses to corresponding state \(\phantom {\dot {i}\!}\vert \psi \rangle _{A_{2}B_{1}}\) if the X-basis measurement results are \(\phantom {\dot {i}\!}\vert t_{1x}\rangle _{A_{1}},\vert t_{2x}\rangle _{B_{2}}\) and \(\phantom {\dot {i}\!}\vert t_{3x}\rangle _{C}\)

$$\begin{array}{@{}rcl@{}} \vert\psi\rangle_{A_{2}B_{1}}=\vert\varphi_{1}^{\prime}\rangle_{A_{2}}\otimes\vert\varphi_{2}^{\prime}\rangle_{B_{1}} \end{array} $$
(15)

where

$$\begin{array}{@{}rcl@{}} \vert\varphi_{1}^{\prime}\rangle_{A_{2}}={\sum}_{i_{1}=0}^{1}(-1)^{i_{1}t_{1}^{\prime}}\alpha_{i_{1}}\vert i_{1}\oplus j_{1}\rangle_{A_{2}}\\ \vert\varphi_{2}^{\prime}\rangle_{B_{1}}={\sum}_{i_{2}=0}^{1}(-1)^{i_{2}t_{2}^{\prime}}\beta_{i_{2}}\vert i_{2}\oplus j_{2}\rangle_{B_{1}}. \end{array} $$
(16)

Similar to Ref. [84], Bob and Alice can reconstruct the original states |φ 2〉,|φ 1〉 on their entangled particles A 2, B 1 by performing corresponding unitary operations on their entangled photons,

$$\begin{array}{@{}rcl@{}} X^{j_{1}}Z^{t_{1}^{\prime}}\vert\varphi_{1}^{\prime}\rangle_{A_{2}}=\vert\varphi_{1}\rangle_{A_{2}}\\ Z^{t_{2}^{\prime}}X^{j_{2}}\vert\varphi_{2}^{\prime}\rangle_{B_{1}}=\vert\varphi_{2}\rangle_{B_{1}}. \end{array} $$
(17)

3 Bidirectional Controlled Remote Preparation of an Arbitrary Single-Photon State with a Five-Photon Cluster-Type State

In real application, the quantum channel is a partially entangled state since it is difficult to prepare and distribute maximally entangled state in the practical environment [4]. In this section, we generalize the scheme for bidirectional controlled remote preparation of an arbitrary single-photon state via a five-photon cluster state to the case with a five-photon cluster-type state.

For controlled remote preparation of an arbitrary single-photon state with a five-photon cluster-type state, all the agents should first share a five-photon entangled state before they remote preparation of an arbitrary single-photon state, and then Alice (Bob) performs single-photon operations via linear optical elements according to the information of prepared state and the coefficients of entangled quantum channel. The controller Charlie performs X-basis measurement on his entangled particle, and Bob(Alice) can reconstruct the original state by performing corresponding unitary operation on his entangled particle.

Suppose the quantum channel shared by Alice, Bob and Charlie is a five-photon cluster-type state [85]:

$$\begin{array}{@{}rcl@{}} \vert{\Psi}_{0}^{\prime}\rangle_{A_{1}A_{2}B_{1}CB_{2}}=&&\gamma_{00}\vert00000\rangle+\gamma_{01}\vert00111\rangle+\gamma_{10}\vert11010\rangle\\&&+\gamma_{11}\vert11101\rangle, \end{array} $$
(18)

where |γ 00|2+|γ 01|2+|γ 10|2+|γ 11|2=1. Similar to the case for bidirectional controlled remote preparation via a cluster state, particles A 1,B 1 belong to Alice, particles A 2,B 2 belong to Bob, and Charlie owns particle C. The arbitrary single-photon state Alice want Bob to prepare can be described as: |φ 1〉=α 0|0〉+α 1|1〉, and the single-photon state Bob want Alice to prepare can be written as: |φ 2〉=β 0|0〉+β 1|1〉.

Without loss of generalization, suppose |α 0|<|α 1|, |β 0|<|β 1|. γ 11 is the smallest coefficient which have the relations |γ 10 γ 11|<|γ 00 γ 01|, |γ 01 γ 11|<|γ 00 γ 10|, and |γ 00 γ 11|<|γ 10 γ 01|(similar to Ref. [97], the case with other coefficients can also be used to controlled remote preparation of single-photon state with a little modification). The basis idea of our bidirectional controlled remote preparation of an arbitrary single-photon state by using a five-photon cluster-type state as the quantum channel with only linear optical elements is shown in Fig. 2. The wave plate \(R(\theta _{i}^{\prime })(i=1,2,3)\) can rotate photon polarization state with an angle \(\theta _{i}^{\prime }\). Similar to Ref. [97], Alice, Bob and Charlie preset the coefficients \(\theta _{i}^{\prime }\)

$$\begin{array}{@{}rcl@{}} &&\theta_{1}^{\prime}=\arccos(\sqrt{\frac{\gamma_{10}\gamma_{11}}{\gamma_{00}\gamma_{01}}}\frac{\alpha_{0}}{\alpha_{1}}),\theta_{2}^{\prime}=\arccos(\sqrt{\frac{\gamma_{01}\gamma_{11}}{\gamma_{00}\gamma_{10}}}\frac{\beta_{0}}{\beta_{1}})\\ &&\theta_{3}^{\prime}=\arcsin(\sqrt{\frac{\gamma_{00}\gamma_{11}}{\gamma_{01}\gamma_{10}}})-\frac{\pi}{2} \end{array} $$
(19)

to rotate photon polarization states to the corresponding states:

$$\begin{array}{@{}rcl@{}} &&\vert0\rangle\xrightarrow[]{R(\theta_{1}^{\prime})}R_{1}\vert0\rangle+\sqrt{1-{R_{1}^{2}}}\vert1\rangle\\ &&\vert0\rangle\xrightarrow[]{R(\theta_{2}^{\prime})}R_{2}\vert0\rangle+\sqrt{1-{R_{2}^{2}}}\vert1\rangle\\ &&\vert1\rangle\xrightarrow[]{R(\theta_{3}^{\prime})}R_{3}\vert1\rangle+\sqrt{1-{R_{3}^{2}}}\vert0\rangle. \end{array} $$
(20)

Here \(R_{1}=\sqrt {\frac {\gamma _{10}\gamma _{11}}{\gamma _{00}\gamma _{01}}}\frac {\alpha _{0}}{\alpha _{1}}\), \(R_{2}=\sqrt {\frac {\gamma _{01}\gamma _{11}}{\gamma _{00}\gamma _{10}}}\frac {\beta _{0}}{\beta _{1}}\) and \(R_{3}=\sqrt {\frac {\gamma _{00}\gamma _{11}}{\gamma _{01}\gamma _{10}}}\).

Fig. 2
figure 2

The quantum circuit for bidirectional controlled remote preparation of an arbitrary single-photon state via a five-qubit cluster-type state. a 0,a 1 , b 0,b 1 and c 0,c 1 represent two spatial modes of photons A 1, B 2 and C. \(a_{0}^{\prime },a_{1}^{\prime }\), \(b_{0}^{\prime },b_{1}^{\prime }\) and \(c_{0}^{\prime },c_{1}^{\prime }\) are another two spatial modes of photons A 1, B 2 and C. \(R(\theta _{i}^{\prime })(i=1,2,3)\) represents a wave plate which rotate photon polarization state with an angle \(\theta _{i}^{\prime }\)

Full size image

For bidirectional controlled remote preparation of an arbitrary single-photon state, Alice, Bob and Charlie first transform the five-photon cluster-type state to the target state according to the information of prepared states with the parameter-splitting method introduced by Ren et al. [38]. After transform the quantum channel to the target state, Alice, Bob and Charlie perform X-basis measurements on their entangled particles and the receiver can reconstruct the original state on their entangled particles by performing corresponding unitary operations if they cooperate with the controller.

To bidirectional controlled remote preparation via linear optical elements, Alice, Bob and Charlie perform corresponding polarization unitary operation according to his knowledge of prepared states by placing the wave plate \(R(\theta _{1}^{\prime })\), \(R(\theta _{2}^{\prime })\) and \(R(\theta _{3}^{\prime })\) in the spatial mode a 0,b 0 and c 1,respectively. As shown in Fig. 2, after the photon A 1,B 2 and C pass through \(PBS_{1},R(\theta _{1}^{\prime })\), \(PBS_{3},R(\theta _{2}^{\prime })\) and \(PBS_{5},R(\theta _{3}^{\prime })\),respectively, the state of composite system composed of particles A 1,A 2,B 1,C,B 2 is transformed from \(\vert {\Psi }_{0}^{\prime }\rangle \) to \(\vert {\Psi }_{1}^{\prime }\rangle \):

$$\begin{array}{@{}rcl@{}} \vert{\Psi}_{1}^{\prime}\rangle&=&\gamma_{00}(R_{1}\vert0_{a_{0}}\rangle+\sqrt{1-{R_{1}^{2}}}\vert1_{a_{0}}\rangle)_{A_{1}}\vert00\rangle_{A_{2}B_{1}}\vert0_{c_{0}}\rangle_{C} \\&&(R_{2}\vert0_{b_{0}}\rangle+\sqrt{1-{R_{2}^{2}}}\vert1_{b_{0}}\rangle)_{B_{2}}+\gamma_{01}(\sqrt{1-{R_{1}^{2}}}\vert1_{a_{0}} \\&&+R_{1}\vert0_{a_{0}}\rangle)_{A_{1}}\vert01\rangle_{A_{2}B_{1}}(\sqrt{1-{R_{3}^{2}}}\vert0_{c_{1}}\rangle +R_{3}\vert1_{c_{1}}\rangle)_{C} \\&&\vert1_{b_{1}}\rangle_{B_{2}}+\gamma_{10}\vert1_{a_{1}}\rangle_{A_{1}}\vert10\rangle_{A_{2}B_{1}}(\sqrt{1-{R_{3}^{2}}}\vert0_{c_{1}}\rangle \\&&+R_{3}\vert1_{c_{1}}\rangle)_{C}\vert0\rangle(R_{2}\vert0_{b_{0}}\rangle+\sqrt{1-{R_{2}^{2}}}\vert1_{b_{0}}\rangle)_{B_{2}} \\&&+\gamma_{11}\vert1_{a_{1}}\rangle_{A_{1}}\vert11\rangle_{A_{2}B_{1}}\vert0_{c_{0}}\rangle_{C}\vert1_{b_{1}}\rangle_{B_{2}} \end{array} $$
(21)

where a 0,a 1,b 0,b 1 and c 0,c 1 represent two spatial modes of P B S 1, P B S 3 and P B S 5, respectively. After the photons A 1 , B 2 and C pass through P B S 2,P B S 4 and P B S 6, the state of composite system is transformed from \(\vert {\Psi }_{1}^{\prime }\rangle \) to \(\vert {\Psi }_{2}^{\prime }\rangle \) [38]:

$$\begin{array}{@{}rcl@{}} \vert{\Psi}_{2}^{\prime}\rangle&=&\gamma_{00}R_{1}R_{2}\vert000_{a_{0}^{\prime}b_{0}^{\prime}c_{0}^{\prime}}\rangle_{A_{1}B_{2}C}\vert00\rangle_{A_{2}B_{1}}+\gamma_{01}R_{1}R_{3} \\&&\vert011_{a_{0}^{\prime}b_{0}^{\prime}c_{0}^{\prime}}\rangle_{A_{1}B_{2}C}\vert01\rangle_{A_{2}B_{1}}+\gamma_{10}R_{2}R_{3}\vert101_{a_{0}^{\prime}b_{0}^{\prime}c_{0}^{\prime}}\rangle_{A_{1}B_{2}C} \\&&\vert10\rangle_{A_{2}B_{1}}+\gamma_{11}\vert110_{a_{0}^{\prime}b_{0}^{\prime}c_{0}^{\prime}}\rangle_{A_{1}B_{2}C}\vert11\rangle_{A_{2}B_{1}}+\gamma_{00} \\&&R_{1}\sqrt{1-{R_{2}^{2}}}\vert010_{a_{0}^{\prime}b_{1}^{\prime}c_{0}^{\prime}}\rangle_{A_{1}B_{2}C}\vert00\rangle_{A_{2}B_{1}}+\gamma_{10}\sqrt{1-{R_{2}^{2}}} \\&&R_{3}\vert111_{a_{0}^{\prime}b_{1}^{\prime}c_{0}^{\prime}}\rangle_{A_{1}B_{2}C}\vert10\rangle_{A_{2}B_{1}}+\gamma_{00}R_{2}\sqrt{1-{R_{1}^{2}}} \\&&\vert100_{a_{1}^{\prime}b_{0}^{\prime}c_{0}^{\prime}}\rangle_{A_{1}B_{2}C}\vert00\rangle_{A_{2}B_{1}}+\gamma_{01}\sqrt{1-{R_{1}^{2}}}R_{3} \\&&\vert111_{a_{1}^{\prime}b_{0}^{\prime}c_{0}^{\prime}}\rangle_{A_{1}B_{2}C}\vert01\rangle_{A_{2}B_{1}}+\gamma_{00}\sqrt{1-{R_{1}^{2}}}\sqrt{1-{R_{2}^{2}}} \\&&\vert110_{a_{1}^{\prime}b_{1}^{\prime}c_{0}^{\prime}}\rangle_{A_{1}B_{2}C}\vert00\rangle_{A_{2}B_{1}}+\gamma_{01}\sqrt{1-{R_{3}^{2}}}R_{1} \\&&\vert010_{a_{0}^{\prime}b_{0}^{\prime}c_{1}^{\prime}}\rangle_{A_{1}B_{2}C}\vert01\rangle_{A_{2}B_{1}}+\gamma_{10}\sqrt{1-{R_{3}^{2}}}R_{2} \\&&\vert100_{a_{0}^{\prime}b_{0}^{\prime}c_{1}^{\prime}}\rangle_{A_{1}B_{2}C}\vert10\rangle_{A_{2}B_{1}}+\gamma_{01}\sqrt{1-{R_{1}^{2}}}\sqrt{1-{R_{3}^{2}}} \\&&\vert110_{a_{1}^{\prime}b_{0}^{\prime}c_{1}^{\prime}}\rangle_{A_{1}B_{2}C}\vert01\rangle_{A_{2}B_{1}}+\gamma_{10}\sqrt{1-{R_{2}^{2}}}\sqrt{1-{R_{3}^{2}}} \\&&\vert110_{a_{0}^{\prime}b_{1}^{\prime}c_{1}^{\prime}}\rangle_{A_{1}B_{2}C}\vert10\rangle_{A_{2}B_{1}} \\&=&\frac{\gamma_{11}}{\alpha_{1}\beta_{1}}(\alpha_{0}\beta_{0}\vert000_{a_{0}^{\prime}b_{0}^{\prime}c_{0}^{\prime}}\rangle_{A_{1}B_{2}C}\vert00\rangle_{A_{2}B_{1}}+\alpha_{0}\beta_{1} \\&&\vert011_{a_{0}^{\prime}b_{0}^{\prime}c_{0}^{\prime}}\rangle_{A_{1}B_{2}C}\vert01\rangle_{A_{2}B_{1}}+\alpha_{1}\beta_{0}\vert101_{a_{0}^{\prime}b_{0}^{\prime}c_{0}^{\prime}}\rangle_{A_{1}B_{2}C} \\&&\vert10\rangle_{A_{2}B_{1}}+\alpha_{1}\beta_{1}\vert110_{a_{0}^{\prime}b_{0}^{\prime}c_{0}^{\prime}}\rangle_{A_{1}B_{2}C}\vert11\rangle_{A_{2}B_{1}})+\cdots \end{array} $$
(22)

Here ⋯ represents terms that photons A 1, B 2 and C do not emit from spatial modes \(a_{0}^{\prime }\), \(b_{0}^{\prime }\) and \(c_{0}^{\prime }\). Similar to Ref. [97], the bidirectional controlled remote state preparation succeeds if photons A 1, B 2 and C emit from spatial modes \(a_{0}^{\prime }\), \(b_{0}^{\prime }\) and \(c_{0}^{\prime }\); otherwise the bidirectional controlled remote state preparation fails. The state of composite system composed of particles A 1, B 2, C, A 2 and B 1 becomes corresponding state \(\vert {\Psi }_{s}^{\prime }\rangle \) if photons A 1, B 2 and C emit from spatial modes \(a_{0}^{\prime }\), \(b_{0}^{\prime }\) and \(c_{0}^{\prime }\):

$$\begin{array}{@{}rcl@{}} \vert{\Psi}_{2}^{\prime}\rangle_{A_{1}B_{2}CA_{2}B_{1}}&=&(\alpha_{0}\beta_{0}\vert00000\rangle+\alpha_{0}\beta_{1}\vert01101\rangle \\&&+\alpha_{1}\beta_{0}\vert10110\rangle +\alpha_{1}\beta_{1}\vert11011\rangle). \end{array} $$
(23)

After transform the five-photon cluster-type state to the target state \(\vert {\Psi }_{2}^{\prime }\rangle \), Alice, Bob and Charlie perform X-basis measurements on their entangled photons A 1, B 2 and C. The receiver can reconstruct the original state by performing corresponding unitary operations according to the X-basis measurement results. In detail, one can rewrite state \(\vert {\Psi }_{2}^{\prime }\rangle \) as fellows(without normalization):

$$\begin{array}{@{}rcl@{}} \vert{\Psi}_{2}^{\prime}\rangle=\sum\nolimits_{i_{1},i_{2},t_{1},t_{2},t_{3}=0}^{1}(-1)^{t_{1}{\prime}i_{1}+t_{2}{\prime}i_{2}}\alpha_{i_1}\beta_{i_2}\vert t_{1x}\rangle_{A_{1}}\vert t_{2x}\rangle_{B_{2}} \vert t_{3x}\rangle_{C}\vert i_{1}\rangle_{A_{2}}\vert i_{2}\rangle_{B_{1}} \end{array} $$
(24)

where \(t_{1}^{\prime }=t_{1}+t_{3}\), \(t_{2}^{\prime }=t_{2}+t_{3}\). The state of photons A 2, B 1 collapses to state \(\phantom {\dot {i}\!}\vert \psi ^{\prime }\rangle _{A_{2}B_{1}}\) if the X-basis measurement results are \(\phantom {\dot {i}\!}\vert t_{1x}\rangle _{A_{1}},\vert t_{2x}\rangle _{B_{2}}\) and \(\phantom {\dot {i}\!}\vert t_{3x}\rangle _{C}\)

$$\begin{array}{@{}rcl@{}} \vert\psi^{\prime}\rangle_{A_{2}B_{1}}=\vert\phi_{1}\rangle_{A_{2}}\otimes\vert\phi_{2}\rangle_{B_{1}} \end{array} $$
(25)

where

$$\begin{array}{@{}rcl@{}} &\vert\phi_{1}\rangle_{A_{2}}=\sum\nolimits_{i_{\!1}= 0}^{1}(-1)^{t_{1}{\prime}}\alpha i_{\!1}\vert i_{\!1}\rangle\\ &\hspace*{6pt} \vert\phi_{2}\rangle_{B_{1}}=\sum\nolimits_{i_{2}=0}^{1}(-1)^{t_{2}{\prime}}\beta_{i2}\vert i_{2}\rangle. \end{array} $$
(26)

Similar to the case for bidirectional remote state preparation via five-photon cluster state, Bob and Alice can prepare the original states |φ 2〉, |φ 1〉 on their entangled photons A 2, B 1 by performing corresponding unitary operations:

$$\begin{array}{@{}rcl@{}} Z^{t_{1}^{\prime}}\vert\phi_{1}\rangle_{A_{2}}=\vert\varphi_{1}\rangle_{A_{2}}\\ Z^{t_{2}^{\prime}}\vert\phi_{2}\rangle_{B_{1}}=\vert\varphi_{2}\rangle_{B_{1}}. \end{array} $$
(27)

From (22), one can see the success probability that the receiver can prepare the original state with linear-optical elements is \(\frac {|\gamma _{11}|^{2}}{|\alpha _{1}|^{2}|\beta _{1}|^{2}}\) [97].

4 Discussion and Summary

It is valuable to emphasize that Alice, Bob and Charlie can also first obtain a five-photon cluster state by performing a entanglement concentration on the five-photon cluster-type state \(\vert {\Psi }_{0}^{\prime }\rangle _{A_{1}A_{2}B_{1}CB_{2}}=\gamma _{00}\vert 00000\rangle +\gamma _{01}\vert 00111\rangle +\gamma _{10}\vert 11010\rangle +\gamma _{11}\vert 11101\rangle \) in the bidirectional controlled remote preparation of arbitrary single-qubit states, then prepare the arbitrary single-qubit states |φ 1〉,|φ 2〉, similar to the case in quantum teleportation. This way will increase the probability preparing the original state at the expense of storing it a long time.

In Ref. [100], the senders exploit some special unitary operations to avoid the requirement that Alice should transform the entangled channel \(\vert {\Phi }\rangle =\frac {1}{\sqrt {2}}(\vert 000\rangle +\vert 111\rangle )\) to the target channel according to the information of the state of quantum channel. But when the quantum channel becomes partially entangled quantum channel \(\vert {\Psi }_{0}^{\prime }\rangle _{A_{1}A_{2}B_{1}CB_{2}}=\gamma _{00}\vert 00000\rangle +\gamma _{01}\vert 00111\rangle +\gamma _{10}\vert 11010\rangle +\gamma _{11}\vert 11101\rangle \), the approach in Ref. [100] does not work. Different to Ref. [96], Alice transform the quantum channel to the target channel not only according to the information of prepared state but also according to the state of quantum channel.

In summary, we have proposed a scheme for bidirectional controlled remote preparation of arbitrary single-qubit states with parameter-splitting method which is first proposed by Ren et al. [38]. Alice can prepare an arbitrary single-qubit state on the remote Bob’s quantum system and at the same time Bob can also prepare an arbitrary single-qubit state on Alice’s quantum system if they cooperate with the controller. This method can help remote parties prepare arbitrary single-qubit states on the quantum system at the node of quantum communication network bidirectionally via a partially entangled cluster-type state with only linear-optical elements. It is more convenient in application since it only requires linear-optical elements for bidirectional controlled remote preparation of an arbitrary single qubit state via partially entangled quantum channel.