1 Introduction

It is well known that quantum entanglement is an important resource [1–4] in the field of quantum information processing, such as quantum teleportation, quantum key distribution, quantum cryptograph, and quantum dense coding. In recent years, quantum phase transition (QPT) has attracted a plenty of attention in condensed matter physics (CMP) and become a hot topic [5–7]. In fact, a remarkable change in the ground state of the system will take place when one considers the connection between entanglement and QPT. This change will occur at zero temperature or final cryogenic situations where all thermal fluctuations get frozen. And quantum fluctuations play a dominant role in driving the phase transition [8–12].

Additionally, quantum renormalization-group (QRG) method is considered as one of the good candidates for investigating quantum properties of multibody systems. In the past, considerable effort had been made on that theme via QRG [13–18]. Specially, performance of coupled quantum entanglement in QPT was studied in different spin systems by means of QRG [18–21]. Generally speaking, QRG method, which is originally designed to investigate the statistical questions of continuum limit, can be used to study the total properties of the model entering a few sites by the renormalizing of coupling constants [21–23]. Via our investigations, we found that the QRG method is efficient for probing the scaling behavior and the nonanalytic near the critical points within some physical systems [22–27].

Some spin models can supply a magnetic term which is called as the Dzyaloshinskii–Moriya (DM) interaction arising from spin-orbit coupling. The DM interaction, firstly proposed by Dzyaloshinsky [28] and Moriya [29], can affect QPT and the critical properties of many spin systems. It is found that the introduction of the DM interaction can cause the ferromagnetic spin line to be a better quantum channel for teleportation [30]. Recently, the relations between two-qubit quantum entanglement or correlation and quantum phase transition of some spin models have been reported by using the QRG method [18, 31]. However, there are some differences in the practical system when a site was traced. Factually, N-qubit \((N>2)\) quantum entanglement and QPT of some spin models have not been studied thoroughly. Motivated by this, in this paper, we will study three-body entanglement by using the global entanglement to indicate the QPT in the XXZ model with DM interaction [32, 33]. Our results show that the global entanglement can develop two different fixed values, which preferably exhibit quantum phase transition at the critical point, and we found that DM interaction not only can control the occurrence of the critical point, but also can recover the spoiled three-block entanglement. At the same time, the scaling behavior and nonanalytic phenomenon have also been revealed.

The paper is arranged as follows. In Sect. 2, multipartite entanglement measure method called as global entanglement is introduced. In Sect. 3, we elaborate how to obtain the fixed points of the spin 1/2 XXZ model with DM interaction by means of QRG method. In Sect. 4, dynamical properties of the renormalized global entanglement and the QPT are shown. In Sect. 5, the scaling behavior and nonanalytic phenomenon in the spin chains are disclosed. Finally, we conclude our results with the summary section.

2 Entanglement measure in N-qubit systems

As we know, the global entanglement was generally introduced to measure multipartite entanglement [33]. Given that there is a state vector \(|\phi \rangle \) describing a pure composite quantum system consisting of N qubits, the global entanglement Q is defined as

$$\begin{aligned} Q(|\phi \rangle )=2\left[ {1-\frac{1}{N}\sum _i^N {\mathrm{Tr}\left( {\rho _i^2}\right) }}\right] , \end{aligned}$$
(1)

where \(\rho _i\) is the reduced density matrix for qubit i. The global entanglement is normalized within the limitation of \(0\le Q\le 1\); explicitly, \(Q=0\) if and only if \(|\phi \rangle \) is a product state; \(Q=1\) when \(\mathrm{Tr}(\rho _i^2 )=0.5\), \(\forall i\), i.e., when the reduced state of each qubit is a maximally mixed state in a state vector \(|\phi \rangle \).

3 Quantum renormalization of the XXZ model with DM interaction

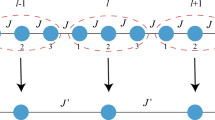
In this section, we will focus on recalling the quantum renormalization-group (QRG) method and its application in the spin 1/2 XXZ model with Dzyaloshinskii–Moriya (DM) interaction. The major aim of QRG method is to gradually reduce the degrees of freedom by iteration until we obtain a controllable state with keeping the low-energy part of the system unvaried. In Kadanoff’s block method, the lattice is grouped into blocks in which the Hamiltonian is precisely diagnosed and solved. Each block can be treated autonomously to obtain the lower-energy renormalized Hilbert subspace. After that, one can get the effective Hamiltonian \(H^\mathrm{eff}\) via the full Hamiltonian being mapped into the renormalized space.

Now, we review the renormalization method in the 1D anisotropic XXZ model with DM interaction in the z direction. The Hamiltonian of the spin 1/2 XXZ model with DM interaction on a periodic chain of N sites is given by

$$\begin{aligned} H(J,\Delta )=\frac{J}{4}\sum _{\mathrm{k}=1}^N {\left[ {\sigma _k^x \sigma _{k+1}^x +\sigma _k^y \sigma _{k+1}^y +\Delta \sigma _k^z \sigma _{k+1}^z +D\left( {\sigma _k^x \sigma _{k+1}^y -\sigma _k^y \sigma _{k+1}^x } \right) } \right] } , \end{aligned}$$
(2)

where J is the exchange constant, \(\Delta \) is the anisotropy parameter, D is the strength of z component of DM interaction, and \(\sigma _k^\alpha (\alpha =x,y,z)\) are the standard Pauli matrices at site k. Besides, the coefficients satisfy \(J,\Delta ,D>0\).

In order to attain a self-similar Hamiltonian after each QRG step, it is necessary to divide the spin chain into three-site blocks. In the standard bases \(\{\left| \uparrow \uparrow \downarrow \right\rangle ,\left| \uparrow \downarrow \uparrow \right\rangle ,\left| \uparrow \downarrow \downarrow \right\rangle ,\left| \downarrow \uparrow \uparrow \right\rangle ,\left| \downarrow \uparrow \downarrow \right\rangle ,\left| \downarrow \downarrow \uparrow \right\rangle ,\left| \downarrow \downarrow \downarrow \right\rangle ,\left| \uparrow \uparrow \uparrow \right\rangle \}\) the degenerate ground states are given by

$$\begin{aligned} \begin{aligned} \left| {\phi _0}\right\rangle&=\frac{1}{\sqrt{2q(\Delta +q)(1+D^{2})}}\{2(1+D^{2})\left| {\downarrow \downarrow \uparrow } \right\rangle -(1-iD)(\Delta +q)\left| {\downarrow \uparrow \downarrow } \right\rangle \\&-\,2[2iD+(D^{2}-1)]\left| {\uparrow \downarrow \downarrow } \right\rangle \} \end{aligned}, \end{aligned}$$
(3)

and

$$\begin{aligned} \begin{aligned} \left| {\phi _0^{\prime }}\right\rangle&=\frac{1}{\sqrt{2q(\Delta +q)(1+D^{2})}}\{2(1+D^{2})\left| {\downarrow \uparrow \uparrow } \right\rangle -(1-iD)(\Delta +q)\left| {\uparrow \downarrow \uparrow } \right\rangle \\&-\,2[2iD+(D^{2}-1)]\left| {\uparrow \uparrow \downarrow } \right\rangle \} \end{aligned}, \end{aligned}$$
(4)

where \(\left| \uparrow \right\rangle \) and \(\left| \downarrow \right\rangle \) are the eigenstates of \(\sigma _z \), and \(q=\sqrt{8(1+D^{2})+\Delta ^{2}}\). Thus, the effective Hamiltonian of the renormalized XXZ chain can be expressed as

$$\begin{aligned} H^{\mathrm{eff}}=\frac{J^{\prime }}{4}\sum _{\mathrm{k}=1}^{N/3} {\left[ {\sigma _k^x \sigma _{k+1}^x +\sigma _k^y \sigma _{k+1}^y +\Delta ^{\prime }\sigma _k^z \sigma _{k+1}^z +D^{\prime }\left( {\sigma _k^x \sigma _{k+1}^y -\sigma _k^y \sigma _{k+1}^x } \right) } \right] } , \end{aligned}$$
(5)

where \(J^{\prime }\) and \(D^{\prime }\) are the renormalized coupling constants. Consequently, the iterative relationship is

$$\begin{aligned} J^{\prime }=J\left( {1+D^{2}} \right) \left( {\frac{2}{q}} \right) ^{2},\,\Delta ^{\prime }=\frac{\Delta \left( {q+\Delta }\right) ^{2}}{16\left( {1+D^{2}}\right) },\,D^{\prime }=D. \end{aligned}$$
(6)

The most important information given in the QRG method is its fixed points. By solving the expression of \(\Delta ^{\prime }=\Delta \), one can obtain a phase boundary \(\Delta =\sqrt{1+D^{2}}\) that detaches the spin-fluid phase \(0\le \Delta <\sqrt{1+D^{2}}\) from the Néel phase \(\Delta >\sqrt{1+D^{2}}\).

4 Dynamical properties of the renormalized global entanglement

In order to exploit the performance of the renormalized global entanglement among three spins located on the side of the block, we here consider one of the degenerate ground states. Correspondingly, the density matrix of a ground state is defined by

$$\begin{aligned} \rho _{123}=\left| {\phi _0}\right\rangle \left\langle {\phi _0}\right| , \end{aligned}$$
(7)

where \(\left| {\phi _0}\right\rangle \) has been defined as Eq. (3). The results will be the same if we consider \(\left| {\phi _0^{\prime }}\right\rangle \) constructing the density matrix. After calculation, one can obtain the global entanglement as follows:

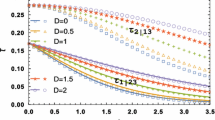
$$\begin{aligned} Q=2\left( {1-\frac{1}{3}\left( {\frac{\left( {4\left( {1+D^{2}} \right) +\left( {\Delta +q} \right) ^{2}} \right) ^{2}}{2q^{2}\left( {\Delta +q} \right) ^{2}}+\frac{\left( {\Delta +q} \right) ^{2}}{4q^{2}}+\frac{24\left( {1+D^{2}} \right) ^{2}}{q^{2}\left( {\Delta +q} \right) ^{2}}} \right) } \right) . \end{aligned}$$
(8)

In Fig. 1, we illuminate the evolution of the global entanglement versus \(\Delta \) for different QRG steps, when \(D=1\). In the calculation, we choose the iteration relation of the Eq. (6) and \(q=\sqrt{8(1+D^{2})+\Delta ^{2}}\). As the iterations are increased, all entanglement crosses each other at the critical point of \(\Delta =\sqrt{2}\). The global entanglement develops two satisfied values, which are two different phases: the spin-fluid phase and the Néel phase. It is worth noting that after enough iteration steps \(Q=\frac{5}{6}\) for \(0\le \Delta <\sqrt{2}\), while \(Q\rightarrow 0\) for \(\Delta >\sqrt{2}\). Compared with the previous works [24–30], the global entanglement Q of three-qubit systems is bigger than that in the arbitrary two-qubit system. What is more, the global entanglement can preferably exhibit a QPT at the critical point. Afterward, the relationship between the global entanglement and DM interaction with the increase in the QRG for \(\Delta =\sqrt{2}\) is shown in Fig. 2. From the figure, one can easily find that the plots of global entanglement exist an intersection each other when \(D=1\) for the different iterations. The global entanglement still can develop two saturated values, which can preferably exhibit QPT at the critical point \(D=1\). After enough iteration steps, we found that \(Q\rightarrow 0\) for \(0\le D<1\), and \(Q=\frac{5}{6}\) for \(D>1\).

Fig. 1
figure 1

Variation of the global entanglement with the anisotropic parameters \((\Delta )\) in the case of different QRG iterations when \(D=1\)

Full size image
Fig. 2
figure 2

Global entanglement as a function of the DM interaction (D) in the case of QRG iterations at a fixed value \(\Delta =\sqrt{2}\)

Full size image
Fig. 3
figure 3

Global entanglement as a function of the anisotropic parameters \((\Delta )\) for the different strength of DM interaction (D)

Full size image

Next, for the sake of developing how the anisotropy parameters and DM interaction influence quantum entanglement, here we have plotted their relation graphs as Fig. 3. One can readily see that global entanglement is decreased with the increase in the anisotropy parameter, when the strength of DM interaction is a constant value. Moreover, the global entanglement is increased with the increase in the strength of DM interaction, when anisotropy parameter is a nonzero value. However, the global entanglement has a maximum constant value \(Q_{\max } =\frac{5}{6}\) when \(\Delta =0\). Hence, one can conclude that the decay of global entanglement can be effectively suppressed by tuning the intensity of DM interaction, i.e., the DM interaction can enhance the global entanglement to some extent, but the anisotropy parameter can weaken the global entanglement.

5 Scaling behaviors and nonanalytic phenomenon

Now, let us illustrate how nonanalytic behavior and no characteristic length scale occur at the intersection point. Remarkably, it indicates that quantum entanglement displays a scaling behavior in the neighborhood of intersection point.

Fig. 4
figure 4

Logarithm of the absolute value of minimum, \(\ln \left( {|\mathrm{d}Q/\mathrm{d}\Delta |_{\min } } \right) \), versus the logarithm of chain size, \(\ln (N)\), which shows a scaling behavior. Each point corresponds to the minimum value of \(\mathrm{d}Q/\mathrm{d}\Delta \)

Full size image

Definitely, we here focus on the behavior of the three-block global entanglement of this large 1D spin 1/2 XXZ model with DM interaction. Firstly, we analyze the scaling behavior of \(y=|\mathrm{d}Q/\mathrm{d}\Delta |_{\Delta _{\min } } \) versus the size of the system N when \(D=1\), where \(\Delta _{\min } \) is the position of the minimum of \(\mathrm{d}Q/\mathrm{d}\Delta \). Distinctly, one can gain that a liner relationship between \(\ln \left( {|\mathrm{d}Q/\mathrm{d}\Delta |_{\min } } \right) \) and \(\ln (N)\) is shown in Fig. 4. At the same time, one can obtain that the position of the minimum \(\Delta _{\min } \) of \(\mathrm{d}Q/\mathrm{d}\Delta \) is slowly close to the intersection point \(\Delta =\sqrt{2}\), which is analyzed in Fig. 5. Through numerical calculation, it is verified that the exponent for this behavior is \(\Delta _{\min } =\Delta _c +N^{-0.461}\).

Subsequently, we also analyze the scaling behavior of \(y=||\mathrm{d}Q/\mathrm{d}D|_{D_{\max } } \) versus the size of the system N for \(\Delta =\sqrt{2}\), where \(D_{\max } \) is the position of the maximum of dQ / dD. In Fig. 6, one can obtain that the position of the maximum \(D_{\max } \) of dQ / dD is slowly close to the critical point \(D=1\), which is analyzed in Fig. 7. After calculation, it is proved that the exponent for this behavior is \(D_{\max } =D_c +N^{-0.111}\). By comparing Figs. 4 with 6, one can find that two straight line slopes are equal, which is equal to 0.72. These results show that the quantum renormalization-group realization is effective and feasible to gain the critical point behavior of the spin 1/2 XXZ model with DM interaction.

Fig. 5
figure 5

Logarithm of \((\Delta _{\min }-\Delta _c)\), \(\ln \left( {\Delta _{\min } -\Delta _c } \right) \), versus the logarithm of chain size, \(\ln (N)\), which shows a scaling behavior. The scaling behavior of \(\Delta _{\min } \) in terms of system size (N) where \(\Delta _{\min } \) is the position of minimum for \(\mathrm{d}Q/\mathrm{d}\Delta \)

Full size image
Fig. 6
figure 6

Logarithm of the absolute value of maximum, \(\ln \left( {|\mathrm{d}Q/\mathrm{d}D|_{\max } } \right) \), versus the logarithm of chain size, \(\ln (N)\), which shows a scaling behavior. Each point corresponds to the maximum value of \(\mathrm{d}Q/\mathrm{d}D\)

Full size image
Fig. 7
figure 7

Logarithm of \((D_{\max } -D_c )\), \(\ln \left( {D_{\max } -D_c } \right) \), versus the logarithm of chain size, \(\ln (N)\), which shows a scaling behavior. The scaling behavior of \(D_{\max } \) in terms of system size (N) where \(D_{\max } \) is the position of maximum for dQ / dD

Full size image

6 Summary

To summarize, we have investigated the dynamical behaviors of the important quantum entanglement witness, the global entanglement in the spin 1/2 XXZ model with DM interaction by the utilization of QRG method. The result shows that the DM interaction can make critical point move backward. Thus, one can modulate the critical point by controlling the DM interaction. Because of this, we claim that our investigation might provide a valid method for studying quantum phase transition in the further. On the other hand, the spoiled entanglement can be recovered by applying the DM interaction for \(\Delta \ne 0\). In addition, after the enough iteration steps, the global entanglement develops two saturated values, which can preferably exhibit QPT at the critical point. Meanwhile, the critical behavior is described by the first derivative of global entanglement of the block, which is increased slowly as the size of the system becomes larger and larger. This indicates that the behavior of the entanglement can perfectly help one observe the quantum critical properties of the spin model. At last, we find that the critical exponent had a relation with the correlation length near the critical point. Thereby, we expect that these results would be helpful for researchers to use the global entanglement as the indicators of the quantum phase transition in the Heisenberg spin models.