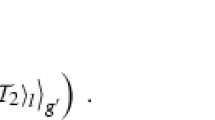Abstract
When a test particle moves about an oblate spheroid, it is acted upon, among other things, by two standard perturbing accelerations. One, of Newtonian origin, is due to the quadrupole mass moment \(J_2\) of the orbited body. The other one, of order \({\mathcal {O}}\left( 1/c^2\right) \), is caused by the static, post-Newtonian field arising solely from the mass of the central object. Both of them concur to induce indirect, mixed orbital effects of order \({\mathcal {O}}\left( J_2/c^2\right) \). They are of the same order of magnitude of the direct ones induced by the post-Newtonian acceleration arising in presence of an oblate source, not treated here. We calculate these less known features of motion in their full generality in terms of the osculating Keplerian orbital elements. Subtleties pertaining the correct calculation of their mixed net precessions per orbit to the full order of \({\mathcal {O}}\left( J_2/c^2\right) \) are elucidated. The obtained results hold for arbitrary orbital geometries and for any orientation of the body’s spin axis \(\hat{\mathbf {{k}}}\) in space. The method presented is completely general, and can be extended to any pair of post-Keplerian accelerations entering the equations of motion of the satellite, irrespectively of their physical nature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
To the first post-Newtonian (1pN) order, the quadrupole mass moment \(J_2\) of an oblate spheroid that is rigidly rotating causes an acceleration of the order \({\mathcal {O}}\left( J_2/c^2\right) \), where c is the speed of light in vacuum, which directly induces long-term orbital variations affecting the motion of a test particle. They have been treated to various levels of completeness elsewhere [3, 10, 11, 25, 27, 28]; the most general calculation, valid for any orbital geometry and arbitrary orientation of the primary’s spin axis can be found in Iorio [15].
Nonetheless, further indirect orbital features of motion of order \({\mathcal {O}}\left( J_2/c^2\right) \) arise due to the interplay of two well known post-Keplerian (pK) accelerations: the Newtonian one induced by \(J_2\), causing the orbital plane of an Earth’s satellite to secularly precess [4, 16, 23], and the 1pN “gravitoelectric" term due to the mass monopole of the body [23, 25, 26], responsible of the formerly anomalous perihelion precession of Mercury [19] of 42.98 arcseconds per century (arcsec cty\(^{-1}\)) [20]. Its explanation by Einstein [7] was the first empirical success of his newborn General Theory of Relativity (GTR). For a recent review, see, e.g., Debono and Smoot [6], and references therein. Calculations for the “mixed" effects resulting from the interplay of the aforementioned pK accelerations, performed mainly recurring to some simplifying assumptions and to various computational schemes, can be found in the literature [9,10,11, 28].
The task of the present work is to calculate them in their full generality, elucidating certain subtleties occurring when one moves from the orbital shifts per revolution to the averaged orbital precessions.
The paper is organized as follows. In Sect. 2, a general overview of the calculation of the mixed effects due to a pair of arbitrary disturbing accelerations is first presented (Sect. 2.1). Then, it is applied to the aforementioned pK perturbations, and explicit expressions for the mixed net shifts per orbit of order \({\mathcal {O}}\left( J_2/c^2\right) \) of all the Keplerian orbital elements, valid for any orbital configurations and arbitrary orientations of the body’s symmetry axis in space, are displayed (Sect. 2.2). Section 3 is devoted to the calculation of the total mixed averaged rates of change of order \({\mathcal {O}}\left( J_2/c^2\right) \) of the orbital elements by elucidating that it is not enough to simply take the ratios of the averaged variations obtained in Sect. 2 to the Keplerian orbital period. Also in this case, explicit expressions of general validity are obtained. In Sect. 4, the results obtained in Sects. 2 to 3 are specialized to two particular configurations: equatorial (Sect. 4.1) and polar (Sect. 4.2) orbits. Section 5 summarizes our results and offers concluding remarks.
2 The mixed net shifts per orbit
2.1 General calculational overview
Let us assume that a perturbing acceleration
made of the sum of two pK accelerations \({\textbf{A}}^\mathrm {\left( 1\right) }\) and \({\textbf{A}}^\mathrm {\left( 2\right) }\) of arbitrary origin, enters the equations of motion of a test particle orbiting a central body in addition to the dominant Newtonian monopole. The osculating Keplerian orbital elements \(\left\{ \kappa \right\} \) of the satellite, i.e. the semimajor axis a, the eccentricity e, the inclination I of the orbital plane to the reference plane \(\left\{ x,\,y\right\} \), the longitude of the ascending node \(\Omega \), the argument of pericenter \(\omega \), and the mean anomaly at epoch \(\eta \) [17, 18], undergo long-term variations; for non-osculating orbital elements in pN dynamics, see Gurfil and Efroimsky [8]. These long-term variations of any one of the Keplerian orbital elements \(\left\{ \kappa \right\} \) can be calculated as averages over one orbital period \(P_{\textrm{b}}\), that are caused not only by each of the two pK accelerations \({\textbf{A}}^\mathrm {\left( 1\right) }\) and \({\textbf{A}}^\mathrm {\left( 2\right) }\) individually as if the other were not present, but also by the simultaneous action of both of them giving rise to indirect, mixed effects. It means
where f is the true anomaly and \(f_0\) is the anomaly at some arbitrary moment of time \(t_0\) assumed as initial instant. Here and in the following, the angular brackets \(\left\langle \cdots \right\rangle \) denoting the average over \(P_{\textrm{b}}\) will be neglected in order to make the overall notation less cumbersome. As it will become clearer below, it is worthwhile noticing that the average is taken over the anomalistic period, i.e., the time elapsed between two successive crossings of the moving pericenter due to the pK acceleration(s). In our work we are interested in the mixed average term, that is
where
It should be noted that \(\partial \left( \textrm{d}\kappa /\textrm{d}f\right) /\partial \eta = 0\) for all the Keplerian orbital elements and for any of the pK accelerations considered here; thus, the summations in Eq. (4) do not run over \(\eta \) as well. In Eq. (4),
is the primary’s gravitational parameter given by the product of the Newtonian constant of gravitation G by its mass M,
is the orbit’s semilatus rectum, and \(A_R,\,A_T\) are the radial and transverse components of the pK acceleration at hand, respectively. Furthermore, the subscript \(``_\textrm{K}"\) means that the quantities in curly brackets to which it is appended are to be evaluated onto the Keplerian ellipse
assumed as unperturbed, reference trajectory. Finally, the derivative \(\textrm{d}\kappa /\textrm{d}f\) of any one of the orbital elements \(\kappa \) with respect to the true anomaly f is given by
where
is the Keplerian expression for the reciprocal of the time derivative of the true anomaly, and \(\textrm{d}\kappa /\textrm{d}t\) is given by the right-hand-side of the corresponding Gaussian equation for its variation. The equations for the variations of the Keplerian osculating elements in the Euler-Gauss form [3, 18, 25, 26] are
is the Keplerian mean motion, which is proportional to the reciprocal of the Keplerian orbital period \(P_{\textrm{b}}^{\left( \textrm{K}\right) }\),
is the argument of latitude, and \(A_N\) is the normal component of the pK acceleration at hand. In Eq. (4), the instantaneous variations of the Keplerian orbital elements \(\Delta \kappa ^{\mathrm {\left( pK\right) }}_j\left( f\right) \) are present; they can be calculated for any of them as
where the derivative, taken from Eqs. (10)–(15), has to be evaluated onto the Keplerian ellipse of Eq. (7) for a given pK acceleration; in this case, the subscript \(``_\textrm{K}"\) is omitted to avoid making the notation too heavy.
Some explanatory remarks about the structure of Eq. (4) are, now, in order. The first two terms of Eq. (2), and the second and the fourth terms in Eq. (4) come from
In obtaining Eq. (19), the pK expression [1, 3, 23]
Equations (8), and (13)–(14) were used. Equation (20) accounts for the fact that, in general, both the nodal and apsidal lines vary instantaneously during an orbital revolution because of pK perturbing accelerations. It does matter since the fast variable of integration is the true anomaly f; as remarked before, the averaging time interval, is the anomalistic period. Going into more detail, the superscripts \(``^\mathrm {\left( 1\right) }"\) and \(``^\mathrm {\left( 2\right) }"\) in Eq. (4) mean that the associated quantities have to be calculated with the pK acceleration \({\textbf{A}}^\mathrm {\left( 1\right) }\) and \({\textbf{A}}^\mathrm {\left( 2\right) }\), respectively. Thus, \(\partial \left( \textrm{d}\kappa /\textrm{d}f\right) ^{\left( 1\right) }/\partial \kappa _j\) and \(\partial \left( \textrm{d}\kappa /\textrm{d}f\right) ^{\left( 2\right) }/\partial \kappa _j\) are to be meant as the partial derivatives of Eq. (8) with respect to \(\kappa _j,\,j = a,\,e,\,I,\,\Omega ,\,\omega \) calculated with the accelerations \({\textbf{A}}^\mathrm {\left( 1\right) }\) and \({\textbf{A}}^\mathrm {\left( 2\right) }\), respectively, onto the Keplerian ellipse. The first and the third terms of Eq. (4), arising from such partial derivatives, occur because, actually, the orbital elements do not stay constant during an orbital revolution; instead, they vary instantaneously because of the pK accelerations. Furthermore, the first term of Eq. (19), calculated with \({\textbf{A}}^\mathrm {\left( 1\right) }\) and \({\textbf{A}}^\mathrm {\left( 2\right) }\) onto the Keplerian ellipse, respectively, yield the first two terms of Eq. (2). The term in square brackets of Eq. (19), calculated with \({\textbf{A}}^\mathrm {\left( 2\right) }\) onto the Keplerian ellipse and multiplied by \(\textrm{d}\kappa /\textrm{d}f\), calculated with \({\textbf{A}}^\mathrm {\left( 1\right) }\) onto the Keplerian ellipse, gives rise to the second mixed term of Eq. (4), while the term in square brackets of Eq. (19), calculated with \({\textbf{A}}^\mathrm {\left( 1\right) }\) onto the Keplerian ellipse and multiplied by \(\textrm{d}\kappa /\textrm{d}f\), calculated with \({\textbf{A}}^\mathrm {\left( 2\right) }\) onto the Keplerian ellipse, gives rise to the fourth mixed term of Eq. (4).
It should be noted that also effects of order \({\mathcal {O}}\left( A^2\right) \) arise from Eq. (4) if it is calculated with the same pK acceleration. They will not be treated here since they would be of order \({\mathcal {O}}\left( J_2^2\right) \) and \({\mathcal {O}}\left( 1/c^4\right) \), respectively.
2.2 The mixed averaged shifts per orbit of order \({\mathcal {O}}\left( J_2/c^2\right) \)
Let us assume that [23]
where R is the body’s equatorial radius, \({\hat{\textbf{k}}}\) is the unit vector directed along its symmetry axis,
is the cosine of the angle between the body’s spin axis and the satellite’s position vector, and
is the radial velocity of the test particle. It turns out that the \(R-T-N\) components of the accelerations of Eqs. (21)–(22) are
and
is the unit vector directed along the line of the nodes toward the ascending node,
is the unit vector directed transversely to the line of the nodes in the orbital plane, and
is the normal unit vector, directed along the orbital angular momentum, such that \({\hat{\textbf{l}}}\mathbf {\times }{\hat{\textbf{m}}}={\hat{\textbf{h}}}\); see, e.g., Brumberg [3]; Soffel [25].
By inserting Eqs. (25)–(27) in Eqs. (10)–(14), one can use Eqs. (18) and (9) to calculate the \(J_2\)-driven instantaneous orbital shifts needed in Eq. (4). They turn out to be
where
The coefficients \({\widehat{T}}_j,\,j=1,\,2,\,\dots 6\) are displayed in Appendix A, while \({\mathcal {A}}_1^{\left( J_2\right) },\ldots {\mathcal {P}}_6^{\left( J_2\right) }\) are shown in Appendix A.1. Equation (18), calculated with Equations (28)–(30) in Eqs. (10)–(14) and (9), yields for the 1pN instantaneous orbital shifts
The instantaneous shifts of \(\eta \) are not displayed since they are not required in Eq. (4). Indeed, as pointed out in Sect. 2.1, the derivatives \(\textrm{d}\kappa /\textrm{d}f\), calculated with either Eqs. (25)–(27) or (28)–(30) in Eqs. (10)–(15), do not contain explicitly \(\eta \).
Equation (4), applied to Eqs. (21)–(22) and calculated with Eqs. (34)–(38) and (44)–(48), allows to obtain the total mixed shifts per orbit of order \({\mathcal {O}}\left( J_2/c^2\right) \). They are
where
The explicit forms of the coefficients \(\mathcal {{\overline{A}}}_1^{\left( J_2/c^2\right) },\ldots \mathcal {{\overline{H}}}_6^{\left( J_2/c^2\right) }\) entering Eqs. (55)–(60) are displayed in Appendix A.2.
3 The mixed averaged precessions
In calculating the mixed averaged orbital precessions \({{\dot{\kappa }}}^{\left( J_2/c^2\right) }_\textrm{mix}\), caution is needed. Their full expressions do not consist only of the ratios
of the mixed net shifts per orbit of Eqs. (49)–(54) to the Keplerian orbital period. Indeed, one has to include also the ratios of the direct averaged variations \(\Delta \kappa ^\mathrm {\left( pK\right) }\) of the orbital elements due to a given pK acceleration \({\textbf{A}}^\mathrm {\left( pK\right) }\) to the total pK period
including the corrections \(\Delta P_{\textrm{b}}^{\left( \textrm{pK}\right) }\) to \(P_{\textrm{b}}^{\left( \textrm{K}\right) }\) due to \({\textbf{A}}^{\left( 1\right) }\) and \({\textbf{A}}^{\left( 2\right) }\), and expanding the resulting expressions to the order required to have just the desired mixed effects. Also in this case, the contributions of order \({\mathcal {O}}\left( A^2\right) \) are neglected.
By following the calculational approach of Iorio [12] for the anomalistic orbital period, it turns out that the corrections to \(P_{\textrm{b}}^{\left( \textrm{K}\right) }\) induced by Eqs. (21)–(22) are
respectively.
The averaged orbital changes due to \(J_2\) are
The 1pN averaged orbital shifts are
Equations (65)–(69) and (71)–(75) are calculated by posing \(f = f_0 + 2\pi \) in Eqs. (34)–(38) and (44)–(48), respectively. Equations (70) and (76) can straightforwardly be obtained from Eqs. (48) and (29), respectively, of Iorio [14] by multiplying the latter ones by \(P_{\textrm{b}}^{\mathrm {\left( K\right) }} = 2\pi /n_{\textrm{b}}^{\mathrm {\left( K\right) }}\).
By using Eq. (64) with Eqs. (65)–(70) and (63) with Eqs. (71)–(76), one finally gets
In Eqs. (81)–(82), it is \(u_0:=f_0 + \omega \). Eqs. (77)–(82) add to the ratios of Eqs. (49)–(54) to the Keplerian orbital period \(P_{\textrm{b}}^{\mathrm {\left( K\right) }}\) in order to give the total mixed orbital precessions of order \({\mathcal {O}}\left( J_2/c^2\right) \); the resulting expressions are too cumbersome to be shown here.
Equations (77)–(82) represent, together with the results of Sect. 2, the primary findings of this investigation. Some special configurations will be investigated in some more detail in the next Sect. 4.
4 Some special orbital configurations
Two peculiar orbital configurations are considered here: a) equatorial (Sect. 4.1) and b) polar (Sect. 4.2) orbits.
By parameterizing \({\hat{\textbf{k}}}\) in terms of the right ascension (RA) \(\alpha \) and declination (DEC) \(\delta \) of the body’s north pole of rotation as
one obtains
These expressions will be used in what follows.
4.1 Equatorial orbit
Let us assume that the satellite’s orbital plane lies in the equatorial plane of the primary, whatever the orientation of the latter in the adopted reference frame, i.e., for generic values of \(\alpha ,\,\delta \): for such an orbital geometry, it is
According to Eqs. (84)–(86), the conditions of Eqs. (87)–(88) are satisfied if
Then, Eqs. (49)–(54) reduce to
4.2 Polar orbit
Let us, now, assume that the body’s spin axis, irrespectively of its orientation, i.e., for generic values of \(\alpha ,\,\delta \), lies somewhere in the satellite’s orbital plane between \({\hat{\textbf{l}}}\) and \({\hat{\textbf{m}}}\). In such a scenario, it is
According to Eqs. (84)–(86), the conditions of Eqs. (103)–(105) are fulfilled if
indeed, with Eqs. (106)–(107), one has just
Thus, Eqs. (49)–(54) reduce to
while Eqs. (77)–(82) can be written as
4.3 Numerical estimates
Here, some order-of-magnitude evaluations of the size of the effects derived in the previous Sects. 4.1 to 4.2 for some natural and artificial bodies in our solar system are given.
For the sake of definiteness, just the amplitude
is calculated.
For Mercury and the Sun, Eq. (123) yields \(5\times 10^{-4}\) microarcseconds per century \(\left( \mu \mathrm {as\,cty}^{-1}\right) \), while for an Earth’s artificial satellite like, e.g., LAGEOS [21], one has \({{\dot{\psi }}} = 0.3\) milliarcseconds per year \(\left( \mathrm {mas\,yr}^{-1}\right) \). For Juno [2], currently orbiting Jupiter, it is \({{\dot{\psi }}} = 0.04\) microarcseconds per year \(\left( \mu \mathrm {as\,yr}^{-1}\right) \). While these figures are only rough indications, they should make it clear how small these effects are. Suffice it to say that, according to the recent planetary ephemerides EPM2017 [22], the current (formal) accuracy in constraining any possible anomalous perihelion precession of Mercury may be calculated to be \(\simeq 10\,\mu \mathrm {as\,cty}^{-1}\) [13]. Furthermore, it is still debated if the satellites of the LAGEOS family were actually able to measure the Lense-Thirring signal of a few tens of mas yr\(^{-1}\) [5] to the per cent level [24].
It is unclear if such mixed effects, which do contribute to the overall orbital evolution, could be actually measurable independently of other dynamical features of motion. Indeed, they do not come from some new pK acceleration, still unmodelled in the softwares used worldwide to process astronomical and geodetic observations of interest. If so, it could be possible, at least in principle, to include it in the dynamical models and estimate some dedicated solve-for parameters in the usual least-square approach of real data reductions. On the other hand, the standard pK accelerations of Eqs. (21) and (22) giving rise to the features of motion which are the subject of this paper are accurately modelled; thus, just very tiny signatures, due to the current level of mismodeling in Eqs. (21)–(22), would impact the post-fit residuals produced in data analyses. Given the already tiny magnitude of the nominal values of such effects, it is even more unlikely than their resulting mismodelled signals may leave any detectable trace.
5 Summary and conclusions
To the 1pN order, the net orbital effects per orbit experienced by a test particle moving around an oblate body include not only those directly induced by the 1pN acceleration of order \({\mathcal {O}}\left( J_2/c^2\right) \), but further ones as well, also of the same order, due to the simultaneous action of two standard pK accelerations: the Newtonian one caused by the quadrupole mass moment \(J_2\) of the primary, and the 1pN gravitoelectric one causing the formerly anomalous perihelion precession of Mercury in the field of the Sun. Such indirect features of motion of order \({\mathcal {O}}\left( J_2/c^2\right) \) arise because, during an orbital revolution, the orbital elements do not remain constant, being instantaneously displaced by each of the pK accelerations. Moreover, the orbital period over which the average is performed is, actually, the time interval between two successive passages at the pericenter which instantaneously moves because of the pK perturbations.
We presented a general approach to analytically calculate the mixed effects arising from the interplay of two pK accelerations, irrespectively of their physical origin. As a result, we, first, explicitly calculated the mixed net shifts per orbit of all the osculating Keplerian orbital elements to the order of \({\mathcal {O}}\left( J_2/c^2\right) \). It turned out that all of them undergo generally non-vanishing changes of this type.
Then, we worked out their mixed averaged rates elucidating that their total expressions can only be obtained if also the ratios of the direct net shifts per orbit due to each pK acceleration to the pK orbital period are taken in addition to the ratios of the mixed ones to the Keplerian one. Also in this case, analytic expressions of general validity were derived: no approximations pertaining both the satellite’s orbital geometry and the spatial orientation of the body’s spin axis were adopted. It turned out that the semimajor axis and the eccentricity stay constant in the aforementioned calculation.
Subsequently, we obtained simplified expressions for all the mixed effects under consideration that are specialized to the equatorial and polar orbit scenarios. In the former case, only the pericenter and the mean anomaly at epoch undergo non-vanishing mixed variations. In the latter, while the mixed net shifts per orbit of the inclination and the node are zero, the precessional contributions due to the pK period are non-vanishing only for the pericenter and the mean anomaly at epoch.
The nominal size of the effects studied in this work is very tiny for various astronomical scenarios of potential interest in our solar system; as an example, the perihelion of Mercury would be impacted at the level of \(\simeq 10^{-4}\,\mu \mathrm {as\,cty}^{-1}\), compared to today’s (formal) accuracy in constraining any possible anomalous precession of just \(\simeq 10\,\mu \mathrm {as\,cty}^{-1}\). Furthermore, since they arise from the interplay of standard accelerations which are routinely modelled to a high level of accuracy in the softwares used in real data reductions, only mismodelled signatures, much smaller than the already tiny nominal ones, should affect the post-fit residuals produced in data analyses.
Data availibility
No new data were generated or analysed in support of this research.
References
Bertotti, B., Farinella, P., Vokrouhlický, D.: Physics of the solar system. Kluwer, Dordrecht, Aug 2003. https://doi.org/10.1007/978-94-010-0233-2
Bolton, S.J., Lunine, J., Stevenson, D., Connerney, J.E.P., Levin, S., Owen, T.C., Bagenal, F., Gautier, D., Ingersoll, A.P., Orton, G.S., Guillot, T., Hubbard, W., Bloxham, J., Coradini, A., Stephens, S.K., Mokashi, P., Thorne, R., Thorpe, R.: The Juno Mission. Space Sci. Rev. 213(1–4), 5–37 (2017). https://doi.org/10.1007/s11214-017-0429-6
Brumberg, V.A.: Essential Relativistic Celestial Mechanics. Adam Hilger, Bristol (1991)
Capderou, M.: Satellites. Orbits and Missions. Springer-Verlag France, Paris, (2005). https://doi.org/10.1007/b139118
Ciufolini, I., Paolozzi, A., Koenig, R., Pavlis, E.C., Ries, J., Matzner, R., Gurzadyan, V., Penrose, R., Sindoni, G., Paris, C.: Fundamental Physics and General Relativity with the LARES and LAGEOS satellites. Nucl. Phys. B Proc. Suppl. 243, 180–193 (2013). https://doi.org/10.1016/j.nuclphysbps.2013.09.005
Debono, I., Smoot, G.F.: General relativity and cosmology: unsolved questions and future directions. Universe 2, 23 (2016). https://doi.org/10.3390/universe2040023
Einstein, A.: Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie. Sitzber. Preuss. Akad. 47, 831–839 (1915)
Gurfil, P., Efroimsky, M.: Analysis of the PPN two-Body Problem using non-osculating orbital elements. Adv. Space Res. 69(1), 538–553 (2022). https://doi.org/10.1016/j.asr.2021.09.009
Heimberger, J., Soffel, M., Ruder, H.: Relativistic effects in the motion of artificial satellites—The oblateness of the central body II. Celest. Mech. Dyn. Astr. 47(2), 205–217 (1989). https://doi.org/10.1007/BF00051205
Huang, C., Liu, L.: Analytical solutions to the four post-Newtonian effects in a near Earth satellite orbit. Celest. Mech. Dyn. Astr. 53(3), 293–307 (1992). https://doi.org/10.1007/BF00052615
Iorio, L.: Post-Newtonian direct and mixed orbital effects due to the oblateness of the central body. Int. J. Mod. Phys. D 24(8), 1550067–59 (2015). https://doi.org/10.1142/S0218271815500674
Iorio, L.: Post-Keplerian corrections to the orbital periods of a two-body system and their measurability. Mon. Not. Roy. Astron. Soc. 460(3), 2445–2452 (2016). https://doi.org/10.1093/mnras/stw1155
Iorio, L.: Calculation of the Uncertainties in the Planetary Precessions with the Recent EPM2017 Ephemerides and their Use in Fundamental Physics and Beyond. Astron J. 157(6), 220 (2019). https://doi.org/10.3847/1538-3881/ab19bf
Iorio, L.: On the mean anomaly and the mean longitude in tests of post-Newtonian gravity. Eur. Phys. J. C 79(10), 816 (2019). https://doi.org/10.1140/epjc/s10052-019-7337-8
Iorio, L.: Post-Newtonian orbital effects induced by the mass quadrupole and spin octupole moments of an axisymmetric body. arXiv e-prints, art. arXiv:2310.02834, (2023). https://doi.org/10.48550/arXiv.2310.02834
King-Hele, D.G.: The effect of the earth’s oblateness on the orbit of a near satellite. Proc. R. Soc. A 247(1248), 49–72 (1958). https://doi.org/10.1098/rspa.1958.0169
Klioner, S.A., Kopeikin, S.M.: The post-keplerian orbital representations of the relativistic two-body problem. Astrophys. J. 427, 951 (1994). https://doi.org/10.1086/174201
Kopeikin, S.M., Efroimsky, M., Kaplan, G.: Relativistic celestial mechanics of the solar System. Wiley-VCH, Weinheim, (2011). https://doi.org/10.1002/9783527634569
Le Verrier, U.: Lettre de M. Le Verrier à M. Faye sur la théorie de Mercure et sur le mouvement du périhélie de cette planète. Cr. Hebd. Acad. Sci., 49:379–383, (1859)
Nobili, A.M., Will, C.M.: The real value of Mercury’s perihelion advance. Nature 320, 39–41 (1986). https://doi.org/10.1038/320039a0
Pearlman, M., Arnold, D., Davis, M., Barlier, F., Biancale, R., Vasiliev, V., Ciufolini, I., Paolozzi, A., Pavlis, E.C., Sośnica, K., Bloßfeld, M.: Laser geodetic satellites: a high-accuracy scientific tool. J. Geod. 93(11), 2181–2194 (2019). https://doi.org/10.1007/s00190-019-01228-y
Pitjeva, E.V., Pitjev, N.P.: Masses of the main asteroid belt and the kuiper belt from the motions of planets and spacecraft. Astron. Lett. 44(8–9), 554–566 (2018). https://doi.org/10.1134/S1063773718090050
Poisson, E., Will, C.M.: Gravity. Cambridge University Press, Cambridge, (2014). https://doi.org/10.1017/CBO9781139507486
Renzetti, G.: History of the attempts to measure orbital frame-dragging with artificial satellites. Centr. Eur. J. Phys. 11(5), 531–544 (2013). https://doi.org/10.2478/s11534-013-0189-1
Soffel, M.H.: Relativity in Astrometry, Celestial Mechanics and Geodesy. Springer, Heidelberg, (1989). https://doi.org/10.1007/978-3-642-73406-9
Soffel, M.H., Han, W.-B.: Applied General Relativity. Astronomy and Astrophysics Library. Springer Nature Switzerland, Cham, (2019). https://doi.org/10.1007/978-3-030-19673-8
Soffel, M.H., Wirrer, R., Schastok, J., Ruder, H., Schneider, M.: Relativistic effects in the motion of artificial satellites—The oblateness of the central body i. Celest. Mech. Dyn. Astr. 42(1–4), 81–89 (1987). https://doi.org/10.1007/BF01232949
Will, C.M.: Incorporating post-Newtonian effects in N-body dynamics. Phys. Rev. D 89(4), 044043 (2014). https://doi.org/10.1103/PhysRevD.89.044043
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
I declare no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Coefficients of some orbital variations
Coefficients of some orbital variations
The coefficients \({\widehat{T}}_j,\,j=1,\,2,\,\dots 6\) entering Eqs. (39)–(43) and (55)–(60) in Sect. 2.2 are
They depend on I and \(\Omega \), and on the polar angles in terms of which \({\hat{\textbf{k}}}\) is parameterized; see, e.g., Eqs. (83)–(86).
1.1 Coefficients of the instantaneous Newtonian shifts due to \(J_2\)
Here, we deal with the instantaneous Newtonian shifts induced by \(J_2\) calculated in Sect. 2.2. We display the explicit expressions of the coefficients \({\mathcal {A}}_1^{\left( J_2\right) },\ldots {\mathcal {P}}_6^{\left( J_2\right) }\) entering Eqs. (39)–(43), which are
1.2 Coefficients of the total mixed shifts per orbit of order \(J_2/c^2\)
Here, the mixed averaged shifts per orbit of order \({\mathcal {O}}\left( J_2/c^2\right) \), calculated in Sect. 2.2, are treated. The explicit expressions of the coefficients \(\mathcal {{\overline{A}}}_1^{\left( J_2/c^2\right) },\ldots \mathcal {{\overline{H}}}_6^{\left( J_2/c^2\right) }\) entering Eqs. (55)–(60) are displayed below. They read
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Iorio, L. The post-Newtonian motion around an oblate spheroid: the mixed orbital effects due to the Newtonian oblateness and the post-Newtonian mass monopole accelerations. Gen Relativ Gravit 55, 136 (2023). https://doi.org/10.1007/s10714-023-03184-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10714-023-03184-7