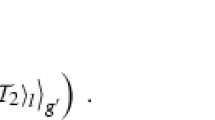1 Introduction

Newtonian gravity is the first-order approximation to Einstein’s covariant and non-linear theory of gravitation; General Relativity (GR) (d’Inverno 1992; Misner et al. 1973; Weinberg 1972). The field equations of GR are a system of ten, non-linear, coupled partial differential equations; hence, obtaining exact analytical solutions (Stephani et al. 2009) is a notoriously formidable task. Notable solutions are given by Schwarzschild (1916) and Kerr (1963) which describe highly ideal gravitational systems for non-rotating, spherically symmetric and rotating, axially symmetric black holes respectfully.

As early as 1916, Einstein hypothesised (Einstein 1916, 1918) the existence of gravitational waves using a weak-field approximation (d’Inverno 1992; Misner et al. 1973; Weinberg 1972) of the field equations of gravity. The first direct observation of gravitational waves was due to the coalescence of a binary black hole system (Abbott et al. 2016), which was detected by the advanced laser interferometer gravitational-wave observatory collaboration (Abbott et al. 2009; Harry 2010). More recently, a simultaneous observation of both gravitational waves (Abbott et al. 2017) and electromagnetic radiation (Goldstein et al. 2017) due to the merger of a binary neutron star system was detected by the collaboration and the low Earth orbit Fermi—Gamma-ray burst monitor (Meegan et al. 2009) respectfully.

The treatment of such binary systems under the full non-linear field equations of GR requires such a spacetime to provide a complete description of the entire history of the binary system. Specifically, the solution is required to describe past events such as the formation of the bodies, and future events such as the final merger of the binary system (Poisson and Will 2014). Due to the complexity of the field equations, no such solution presently exists. Hence, to accommodate the complexities associated with Einstein’s non-linear theory of gravity, approximation methods have been developed to determine solutions of the field equations and the accurate modelling of \(n\)-body systems. This is achieved using the Post-Newtonian (PN) approximation (Brumberg 2017; Poisson and Will 2014; Soffel 1989) which has proven to be an important practical approximation for gravitational wave astronomy and has been coined unreasonably effective (Poisson and Will 2014) in the description of gravitational physics. The PN approximation is relied upon in areas such as astronomy, geodesy (Müller et al. 2008) and deep space navigation (Moyer 2005) for successfully accounting for the departure from Newtonian gravity due to GR. Furthermore, in order to accurately describe the binary or one-body systems in the PN regime, a complete understanding of the governing mechanics is required.

The present paper derives a new Binet equation in the first post-Newtonian regime which characterises the orbit of test particles. The PN Binet equation is obtained by direct integration of the associated planar equations of motion, where the expression so obtained does not appear to have been given in the literature. The newly obtained expression contains exponential functions that when approximated can produce known linear results. The accuracy of the PN Binet equation is verified by comparing the long-term secular variations of both orbit equations (12) and (13) with the full non-linear general relativistic orbit equation (16). The results of the numerical simulation suggest that retaining the exponential functions produces precessing orbits which closely resemble that of GR. The paper is organised as follows: in Sect. 2, we outline the procedure required to derive the relativistic \(n\)-body equations of motion associated with non-spinning point particles that are sufficiently separated such that the only gravitational contribution to each body is given by their respective monopole moment. In Sect. 3, we derive a new PN Binet equation associated with the relativistic Kepler problem offering insight in to the mechanics of orbiting bodies in the relativistic domain for both near-Earth objects and astronomical binary systems which are currently of significant interest to astronomical communities. The expression obtained confirms the same formal mathematical structure as the energy integral given by the present authors O’Leary et al. (2018) and is discussed in Sect. 4.

2 Post-Newtonian equations of motion

In this section, we derive the PN equations of motion for a test particle containing arbitrary, spatially and temporally dependent, scalar, vector and PN gravitational potentials \(U\), \(U_{j}\) and \(\varPsi \) respectively (Poisson and Will 2014). This is then generalised to describe a system of \(n\) gravitationally interacting mass monopoles (Poisson and Will 2014). The \(n\)-body relativistic equations of motion are known as the Einstein-Infeld-Hoffmann (EIH) equations (Einstein et al. 1938) and form the foundation in computing modern planetary ephemeris files (Soffel 1989). The convention we adopt here is as follows: Latin indices are reserved for spatial variables \((i,j = 1,2,3)\) while Greek indices \((\alpha ,\beta = 0,1,2,3)\) are used for spacetime variables, with the \(0^{\mbox{th}}\) designated for time. Finally, the Einstein summation convention is assumed for repeated indices unless otherwise stated.

The 10 independent components describing the gravitational field are contained within the metric tensor \(g_{\mu \nu }\) (d’Inverno 1992; Weinberg 1972) which depends on the spacetime variables \(x^{\alpha }= (ct,x^{j}) = (ct, \mathbf{r})\), where the speed of light and coordinate time are given by \(c\) and \(t\) respectively. The position of the test particle is given by \(\mathbf{r} = r\hat{\mathbf{r}}\) where \(\hat{\mathbf{r}}\) is a unit vector in Cartesian coordinates and \(r\) denotes the magnitude of the position vector. The first-PN metric tensor components \(g_{\mu \nu }\) are formally obtained by performing two iterations of the relaxed Einstein field equations and are given by (Poisson and Will 2014)

$$ \begin{aligned} g_{00} &= -1 + 2U/c^{2} + 2\bigl(\varPsi - U^{2}\bigr)/c^{4}, \\ g_{0j} & = -4U_{j} /c^{3}, \\ g_{ij} & = \delta _{ij} \bigl(1 + 2U/c^{2}\bigr), \end{aligned} $$
(1)

where the Kronecker delta function is given by \(\delta _{ij}\). The reader is referred to Poisson and Will (2014) for detailed discussions on the origin and integral representations of potentials \(U\), \(U_{j}\) and \(\varPsi \). The motion of a test particle in the spacetime governed by the metric tensor components (1) is described by a modified geodesic equation (Weinberg 1972)

$$\begin{aligned} \frac{d^{2} x^{\alpha }}{dt^{2}} &= \biggl( \frac{d t}{d \tau } \biggr) ^{-1} \frac{d}{d \tau } \biggl( \biggl( \frac{d t}{d \tau } \biggr) ^{-1} \frac{d x^{\alpha }}{d \tau } \biggr) , \\ &= - \biggl( \varGamma ^{\alpha }_{\beta \gamma } - \frac{v^{\alpha }}{c} \varGamma ^{0}_{\beta \gamma } \biggr) v^{\beta }v^{\gamma }, \end{aligned}$$
(2)

where the proper time of the test particle is given by \(\tau \) and the associated coordinate velocity is defined by \(v^{\alpha }= (c,v^{j}) = (c,\mathbf{v})\) and \(\mathbf{v} = d \mathbf{r} /dt\). The Christoffel symbols of the second kind \(\varGamma ^{\alpha }_{\beta \gamma }\) are expressed in terms of first derivatives of the metric tensor components (1) and are defined by

$$ \varGamma ^{\alpha }_{\beta \gamma } = g^{\alpha \delta } ( \partial _{ \gamma } g_{\delta \beta } + \partial _{\beta } g_{\delta \gamma } - \partial _{\delta }g_{\beta \gamma })/2, $$
(3)

where \(\partial _{\gamma } \equiv \partial / \partial x^{\gamma }\) and explicit calculations of (3) can be found in Poisson and Will (2014). Finally, the equations of motion are obtained by substituting the non-zero, independent Christoffel symbols in (2) and are given by (Poisson 2007; Poisson and Will 2014)

$$\begin{aligned} \frac{d^{2} x^{j}}{dt^{2}} = & \partial _{j} U + \frac{1}{c^{2}} \bigl[ \bigl(v ^{k} v_{k} - 4U\bigr) \partial _{j} U \\ &- \bigl(4 v^{m} \partial _{m} U + 3 \partial _{t} U\bigr) v^{j} \\ & - 4 v^{n} (\partial _{j} U_{n} - \partial _{n} U_{j}) + 4\partial _{t} U_{j} + \partial _{j} \varPsi \bigr]. \end{aligned}$$
(4)

We note the equations of motion (4) are characterised by spatial variables only i.e. the case \(\alpha = 0\) in (2) is trivial. In order to derive the EIH equations using (4), a decomposition of \(U\), \(U_{j}\), \(\varPsi \) into internal and external components is required where the reader is referred to Poisson (2007) and Poisson and Will (2014) for the associated lengthy and laborious calculations. The case where \(n=2\) for the EIH equations is of particular interest and is discussed in the following section.

3 The post-Newtonian Kepler problem

The Kepler problem is the most well studied problem in classical celestial mechanics. It describes the motion of two spherically symmetric bodies about a common barycentre due to their mutual gravitational attraction. The general relativistic and Newtonian two-body problems are covered extensively in the literature (Blanchet et al. 2011; Damour 1987; Damour and Deruelle 1985) with the perturbed Kepler problem playing a central role in fields such as precise satellite orbit propagation and prediction (Montenbruck and Gill 2012; Vallado 2001). In this section, we present a new formal solution to the first-PN Kepler problem and derive the associated PN Binet equation characterising the orbit of test particles.

The PN two-body equations of motion are given by (Poisson 2007; Poisson and Will 2014)

$$\begin{aligned} \frac{d^{2} \mathbf{r}}{dt^{2}} =& -\frac{\mu }{r^{2}}\hat{\mathbf{r}}\\ & - \frac{\mu }{c^{2}r^{2}} \biggl[ (1+3\eta ) (\mathbf{v} \cdot \mathbf{v}) - \frac{3}{2}\eta \dot{r}^{2} - 2(2+\eta ) \frac{\mu }{r} \biggr] \hat{\mathbf{r}} \\&+ \frac{2\mu }{c^{2}r^{2}}(2-\eta ) \dot{r} \mathbf{v}, \end{aligned}$$
(5)

where we introduce \(\mu = G (m_{1} + m_{2})\), \(\eta = m_{1}m_{2}/(m _{1} +m_{2})^{2}\) and we denote the mass of body \(i\) (for \(i=1,2\)), Newton’s gravitational constant and the radial component of the velocity as \(m_{i}\), \(G\) and \(\dot{r}\) respectively. Finally, derivatives with respect to time are denoted using the usual dot notation. We note that \(\eta \) is given as a reduced mass term (Poisson and Will 2014) synonymous with the gravitational two-body problem and in the limit \(\eta \rightarrow 0\), we recover the one-body problem.

The corresponding system of coupled differential equations associated with (5) are given by (Poisson 2007; Poisson and Will 2014)

$$\begin{aligned} \ddot{r} = {}&r \dot{\theta }^{2} - \frac{\mu }{r^{2}} + \frac{\mu }{c ^{2}r^{2}} \biggl[ 3\dot{r}^{2} - \frac{7}{2}\eta \dot{r}^{2}\\&{} - (1+3 \eta ) (r\dot{\theta })^{2} + 2(2+\eta ) \frac{\mu }{r} \biggr] , \end{aligned}$$
(6a)
$$ 2r\dot{r} \dot{\theta } + r^{2} \ddot{\theta } = 2(2- \eta ) \frac{ \mu }{c^{2}} \dot{r}\dot{\theta }, $$
(6b)

where Eqs. (6a), (6b) are separated in to respective radial and angular components. The integration of (6b) with respect to time produces an alternative expression for the classical angular momentum in the PN Kepler problem in plane polar coordinates given by

$$ r^{2} \dot{\theta } = h_{0} e^{-2(2-\eta ) \mu / (c^{2} r)}, $$
(7)

where \(h_{0}\) is a constant of integration. The formal procedure adopted in celestial mechanics is to introduce a Binet transformation (d’Inverno 1992) where \(\theta \) replaces time as the independent variable through the relations

$$ \begin{aligned} r &= \frac{1}{u}, \qquad \dot{r} = -h_{0} u' e^{-2(2-\eta )\mu u / c^{2}}, \\ \ddot{r} &= -h_{0}^{2} u^{2} \biggl[ u'' - \frac{2(2-\eta )\mu }{c ^{2}}\bigl(u' \bigr)^{2} \biggr] e^{-4(2-\eta )\mu u / c^{2}}, \end{aligned} $$
(8)

where \(u = u(\theta )\) and \(u' = du/d\theta \). The simplification of (6a) is greatly facilitated by multiplication of \(-2u'/(u h_{0})^{2}\) and substitution of the relations (8) given by

$$\begin{aligned} & \biggl[ 2u' \bigl(u'' + u\bigr) - \frac{\mu u' (2 + 3\eta )}{c^{2}}\bigl( \bigl(u'\bigr)^{2} + u^{2}\bigr) \biggr] e^{-4(2-\eta )\mu u / c^{2}} \\ &\quad = \frac{2\mu u'}{h_{0} ^{2}} \\ &\qquad {}- \frac{4\mu ^{2}uu'(2+\eta )}{h_{0}^{2}c^{2}} + \frac{3\eta \mu u ^{2}u'}{c^{2}} e^{-4(2-\eta )\mu u / c^{2}}. \end{aligned}$$
(9)

We note that in the test particle (\(\eta \rightarrow 0\)) and Newtonian limits (\(c \rightarrow \infty \)), Eq. (9) reduces to the well known classical Binet equation (d’Inverno 1992) with associated solution describing conic sections. A new method to derive the equivalent first-PN Binet equation is presented below.

By introducing \(\delta \equiv (u')^{2} + u^{2}\), we express Eq. (9) as a first order differential equation given by

$$\begin{aligned} \bigl( \delta e^{-(2+3 \eta )\mu u/c^{2}} \bigr) ' ={}&\frac{2 \mu u'}{h_{0}^{2}} \biggl[ 1 - \frac{2\mu u (2+\eta )}{c^{2}} \biggr] e^{(6-7\eta )\mu u/c^{2}} \\ &{} + \frac{3\eta \mu u^{2}u'}{c^{2}}e^{-(2+3\eta )\mu u / c^{2}} , \end{aligned}$$
(10)

where we note Eq. (10) has been multiplied by \(\exp {[(6-7\eta )\mu u/c^{2}]}\) in order to obtain the appropriate integrating factor.

The analytical solution to Eq. (10) can be reduced to quadrature and would need to be evaluated numerically as an integral. The corresponding second order differential equations characterising orbits for binary and one-body systems in the first PN regime are given by

$$\begin{aligned} &u'' + \biggl( 1+ \frac{3\eta }{2+3\eta } + \frac{8\mu ^{2} (4-\eta ^{2})}{h_{0}^{2} c^{2} (6-7\eta )}e^{4 (2 - \eta ) \mu u/c^{2}} \biggr) u \\ &\quad =\frac{\delta _{0} \mu (2+3\eta )}{2c^{2}} e^{ (2+3\eta ) \mu u/c^{2}} \\&{}\qquad + \frac{2\mu (17\eta ^{2} - 32\eta + 28)}{h_{0}^{2} (6-7\eta )^{2}} e ^{4 (2 - \eta ) \mu u/c^{2}} - \frac{3\eta c^{2}}{\mu (2+3\eta )^{2}}, \end{aligned}$$
(11)

and

$$ u'' + \biggl( 1 + \frac{16 \mu ^{2}}{3h_{0}^{2} c^{2}} e^{8\mu u /c ^{2}} \biggr) u = \frac{14 \mu }{9 h_{0}^{2}}e^{8\mu u /c^{2}} - \frac{5 \mu }{9h_{0}^{2}} e^{2 \mu u /c^{2}}, $$
(12)

respectfully. We note that \(\delta _{0}\) is introduced above as an arbitrary constant of integration arising from (10). Equation (12) is the first PN Binet equation which does not appear to have been given in the literature. The value of \(\delta _{0}\) is determined by adding the requirement that in the Newtonian limit we recover the classical Binet equation and is given by \(\delta _{0} = -5c^{2}/9h_{0}^{2}\). Again, we note, the value of \(\delta _{0}\) is consistent with results in O’Leary et al. (2018).

4 Discussion

The problem of motion in GR (see Damour 1987 for a thorough review) has a vast and extensive literature. Many authors have approached the two-body problem in the first-PN approximation by formulating the problem in terms of osculating elements (see Kopeikin et al. 2011, Soffel 1989, Will 2011 and references therein). In contrast to this, we have developed the corresponding solutions by adopting a direct integration approach. In doing so, we obtain the fully analytical PN Binet equation and as expected, in the appropriate limit we recover known results.

The PN orbit equation (11) describes the motion of a binary system of arbitrary masses \(m_{1}\) and \(m_{2}\). Expanding the exponential functions (to PN order) in (12) using a Taylor series approximation gives

$$ u'' + \biggl( 1 - \frac{6\mu ^{2}}{h_{0}^{2} c^{2}} \biggr) u = \frac{ \mu }{h_{0}^{2}}. $$
(13)

The solution to (13) is well known and given by

$$ u(\theta ) = \frac{\mu }{h_{0}^{2}} + \frac{6 \mu ^{3}}{h_{0}^{4} c ^{2}} + u_{0} \cos \biggl( \biggl[ 1 - \frac{6\mu ^{2}}{h_{0}^{2} c ^{2}} \biggr] ^{1/2} \theta - \theta _{0} \biggr) , $$
(14)

where \(u_{0}\), \(\theta _{0}\) are arbitrary constants of integration. The orbit described by Eq. (14) is no longer \(2\pi \)-periodic but precesses about an angle

$$ \Delta \theta = 2\pi \biggl( 1 - \frac{6 \mu ^{2}}{h_{0}^{2} c^{2}} \biggr) ^{-1/2} \approx 2\pi + \frac{6 \pi \mu ^{2}}{h_{0}^{2} c^{2}}. $$
(15)

Equation (15) is well-known and accounts for the relativistic contribution to planetary perihelion precession such as the anomalous precession associated with Mercury.

We note that Eq. (12) is the exact analytical first-PN Binet equation which does not appear in the literature. Interestingly, the same mathematical structure arises when deriving the energy associated with a test particle in the first-PN approximation (O’Leary et al. 2018). With this, the question arises as to whether there is a benefit in retaining the exponential terms in (12) over the corresponding series expansion (13); this answer is in the affirmative and is presented below.

The general relativistic Binet equation is well known and presented in most GR undergraduate textbooks (d’Inverno 1992; Weinberg 1972) given by

$$ u'' + u = \frac{\mu }{h_{0}^{2}} + \frac{3\mu }{c^{2}} u^{2}. $$
(16)

Equation (16) can be derived from a variational formulation and describes the geodesic motion of a test particle in Schwarzschild geometry. Introducing \(\xi = u/u_{c}\) in Eqs. (12), (13) and (16) we obtain the corresponding non-dimensionalised equations given by

$$ \xi ''+ \biggl( 1 + \frac{16 \beta }{3} e^{8 \beta \xi } \biggr) \xi = \frac{14}{9}e^{8 \beta \xi } - \frac{5}{9}e^{2 \beta \xi }, $$
(17)
$$ \xi '' + ( 1 - 6\beta ) \xi = 1, $$
(18)
$$ \xi '' + \xi = 1 + 3 \beta \xi ^{2}, $$
(19)

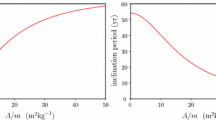
respectfully where \(u_{c}\) is a characteristic unit with the same dimensions as \(u\) and \(\beta \equiv \mu ^{2}/(h_{0}^{2} c^{2})\) is a dimensionless parameter. To demonstrate the advantage of retaining the exponential functions in (12) we adopt the approach given in Koberlein and Meisel (2013) by identifying the long-term secular changes in the positions of (12) and (13) when compared with the full GR Binet equation (16) discussed in Fig. 1. We perform an orbit simulation by numerically integrating the non-dimensionalised differential equations given above subject to the initial conditions \(\xi (0) = 1.3\) and \(\xi '(0) = 0\) and \(\beta = 0.01\) which approximately corresponds to an orbit with semi-major axis \(a=1\) and eccentricity \(e = 0.5\). The results given in Fig. 1 suggest that the characterisation of relativistic orbits in the PN regime should retain the exponential terms associated with the newly derived PN Binet equation in order to closely resemble the orbit of a test particle in GR.

Fig. 1
figure 1

Comparisons of secular variation in PN orbits. (a) and (b) demonstrate the secular variations of Eqs. (17) and (18) when compared with (19) by computing the differences in positions \(u\) at each integration step. (c) Simultaneously compares (a) and (b) indicating that retaining the exponential terms in (12) and (17) is more consistent with the well-known general relativistic Binet equation. The simulation uses initial conditions given by \(\xi (0) = 1.3, \xi '(0) = 0\) and \(\beta = 0.01\) which approximately correspond to an orbit with semi-major axis \(a=1\) and eccentricity \(e = 0.5\)

Full size image