Quasi-Keplerian motion under the generally parameterized post-Newtonian force

Abstract

The analytical solutions for the quasi-Keplerian motion under the generally parameterized post-Newtonian force are derived in the Brumberg–Damour–Deruelle representation. The solutions are formulated in terms of the orbital energy and angular momentum. The achieved results can be applied to not only the motion of a test particle but also the relative motion of a binary system in a broad spectrum of gravitation theories.

1 Introduction

Newton theory cannot be applied to the cases of the strong gravitational fields, and we need consider other gravitation theories. For the first post-Newtonian (PN) approximation, the general model for the dynamics of a test particle in the spherically symmetric gravitational field can be described by the force [1,2,3,4]

$$\begin{aligned} \varvec{F} = -\frac{m\varvec{x}}{r^3}+\frac{m\varvec{x}}{r^3} \Big [2\sigma \frac{m}{r}-2\epsilon \varvec{v}^2+3\alpha \frac{(\varvec{v}\cdot \varvec{x})^2}{r^2}\Big ]+2\mu \frac{m(\varvec{v}\cdot \varvec{x})}{r^3}\varvec{v}~, \end{aligned}$$

(1)

where we use the natural units in which the gravitational constant and the speed in the vacuum are set as 1. m is the gravitational source’s mass. $\varvec{x}$ and $\varvec{v}$ denote the position and velocity vectors of the test particle. $r\equiv |\varvec{x}|$ is the distance between the test particle and the source which is located at the origin of the coordinates. The combinations of the parameters $\sigma ,~\epsilon ,~\alpha$ and $\mu$ can characterize the force in various gravitation theories. In fact, this force can also cover the two-body problems in the parameterized post-Newtonian (PPN) frame [3, 4]. The relations between these four parameters and the PPN parameters have been given in Ref. [4], and the constraints on the latter can be found in Ref. [5]. The comprehensive discussions on the motion in the PN Schwarzschild field can also be found in Ref. [6].

Table 1 gives the values of these parameters for general relativity (GR) and the Brans–Dicke (B–D) theory in the harmonic coordinates [7], as well as GR being applied for a binary system [4]. $\omega$ is the constant of the B–D theory. For a binary system with masses $M_1$ and $M_2$, $m\!\equiv \!M_1\!+\!M_2$ is the total mass of the system, and $\nu \!\equiv \!\frac{M_1M_2}{m^2}$ is called as the dimensionless reduced mass [5].

Table 1 The values of $\sigma ,~\epsilon ,~\alpha ,~\mu$ of GR and the B–D theory with constant $\omega$ in the harmonic coordinates as well as GR being applied to a binary system with the dimensionless reduced mass $\nu$

Brumberg first obtains the quasi-Keplerian solution for this force in terms of the osculating elements [1]. Later, Klioner and Kopeikin present the formulations of the analytical solution in the Damour–Deruelle representation [8], the Epstein-Haugan representation [9, 10], as well as the Brumberg representation [2], and explicitly give the relations of the PN semi-major axis and eccentricity in these representations to the constants of the Brumberg’s osculating-element solution [4].

In this work, we follow the approaches given by Brumberg [2] and Soffel et al. [11], to derive the solution for the quasi-Keplerian motion under the generally PN force in Brumberg–Damour–Deruelle representation. The analytical solution is formulated in terms of the orbital energy and angular momentum, being different from those in Ref. [4].

The rest of paper is organized as follows. In Sect. 2 we calculate the Lagragian, energy and angular momentum of a test particle under the generally parameterized force. In Sect. 3 we present two slightly different formulations of the quasi-Keplerian solution, as well as the detailed derivations. Section 4 gives some applications. Summary is given in Sect. 5.

2 The Lagrangian, energy, angular momentum under the generally parameterized force

With the force Eq. (1), following the Euler-Lagrange equation

$$\begin{aligned} \frac{d}{dt}\frac{\partial \mathrm {L}}{\partial \varvec{v}}= \frac{\partial \mathrm {L}}{\partial \varvec{x}}~, \end{aligned}$$

(2)

we can obtain the corresponding Lagrangian of the test particle

$$\begin{aligned}&\mathrm{L} \!= \!\frac{\varvec{v}^{2}}{2}\!+\!\frac{m}{r} \!-\!\Big (\!\frac{\epsilon }{4}\!-\!\frac{\alpha }{4}\!-\!\frac{\mu }{8}\!\Big )\!\varvec{v}^{4}\! \!+\!\Big (\!\epsilon \!-\!\alpha \!+\!\frac{\mu }{2}\!\Big )\!\frac{m}{r}\varvec{v}^{2}\!\!-\! \Big (\!\sigma \!-\!\epsilon \!-\!\frac{\mu }{2}\!\Big )\!\frac{m^2}{r^2}\!+\!\alpha \frac{m(\varvec{v}\!\cdot \!\varvec{x})^2}{r^3}\!.\nonumber \\ \end{aligned}$$

(3)

Based on this Lagrangian, we can calculate the energy $\mathcal {E}$ and the angular momentum $\mathcal {J}$ of the post-Newtonian motion as follows

$$\begin{aligned}&\mathcal {E} \equiv \varvec{v}\cdot \frac{\partial \mathrm {L}}{\partial \varvec{v}}-\mathrm{L}\nonumber \\&\quad =\frac{\varvec{v}^{2}}{2}\!\!-\!\frac{m}{r}\!-\!\frac{3}{4}\Big (\!\epsilon \!-\!\alpha \!-\!\frac{\mu }{2}\!\Big )\varvec{v}^{4}\! +\!\Big (\!\epsilon \!-\!\alpha \!+\!\frac{\mu }{2}\!\Big )\!\frac{m}{r}\varvec{v}^{2}\!\!+\!\Big (\!\sigma \!-\!\epsilon \!-\!\frac{\mu }{2}\!\Big )\!\frac{m^2}{r^2} \!+\!\alpha \frac{m(\varvec{v}\!\cdot \!\varvec{x})^2}{r^3},\nonumber \\ \end{aligned}$$

(4)

$$\begin{aligned}&\mathcal {J} \equiv \Big |\varvec{x}\times \frac{\partial \mathrm {L}}{\partial \varvec{v}}\Big |=|\varvec{x}\!\times \!\varvec{v}|\Big [1\!-\!\Big (\epsilon \!-\!\alpha \!-\!\frac{\mu }{2}\Big )\varvec{v}^{2} \!+\!(2\epsilon \!-\!2\alpha \!+\!\mu )\frac{m}{r}\Big ]. \end{aligned}$$

(5)

Since the force has a spherical symmetry, without loss of generality, we take the plane in which the test particle moves as the equatorial plane, and express the particle’s trajectory as

$$\begin{aligned} \varvec{x} = r(\cos \phi \,\varvec{e}_{x}+\sin \phi \,\varvec{e}_{y})~, \end{aligned}$$

(6)

where $\phi$ is the azimuthal angle. $\varvec{e}_{x}$ and $\varvec{e}_{y}$ are the unit vectors of the x-axis and y-axis.

3 Quasi-Keplerian motion under the generally parameterized post-Newtonian force

In order to deliver the formulations more clearly, we will first give the analytical solution directly, and then present the detailed derivations.

3.1 Results

The first formulation for the quasi-Keplerian motion can be expressed as

$$\begin{aligned} \varvec{x}= & {} r(\cos \phi \,\varvec{e}_{x}+\sin \phi \,\varvec{e}_{y})~, \end{aligned}$$

(7)

$$\begin{aligned} \varvec{v}= & {} \frac{2\pi a_r e_r\sin u}{\mathrm{T}_u(1\!-\!e_t\cos u)}( \cos \phi \,\varvec{e}_{x}\!+\sin \phi \,\varvec{e}_{y})\nonumber \\&- \frac{ a_r\varPhi (1\!-\!e_r^2)^{\frac{1}{2}} }{\mathrm{T}_u(1\!-\!e_t\cos u)}\Big (1\!+\!N \frac{\cos u\!-\!e_r}{1\!-\!e_r \cos u}\Big )( \sin \phi \,\varvec{e}_{x}\! -\cos \phi \,\varvec{e}_{y})~, \end{aligned}$$

(8)

$$\begin{aligned} r= & {} a_{r}(1-e_{r} \cos u)~, \end{aligned}$$

(9)

$$\begin{aligned}&\phi \Big (\frac{2\pi }{\varPhi }\Big )=f+ N \sin f~, \end{aligned}$$

(10)

$$\begin{aligned} f= & {} 2 \arctan \Big (\sqrt{\frac{1+e_{r}}{1-e_{r}}}\tan \frac{u}{2}\Big )~, \end{aligned}$$

(11)

$$\begin{aligned}&t\Big (\frac{2\pi }{\mathrm{T}_u}\Big ) = u-e_t \sin {u}~, \end{aligned}$$

(12)

and the second formulation can be expressed as

$$\begin{aligned}&\varvec{x} = r(\cos \phi \,\varvec{e}_{x}+\sin \phi \,\varvec{e}_{y})~, \end{aligned}$$

(13)

$$\begin{aligned}&\varvec{v} = \frac{2\pi a_r e_r\sin u}{\mathrm{T}_u(1\!-\!e_t\cos u)}( \cos \phi \,\varvec{e}_{x}\!+\sin \phi \,\varvec{e}_{y})\nonumber \\&\qquad - \frac{ a_r\varPhi (1-e_{\phi }^2)^{\frac{1}{2}} }{\mathrm{T}_u(1\!-\!e_t\cos u)}\frac{1\!-\!e_r \cos u}{1\!-\!e_{\phi } \cos u}( \sin \phi \,\varvec{e}_{x}\! -\cos \phi \,\varvec{e}_{y})~, \end{aligned}$$

(14)

$$\begin{aligned}&r=a_{r}(1-e_{r} \cos u)~, \end{aligned}$$

(15)

$$\begin{aligned}&\phi \Big (\frac{2\pi }{\varPhi }\Big )= \upsilon ~, \end{aligned}$$

(16)

$$\begin{aligned}&\upsilon =2 \arctan \Big (\sqrt{\frac{1+e_{\phi }}{1-e_{\phi }}}\tan \frac{u}{2}\Big )~, \end{aligned}$$

(17)

$$\begin{aligned}&t\Big (\frac{2\pi }{\mathrm{T}_u}\Big ) = u-e_t \sin {u}~, \end{aligned}$$

(18)

where

$$\begin{aligned}&a_{r}=\frac{m}{-2\mathcal {E}}\Big [1\!+\!\Big (\epsilon \!-\!\alpha \!+\!\frac{3}{2}\mu \Big )\mathcal {E}\Big ]~,\end{aligned}$$

(19)

$$\begin{aligned}&e_r^2=1\!+\!\frac{2\mathcal {E}\mathcal {J}^2}{m^2}\!+\mathcal {E}\Big [4(\sigma \!-\!2\epsilon \!+\!\alpha \!-\!2\mu )\!-\!(2\epsilon \!-\!2\alpha \!+\!7\mu ) \frac{\mathcal {E}\mathcal {J}^2}{m^2}\Big ]~,\end{aligned}$$

(20)

$$\begin{aligned}&e_t=e_r\Big [1\!+\!2(\alpha \!+\!2\mu )\mathcal {E}\Big ]~,\end{aligned}$$

(21)

$$\begin{aligned}&e_{\phi } = e_r \Big (1\!-2\alpha \,\mathcal {E}\Big )~,\end{aligned}$$

(22)

$$\begin{aligned}&\varPhi =2\pi \Big [1\!+\!(2\epsilon \!+\!2\mu \!-\!\sigma \!)\frac{m^2}{\mathcal {J}^2}\Big ]~,\end{aligned}$$

(23)

$$\begin{aligned}&N= \alpha \frac{m^2}{\mathcal {J}^2}\Big (1\!+\!\frac{2\mathcal {E}\mathcal {J}^2}{m^2}\Big )^{\!\frac{1}{2}}~,\end{aligned}$$

(24)

$$\begin{aligned}&\mathrm{T}_u=\frac{2\pi m}{(-2\mathcal {E})^{\frac{3}{2}}}\Big [1\!-\!\Big (\frac{1}{2}\epsilon \!+\!\frac{3}{2}\alpha \!+\!\frac{7}{4}\mu \Big )\mathcal {E}\Big ]. \end{aligned}$$

(25)

In the formulations, $a_{r}$, $e_{r}$, f and u and can be regarded as the semi-major axis, the eccentricity, the true anomaly and the eccentric anomaly of the quasi-Keplerian orbit in the post-Newtonian approximation, respectively. $\upsilon$ is another definition of the true anomaly [11]. $\mathrm{T}_u$ denotes the orbital period.

It is worth emphasizing that these two formulations of the quasi-Keplerian solution are equivalent in the 1PN approximation.

3.2 Derivations

We follow the same procedure given by Soffel et al. [11] to derive the analytical solution for the post-Newtonian motion.

The expressions for the orbital energy and angular momentum in Eqs. (4)–(5) can be written as:

$$\begin{aligned} \mathcal {E}= & {} \frac{1}{2}(\dot{r}^2\!+\!r^2\dot{\phi }^2)\!-\!\frac{m}{r}\!-\!\Big (\frac{3}{4}\epsilon \!-\!\frac{3}{4}\alpha \!-\!\frac{3}{8}\mu \Big )(\dot{r}^2\!+\!r^2\dot{\phi }^2)^2\nonumber \\&+\,\frac{m}{2r} \Big [(2\epsilon \!+\!\mu )\dot{r}^2\!+\!(2\epsilon \!-\!2\alpha \!+\!\mu )r^2\dot{\phi }^2\!+\!(2\sigma \!-\!2\epsilon \!-\!\mu )\frac{m}{r}\Big ], \end{aligned}$$

(26)

$$\begin{aligned}&\mathcal {J}=r^2\dot{\phi } \Big [1\!-\!\Big (\epsilon \!-\!\alpha \! -\!\frac{\mu }{2}\Big )(\dot{r}^2\!+\!r^2\dot{\phi }^2)\!+\!(2\epsilon \!-\!2\alpha \!+\!\mu )\frac{m}{r}\Big ], \end{aligned}$$

(27)

where the dot denotes the derivative with respect to the time. These formulas lead to the first-order equations of motion

$$\begin{aligned} r^2\dot{\phi }=\mathcal {J}\Big [1\!+\!(2\epsilon \!-\!2\alpha \!-\!\mu )\mathcal {E}\!-\!2\mu \frac{m}{r}\Big ]~, \end{aligned}$$

(28)

and

$$\begin{aligned} \dot{r}^2=A+\frac{B}{r}+\frac{C}{r^2}+\frac{D}{r^3}~, \end{aligned}$$

(29)

with

$$\begin{aligned}&A=2\mathcal {E}\Big [1\!+\!\Big (3\epsilon \!-\!3\alpha \!-\!\frac{3}{2}\mu \Big )\mathcal {E}\Big ]~,\\&B=2m\Big [1\!+\!2(2\epsilon \!-\!3\alpha \!-\!2\mu )\mathcal {E}\Big ]~,\\&C=-\mathcal {J}^2\Big [1\!+\!2(2\epsilon \!-\!2\alpha \!-\!\mu )\mathcal {E}\!+\!2(\sigma \!-\!2\epsilon \!+\!3\alpha \!+\!2\mu )\frac{m^2}{\mathcal {J}^2}\Big ]~,\\&D=2(\alpha \!+\!2\mu )m \mathcal {J}^2. \end{aligned}$$

Making use of the relation

$$\begin{aligned} \dot{r}^2 \equiv \Big [\frac{d(1/r)}{d\phi }\Big ]^2(r^4\dot{\phi }^2)~, \end{aligned}$$

(30)

and plugging Eqs. (28)–(29) into (30), we can write the radial equation in the form

$$\begin{aligned} \Big [\frac{d(1/r)}{d\phi }\Big ]^2=A'+\frac{B'}{r} +\frac{C'}{r^2}+\frac{D'}{r^3}~, \end{aligned}$$

(31)

with

$$\begin{aligned}&A'=\frac{2\mathcal {E}}{\mathcal {J}^2}\Big [1\!-\!\Big (\epsilon \!-\!\alpha \!-\!\frac{\mu }{2}\Big )\mathcal {E}\Big ]~,\\&B'=\frac{2m}{\mathcal {J}^2}\Big [1\!-\!2(\alpha \!-\!\mu )\mathcal {E}\Big ]~,\\&C'=-1\!-\!2(\sigma \!-\!2\epsilon \!+\!3\alpha \!-\!2\mu )\frac{m^2}{\mathcal {J}^2}~,\\&D'=2\alpha \,m. \end{aligned}$$

Since the right hand side of Eq. (31) is a third-order polynomial in $r^{-1}$, we can further re-write it as

$$\begin{aligned} \Big [\frac{d(1/r)}{d\phi }\Big ]^2=\Big [\frac{1}{r}\!-\!\frac{1}{a_{r} (1+e_{r})}\Big ]\Big [\frac{1}{a_{r}(1-e_{r})}\!-\!\frac{1}{r}\Big ] \Big (C_{1}+\frac{C_{2}}{r}\Big ). \end{aligned}$$

(32)

Comparing the coefficients between Eq. (31) and Eq. (32), we have

$$\begin{aligned} a_{r}= & {} \frac{m}{-2\mathcal {E}}\Big [1\!+\!\Big (\epsilon \!-\!\alpha \!+\!\frac{3}{2}\mu \Big )\mathcal {E}\Big ]~, \end{aligned}$$

(33)

$$\begin{aligned} e_r^2= & {} 1\!+\!\frac{2\mathcal {E}\mathcal {J}^2}{m^2}\!+\mathcal {E}\Big [4(\sigma \!-\!2\epsilon \!+\!\alpha \!-\!2\mu )\!-\!(2\epsilon \!-\!2\alpha \!+\!7\mu ) \frac{\mathcal {E}\mathcal {J}^2}{m^2}\Big ]~, \end{aligned}$$

(34)

$$\begin{aligned} C_{1}= & {} 1\!+\!2(\sigma \!-\!2\epsilon \!+\!\alpha \!-\!2\mu )\frac{m^2}{\mathcal {J}^2}~, \end{aligned}$$

(35)

$$\begin{aligned} C_{2}= & {} -2\alpha m. \end{aligned}$$

(36)

It can be seen from Eq. (32) that $r_{\pm }=a_{r}(1\pm e_{r})$ represent the maximal and minimal values for r. Hence, $a_{r}$ and $e_{r}$ can be regarded as the semi-major axis and the eccentricity of the quasi-Keplerian orbit.

The solution of Eq. (32) can be written as:

$$\begin{aligned} r=\frac{a_{r}(1-e_{r}^2)}{1+e_{r}\cos {f}}~, \end{aligned}$$

(37)

with f being the true anomaly for the quasi-Keplerian orbit and obeying

$$\begin{aligned} \Big (\frac{df}{d\phi }\Big )^2=C_{1}+\frac{C_{2}}{r}. \end{aligned}$$

(38)

Substituting Eqs. (35)–(37) into Eq. (38), we have

$$\begin{aligned} \frac{df}{d\phi }=\Big [1\!+\!(\sigma \!-\!2\epsilon \!-\!2\mu ) \frac{m^2}{\mathcal {J}^2}\Big ]\Big (1\!-\! \alpha \frac{m^2}{\mathcal {J}^2}e_{r} \cos f\Big )~, \end{aligned}$$

(39)

and then integrate this equation, we obtain

$$\begin{aligned} \phi \Big (\frac{2\pi }{\varPhi }\Big )=f+\alpha \frac{m^2}{\mathcal {J}^2}e_{r} \sin f~, \end{aligned}$$

(40)

with

$$\begin{aligned} \varPhi =2\pi \Big [1\!-\!(\sigma \!-\!2\epsilon \!-\!2\mu )\frac{m^2}{\mathcal {J}^2}\Big ]. \end{aligned}$$

(41)

Finally, we derive the time dependence of the quasi-Keplerian motion. Combining Eqs. (28) and (39), we have

$$\begin{aligned} r^2\dot{f}=\mathcal {J}\Big [1\!+\!(2\epsilon \!-\!2\alpha \!-\!\mu ) \mathcal {E}\!-\!2\mu \frac{m}{r}\!+\!(\sigma \!-\!2\epsilon \!-\!2\mu ) \frac{m^2}{\mathcal {J}^2}-\alpha \frac{m^2}{\mathcal {J}^2}e_{r} \sin f \Big ]. \end{aligned}$$

(42)

Introducing the post-Newtonian eccentric anomaly u by the relations

$$\begin{aligned} \sin f\!=\!\frac{(1\!-\!e_{r}^{2})^{\frac{1}{2}}\!\sin u}{1\!-\!e_{r}\!\cos u};\,\,\cos f\!=\!\frac{\cos u\!-\!e_{r}}{1\!-\!e_{r}\cos u};\,\, f\!=\!2 \arctan \Big (\!\sqrt{\frac{1\!+\!e_{r}}{1\!-\!e_{r}}}\tan \frac{u}{2}\!\Big ), \end{aligned}$$

(43)

we have

$$\begin{aligned} \frac{df}{dt}=\frac{(1-e_{r}^2)^{1/2}}{1-e_{r}\cos u}\frac{du}{dt}~, \end{aligned}$$

(44)

and we can formulate the orbit given in Eq. (37) in terms of u as

$$\begin{aligned} r=a_{r}(1-e_{r} \cos u). \end{aligned}$$

(45)

Integrating Eq. (42) and making use of Eqs. (43)–(45), we can achieve the quasi-Keplerian equation

$$\begin{aligned} t\Big (\frac{2\pi }{\mathrm{T}_u}\Big ) = u-e_t \sin {u}~, \end{aligned}$$

(46)

with $\mathrm{T}_{\!u}$ being the period for the eccentric anomaly u of the quasi-Keplerian motion

$$\begin{aligned} \mathrm{T}_u=\frac{2\pi m}{(-2\mathcal {E})^{\frac{3}{2}}}\Big [1\!-\!\Big (\frac{1}{2} \epsilon \!+\!\frac{3}{2}\alpha \!+\!\frac{7}{4}\mu \Big )\mathcal {E}\Big ]~, \end{aligned}$$

(47)

and $e_t$ being the time eccentricity

$$\begin{aligned} e_t=e_r\Big [1\!+\!2(\alpha \!+\!2\mu )\mathcal {E}\Big ]. \end{aligned}$$

(48)

In the literatures, one usually uses the “true anomaly” $\upsilon$ to replace the true anomaly f in the formula of the quasi-Keplerian equation, requiring that the $\sin \upsilon$ contribution in $\phi (\frac{2\pi }{\varPhi })$ vanish at each PN order [12,13,14]. Following the same method given in Ref [14], we set

$$\begin{aligned} \upsilon =2 \arctan \Big (\sqrt{\frac{1+e_{\phi }}{1-e_{\phi }}}\tan \frac{u}{2}\Big )~, \end{aligned}$$

(49)

with

$$\begin{aligned} e_\phi =e_r(1+c_1)~, \end{aligned}$$

(50)

being different from the radial eccentricity $e_r$ by the 1PN correction $c_1$. Notice that here we only need consider the 1PN case.

Eliminating u in Eq. (43) with the help of Eq. (49) and inserting the result into Eq. (40), we have [14]

$$\begin{aligned} f=\upsilon +c_1\frac{e_r}{e_r^2-1}\sin \upsilon . \end{aligned}$$

(51)

Requiring the $\sin \upsilon$ term to vanish in $\phi (\frac{2\pi }{\varPhi })$ yields

$$\begin{aligned} c_1=-2\alpha \mathcal {E}~, \end{aligned}$$

i.e.,

$$\begin{aligned} e_{\phi } = e_r \Big (1\!-2\alpha \mathcal {E}\Big ). \end{aligned}$$

(52)

Substituting Eq. (51) into Eq. (40), we can obtain

$$\begin{aligned} \phi \Big (\frac{2\pi }{\varPhi }\Big ) = \upsilon . \end{aligned}$$

(53)

To the 1PN accuracy, the time dependance of the quasi-Keplerian motion, depicted by Eqs. (46)–(48), does not need change when the “true anomaly” $\upsilon$ is used in the formulation.

The derivations for the velocity $\varvec{v}$ of the post-Keplerian motion will be given in the next section.

4 Some applications

Here we discuss some potential applications of the achieved solutions.

The orbital period $\mathrm{T}_u$ and perihelion precession $\varDelta \phi$ of the celestial bodies are two important quantities in the astronomical observations. The perihelion precession can be obtained from Eq. (2324), which reads

$$\begin{aligned} \varDelta \phi \equiv \varPhi -2\pi =2\pi (2\epsilon +2\mu -\sigma )\frac{m^2}{\mathcal {J}^2}. \end{aligned}$$

(54)

It can be seen that it is independent on the parameter $\alpha$. The orbital period is given in Eq. (25), from which we can see that it is independent on the parameter $\sigma$. The corrections to the Keplerian period $\mathrm{T}_{\text {K}} \!\equiv \! 2\pi m/(-2\mathcal {E})^{\frac{3}{2}}$ can be written as

$$\begin{aligned} \frac{\varDelta \mathrm{T}}{\mathrm{T}_{\text {K}}} \equiv \frac{\mathrm{T}_u-\mathrm{T}_{\text {K}}}{\mathrm{T}_{K}} = -\Big (\frac{1}{2}\epsilon \!+\!\frac{3}{2}\alpha \!+\!\frac{7}{4}\mu \Big )\mathcal {E}. \end{aligned}$$

(55)

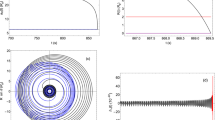
Figures 1 and 2 present the perihelion precession and the corrections to the orbital period predicted by the B–D theory with different constant $\omega$. Notice that the B–D theory reduces to GR in the limit of $\omega \!\rightarrow \! \infty$, and the relations between the parameters in the general force and $\omega$ are given in Table 1.

Fig. 1

The perihelion precession varies with $\omega$ in the B–D theory

Fig. 2

The corrections to the orbital period varies with $\omega$ in the B–D theory

Next, we consider the effects of the dimensionless reduced mass $\nu$ of the binary systems on the perihelion precession and the orbital period. The relations between the parameters in the general force and $\nu$ are given in Table 1. Figure 3 and 4 show the dependence of the perihelion precession and the corrections to the orbital period on the dimensionless reduced mass in the GR frame.

Fig. 3

The perihelion precession predicted by GR varies with the dimensionless reduced mass of the binary systems

Fig. 4

The GR corrections to the orbital period varies with the dimensionless reduced mass of the binary systems

Finally, with the orbital solutions, we can further derive the celestial body’s velocity $\varvec{v}$, which is needed in calculating the waveform of gravitational-wave radiation.

For the first formulation, from Eqs. (9), (10) and (12), we have

$$\begin{aligned} \frac{dr}{dt}= & {} a_re_r \sin u \frac{du}{dt}~, \end{aligned}$$

(56)

$$\begin{aligned} \frac{d\phi }{df}= & {} \frac{\varPhi }{2\pi }(1+N \cos f)~, \end{aligned}$$

(57)

$$\begin{aligned} \frac{du}{dt}= & {} \frac{2\pi }{\mathrm{T}_u(1-e_t\cos u)}. \end{aligned}$$

(58)

Taking the time derivation of Eq. (7), and making use of Eqs. (9), (43), (44), (56), (57) and (58), we can obtain the velocity for the quasi-Keplerian motion under the first formulation as follow

$$\begin{aligned} \varvec{v}= & {} \frac{2\pi a_r e_r\sin u}{\mathrm{T}_u(1\!-\!e_t\cos u)}( \cos \phi \,\varvec{e}_{x}\!+\sin \phi \,\varvec{e}_{y})\nonumber \\&- \frac{ a_r\varPhi (1\!-\!e_r^2)^{\frac{1}{2}} }{\mathrm{T}_u(1\!-\!e_t\cos u)}\Big (1\!+\!N \frac{\cos u\!-\!e_r}{1\!-\!e_r \cos u}\Big )( \sin \phi \,\varvec{e}_{x}\! -\cos \phi \,\varvec{e}_{y})~, \end{aligned}$$

(59)

For the second formulation, from Eq. (16), we have

$$\begin{aligned} \frac{d\phi }{d\upsilon } = \frac{\varPhi }{2\pi }. \end{aligned}$$

(60)

In addition, following Eq. (17), we can obtain

$$\begin{aligned} \sin \upsilon \!=\!\frac{(1\!-\!e_{\phi }^2)^{\frac{1}{2}}\!\sin u}{1\!-\!e_{\phi }\cos u};\,\,\,\cos \upsilon \!=\!\frac{\cos u\!-\!e_{\phi }}{1\!-\!e_{\phi }\cos u};\,\,\,\frac{d\upsilon }{dt}=\frac{(1-e_{\phi }^2)^{\frac{1}{2}}}{1-e_{\phi }\cos u}\frac{du}{dt}. \end{aligned}$$

(61)

Taking the time derivation of Eq. (13), and making use of Eqs. (15), (56), (58) and (61), we can obtain the velocity for the quasi-Keplerian motion under the second formulation as follow

$$\begin{aligned} \varvec{v}= & {} \frac{2\pi a_r e_r\sin u}{\mathrm{T}_u(1\!-\!e_t\cos u)}( \cos \phi \,\varvec{e}_{x}\!+\sin \phi \,\varvec{e}_{y})\nonumber \\&- \frac{ a_r\varPhi (1-e_{\phi }^2)^{\frac{1}{2}} }{\mathrm{T}_u(1\!-\!e_t\cos u)}\frac{1\!-\!e_r \cos u}{1\!-\!e_{\phi } \cos u}( \sin \phi \,\varvec{e}_{x}\! -\cos \phi \,\varvec{e}_{y}). \end{aligned}$$

(62)

5 Summary

We derive two slightly different but equivalent 1PN formulations of the solution for the particle’s motion under the generally parameterized force, through an iterative method and a function-fitting method. The formulas are expressed in terms of the orbital energy and angular momentum, which have direct physical meaning. The achieved solutions can be used in fitting the motion of the test particle as well as the relative motion of the binary systems under various gravitation theories. Moreover, since the generally parameterized force can characterize the dynamic equations for these kinds of systems under various gravitation theories in the harmonic coordinates, the analytical orbit and velocity can also be directly used to calculate the waveform of gravitational wave, and thus are useful in building the theoretical templates of the gravitational-wave radiation for the binary systems including the extreme-mass-ratio inspirals.